От характеристических значений системы
зависит ее динамические свойства.
у = Ах, гдеу
их–
векторы столбцы, а А – квадратная матрица
(n×n).
у = Ах= λх, гдеλ– скалярный коэффициент пропорциональности.
Значение λ(λi),
для которого уравнение у = Ахимеет
решениеxi≠ 0 называетсяхарактеристическим
числом А.Соответственный вектор
решения xi≠ 0 называетсяхарактеристическим
вектором А.
4.1. Характеристическое уравнение.
Многочлен n-й
степени относительно А, определенный
уравнением,
называетсяхарактеристическим
уравнением А.
Р(λ) = λn
+ a1
λn-1
+ a2
λn-2
+…+ an-1
λ + an
= 0. Корни характеристического
уравнения равны характеристическим
значениям А.
4.2. Модальная матрица.
Для каждого из (n)
характеристических чисел
λi(i= 1, 2,…,n)
матрицы А можно получить решением
уравненияотносительно
х. Векторыхi,
представленные решением системы(i= 1, 2,…,n),
является характеристический вектор А.ki– произвольная скалярная величина –
решение (уравнение однородное). Матрица,
образованная векторами-столбцами
kiхiназываетсямодальной матрицей.
Симметрические матрицы. Свойство
заключается в том, что характеристические
числа симметрической матрицы должны
быть действительными.
4.3. Диагонализация квадратной матрицы.
Рассмотрим несобственную модальную
матрицу М (М-1).
Решение уравненияв виде
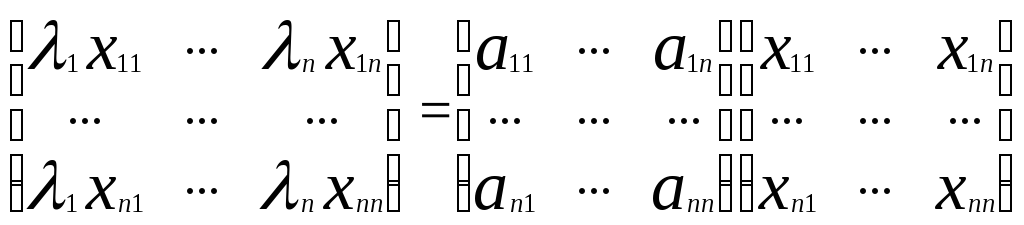

характеристических чиселλ1,λ2,…,λn.
Умножим обе части уравнения на М-1:
Λ = М-1АМ. Более высокие степени
матрицы А приводится к диагональному
ряду так же. Преобразование вида В =Q-1AQ,
где А и В – квадратные матрицы,q– неособенная квадратная матрица,
называетсяколлинеарным преобразованием
илипреобразованием подобия.
5. Матричные преобразования.
Эквивалентные матрицы А и В считаются,
если одна из матриц получается посредством
выполнения ряда элементарных операций
над другой. Матрица В эквивалентна
матрице А, когда существуют такие две
неособенные матрицы Р и Q,
что В =PAQ.
Нормальная форма. Матрицу А ранга
> 0 можно привести к эквивалентной
матрице вида:Ir,

или
,
гдеIr– единичная матрица (r×r).
Данный вид называется нормальнойиликанонической формой матриц.
Если А приводится к единичной матрице
посредством ряда элементарных операций,
то
А = Р-1РАQQ-1=
Р-1IQ-1=P-1Q-1
Преобразование В = РАQ–
общий вид матричного преобразования.
Отдельные преобразования определяются
из взаимосвязиPиQ.
В частности преобразование подобия: В
=Q-1АQили Р =Q-1.
Ортогональное преобразование.
В = QтАQ=Q-1АQили Р =Qт=Q-1преобразование: В =QтАQили Р =Qт.
Для эрнитовой матрицы А определяются:
а) коньютивное: В =Q*ТАQили Р =Q*Т.
б) унитарное: В =Q*ТАQ=Q-1АQили Р =Q*Т=Q-1.
6. Билинейная и квадратичная формы.
Билинейной формойотносительно
переломныххi,уi,
называется выражение вида:
В = a11x1y1+a12x1y2+…+a1nx1yn+a21x2y1+a22x2y2+…+a2nx2yn+…+an1xny1+…+annxnyn,
где все составляющие – действительные
величины.
Комплексная форма:
,
или в матричной форме:
Матрица А – матрица коэффициентов
формы, ранг А – ранг формы. Если х
=у, то
предыдущее уравнение превратится в:Q=xTAx= <x,Ax>.
Qназываетсяквадратичной
формойx1,x2,…,xn.
Или:.
Преобразование переменных.
Линейное преобразование х = Ву, где В –
произвольная неособенная матрица (n×n),
преобразуетQв квадратичную
форму относительноу1,у2,…,уn:Q=yTBTAByилиQ= утСу, где С =
ВтАВ.
Соседние файлы в папке лекции МОТС
- #
- #
- #
- #
- #
- #
- #
Содержание
Характеристический полином, собственные числа, собственные векторы матрицы
§
В настоящем разделе $ n_{} $ означает порядок квадратной матрицы $ A_{} $.
Характеристический полином
определяется для произвольной квадратной матрицы $ A_{} $ как1)
$ det (A_{}-lambda E) $, где $ E_{} $ – единичная матрица одинакового с $ A_{} $ порядка.
П
Пример. Для $ n=2_{} $:
$$ det (A-lambda E)=
begin{vmatrix}
a_{11}-lambda & a_{12}\
a_{21}& a_{22}-lambda
end{vmatrix}=
$$
$$
=lambda^2-(a_{11}+a_{22})lambda + (a_{11}a_{22}-a_{12}a_{21}) ;
$$
для $ n=3_{} $:
$$
det (A-lambda E)=
begin{vmatrix}
a_{11}-lambda & a_{12} & a_{13}\
a_{21}& a_{22}-lambda & a_{23} \
a_{31}& a_{32} & a_{33}-lambda
end{vmatrix}=
$$
$$
=-lambda^3+(a_{11}+a_{22}+a_{33})lambda^2 —
$$
$$
-left {
begin{vmatrix}
a_{11}& a_{12}\
a_{21}& a_{22}
end{vmatrix}
+begin{vmatrix}
a_{22}& a_{23}\
a_{32}& a_{33}
end{vmatrix}+
begin{vmatrix}
a_{11}& a_{13}\
a_{31}& a_{33}
end{vmatrix}
right }lambda+
det A .
$$
Т
Теорема 1.
$$ det (A-lambda E)=
(-1)^nBigg(
lambda^n — lambda^{n-1}sum_{1le jle n} a_{jj}
+ lambda^{n-2}sum_{1le j_1< j_2 le n} left|begin{array}{ll}
a_{j_1j_1}& a_{j_1j_2}\
a_{j_2j_1}& a_{j_2j_2}
end{array}right| — dots +
$$
$$
+(-1)^k lambda^{n-k}
sum_{1le j_1< j_2 < dots < j_kle n} left|begin{array}{llll}
a_{j_1j_1}& a_{j_1j_2} & dots & a_{j_1j_k}\
a_{j_2j_1}& a_{j_2j_2} & dots & a_{j_2j_k}\
vdots & & & vdots \
a_{j_kj_1}& a_{j_kj_2} & dots & a_{j_kj_k}
end{array}right|+ dots + (-1)^n det A
Bigg) .
$$
Образно говоря, коэффициент при $ (-1)^{k}lambda^{n-k} $ получается
суммированием всех миноров $ k_{} $-го порядка матрицы $ A_{} $, построенных на
элементах, стоящих в строках и столбцах с одинаковыми номерами..
Такой минор матрицы
$$
left|begin{array}{cccc}
a_{j_1j_1} & a_{j_1j_2} & dots & a_{j_1j_k} \
a_{j_2j_1} & a_{j_2j_2} & dots & a_{j_2j_k} \
vdots & & ddots & vdots \
a_{j_kj_1} & a_{j_kj_2} & dots & a_{j_kj_k}
end{array}
right|
, quad 1le j_1<j_2< dots < j_k le n
$$
в настоящем ресурсе называется ведущим минором ($k$-го порядка). См. замечание о терминологии
☞
ЗДЕСЬ.
Результат теоремы имеет исключительно теоретическое значение: практическое вычисление характеристического полинома матрицы большого порядка по этой теореме обычно крайне неэффективно. Методы практического вычисления характеристического полинома разбираются
☟
НИЖЕ.
П
Пример. Характеристический полином матрицы Фробениуса
$$
mathfrak F=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n}
$$
равен $ (-1)^n(lambda^n-a_1lambda^{n-1}-dots-a_{n}) $.
Характеристический полином линейного оператора
определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее
☞
ЗДЕСЬ.
Характеристический полином линейного однородного разностного уравнения
$ n_{} $-го порядка
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K, quad a_n ne 0,
$$
определяется как
$$ lambda^n — a_1 lambda^{n-1} — dots — a_n . $$
Подробнее
☞
ЗДЕСЬ.
Свойства
Т
Теорема 2. Характеристический полином матрицы не меняется
1.
при ее транспонировании:
$$ det (A-lambda E) = det (A^{top}-lambda E_{}) , ;$$
2.
при переходе к подобной матрице: если $ B=C^{-1}AC^{} $ при произвольной неособенной матрице $ C_{} $, то
$$ det (A-lambda E) equiv det (B-lambda E_{}) , . $$
Т
Теорема 3. Пусть матрица $ A_{} $ имеет порядок $ mtimes n_{} $, а $ B_{} $ — порядок $ ntimes m_{} $. Тогда эти матрицы допускают умножение в любом порядке, т.е. определены $ AB_{} $ и $ BA_{} $ и оба произведения будут квадратными матрицами — порядков $ m_{} $ и $ n_{} $ соответственно. Тогда характеристические полиномы этих произведений различаются лишь на степень $ lambda_{} $:
$$
lambda^n det (AB — lambda E_{m times m})equiv lambda^m det (BA — lambda E_{n times n}) .
$$
=>
Если матрицы $ A_{} $ и $ B_{} $ — квадратные одинакового порядка, то характеристические полиномы матриц $ AB_{} $ и $ BA_{} $ тождественны.
Т
Теорема 4. Если характеристический полином матрицы $ A_{} $ равен
$$ f(lambda)=(-1)^n lambda^n+a_1lambda^{n-1}+dots+a_{n-1}lambda+a_n $$
и $ a_{n} ne 0 $, то характеристический полином матрицы $ A^{-1}_{} $ равен
$$ f^{ast}(lambda)=frac{(-lambda)^n}{a_n} f(1/lambda) = frac{(-1)^n}{a_n} left[ (-1)^n+a_1 lambda + dots+
a_{n-1}lambda^{n-1}+a_nlambda^{n} right] . $$
Теорема Гамильтона-Кэли
Т
Теорема 5. Результатом подстановки в характеристический полином $ det (A_{}-lambda E) $ самой матрицы $ A_{} $ будет нулевая матрица:
$$
det (A-lambda E)= (-1)^n lambda^n +a_1 lambda^{n-1}+dots+a_{n-1}lambda+ a_n Rightarrow
$$
$$
Rightarrow
(-1)^n A^n +a_1 A^{n-1}+dots+a_{n-1}A+ a_n E = {mathbb O}_{ntimes n} .
$$
В литературе эта теорема обычно приводится в иной формулировке:
матрица является корнем своего характеристического полинома.
Доказательство
☞
ЗДЕСЬ.
П
Пример. Для $ n_{}=2 $:
$$
left(begin{array}{ll} a_{11} & a_{12} \ a_{21} & a_{22}
end{array} right)^2 — (a_{11}+a_{22})left(begin{array}{ll} a_{11} & a_{12} \ a_{21} & a_{22}
end{array} right) +
(a_{11}a_{22}-a_{12}a_{21})
left(begin{array}{ll} 1 & 0 \ 0 & 1
end{array} right) = left(begin{array}{ll} 0 & 0 \ 0 & 0
end{array} right) .
$$
Собственное число
Собственное (или характеристическое) число2) определяется для квадратной матрицы $ A_{} $ как произвольный корень ее характеристического полинома $ det (A_{}-lambda E) $. Уравнение
$$
det(A-lambda E)=0
$$
называется характеристическим уравнением матрицы $ A $.
И
Понятие характеристического уравнения было введено Коши в 1840 г. В литературе XIX века известно также как вековое уравнение.
Набор всех собственных чисел матрицы $ A_{} $ (с учетом их кратностей) называется спектром матрицы3) (таким образом спектр матрицы $ A_{} $ порядка $ n_{} $ всегда состоит из $ n_{} $ чисел, часть из которых могут быть одинаковыми). Максимальный из модулей собственных чисел матрицы $ A_{} $ называется ее спектральным радиусом4), он иногда обозначается $ rho(A) $.
П
Пример. Найти спектр матрицы
$$
A=
left(begin{array}{rrrr}
0&1&2&3\
-1&0&4&7\
-2&-4&0&2\
-3&-7&-2&0
end{array}right).
$$
Решение. Характеристический полином
$$ det (A-lambda E)=left|begin{array}{rrrr}
-lambda&1&2&3\
-1&-lambda&4&7\
-2&-4&-lambda&2\
-3&-7&-2&-lambda
end{array}right|=lambda^4+
83lambda^2
$$
имеет корни $ lambda_1=0, lambda_2 = {mathbf i}sqrt{83}, lambda_3 = — {mathbf i} sqrt{83} $, причем $ lambda_{1} $ — второй кратности.
Ответ. Спектр матрицы $ A_{} $:
$ {0,0, {mathbf i} sqrt{83},- {mathbf i} sqrt {83} } $. Спектральный радиус матрицы $ A_{} $: $ rho(A)= sqrt {83} $.
Т
Теорема 6. Если $ {lambda_{1},lambda_{2},dots,lambda_{n} } $ — спектр матрицы $ A_{} $, то
$$ lambda_1+lambda_{2}+dots+lambda_n = operatorname{Sp}(A)=a_{11}+a_{22}+dots+a_{nn}, $$
$$ lambda_1cdotlambda_{2}times dots times lambda_n = (-1)^ndet (A) . $$
Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета.
♦
Можно, разумеется, привести еще $ n-2 $ зависимостей между собственными числами матрицы и ее минорами, но они редко нужны — а вот равенства из теоремы полезно запомнить.
=>
Для того, чтобы матрица $ A_{} $ была неособенной необходимо и достаточно, чтобы среди ее собственных чисел не было нулевого.
Т
Теорема 7. Пусть $ g(x)=b_{0}x^m+dots+b_m in {mathbb C}[x] $ — произвольный полином. Вычислим полином от матрицы $ A_{} $:
$$ g(A)=b_{0}A^m+dots+b_m E , . $$
Тогда если $ {lambda_{1},dots,lambda_{n} } $ — спектр матрицы $ A_{} $, то $ {g(lambda_{1}),dots,g(lambda_n) } $ — спектр матрицы $ g(A_{}) $.
=>
Результат теоремы обобщается и на более широкий класс функций $ g_{}(x) $ — фактически на любую функцию, которая, вместе со своими производными, может быть определена на спектре матрицы $ A_{} $. В частности, если $ det A_{} ne 0 $, то спектр матрицы $ A^{-1}_{} $ совпадает с $ {1/lambda_j}_{j=1}^n $.
=>
Имеет место следующее равенство, связывающее степени матрицы $ A_{} $ с суммами Ньютона ее характеристического полинома:
$$ operatorname{Sp}(A^k)=lambda_1^k+dots+lambda_n^k . $$
Здесь $ operatorname{Sp}_{} $ обозначает след матрицы (т.е. сумму ее диагональных элементов). Утверждение остается справедливым и для отрицательных показателей $ k_{} $ при условии, что $ det A_{} ne 0 $.
=>
Имеет место следующее равенство:
$$ det g(A) = (-1)^{mn} {mathcal R}(f,g_{}) , $$
где $ {mathcal R}(f,g_{}) $ означает результант полиномов $ f(x) =det (A-x_{} E) $ и $ g_{}(x) $.
Т
Теорема 8. Собственные числа вещественной симметричной матрицы $ A_{} $ все вещественны.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 9. Собственные числа вещественной кососимметричной матрицы $ A_{} $ все мнимы, за исключением, возможно, $ lambda_{} = 0 $.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 10. Собственные числа вещественной ортогональной матрицы все равны $ 1_{} $ по абсолютной величине (модулю). Характеристический полином ортогональной матрицы является возвратным если $ +1 $ не является его корнем или является корнем четной кратности. Хотя бы одно собственное число ортогональной матрицы нечетного порядка равно $ +1 $ или $ (-1) $.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема 11. Спектр циклической матрицы
$$
left(begin{array}{lllll}
a_1 & a_2 & a_3 & dots & a_n \
a_n & a_1 & a_2 & dots & a_{n-1} \
a_{n-1} & a_n & a_1 & dots & a_{n-2} \
vdots & & & & vdots \
a_2 & a_3 & a_4 & dots & a_1
end{array}
right) .
$$
совпадает с набором чисел
$$ {f(1),f(varepsilon_1), dots, f(varepsilon_{n-1}) } ,$$
при
$$ f(x)=a_{1}+a_2x+a_3x^2+dots+a_nx^{n-1} $$
и
$$
varepsilon_k=cos frac{2,pi k}{n} + {mathbf i} sin frac{2,pi k}{n}
$$
— корне n-й степени из единицы.
Доказательство
☞
ЗДЕСЬ.
Локализация собственных чисел
Т
Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть
$$A=left[a_{jk} right]_{j,k=1}^n quad , quad B=left[b_{jk} right]_{j,k=1}^n
.
$$
Обозначим
$$M= max_{j,kin{1,dots,n}} left{|a_{jk} |, |b_{jk} | right} quad ,
quad delta = frac{1}{nM}sum_{j,k=1}^n |a_{jk} — b_{jk} | . $$
Тогда любому собственному числу $ lambda_{ast}^{} $ матрицы $ A_{} $ можно поставить
в соответствие такое собственное число $ mu_{ast}^{} $ матрицы $ B_{} $, что
$$ |lambda_{ast}-mu_{ast} | le (n+2) M sqrt[n]{delta} . $$
Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы
☞
ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы.
Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.
Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.
П
Пример [Уилкинсон] [2]. Найти собственные числа матрицы
$$
A=
left(
begin{array}{cccccc}
20 & 20 & & & & \
& 19 & 20 & & & \
& & 18 & 20 & & \
& & & ddots & ddots & \
& & & & 2 & 20 \
{color{Red} varepsilon } & & & & & 1 \
end{array}
right)_{20times 20}
$$
при $ {color{Red} varepsilon }=10^{-10} $
(все неуказанные элементы матрицы считаются равными нулю).
Решение. Характеристический полином
$$
det(A-lambda E) = prod_{j=1}^{20} (j-lambda) — 20^{19} {color{Red} varepsilon } =
$$
$$
=lambda^{20}-{scriptstyle 210},lambda^{19}+{scriptstyle 20615},lambda^{18}-{scriptstyle 1256850}, lambda^{17}
+{scriptstyle 53327946}, lambda^{16}-{scriptstyle 1672280820}, lambda^{15}+
{scriptstyle 40171771630}, lambda^{14}-{scriptstyle 756111184500}, lambda^{13}+
$$
$$
+{scriptstyle 11310276995381}, lambda^{12} —
{scriptstyle 135585182899530}, lambda^{11}
+{scriptstyle 1307535010540395}, lambda^{10}-{scriptstyle 10142299865511450}, lambda^9 +
$$
$$
+{scriptstyle 63030812099294896}, lambda^8 —
{scriptstyle 311333643161390640}, lambda^7+{scriptstyle 1206647803780373360}, lambda^6 -{scriptstyle 3599979517947607200}, lambda^5
+{scriptstyle 8037811822645051776}, lambda^4-
$$
$$
-{scriptstyle 12870931245150988800}, lambda^3
+{scriptstyle 13803759753640704000}, lambda^2
-{scriptstyle 8752948036761600000},lambda +{scriptstyle 2432377720176640000}
$$
очень похож на полином из другого
☞
ПРИМЕРА Уилкинсона. Он имеет корни
$$
lambda_1=0.995754, lambda_2=2.109241, lambda_3=2.574881,
$$
$$
lambda_{4,5}=3.965331pm 1.087735, mathbf i, lambda_{6,7}=5.893977pm 1.948530 , mathbf i,
$$
$$
lambda_{8,9}=8.118073 pm
2.529182 , mathbf i,
lambda_{10,11}=10.5pm 2.733397 , mathbf i,
$$
$$
lambda_{12,13}=12.881926pm 2.529182 , mathbf i, lambda_{14,15}=15.106022 pm 1.948530
, mathbf i, $$
$$
lambda_{16,17}=17.034669pm 1.087735 , mathbf i,
$$
$$
lambda_{18}=18.425118, lambda_{19}=18.890758, lambda_{20}=20.004245 .
$$
Итак, нановозмущение5) в одном-единственном элементе матрицы приводит к существенному изменению спектра: из $ 20 $ вещественных собственных чисел «остаются в живых» только $ 6_{} $; кроме того, у образовавшихся мнимых корней оказываются достаточно большими мнимые части. В данном примере допустимые возмущения для $ {color{Red} varepsilon } $, т.е. такие, при
которых сохранится
свойство вещественности всех корней характеристического полинома, находятся в пределах6)
$$ -8.636174times 10^{-14} < {color{Red} varepsilon } le frac{685872258640569}{8796093022208000000000000000} approx +7.797464 times 10^{-14} .$$
♦
Т
Теорема 13 [Гершгорин].7) Обозначим $ mathbb D_{j} $ круг на комплексной
плоскости $ mathbb C_{} $ с центром в точке $ a_{jj}^{} $ и радиуса
$$ r_j=sum_{ell=1 atop ellne j}^n left|a_{j ell}right| .$$
Тогда спектр матрицы $ A_{} $ лежит внутри объединения этих кругов:
$$ {lambda_1,dots, lambda_n } subset bigcup_{j=1}^n mathbb D_j . $$
Иными словами: любое собственное число матрицы должно удовлетворять хотя бы одному из
неравенств
$$ |z- a_{jj} | < r_j . $$
Доказательство
☞
ЗДЕСЬ
П
Пример. Построить круги Гершгорина для матрицы
$$ A=left(
begin{array}{crr}
-1+3,{mathbf i} & 2- {mathbf i} & 3+2, {mathbf i} \
-1+{mathbf i} & 4+ {mathbf i} & 3, {mathbf i} \
-1& 2-2,{mathbf i}& -2-3, {mathbf i}
end{array}
right) . $$
Решение.
$$|lambda + 1 — 3,{mathbf i} |le | 2-{mathbf i} |+| 3+2,{mathbf i} |=sqrt{5}+sqrt{13}, $$
$$|lambda — 4 — {mathbf i} |le 3+sqrt{2}, $$
$$ |lambda + 2+ 3, {mathbf i} |le 1 + 2sqrt{2} . $$

Проверка. Собственные числа матрицы $ A_{} $ (на рисунке обозначены красными крестиками):
$$ { -2.509081750-3.442241533,{mathbf i} , -1.041999986+2.655757676,{mathbf i} , 4.551081736+1.786483857, {mathbf i} } .$$
Локализация вещественных собственных чисел
Симметричная матрица
Т
Теорема 14 [Коши].
Для вещественной симметричной матрицы $ A_{} $ число ее собственных чисел, лежащих на интервале $ ]a,b_{}[ $, определяется по формуле:
$$operatorname{nrr} { det (A-lambda E) =0 | a< lambda<b }= $$
$$= {mathcal P}(1, H_1(a), H_2(a),dots, H_n(a))-
{mathcal P}(1, H_1(b), H_2(b),dots, H_n(b)) . $$
Здесь $ H_1(lambda), H_2(lambda),dots, H_n(lambda) $ —
главные миноры матрицы $ A-lambda, E $, а $ {mathcal P}_{} $ — число знакопостоянств.
Доказательство
☞
ЗДЕСЬ.
Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы
полиномов Штурма для характеристического полинома симметричной матрицы $ A_{} $.
=>
Если все главные миноры $ A_1,A_2,dots,A_{n} $ симметричной матрицы $ A_{} $ отличны от нуля, то
число положительных собственных чисел матрицы $ A_{} $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:
$$ operatorname{nrr} { det (A-lambda E) =0 | lambda>0 } = {mathcal P}(1,A_1,dots,A_n),
$$
$$
operatorname{nrr} { det (A-lambda E) =0 | lambda<0 }={mathcal V}(1,A_1,dots,A_n) .
$$
П
Пример. Локализовать собственные числа матрицы
$$
left(
begin{array}{rrr}
11 & 2 & -8 \
2 & 2 & 10 \
-8 & 10 & 5
end{array}
right)
$$
Решение.
$$ H_1(lambda)=11- lambda, H_2(lambda)=lambda^2-13, lambda+18,
$$
$$
f(lambda)= H_3(lambda)=-lambda^3+18, lambda^2 +81, lambda -1458
.
$$
| $ lambda $ | $ 1_{} $ | $ H_1(lambda) $ | $ H_2(lambda) $ | $ H_3(lambda) $ | $ {mathcal P} $ | Комментарии |
|---|---|---|---|---|---|---|
| $ 0_{} $ | $ + $ | $ + $ | $ + $ | $ — $ | 2 | число положительных =2 |
| $ -10 $ | $ + $ | $ + $ | $ + $ | $ + $ | 3 | собственное число |
| $ -5 $ | $ + $ | $ + $ | $ + $ | $ — $ | 2 | лежит на $ ]-10,-5[ $ |
| $ 5 $ | $ + $ | $ + $ | $ — $ | $ — $ | 2 | собственное число |
| $ 10 $ | $ + $ | $ + $ | $ — $ | $ + $ | 1 | лежит на $ ]5,10[ $ |
| $ 15 $ | $ + $ | $ — $ | $ — $ | $ + $ | 1 | собственное число |
| $ 20 $ | $ + $ | $ — $ | $ + $ | $ — $ | 0 | лежит на $ ]15,20[ $ |
Проверка. Спектр матрицы: $ {-9,9,18 } $.
П
Пример. Локализовать собственные числа матрицы
$$
left(
begin{array}{rrr}
1 & -2 & 2 \
-2 & -2 & 4 \
2 & 4 & -2
end{array}
right) .
$$
Решение.
$$H_1(lambda)=1- lambda, H_2(lambda)=lambda^2+, lambda-6,
f(lambda)=H_3(lambda)=-lambda^3-3, lambda^2 +24, lambda -28
.
$$
| $ lambda_{} $ | $ 1_{} $ | $ H_1(lambda) $ | $ H_2(lambda) $ | $ H_3(lambda) $ | $ {mathcal P} $ | Комментарии |
|---|---|---|---|---|---|---|
| $ 0_{} $ | $ + $ | $ + $ | $ — $ | $ — $ | 2 | число положительных =2 |
| $ -8 $ | $ + $ | $ + $ | $ + $ | $ + $ | 3 | собственное число |
| $ -6 $ | $ + $ | $ + $ | $ + $ | $ — $ | 2 | лежит на $ ]-8,-6[ $ |
| $ 1.5 $ | $ + $ | $ — $ | $ — $ | $ — $ | 2 | два собственных числа |
| $ 3_{} $ | $ + $ | $ — $ | $ + $ | $ — $ | 0 | лежат на $ ]1.5,3[ $ |
Никаким дроблением интервала $ ]1.5, , , 3[ $ не удается отделить
два вещественных собственных числа. Вывод: имеется кратное собственное
число.
Проверка. Спектр матрицы: $ {-7,2,2 } $.
Произвольная матрица
Собственный вектор
Собственный вектор матрицы 
$$
X_{ast}= left(
begin{array}{c} x_{1}^{ast} \ vdots \ x_{n}^{ast}
end{array} right)
in mathbb{C}^n
$$
такой, что
$$ AX_{ast}=lambda_{ast} X_{ast} quad iff quad (A -lambda_{ast}E) X_{ast} = mathbb O_{ntimes 1} . $$
По определению собственного числа, $ det (A^{} -lambda_{ast}E) = 0 $ и, следовательно,
система однородных уравнений $ (A -lambda_{ast}E) X^{} = mathbb O $ всегда имеет нетривиальное решение; более того, этих решений бесконечно много. Таким образом, одному и тому же собственному числу матрицы принадлежит бесконечное множество собственных векторов. Эту бесконечность можно описать с помощью фундаментальной системы решений (ФСР).
Строго говоря, только что введено определение правого собственного вектора матрицы $ A $. Потому как для
этой же матрицы определяется и левый собственный вектор — как строка $ Y_{ast}=(y_1^{ast},dots, y_n^{ast}) ne mathbb O $, такая, что
$$ Y_{ast} A= mu_{ast} A quad mbox{ при некотором } mu_{ast} in mathbb C , . $$
Очевидно, что $ Y_{ast} $ является левым собственным вектором $ A $ тогда и только тогда, когда столбец $ Y_{ast}^{top} $ является правым собственным вектором матрицы $ A^{^{top}} $. Кроме того, поскольку спектры матриц $ A $ и $ A^{^{top}} $ совпадают, то все результаты, полученные для правых собственных векторов, автоматически переносятся и на левые. Традиционно принято рассматривать правые собственные векторы; в этом случае слово «правый» опускают.
П
Пример. Найти собственные векторы матрицы
$$
A=
left(begin{array}{rrrr}
0&1&2&3\
-1&0&4&7\
-2&-4&0&2\
-3&-7&-2&0
end{array}right).
$$
Решение. Спектр матрицы найден выше.
$$(A-0 cdot E)X=mathbb O quad Longrightarrow mbox{ ФСР}=
left{
{mathfrak X}_1=left(begin{array}{r}
4 \ -2 \ 1 \ 0 end{array}right),
{mathfrak X}_2=left(begin{array}{r}
7 \ -3 \ 0 \ 1 end{array} right) right}.$$
Любой вектор вида $ alpha_{1} {mathfrak X}_1 + alpha_2 {mathfrak X}_2 $ будет собственным,
принадлежащим $ lambda_{}=0 $.
$$ begin{array}{c}
(A- mathbf i, sqrt {83} E)X=mathbb O \ \ Downarrow \ \ {mathfrak X}_3=
left(begin{array}{c}
1- mathbf i , sqrt {83} \ 8-2, mathbf i , sqrt {83} \ 12 \ 17+mathbf i , sqrt {83}
end{array}right)
end{array}
qquad
begin{array}{c}
(A+mathbf i sqrt {83} E)X=mathbb O \ \ Downarrow \ \ {mathfrak X}_4=
left(begin{array}{c}
1+mathbf i , sqrt {83} \ 8+2mathbf i , sqrt {83} \ 12 \ 17- mathbf i ,sqrt {83}
end{array}right)
end{array} .
$$
♦
Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.
Т
Теорема 15. Пусть $ lambda_{ast}^{} $ — собственное число матрицы $ A_{} $. Обозначим частное от деления характеристического полинома на линейный множитель $ lambda_{} — lambda_{ast} $ через $ f_{ast}(lambda)^{} $:
$$ f_{ast}(lambda) equiv f(lambda) / (lambda-lambda_{ast}) . $$
Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ является собственным вектором, принадлежащим $ lambda_{ast}^{} $.
Доказательство следует из равенства
$$(A-lambda_{ast} E)f_{ast}(A)=mathbb O_{ntimes n} . $$
На основании определения любой ненулевой столбец $ f_{ast}(A)^{} $ должен быть
собственным вектором матрицы $ A_{} $.
♦
П
Пример. Найти собственные векторы матрицы
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right) .
$$
Решение.
$$ det (A-lambda E)=-lambda^3+ 7, lambda + 6 equiv -(lambda_{}-3) (lambda+2)(lambda+1) , .$$
Пренебрегая знаком – , имеем:
$$
begin{matrix}
f_1(lambda)=lambda^2+3lambda+2 & u & f_1(A)=
left( begin{array}{rrr}
40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20
end{array}
right) , \
f_2(lambda)=lambda^2-2lambda-3 & u & f_2(A)=
left( begin{array}{rrr}
-10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0
end{array}
right) , \
f_3(lambda)=lambda^2-lambda-6 & u & f_3(A)=
left( begin{array}{rrr}
-4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8
end{array}
right) .
end{matrix}
$$
Ответ. $ {mathfrak X}_{1}=[1,0,1]^{^{top}} $ принадлежит $ lambda_{1}^{}=3 $,
$ {mathfrak X}_{2}=[-2,1,0]^{^{top}} $ принадлежит $ lambda_{2}^{}=-2 $,
$ {mathfrak X}_{3}=[-1,1,2]^{^{top}} $ принадлежит $ lambda_{3}^{}=-1 $.
=>
Если $ lambda_{ast}^{} $ является простым корнем характеристического полинома9), то ненулевые столбцы $ f_{ast}(A)^{} $ будут пропорциональными. Или, что то же, $ operatorname{rank} f_{ast}(A)^{} = 1 $.
Тогда очевидно, что и строки матрицы $ f_{ast}(A)^{} $ тоже должны быть пропорциональны!
На практике вычисление полинома $ f_{ast}(lambda)^{} $ может быть осуществлено с помощью схемы Хорнера.
П
Пример. Вычислить собственный вектор матрицы
$$
A=left( begin{array}{rrr}
23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87
end{array}
right) ,
$$
принадлежащий ее вещественному собственному числу.
Решение. Характеристический полином
$$ f(lambda)= -lambda^3+184,lambda^2-14751,lambda+611404 $$
имеет единственное вещественное собственное число $ lambda_{ast} approx 96.8817 $. Составляем схему Хорнера
$$
begin{array}{c|cccc}
& -1 & 184 & -14751 & 611404 \
hline
96.8817 & -1 & 87.1183 & -6310.8310 & -0.0352
end{array}
$$
За счет ошибок округления мы получили ненулевое значение для $ f(lambda_{ast}) $. В качестве частного от деления $ f(lambda) $ на $ lambda-lambda_{ast} $ берем
$$
f_{ast}(lambda)= -lambda^2 + 87.1183, lambda — 6310.8310 .
$$
Подставляем в него матрицу $ A_{} $ и вычисляем первый столбец матрицы
$$ -A^2+87.1183,A -6310, E =
left( begin{array}{rrr}
-1882.1101 & * & * \ -2723.2902 & * & * \ -708.6229 & * & *
end{array}
right) .$$
Проверяем:
$$
left( begin{array}{rrr}
23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87
end{array}
right)
left( begin{array}{r}
-1882.1101 \ -2723.2902 \ -708.6229
end{array}
right) — 96.8817 left( begin{array}{r}
-1882.1101 \ -2723.2902 \ -708.6229
end{array}
right)= left( begin{array}{r}
0.0356 \ 0 \ -0.0002
end{array}
right) .
$$
♦
Можно развить последний метод далее: найти универсальную формулу для собственного вектора как функции ее собственного числа. Действительно, найдем частное от деления характеристического полинома
$$ f(lambda) =a_0lambda^n+a_0lambda^{n-1}+dots+ a_n, quad a_0=(-1)^n $$
на линейный полином $ lambda- lambda_{ast} $, где $ lambda_{ast} $ — произвольное число из $ mathbb C $. С помощью той же схемы Хорнера, получаем
$$ q(lambda)= $$
$$
=a_0lambda^{n-1}+(a_0lambda_{ast}+a_1)lambda^{n-2}+(a_0lambda_{ast}^2+a_1lambda_{ast}+a_2)lambda^{n-3}+dots+ (a_0lambda_{ast}^{n-1}+a_1lambda_{ast}^{n-2}+dots+a_{n-1}) , .
$$
Если $ lambda_{ast} $ является собственным числом матрицы $ A_{} $, то любой ненулевой столбец матрицы
$$ q(A)= $$
$$
=a_0A^{n-1}+(a_0lambda_{ast}+a_1)A^{n-2}+(a_0lambda_{ast}^2+a_1lambda_{ast}+a_2)A^{n-3}+dots+ (a_0lambda_{ast}^{n-1}+a_1lambda_{ast}^{n-2}+dots+a_{n-1})E
$$
будет собственным вектором, принадлежащим $ lambda_{ast} $.
П
Пример. Найти представление всех собственных векторов матрицы
$$
A=left( begin{array}{rrr}
9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5
end{array}
right)
$$
в виде функции ее собственных чисел.
Решение. Характеристический полином матрицы был вычислен выше: $ f(lambda)=-lambda^3+ 7, lambda + 6 $. Имеем,
$$
q(lambda)=-lambda^2-lambda_{ast}lambda+(7-lambda_{ast}^2)
$$
и
$$
q(A)=-A^2-lambda_{ast}A+(7-lambda_{ast}^2)E=
left(begin{array}{ccc} -lambda_{ast}^2-9lambda_{ast}-4 & -22lambda_{ast}-14 & 6lambda_{ast}+2 \
lambda_{ast}-3 & -lambda_{ast}^2+4lambda_{ast}-3 & -lambda_{ast}+3 \
-8lambda_{ast}-16 & -16lambda_{ast}-32 & -lambda_{ast}^2+5lambda_{ast}+14
end{array} right) , .
$$
Берем произвольный столбец этой матрицы, например, первый:
$$
X_{ast}(lambda_{ast})=
left(begin{array}{c}
-lambda_{ast}^2-9lambda_{ast}-4 \
lambda_{ast}-3 \ -8lambda_{ast}-16
end{array} right) , .
$$
Утверждается, что $ X_{ast} (lambda_{ast}) $ — универсальное представление всех собственных векторов матрицы. Действительно,
$$
X_{ast}(-1)
=
left(begin{array}{r}
4 \
-4 \
-8
end{array} right),
X_{ast}(-2)
=
left(begin{array}{r}
10 \
-5 \ 0
end{array} right),
X_{ast}(3)
=
left(begin{array}{r}
-40 \
0 \
-40
end{array} right) , .
$$
♦
Матрица $ q(A) $, которую мы построили для нахождения универсального представления собственного вектора, может быть получена другим способом. В самом деле, поскольку
$$ f(lambda)equiv q(lambda)(lambda-lambda_{ast})+ f(lambda_{ast}), $$
то имеем справедливость матричного равенства:
$$ f(A)equiv q(A)(A-lambda_{ast}E)+ f(lambda_{ast})E , . $$
Откуда, на основании теоремы Гамильтона-Кэли, получаем равенство
$$ q(A)(A-lambda_{ast}E) = — E det (A-lambda_{ast}E) , . $$
Это равенство означает, что матрица $ (- q(A)) $ является взаимной матрице $ A-lambda_{ast}E $:
$$ — q(A)=operatorname{adj}(A-lambda_{ast}E) , . $$
Следовательно, ее выражение (а нам, собственно, нужно только выражение для какого-то ее столбца)
может быть получено с помощью алгебраических дополнений элементов матрицы $ A-lambda_{ast}E $. Именно такой способ вычисления взаимной матрицы использовался при доказательстве теоремы Гамильтона-Кэли.
Т
Теорема 16. Пусть $ g(x)=b_0x^m+dots+b_{m} in {mathbb C}[x] $ – произвольный полином. Если $ X_{ast}in mathbb C^{n} $ — собственный вектор матрицы $ A_{} $,
соответствующий собственному числу $ lambda_{ast}^{} $, то он же будет собственным и для матрицы $ g(A)^{} $, принадлежащим собственному числу $ g(lambda_{ast})^{} $.
Доказательство. Домножим равенство $ A{mathfrak X}_{ast}=lambda_{ast}^{}{mathfrak X}_{ast} $ слева
на матрицу $ A_{} $:
$$ A^2{mathfrak X}_{ast}=lambda_{ast}A{mathfrak X}_{ast}=lambda_{ast}^2{mathfrak X}_{ast} .$$
По индукции доказывается и общее равенство:
$$ A^k{mathfrak X}_{ast}=lambda_{ast}^k{mathfrak X}_{ast} .$$
Домножим его на $ b_{m-k}^{} $ и просуммируем по $ k_{} $ от $ 0_{} $ до $ m_{} $:
$$ g(A){mathfrak X}_{ast}=g(lambda_{ast}){mathfrak X}_{ast} ,$$
что и доказывает утверждение теоремы.
♦
=>
Если матрица $ A $ невырождена, то теорема остается справедливой и для произвольного полинома от $ A^{-1} $. В частности, собственные векторы $ A^{-1} $ совпадают с собственными векторами матрицы $ A $.
Т
Теорема 17. Собственные векторы, принадлежащие различным собственным числам матрицы $ A_{} $, линейно независимы.
Т
Теорема 18. Собственные векторы, принадлежащие различным собственным числам вещественной симметричной матрицы $ A_{} $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_{1} $, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_{2} $ и $ lambda_1 ne lambda_2 $, то
$$ langle mathfrak X_1, mathfrak X_2 rangle =0 , $$
где $ langle , rangle $ означает скалярное произведение, определяемое стандартным образом: $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.
Доказательство
☞
ЗДЕСЬ.
Теорема Перрона-Фробениуса
Т
Теорема 19 [Перрон, Фробениус]. Для положительной матрицы $ A_{} $ существует положительное собственное число $ lambda_{+} $ такое, что все остальные собственные числа этой матрицы меньше $ lambda_{+} $ по абсолютной величине (модулю). Соответствующий этому собственному числу собственный вектор может быть выбран положительным:
$$ exists mathfrak X_{+} > mathbb O: quad A mathfrak X_{+} = lambda_{+} mathfrak X_{+} . $$
Число $ lambda_{+} $ из теоремы называется собственным числом Перрона или собственным числом Перрона-Фробениуса матрицы $ A_{} $, а соответствующий ему произвольный положительный собственный вектор —
собственным вектором Перрона-Фробениуса матрицы $ A_{} $.
=>
Спектральный радиус положительной матрицы $ A_{} $ совпадает с ее собственным числом Перрона-Фробениуса:
$$ rho(A)=lambda_{+} . $$
П
Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы
$$
A=
left(begin{array}{rrrr}
2 & 7 & 18 & 28 \
1 & 8 & 2 & 8 \
3 & 1 & 4 & 1 \
5 & 9 & 26 & 5
end{array}
right) , .
$$
Решение. Характеристический полином матрицы $ A_{} $
$$
det(A-lambda E)=lambda^4-19, lambda^3-175, lambda^2-285, lambda+10390
$$
имеет корнями
$$
lambda_{1,2} approx -6.260463 pm 5.452465 mathbf i, lambda_3 approx 5.878976, lambda_4 approx 25.641950 .
$$
Числом Перрона-Фробениуса является $ lambda_4 $, а соответствующий ему собственный вектор Перрона-Фробениуса можно взять равным
$$
left(
begin{array}{c}
1 \
0.365240 \ 0.184802 \ 0.634244
end{array}
right) quad mbox{ или } quad
left(
begin{array}{c}
2.737922 \ 1 \ 0.505974 \ 1.736510
end{array}
right) quad mbox{ или }
left(
begin{array}{c}
5.411185 \ 1.976383 \ 1 \ 3.432010
end{array}
right) quad mbox{ или } quad
left(
begin{array}{c}
1.576681 \ 0.575868 \ 0.291374 \ 1
end{array}
right) quad mbox{ или } quad
left(
begin{array}{r}
0.798133 \
0.291510 \
0.147496\
0.506210
end{array}
right) quad mbox{ или } dots
$$
(напоминаю: собственный вектор определяется с точностью до ненулевого сомножителя!). Последний вектор имеет длину равную $ 1_{} $.
♦
Свойства.
1.
Собственное число Перрона-Фробениуса всегда простое для характеристического полинома матрицы $ A_{} $. Отсюда следует, что собственный вектор Перрона-Фробениуса определяется единственным образом — с точностью до домножения на положительный скаляр.
2.
Любой собственный вектор положительной матрицы $ A_{} $, не соответствующий собственному числу Перрона-Фробениуса, не может состоять исключительно только из положительных элементов. Иными словами, хотя бы одна компонента такого вектора должна быть либо отрицательной либо мнимой.
3.
Для собственного числа Перрона-Фробениуса справедливо неравенство
$$ min_{jin{1,dots,n}} sum_{k=1}^n a_{jk} le lambda_{+} le max_{jin{1,dots,n}} sum_{k=1}^n a_{jk} . $$
4.
Собственное число Перрона-Фробениуса матрицы $ A_{} $ совпадает с собственным числом Перрона-Фробениуса матрицы $ A^{top} $.
Какие из перечисленных свойств можно распространить на случай неотрицательных матриц ? Каждую такую матрицу можно рассматривать как предел последовательности (строго)
положительных матриц.
Воспользовавшись теоремой о непрерывной зависимости собственных чисел матрицы от ее элементов, можем сделать вывод, о том, что для неотрицательной матрицы $ A_{} $ всегда найдется вещественное неотрицательное собственное число, которое будет являться максимальным по модулю среди всех собственных чисел матрицы. Другое дело, что в данном случае — в отличие от случая положительных матриц — такое мажорирующее собственное число может оказаться не единственным.
П
Пример. Спектр неотрицательной матрицы
$$ A=left( begin{array}{cc} 0 & 1 \ 1 & 0 end{array} right) $$
состоит из чисел $ lambda_1=+1 $ и $ lambda_1=-1 $ одинакового модуля.
♦
Однако, по-прежнему, хотя бы одно неотрицательное вещественное число $ lambda_{+} $ со свойством $ rho(A) = lambda_{+} $ существовать будет; более того, ему будет соответствовать неотрицательный собственный вектор $ mathfrak X ge mathbb O $. Это число (вектор) по-прежнему называются числом (вектором) Перрона-Фробениуса10) матрицы $ A_{} $.
Частным случаем неотрицательных матриц являются стохастические матрицы, т.е. неотрицательные матрицы, в которых сумма элементов
каждой строки равна $ 1_{} $:
$$
mathfrak P=left[p_{jk}right]_{j,k=1}^n, {p_{jk}ge 0 }_{j,k=1}^n, sum_{k=1}^n p_{jk} = 1 npu quad j in {1,2,dots,n} .
$$
Т
Теорема 20. Собственное число Перрона-Фробениуса стохастической матрицы равно $ 1_{} $. Этому собственному числу соответствует собственный вектор $ X=[1,1,dots,1]^{top} $.
Доказательство существования собственного числа равного $ 1_{} $ и соответствующего ему собственного вектора $ X=[1,1,dots,1]^{top} $ следует из равенства
$$mathfrak P left(
begin{array}{c}
1 \
1 \ vdots \ 1
end{array}
right) =
left(
begin{array}{c}
1 \ 1 \ vdots \ 1
end{array}right) .
$$
Далее, из теоремы Гершгорина следует, что любое собственное
число $ lambda_{}in mathbb C $ стохастической матрицы должно удовлетворять неравенству
$$|lambda — p_{jj}|le sum_{kne j} |p_{jk}|=1-p_{jj} $$
хотя бы при одном $ j_{} $. Воспользовавшись следствием к неравенству треугольника получаем:
$$|lambda| — |p_{jj}|le |lambda — p_{jj}| le 1-p_{jj} Rightarrow
|lambda| le 1 . $$
♦
Численное нахождение собственного числа и собственного вектора Перрона-Фробениуса возможно по методу, разобранному в пункте
☞
ЧАСТИЧНАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ.
Методы вычисления характеристического полинома
Вычисление коэффициентов характеристического полинома матрицы $ A_{} $
непосредственным разложением определителя $ det (A-lambda_{} E) $ на $ n!_{} $ слагаемых — крайне неэффективно. Элементами этого разложения являются выражения, полиномиально зависящие от параметра $ lambda_{} $. На каждом этапе вычислений мы получаем проблему символьных вычислений: хранения таких полиномов и действий над ними.
Основной метод вычисления числовых определителей — метод Гаусса — также неэффективен в приложении к вычислению определителя, элементы которого зависят от параметра.
Источником вычислительных проблем является неудобное расположение переменной $ lambda_{} $ — на главной диагонали матрицы. Первый же шаг метода Гаусса приводит к делению на элемент $ a_{11} — lambda $, и, в дальнейшем, элементы преобразованной матрицы будут уже не полиномами, а рациональными функциями относительно $ lambda_{} $. Следующие шаги метода приводят к возрастанию степеней знаменателей. Необходимость в организации хранения рациональных функций и программировании действий с ними кажется тем более неоправданной, если вспомнить, что окончательный ответ — выражение для $ det (A-lambda_{} E) $ — должно быть полиномом по $ lambda_{} $; т.е. знаменатели дробей в конечном ответе сократятся.
А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.
Какой выход предлагается? — Предварительно преобразовать определитель $ det (A-lambda_{} E) $ к виду, когда переменная $ lambda_{} $ оказывается «выметенной» с диагонали на крайний ряд (в столбец или в строку). При этом допускается увеличение размеров (порядка) определителя. Такое представление дает возможность разложения определителя по этому исключительному ряду, и, тем самым, позволяет свести задачу к вычислению числовых
определителей — а уж для этой задачи применение метода Гаусса вполне эффективно.
Метод Леверье
Метод основан на формуле (см. следствие к теореме $ 7 $
☞
ЗДЕСЬ ):
$$ operatorname{Sp} (A^k)=lambda_1^k+dots+lambda_n^k=s_k , $$
т.е. след $ k_{} $-й степени матрицы $ A_{} $ равен $ k_{} $-й сумме Ньютона ее характеристического полинома $ f(lambda)=det (A-lambda E ) $.
Вычисляем последовательные степени матрицы $ A_{} $:
$$s_1=operatorname{Sp} (A), s_2=operatorname{Sp} (A^2), dots, s_n=operatorname{Sp} (A^n) .$$
Неизвестные коэффициенты $ f(lambda)=(-1)^n(lambda^n+a_1lambda^{n-1}+
dots+a_n) $ находим по рекурсивным формулам Ньютона:
$$
a_1=-s_1, a_2=-(s_2+a_1s_1)/2,
$$
$$
a_k=-(s_{k}+a_1s_{k-1}+a_2s_{k-2}+dots+a_{k-1}s_1)/k npu k le n.
$$
Очевидно, что не имеет смысла вычислять все элементы матрицы $ A^{n} $ — достаточно обойтись лишь элементами ее главной диагонали.
П
Пример [Леверье]. Найти характеристический полином матрицы
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение.
$$
A^2=left(begin{array}{rrrr}
30.91795128&-30.56848188&2.878480155&0.0031325713\
-4.705449283&164.6764010&-141.3504639&-0.4143169528\
0.3341843103&-106.6094396&193.1869924& -6.756396001\
0.0022236138&-1.904168948&-41.16923134& 309.9628536
end{array}
right),
$$
$$
A^3=left(begin{array}{rrrr}
-179.0125092&431.2849919&-198.8601505& -0.9173897610\
66.38829278&-2562.954533& 2771.458834& -15.49709921\
-23.08728044&2090.291485&-3124.010318& 156.9329019\
-0.649145142&-71.21907809&956.2502143& -5463.723497
end{array}
right),
$$
$$
A^4=left(begin{array}{cccc}
1100.720103& ast& ast& ast \
ast& 42332.23816& ast& ast \
ast& ast& 52669.62534& ast \
ast& ast& ast& 96355.91518
end{array}
right) .
$$
Вычисляем следы матриц:
$$s_1=-47.888430, s_2=698.7441983, s_3=-11329.70086, s_4= 192458.4988 ,$$
и по формулам Ньютона получаем:
$$a_1= 47.888430, a_2 = 797.278764_{displaystyle 8}
, a_3 = 5349.45551_{displaystyle 3},
a_4 = 12296.550_{displaystyle 68} . $$
♦
После нахождения коэффициентов характеристического полинома можно найти его корни каким-либо11) методом. Если $ lambda_{ast}^{} $ — одно
из собственных чисел, то для нахождения соответствующего собственного
вектора воспользуемся алгоритмом из
☞
ПУНКТА. Предположив дополнительно, что это собственное число простое12), обозначим
$$
f_{ast}(lambda)= f(lambda)/(lambda-lambda_{ast})=(-1)^n(lambda^{n-1}
+p_1lambda^{n-2}+dots+p_{n-2}lambda+p_{n-1})
$$
т.е. частное от деления $ f(lambda_{}) $ на $ lambda-lambda_{ast} $. Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ будет собственным вектором, принадлежащим $ lambda_{ast}^{} $. Как правило, собственным вектором можно взять комбинацию

Степени матрицы $ A_{} $ уже нами посчитаны при вычислении коэффициентов характеристического полинома.
П
Пример. Для приведенного выше примера находим собственные числа:
$$
lambda_1=-17.86326,
lambda_2=-17.15242, lambda_3=-7.57404,
lambda_4= -5.29869 .
$$
Коэффициенты $ f_1(lambda) $ можно определить по схеме Хорнера:
$$
begin{array}{r|r|r|r|r|r}
&1 & 47.888430 & 797.2787648 & 5349.455513 & 12296.55068 \ hline
-17.86326 & 1 & underbrace{30.025170}_{p_{_1}}&
underbrace{260.9313465}_{p_{_2}} &underbrace{688.371028}_{p_{_3}}&
approx 0 \
end{array}
$$
Собственным вектором, принадлежащим $ lambda_{1} $, будет
$$left[ -0.0256_{displaystyle 67},
0.21938_{displaystyle 0},
-0.24187_{displaystyle 1},
1.044526 right]^{^{top}} .$$
♦
Т
Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:
$$
f(lambda)=frac{1}{n!}left|
begin{array}{llllll}
s_1 &1 & & & &\
s_2&s_1& 2 & &mathbb O & \
s_3&s_2&s_1&3& & \
vdots& & & ddots &ddots & \
s_n&s_{n-1}& s_{n-2} & dots &s_1&n \
lambda^n&lambda^{n-1}&lambda^{n-2}& dots &lambda&1
end{array}
right|_{(n+1)times (n+1)} .
$$
Этот определитель имеет порядок больший, чем исходный $ det (A_{}-lambda E) $, однако в нем все включения переменной $ lambda_{} $ локализованы в одной строке — именно такое размещение трактовалось как «хорошее» в смысле вычисления определителя
☝
ВЫШЕ.
И
Биографические заметки о Леверье
☞
ЗДЕСЬ.
Существует модификация метода Леверье, позволяющая организовать одновременное вычисление как самого характеристического полинома матрицы $ A_{} $, так и матрицы взаимной к матрице $ A_{}-lambda E $ (что делает возможным получение универсальной формулы для всех собственных векторов матрицы $ A_{} $); этот метод известен как метод Леверье-Фаддеева.
Метод Крылова
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_{1}^{[0]},dots,y_{n}^{[0]} right]^{^{top}} in mathbb C^n $. Cоставим итерационную векторную
последовательность
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{n}=Acdot Y_{n-1} .
$$
Т
Теорема 22. Определитель
$$
det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&Y_{n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]_{(n+1)times (n+1)}
$$
совпадает — с точностью до постоянного множителя — с характеристическим полиномом матрицы $ A_{} $. Здесь $ |_{} $ означает конкатенацию.
Доказательство. Легко видеть, что
$$ Y_K=A^KY_0 quad npu quad K in {1,dots,n} . $$
Если
$$ f(lambda)=det(A-lambda E) =(-1)^n lambda^n+a_1 lambda^{n-1}+a_2 lambda^{n-2}+dots+a_n , $$
то по теореме Гамильтона-Кэли:
$$
(-1)^n A^n+a_1A^{n-1}+dots+a_nE=mathbb O_{n times n} .
$$
Это равенство останется справедливым и после умножения его на произвольный вектор, в том числе на $ Y_{0} $:
$$
(-1)^n A^ncdot Y_0+a_1A^{n-1} cdot Y_0 +dots+a_ncdot Y_0=mathbb O_{n times 1} iff
$$
$$
iff quad (-1)^n Y_n+a_1Y_{n-1} +dots+a_nY_0=mathbb O .
$$
Последнее равенство представляет линейную систему относительно неизвестных коэффициентов характеристического полинома. Можно решать ее по формулам Крамера, но мы пойдем другим путем. Дополним эту систему тождеством $ f(lambda)=(-1)^n lambda^n+a_1 lambda^{n-1}+a_2 lambda^{n-2}+dots+a_n $. Рассмотрим получившуюся систему как линейную однородную относительно столбца $ left[ a_n,a_{n-1},dots,a_1,1right]^{top} $. Поскольку эта система имеет нетривиальное решение, то ее определитель должен равняться нулю:
$$
0=det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&(-1)^nY_{n}\
1& lambda&dots&lambda^{n-1}&(-1)^nlambda^n-f(lambda)
end{array}
right]=
$$
(представляем последний столбец в виде суммы двух столбцов и используем свойство
5
определителя)
$$
=det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&(-1)^nY_{n}\
1& lambda&dots&lambda^{n-1}&(-1)^nlambda^n
end{array}
right]-f(lambda)
det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right] .
$$
Таким образом,
$$ f(lambda)=(-1)^n frac{det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}&Y_{n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]}{det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right]} ,
$$
если только знаменатель в этой дроби не обратится в нуль.
♦
П
Пример. Найти характеристический полином матрицы примера Леверье
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение. Возьмем $ Y_0=left[ 1,0,0,0 right]^{top} $. Имеем
$$
begin{array}{cccc}
Y_1=A Y_0= & Y_2=AY_1= & Y_3=AY_2= & Y_4=AY_3= \
left(begin{array}{r}
-5.509882\
0.287865 \
0.049099 \
0.006235
end{array}
right), &
left(begin{array}{r}
30.917951\
-4.705449 \
0.334184 \
0.002223
end{array}
right), &
left(begin{array}{r}
-179.012509\
66.388293 \
-23.087280\
-0.649145
end{array}
right), &
left(begin{array}{r}
1100.720101\
-967.597333\
576.522644\
-4.040153
end{array}
right) .
end{array}
$$
$$
det left[begin{array}{c|c|c|c|c}
Y_0&Y_{1}&Y_2& Y_{3}& Y_{4}\
1& lambda&lambda^2 &lambda^{3}&lambda^4
end{array}
right]=
left| begin{array}{rrrrr}
1 & -5.509882 & 30.917951 & -179.012509 & 1100.720101 \
0 & 0.287865 & -4.705449 & 66.388293 & -967.597333\
0 & 0.049099 & 0.334184 & -23.087280 & 576.522644\
0 & 0.006235 & 0.002223 & -0.649145 & -4.040153 \
1 & lambda & lambda^2 & lambda^3 & lambda^4
end{array}
right|=
$$
$$
=0.348621 lambda^4+16.694915lambda^3+277.948166lambda^2+1864.932835lambda+4286.836454 =
$$
$$
=0.348621 left(lambda^4+47.888430lambda^3+797.27876_{displaystyle 3}lambda^2+5349.4555_{displaystyle 0}lambda+12296.550_{displaystyle 5} right) .
$$
♦
После нахождения характеристического полинома можно найти его корни каким-либо13) методом. Пусть $ lambda_{ast}^{} $ — одно из собственных чисел, и оно —
простое; тогда для нахождения соответствующего собственного вектора можно воспользоваться тем же приемом, что был задействован в предыдущем ПУНКТЕ. Вычислим14) частное от деления $ f(lambda_{}) $ на $ lambda-lambda_{ast} $
$$
f_{ast}(lambda)= f(lambda)/(lambda-lambda_{ast})=(-1)^n(lambda^{n-1}
+p_1lambda^{n-2}+dots+p_{n-2}lambda+p_{n-1}) .
$$
Тогда любой ненулевой столбец матрицы $ f_{ast}(A)^{} $ будет собственным вектором, принадлежащим $ lambda_{ast}^{} $. Но тогда и произвольная комбинация столбцов этой матрицы тоже будет собственным вектором (если только не обратится в нулевой вектор). В частности, это относится и к комбинации, записываемой в матричном виде
$$ (-1)^n f_{ast}(A) Y_0 = A^{n-1}Y_0 +p_1A^{n-2}Y_0+dots+p_{n-1}Y_0=Y_{n-1}+p_1Y_{n-2}+dots+p_{n-1}Y_0 . $$
А комбинируемые векторы уже посчитаны.
Теперь обсудим исключительные случаи. При неудачном выборе $ Y_{0} $ определитель
$$
det left[begin{array}{c|c|c|c}
Y_0&Y_{1}&dots&Y_{n-1}
end{array}
right]
$$
может обратиться в нуль. Эта неприятность обязательно произойдет если, например, наш выбор пал на вектор $ Y_0 $, совпадающий с собственным вектором матрицы $ A_{} $. Вероятность такого события — нулевая. В общем же случае, трудно ожидать, чтобы $ n_{} $ почти произвольных столбцов
$ Y_0,Y_{1},dots,Y_{n-1} $ оказались линейно зависимыми — если только сама матрица $ A_{} $ не обладает «скрытым дефектом» — типа рассмотренного в следующем примере.
П
Пример. Найти характеристический полином матрицы
$$A=left( begin{array}{ccc}
2&1&1 \
1&2&1 \
1&1&2
end{array}
right) .
$$
Решение. При любом выборе $ Y_0 $ векторы $ {Y_0,Y_1,Y_2 } $ оказываются линейно зависимыми:
$$
Y_0=
left(begin{array}{r}
1\
0\
0
end{array}
right),
Y_1=
left(begin{array}{r}
2\
1\
1
end{array}
right),
Y_2=
left(begin{array}{r}
6\
5\
5
end{array}
right),dots ;
Y_0=
left(begin{array}{r}
1\
1\
1
end{array}
right),
Y_1=
left(begin{array}{r}
4\
4\
4
end{array}
right),dots
$$
Объяснение этого феномена состоит в том, что для матрицы $ A_{} $ ее аннулирующий полином имеет степень меньшую ее порядка:
$$ A^2-5 A+4 E = mathbb O . $$
Домножение этого равенства на произвольный столбец $ Y_0 $ и доказывает линейную зависимость системы $ {Y_0,Y_1,Y_2} $.
♦
Такая ситуация возможна только в случае, когда характеристический полином матрицы $ A_{} $ имеет кратные корни (в рассмотренном выше примере $ lambda_{}=1 $ являлся двойным корнем $ det (A-lambda_{} E) $); она исключительно редко встречается на практике.
Поиск всех собственных чисел
Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.
QR-алгоритм
Этот алгоритм основан на QR-разложении матрицы $ A $.
Т
Теорема 23. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^{top} A P $ при произвольной ортогональной матрице $ P $.
Доказательство.
$$ det (P^{top} A P-lambda E)=det (P^{top} A P- lambda P^{top} E P)=det P^{top} (A -lambda E ) P =
det (A -lambda E ) P P^{top} = det (A -lambda E ) , .
$$
♦
Пусть QR-разложение матрицы $ A $ имеет вид
$$ A=Q_1R_1 , , $$
где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица
$$ A_2=R_1Q_1 $$
имеет тот же спектр, что и матрица $ A $. Действительно, поскольку
$$ A_2=Q_1^{top} A Q_1 , $$
то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $
$$ A_2=Q_2R_2 $$
и переставим местами матрицы этого произведения:
$$ A_3=R_2Q_2 , . $$
Матрица
$$ A_3= Q_2^{top} A_2 Q_2=Q_2^{top} Q_1^{top} A Q_1 Q_2 $$
продолжаем иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц
$$ {A_j=R_{j-1}Q_{j-1}}_{j=1}^{infty} $$
как правило, сходится к матрице $ A_{infty} $, которая будет верхнетреугольной.
Т
Теорема 24 [4]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_{infty} $ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.
П
Пример. Найти все собственные числа матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & 4
end{array}
right) , .
$$
Решение.
$$
A_1=Aapprox
underbrace{left(begin{array}{rrr}
0.272165 & 0.759752 & 0.590511 \
0.952579 & -0.299517 & -0.053683 \
-0.136083& -0.577119 & 0.805242
end{array}
right)}_{Q_1}
underbrace{left(begin{array}{rrr}
7.348469 & 3.946400 & 2.041241\
0 & 2.534941 & -3.966781 \
0 & 0 & 2.469409
end{array}
right)}_{R_1}
$$
Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы:
$$
quad Rightarrow quad A_2 = R_1Q_1approx
left(begin{array}{rrr}
5.481481 & 3.222957 & 5.771191 \
2.954542 & 1.530046 & -3.3303021 \
-0.336044 & -1.425143 & 1.988472
end{array}
right)approx
$$
$$
approxunderbrace{left(begin{array}{rrr}
-0.878992 & 0.022595 & 0.476300\
0.473781 & -0.154267 & -0.867026 \
0.053886 & -0.987771 & 0.146304
end{array}
right)}_{Q_2}
underbrace{left(begin{array}{rrr}
-6.236096& -3.634658 & -3.387848\
0 & 1.244502 & -1.319999\
0 & 0 & 5.927198
end{array}
right)}_{R_2}
$$
Продолжим процесс:
$$
quad Rightarrow quad A_3 = R_2Q_2approx
left(begin{array}{rrr}
7.020952& 3.766220 & -0.314568\
-0.660752 & 1.111870 & -1.272137\
0.319398 & -5.854713 & 0.867177
end{array}
right) approx
$$
$$
approx
underbrace{left(begin{array}{rrr}
-0.994581 & -0.065879 & 0.080426 \
0.093601 & -0.230749 & 0.968501 \
-0.045246 & 0.970780 & 0.235665
end{array}
right)}_{Q_3}
underbrace{left(begin{array}{rrr}
-7.059205 & -3.376839 & 0.154554 \
0 & -6.188319 & 1.156106 \
0 & 0 & -1.053002
end{array}
right)}_{R_3}
$$
Замечаем тенденцию убывания элементов матриц $ {A_j} $, стоящих под главной диагональю.
$$
Rightarrow dots Rightarrow A_{10} approx
left(begin{array}{rrr}
mathbf{6.}_{246022} & 2.758769 & -2.160057\
-0.0467437 & mathbf{4.4}_{09292} & -5.341014\
0.000018 &-0.005924 & mathbf{-1.6}_{55314}
end{array}
right) approx
$$
$$
underbrace{left(begin{array}{rrr}
-0.999972 & -0.007483 & 0.000007 \
0.007483 & -0.999971 & 0.001339 \
-0.000003 & 0.001339 & 0.999999
end{array}
right)}_{Q_{10}}
underbrace{left(begin{array}{rrr}
-6.246197 & -2.725694 & 2.120031\
0 & -4.429817 & 5.354807 \
0 & 0 & -1.662479
end{array}
right)}_{R_{10}} , .
$$
Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна.
$$
Rightarrow dots Rightarrow A_{20} approx
left(begin{array}{rrr}
mathbf{6.17}_{5608} & 2.805821 & -2.020513 \
-0.001776 & mathbf{4.48}_{4917} & -5.388407\
0 & 0 & -mathbf{1.660525}
end{array}
right) approx
$$
Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел.
$$
Rightarrow dots Rightarrow A_{30} approx
left(begin{array}{rrr}
mathbf{6.172}_{778} & 2.807524 & -2.015076\
-0.000073 & mathbf{4.487}_{747} & -5.390442\
0 & 0 & -mathbf{1.660525}
end{array}
right) , .
$$
♦
К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю.
§
Как это обстоятельство сказывается на структуре матрицы $ A_{infty} $ и дальнейшее развитие метода
☞
ЗДЕСЬ
Частичная проблема собственных чисел
Задача. Найти максимальное по модулю собственное число матрицы $ A_{} $.
Предположение
. Будем считать сначала, что максимальное по модулю собственное число матрицы единственно.
Излагаемый ниже метод поиска этого собственного числа называется методом степенны́х итераций15).
Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_{1}^{[0]},dots,y_{n}^{[0]} right]^{^{top}} in mathbb C^n $. Cоставим такую же итерационную векторную
последовательность, как и в методе Крылова
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{K}=Acdot Y_{K-1},dots ,
$$
(только теперь, в отличие от метода Крылова, считаем ее неограниченно продолжающейся) и выделим последовательность первых элементов этих векторов:
$$y_{1}^{[1]},y_{1}^{[2]},dots,y_{1}^{[K]},dots $$
Т
Теорема 25. Как правило, предел
$$
lim_{Kto +infty}frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}
$$
существует и он равен максимальному по модулю собственному числу матрицы $ A_{} $.
Доказательство. Перенумеруем собственные числа $ lambda_{1},dots,lambda_n $ матрицы $ A_{} $ так, чтобы $ lambda_{1} $ обозначило максимальное по модулю:
$$|lambda_1|= max_{jin {1,dots,n}} |lambda_j| , quad |lambda_1|>|lambda_j| quad npu quad jin {2,dots,n} . $$
Очевидно,
$$
Y_{K}=A^Kcdot Y_0 ;
$$
отсюда следует, что любой элемент столбца $ Y_{K} $ может быть линейно выражен через $ lambda_{1}^K,dots,lambda_n^K $.
В частности, это справедливо и для первого элемента:
$$
y_{1}^{[K]}=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K .
$$
В этом представлении $ {C_j}_{j=1}^n $ — будут константами из $ mathbb C_{} $ в случае если все собственные числа являются простыми, и полиномами из $ mathbb C[K] $ в случае, если имеются кратные собственные числа. Действительно, в первом случае существует базис пространства $ mathbb C^n $, состоящий из собственных векторов матрицы $ A_{} $:
$$ A{mathfrak X}_j=lambda_j{mathfrak X}_j quad npu quad jin {1,dots,n} . $$
Вектор $ Y_0 $ можно разложить по этому базису:
$$Y_0=alpha_1{mathfrak X}_1+dots+alpha_n{mathfrak X}_n .$$
Тогда последовательным домножением на матрицу $ A_{} $ получаем :
$$begin{matrix}
Y_1=AY_0&=& alpha_1 lambda_1{mathfrak X}_1+dots+alpha_nlambda_n{mathfrak X}_n, \
dots & & dots \
Y_K=A^KY_0&=& alpha_1 lambda_1^K{mathfrak X}_1+dots+alpha_nlambda_n^K{mathfrak X}_n
end{matrix}
$$
откуда и следует доказываемое равенство.
Во втором случае — когда имеются кратные собственные числа матрицы $ A_{} $ — придется применять «тяжелую артиллерию» в виде жордановой нормальной формы; см. теорему $ 5 $
☞
ЗДЕСЬ. Для простоты рассуждений, будем в оставшейся части доказательства считать все собственные числа матрицы различными. Имеем тогда
$$
lim_{K to +infty} frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}=
lim_{K to +infty} frac{lambda_1^{K+1} left[C_1+
C_2(lambda_2/lambda_1)^{K+1}+dots+
C_n(lambda_n/lambda_1)^{K+1} right]}
{lambda_1^{K} left[C_1+C_2(lambda_2/lambda_1)^{K}+dots+
C_n(lambda_n/lambda_1)^{K} right]}
=lambda_1
$$
поскольку
$$
lim_{K to +infty} left| frac{lambda_j}{lambda_1} right|^K = 0 quad
npu quad jin {2,dots,n} .
$$
Исключительным случаем является ситуация $ C_1=0 $, в этом случае утверждение теоремы может оказаться несправедливым16).
♦
=>
Как правило, вектор
$$
left[1, lim_{Kto +infty}frac{y_{2}^{[K]}}{y_{1}^{[K]}},dots,
lim_{Kto +infty}frac{y_{n}^{[K]}}{y_{1}^{[K]}}right]^{^{top}}
$$
будет собственным, принадлежащим максимальному по модулю собственному числу матрицы $ A_{} $.
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & -4
end{array}
right)
$$
найти максимальное по модулю собственное число и принадлежащий ему собственный вектор.
Решение. Возьмем в качестве стартового столбца $ Y_0=[1,0,0]^{^{top}} $. Имеем:
$$
Y_1=AY_0=left( begin{array}{r} 2 \ 7 \ -1 end{array} right),
Y_2=AY_1=left( begin{array}{r} 26 \ 32 \ -12 end{array} right),
Y_3=AY_2=left( begin{array}{r} 160 \ 242 \ -42 end{array} right),dots,
$$
$$
Y_{19}=left( begin{array}{r}
{scriptstyle 4259667747238636} \ {scriptstyle 6435097324667832} \ {scriptstyle -1571397155909260}
end{array} right), Y_{20}=AY_{19}=left( begin{array}{r}
{scriptstyle 29396024624390028} \ {scriptstyle 44408774736946168} \ {scriptstyle -10844273772937260}
end{array} right)
$$
Смотрим на отношения первых элементов векторов:
$$
begin{array}{c|c|c|c|c|c|c|c|c|c}
K & 1 & 2 & 3 & 4 & 5 & dots & 15 & dots & 19 \
hline
y_{1}^{[K+1]}/y_{1}^{[K]} & 2 & 13 & 6.153846 & 6.8 & 7.180147 & dots & 6.900726 & dots & mathbf{6.90101}_{displaystyle 3}
end{array}
$$
Далее, в соответствии со следствием, собственный вектор, принадлежащий найденному числу
$$
approx left[1, frac{y_{2}^{[20]}}{y_{1}^{[20]}},frac{y_{3}^{[20]}}{y_{1}^{[20]}}right]^{^{top}} approx left[1, 1.51070_{displaystyle 6}, -0.368902 right]^{^{top}}
$$
♦
Результат теоремы представляет собой обобщение метода Бернулли поиска максимального по модулю корня полинома. Если в качестве матрицы $ A_{} $ взять матрицу Фробениуса
$$
mathfrak F=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n} ,
$$
то равенство
$$ X_K=mathfrak F X_{K-1} npu Kin {1,2,dots } $$
определяет — при задании (произвольным образом) чисел $ x_0,x_1,dots,x_{n-1} $ — линейную рекуррентную последовательность порядка $ n_{} $:
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K .
$$
Здесь столбцы $ X_K $ определяются формулами
$$
X_0=left( begin{array}{l}
x_0 \ x_1 \ vdots \ x_{n-1}
end{array}
right), X_1=left( begin{array}{l}
x_1 \ x_2 \ vdots \ x_{n}
end{array}
right), X_2=left( begin{array}{l}
x_2 \ x_3 \ vdots \ x_{n+1}
end{array}
right), dots,
X_K=left( begin{array}{l}
x_K \ x_{K+1} \ vdots \ x_{K+n-1}
end{array}
right),dots ;
$$
Характеристический полином последовательности совпадает с характеристическим полиномом матрицы $ mathfrak F $, т.е. с $ lambda^n-a_1 lambda^{n-1} -a_2 lambda^{n-2} -dots — a_n $.
Метод степенных итераций используется в поисковике Google для вычисления PageRank.
Теперь обсудим исключительные случаи алгоритма.
1.
Нарушение сходимости итерационного процесса за счет неудачного выбора стартового вектора. Если в качестве $ Y_{0} $ оказался случайно взят собственный вектор $ mathfrak X_{ast} $ матрицы $ A_{} $, принадлежащий произвольному ее собственному числу $ lambda_{*} $, то предел последовательности из теоремы будет равен именно этому числу; если при этом $ |lambda_{*} | ne max_{1le j le n} | lambda_j | $, то мы выйдем за пределы смысла выражения «как правило». Понятно, что вероятность настолько плохого выбора нулевая, но и выбор $ Y_0 $ вблизи $ mathfrak X_{ast} $ также может существенно замедлить скорость сходимости. Поэтому если возникает ситуация медленной «стабилизации» значащих цифр в десятичном приближении собственного числа, попробуйте сменить начальный вектор.
2.
Нарушение условия
предположения
,
выдвинутого в начале пункта: максимальное по модулю собственное число неединственно.
П
Пример. Найти максимальное по модулю собственное число матрицы примера Леверье
$$
A=left(begin{array}{rrrr}
-5.509882&1.870086&0.422908&0.008814 \
0.287865&-11.811654&5.711900&0.058717 \
0.049099&4.308033&-12.970687&0.229326 \
0.006235&0.269851&1.397369&-17.596207
end{array}
right) .
$$
Решение. Для столбца $ Y_0=[1,0,0,0]^{^{top}} $ имеем
$$y_{1}^{[100]}/y_{1}^{[99]}=-17.8_{displaystyle 3113} ,$$
т.е. на $ 100 $-й итерации получаем лишь $ 3_{} $ истинные десятичные цифры в представлении собственного числа. При этом
компонентами векторов $ Y_{K} $ являются числа порядка $ 10^{123} $. Если мы
посмотрим на ответ примера Леверье, то увидим, что имеются два собственных числа матрицы, близких по модулю.
♦
К сожалению, вероятность того факта, что у случайно выбранной матрицы два ее собственных числа будут иметь одинаковый модуль становится ненулевой если эта матрица выбирается из множества вещественных матриц. Дело в том, что в этом случае ее характеристический полином будет иметь вещественные коэффициенты, а мнимые корни такого полинома всегда пáрные — для любого невещественного корня $ lambda_{ast}^{} $ полинома, комплексно сопряженное к нему число $ overline{lambda_{ast}} $ также будет корнем. При этом $ |lambda_{ast}|= |overline{lambda_{ast}} | $.
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
3 & 2 &7\
-2 & -8 & 2 \
5 & -3 & -2
end{array}
right)
$$
итерационная последовательность из теоремы ведет себя хаотически: при выборе $ Y_0=[1,0,0]^{top} $ получим
$$
left{frac{y_{1}^{[K+1]}}{y_{1}^{[K]}}right}_{K=1}^{infty} = 3; 13.3333; 5.9250;
4.6455; 15.9273; 0.8546; 68.0186;
$$
$$
0.4543; 91.7873; dots
$$
Спектр матрицы: $ { 6.9363, -6.9682pm 3.0186 mathbf i} $, и максимальное по модулю собственное число неединственно.
♦
Существуют приемы, позволяющие модифицировать метод на случай когда два числа спектра матрицы близки по модулю к максимальному; они подробно обсуждаются в [3].
Предположение 2
. Пусть два максимальных по модулю собственных числа матрицы разнесены по величине, например
$$ |lambda_1| > | lambda_2 | > | lambda_ j | quad npu j in {2,dots, n } . $$
Обобщение степенного метода основывается на использовании последовательностей из каких-то двух компонент векторов $ Y_{K+1}=AY_K $, например, наряду с уже использованной выше последовательностью первых компонент
$$y_{1}^{[1]},y_{1}^{[2]},dots,y_{1}^{[K]},dots $$
возьмем еще и аналогичную для вторых:
$$y_{2}^{[1]},y_{2}^{[2]},dots,y_{2}^{[K]},dots $$
Т
Теорема 26 [Эйткен]. При практически любом выборе стартового вектора $ Y_0 ne mathbb O $ для последовательности
$$
Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_{K}=Acdot Y_{K-1},dots ,
$$
имеет место равенство
$$
lambda_1 lambda_2 = lim_{Kto +infty} frac{left|begin{array}{ll} y_1^{[K+1]} & y_1^{[K+2]} \ y_2^{[K+1]} & y_2^{[K+2]} end{array} right|}
{left|begin{array}{ll} y_1^{[K]} & y_1^{[K+1]} \ y_2^{[K]} & y_2^{[K+1]} end{array} right|} , .
$$
Доказательство. Построим квадратное уравнение
$$ p_0x^2+p_1x+p_2 = 0 $$
имеющее корнями $ lambda_1 $ и $ lambda_2 $.
Если существует базис рпостранства $ mathbb C^n $
$$Y_0=alpha_1{mathfrak X}_1+alpha_2{mathfrak X}_2+dots+alpha_n{mathfrak X}_n .$$
Тогда последовательным домножением на матрицу $ A_{} $ получаем :
$$begin{array}{llll}
Y_K=& alpha_1 lambda_1^K{mathfrak X}_1 &+alpha_2 lambda_2^K{mathfrak X}_2+dots &+alpha_nlambda_n^K{mathfrak X}_n, \
Y_{K+1}=& alpha_1 lambda_1^{K+1}{mathfrak X}_1 &+alpha_2 lambda_2^{K+1}{mathfrak X}_2+dots &+alpha_nlambda_n^{K+1}{mathfrak X}_n,\
Y_{K+2}=& alpha_1 lambda_1^{K+2}{mathfrak X}_1 & +alpha_2 lambda_2^{K+2}{mathfrak X}_2+dots &+alpha_nlambda_n^{K+2}{mathfrak X}_n.
end{array}
$$
Отбрасываем из правых частей равенств слагаемые порядков возрастания ниже, чем $ lambda_2^K, lambda_2^{K+1}, lambda_2^{K+2} $ соответственно, домножаем получившиеся приближенные равенства
$$begin{array}{lll|l}
Y_K & approx alpha_1 lambda_1^K{mathfrak X}_1 &+alpha_2 lambda_2^K{mathfrak X}_2, & color{Red} times p_2 \
Y_{K+1}& approx alpha_1 lambda_1^{K+1}{mathfrak X}_1 &+alpha_2 lambda_2^{K+1}{mathfrak X}_2, & color{Red} times p_1\
Y_{K+2} & approx alpha_1 lambda_1^{K+2}{mathfrak X}_1 & +alpha_2 lambda_2^{K+2}{mathfrak X}_2, & color{Red} times p_0
end{array}
$$
и складываем:
$$ p_2 Y_K + p_1Y_{K+1} + p_0 Y_{K+2} approx mathbb O , . $$
В получившемся векторном равенстве выбираем первые две компоненты:
$$
left{
begin{array}{ll}
p_2 y_1^{[K]} + p_1 y_1^{[K+1]} + p_0 y_1^{[K+2]} approx 0 , , \
p_2 y_2^{[K]} + p_1 y_2^{[K+1]} + p_0 y_2^{[K+2]} approx 0 , ,
end{array}
right.
$$
которые и позволят определить приближенное значение набора $ p_0,p_1,p_2 $. С точностью до числового сомножителя, искомый полином можно представить в виде определителя
$$
p_0x^2+p_1x+p_2 approx
left|begin{array}{lll}
y_1^{[K]} & y_1^{[K+1]} & y_1^{[K+2]} \
y_2^{[K]} & y_2^{[K+1]} & y_2^{[K+2]} \
1 & x & x^2
end{array}
right| , .
$$
Формулы Виета завершат доказательство.
♦
=>
При выполнении условия
предположения 2
имеет место равенство
$$ lambda_2 =
lim_{Kto +infty} frac{left|begin{array}{ll} y_1^{[K+1]} & y_1^{[K+2]} \ y_2^{[K+1]} & y_2^{[K+2]} end{array} right| y_{1}^{[K+1]}}
{left|begin{array}{ll} y_1^{[K]} & y_1^{[K+1]} \ y_2^{[K]} & y_2^{[K+1]} end{array} right| y_{1}^{[K+2]} } , .
$$
П
Пример. Для матрицы
$$
A=left(begin{array}{rrr}
2 & 3 &-1\
7 & 3 & 3 \
-1 & -2 & 4
end{array}
right)
$$
найти первые два по порядку убывания модулей собственных числа.
Решение. Для $ Y_0= [1,0,0]^{top} $ имеем:
$$
Y_1=left( begin{array}{r} 2 \ 7 \ -1 end{array} right),
Y_2=left( begin{array}{r} 26 \ 32 \ -20 end{array} right), dots,
$$
$$
Y_{18}=left( begin{array}{r} {scriptstyle 164983395620948} \ {scriptstyle 156537857759336} \ -{scriptstyle 219402049179956} end{array} right),
Y_{19}=left( begin{array}{r} {scriptstyle 1018982413699860} \ {scriptstyle 966291195084776} \ -{scriptstyle 1355667307859444} end{array} right),
Y_{20}=left( begin{array}{r} {scriptstyle 6292505720513492} \ {scriptstyle 5964748557575016} \ -{scriptstyle 8374234035307188} end{array} right), .
$$
Таким образом,
$$
lambda_1 approx frac{y_1^{[20]}}{y_1^{[19]}}= frac{1573126430128373}{254745603424965} approx mathbf{6.17}_5 ,
$$
$$
lambda_2 approx
frac{left|begin{array}{ll} y_1^{[19]} & y_1^{[20]} \ y_2^{[19]} & y_2^{[20]} end{array} right| y_{1}^{[19]}}
{left|begin{array}{ll} y_1^{[18]} & y_1^{[19]} \ y_2^{[18]} & y_2^{[19]} end{array} right| y_{1}^{[20]} }=
frac{300892177677465751832368453246033765185}{67074186846991590001957412392957971737 }
approx mathbf{4.48}_5
$$
♦
Обобщение этого подхода для поиска следующих по убыванию модулей собственных чисел проводится по аналогии с деления-вычитания вычисления корня полинома. Кстати, теоретически можно довести этот метод и до построения характеристического (точнее, минимального аннулирующего) полинома матрицы: при любом $ K in {0,1,2,dots } $ определитель
$$
left|begin{array}{llll}
y_1^{[K]} & y_1^{[K+1]} & dots & y_1^{[K+n]} \
y_2^{[K]} & y_2^{[K+1]} & dots & y_2^{[K+n]} \
vdots & vdots & & vdots \
y_n^{[K]} & y_n^{[K+1]} & dots & y_n^{[K+n]} \
1 & lambda & dots & lambda^n
end{array}
right|=
det left[begin{array}{c|c|c|c|c}
Y_K&Y_{K+1}&dots&Y_{K+n-1}&Y_{K+n}\
1& lambda&dots&lambda^{n-1}&lambda^n
end{array}
right]
$$
совпадает — с точностью до числового сомножителя — с $ det (A-lambda E) $. И мы вернулись к
☝
методу Крылова вычисления характеристического полинома!
Для случая симметричной матрицы альтернативное обобщение степенного метода для поиска ранжированных по убыванию модулей собственных чисел и соответствующих им собственных векторов разбирается
☞
ЗДЕСЬ.
Задачи
Источники
[1]. Островский А.М. Решение уравнений и систем уравнений. М. ИЛ, 1963, c. 137-142
[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94
[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960
[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989
Нахождение собственных чисел и собственных векторов
Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.
Больше:
Выводить десятичную дробь
,
- Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.
-
Элементы матриц — десятичные (конечные и периодические) дроби:
1/3,3,14,-1,3(56)или1,2e-4; либо арифметические выражения:2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2).-
decimal (finite and periodic) fractions:
1/3,3,14,-1,3(56)или1,2e-4 -
2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2) -
matrix literals:
{{1,3},{4,5}} -
operators:
+,-,*,/,,!,^,^{*},,,;,≠,=,⩾,⩽,>и< -
functions:
sqrt,cbrt,exp,log,abs,conjugate,min,max,gcd,rank,adjugate,inverse,determinant,transpose,pseudoinverse,cos,sin,tan,cot,cosh,sinh,tanh,coth,arccos,arcsin,arctan,arccot,arcosh,arsinh,artanhиarcoth -
units:
rad,deg -
special symbols:
pi,e,i— mathematical constantsk,n— integersIorE— identity matrixX,Y— matrix symbols
-
- Используйте ↵ Ввод, Пробел, ←↑↓→, Backspace и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V — для копирования матриц.
- Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
- За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.
Примеры
- Найти собственные векторы
({{-26,-33,-25},{31,42,23},{-11,-15,-4}})

