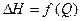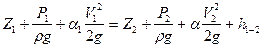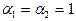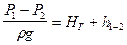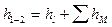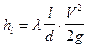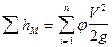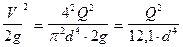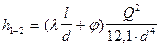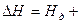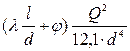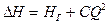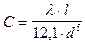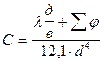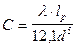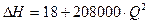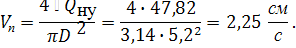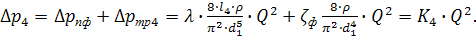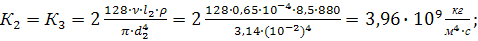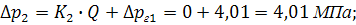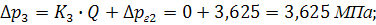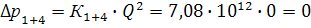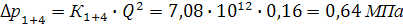В гидравлических расчетах простых и
сложных трубопроводов используют
графические методы, которые во многих
случаях облегчают решение задач. Эти
методы основаны на графическом построении
характеристик трубопроводов.
Характеристикой трубопровода называется
график зависимости суммарных потерь
напора в трубопроводе от расхода.
Для простого трубопровода потери равны
требуемому напору, который в общем
случае может быть найден по формуле
(11.1)
,
которая
при заданных значениях l,
d,
∑ζi,
Кэ однозначно
отражает зависимость напора Н от расхода
Q.
Д
(11.2)
ля квадратной области зависимость
(11.1) переходит в следующую
hW
= H = KQ2
,
а если учитывать
только сопротивления по длине, то (11.2)
примет вид
h
(11.3)
W
= H = A · l · Q2
Зависимости
(11.1) и (11.2) возможно представить в
координатах H
– Q,
задавая ряд значений Q
и определяя соответствующие им значения
Н.
Рис.11.1
Рис.
11.2
Полученная
на рис. 11.1 кривая представляет
геометрический образ характеристики
трубопровода. Если помимо гидравлических
сопротивлений необходимо еще преодолеть
геометрический напор Нг
(высоту Нг
или эквивалентную разность давлений),
то график (характеристика трубопровода)
будет иметь вид как на рис. 11.2 (Н = Нг
при Q=0).
П
ример.Рассмотрим расчет
параллельного соединения простых
трубопроводов в общем случае, когда
заранее неизвестны зоны сопротивления
в ветвях. Допустим, что имеются три ветви
(число их на ход расчета не влияет).
Заданы:общий
расход и параметры каждой из ветвей.
Необходимо найти потери напора и расход
в каждой из них.
Д
Рис.
11.3
ля решения задачи строим на одном
графике в координатахH–Qхарактеристики всех
ветвей, рис. 11.3 (в общем случае все они
будут разные). Затем строим результирующую
характеристику по нескольким точкам.
Для этого при некотором значении Н,
одинаковом для всех характеристик
суммируем расходы и получаем точку для
построения результирующей характеристики.
После того, как она построена по нескольким
точкам, откладываем на осиQзаданный суммарный (общий) расход,
находим искомое значение Н и по каждой
из характеристик ветвей находим значения
расходовQ1,Q2иQ3.
Задача 11.1.Построить характеристику трубопровода,
по которому при ламинарном режиме
жидкость перетекает из одного резервуара
в другой при постоянной разности уровней
Н (принять, что местные потери отсутствуют
и давление на свободной поверхности
резервуаров атмосферное).
УказаниеУчесть
выражение для λ при ламинарном режиме
в формуле
.
12. Трубопроводы с насосной подачей жидкости
Рассмотрим совместную работу трубопровода
с насосом (такая система еще называется
– трубопровод с насосной подачей). В
общем случае это трубопровод, по которому
насос перекачивает жидкость из нижнего
резервуара с давлением на поверхности
р0в другой резервуар с давлением
на поверхности рз, рис. 12.1
|
|
Высота Высота |
Составим уравнение Бернулли для потока
во всасывающем трубопроводе, т. е. для
сечений 0 – 0 и 1 – 1 (принимается α=1):
(12.1)
Это уравнение является основным для
расчета всасывающих трубопроводов. Оно
показывает, что процесс всасывания, т.
е. подъем жидкости на высоту Н1,
сообщение ей кинетической энергии и
преодоление всех гидравлических
сопротивлений происходит за счет
использования (с помощью насоса) давления
р0. Во время работы насоса на его
входе создается вакуум и жидкость под
действием разности давлений (атмосферного
и низкого давления на входе) поступает
в насос. Возможны следующие задачи
расчета всасывающего трубопровода.
Задача 1.Даны все геометрические
параметры трубопровода и расход.
Требуется найти абсолютное давление
перед входом в насос.
Решение этой задачи представляет
поверочный расчет всасывающего
трубопровода. Абсолютное давление Р1,
полученное по уравнению (12.1) сравнивают
с тем, которое является минимально
допустимым.
Задача 2. Дано минимально допустимое
абсолютное давление перед входом в
насос Р1.
Требуется найти одну из следующих
предельных величин: H1min,
Qmax,
dmin,
p0min.Эта задача также решается с помощью
уравнения (12.1).
Для уравнения запишем уравнение Бернулли
для напорного трубопровода, т. е. для
сечений 2 – 2 и 3 – 3:
(12.2)
Левая часть уравнения (12.2) представляет
энергию жидкости на выходе из насоса,
отнесенную к единице веса. Энергия
жидкости перед входом в насос может
быть найдена из уравнения (12.1)
(12.3)
найдем приращение энергии жидкости в
насосе, т. е. определим ту энергию, которую
приобретает, проходя через насос каждая
единица веса. Эта энергия сообщается
жидкости насосом, поэтому она носит
название напора, создаваемого насосоми обозначается обычно Ннас.
Для определения Ннасвычтем
уравнение (12.3) из уравнения (12.2)
или
(12.4)
где Δz– полная геометрическая
высота подъема жидкости, Σhw
– сумма гидравлических потерь во
всасывающем и напорном трубопроводах.
Если к действительной разности уровней
Δzприбавить разность
пьезометрических высот (p3–p0)/ρg,
то можно рассматривать как бы увеличенную
разность уровней
и
(12.5)
(12.4) примет вид
Ннас = Нст
+ Σhw
С
(12.6)
равнивая (12,5) с основным уравнением
для расчета простого трубопровода,
получим
Ннас = Н.
Это равенство можно распространить на
все случаи устойчивой работы насоса,
соединенного с трубопроводом и
сформулировать в виде правила: при
установившемся течении в трубопроводе
насос развивает напор, равный требуемому.
На равенстве (12.6) основывается метод
расчета трубопроводов, питаемых насосом,
который заключается в совместном
построении, в одном масштабе и на одном
графике двух кривых: напора H=f1(Q)по (12.5) – это фактически характеристика
всех трубопроводов и характеристики
насосаHнас=f2(Q)и в нахождении точки их пересечения,
рис. 12.2.
Характеристикой насоса называется
зависимость напора, создаваемого
насосом, от его подачи расхода жидкости.
В точке пересечения кривой напора Н по
(12.5) и характеристики насоса имеем
равенство между требуемым напором и
напором, создаваемым насосом. Эта точка
называется рабочей точкой, так как
всегда реализуется режим работы насоса,
ей соответствующий. Чтобы получить
другую рабочую точку, необходимо или
изменить открытие регулировочного
крана (вентиля, задвижки), т. е. изменить
характеристику трубопровода или изменить
частоту вращения вала насоса (т. е.
изменить характеристику насоса).
Задача 12.1:
Показать, что насос не может работать
в режиме, отличном от режима А, рис 12.2.
|
Рис.12.2. |
Решение: |
Если предположить,
что сообщаемый насосом напор меньше
требуемого. Недостаток энергии
восполняется за счет собственной
кинетической энергии жидкости. Это
приводит к уменьшению скорости движения
и, следовательно, к уменьшению расхода
до QA.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5 ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ
5.1 Простой трубопровод постоянного сечения
Трубопровод называется простым, если он не имеет ответвлений. Простые трубопроводы могут образовывать соединения: последовательное, параллельное или разветвленное. Трубопроводы могут быть сложными, содержащими как последовательное, так и параллельное соединения или разветвления.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад (разность) уровней энергии может быть создан тем или иным способом: работой насоса, благодаря разности уровней жидкости, давлением газа. В машиностроении приходится иметь дело главным образом с трубопроводами, движение жидкости в которых обусловлено работой насоса.
При гидравлическом расчете трубопровода чаще всего определяется его потребный напор Hпотр — величина, численно равная пьезометрической высоте в начальном сечении трубопровода. Если потребный напор задан, то его принято называть располагаемым напором Hрасп. В этом случае при гидравлическом расчете может определяться расход Q жидкости в трубопроводе или его диаметр d. Значение диаметра трубопровода выбирается из установленного ряда в соответствии с ГОСТ 16516—80.
Пусть простой трубопровод постоянного проходного сечения, произвольно расположенный в пространстве (рисунок 5.1, а), имеет общую длину l и диаметр d и содержит ряд местных гидравлических сопротивлений I и II.
Запишем уравнение Бернулли для начального 1-1 и конечного 2-2 сечений этого трубопровода, считая, что коэффициенты Кориолиса в этих сечениях одинаковы (α1=α2). После сокращения скоростных напоров получим

Рекомендуемые материалы
где z1, z2 — координаты центров тяжести соответственно начального и конечного сечений;
p1, p2 — давления в соответственно начальном и конечном сечениях трубопровода;

Отсюда потребный напор

Как видно из полученной формулы, потребный напор складывается из суммарной геометрической высоты Δz = z2 – z1, на которую поднимается жидкость в процессе движения по трубопроводу, пьезометрической высоты в конечном сечении трубопровода и суммы гидравлических потерь напора, возникающих при движении жидкости в нем.
В гидравлике принято под статическим напором трубопровода понимать сумму 

Рисунок 5.1 – Простой трубопровод:
а – расчетная схема; б – характеристики потребного напора при ламинарном режиме течения;
в – то же при турбулентном режиме
Тогда, представляя суммарные потери 

где т — величина, зависящая от режима течения жидкости в трубопроводе;
К — сопротивление трубопровода.
При ламинарном режиме течения жидкости и линейных местных сопротивлениях (заданы их эквивалентные длины lэкв) суммарные потери

где lрасч = l + lэкв — расчетная длина трубопровода.
Следовательно, при ламинарном режиме т = 1, 
При турбулентном течении жидкости

Заменяя в этой формуле среднюю скорость жидкости через расход, получим суммарные потери напора

Тогда при турбулентном режиме 

Поступая аналогично в каждом конкретном случае, после несложных алгебраических преобразований и вычислений можно получить формулу, определяющую аналитическую зависимость потребного напора для данного простого трубопровода от расхода в нем. Примеры таких зависимостей в графическом виде приведены на рисунке 5.1, б, в.
Анализ формул, приведенных выше, показывает, что решение задачи по определению потребного напора Hпотр при известных расходе Q жидкости в трубопроводе и его диаметре d несложно, так как всегда можно провести оценку режима течения жидкости в трубопроводе, сравнивая критическое значение Reкp = 2300 с его фактическим значением, которое для труб круглого сечения может быть вычислено по формуле

После определения режима течения можно вычислить потери напора, а затем потребный напор по формуле (5.2).
Если же величины Q или d неизвестны, то в большинстве случаев сложно оценить режим течения, а, следовательно, обоснованно выбрать формулы, определяющие потери напора в трубопроводе. В такой ситуации можно рекомендовать использовать либо метод последовательного приближения, обычно требующий достаточно большого объема вычислительной работы, либо графический метод, при применении которого необходимо строить так называемую характеристику потребного напора трубопровода.
5.2. Построение характеристики потребного напора простого трубопровода
Графическое представление в координатах Н—Q аналитической зависимости (5.2), полученной для данного трубопровода, в гидравлике называется характеристикой потребного напора. На рисунке 5.1, б, в приведено несколько возможных характеристик потребного напора (линейные — при ламинарном режиме течения и линейных местных сопротивлениях; криволинейные — при турбулентном режиме течения или наличии в трубопроводе квадратичных местных сопротивлений).
Как видно на графиках, значение статического напора Нст может быть как положительным (жидкость подается на некоторую высоту Δz или в конечном сечении существует избыточное давление p2), так и отрицательным (при течении жидкости вниз или при ее движении в полость с разрежением).
Крутизна характеристик потребного напора зависит от сопротивления трубопровода и возрастает с увеличением длины трубы и уменьшением ее диаметра, а также зависит от количества и характеристик местных гидравлических сопротивлений. Кроме того, при ламинарном режиме течения рассматриваемая величина пропорциональна еще и вязкости жидкости. Точка пересечения характеристики потребного напора с осью абсцисс (точка А на рисунке 5.1, б, в) определяет расход жидкости в трубопроводе при движении самотеком.
Графические зависимости потребного напора широко используются для определения расхода Q при расчете как простых трубопроводов, так и сложных. Поэтому рассмотрим методику построения такой зависимости (рисунок 5.2, а). Она состоит из следующих этапов.
1-й этап. Используя формулу (5.4) определяем значение критического расхода Qкр, соответствующее Reкp=2300, и отмечаем его на оси расходов (ось абсцисс). Очевидно, что для всех расходов, расположенных левее Qкр, в трубопроводе будет ламинарный режим течения, а для расходов, расположенных правее Qкр, — турбулентный.
2-й этап. Рассчитываем значения потребного напора Н1 и Н2 при расходе в трубопроводе, равном Qкр, соответственно предполагая, что Н1 — результат расчета при ламинарном режиме течения, а Н2 — при турбулентном.
3-й этап. Строим характеристику потребного напора для ламинарного режима течения (для расходов, меньших Qкр). Если местные сопротивления, установленные в трубопроводе, имеют линейную зависимость потерь от расхода, то характеристика потребного напора имеет линейный вид.
4-й этап. Строим характеристику потребного напора для турбулентного режима течения (для расходов, больших Qкp). Во всех случаях получается криволинейная характеристика, близкая к параболе второй степени.
Имея характеристику потребного напора для данного трубопровода, можно по известному значению располагаемого напора Hрасп найти искомое значение расхода Qx (см. рисунок 5.2, а).
Если же необходимо найти внутренний диаметр трубопровода d, то, задаваясь несколькими значениями d, следует построить зависимость потребного напора Hпотр от диаметра d (рис. 5.2, б). Далее по значению Нрасп выбирается ближайший больший диаметр из стандартного ряда dст.
В ряде случаев на практике при расчете гидросистем вместо характеристики потребного напора используют характеристику трубопровода. Характеристика трубопровода — это зависимость суммарных потерь напора в трубопроводе от расхода. Аналитическое выражение этой зависимости имеет вид

Сравнение формул (5.5) и (5.2) позволяет заключить, что характеристика трубопровода отличается от характеристики потребного напора отсутствием статического напора Hст, а при Hст = 0 эти две зависимости совпадают.
5.3 Соединения простых трубопроводов.
Аналитические и графические способы расчета
Рассмотрим способы расчета соединений простых трубопроводов.
Пусть имеем последовательное соединение нескольких простых трубопроводов (1, 2 и 3 на рисунке 5.3, а) различной длины, разного диаметра, с различным набором местных сопротивлений. Так как эти трубопроводы включены последовательно, то в каждом из них имеет место один и тот же расход жидкости Q. Суммарная потеря напора для всего соединения (между точками М и N) 




Рисунок 5.3 — Схема последовательного (а), параллельного (в) и сложного (д) соединений трубопроводов и соответствующие им характеристики (б, г, е):
1,2,3 — трубопроводы
Потери напора в каждом простом трубопроводе могут быть определены через значения соответствующих расходов:



Система уравнений (5.6), дополненная зависимостями (5.7), является основой для аналитического расчета гидросистемы с последовательным соединением трубопроводов.
Если используется графический метод расчета, то при этом возникает необходимость в построении суммарной характеристики соединения.
На рисунке 5.3, б показан способ получения суммарной характеристики последовательного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).
Для построения точки, принадлежащей суммарной характеристике последовательного соединения, необходимо в соответствии с (5.6) сложить потери напора в исходных трубопроводах при одинаковом расходе. С этой целью на графике проводят произвольную вертикальную линию (при произвольном расходе Q‘). По этой вертикали суммируют отрезки (потери напора 


Параллельным называется соединение трубопроводов, имеющих две общие точки (точку разветвления и точку смыкания). Пример параллельного соединения трех простых трубопроводов приведен на рисунке 5.3, в. Очевидно, что расход Q жидкости в гидросистеме до разветвления (точка М) и после смыкания (точка N) один и тот же и равен сумме расходов Q1, Q2 и Q3 в параллельных ветвях.
Если обозначить полные напоры в точках M и N через НM и HN, то для каждого трубопровода потеря напора равна разности этих напоров:



т. е. в параллельных трубопроводах потери напора всегда одинаковы. Это объясняется тем, что при таком соединении, несмотря на разные гидравлические сопротивления каждого простого трубопровода, расходы Q1, Q2 и Q3 распределяются между ними так, что потери остаются равными.
Таким образом, система уравнений для параллельного соединения имеет вид

Потери напора в каждом трубопроводе, входящем в соединение, могут быть определены по формулам вида (5.7). Таким образом, система уравнений (5.8), дополненная формулами (5.7), является основой для аналитического расчета гидросистем с параллельным соединением трубопроводов.
На рисунке 5.3, г показан способ получения суммарной характеристики параллельного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).
Для получения точки, принадлежащей суммарной характеристике параллельного соединения, необходимо в соответствии с (5.8) сложить расходы в исходных трубопроводах при одинаковых потерях напора. С этой целью на графике проводят произвольную горизонтальную линию (при произвольной потере 
По аналогичному методу строятся суммарные характеристики для разветвленных трубопроводов. Разветвленным соединением называется совокупность нескольких трубопроводов, имеющих одну общую точку (место разветвления или смыкания труб).
Рассмотренные выше последовательное и параллельное соединения, строго говоря, относятся к разряду сложных трубопроводов. Однако в гидравлике под сложным трубопроводом, как правило, понимают соединение нескольких последовательно и параллельно включенных простых трубопроводов.
На рисунке 5.3, д приведен пример такого сложного трубопровода, состоящего из трех трубопроводов 1, 2 и 3. Трубопровод 1 включен последовательно по отношению к трубопроводам 2 и 3. Трубопроводы 2 и 3 можно считать параллельными, так как они имеют общую точку разветвления (точка М) и подают жидкость в один и тот же гидробак.
Для сложных трубопроводов расчет, как правило, проводится графическим методом. При этом рекомендуется следующая последовательность:
1) сложный трубопровод разбивается на ряд простых трубопроводов;
2) для каждого простого трубопровода строится его характеристика;
3) графическим сложением получают характеристику сложного трубопровода.
На рисунке 5.3, е показана последовательность графических построений при получении суммарной характеристики (





Имея построенный таким образом график (см. рисунок 5.3, е) для сложного трубопровода, можно достаточно просто по известному значению расхода Q1, поступающего в гидросистему, определить потребный напор Hпотр = 



5.4 Трубопровод с насосной подачей
Как уже отмечалось, основным способом подачи жидкости в машиностроении является принудительное нагнетание ее насосом. Насосом называется гидравлическое устройство, преобразующее механическую энергию привода в энергию потока рабочей жидкости. В гидравлике трубопровод, в котором движение жидкости обеспечивается за счет насоса, называется трубопроводом с насосной подачей (рисунок 5.4, а).
Целью расчета трубопровода с насосной подачей, как правило, является определение напора, создаваемого насосом (напора насоса). Напором насоса Нн называется полная механическая энергия, переданная насосом единице веса жидкости. Таким образом, для определения Нн необходимо оценить приращение полной удельной энергии жидкости при прохождении ее через насос, т.е.

где Нвх, Нвых — удельная энергия жидкости соответственно на входе и выходе из насоса.
Рассмотрим работу разомкнутого трубопровода с насосной подачей (см. рисунок 5.4, а). Насос перекачивает жидкость из нижнего резервуара А с давлением над жидкостью p0 в другой резервуар Б, в котором давление р3. Высота расположения насоса относительно нижнего уровня жидкости H1 называется высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом, или гидролинией всасывания. Высота расположения конечного сечения трубопровода или верхнего уровня жидкости Н2 называется высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным, или гидролинией нагнетания.
 |
Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1:

где 
Уравнение (5.10) является основным для расчета всасывающих трубопроводов. Давление p0 обычно ограничено (чаще всего это атмосферное давление). Поэтому целью расчета всасывающего трубопровода, как правило, является определение давления перед насосом. Оно должно быть выше давления насыщенных паров жидкости. Это необходимо для исключения возникновения кавитации на входе в насос. Из уравнения (5.10) можно найти удельную энергию жидкости на входе в насос:

Запишем уравнение Бернулли для потока жидкости в напорном трубопроводе, т. е. для сечений 2-2 и 3-3:

где 
Левая часть этого уравнения представляет собой удельную энергию жидкости на выходе из насоса Hвых. Подставив в (5.9) правые части зависимостей (5.11) для Hвх и (5.12) для Hвых, получим

Как следует из уравнения (5.13), напор насоса Hн обеспечивает подъем жидкости на высоту (Н1+H2), повышение давления с р0 до p3 и расходуется на преодоление сопротивлений во всасывающем и напорном трубопроводах.
Если в правой части уравнения (5.13) 

Сравним последнее выражение с формулой (5.2), определяющей потребный напор для трубопровода. Очевидна их полная идентичность:

т.е. насос создает напор, равный потребному напору трубопровода.
Полученное уравнение (5.14) позволяет аналитически определить напор насоса. Однако в большинстве случаев аналитический способ достаточно сложен, поэтому получил распространение графический метод расчета трубопровода с насосной подачей.
Этот метод заключается в совместном построении на графике характеристики потребного напора трубопровода 


На рисунке 5.4, б приведен пример такого графического решения. Здесь точка А и есть искомая рабочая точка гидросистемы. Ее координаты определяют напор Hн, создаваемый насосом, и расход Qн жидкости, поступающей от насоса в гидросистему.
Если по каким-то причинам положение рабочей точки на графике не устраивает проектировщика, то это положение можно изменить, если скорректировать какие-либо параметры трубопровода или насоса.
7.5. Гидравлический удар в трубопроводе
Гидравлическим ударом называется колебательный процесс, возникающий в трубопроводе при внезапном изменении скорости жидкости, например при остановке потока из-за быстрого перекрытия задвижки (крана).
Этот процесс очень быстротечен и характеризуется чередованием резкого повышения и понижения давления, что может привести к разрушению гидросистемы. Это вызвано тем, что кинетическая энергия движущегося потока при остановке переходит в работу по растяжению стенок труб и сжатию жидкости. Наибольшую опасность представляет начальный скачок давления.
Проследим стадии гидравлического удара, возникающего в трубопроводе при быстром перекрытии потока (рисунок 7.5).
Пусть в конце трубы, по которой жидкость движется со скоростью vq, произведено мгновенное закрытие крана А. Тогда (см. рисунок 7.5, а) скорость частиц жидкости, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается. Давление в остановившейся жидкости возрастает на Δpуд. На заторможенные частицы жидкости у крана набегают другие частицы и тоже теряют скорость, в результате чего сечение п—п перемещается вправо со скоростью с, называемой скоростью ударной волны, сама же переходная область (сечение п—п), в которой давление изменяется на величину Δpуд, называется ударной волной.
Когда ударная волна достигнет резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления Δpуд распространится на всю трубу (см. рис. 7.5, б).
Но такое состояние не является равновесным. Под действием повышенного давления (р0 + Δpуд) частицы жидкости устремятся из трубы в резервуар, причем это движение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение п—п перемещается по трубопроводу в обратном направлении — к крану — с той же скоростью с, оставляя за собой в жидкости давление p0 (см. рисунке 7.5, в).
Рисунок 7.5 — Стадии гидравлического удара в трубопроводе
Жидкость и стенки трубы возвращаются к начальному состоянию, соответствующему давлению p0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость 
С этой скоростью «жидкая колонна» (см. рисунок 7.5, г) стремится оторваться от крана, в результате возникает отрицательная ударная волна (давление в жидкости уменьшается на то же значение Δpуд). Граница между двумя состояниями жидкости направляется от крана к резервуару со скоростью с, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость (см. рисунок 7.5, д). Кинетическая энергия жидкости вновь переходит в работу деформации, но с противоположным знаком.
Состояние жидкости в трубе в момент прихода отрицательной ударной волны к резервуару показано на рисунке 7.5, е. Так же как и для случая, изображенного на рисунке 7.5, б, оно не является равновесным, так как жидкость в трубе находится под давлением (р0 + Δpуд), меньшим, чем в резервуаре. На рисунке 7.5, ж показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью 
Очевидно, что как только отраженная от резервуара ударная волна достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Теоретическое и экспериментальное исследования гидравлического удара в трубах было впервые выполнено Н.Е.Жуковским. В его опытах было зарегистрировано до 12 полных циклов с постепенным уменьшением Δpуд. В результате проведенных исследований Н.Е.Жуковский получил аналитические зависимости, позволяющие оценить ударное давление Δpуд. Одна из этих формул, получившая имя Н.Е.Жуковского, имеет вид

где скорость распространения ударной волны с определяется по формуле

Рекомендуем посмотреть лекцию «8. Постановка задачи идентификации».
где К — объемный модуль упругости жидкости; Е — модуль упругости материала стенки трубопровода; d и δ — соответственно внутренний диаметр и толщина стенки трубопровода.
Формула (7.14) справедлива при прямом гидравлическом ударе, когда время перекрытия потока tзакр меньше фазы гидравлического удара t0:

где l — длина трубы.
Фаза гидравлического удара t0 — это время, за которое ударная волна движется от крана к резервуару и возвращается обратно. При tзакр > t0 ударное давление получается меньше, и такой гидроудар называют непрямым.
При необходимости можно использовать известные способы «смягчения» гидравлического удара. Наиболее эффективным из них является увеличение времени срабатывания кранов или других устройств, перекрывающих поток жидкости. Аналогичный эффект достигается установкой перед устройствами, перекрывающими поток жидкости, гидроаккумуляторов или предохранительных клапанов. Уменьшение скорости движения жидкости в трубопроводе за счет увеличения внутреннего диаметра труб при заданном расходе и уменьшение длины трубопроводов (уменьшение фазы гидравлического удара) также способствуют снижению ударного давления.
Содержание: [Скрыть]
-
- 1. Постановка задачи
- 2. Основные положения гидравлического расчета
- 3. Подбор оптимального диаметра трубопровода
- 4. Расчет падения напора и гидравлического сопротивления
- 5. Расчет потерь давления
- 6. Примеры задач гидравлического расчета трубопровода с решениями
Постановка задачи
Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

- минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
- круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
- форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
- процесс изготовления труб круглой формы относительно простой и доступный.
Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.
Основными параметрами, характеризующими трубопровод являются:
- условный (номинальный) диаметр – DN;
- давление номинальное – PN;
- рабочее допустимое (избыточное) давление;
- материал трубопровода, линейное расширение, тепловое линейное расширение;
- физико-химические свойства рабочей среды;
- комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
- изоляционные материалы трубопровода.

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.
Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.
Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.
Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.
Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.
Основные положения гидравлического расчета
Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.
Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:
Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:
- ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
- переходный режим (2300<Re<4000), который характеризуется нестабильной структурой потока, когда отдельные слои жидкости перемешиваются;
- турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.
Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.
Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.
Подбор оптимального диаметра трубопровода
Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.
Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:
При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).
Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:
Расчет падения напора и гидравлического сопротивления
Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.
Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.
Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.
Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.
Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:
В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы:

Расчет потерь давления
Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.
Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:
Примеры задач гидравлического расчета трубопровода с решениями
Задача 1
В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м3/час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.
Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.
Исходные данные:
Расход Q = 80 м3/час = 80·1/3600 = 0,022 м3/с;
эффективный диаметр d = 24 мм;
длина трубы l = 32 м;
коэффициент трения λ = 0,028;
давление в аппарате Р = 2,2 бар = 2,2·105 Па;
общий напор Н = 20 м.
Решение задачи:
Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:
w=(4·Q) / (π·d2) = ((4·0,022) / (3,14·[0,024]2)) = 48,66 м/с
Потери напора жидкости в трубопроводе на трение определяются по уравнению:
HТ = (λ·l) / (d·[w2/(2·g)]) = (0,028·32) / (0,024·[48,66]2) / (2·9,81) = 0,31 м
Общие потери напора носителя рассчитываются по уравнению и составляют:
hп = H — [(p2-p1)/(ρ·g)] — Hг = 20 — [(2,2-1)·105)/(1000·9,81)] — 0 = 7,76 м
Потери напора на местные сопротивления определяется как разность:
7,76 — 0,31=7,45 м
Ответ: потери напора воды на местные сопротивления составляют 7,45 м.
Задача 2
По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.
Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10-5.
Исходные данные:
Скорость потока жидкости W = 2,0 м/с;
диаметр трубы d = 100 мм;
общий напор Н = 8 м;
относительная шероховатость 4·10-5.
Решение задачи:
Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.
Значение скоростного напора определяется по соотношению:
w2/(2·g) = 2,02/(2·9,81) = 0,204 м
Потери напора воды на местные сопротивления составят:
∑ζМС·[w2/(2·g)] = (4,1+1)·0,204 = 1,04 м
Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):
hп = H — (p2-p1)/(ρ·g) — = 8 — ((1-1)·105)/(1000·9,81) — 0 = 8 м
Полученное значение потери напора носителя на трение составят:
8-1,04 = 6,96 м
Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10-3 Па·с, плотность воды – 1000 кг/м3):
Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10-3) = 200000
Согласно рассчитанному значению Re, причем 2320 <Re< 10/e, по справочной таблице рассчитаем коэффициент трения (для режима гладкого течения):
λ = 0,316/Re0,25 = 0,316/2000000,25 = 0,015
Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:
l = (Hоб·d) / (λ·[w2/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м
Ответ:требуемая длина трубопровода составит 213,235 м.
Задача 3
В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м3/час. Длина прямого трубопровода l = 26 м, материал — сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.
Исходные данные:
Расход Q = 18 м3/час = 0,005 м3/с;
длина трубопровода l=26 м;
для воды ρ = 1000 кг/м3, μ = 653,3·10-6 Па·с (при Т = 40°С);
шероховатость стальной трубыε = 50 мкм;
коэффициент трения λ = 0,026;
Δp=0,01 МПа;
ΔH=1,2 м.
Решение задачи:
Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:
∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d5 = (8·26·0.005²)/(9,81·3,14²)· λ/d5 = 5,376·10-5·λ/d5
Выразим диаметр:
d5 = (5,376·10-5·λ)/∆H = (5,376·10-5·0,026)/1,2 = 1,16·10-6
d = 5√1,16·10-6 = 0,065 м.
Ответ: оптимальный диаметр трубопровода составляет 0,065 м.
Задача 4
Проектируются два трубопровода для транспортировки невязкой жидкости с предполагаемой производительностью Q1 = 18 м3/час и Q2 = 34 м3/час. Трубы для обоих трубопроводов должны быть одного диаметра.
Определите эффективный диаметр труб d, подходящих под условия данной задачи.
Исходные данные:
Q1 = 18 м3/час;
Q2 = 34 м3/час.
Решение задачи:
Определим возможный интервал оптимальных диаметров для проектируемых трубопроводов, воспользовавшись преобразованным видом уравнения расхода:
d = √(4·Q)/(π·W)
Значения оптимальной скорости потока найдем из справочных табличных данных. Для невязкой жидкости скорости потока составят 1,5 – 3,0 м/с.
Для первого трубопровода с расходом Q1 = 18 м3/час возможные диаметры составят:
d1min = √(4·18)/(3600·3,14·1,5) = 0,065 м
d1max = √(4·18)/(3600·3,14·3.0) = 0,046 м
Для трубопровода с расходом 18 м3/час подходят трубы с диаметром поперечного сечения от 0,046 до 0,065 м.
Аналогично определим возможные значения оптимального диаметра для второго трубопровода с расходом Q2 = 34 м3/час:
d2min = √(4·34)/(3600·3,14·1,5) = 0,090 м
d2max = √(4·34)/(3600·3,14·3) = 0,063 м
Для трубопровода с расходом 34 м3/час возможные оптимальные диаметром могут быть от 0,063 до 0,090 м.
Пересечение двух диапазонов оптимальных диаметров находится в интервале от 0,063 м до 0,065 м.
Ответ: для двух трубопроводов подходят трубы диаметром 0,063–0,065 м.
Задача 5
В трубопроводе диаметром 0,15 м при температуре Т = 40°C движется поток воды производительностью 100 м3/час. Определите режим течения потока воды в трубе.
Дано:
диаметр трубы d = 0,25 м;
расход Q = 100 м3/час;
μ = 653,3·10-6 Па·с (по таблице при Т = 40°С);
ρ = 992,2 кг/м3 (по таблице при Т = 40°С).
Решение задачи:
Режим течения потока носителя определяется по значению числа Рейнольдса (Re). Для расчета Re определим скорость движения потока жидкости в трубе (W), используя уравнение расхода:
W = Q·4/(π·d²) = [100/3600] · [4/(3,14·0,25²)] = 0,57 м/c
Значение числа Рейнольдса определим по формуле:
Re = (ρ·W·d)/μ = (992,2·0,57·0,25) / (653,3·10-6) = 216422
Критическое значение критерия Reкр по справочным данным равно 4000. Полученное значение Re больше указанного критического, что говорит о турбулентном характере течения жидкости при заданных условиях.
Ответ: режим потока воды – турбулентный.
Вывод уравнения гидравлической характеристики трубопровода.
При гидравлическом расчете трубопроводов весьма широко используется гидравлические методы расчета. Применение этого метода значительно облегчает и улучшает решение некоторых сложных задач, а в отдельных случаях (например, при исследовании совместной работы некоторых центробежных насосов на один общий трубопровод) является практически единственно возможным приемом, позволяющим получать искомое решение.
Гидравлической характеристикой трубопровода называется графическая зависимость напора, необходимого для перемещения жидкости по трубопроводу, от заданного расхода, т.е.
Для построения графической характеристики трубопровода необходимо знать уравнение, которым выражается интересующая нас зависимость.
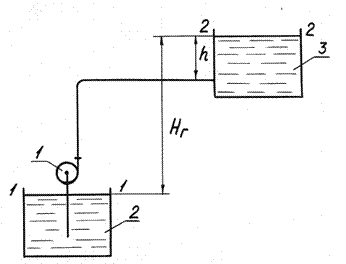
Рассмотрим схему насосной установки, подающей жидкость из одного резервуара в другой (рисунок. 1).
На рисунке представлена производная схема трубопровода, соединяющего приемный резервуар (2) с напорным резервуаром (3). Из рисунка видно, что напор, созданный в начальном сечении трубопровода насосом (1), затрачивается на:
— сообщение жидкости геометрического напора путем поднятия её с приемного резервуара в напорный;
— создание скоростного напора;
— преодоление гидравлических сопротивлений трубопровода;
— поддержание избыточного давления в конечном сечении трубопровода, которое необходимо для преодоления гидростатического давления в напорном резервуаре на уровень конечного сечения.
Величина гидростатического давления в напорном резервуаре определяется расстоянием h от оси трубопровода, входящего в резервуар 3, и равна
PK = 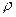
где PK — величина давления в конечном сечении трубопровода.
Для вывода уравнение, характеризующего зависимость
воспользуемся уравнением Бернулли для реальной жидкости и применим его к схеме насосной установки (рисунок 1).
Выберем два сечения, проходящих по свободной поверхности жидкости в резервуарах 2 и 3 (сечения 1-1 и 2-2). За плоскость отсчета принимаем свободную поверхность жидкости в резервуаре 2.
Для выбранных двух сечений напишем уравнение Бернулли
Проанализируем члены уравнения Бернулли:
z1=0 ; z2=НГ; 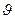
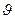
Тогда уравнение Бернулли примет вид
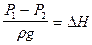
где 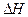
Потери напора между сечениями 1-1 и 2-2 складывается из суммы напора по длине трубопровода и суммы потерь напора на местные сопротивления:
Потер напора по длине трубопровода определяются по формуле Дарси-Вейсбаха
Потери напора на местные сопротивления определяются из выражения :
Тогда общие потери будут равны
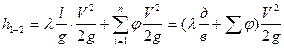
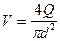

С учетом принятых значений 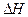
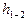

Обозначим 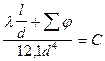
где 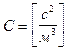
Характеристический коэффициент определяется длиной трубопровода, его диаметром, шероховатостью, местными сопротивлениями и для данного трубопровода является постоянной величиной.
Окончательное уравнение гидравлической характеристики трубопровода имеет вид
Для полевых магистральных трубопроводов потеря напора на местные сопротивления по сравнению с потерями по длине трубопровода являются незначительными и при гидравлических расчетах ПМТ ими пренебрегают. С учетом этого характеристический коэффициент для ПМТ имеет вид
По виду уравнение
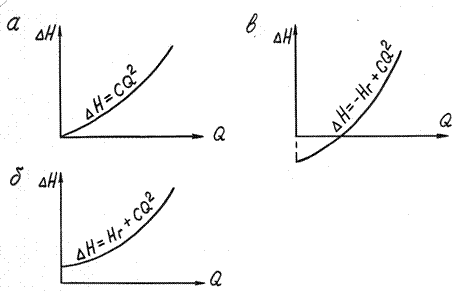
можно заключить, что гидравлическая характеристика трубопровода представляет собой параболу, симметричную относительно вертикальной оси, направленную выпуклостью вниз с вершиной, смещенной относительно начала координат на величину НГ.
Если конечное сечение трубопровода размещено на одном уровне с начальным сечением трубопровода относительно плоскости отсчета (т.е. Z2-Z1=0), тогда геометрическая высота НГ равна нулю, а вершина параболы совпадает с началом осей координат (рисунок 2а).
Если конечное сечение трубопровода расположено выше начального сечения, тогда геометрическая высота НГ будет иметь знак плюс и вершина параболы будет лежать выше начала координат на величину Z2-Z1 (рисунок 2б).
Если конечное сечение трубопровода лежит ниже начального сечения трубопровода, тогда геометрическая высота НГ будет иметь знак минус и вершина параболы будет лежать ниже начала координат на величину Z2-Z1 (рисунок 2в).
Гидравлическая характеристика трубопровода может выражаться одним из трех графиков (рисунок 2 а,б,в.)
Вывод по первому вопросу
Полученное уравнение гидравлической характеристики может быть использовано при решении задач по определению режимов работы насосных агрегатов на трубопровод.
2. Методика построения гидравлической характеристики трубопровода.
Чтобы построить график гидравлической характеристики трубопровода необходимо выдержать следующую последовательность.
1. Вычислить характеристический коэффициент “С” и составить уравнение.
Характеристический коэффициент определяют по формуле:
Если вместо коэффициентов местных сопротивлений дана эквивалентная длина местных сопротивлений, то в уравнение подставляется расчетная длина трубопровода lp , которая равна
где l — фактическая длина трубопровода;
lэ — эквивалентная длина местных сопротивлений.
Тогда уравнение для определения характеристического коэффициента трубопровода примет вид
При составлении расчетного уравнения
в него подставляются значение Нг и определено по уравнению значение С.
2. Задаться расходом жидкости Q и вычислить для каждого заданного значения расхода Q значение 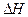
а) расход жидкости не задан. Тогда задаются произвольным значением расхода по арифметической прогрессии, начиная с нуля, с одной и той же разностью;
б)расход жидкости задан. Тогда заданный расход необходимо взять в “вилку” расходов, начиная с нуля.
3. Построить гидравлическую характеристику трубопровода.
Для этого выбирают два масштаба — горизонтальный по оси расхода в м 2 /с и вертикальный для разности напоров в метрах. Нанести точки и соединить их плавной кривой.
Методику построения гидравлических характеристик трубопровода рассмотрим на примере практического решения задачи.
ЗАДАЧА.
Построить гидравлическую характеристику трубопровода, подающего автобензин, если :
— длина трубопровода l=6000 м
— диаметр d=150 мм
— геометрическая высота Нг=18 м
— коэффициент Дарси 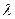
— эквивалентная длина местных сопротивлений lэ=4% от l
1. Вычислим характеристический коэффициент С и составим расчетное уравнение
lp = l + lэ=6000 + 240 = 6240 м
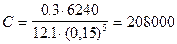
Расчетное уравнение будет иметь вид
2. Задаемся расходом и вычисляем
| Q м 3 /с | 0.004 | 0.008 | 0.012 | 0.016 | 0.02 |
| H м |
При Q2=0/004 H2= 18+208000*(0.004) 2 = 21 м и т.д.
— горизонтальный — в 1 см — 0.004 м 3 /с
— вертикальный — в 1 см — 10 м
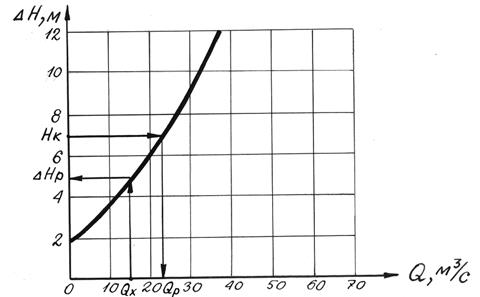
3. Строим гидравлическую характеристику трубопровода (рисунок 3).
По построенной характеристике мы можем для данного трубопровода решать следующие задачи без вычислений :
— определять необходимый напор для перекачки горючего с заданной производительностью;
— определять производительность трубопровода при заданном напоре.
Вывод по второму вопросу.
Рассмотренная методика облегчает процесс построения гидравлических характеристик простых трубопроводов.
3.Принцип построения гидравлических характеристик сложных трубопроводов.
В зависимости от конфигурации трубопроводы делятся на простые и сложные.
Простым трубопроводом называется трубопровод не имеющий разветвлений на пути движения жидкости от точки забора до точки потребления. Примером такого трубопровода может быть ПМТ, развернутый от фронтового склада до его отделения.
Сложным трубопроводом называется трубопровод, который представляет собой сеть труб, состоящую из основной магистральной линии и ряда отходящих от нее ответвлений.
Сложные трубопроводы делятся на следующие основные виды: последовательное соединение, параллельное соединение, разветвленные трубопроводы и др.
Рассмотренная во втором вопросе лекции методика построения гидравлической характеристики относится к простому трубопроводу. Построение гидравлической характеристики сложного трубопровода имеет ряд особенностей.
Рассмотрим принцип построения гидравлических характеристик для некоторых сложных трубопроводов.
а) Последовательное соединение трубопроводов
Схему последовательного соединения трубопроводов можно представить так :




Расход жидкости в любом сечении трубопровода, исходя из уравнения неразрывности потока будет одинаковым, т.е.
а общие потери напора будут равны сумме потерь напора на отдельных участках
Для построения гидравлической характеристики такого трубопровода необходимо построить гидравлические характеристики каждого участка трубопровода отдельно (по методике построения гидравлической характеристики для простого трубопровода), а затем построить суммарную гидравлическую характеристику для всей линии трубопровода.
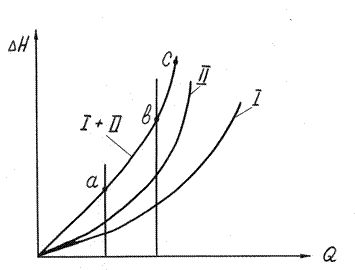
На рисунке 5 построены характеристики участков последовательного включения трубопроводов: кривая I представляет собой характеристику участка 1, крива II — участка 2.
Дальнейшее построение суммарной характеристики ведут следующим порядком. Так как при последовательном соединении потери напора суммируются, то кривые I и II сложим по вертикали. Для этого проведем ряд прямых параллельных оси ординат, каждая из которых пересечет обе кривые, сложим ординаты точек этих прямых с кривыми
В результата получим ряд точек а, б, с принадлежащих новой кривой I+II. Соединив эти точки плавной кривой, получим искомую суммарную характеристику всего рассматриваемого трубопровода, кривая I+II (рисунок 5).
б) Параллельное соединение трубопроводов
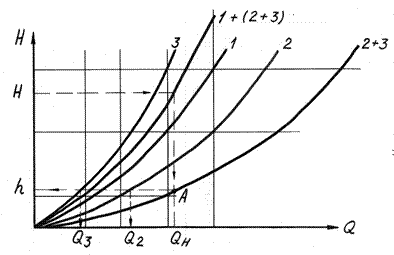
При параллельном соединении трубопроводов (рисунок 3, участки 2, 3, 4) построение характеристики этого сложного трубопровода следует начинать с построения




гидравлических характеристик отдельных параллельно включенных участков трубопровода по известной методике.
На рисунке 4 кривые II, III, IV представляют собой такие характеристики участков 2, 3 и 4.
Рисунок 7
При параллельном соединении трубопроводов жидкость, подходя с определенным расходом к точке их разветвления, проходит по разветвлениям и далее снова сливается в точке соединения этих трубопроводов. При этом общий расход определяется как сумма расходов в отдельных параллельно включенных участках, т.е.
Потери же напора в этих участках одинаковы, и полная потеря напора определяется как потеря в одном из них, т.е.
Поэтому для полстроения суммарной характеристики необходимо провести ряд горизонтальных прямых, параллельных оси абсцисс, и сложить при постоянных ординатах абсциссы точек их пересечения с характеристиками отдельных участков. В результате получим ряд точек а, б, с, определяющих суммарную характеристику II+III+IV трубопровода при параллельном включении
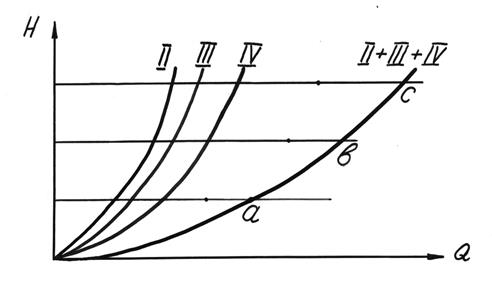
Разветвленный трубопровод можно представить в виде схемы (рисунок 5)
Если длина и диаметр каждого из участков трубопровода, известен коэффициент гидравлического сопротивления, то можно построить гидравлическую характеристику каждого из этих участков.
По известной методике построим гидравлические характеристики каждого участка трубопровода (1, 2 и 3) в отдельности (рисунок 8).
Решение разветвленной системы трубопровода начнем со второго и третьего участков, которые соединены параллельно.
Заменим участки 2 и 3 эквивалентным трубопроводом (2+3), т.е. сложим гидравлические характеристики участков трубопровода 2 и 3 по оси расходов. После чего получим два участка трубопровода, соединенных последовательно (рисунок 9 ).
Далее строим суммарную характеристику двух последовательно соединенных трубопроводов 1+(2+3). Таким образом, мы получили суммарную характеристику развернутой сети трубопровода 1 + 2 + 3 ( рисунок 9).
о суммарной характеристике разветвленного трубопровода можно решать следующие задачи :
— задать напор Н, определить расход при этом напоре. Для решения этой задачи необходимо на оси ординат найти напор Н, и двигаясь от этой точки слева направо дойти до характеристики 1+(2+30, и опустив перпендикуляр на ось абсцисс получим искомый расход (QH) (рисунок 6).
— чтобы определить расход отдельно по трубопроводам 2 и 3 необходимо от QH восстановить перпендикуляр до пересечения с характеристикой (2+3), точка пересечения А (Рис. 6) дает напор, который одинаков для обеих участков 2 и 3 (рисунок 7 ). Двигаясь от точки А справа налево до точек пересечения с характеристиками 2 и 3 и, опускаясь по перпендикуляру от этих точек, найдем расходы Q2 и Q3.
Вывод по третьему вопросу
Рассмотренные способы построения суммарной гидравлической характеристики сложных трубопроводов имеет важное прикладное значение для специалистов службы горючего.
Заключение .
В лекции дано определение гидравлической характеристики трубопровода. выведено уравнение гидравлической характеристики простого трубопровода и на конкретном примере рассмотрена методика построения гидравлической характеристики простого трубопровода. изложен принцип построения гидравлической характеристики сложных трубопроводов.
Умение рассчитывать и строить гидравлическую характеристику трубопровода позволит офицеру службы горючего грамотно принимать решение при эксплуатации перекачивающих средств и трубопроводов.
| | | следующая лекция ==> | |
| Расчет статически неопределимых плоско-пространственных рам методом сил | | | Морфологический критерий |
Дата добавления: 2016-11-29 ; просмотров: 5725 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Характеристика трубопровода ее уравнение и построение
При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора.
В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач.
Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.
Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые исложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z1 и избыточное давление Р1, а в конечном сечении 2-2 — соответственно z2 и Р2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν.
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α1 = α2, то скоростной напор можно не учитывать. При этом получим
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту
а последнее слагаемое Σh — как степенную функцию расхода
где K — величина, называемая сопротивлением трубопровода;
Q — расход жидкости;
m — показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Нпотр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при турбулентном — параболой с показателем степени равном двум (рис.6.2, б).
Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
Простые трубопроводы могут соединяться между собой, при этом их соединение может бытьпоследовательным или параллельным.
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и Nравна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.
Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.
Обозначим полные напоры в точках М и N соответственно HM и HN , расход в основной магистрали (т.е. до разветвления и после слияния) — через Q, а в параллельных трубопроводах через Q1, Q2 и Q3; суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что расход жидкости в основной магистрали
Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :
Отсюда делаем вывод, что
т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом
где K и m — определяются в зависимости от режима течения.
Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб.
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а). Геометрические высоты z1, z2 и z3 конечных сечений и давления P1, P2 и P3 в них будут также различны.
Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:
Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)
Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем
Аналогично для двух других трубопроводов можно записать
Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) — сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM > Hст1.
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M — N и избыточные давления в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М.
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:
уравнение равенства потребных напоров для ветвей CD и CE
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
выражение для потребного напора в точке М
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.
Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее.
Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 6.8, б).
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P 0 в другой резервуар с давлением P3 (рис. 6.8, а). Высота расположения оси насоса H1 называетсягеометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу,всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.
Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):
Это уравнение является основным для расчета всасывающих трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2и 3-3:
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
где Δz — полная геометрическая высота подъема жидкости, Δz = H 1 + H2;
КQ m — сумма гидравлических потерь,
P3 и Р0 — давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P3 — Р0 ) ( ρg ), то можно рассматривать увеличенную разность уровней
и формулу можно переписать так:
Из этой формулы делаем вывод, что
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр = f1(Q)и характеристики насоса Hнас = f2(Q) и в нахождении их точки пересечения (рис. 6.9).
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а — для турбулентного режима; б — для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено мгновенное закрытие крана (рис. 6.10, а).
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔPуд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-nперемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P0 (рис. 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P0 — ΔPуд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Повышение давления при гидравлическом ударе можно определить по формуле
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:
где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = 
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:
где k0 — абсолютная шероховатость для новых труб, (мм),
kt — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).
Построение характеристики трубопровода и определение рабочей точки гидросистемы.
Подставив данные из условия задачи, получим:
Определяем значения 5 точек в рабочем диапазоне значений расходов для Q = 0:
для Q = 50·10 -6 м 3 /с:
для Q = 100·10 -6 м 3 /с:
для Q = 150·10 -6 м 3 /с:
для Q = 200·10 -6 м 3 /с:
Таблица 1. Результаты расчета характеристики трубопровода
| Q (м 3 /с) | 50×10 -6 | 100×10 -6 | 150×10 -6 | 200×10 -6 | |
| ΔpΣ (мПа) | 5,65 | 5,8 | 6,13 | 6,64 | 7,33 |
По этим данным строится характеристика трубопровода (кривая 3). Точка пересечения линии 3 с CD дает рабочую точку гидросистемы (точка R). Ее координаты:
Qну = 47,82 см 3 /с; рн = 5,79 МПа.
5. Определение искомых величин
Так как вся подача насосной установки Qну поступает в гидроцилиндр, то скорость движения его штока определяется по формуле (в соответствии с рекомендациями принимаем объемный КПД гидроцилиндра равным единице)
Мощность, потребляемая гидроприводом, равна мощности, потребляемой насосной установкой, и в данном случае определяется по формуле
Для определения КПД гидропривода ηгп вначале необходимо рассчитать полезную мощность, развиваемую на его выходном звене
N вых F Vп 12·10 3 ·0,0225 = 270 Вт

Гидропривод вращательного движения
Рис.1. Схема гидропривода вращательного движения
Дано:вес грузов G1 = 2,1 кН и G2 = 1,9 кН; параметры насоса: максимальный рабочий объем Wон = 30 см3, частота вращения валаnн=25об/с, объемный КПД ηон = 0,82 при давлении р’ = 6 МПа, механический КПД ηмн= 0,9; параметры регулятора подачи: давление настройки pр=4,85 МПа, Kр=0,001м3/(МПа·с); размеры гидролиний:d1 = d2 = 1 см, l1 = 3 м, l2 = l3 = 8,5м, l4 = 5 м; коэффициент сопротивленияфильтра ζф=3; параметры гидродросселя: площадь проходного сечения Sдр = 14 мм2, коэффициент расхода µдр = 0,7; параметры гидромоторов: рабочий объем Wг = 32 см3, механический КПД ηмг = 0,9, объемный КПДпринять ηог=0,99; передаточное число механического редуктора inвх /nвых=40, диаметр шкива D = 0,7 м; параметры рабочей жидкости: кинематическая вязкость ν = 0,65 см2/с, плотность ρ = 880 кг/м3. Принять, что в трубах с диаметром d1 режим течения турбулентный и λ = 0,04, а с диаметром d2 – ламинарный.
– скорости движения тросов грузов;
– мощность, потребляемую гидроприводом;
– коэффициент полезного действия гидропривода.
1) Замена принципиальной схемы гидропривода эквивалентной
На рис. 2 приведена эквивалентная, или расчетная, схема, полученная на основании принципиальной схемы гидропривода (см. рис. 1).
Из анализа расчетной схемы ясно, что рассматриваемый гидропривод представляет собой сложный трубопровод с последовательно-параллельным соединением отдельных участков. Его целесообразно разбить на 4 простых трубопровода: 1, 2, 3 и 4 (рис. 2).
Рис. 2. Эквивалентная схема
2) Построение характеристики насосной установки
Учитывая линейность характеристик насоса и насосной установки с регулятором подачи, построение каждой из них проводим по двум точкам в соответствии с вышеизложенной методикой.
Для насоса: первая точка А — при р = 0,
вторая точка В — при р’ = 6 МПа,
Q’ = QTmax ·ηон =0,75·10 -3 ·0,82=0, 615· 10 -3 м 3 /с.
Соединяя точки А и В, получаем характеристику насоса (рис. 3).
Для насосной установки с регулятором подачи:
первая точка С — это точка пересечения горизонтали, соответствующей давлению настройки регулятора pp = 4,85 МПа, с характеристикой насоса. Подача насосной установки при этом равна Q’ну = 0,641·10 -3 м 3 /с;
вторая точка С’ — ее координаты определяются, зная Q’ну и произвольно задаваясь давлением на выходе насоса, при p»н=5,25 МПа,
Проведя прямую через точки С и С’ до пересечения с осью ординат в точке D, получаем характеристику насосной установки (ломаная линия АCD на рис. 3).
3) Составление уравнений характеристик простых трубопроводов
Составление уравнений характеристик простых трубопроводов 1, 2, 3 и 4 базируется на заданном условии: на участках 1 и 4 — режим течения турбулентный, а на участках 2 и 3 — ламинарный. Отсюда:
для 1:
для 2:
для 3:
ддя4:
В этих уравнениях значение моментов на валах гидромоторов М1 и М2 определяются с учетом передаточных отношений редукторов
4) Построение суммарной характеристики сложного трубопровода и определение рабочей точки гидросистемы
Заметим, что участки 1 и 4 включены последовательно, поэтому для них можно написать общее уравнение
и сразу построить их суммарную характеристику. Подставив данные из условия задачи, получим:
Поскольку характеристики 2 и 3 трубопроводов линейны, для их построения достаточно двух точек, а для построения нелинейной характеристики К1+4 = f(Q) используем 6 точек. Результаты расчетов заносим в таблицу 1.
Для Q = 0,2 м 3 /с:
Для Q = 0,3 м 3 /с:
Для Q = 0,4 м 3 /с:
Для Q = 0,5 м 3 /с:
Для Q = 0,6 м 3 /с:
Таблица 1. Результаты расчета характеристик трубопровода
| Q (м 3 /с) | 0,2·10 -3 | 0,3·10 -3 | 0,4·10 -3 | 0,5·10 -3 | 0,6·10 -3 |
| Δp2 (МПа) | 4,01 | 5,99 | |||
| Δp3 (МПа) | 3,625 | 5,605 | |||
| Δp1+4 (МПа) | 0,28 | 0,64 | 1,13 | 1,77 | 2,55 |
По данным таблицы на графике (см. рис. 3) строим характеристики каждого простого трубопровода (линии 1+4, 2 и 3).
Затем по правилам графического сложения характеристик параллельных участков (они складываются за счет суммирования отрезков вдоль оси расходов) получаем суммарную характеристику участков 2 и 3 (ломаная линия 2+3). Далее проводим графическое сложение полученной характеристики Δр2+3 =f(Q) c характеристикой Δр2+3 =f(Q).

Эти характеристики складываются по правилу сложения характеристик последовательно соединенных трубопроводов, т.е. за счет суммирования отрезков вдоль оси давлений. В результате получаем суммарную характеристику всего сложного трубопровода (линия Σ).
Пересечение полученной характеристики сложного трубопровода с характеристикой насосной установки определяет рабочую точку гидросистемы (точка R на рис.3). Ее координаты рн = 5,17 МПа и Qну=0,319·10 -3 м 3 /с
5) Определение искомых величин
Определим потребляемую гидроприводом мощность, для этого через точку R проводим прямую параллельно АВ и определяем Q’т = 0,436·10 -3 м 3 /с. Тогда
Чтобы определить скорости подъема грузов и КПД гидропривода, необходимо найти частоту вращения вала каждого гидромотора. Для этого необходимо знать величины расходов Q2 и Q3 в параллельных трубопроводах 2 и 3.
Эту задачу можно решить графически, исходя из того, что при наличии графической зависимости р = f(Q) по одной из известных координат легко определяется другая.
Опустив вертикаль из точки R, соответствующую подаче насосной установки Qну, находим точку R1 пересечения этой вертикали с кривой 2+3 и, следовательно, потерю давления Δр2+3 на участке параллельного соединения, где Δр2+3 = Δр2 = Δр3.
Проведя теперь горизонталь через точку R1, соответствующую потерям давления Δр2 = Δр3, находим точки ее пересечения с характеристиками 2-го и 3-го трубопроводов (соответственно, точки R2 и R3). Опустив вертикали из точек R2 и R3, находим расходы Q2 = 0,111·10 -3 м 3 /с и Q3 = 0,208·10 -3 м 3 /с.
По известным расходам Q2 и Q3 с учетом передаточного отношения i механического редуктора и диаметра D шкива определяем скорости подъема левого V1 и правого V2 грузов. При этом целесообразно использовать формулу
Отсюда, подставив соответствующие значения, получим:
V1 = 3,14·0,7·0,111·10 -3 ·0,99/(40·32·10 -6 ) = 0,189 м/с;
V2 = 3,14·0,7·0,208·10 -3 ·0,99/(40·32·10 -6 ) = 0,354 м/с.
Полезная мощность, развиваемая гидроприводом, складывается из мощностей, затрачиваемых на подъем обоих грузов:
Тогда коэффициент полезного действия гидропривода равен
http://www.sites.google.com/site/kursgidravliki/6-igidravliceskij-rascet-prostyh-truboprovodov
http://poisk-ru.ru/s38898t19.html
4
Введение
Настоящее пособие предназначено для студентов машиностроительных
специальностей, в учебных планах которых предусмотрено выполнение домашних расчетно-графических заданий по расчету установившегося режима
работы гидравлических систем в рамках дисциплин «Механика жидкости и газа», «Гидравлика и гидропневмопривод», «Гидравлические системы» и др.
В данном учебном пособии рассматриваются методики расчета установившихся режимов работы как простых трубопроводов, не имеющих ответвлений, так и разных вариантов их соединения, а также особенности расчета трубопроводов, содержащих гидродвигатели. Кроме этого определяются условия,
обеспечивающие требуемый установившийся режим работы трубопровода, необходимая дополнительная избыточная энергия в котором передается жидкости за счет работы насоса.
В основе всех этих методик гидравлического расчета трубопроводов лежит использование уравнения Бернулли для установившегося течения реальной жидкости, которое с энергетической точки зрения есть уравнение баланса
удельной механической энергии жидкости в потоке. Таким образом, изучаемые
в данном пособии методы гидравлического расчета трубопроводов – это методы расчета условий установившегося движения жидкости в трубопроводе в
требуемом количестве с энергетической точки зрения.
Учебное пособие состоит из трех разделов: «Построение характеристики
сложного трубопровода», «Построение характеристики насосной установки» и
«Определение параметров совместной работы насосной установки и сложного
трубопровода». При этом каждый из этих разделов посвящен выполнению одного из трех домашних расчетно-графических заданий учебного плана.
В каждом разделе рассматриваются:
основные законы и расчетные формулы, необходимые для решения задач
данного раздела;
графо-аналитические методы расчета, использующие указанные законы и
5
формулы;
примеры расчета, сопровождающиеся рекомендациями, облегчающими решение задач;
контрольные задания для самостоятельного решения.
Незаданные в условиях контрольных задач числовые значения обозначенных величин берутся в соответствии с номером варианта задания из таблиц
исходных данных, приведенных в конце каждого раздела.
При выполнении расчетов особое внимание следует уделить размерностям используемых физических величин. Все расчеты рекомендуется делать в
системе СИ. В пособии примеры расчетов проведены в этой системе.
Рассмотренные в учебном пособии методы могут также применяться при
решении подобных задач с использованием ЭВМ, когда вместо графических
построений используются численные математические способы решения инженерных задач.
6
1. Расчетно-графическая работа № 1
ПОСТРОЕНИЕ ХАРАКТЕРИСТИКИ СЛОЖНОГО ТРУБОПРОВОДА
1.1 Общие положения.
Под сложным трубопроводом понимаем трубопровод, содержащий соединения простых трубопроводов.
Простым называют трубопровод, не имеющий ответвлений и содержащий ряд последовательно включенных элементов. К таким элементам относятся распределители, дроссели, клапаны, фильтры, теплообменники, гидравлические двигатели и т.д.
Гидравлический расчет трубопроводов состоит в определении следующих параметров: величин расходов и давлений в определенных сечениях, а
также перепадов (потерь) давления на элементах трубопровода.
Для расчета трубопроводов используются характеристики потребных напоров и характеристики трубопроводов. При расчете машиностроительных
гидросистем, в большинстве случаем, применяются характеристики трубопроводов.
1.2 Простой трубопровод
Под характеристикой трубопровода понимается зависимость потерь в
трубопроводе от расхода.
В гидравлике потери принято делить на потери на трение по длине трубы
и потери в местных сопротивлениях (местные потери).
Потери на трение Δртр в трубе длиной l и внутренним диаметром dт при
расходе Q в общем случае определяются по формуле, полученной из канонической формулы Вейсбаха-Дарси:
pтр
l
8
2 4 Q2 ,
d т d
(1.1)
где: ρ – плотность рабочей жидкости;
λ – коэффициент Дарси, величина которого определяется в зависимости от
режима течения жидкости.
7
Оценка режима течения жидкости в трубопроводе проводится по величине числа Рейнольдса:
Re
4Q
,
d т
(1.2)
где: ν – кинематическая вязкость рабочей жидкости.
Если число Re, рассчитанное по формуле (1.2), больше 2300, то режим
течения следует принять турбулентным. Тогда, учитывая, что трубы в машиностроительных гидросистемах, как правило, рассматриваются технически гладкие, то коэффициент λ целесообразно определять по формуле Блазиуса:
0.316
,
4
Re
(1.3)
где: Re – число Рейнольдса, вычисленное по формуле (1.2).
Если полученное число Re меньше 2300, режим течения следует принять
ламинарным, и тогда формула (1.1) после подстановки в нее значения
64
,
Re
преобразуется в формулу закона Пуазейля:
pтр
128 l Q
.
d т4
(1.4)
Формулы (1.1) и (1.4) можно представить в виде:
при турбулентном режиме течения – pтр Kт Q2 , где K т
при ламинарном режиме течения – pтр Kл Q , где K л
8 l
;
2 d т5
128 l
.
d т4
Следует отметить, что если при турбулентном режиме величина коэффициента λ задана по условию задачи, то в расчете он принимается постоянным,
и, следовательно, постоянным будет оставаться коэффициент Кт. Если же коэффициент λ по условию задачи не задан, то в расчете следует учитывать его
зависимость от расхода по формуле (1.3), а коэффициент Кт корректировать в
процессе расчета.
Местные потери Δрм происходят в местных гидравлических сопротивлениях, имеющихся в трубопроводе.
8
Заметим, что в данном пособии потери, связанные с прохождением жидкости через соединительные элементы трубопроводов, места поворота, разветвления и объединения потоков, не рассматриваются. Здесь под местными
сопротивлениями понимаются такие элементы гидравлических систем как гидравлические дроссели, распределители, фильтры, теплообменники и т.п.
В связи с этим для характеристики местных гидравлических сопротивлений в условии задач могут быть заданы следующие параметры:
– коэффициент потерь ζ;
– площадь проходного сечения S и коэффициент расхода μ;
– эквивалентная длина lэ.
Определение потерь в рассматриваемом местном сопротивлении рекомендуется проводить, в зависимости от заданных параметров, по одной из трех
формул:
при известном коэффициенте потерь зависимость потерь от расхода выражается формулой, полученной из канонической формулы Вейсбаха:
pм
8
Q2 ,
2
4
dт
(1.5)
где dт – диаметр трубопровода, в котором установлено местное сопротивление;
если задана площадь S проходного сечения и коэффициент расхода μ, то потери определяются из формулы истечения, которая приводится к виду:
pм
Q2 ;
2
2
2 S
(1.6)
если задана эквивалентная длина lэ трубопровода, то считается, что потери в
рассматриваемом местном сопротивлении эквивалентны потерям на трение
в трубе длиной lэ с диаметром dт трубопровода, в котором это местное сопротивление установлено. Тогда при ламинарном режиме течения потери в
таком местном сопротивлении определяются по формуле:
pм
128 lэ
Q .
d т4
(1.7)
По аналогии с потерями на трение формулы (1.5), (1.6) и (1.7) можно
9
представить в виде Δрм = Км·Q2 или Δрм = Км·Q.
Очевидно, имея для конкретного простого трубопровода набор формул,
оценивающих гидравлические потери в его элементах, при их сложении можно
получить зависимость суммарных потерь давления ΔрΣ в этом простом трубопроводе от расхода, которая является характеристикой простого трубопровода.
Эта зависимость в общем случае может быть представлена в виде:
p pтр pм K1 Q K2 Q 2 ,
(1.8)
где коэффициенты К1и К2 получаются в результате суммирования соответствующих коэффициентов Кт, Кл и Км.
1.3 Простой трубопровод, содержащий гидродвигатель
В машиностроении наибольшее распространение получили гидросистемы, предназначенные для передачи механической энергии, которые называются гидравлическими приводами. Если в гидроприводе используются объемные
гидромашины, то он называется объемным. Любой объемный гидропривод
включает в себя хотя бы один гидравлический двигатель.
Гидродвигатель – это гидромашина, преобразующая часть энергии потока жидкости в механическую работу.
При гидравлическом расчете трубопровода, содержащего гидродвигатель, гидродвигатель рекомендуется рассматривать как местное гидравлическое сопротивление, в котором потери давления Δргд идут на совершение полезной работы – перемещение выходного звена, преодолевающего внешнюю
нагрузку.
Поэтому в уравнение характеристики простого трубопровода (1.8), при
наличии в нем гидродвигателя, добавляется дополнительное слагаемое, и уравнение принимает вид:
p pтр pм pгд .
(1.9)
Определение величины Δргд зависит от типа гидродвигателя. Самыми
распространенными гидродвигателями являются роторные гидромоторы и
гидроцилиндры. Роторный гидромотор – это гидродвигатель с вращательным
10
движением выходного звена, а гидроцилиндр – это гидродвигатель с возвратно-поступательным движением выходного звена.
Роторные гидромоторы по устройству аналогичны соответствующим
роторным насосам. Например, конструкция шестеренного гидромотора аналогична конструкции шестеренного насоса с внешним зацеплением, конструкция
аксиально-поршневого гидромотора – конструкции аксиально-пошневоого насоса и т.д.
Условное обозначение гидромотора на схемах приведено на рис. 1.1.
Рисунок 1.1. Условное обозначение гидромотора
Режим работы гидромотора, характеризуют параметры:
Q1 и р1 – расход и давление на входе в гидромотор;
Q2 и р2 – расход и давление на выходе из гидромотора;
М – крутящий момент на валу гидромотора;
n – частота вращения вала гидромотора.
При расчете гидромоторов следует использовать следующие формулы:
pгд pгм p1 p2
n
2 M
,
Wо мм
Q о м
,
Wо
(1.10)
(1.11)
где: Δргм – перепад (потеря) давления на гидромоторе;
Wо – рабочий объем гидромотора;
Q – расход жидкости, потребляемый гидромотором (для большинства
гидромоторов с достаточной точностью можно считать Q = Q1 = Q2);
ηмм – механический КПД гидромотора;
ηом – объемный КПД гидромотора.
Гидроцилиндр. Самым распространенным типом гидроцилиндра является гидроцилиндр с односторонним штоком.
11
В зависимости от направления движения жидкости в трубопроводе различают два варианта режима работы гидроцилиндра, представленные на рисунке 1.2.
Рисунок 1.2. Гидроцилиндр с односторонним штоком
Режим работы гидроцилиндра, характеризуют параметры:
Q1 и р1 – расход и давление на входе в гидроцилиндр;
Q2 и р2 – расход и давление на выходе из гидроцилиндра;
F – сила штоке гидроцилиндра;
V – скорость штока гидроцилиндра.
Для гидроцилиндра, включенного по схеме на рисунке 1.3 а, с достаточной степенью точности при расчете можно принять:
pгд pгц p1 p2
V
4 Q1 о ц
D 2
4 F
,
D 2 м ц
.
(1.12)
(1.13)
Для схемы на рисунке 1.3,б соответственно:
pгд pгц p1 p2
V
4 F
,
D dш2 м ц
4 Q2 о ц
D 2 dш2
2
(1.14)
.
(1.15)
В формулах (1.12) ÷ (1.15) приняты следующие обозначения:
Δргц – перепад (потеря) давления на гидроцилиндре;
D и dш – диаметры поршня и штока гидроцилиндра;
ηмц – механический КПД гидроцилиндра;
12
ηоц – объемный КПД гидроцилиндра.
Заметим, что, если ηоц по условию задачи не задан, то в расчете из-за малости объемных потерь в гидроцилиндрах следует принять ηоц = 1.
Важной особенностью гидроцилиндра с односторонним штоком является
то, что из-за неравенства эффективных площадей поршня с его правой и левой
стороны, расходы жидкости на входе и на выходе гидроцилиндра различны.
Поэтому в расчете рекомендуется расход Q2 выражать через расход Q1.
Для схемы на рис. 1.3,а
Q2
D
Q
1
2
dш2
D2
,
(1.16)
а для схемы на рис. 1.3,б
D2
Q2 Q1 2
.
D dш2
(1.17)
Для гидроцилиндров с двухсторонним штоком (эффективные площади с
обеих сторон поршня равны) расходы на входе Q1 и выходе Q2 гидроцилиндра одинаковы.
Для гидроцилиндров одностороннего действия давление р2 в формулах
(1.12) и (1.14) следует принимать равным нулю.
Из формул (1.10), (1.12) и (1.14) видно, что при принятых допущениях
потери давления в гидродвигателе Δргд не зависят от расхода Q, а определяются преодолеваемой внешней нагрузкой (М или F) на его выходном звене и его
конструктивными параметрами. Поэтому в общем случае аналитическое выражение характеристики простого трубопровода (1.9), содержащего гидродвигатель, имеет вид:
p pгд K1 Q K2 Q 2 .
(1.18)
В качестве примера рассмотрим простой трубопровод, схема которого
приведена на рисунке 1.3, и получим его характеристику.
13
Рисунок 1.3. Простой трубопровод, содержащий гидроцилиндр
Трубопровод состоит из последовательно соединенных: фильтра 1, дросселя 2, гидроцилиндра 3 и труб (гидролиний), соединяющих эти элементы. Заметим, что если для некоторого отрезка трубопровода длина l на схеме не указана, то при расчете потерями на трение на этом участке следует пренебречь.
Предположим, что режим течения жидкости в трубопроводе ламинарный, потери в фильтре 1 заданы эквивалентной длиной lэ, потери в дросселе 2
заданы площадью проходного сечения S и коэффициентом расхода μ. Тогда
суммарные потери давления в трубопроводе ΔрΣ складываются из потерь в
гидролиниях Δртр1 и Δртр2, в фильтре Δрф, в дросселе Δрдр и в гидроцилиндре
Δргц и в общем виде равны:
p pф pтр1 pгц pдр pтр2 .
(1.19)
Подставив в формулу (1.19) значения Δртр1 и Δртр2 по формуле (1.4), Δрф –
по формуле (1.7), ΔрГц – по формуле (1.12), и Δрдр – по формуле (1.6), получим:
p
128 lэ
128 l1
4 F
128 l2
Q1
Q1
Q12
Q2 .
4
4
2
2
2
d1
d1
2 S
D м ц
d 24
Поскольку в нашем случае в качестве гидродвигателя используется гидроцилиндр с односторонним штоком, то, используя формулу (1.16), после преобразований получим характеристику рассматриваемого трубопровода в виде:
D 2 dш2
2
p pгд K1 K 2
Q K3 Q ,
2
D
где: pгд
(1.20)
128 lэ l1
4 F
128 l2
, K1
, K2
, K3
.
2
4
4
D м ц
d1
2 2 S 2
d 2
Таким образом, полученная формула соответствует зависимости (1.18)
14
характеристики простого трубопровода, содержащего гидродвигатель.
После вычисления (по известным значениям F, D, d, ηцм, l1,
l2, d1, d2, lэ, µ, S, μ и ρ) постоянных
величин Δргд, К1, К2 и К3, входящих в уравнение (1.20), можно построить в координатах p–Q характеристику данного простого трубопровода (рис. 1.4).
Рис. 1.4. Характеристика трубопровода,
содержащего гидродвигатель.
Заметим, что если функция (1.20) получилась линейной, то характеристику строят по двум значениям Q, одно из которых, как правило, Q = 0. Построение нелинейной характеристики проводят по 5 7 точкам.
1.4. Характеристика сложного трубопровода
Сложный трубопровод следует рассматривать как соединение нескольких простых трубопроводов. Тогда задача построения характеристики сложного трубопровода сводится к построению в координатах p – Q характеристик
простых трубопроводов, входящих в соединение, и последующему графическому сложению этих характеристик.
Графическое сложения характеристик простых трубопроводов осуществляется в соответствии со следующими системами уравнений, характеризующими данное соединение:
– для последовательного соединения 1, 2, …, n трубопроводов
Q1 Q2 Qn
;
p
p
p
p
1
2
n
(1.21)
– для параллельного соединения 1, 2, …, n трубопроводов
Q Q1 Q2 Qn
.
p
p
p
2
n
1
(1.22)
15
Из соотношений (1.21) и (1.22) следует, что сложение характеристик трубопроводов в координатах p – Q при их последовательном соединении происходит по вертикали (вдоль оси p при Q = const), а при параллельном – по горизонтали (вдоль оси Q при p = const).
Если сложный трубопровод включает в себя участки параллельного и последовательного соединения простых трубопроводов, то сначала необходимо
построить суммарные характеристики участков с параллельным соединением, а
затем общую суммарную характеристику всего трубопровода представить в
виде суммы характеристик последовательных соединений.
В качестве примера рассмотрим сложный трубопровод, представленный
на рис. 1.5.
Рис. 1.5. Схема сложного трубопровода.
Жидкость плотностью ρ и вязкостью ν движется от точки К по трубопроводу длиной l1 и диаметром d1, содержащем фильтр 1, потери в котором заданы эквивалентной длиной lэ. В точке L трубопровод разветвляется на два. В
одном из них длиной l2 диаметром d2, содержит гидромотор 2, рабочим объем
которого Wo, а механический КПД ηмм. Вал гидромотора преодолевает крутящий момент М. Второй трубопровод длиной l3 диаметром d3 содержит дроссель
3 с коэффициентом сопротивления ζ. Оба эти трубопровода находятся в одной
горизонтальной плоскости и имеют в конечных точках T1 и T2 одинаковые давления, равные атмосферному. Исходя из этого, данные трубопроводы включены параллельно.
Предположим, что во всех трубопроводах режим течения ламинарным.
16
Анализ схемы на рис. 1.5 позволяет сделать вывод о том, что рассматриваемый сложный трубопровод состоит из трех простых:
– 1-ый простой трубопровод – от точки К до точки L;
– 2-ой простой трубопровод – от точки L до точки T 1;
– 3-ий простой трубопровод – от точки L до точки T 2.
Получим аналитические выражения характеристик для каждого простого
трубопровода.
Для 1-го трубопровода, используя формулы (1.7) и (1.4), после алгебраических преобразований получим:
p1
128 lэ l1
Q
d14
или
p1 К1 Q .
(1.23)
K1
Для 2-го трубопровода, используя формулы (1.4) и (1.10), после алгебраических преобразований получим:
p2
128 l2
2 M
Q
4
d2
Wo мм
K2
или
p3 ргд К 2 Q .
(1.24)
pгд
Для 3-го трубопровода, используя формулы (1.4) и (1.5), после алгебраических преобразований получим:
p3
128 l3
Q
Q 2 или p3 К3 Q К 4 Q2 . (1.25)
4
2
2
d3
2 S
K3
K4
После вычисления постоянных величин Δргд, К1, К2, К3 и К4. входящих в
уравнения (1.23) ÷ (1.25), строим графики характеристик простых трубопроводов в координатах p–Q (рис. 1.6).
Получение суммарной характеристики начинается со сложения характеристик параллельно включенных простых трубопроводов 2 и 3. В соответствии
с системой уравнений (1.22), это сложение проводиться по горизонтали (вдоль
оси Q при p = const).
Очевидно, что в диапазоне изменения давления от нуля до Δргд суммарная характеристика совпадает с кривой 3, так как в этом диапазоне абсциссы
характеристики 2 равны нулю. Начиная с точки А, их суммарная характеристи-
17
ка уже получается в результате суммирования соответствующих абсцисс характеристик 2 и 3. Например, при ординате p* точка В получается в результате
сложения отрезков a и b. Таким образом, задаваясь несколькими значениями
p*, строим суммарную характеристику параллельного соединения (2+3).
Рис. 1.6. Пример построения характеристики сложного трубопровода.
Теперь сложный трубопровод можно условно считать, состоящим из двух
последовательно соединенных простых трубопроводов с характеристиками 1 и
(2+3). Тогда для получения характеристики всего сложного трубопровода необходимо сложить эти две характеристики в соответствии с системой уравнений (1.21). Это сложение проводиться по вертикали (вдоль оси р при Q = const).
Так, например, при произвольном значение расхода Q* точка С получается как сумма отрезков c и е. Таким образом, задаваясь несколькими значениями расхода Q*, строим суммарную характеристику Σ всего сложного трубопровода. При этом, с целью получения более точного результата, рекомендуется при наличии точки перелома характеристик, подобной точки А, обязательно провести сложение на вертикали, проходящей через эту точку. На рис. 1.6
так получена точка Е.
1.5. Пример выполнения расчетно-графической работы
Далее рассмотрим пример определения параметров сложного трубопровода с использованием характеристик простых трубопроводов.
18
Сложный трубопровод, схема которого приведена на рисунке 7, включает: распределители 3 и 7, регулируемые дроссели 4 и 6, гидромотор 5, гидроцилиндр 8, фильтр 1, бак 2, а также соединительные гидролинии.
Рис. 1.7. Схема сложного трубопровода.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость перемещения поршня
гидроцилиндра 8 при заданной скорости вращения гидромотора 5 ω = 37 рад/с.
Все соединительные гидролинии имеют одинаковые диаметры dт = 10 мм
и следующие длины:
– от точки K до точки L – l1 = 6 м;
– от точки L до гидромотора 4 и далее до точки L′ – l2 = 3 м;
– от точки L до гидроцилиндра 8 – l3 = 1,5 м;
–от гидроцилиндра 8 до точки L′ l3 = 1,5 м;
–от точки L′ до бака 5 (точка Т) – l4 = 4м.
Известны также: момент на валу гидромотора М = 28 Н·м, сила на штоке
цилиндра F = 6,5 кН, рабочий объем гидромотора Wо = 30 см3, диаметр поршня
D = 50 мм, диаметр штока dш = 30 мм.
19
Учесть потери в трубопроводах при вязкости жидкости = 0,75 см2/с
(плотность ρ = 900 кг/м3), а также потери в распределителях 3 и 7 (эквивалентная длина каждого канала lэр = 2 м), в дросселе 4 (коэффициент сопротивления
ζ = 30), в дросселе 6 (коэффициент расхода μ = 0,7, проходное сечение S = 18
мм2) и в фильтре 1 (эквивалентная длина lэф = 10 м).
Принять: механический КПД гидромотора – ηмм = 0,94, его объемный
КПД – ηмо = 0,92, механический КПД гидроцилиндра – ηцм = 0,97, , а режим течения – ламинарным.
Принципиальная гидравлическая схема, приведенная в условии задачи,
сложна для восприятия. Поэтому облегчения решения ее целесообразно заменить эквивалентной (расчетной).
На рис. 1.8 представлен один из возможных вариантов эквивалентной
схемы, полученной из заданной принципиальной схемы (рис. 1.7).
Рис. 1.8. Эквивалентная схема сложного трубопровода
Данная эквивалентная схема дает наглядное представление о том, какие
гидравлические сопротивления будут учтены при расчете, а также их расположение в трубопроводе. Ее анализ позволяет сделать вывод о том, что рассматриваемый сложный трубопровод состоит из четыре простых трубопроводов:
– 1-ый трубопровод от точки К до точки L;
– 2-ой трубопровод от точки L через гидромотор (Гм) до точки L′ (верхняя ветвь параллельного соединения);
– 3-ий трубопровод от точки L через гидроцилиндр (Гц) до точки L′
(нижняя ветвь параллельного соединения);
– 4-ый трубопровод от точки L′ до точки T;
20
Для каждого из этих простых трубопроводов получим аналитические выражения их характеристик.
Для 1-ого простого трубопровода характеристика примет вид:
p1
128 l1
Q К1 Q .
d т4
Определим численное значение коэффициента К1, т.е.
128 l1 128 0, 75 104 6 900
с
К1
1, 72 109 Па 3 .
4
4
d т
3,14 0, 01
м
В результате получим характеристику 1-го трубопровода в виде:
p1 1,72 109 Q .
(1.26)
Для 2-ого простого трубопровода характеристика примет вид:
p2
2 M 128 l2 2lэр lэф
8
Q 2 4 Q 2 pгд К 2 Q К 2 Q 2 .
4
Wо мм
d т
dт
Определим численные значения постоянных величин:
pгд
К2
2 3,14 28
6, 24 106 Па ;
6
30 10 0,94
128 l2 2lэр lэф 128 0,75 104 3 2 2 10 900
с
4,68 109 Па 3 ;
4
4
d т
3,14 0,01
м
8 900
с
K 2 30
2,19 1012 Па 3 .
2
4
3,14 0, 01
м
2
В результате получим характеристику 2-го трубопровода в виде:
p2 6,24 106 4,68 109 Q 2,19 1012 Q2 .
(1.27)
Для 3-ого простого трубопровода характеристика примет вид:
p3
128 2l3 2lэр
4F
Q
Q 2 pгд К3 Q К3 Q 2 .
4
2
2
2
2
d т
2 S
D dш цм
Определим численные значения постоянных величин:
pгд
К3
4F
4 6,5 103
5,34 106 Па ;
2
2
2
2
D dш цм 3,14 0,05 0,03 0,97
128 2l3 2lэр
d
4
т
128 0, 75 104 2 1,5 2 2 900
3,14 0, 01
4
1,93 109 Па
с
;
м3
21
K3
2
900
2 0, 7 2 18 106
2
с
2,83 1012 Па 3 .
м
В результате получим характеристику 3-го трубопровода в виде:
p3 5,34 106 1,93 109 Q 2,83 1012 Q2
(1.28)
Для 4-ого простого трубопровода характеристика примет вид:
p4
128 l4
Q К4 Q ,
d т4
Определим численное значение коэффициента К4, т.е.
К4
128 l1 128 0, 75 104 4 900
с
1, 03 109 Па 3 .
4
4
d т
3,14 0, 01
м
В результате получим характеристику 4-го трубопровода в виде:
p1 1,03 109 Q .
(1.29)
Далее строим графики зависимостей (1.26) ÷ (1.29). При этом следует
учитывать, что зависимости (1.26) и (1.29) являются линейными, а зависимости
1.27 и 1.28 носят квадратичный характер. Построение линейных характеристик
проводят по двум точкам, а при построении парабол необходимо использовать
не менее 5 7 точек.
Для удобства необходимые для построения данные целесообразно свести
в таблицу (таблица 1.1).
Таблица 1.1.
Q
[м3/с]
0.210-3
0.410-3
0.610-3
0.810-3
1,010-3
Δp1
[МПа]
0,00
–
–
–
–
1,72
Δp2
[МПа]
6,24
7,26
8,46
9,83
11,38
13,10
Δp3
[МПа]
5,34
5,83
6,56
7,51
8,69
10,10
Δp4
[МПа]
0,00
–
–
–
–
1.03
На рис. 1.9 по данным, приведенным в таблице 1.1, построены линии 1, 2,
3 и 4.
Используя рекомендации, изложенные в разделе 1.4, получим суммарную
характеристику всего сложного трубопровода.
Для этого, прежде всего, следует сложить параллельные трубопроводы 2
22
и 3. Построенная ломанная линия (2+3) является характеристикой условного
трубопровода (2+3), которым можно заменить параллельное соединение трубопроводов 2 и 3 (рис. 1.10).
Рис. 1.9. Построения характеристики сложного трубопровода и определение
параметров его работы
Рис. 1.10. Преобразованная эквивалентная схема сложного трубопровода.
Из преобразованной эквивалентной схемы сложного трубопровода (рис.
1.10) следует, что он состоит из трех последовательно соединенных простых
трубопроводов: 1, (2+3) и 4. Воспользуемся правилами графического сложения
23
характеристик последовательного соединения трубопроводов, рассмотренными
в подразделе 1.4. В результате получаем суммарную характеристику участков
1, (2+3) и 4 (линия Σ), представленную на рис. 1.9. Она является характеристикой всего сложного трубопровода.
Заметим, что при сложении линейных характеристик следует получить
две точки, а при сложении характеристик в виде квадратичных парабол или
прямых с параболами необходимо 5 7 точек.
Получив суммарную характеристику сложного трубопровода, ответим на
вопросы, поставленные в условиях задачи, т.е. определим параметры потока в
точке К и скорость поршня гидроцилиндра 8.
Для этого необходимо найти рабочую точку на его суммарной характеристике, исходя из значений параметров, заданных по условию задачи.
В данной задаче для этого, по известной величине угловой скорости вращения ω вала гидромотора 5 найдем расход во 2-ом простом трубопроводе Q2.
Из формулы (1.11) получим:
Q2
n Wо
Wо
37 30
м3
.
0,192 103
мо
2 мо 2 3,14 0,92
с
По этой величине расхода во 2-ом трубопроводе Q2 находим точку на его
характеристике (точка R2 на рис. 1.9).
Потом графически определим соответствующую этому режиму точку R′
на характеристике (2+3) и далее R на характеристике Σ (рис. 1.9). Последняя
будет являться рабочей точкой для данного сложного трубопровода. Положение точки R на характеристике сложного трубопровода позволяет найти искомые параметры потока в точке К: pК = 9,24 МПа и QК = 0,735·10-3 м3/с.
Для определения скорости перемещения поршня гидроцилиндра 8 найдем рабочую точку на характеристике 3-его трубопровода, в котором установлен гидроцилиндр. Так как 3-ий трубопровод параллелен 2-ому, то эту точку R3
(рис. 1.11) определим, на той же горизонтали, что и точка R2.
Величина расхода Q3 для точки R3 равна: Q3 = 0,543·10-3 м3/с.
24
По величине Q3, используя формулу (1.15) (принимаем ηоц = 1), вычисляем искомую величину скорости поршня:
V
4 Q2 о ц
D 2 dш2
4 0,543 103 1
м
cм
.
0,
432
43,
2
с
с
3,14 0, 052 0, 032
Таким образом, в результате построена суммарная характеристика сложного трубопровода, определены параметры потока в начальной точке этого
трубопровода: pК = 9,24 МПа и QК = 0,735 л/с, а также скорость перемещения
поршня гидроцилиндра: V = 43,2 см/с.
1.6. Контрольные задания для самостоятельного выполнения
Далее приводятся варианты заданий для самостоятельной работы. Шифр
каждого варианта включает числовой номер и букву русского алфавита. По
номеру выбирается соответствующее условие, а буква определяет вариант значений физических величин не заданных в тексте. Эти численные значения приведены в таблице 1.2 в конце подраздела после текстов вариантов заданий.
25
Вариант 1.1
Сложный трубопровод содержит регулируемый дроссель 1, распределитель 5, гидроцилиндр 6, переливной клапан 2, фильтр 4 и бак 3, соединенные
по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и расход через фильтр 4 при известном расходе через клапан 2 (Q0).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до гидроцилиндра 6 – l1;
– длина от гидроцилиндра 6 до точки L – l2;
– длины разветвленных участков (от точки L до бака 3) одинаковы и равны l3.
Известны также: сила на штоке поршня F = F2, его размеры D и dш.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
дросселе 1 (коэффициент расхода μ = 0,7 проходное сечение S2), в распределителе 5 (эквивалентная длина одного канала lэ1), в фильтре 4 (эквивалентная
длина lэ2) и в клапане 2, характеристика которого Δрк = р0 + k · Q. Принять для
клапана k = 2·103 МПа·с/м3, механический КПД гидроцилиндра ηм = 0,97,
плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l2, l3, lэ1, lэ2, dт, S2, D, dш, F2, р0, и Q0 взять из таблицы 1.2).
26
Вариант 1.2
Сложный трубопровод содержит регулируемый дроссель 1, распределители 2 и 5, гидроцилиндр 6, радиатор 3 и бак 4, соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и расход через радиатор 3 при заданной скорости поршня гидроцилиндра 6 (V = V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длина от точки L до гидроцилиндра – l1;
– длина от цилиндра до бака – l1:
– длина от точки L через охладитель до бака l3
Известны также: сила на штоке поршня F = F2, его размеры D и dш.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
дросселе 1 (коэффициент расхода μ = 0,7, проходное сечение S1), в распределителях 2 и 5 (эквивалентная длина одного канала lэ2) и в радиаторе 3 (эквивалентная длина lэ3). Принять механический КПД гидроцилиндра ηм = 0,98, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ2, lэ3, dт, S1, D, dш, F2 и V1 взять из таблицы 1.2).
27
Вариант 1.3
Сложный трубопровод содержит регулируемый дроссель 1, распределитель 2, гидроцилиндр 6, фильтр 5, обратный клапан 4, бак 3, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и расход через фильтр 5 при заданной скорости поршня гидроцилиндра 6 (V = V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длины от точки L до цилиндра 6 и от него до точки L’ одинаковы и равны l1;
– длина от точки L’ до бака 3 – l1;
– другими длинами пренебречь.
Известны также: сила на штоке поршня F = F2, его размеры D и dш.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
дросселе 1 (коэффициент сопротивления ζ2), в распределителе 2 (эквивалентная
длина одного канала lэ1), в фильтре 5 (эквивалентная длина lэ3) и в клапане 4
(эквивалентная длина lэ2). Принять механический КПД гидроцилиндра ηм =
0,97, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, lэ1, lэ2, lэ3, dт, ζ2, D, dш, F2 и V1 взять из таблицы 1.2).
28
Вариант 1.4
Сложный трубопровод содержит регулируемый дроссель 3, распределитель 5, гидроцилиндр 6, бак 4, редукционный клапан 1, гидроаккумулятор 2
(для вспомогательной системы подачи жидкости), соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость поршня гидроцилиндра
6, при заданном расходе жидкости, направляемом в гидроаккумулятор 2 (Q0),
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длина от точки L до гидроцилиндра 6 – l1;
– длина от гидроцилиндра 6 до бака 4 – l1;
– длина от точки L до клапана 1 – l3.
Известны также: давление в аккумуляторе рак = 8 · р0, сила на штоке
поршня F = F1, его размеры D и dш. Учесть потери в трубопроводах при вязкости жидкости , а также потери в клапане 1 (эквивалентная длина lэ2), в дросселе 3 (коэффициент расхода μ = 0,7, проходное сечение S2) и в распределителе 5
(эквивалентная длина одного канала lэ1). Принять механический КПД цилиндра ηм = 0,98, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ1, lэ2, dт, S2, D, dш, F1, р0 и Q0 взять из таблицы 1.2).
29
Вариант 1.5
Сложный трубопровод содержит регулируемый дроссель 1, распределитель 2, гидроцилиндр 3, переливной клапан 2, охладитель жидкости 4, бак 5,
соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и расход через охладитель 4 при
заданной скорости поршня гидроцилиндра 3 (V = V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до распределителя (до точки L) – l1;
– длина от распределителя до гидроцилиндра 3 – l2;
– длина от гидроцилиндра 3 до бака 5 – l2;
– длина от распределителя 2 через охладитель 4 до бака 5 – 2·l1.
Известны также: сила на штоке поршня F2, его размеры D и dш. Учесть
потери в трубопроводах при вязкости жидкости , а также потери в дросселе 1
(коэффициент сопротивления ζ2), в распределителе 2 (эквивалентная длина одного канала lэ2) и в охладителе 4 (эквивалентная длина lэ2). Принять механический КПД гидроцилиндра ηм = 0,97, плотность жидкости ρ = 900 кг/м3, а режим
течения ламинарным.
(Величины , l1, l2, lэ2, dт, ζ2, D, dш, F2 и V1 взять из таблицы 1.2).
30
Вариант 1.6
Сложный трубопровод содержит распределитель 3, регулируемые дроссели 4 и 5, гидроцилиндры 6 и 7, фильтр 1, бак 2, соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость поршня гидроцилиндра
6 (V1) при заданной скорости поршня гидроцилиндра 7 (V2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длина точки L’ до бака 2 l1;
– другими длинами пренебречь.
Известны также: силы на штоках поршней F1, F2, их диаметры – D, dш
(они для цилиндров 6 и 7 одинаковы). Учесть потери в трубопроводах при вязкости жидкости , а также потери в распределителе 3 (эквивалентная длина
каждого канала lэ1), в дросселе 4 (коэффициент сопротивления ζ1), в дросселе 5
(коэффициент сопротивления ζ2) и в фильтре 1 (эквивалентная длина lэ2). Принять механические КПД гидроцилиндров ηм = 0,95, плотность жидкости ρ =
900 кг/м3, а режим течения ламинарным.
(Величины , l1, lэ1, lэ2, dт, ζ1, ζ2, D, dш, F1, F2, и V2 взять из таблицы 1.2).
31
Вариант 1.7
Сложный трубопровод содержит распределитель 2, регулируемые дроссели 3 и 4, гидроцилиндры одностороннего действия 5 и 6, бак 1, соединенные
по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость поршня гидроцилиндра
6 (V2) при заданной скорости поршня гидроцилиндра 5 (V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – 2·l1;
– длины от точки L до гидроцилиндров 5 и 6 одинаковы и равны l1.
Известны также: силы на штоках поршней F1, F2, и диаметры – D, dш (они
для цилиндров 5 и 6 одинаковы) и вязкость жидкости . Учесть потери в трубопроводах, длины которых заданы, а также в распределителе 2 (эквивалентная
длина lэ2), в дросселе 3 (проходное сечение 0,6·S1) и в дросселе 4 (проходное
сечение S2). Принять коэффициент расхода дросселей μ = 0,7, механические
КПД гидроцилиндров ηм = 0,95, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, lэ2, S1, S2, dт, D, dш, F1, F2 и V1 взять из таблицы 1.2).
32
Вариант 1.8
Сложный трубопровод содержит регулируемый дроссель 3, распределитель 4, гидроцилиндры 5 и 6, охладитель жидкости 7, фильтр 2, бак 1, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость поршня гидроцилиндра
5 (V2) при заданной скорости поршня гидроцилиндра 6 (V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длины от точки L до гидроцилиндров 5 и 6 одинаковы и равны – l1;
– длина от гидроцилиндра 5 до точки L’ – 2·l1;
– длина от точки L’ до бака 1 l1.
Известны также: силы на штоках поршней F1, F2, их диаметры – D, dш
(они для цилиндров 5 и 6 одинаковы) dш. Учесть потери в трубопроводах при
вязкости жидкости , а также потери в распределителе 3 (эквивалентная длина
одного канала lэ1), в дросселе 4 (коэффициент сопротивления ζ1), в охладителе
7 (эквивалентная длина lэ2) и в фильтре 2 (эквивалентная длина lэ2). Принять
механические КПД гидроцилиндров ηм = 0,97, плотность жидкости ρ = 900
кг/м3, а режим течения ламинарным.
(Величины , l1, lэ1, lэ2, dт, ζ1, D, dш, F1, F2, и V1 взять из таблицы 1.2).
33
Вариант 1.9
Сложный трубопровод содержит распределитель 3, регулируемый дроссель 4, гидроцилиндры 5 и 6, фильтр 1, бак 2, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость поршня гидроцилиндра
5 (V2) при заданной скорости поршня гидроцилиндра 6 (V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l3;
– длины от точки L до гидроцилиндров 5 и 6 одинаковы и равны l1;
– длины от цилиндров 5 и 6 до точки L’ также одинаковы и равны l1;
– длина от точки L’ до бака 2 – l1;
– другими длинами пренебречь.
Известны также: силы на штоках поршней F1, F2, их диаметры – D, dш
(они для цилиндров 5 и 6 одинаковы). Учесть потери в трубопроводах при вязкости жидкости , а также потери в распределителе 3 (эквивалентная длина одного канала lэ2), в дросселе 4 (коэффициент расхода μ = 0,7, проходное сечение
S2) и в фильтре 1 (эквивалентная длина lэ3). Принять механические КПД гидроцилиндров ηм = 0,96, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ2, D, dш, S2, dт, F1, F2 и V2 взять из таблицы 1.2).
34
Вариант 1.10
Сложный трубопровод содержит регулируемый дроссель 1, распределители 2 и 5, гидроцилиндры 6 и 7, фильтр 3, бак 4, соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и расход жидкости через фильтр 3
при заданной скорости поршня гидроцилиндра 5 (Vп1 = V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l3;
– длина от точки L до гидроцилиндра 6 – l3;
– длина от гидроцилиндра 6 до гидроцилиндра 7 – l3;
– длина от гидроцилиндра 7 до бака4 – l1;
– длина от точки L через фильтр 3 до бака 4 – l1.
Известны также: силы на штоках поршней Fп1 = 0,5·F1, Fп2 = 0,5·F2, и их
диаметры – D, dш (они для цилиндров 6 и 7 одинаковы). Учесть потери в трубопроводах при вязкости жидкости , а также потери в дросселе 1 (коэффициент расхода μ = 0,7, проходное сечение S2), в распределителях 2 и 5 (эквивалентная длина одного канала lэ1), и в фильтре 3 (эквивалентная длина lэ3). Принять механические КПД гидроцилиндров ηм = 0,97, плотность жидкости ρ =
900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ1, lэ3, dт, S2, D, dш, F1, F2 и V1 взять из таблицы 1.2).
35
Вариант 1.11
Сложный трубопровод содержит регулируемый дроссель 1, распределители 2 и 6, гидромотор 7, фильтр 5, охладитель жидкости 3, бак 4, соединенные
по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и расход через охладитель 3 при
заданной скорости вращения вала гидромотора 7 (ω = ω1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l3;
– длина от точки L до гидромотора 7 – l1;
– длина от гидромотора 7 до бака 4 – l1;
– длина от точки L через охладитель 3 до бака 4 – l2.
Известны также: сила на гидромоторе М = М2 и его рабочий объем Wo.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
дросселе 1 (коэффициент сопротивления ζ2), в распределителях 2 и 6 (эквивалентная длина одного канала lэ1), в фильтре 5 (эквивалентная длина lэ3) и в охладителе 2 (эквивалентная длина lэ3). Принять КПД гидромотора: механический – ηм = 0,94, объемный – ηо = 0,96; плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l2, l3, lэ1, lэ3, dт, ζ2, Wo, М2 и ω1 взять из таблицы 1.2).
36
Вариант 1.12
Сложный трубопровод содержит распределитель 4, регулируемый дроссель 5, гидромотор 6, фильтр 1, переливной клапан 3, бак 2, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и расход через клапан 3 при известном расходе фильтр 1 (Q0).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до гидромотора 6 – l1;
– длина от гидромотора 6 до точки L – l1;
– длины разветвленных участков от точки L до бака 2 одинаковы и равны l1.
Известны также: сила на гидромоторе М = М2 и его рабочий объем Wo.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
распределителе 4 (эквивалентная длина одного канала lэ1), в дросселе 5 (коэффициент сопротивления ζ1), в фильтре 1 (эквивалентная длина lэ3) и в клапане 3,
характеристика которого Δрк = р0 + k · Q. Принять КПД гидромотора: механический – ηм = 0,95, объемный – ηо = 0,95; коэффициент k = 2·103 МПа·с/м3, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, lэ1, lэ3, dт, ζ1, Wo, М2, р0, и Q0 взять из таблицы 1.2).
.
37
Вариант 1.13
Сложный трубопровод содержит регулируемый дроссель 1, распределитель 2, гидромотор 4, фильтр 3, охладитель жидкости 5, бак 6, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и расход через фильтр 3 при заданной скорости вращения вала гидромотора 4 (ω = ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до распределителя 2 (до точки L) – l1;
– длина от распределителя 2 до гидромотора 4 – l1;
– длина от гидромотора 4 до бака 6 – l1;
– длина от распределителя через фильтр 3 и охладитель 2 до бака 6 – l2.
Известны также: сила на гидромоторе М = М1 и его рабочий объем Wo.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
дросселе 1 (коэффициент расхода μ = 0,7, проходное сечение S2), в распределителе 2 (эквивалентная длина одного канала lэ1), в фильтре 3 (эквивалентная
длина lэ3) и в охладителе 5 (эквивалентная длина lэ3). Принять КПД гидромотора: механический – ηм = 0,92, объемный – ηо = 0,98; плотность жидкости ρ =
900 кг/м3, а режим течения ламинарным.
(Величины , l1, l2, lэ1, lэ3, dт, S2, Wo, М1 и ω2 взять из таблицы 1.2).
38
Вариант 1.14
Сложный трубопровод содержит регулируемый дроссель 1, распределитель 3, гидромотор 5, фильтр 4, обратный клапан 6, бак 2, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и расход через фильтр 4 при заданной скорости вращения вала гидромотора 5 (ω = ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длины параллельных участков от точки L до точки L’ одинаковы и равны l1;
– длина от точки L’ до бака 2 – l1.
Известны также: сила на гидромоторе М = М2 и его рабочий объем Wo.
Учесть потери в трубопроводах при вязкости жидкости , а также потери в
дросселе 1 (коэффициент сопротивления ζ1), в распределителе 3 (эквивалентная
длина одного канала lэ1), в фильтре 4 (эквивалентная длина lэ3) и в клапане 6
(эквивалентная длина lэ2). Принять КПД гидромотора: механический – ηм =
0,94, объемный – ηо = 0,96; плотность жидкости ρ = 900 кг/м3, а режим течения
ламинарным.
(Величины , l1, lэ2, lэ3, dт, ζ1, Wo, М2 и ω2 взять из таблицы 1.2).
39
Вариант 1.15
Сложный трубопровод содержит охладитель жидкости 1, распределитель
2, регулируемый дроссель 3, гидромотор 4, фильтр 6, редукционный клапан 8,
гидроаккумулятор 7 (для вспомогательной системы), бак 5, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и расход через клапан 8 при заданной скорости вращения вала гидромотора 4 (ω = ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до распределителя 2 (до точки L) – l3;
– длина от распределителя 2 через фильтр 6 до клапана 8 – l1;
– длина от распределителя 2 через дроссель 3 и гидромотор 4 до бака 5 – l3.
Известны также: давление аккумулятора 7 рак = 2· р0, сила на гидромоторе
М = М1 и его рабочий объем Wo. Учесть потери в трубопроводах при вязкости
жидкости , а также потери в охладителе 1 (эквивалентная длина lэ3), в распределителе 2 (эквивалентная длина одного канала lэ1), в дросселе 3 (коэффициент
расхода μ = 0,7, проходное сечение S2), в фильтре 6 (эквивалентная длина lэ3) и
потери в клапане 8 (эквивалентная длина lэ2). Принять КПД гидромотора: механический – ηм = 0,96, объемный – ηо = 0,94; плотность жидкости ρ = 900
кг/м3, а режим течения ламинарным.
(Величины , l1, l2, lэ1, lэ2, lэ3, dт, S2, Wo, М1 и ω2 взять из таблицы 1.2).
40
Вариант 1.16
Сложный трубопровод содержит регулируемый дроссель 1, распределители 4 и 5, гидромоторы 6 и 7, нерегулируемый дроссель 5, фильтр 2, бак 3, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
6 (ω1) при заданной скорости гидромотора 7 (ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l3;
– длины от точки L до гидромоторов 6 и 7 одинаковы и равны l1;
–длины от гидромоторов 6 и 7 до точки L’ также одинаковы и равны l1;
– длина от точки L’ до бака 3 – l2.
Известны также: моменты на валах гидромоторов М1, М2, их рабочие
объемы – Wо. Учесть потери в трубопроводах при вязкости жидкости , а также
потери в дросселе 1 (коэффициент расхода μ = 0,7, проходное сечение S1), в
распределителях 4 и 5 (эквивалентная длина одного канала lэ1) и в фильтре 2
(эквивалентная длина lэ2). Принять КПД гидромоторов: механические – ηм =
0,95, объемные – ηо = 0,95; плотность жидкости ρ = 900 кг/м3, а режим течения
ламинарным.
(Величины , l1, l3, lэ1, lэ2 dт, S1, Wo, М1, М2, и ω2 взять из таблицы 1.2).
41
Вариант 1.17
Сложный трубопровод содержит распределитель 3, регулируемые дроссели 4 и 5, гидромоторы 6 и 7, фильтр 2, бак 1, соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
7 (ω2) при заданной скорости вращения гидромотора 6 (ω1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l3;
– суммарная длина от точки L до гидромотора 6 и далее до точки L’ – 2·l2;
– суммарная длина от точки L до гидромотора 7 и далее до точки L’ – 3·l1;
– длина от точки L’ до бака 2 – l2.
Известны также: моменты на валах гидромоторов М1, М2, их рабочие
объемы – Wо. Учесть потери в трубопроводах при вязкости жидкости , а также
потери в распределителе 3 (эквивалентная длина одного канала lэ1), в дросселе
4 (коэффициент сопротивления ζ1), в дросселе 5 (коэффициент сопротивления
ζ2) и в фильтре 2 (эквивалентная длина lэ2). Принять КПД гидромоторов: механические – ηм = 0,97, объемные – ηо = 0,92; плотность жидкости ρ = 900 кг/м3, а
режим течения ламинарным.
(Величины , l1, l2, l3, lэ1, lэ2, dт, ζ1, ζ2, Wo, М1, М2 и ω1 взять из таблицы 1.2).
42
Вариант 1.18
Сложный трубопровод содержит распределитель 3, регулируемые дроссели 4 и 6, гидромоторы 5 и 7, охладитель жидкости 1, бак 2, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
5 (ω1) при заданной скорости гидромотора 7 (ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– суммарная длина от точки L через гидромотор 5 до точки L’ – l2;
– суммарная длина от точки L через гидромотор 7 до точки L’ – l1;
– длина от точки L’ до бака 2 – l1.
Известны также: моменты на валах гидромоторов М1, М2, их рабочие
объемы – Wо. Учесть потери в трубопроводах при вязкости жидкости , а также
потери в распределителе 3 (эквивалентная длина одного канала lэ1), в дросселях
4 и 6 (коэффициент расхода μ = 0,7, проходные сечения одинаковы – S1) и в охладителе 1 (эквивалентная длина lэ2). Принять КПД гидромоторов: механические – ηм = 0,94, объемные – ηо = 0,96; плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l2, lэ1, lэ2, dт, S1, Wo, М1, М2 и ω2 взять из таблицы 1.2).
43
Вариант 1.19
Сложный трубопровод содержит распределители 1 и 6, регулируемый
дроссель 5, гидромоторы 7 и 8, фильтр 2, охладитель жидкости 3, бак 4, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и расход через фильтр 2 при заданной скорости вращения гидромотора 8 (ω1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – 3·l1;
– длина от точки L до гидромотора 8 – l1;
– длина от гидромотора 8 до гидромотора 7 – l3;
– длина от гидромотора 7 до бака – l1:
– длина от точки L через фильтр 3 и охладитель 2 до бака – l1.
Известны также: моменты на валах гидромоторов М1, М2, их рабочие
объемы – Wо. Учесть потери в трубопроводах при вязкости жидкости , а также
потери в распределителях 1 и 6 (эквивалентная длина одного канала lэ2), в
дросселе 5 (коэффициент сопротивления ζ2), в фильтре 3 (эквивалентная длина
lэ3) и в охладителе 2 (эквивалентная длина lэ3). Принять КПД гидромоторов:
механические – ηм = 0,96, объемные – ηо = 0,92; плотность жидкости ρ = 900
кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ2, lэ3, dт, ζ2, Wo, М1, М2, и ω1 взять из таблицы 1.2).
44
Вариант 1.20
Сложный трубопровод содержит распределитель 1, регулируемые дроссели 4 и 6, гидромоторы 5 и 7, фильтр 3, бак 2, соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
5 (ω1) при заданной скорости гидромотора 7 (ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – 2·l1;
– суммарная длина от точки L до гидромотора 5 и далее до бака 2 – l2;
– суммарная длина от точки L до гидромотора 7 и далее до бака 2 – 2·l1..
Известны также: моменты на валах гидромоторов М1, М2, их рабочие
объемы одинаковы – Wо. Учесть потери в трубопроводах при вязкости жидкости , а также потери в распределителе 3 (эквивалентная длина lэ2), в дросселе 4
(проходное сечение – S2) и в дросселе 6 (проходное сечение – S1). Принять КПД
гидромоторов: механические – ηм = 0,93, объемные – ηо = 0,96; коэффициент
расхода дросселей μ = 0,7, плотность жидкости ρ = 900 кг/м3, а режим течения
ламинарным.
(Величины , l1, l2, lэ2, dт, S1, S2, Wo, М1, М2, ω2 и взять из таблицы 1.2).
45
Вариант 1.21
Сложный трубопровод содержит распределитель 3, регулируемые дроссели 4 и 6, гидроцилиндр 5, гидромотор 7, фильтр 2, бак 1, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
7 (ω2) при заданной скорости поршня гидроцилиндра 5 (V1).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l2;
– длина от точки L до гидроцилиндра 5 и далее до точки L’ – l2;
– длина от точки L до гидромотора 7 и далее до точки L’ – l1;
– длина от точки L’ до бака 2 – l2.
Известны также: момент на валу гидромотора М2, сила на штоке гидроцилиндра F1, рабочий объем гидромотора Wо, диаметры поршня и штока цилиндра – D, dш. Учесть потери в трубопроводах при вязкости жидкости , а
также потери в распределителе 3 (эквивалентная длина одного канала lэ1), в
дросселях 4 и 6 (коэффициенты сопротивления соответственно ζ 1 и ζ2) и в
фильтре 1 (эквивалентная длина lэ2). Принять механические КПД гидромотора
и цилиндра одинаковыми – ηмм = 0,93, объемный КПД гидромотора – ηмо =
0,97, плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l2, lэ1, lэ2, dт, ζ1, ζ2, D, dш, Wo, F1, М2 и V1 взять из таблицы 1.2).
46
Вариант 1.22
Сложный трубопровод содержит распределители 4 и 6, гидромотор 3, регулируемый дроссель 5, гидроцилиндр 7, фильтр 2, бак 1, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
4 (ω1) при заданной скорости поршня гидроцилиндра 7 (V2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длина от точки L до гидромотора 3 и далее до точки L’ – 2·l1;
– длина от точки L до гидроцилиндра 7 и далее до точки L’ – 2·l3;
– длина от точки L’ до бака 1 – l1.
Известны также: момент на валу гидромотора М1, сила на штоке цилиндра F2, рабочий объем гидромотора Wо, диаметры поршня и штока цилиндра –
D, dш. Учесть потери в трубопроводах при вязкости жидкости , а также потери
в распределителях 4 и 6 (эквивалентная длина одного канала lэ2), в дросселе 5
(коэффициент расхода μ = 0,7, проходное сечение – S2) и в фильтре 1 (эквивалентная длина lэ2). Принять механический КПД гидромотора – ηмм = 0,94, его
объемный КПД – ηмо = 0,96, механический КПД гидроцилиндра – ηцм = 0,95,
плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ2, dт, S2, D, dш, Wo, F2, М1, и V2 взять из таблицы 1.2).
47
Вариант 1.23
Сложный трубопровод содержит распределители 1 и 6, регулируемые
дроссели 2 и 3, гидромотор 4, гидроцилиндр 7, бак 5, соединенные по следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
4 (ω1) при заданной скорости поршня гидроцилиндра 7 (V2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – 2·l1;
– длина от точки L до гидромотора 4 и далее до бака 5 – l2;
– длина от точки L до гидроцилиндра 7 – l1.
Известны также: момент на валу гидромотора М1, сила на штоке гидроцилиндра F2, рабочий объем гидромотора Wо, диаметры поршня и штока гидроцилиндра – D, dш. Учесть потери в трубопроводах при вязкости жидкости ,
а также потери в распределителях 1 и 6 (эквивалентная длина одного канала
lэ2), в дросселях 2 и 3 (коэффициенты сопротивления одинаковы – ζ2). Принять:
механический КПД гидромотора – ηмм = 0,95, его объемный КПД – ηмо = 0,95,
механический КПД гидроцилиндра – ηцм = 0,97, плотность жидкости ρ = 900
кг/м3, а режим течения ламинарным.
(Величины , l1, l2, lэ2, dт, ζ2, D, dш, Wo, F2, М1 и V2 взять из таблицы 1.2).
48
Вариант 1.24
Сложный трубопровод содержит регулируемый дроссель 1, распределители 3, 4 и 6, гидромотор 5, гидроцилиндр 7, бак 2, соединенные по следующей
схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость вращения гидромотора
5 (ω1) при заданной скорости поршня гидроцилиндра 7 (V2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l3;
– длина от точки L до гидромотора 5 и далее до точки L’ – 2·l1;
– длина от точки L до гидроцилиндра 7 и далее до точки L’ – 2·l1;
– длина от точки L’ до бака 2 – l3.
Известны также: момент на валу гидромотора М1, сила на штоке гидроцилиндра F2, рабочий объем гидромотора Wо, диаметры поршня и штока цилиндра – D, dш. Учесть потери в трубопроводах при вязкости жидкости , а
также потери в дросселе 5 (коэффициент расхода μ = 0,7, проходное сечение –
1,2·S2), в распределителях 3, 4 и 6 (эквивалентная длина одного канала lэ1).
Принять: механический КПД гидромотора – ηмм = 0,96, его объемный КПД –
ηмо = 0,94, механический КПД цилиндра – ηцм = 0,93, плотность жидкости ρ =
900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ1, dт, S2, D, dш, Wo, F2, М1 и V2 взять из таблицы 1.2).
49
Вариант 1.25
Сложный трубопровод содержит регулируемый дроссель 1, распределители 2 и 4, гидроцилиндр 5, гидромотор 6, фильтр 7, бак 3, соединенные по
следующей схеме.
Построить суммарную характеристику сложного трубопровода в координатах p– Q. При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК), и скорость поршня гидроцилиндра 5 (V1) при заданной скорости вращения гидромотора 6 (ω2).
Трубопроводы имеют одинаковый диаметр dт и следующие длины:
– длина от точки K до точки L – l1;
– длина от точки L до гидромотора 6 и далее до бака 3 – 2·l1;
– длина от точки L до гидроцилиндра 7 – l3;
– длина от гидроцилиндра 7 до бака 3 – l3.
Известны также: момент на валу гидромотора М2, сила на штоке гидроцилиндра F1, рабочий объем гидромотора Wо, диаметры поршня и штока гидроцилиндра – D, dш. Учесть потери в трубопроводах при вязкости жидкости ,
а также потери в дросселе 1 (коэффициент сопротивления – ζ1), в распределителях 2 и 4 (эквивалентная длина одного канала lэ1), и в фильтре 7 (эквивалентная длина 2·lэ2). Принять: механический КПД гидромотора – ηмм = 0,93, его
объемный КПД – ηмо = 0,95, механический КПД гидроцилиндра – ηцм = 0,96,
плотность жидкости ρ = 900 кг/м3, а режим течения ламинарным.
(Величины , l1, l3, lэ1, lэ2 dт, ζ1, D, dш, Wo, F1, М2, и ω2 взять из таблицы 1.2).
50
1.7. Значения параметров элементов гидравлических систем
Таблица 1.2
Вариант
Параметры гидравлических систем
ν
А
см2/с 0,55
Б
В
Г
Д
Е
Ж
З
0,7
0,95
0,5
0,9
0,75
0,6
0,8
И
К
0,85 0,65
l1
м
7
2,5
9
8,5
9,5
2
6,5
1,8
10
6
l2
м
3,5
1,2
4,2
4
4,5
1
3
0,8
5
2,5
l3
м
1,8
0,6
2,2
2,2
2,4
0,5
1,5
0,4
2,5
1,2
lэ1
м
4,5
1,5
5,3
5
5,5
1,5
4
1,2
6
3,5
lэ2
м
12
4,5
16
15
17
4
11
3,8
18
10
lэ3
м
40
14
45
45
50
12
36
10
55
32
dт
мм
10
8
12
10
12
8
10
8
12
10
ζ1
–
35
15
50
40
60
18
45
14
80
30
ζ2
–
85
30
130
80
140
35
75
28
150
70
S1
мм2
6
6
6,5
5,5
6
6,5
5,5
6
5,5
6,5
S2
мм2
7,5
7,5
8,5
8,5
8,5
8
8
8
7,5
9
D
мм
45
40
50
35
30
30
40
50
45
35
dш
мм
22
20
25
18
15
15
20
25
22
18
Wо
см3
55
23
28
32
40
28
23
40
32
55
F1
кН
6
5
8
4
2,8
3
4,8
8
6,5
4
F2
кН
4
3
5
2,5
1,8
2
3
5
4
2,5
M1
Н·м
25
11
13
15
20
14
10
20
15
28
M2
Н·м
17
7
9
10
13
10
7
14
10
20
р0
МПа 0,55 0,55 0,55 0,65 0,55 0,65
0,6
0,6
V1
см/с
10
12
8
16
20
20
12
8
10
12
V2
см/с
22
28
18
36
48
44
28
18
22
36
ω1
рад/с
17
40
35
30
25
35
40
25
30
17
ω2
рад/с
35
80
70
60
50
70
80
50
60
35
Q0
л/с
0,22
0,2
0,2
0,18
0,2
0,24 0,18 0,24 0,22 0,18
0,65 0,65
51
2. Расчетно-графическая работа № 2
ПОСТРОЕНИЕ ХАРАКТЕРИСТИКИ НАСОСНОЙ УСТАНОВКИ
2.1 Общие положения
В большинстве современных машиностроительных гидросистем, в том
числе в объемных гидроприводах, для подачи жидкости используются насосные установки, построенные на основе объемных роторных насосов.
Под насосной установкой при этом понимают насос с дополнительными
устройствами, обеспечивающие необходимые параметры потока, поступающего в гидросистему.
В простейшем случае, когда не требуется автоматическое регулирование
подачи жидкости, поступающей в гидросистему, насосная установка состоит из
нерегулируемого насоса и предохранительного клапана.
В насосных установках, от которых во время работы требуется автоматическое регулирование подачи, поступающей в гидросистему, используют нерегулируемый насос с переливным клапаном или регулируемый насос с автоматическим регулятором подачи.
Расчет режима работы насосной установки, как правило, состоит в определении его рабочих параметров: подачи Q и давления p на выходе, а также
полезной Nпол, потребляемой Nпотр мощности и кпд η.
Основой для расчета параметров, характеризующих режим работы насосной установоки, является ее характеристика, под которой понимают зависимость p = f(Q).
На практике рекомендуется использовать приведенные ниже методики
построения характеристики насосной установки.
2.2. Рабочий объем насоса
Подача жидкости объемного насоса происходит из его рабочих камер.
Обычно роторный насос имеет несколько рабочих камер, число которых определяет рабочий объем насоса. Под рабочим объемом Wo понимают максимальное количество жидкости, которое насос может подать в гидросистему за один
52
рабочий цикл. Для большинства насосов рабочим циклом является один оборот
его вала. За один рабочий цикл каждая рабочая камера насоса обычно совершает одну подачу жидкости. Такие насосы называют насосами однократного действия. Существуют также насосы много кратного действия, у которых за один
оборот вала каждая рабочая камера совершает несколько раз подачу жидкости.
Исходя из этого, рабочий объем насоса равен:
Wo Wк z i ,
(2.1)
где Wк – рабочий объем одной рабочей камеры;
z – количество рабочих камер в насосе;
i – кратность действия насоса.
Объем рабочей камеры насоса зависит от его конструкции. Рассмотрим
способы определение объема рабочей камеры для некоторых наиболее часто
используемых роторных насосов. Для этого выделим две группы насосов.
К первой группе отнесем насосы с
рабочими камерами постоянной ширины, например, шестеренные, пластинчатые и др. При определении объема рабочей камеры такого насоса, прежде всего,
целесообразно определить ее площадь
поперечного сечения. В качестве примера рассмотрим определение объема рабочей камеры для шестеренного насоса с
внешним зацеплением, поперечный разрез которого представлено на рис. 2.1.
Рис. 2.1. Шестеренный насос
с внешним зацеплением.
Поперечное сечение рабочей камеры насоса выделено штриховкой, и оно
представляет собой сложную геометрическую фигуру. Ее площадь S следует
вычислять по формулам теории эвольвентного зацепления или известными
приближенными методами определения площадей геометрических фигур. После определения площади S объем рабочей камеры, при известной ее ширине b,
53
найдем из формулы:
Wк S b .
Заметим, что рассмотренный шестеренный насос является нерегулируемым насосом, то есть его конструкция не позволяет регулировать величину его
рабочего объема.
К второй группе насосов отнесем насосы с рабочими камерами в форме цилиндров, например, роторно-поршневые. При
вычислении объема цилиндра важным является определение его высоты. В качестве
примера рассмотрим определение объема
рабочей камеры для аксиально-поршневого
Рис. 2.2. Аксиально-поршневой
насос с наклонным диском.
насоса с наклонным диском, поперечный
разрез которого представлено на рис. 2.2.
Рабочий объем камеры насоса имеет цилиндрическую форму и выделен
штриховкой – цилиндр диаметром d и высотой h. Из рисунка видно, что высота
этого цилиндра равна ходу поршня и зависит от диаметра расположения цилиндров D и угла наклона диска γ. Тогда объем рабочей камеры равен:
d2
d2
Wк
h
D tg .
4
4
Заметим, что рассмотренный аксиально-поршневой насос может быть
выполнен регулируемым, то есть, если в его конструкции имеется возможность
изменять величину угла γ наклона диска, то это позволяет регулировать величину рабочего объема насоса.
Отметим, что величина рабочего объема насоса обычно известна из его
технического паспорта или из справочника.
2.3. Насос с предохранительным клапаном
На рис. 2.3,а представлены гидравлическая схема насосной установки состоящей из нерегулируемого насоса 1 и предохранительного клапана 2.
54
Предохранительный клапан 2, срабатывает только в аварийных ситуациях, а при нормальной работе закрыт, т.е. Qкл = 0 и подача насосной установки
Qну равна подаче насоса, т.е. Qну = Qн. Следовательно, характеристика насосной установки совпадает с характеристикой роторного насоса.
Рис. 2.3. Насос с предохранительным клапаном.
Характеристика нерегулируемого роторного насоса приведена на рис.
2.3,б. Она представляет собой прямую линию и, следовательно, может быть построена по двум точкам:
– точка А соответствует теоретической подачи насоса Qт, вал которого
вращается с частотой n. Она определяется по формуле:
Qт Wo n ;
(2.2)
– абсцисса точки B Q*определяются по величине объемного к.п.д. насоса
ηон при определенном давлении р*
Q* Qт о н .
(2.3)
По двум точкам проводится прямая линия AB, которая является характеристикой насосной установки с предохранительным клапаном. Как было отмечено ранее, она совпадает с собственной характеристикой насоса.
2.4. Нерегулируемый насос с переливным клапаном
Конструктивная схема переливного клапана 2 приведена на рис. 2.4,а.
Его основными элементами являются подвижный плунжер 4 и пружина 3. Переливной клапан является постоянно действующим и при нормальной работе
насосной установки он частично открыт. Поэтому часть расхода Qн, посту-
55
пающего от насоса 1 (рис. 2.4,а), сливается через клапан 2 в бак Qкл, а оставшаяся часть и является подачей насосной установки Qну, т.е.
Qну Qн Qкл .
(2.4)
Таким образом, в данном случае имеем гидравлическую систему, состоящую из насоса 1 и клапана 2. Характеристика такой системы может быть
получена графически по известным характеристикам насоса и переливного
клапана.
Рис. 2.4. Насос с переливным клапаном.
Способ построения характеристики насоса рассмотрен в подразделе 2.3
(линия I на рис 2.4,б).
Известно, что характеристика переливного клапана с достаточной степенью точности может быть представлена в виде математического выражения:
Δр = ркл0 + k · Q,
(2.5)
где ркл0 – давление срабатывания (настройки) клапана;
k – коэффициент, величина которого зависит от жесткости пружины 3.
Давление срабатывания клапана может быть вычислено по формуле
pк0
Fпр
Sп
4 Fпр
d п2
,
(2.6)
где Fпр – сила предварительного поджатия пружины 3;
Sп и dп – площадь и диаметр плунжера клапана 4.
Коэффициент k является постоянной характеристикой данного клапана,
56
поэтому обычно задается. Таким образом, при известном давлении срабатывания переливного клапана рк0 (2.6) и коэффициенте k может быть построена его
характеристика (2.5). Она приведена на рис. 2.4,б (линия II).
Характеристику насосной установки получают в результате графического
вычитания характеристики клапана из характеристики насоса при постоянном
значении давления pн в соответствии с (2.4). При этом рекомендуется следующая методика:
– точку В′ переносят с оси ординат на линию I, т.е. получают точку В;
– точку С′ (пересечения линий I и II) переносят на ось ординат, т.е. получают точку С;
– соединяют точки В и С.
В результате получается характеристика насосной установки с переливным клапаном (ломаная линия АВС на рис. 2.4,б).
2.5. Регулируемый насос с автоматическим регулятором подачи
Регулятор подачи может использоваться в составе насосной установки
только совместно с регулируемым насосом. Он обеспечивает автоматическое
изменение рабочего объема насоса и, следовательно, изменение его подачи.
На рис. 2.5,а представлена схема насосной установки с регулируемым
роторным насосом 1 и простейшим регулятором подачи 2, основными элементами которого является пружина 3 и поршень 4. В процессе работы поршень
регулятора перемещаясь, воздействует на управляющий элемент насоса (на
рис. 2.5,а условно показан в виде наклонной стрелки). За счет этого меняется
рабочий объем насоса и, следовательно, его подача Qн.
В такой насосной установке регулятор изменяет подачу за счет изменения рабочего объема насоса, поэтому подача насосной установки всегда равна
подаче насоса, то есть справедливо равенство Qн = Qну.
При давлении р на выходе насоса, меньшем давления рр0 срабатывания
(настройки) регулятора, поршень 4 регулятора занимает крайнее правое положение, Тогда рабочий объем насоса и, следовательно, его подача максимальна.
57
Рис. 2.5. Насос с регулятором подачи.
Давление срабатывания регулятора может быть вычислено по формуле:
pp0
Fпр
Sп
4 Fпр
d п2
,
(2.7)
где Fпр – сила предварительного поджатия пружины 3;
Sп и dп – площадь и диаметр плунжера 4.
При р > рр0 поршень 4 под действием жидкости начинает перемещаться
влево, уменьшая рабочий объем насоса. На рис. 2.5,а показано положение
поршня 4 со смещением х. В результате уменьшается подача насоса и насосной установки. При смещении поршня 4 в крайнее левое положение подача
становиться равной нулю, т.е. Qн = Qну = 0. На этом режиме работы давление в
системе будет максимальным рmax. Это давление определиться по формуле
pmax
Fпр, max
Sп
4 Fпр c x max
d п2
,
(2.8)
где с – жесткость пружины 3;
xmax – величина максимального смещения поршня 4.
При построении характеристики насосной установки с регулятором подачи рекомендуется использовать следующую методику:
– в координатах p .– Q с использованием формул (2.2)÷(2.3) по методике,
изложенной в подразделе 2.3, строят характеристику объемного насоса
при максимальном значении его рабочего объема (линия I на рис.
2.5,б);
58
– на ось ординат наносят давление срабатывания регулятора рр0, определенное по формуле (2.7), точка В′ на рис. 2.5,б;
– точку В′ переносят с оси ординат на линию I, т.е. получают точку В;
– на ось ординат наносят величину максимального давления рmax, определенное по формуле (2.8), точка С на рис. 2.5,б;
– соединяют точки В и С.
В результате получена характеристика насосной установки с регулятором
подачи (ломаная линия АВС на рис. 2.5,б).
Полученная характеристика насосной установки с регулятором подачи
имеет тот же внешние вид (рис. 2.5,б), что и характеристика роторного насоса
с переливным клапаном (рис. 2.4,б). Однако, необходимо помнить, что при использовании переливного клапана эффект снижения подачи насосной установки получен за счет слива части подаваемой насосом жидкости обратно в бак
без совершения полезной работы. При использовании регулятора подачи аналогичный эффект получается за счет уменьшения величины рабочего объема
насоса, что более экономично.
2.6. Определение мощности насосной установки
Для определения величины полезной и потребляемой мощности необходимо знать режим работы насосной установки, т.е. положение рабочей точки
на характеристике насоса.
Наиболее просто ответь на эти
вопросы для насосной установки, состоящей из насоса и предохранительного клапана. В условиях ее
нормальной работы вся подача насоса
направляется в гидросистему, следовательно, подача насоса и насосной
установки одинаковы Qн = Qну.
Рис. 2.6. Работа насосной установки с
предохранительным клапаном.
При известном режиме работы, т.е. определенном положении точки R на
59
характеристике АВ (рис. 2.6), по графику определяют подачу Qн = Qну и давление насоса рн (рис. 2.6) и вычисляют полезную мощность:
Nпол pн Qн pн Qну .
(2.9)
Потребляемую насосом мощность, которая одновременно является мощностью, потребляемой насосной установкой, вычисляют по формуле:
Nпотр
N пол pн Qн
,
н
н
(2.10)
где ηн – п+олный КПД насоса равный произведению его механического ηмн и
объемного ηон КПД, т.е.
н м н о н .
(2.11)
Используя зависимость (2.11) и с учетом (2.3), которая позволяет выразить действительную подачу Qн через теоретическую Qт, формулу (2.10) можно
свести к виду:
Nпотр
pн Qн
p Q
н т .
о н м н
м н
(2.12)
Формула (2.12) более удобна для практического использования, чем
(2.10), так она учитывает зависимость объемного КПД насоса от давления, которое может быть весьма значительным.
Для насосной установки с переливным клапаном определение полезной и потребляемой мощностей зависит от того, где располагается рабочая
точка: на участке АВ характеристики
насосной установки, или на участке ВС
(рис. 2.7).
Если рабочая точка располагает- Рис. 2.7. Работа насосной установки
с переливным клапаном.
ся на участке АВ (точка R1 на рис, 2.7),
т.е. насосная установка работает при закрытом переливном клапане (рис. 2.4,а),
то задача определения мощностей аналогична рассмотренному ранее случаю, и
при расчете используют формулы (2.9)÷(2.12).
60
Если рабочая точка располагается на участке ВС (точка R2 на рис, 2.7), то
полезные мощности насоса и насосной установки не одинаковы. Действительно, в этом случае подача насосной установки Qну определяется точкой R2, а подача насоса Qн – точкой R2′. Их разница, в соответствии с формулой (2.4), равна
расходу жидкости через клапан Qкл (рисунки 2.4,а и 2.7).
Полезная мощность насосной установки вычисляется по формуле:
N пол pн Qну ,
(2.13)
а полезная мощность насоса по формуле:
pн Qн .
N пол
(2.14)
Потребляемая мощность насосной установки равна мощности, потребляемой насосом, и определяется по формуле (2.12).
Отметим, что насосная установка с переливным клапаном имеет, как
правило, низкие значения КПД, так как у нее на большинстве режимах работы
часть подачи насоса не производительно сливается в бак через клапан.
Для насосной установки, состоящей из регулируемого насоса с
регулятором подачи (рис. 2.5,а), рабочая точка гидросистемы также может располагаться либо на участке АВ
характеристики насоса при максимальном рабочем объеме, либо на участке ВС (рис. 2.8).
Рис. 2.8. Работа насосной установки
с регулятором подачи.
Если рабочая точка располагается на участке АВ (точка R1 на рис, 2.8), то
мощности определяются по аналогии со случаями, рассмотренными ранее, и
при расчете используются формулы (2.9)÷(2.12).
Если рабочая точка R2 лежит на участке ВС, то благодаря регулятору подачи (рис. 2.5,а) уменьшается рабочий объем насоса. Поэтому фактически изменилась и его характеристика, т.е. вместо линии АВС (рис. 2.8) характеристи-
61
кой стала линия ЕR2С. При этом точка Е соответствует теоретической подаче
насоса с новым значением рабочего объема, равной Q′т.
Заметим, что линии ЕR2 и АВ параллельны, так как при изменении рабочего объема насоса объемные потери в нем при равных давлениях остаются
практически одинаковыми.
Отсюда полезная мощность насоса определяется по формуле (2.13), а
мощность, потребляемая насосной установкой, вычисляется с использованием
формулы (2.12), в которой принимается Qт = Q′т, т.е.
N потр
pн Qт
нм
(2.15)
При использовании формулы (2.15) следует иметь в виду, что уменьшение рабочего объема насоса влечет за собой некоторое снижение механического КПД. Однако этим снижением нередко пренебрегают.
В заключение отметим, что кпд насосной установки с регулятором подачи всегда выше, чем кпд соответствующей установки с переливными клапанами, но регулируемые насосы существенно дороже нерегулируемых. Поэтому
вопрос о целесообразности использования того или иного варианта насосной
установки должен решаться с учетом экономической обоснованности.
2.7. Пример выполнения расчетно-графической работы
Рассмотрим метод построения характеристики насосной установки и определения параметров ее режима работы.
На рис. 2.9 приведена схема насосной установки состоящей из пластинчатого насоса 1 и регулятора подачи 4, для которой следует построить характеристику в координатах p – Q. Кроме того, необходимо определить ее подачу,
полезную и потребляемую мощности при напорном давлении pн = 6,4 МПа. Затем повторить вычисления при увеличении давления на 50%.
Насос 1 подает жидкость по трубопроводу вправо от точки К, от которой
информация о величине давления на выходе насоса поступает в регулятор подачи 4. В процессе работы поршень 5 регулятора имеет возможность смещать
62
ротор 3 вправо, сжимая пружину 6, и изменять подачу насоса.
При определении рабочего объема насоса следует
учесть, что его рабочей камерой является полость между
двумя соседними пластинами 2.
На рисунке одна из рабочих
камер выделена штриховкой.
Рис. 2.9. Схема насосной установки.
Предположим, что вычисления следует провести для насоса с диаметром
ротора D = 48 мм, при толщине пластин δ = 2 мм, ширине ротора b = 25 мм и
смещении ротора относительно корпуса е = 5 мм . Для определения площади
рабочей камеры воспользуемся формулой:
D e
S 2e
,
z
где z – число рабочих камер.
Кроме того, заданы следующие параметры: частота вращения насоса n =
1450 об/мин, диаметр поршня регулятора dп = 8 мм, сила предварительного
поджатия пружины 5 F0 = 0,45 кН и ее жесткость с = 20 Н/мм. Принять объемный КПД насоса ηон = 0,83 при давлении p = 12 МПа, а его механический КПД
считать равным ηмн = 0,95.
Используя приведенную зависимость, вычислим площадь поперечного
сечения рабочей камеры и ее объем:
3,14 48 5 103
D e
3
Wк S b 2e
b 2 5 10
2 103 25 103 6,43 106 м3 .
6
z
По формуле (2.1) найдем рабочий объем насоса:
Wo Wк z i 6, 43 106 6 1 38,61 10 6 м-6 .
Пользуясь методикой, изложенной в подразделе 2.3, построим характери-
63
стику насоса (линия I на рис. 2.5,б). Для этого сначала по формуле (2.2) найдем
Qт Wo n 38, 61106
1450
м3
,
0,933 106
60
с
а затем по (2.3) –
6
Q* Qт о н 0,933 10 0,83 0, 774 10
6
м3
.
с
Соединяя точки линией AB′, получаем характеристику пластинчатого насоса (рис. 2.10).
Рис. 2.10. Характеристика насосной установки.
Далее, используя методику подраздела 2.5, строим линию BС (рис. 2.5,б),
которая получается в результате совместной работы пластинчатого насоса и
регулятора подачи. Для этого, прежде всего, по формуле (2.7) находим давле-
64
ние срабатывания регулятора подачи:
pp0
4 Fпр
dп2
4 0, 45 103
8,96 106 Па 8,960 М Па .
3,14 0,0082
Определим максимальное давление регулятора рmax, которое будет иметь
место при нулевой подаче насоса, т.е. при максимальном перемещении xmax
поршня 5 вправо. Анализ конструкции насоса (рис. 2.9) позволяет сделать вывод, что xmax = е = 5 мм. Тогда по формуле (2.8) получим:
pmax
4 Fпр c x max
d
2
п
4 0, 45 103 20 5
3,14 0,008
2
10,95 106 Па 10,95 М Па .
После определения параметров работы регулятора, применяя методику
рассмотренную в подразделе 2.5, строим точки В и С, и соединяя их проводим
прямую ВС (рис. 2.10).
В результате получена характеристика рассматриваемой насосной установки с регулятором подачи (ломаная линия АВС на рис. 2.10).
Полученная характеристика (рис. 2.10) позволяет определить подачу насоса при давлении pн = 6,4 МПа. Этому значению соответствует рабочая точка
R1, в которой подача насосной установки равна Qн = Qну = 1,05·10-3 м3/с.
Отметим, что на данном режиме поршень 5 регулятора (рис. 2.9) занимает крайнее правое положение. Полезная мощность при этом равна:
Nпол pн Qн pн Qну 6, 4 106 0,848 103 5, 43 103 Вт 5, 43 кВт .
Потребляемую мощность вычисляем по формуле (2.12). При этом учтем,
что Qт = 0,933 ·10-3 м3/с.
Nпотр
pн Qт 6, 4 106 0,943 103
6,35 103 Вт 6,35 кВт .
нм
0,95
Далее определим подачу насосной установки при повышении давления
на 50%, т.е. при p′н = 1,5·6,4 = 9,6 МПа. Этому давлению на характеристике насосной установки соответствует рабочая точка R2, которая определяет величину подачи Q′ну = 0,551·10-3 м3/с.
На этом режиме (точка R2 на рис. 2.10) регулятор уже включился в работу
и уменьшил рабочий объем насоса. Полезная мощность при этом равна:
65
pн Qну
9,6 106 0,551103 5, 29 103 Вт 5, 29 кВт .
Nпол
На этом режиме (точка R2 на рис. 2.10) с уменьшенным рабочим объемом
насоса его теоретическая подача составляет Q′т = 0,678·10-3 м3/с. Поэтому потребляемую мощность насосной установки найдем, как рекомендуется в подразделе 2.6, по формуле (2.15):
Nпотр
pн Qт 9, 6 106 0, 678 103
6,85 103 Вт 6,85 кВт.
нм
0,95
Таким образом, в результате построена характеристика насосной установки и определены ее параметры на двух режимах работы:
при давлении 6,4 МПа подача насосной установки составила Qну = 0,848 ·103
м3/с, полезная мощность Nпол = 5,43 кВт, а потребляемая мощность Nпотр =
6,35 кВт;
при давлении 9,6 МПа подача насосной установки составила Q′ну = 0,551·10-3
м3/с, полезная мощность Nпол = 5,29 кВт, а потребляемая мощность N′потр =
6,85 кВт.
В заключение следует отметить, что при повышении давления на 50 %
потребляемая мощность насосной установкой увеличилась только на 8 %. Это
объясняется работой насоса на экономичном режиме – режиме уменьшенного
рабочего объема насоса.
2.8. Контрольные задания для самостоятельного выполнения
Далее приводятся варианты заданий расчетно-графических работ для самостоятельной работы. Шифр каждого варианта включает численный номер и
букву русского алфавита. По номеру выбирается соответствующий текст, а буква определяет набор численных значений физических величин не заданных в
тексте. Эти численные значения представлены в таблице 2.1, которая приведена в конце подраздела (после текстов вариантов заданий).
66
Вариант 2.1
На рисунке приведена схема насосной установки состоящей из нерегулируемого насоса 1 и переливного клапана 2, для которой следует построить
характеристику в координатах p .– Q, а также определить ее подачу и потребляемую мощность, если напорное давление на 15% выше давления срабатывания клапана. При построении характеристики принять пределы изменения:
давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется
на два. По одному из них жидкость направляется в гидросистему, которая подсоединяется к насосной установке в точке
К.. По второму трубопроводу жидкость
через переливной клапан 2 сливается в бак.
В процессе работы плунжер 3 перемещается и ограничивает давление на выходе насосной установки.
Построение провести для насоса, имеющего z рабочих камер объемом Wк
каждая. Частота вращения насоса n. Заданы следующие параметры клапана:
диаметр dп плунжера и сила предварительного поджатия пружины 4 Fпр =
1,1·F0. Для построения характеристики клапана воспользоваться формулой Δр
= ркл0 + k · Q, где ркл0 – давление срабатывания клапана. Принять механический
КПД насоса ηнм = 0,94, его объемный КПД – ηно = 0,9 при давлении p = 10 МПа,
а коэффициент – k = 2·103 МПа·с/м3.
(Величины n, Wк, z, dп, и F0 взять из таблицы 2.1).
67
Вариант 2.2
На рисунке приведена схема насосной установки состоящей из регулируемого насоса 1 и регулятора подачи 2, для которой следует построить
характеристику в координатах p – Q, а
также определить ее подачу и потребляемую мощность, если напорное давление на 6% выше давления срабатывания регулятора. При построении характеристики принять пределы изменения:
давления p от 0 до 12 МПа, расхода Q –
от 0 до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется на два. По одному из них жидкость направляется в гидросистему, которая
подсоединяется к насосной установке в точке К.. По второму трубопроводу
жидкость поступает в регулятор подачи 2. В процессе работы поршень 4 регулятора 2 перемещается, изменяя величину х, и воздействует на управляющий
элемент насоса, который изменяет его подачу.
Построение характеристики провести для насоса, имеющего z рабочих
камер объемом Wк каждая. Частота вращения насоса n. Заданы следующие параметры регулятора подачи: диаметр dп, его максимальное перемещение хmax,
сила предварительного поджатия пружины 3 Fпр = 0,95·F0, а ее жесткость с =
2,5 Н/мм. Принять механический КПД насоса ηнм = 0,95, а объемный КПД – ηно
= 0,96 при давлении p = 8 МПа.
(Величины n, Wк, z, dп, F0 и xmax взять из таблицы 2.1).
68
Вариант 2.3
На рисунке приведена схема насосной установки состоящей из шестеренного насоса 1 и переливного клапана 2, для которой следует построить характеристику в координатах p – Q, а также определить ее подачу и потребляемую мощность, если напорное давление на 18% выше давления срабатывания
клапана. При построении характеристики принять пределы изменения: давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость по
трубопроводу, который в точке Е разделяется на два. По одному из них жидкость направляется
в гидросистему,
которая подсоединяется к насосной установке в точке К.. По второму трубопроводу жидкость через переливной клапан 2 сливается в бак. В процессе работы плунжер 4 клапана 2 перемещается, за счет чего ограничивается давление
на выходе насосной установки.
При определении рабочего объема насоса учесть, что его рабочей камерой является объем между двумя соседними зубьями. На рисунке одна из рабочих камер выделена штриховкой. Построение характеристики провести для насоса с двумя одинаковыми шестернями модулем m, шириной b и с числом
зубьев на каждой z = 9. Для определения площади впадины использовать формулу S = 3,5· m2. Частота вращения насоса n. Заданы следующие параметры
клапана: диаметр dп плунжера 4 и сила предварительного поджатия пружины
Fпр = F0. Для построения характеристики клапана воспользоваться формулой
р = ркл0 + k · Q, где ркл0 – давление срабатывания клапана. Принять механический КПД насоса ηнм = 0,91, его объемный КПД – ηно = 0,88 при давлении p = 8
МПа, а коэффициент k = 2,5·103 МПа·с/м3.
(Величины n, m, b, dп и F0 взять из таблицы 2.1).
69
Вариант 2.4
На рисунке приведена схема насосной установки состоящей из героторного насоса 1 и переливного клапана 2, для которой следует построить характеристику в координатах p – Q, а также определить ее подачу и потребляемую
мощность, если напорное давление на 20% выше давления срабатывания клапана. При построении характеристики принять пределы изменения: давления p
от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость
по трубопроводу, который в точке
Е разделяется на два. По одному из
них жидкость направляется в гидросистему, которая подсоединяется к насосной установке в точке
К.. По второму трубопроводу
жидкость через переливной клапан 2 сливается в бак. В процессе работы плунжер 4 клапана 2 перемещается, за счет чего ограничивается давление на выходе
насосной установки.
При определении рабочего объема насоса учесть, что его рабочей камерой является объем, возникающей в нижнем положении внутренней и внешней
шестерен. На рисунке рабочая камера выделена штриховкой. Построение характеристики провести для насоса с внутренней шестерней диаметром D и шириной b, и с числом зубьев z = 6. Для определения площади рабочей камеры
использовать формулу S = 0,056 · D 2. Частота вращения насоса n. Заданы следующие параметры клапана: диаметр dп плунжера 4 и сила предварительного
поджатия пружины 3 Fпр = 0,85·F0. Для построения характеристики клапана
воспользоваться формулой р = ркл0 + k · Q, где ркл0 – давление срабатывания
клапана. Принять механический КПД насоса ηнм = 0,94, его объемный КПД –
ηно = 0,89 при давлении p = 6 МПа, а коэффициент k = 3·103 МПа·с/м3.
(Величины n, b, D, dп и F0 взять из таблицы 2.1).
70
Вариант 2.5
На рисунке приведена схема насосной установки состоящей из нерегулируемого пластинчатого насоса 1 и переливного клапана 4, для которой следует
построить характеристику в координатах p – Q, а также определить ее подачу и
потребляемую мощность, если напорное давление на 12% выше давления срабатывания клапана. При построении характеристики принять пределы изменения: давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется на
два. По одному из них жидкость направляется в гидросистему, которая подсоединяется
к насосной установке в точке
К.. По второму трубопроводу
жидкость через переливной
клапан 6 сливается в бак. В процессе работы плунжер 4 клапана 6 перемещается, за счет чего ограничивается давление на выходе насосной установки.
При определении рабочего объема насоса учесть, что его рабочей камерой является объем между двумя соседними пластинами 3, который на рисунке
выделен штриховкой. Построение характеристики провести для насоса с диаметром ротора D р = 0,7·D, при толщине пластин δ = 2 мм и ширине ротора b =
0,55·D р. Для определения площади рабочей камеры использовать формулу S =
2·е·(0,6·D р – δ). Смещение ротора относительно корпуса принять е = 0,1·D р.
Кроме того, заданы следующие параметры: частота вращения насоса n, диаметр dп плунжера 4 и сила предварительного поджатия пружины 5 Fпр = 0,95·F0.
Для построения характеристики клапана воспользоваться уравнением р = ркл0 +
k · Q, где ркл0 – давление срабатывания клапана. Принять механический КПД
насоса ηнм = 0,88, его объемный КПД – ηно = 0,85 при давлении p = 8 МПа, а коэффициент k = 2·103 МПа·с/м3.
(Величины n, b, D, dп и F0 взять из таблицы 2.1).
71
Вариант 2.6
На рисунке приведена схема насосной установки состоящей из регулируемого пластинчатого насоса 1 и регулятора подачи 4, для которой следует
построить характеристику в координатах p – Q, а также определить ее подачу и
потребляемую мощность, если
напорное давление на 8% выше давления срабатывания регулятора. При построении характеристики принять пределы изменения: давления p от 0
до 12 МПа, расхода Q – от 0
до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется на два. По одному из них жидкость направляется в гидросистему, которая подсоединяется к насосной установке в точке К.. По второму трубопроводу
жидкость поступает в регулятор подачи 4. В процессе работы поршень 6 регулятора 4 перемещается, изменяя величину х и смещение е ротора 2 относительно корпуса насоса 1. Следовательно, изменяется подача насоса.
При определении рабочего объема насоса учесть, что его рабочей камерой является объем между двумя соседними пластинами 3, который на рисунке
выделен штриховкой. Построение провести для насоса с диаметром ротора D р
= 0,7·D, при толщине пластин δ = 2 мм и ширине ротора b = 0,55·D р. Для определения площади рабочей камеры использовать формулу S = 2·е·(0,6·D – δ).
Максимальное смещение ротора относительно корпуса при максимальной подаче принять е = 0,1·D р.
Кроме того, заданы следующие параметры: частота вращения насоса n,
диаметр поршня регулятора dп, его максимальное перемещение хmax = е, сила
предварительного поджатия пружины Fпр = 0,9·F0 и ее жесткость с = 20 Н/мм.
Принять механический КПД насоса ηнм = 0,89, а объемный КПД – ηно = 0,9 при
давлении p = 6 МПа. (Величины n, b, D, dп и F0 взять из таблицы 2.1).
72
Вариант 2.7
На рисунке приведена схема насосной установки состоящей из нерегулируемого аксиально-поршневого насоса 1 и переливного клапана 6, для которой
следует построить характеристику в координатах p – Q, а также определить ее
подачу и потребляемую мощность,
если напорное давление на 10%
выше давления срабатывания клапана. При построении характеристики принять пределы изменения:
давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется на два. По одному из них жидкость направляется в гидросистему, которая подсоединяется к насосной установке в точке К. По второму трубопроводу
жидкость через переливной клапан 6 сливается в бак. В процессе работы поршень 4 клапана 6 перемещается, за счет чего ограничивается давление на выходе установки.
При определении рабочего объема насоса следует учесть, что его рабочей
камерой является цилиндрический объем, в котором совершает возвратнопоступательное движения плунжер 2 насоса. На рисунке рабочая камера выделена штриховкой.
Построение характеристики провести для насоса, с диаметром плунжеров
d, диаметром их расположения в блоке D, у которого максимальный угол наклона диска 3 составляет γmax = 25°. Кроме того, заданы следующие параметры:
частота вращения насоса n, диаметр поршня 4 dп и сила предварительного поджатия пружины 5 Fпр = 1,05·F0. Для построения характеристики клапана воспользоваться формулой р = ркл0 + k · Q, где ркл0 – давление срабатывания клапана. Принять количество плунжеров z = 11, механический КПД насоса ηнм =
0,97, его объемный КПД – ηно = 0,95 при давлении p = 12 МПа, а коэффициент
k = 1,5·103 МПа·с/м3.
(Величины n, D, d, dп и F0 взять из таблицы 2.1).
73
Вариант 2.8
На рисунке приведена схема насосной установки состоящей из регулируемого аксиально-поршневого насоса 1 и регулятора подачи 4, для которой следует построить характеристику в координатах p – Q, а также определить ее подачу и потребляемую мощность, если напорное давление на 4% выше
давления срабатывания регулятора. При построении характеристики принять
пределы изменения: давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется на
два. По одному из них жидкость направляется в гидросистему, которая подсоединяется к насосной установке в точке К.. По второму трубопроводу жидкость
поступает в регулятор подачи 4. В процессе работы поршень 6 регулятора 4
перемещается, изменяя угол γ наклона диска 3 и, следовательно, подачу насоса.
При определении рабочего
объема насоса следует учесть, что
его рабочей камерой является цилиндрический объем, в котором совершает возвратно-поступательное
движения плунжер 2 насоса. На рисунке рабочая камера выделена штриховкой.
Построение характеристики провести для насоса с диаметром плунжеров
d, диаметром их расположения в блоке D, у которого максимальный угол наклона диска 3 составляет γmax = 25°. Также заданы: частота вращения насоса n,
диаметр поршня регулятора dп, его максимальное перемещение хmax, сила предварительного поджатия пружины 5 Fпр = F0 и ее жесткость с = 2 Н/мм. Принять
количество плунжеров z = 11, механический КПД насоса ηнм = 0,95, а объемный
КПД – ηно = 0,95 при давлении p = 10 МПа.
(Величины n, D, d, dп, F0 и xmax взять из таблицы 2.1)
74
Вариант 2.9
На рисунке приведена схема насосной установки состоящей из нерегулируемого радиально-поршневого насоса 1 и переливного клапана 6, для которой
следует построить характеристику в координатах p – Q, а также определить ее
подачу и потребляемую мощность, если напорное давление на 14% выше давления срабатывания клапана. При построении характеристики принять пределы изменения: давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос 1 нагнетает жидкость по трубопроводу, который в точке Е разделяется на два. По одному из них жидкость направляется в гидросистему, которая
подсоединяется к насосной установке в точке К. По второму трубопроводу
жидкость через переливной клапан 6
сливается в бак. В процессе работы
поршень 4 клапана 6 перемещается, за
счет чего ограничивается давление на
выходе насосной установки.
При определении рабочего объема насоса учесть, что его рабочей камерой является цилиндрический объем,
в котором совершает возвратно-поступательное движения плунжер 3 (на рисунке рабочая камера выделена штриховкой). Поэтому ее длина равна ходу
поршня и равна удвоенному смещению ротора 2 относительно корпуса 1, т.е. –
величине 2·е.
Построение характеристики провести для насоса с диаметром ротора Dр
= 2·D, диаметром плунжеров dр = 2·d. Значение смещения ротора 2 относительно корпуса 1 принять е = 0,1·Dр. Кроме того, заданы следующие параметры: частота вращения насоса nр = 0,5· n, диаметр dп поршня 4 и сила предварительного поджатия пружины 5 Fпр = F0. Для построения характеристики клапана воспользоваться формулой р = ркл0 + k · Q, где ркл0 – давление срабатывания
клапана. Принять механический КПД насоса ηнм = 0,96, его объемный КПД –
ηно = 0,92 при давлении p = 10 МПа, а коэффициент k = 2·103 МПа·с/м3.
(Величины n, D, d, dп и F0 взять из таблицы 2.1).
75
Вариант 2.10
На рисунке приведена схема насосной установки состоящей из регулируемого радиально-поршневого насоса 1 и регулятора подачи 4, для которой
следует построить характеристику в координатах p – Q, а также определить ее
подачу и потребляемую мощность, если напорное давление на 5% выше давления срабатывания регулятора. При построении характеристики принять пределы изменения: давления p от 0 до 12 МПа, расхода Q – от 0 до 1 л/с.
Насос нагнетает жидкость по
трубопроводу, который в точке Е
разделяется на два. По одному из
них жидкость направляется в гидросистему, которая подсоединяется к
насосной установке в точке К.. По
второму
трубопроводу
жидкость
поступает в регулятор подачи 4. В
процессе работы поршень 6 регулятора 4 перемещает опорное кольцо 1 плунжеров 3. При этом вращающийся ротор 2 остается на месте и поэтому меняется
смещение ротора е относительно кольца 1. Следовательно, изменяется подача
насоса.
При определении рабочего объема насоса учесть, что его рабочей камерой является цилиндрический объем, в котором совершает возвратнопоступательное движения плунжер 3 (на рисунке она выделена штриховкой).
Поэтому длина рабочей камеры равна ходу поршня, т.е. – величине 2·е.
Построение характеристики провести для насоса с диаметром ротора Dр
= 2·D, диаметром плунжеров dр = 2·d. Значение смещения ротора относительно корпуса при максимальной подаче принять е = 0,1·Dр. Также заданы: частота вращения насоса nр = 0,5· n, диаметр поршня 6 регулятора dп, его максимальное перемещение хmax = е, сила предварительного поджатия пружины 5 Fпр =
0,9·F0 и ее жесткость с = 6 Н/мм.. Принять механический КПД насоса ηнм =
0,94, а объемный КПД – ηно = 0,9 при давлении p = 8 МПа.
(Величины n, D, d, dп и F0 взять из таблицы 2.1).
76
2.9. Значения параметров насосной установки
Таблица 2.1
Вариант
Параметры насосных установок
n
А
Б
В
Г
Д
Е
Ж
И
К
Л
об/мин 1800 900 2250 1350 850 1100 2500 2000 1000 1500
Wк
см3
3
4,2
2,8
3,4
4,6
4
2,6
3
3,6
3,6
z
–
11
15
9
13
15
13
9
9
15
11
m
мм
4,5
6
4
5
6
5,5
4
4,5
5,5
5
b
мм
24
28
24
25
30
28
22
23
28
25
D
мм
62
80
56
68
80
74
56
62
78
68
d
мм
11
14
10
12
14
13
10
11
13
12
dп
мм
7
9
10
8
11
10
8
9
7
10
F
кН
xmax
мм
0,36 0,56 0,83 0,47 0,88 0,69 0,44 0,55 0,34 0,72
40
55
60
45
60
50
50
55
45
40
77
3. Расчетно-графическая работа № 3
РАСЧЕТ СЛОЖНОГО ТРУБОПРОВОДА С НАСОСНОЙ ПОДАЧЕЙ
3.1 Общие положения
В большинстве современных гидравлических систем движение жидкости
происходит за счет принудительного нагнетания ее насосом (насосной установкой). Такие гидросистемы называются трубопроводами с насосной подачей.
В машиностроении наиболее распространенными гидросистемами с насосной
подачей являются объемные гидравлические приводы, которые служат для передачи и преобразования энергии.
Гидравлический расчет установившегося режима работы трубопровода с
насосной подачей, в том числе объемных гидроприводов, представляет собой
достаточно сложную задачу. Обусловлено это тем, что эти гидравлические системы являются сложными техническими устройствами, элементы которых
имеют существенно нелинейные характеристики.
При расчете сложных трубопроводов с насосной подачей используют
рассмотренные ранее характеристики насосных установок и характеристики
сложных трубопроводов. Целью расчета при этом является анализ их совместной работы, в результате которого определяют параметры, характеризующие
как работу гидравлической системы в целом, так и отдельных ее элементов.
3.2 Расчетные зависимости, характеризующие работу трубопровода с
насосной подачей
Как известно, в общем случае для установившегося режима работы трубопровода с насосной подачей насосная установка всегда создает напор равный
потребному для данного трубопровода.
В аналитическом виде это утверждение означает равенство:
H н H потр .
(3.1)
Следует отметить, что аналитические выражения величин, входящих в
уравнение (3.1), от расхода (подачи) представляют собой в общем случае существенно нелинейные зависимости. Поэтому поиск аналитических решений
78
уравнения (3.1) имеет определенную сложность.
Этим обусловлено широкое распространение в практике гидравлических
расчетов графоаналитического метода. Использование этого метода позволяет
не только без особых затруднений получить с необходимой для инженерных
расчетов точностью значения параметров, характеризующих режимы работы
элементов рассматриваемой гидросистемы, но и на основании анализа их значений дать рекомендации о возможно необходимой коррекции рассмотренного
режима ее работы.
Графоаналитический метод гидравлического расчета трубопроводов с
насосной подачей заключается в том, что на одном графике в координатах H–
Q (рис. 3.1) в едином масштабе строят характеристику используемой в гидросистеме насосной установки Hн = f(Q) и характеристику потребного напора
трубопровода Hпотр = f(Q). Очевидно, что точка пересечения R этих характеристик является результатом графического решения уравнения (3.1).
Рис. 3.1. Графическое определение рабочей точки гидросистемы
Эта найденная в результате построений точка R пересечения характеристик (рис. 3.1) называется рабочей точкой гидросистемы. Она определяет параметры, характеризующие рассмотренный режим работы гидросистемы.
Например, на рис. 3.1 показано определение величин напора Hн и подачи
Qн насоса (насосной установки). Причем, напор насоса Hн, в соответствии с
(3.1), равен потребному напору Hпотр для рассматриваемого трубопровода, а
подача насосной установки Qн равна расходу в его начальном сечении Q.
При гидравлическом расчете объемных гидроприводов, которые, как
правило, представляют собой замкнутые трубопроводы с насосной подачей,
79
вместо уравнения (3.1) используется уравнение (3.2):
H н h .
(3.2)
Поэтому при выполнении графоаналитического расчета таких гидросистем используют не характеристики потребных напоров, а характеристики трубопроводов, которые определяют зависимость Σh = f(Q).
Кроме этого, при расчете объемных гидроприводов вместо величин напоров Н используют величины давлений р. Поэтому, учитывая что рн = Нн·ρ·g и
ΔрΣ = ρ·g·Σh, вместо уравнения (3.2) используют выражение:
pн p .
(3.3)
В этом случае при графоаналитическом методе расчете график строится в
координатах р–Q, т.е. по оси ординат откладывается величина давления р, а
получающаяся в результате рабочая точка R определяет подачу Qн и давление
рн, создаваемое насосом.
3.3 Методика графоаналитического расчета трубопроводов с насосной
подачей
При графоаналитическом расчете сложных трубопроводов с насосной
подачей, в том числе объемных гидроприводов, рекомендуется следующая последовательность действий.
1. Для удобства анализа и проведения расчетов целесообразно заменяют заданную принципиальную гидравлическую схему расчетной. Пример расчетной схемы приведен на рис. 1.8. Причем чем сложнее гидравлическая
система, тем полезнее эта замена.
2. Разбивают сложный трубопровод на простые и получают аналитические
выражения характеристик для каждого простого трубопровода. Получение таких характеристик рассмотрено в подразделах 1.2 и 1.3.
3. На графике в координатах р–Q строят характеристики простых трубопроводов. Затем, используя правила сложения характеристик трубопроводов, получают суммарную характеристику сложного трубопровода. Рекомендации для этого приведены в подразделе 1.4.
80
4. На этом же графике строят характеристику насосной установки. Причем,
в зависимости от схемы этой установки используют рекомендации, приведенные в одном из подразделов 2.3, 2.4 или 2.5.
5. Определяют положение рабочей точки, например, точка R на рис. 3.1, по
графику находят необходимые величины, характеризующие режим работы рассматриваемой гидросистемы.
При выполнении пункта 5 методики могут определяться различные параметры. Рассмотрим определение некоторых из них.
При известном расположении рабочей точки R на графике определяется
подача насосной установки Qн и, следовательно, расход жидкости в начальном
сечении трубопровода. Причем, если трубопровод содержит гидродвигатель, то
при известном расходе по (1.11), (1.14) или (1.15) может быть вычислена скорость его выходного звена.
Рабочая точка позволяет также найти давление рн, создаваемое насосом,
по которому при известном Qн может быть определена полезная мощность насоса или насосной установки по формуле (2.9).
По известной полезной мощности с использованием методики, приведенные в подразделе 2.6, может быть определена потребляемая насосом мощность, которая также является мощностью, потребляемой гидросистемой.
По найденной скорости движения выходного звена гидродвигателя (V
или ω) и заданной нагрузке (М или F) можно вычислить полезную мощность,
реализуемую гидроприводом. Если в гидроприводе используется гидромотор,
то мощность, реализуемая на его выходном звене, равна:
N гм M M n ,
(3.4)
если гидроцилиндр, то
N гц F V .
(3.5)
Зная сумму полезных мощностей, реализуемых на выходных звеньях
гидродвигателей (ΣNгд), и мощность Nпотр, потребляемую гидросистемой, кпд
гидросистемы определяют из формулы:
81
N гд
N потр
.
(3.6)
Приведенная методика расчета сложных трубопроводов с насосной подачей позволяет определить рабочий режим системы (рабочую точку) и параметры, характеризующие этот режим. Такую задачу можно считать прямой. Однако при расчете трубопроводов кроме прямой задачи по определению рабочей
точки и вычислению необходимых параметров могут быть решены и другие
«обратные» задачи. В качестве примера ниже приводятся две из возможных задач.
При известной суммарной характеристике трубопровода требуется подобрать характеристику насосной установки, которая обеспечивает заданный
расход Q*. Характеристика насосной установки (линия ВC на рис. 3.2, а) может
смещаться вверх или вниз за счет регулировки давления срабатывания переливного клапана или регулятора подачи р0. Поэтому по величине расхода Q* на
характеристике насоса наносят точку R, а затем через нее проводят линию ВС,
которая обеспечивает требуемую величину расхода Q*.
Рис. 3.2. Возможные задачи при расчете трубопроводов с насосной подачей
Пусть после расчета гидросистемы по рабочей точке R1 получен расход
Q1 не удовлетворяющий проектировщика (рис. 3.2, б). Тогда может быть найдена новая рабочая точка R2, обеспечивающая требуемый расход Q2. Это может
быть достигнуто за счет изменения сопротивления в одной или нескольких
гидролиний, которое обеспечит прохождение характеристики трубопровода
через новую точку R2 (рис. 3.2, б). Отметим, что сопротивление гидролинии
82
можно скорректировать за счет, например, изменения проходного сечения
дросселя или диаметра трубопровода.
При расчете сложных трубопроводов могут возникать и другие задачи,
которые решаются подобными методами.
3.4. Пример графоаналитического расчета сложного трубопровода с
насосной подачей
Пусть необходимо провести анализ работы гидропривода, состоящего из
сложного трубопровода, рассмотренного в подразделе 1.5 (рис. 1.7) и насосной
установки, рассмотренной в подразделе 2.7 (рис. 2.9). При проведении анализа
использовать характеристику сложного трубопровода (рис. 1.9) и характеристику насосной установки (рис. 2.10). По результатам определить скорость
движения поршня и частоту вращения вала гидромотора, а также полезную и
потребляемую мощности гидропривода и его КПД.
Для решения поставленной задачи воспользуемся методикой приведенной в подразделе 3.3 (пункты 1÷5).
Эквивалентная схема рассматриваемого гидропривода (пункт 1) получена
ранее и приведена на рис. 1.9. Для удобства проведения анализа в данном разделе целесообразно ее еще более упростить, указав взаимосвязь простых трубопроводов, расходы в них, места установки гидродвигателей и насосной установки (НУ). Упрощенная эквивалентная схема приведена на рис. 3.3.
Рис. 3.3. Упрощенная эквивалентная схема рассматриваемого трубопровода
Пункты 2÷4 также выполнены ранее, т.е. получены необходимые характеристики трубопроводов (рис. 1.10) и насосной установки (рис. 2.10). В дан-
83
ном разделе указанные характеристики нанесем на общий график (рис. 3.4).
Рис. 3.4. Характеристики рассматриваемого трубопровода с насосной
подачей
Выполнение пункта 5 методики рассмотрим подробнее с использованием
имеющихся характеристик трубопроводов и насосной установки (рис. 3.4).
Пересечение характеристики сложного трубопровода Σ с характеристикой насосной установки НУ определяет рабочую точку гидросистемы (точка R
на рис. 3.4) с координатами рн = 9,18 МПа и Qну = 0,72410-3 м3/с.
Используя положение точки R, определим расходы в параллельных трубопроводах 2 и 3 (рис. 3.3). Для этого необходимо перейти от точки R (рис. 3.4)
через промежуточную точку R′ к точкам R2 и R3, расположенным на характери-
84
стиках трубопроводов 2 и 3. Наконец по положению точек R2 и R3 (рис. 3.4)
найдем величины расходов в параллельных трубопроводах: Q2 = 0,18710-3 м3/с
и Q3 = 0,53710-3 м3/с.
После определения расходов в параллельных трубопроводах найдем скорости выходных звеньев гидродвигателей. Гидромотор установлен во 2-ом
простом трубопроводе (рис. 3.3), поэтому его частоту вращения найдем по
формуле (1.11) с использованием расхода Q2, т.е.
n
Q2 о м
0,187 103 0,95
5,92 об/с 355 об/мин .
Wо
30 106
Гидроцилиндр установлен во 3-ем простом трубопроводе (рис. 3.3), поэтому скорость движения его поршня найдем по формуле (1.15) с использованием величины Q3 при ηоц = 1, т.е.
4 Q3 о ц
4 0,537 10 3 1
V
0, 427 м/с .
D 2 dш2 3,14 0,052 0,032
После определения скоростей при известных нагрузках (М или F) вычислим полезную мощность гидропривода как сумму мощностей на валу гидромотора (3.8) и на штоке гидроцилиндра (3.9). Тогда
Nгп Nгм Nгц M 2 n F V 28 3,14 2 5,92 6,5 103 0,537 4,53103 Вт 4,53 кВт. .
Далее найдем мощность, потребляемую насоса, которая одновременно
является мощностью, потребляемой гидроприводом.
Для этого воспользуемся методикой, приведенной в подразделе 2.6 для
установки с регулятором подачи. Согласно ей определяем теоретическую подачу насоса Q′т на расчетном режиме, которая для рассматриваемого случая составила Q′т = 0,84510-3 м3/с (рис. 3.4).
Отсюда, используя формулу (2.15), получим:
Nпотр
pн Qт 9,18 106 0,845 103
8,17 103 Вт 8,17 кВт .
м н
0,95
В заключение по формуле (3.10) найдем КПД гидропривода:
Nгд 4,53
0,554 .
N потр 8,17
85
Таким образом, в результате проведенных расчетов получены следующие
параметры, характеризующие режим работы данного гидропривода:
o частота вращения вала гидромотора – n = 355 об/мин;
o скорость поршня гидроцилиндра – V = 0,427 м/с;
o полезная мощность гидропривода – Nпол = 4,53 кВт;
o мощность, потребляемая гидроприводом, – Nпол = 8,17 кВт;
o КПД гидропривода – η = 0,554.
3.5. Контрольные задания для самостоятельного выполнения
Используя данные сложного трубопровода из РГР-1 и данные насосной
установки из РГР-2, создать схему объемного гидропривода с регулированием
скоростей движения выходных звеньев (звена) гидродвигателей.
Провести анализ совместной работы насосной установки и сложного
трубопровода, образующих гидропривод. Для проведения анализа использовать характеристики сложного трубопровода, полученную при выполнении
РГР-1, и характеристику насосной установки, полученную при выполнении
РГР-2.
По результатам анализа определить скорости движения выходных звеньев гидродвигателей (скорости движения поршней гидроцилиндров или скорости вращения валов гидромоторов), а также полезную и потребляемую мощности гидропривода и его КПД.
Литература
1. Беленков Ю.А., Лепешкин А.В., Михайлин А.А., Суздальцев В.Е., Шейпак
А.А. Гидравлика и гидропневмопривод. Задачник. / Под редакцией Ю.А.
Беленкова. М., «Экзамен», 2009. 286 с.
2. Вильнер Я.М. и др. Справочное пособие по гидравлике, гидромашинам и
гидроприводам. / Под редакцией Некрасова Б.Б. Минск, «Вышэйшая школа», 1985. 382 с.
3. Лепешкин А.В., Михайлин А.А. Гидравлические и пневматические системы.
/ Под редакцией Беленкова Ю.А. М., «Академия», 2009. 336 с.
4. Лепешкин А.В., Михайлин А.А., Фатеев И.В. Расчет сложных трубопроводов с насосной подачей. / Под редакцией Беленкова Ю.А. М., МАМИ, 2000.
48 с.




 Рис.12.1.
Рис.12.1.