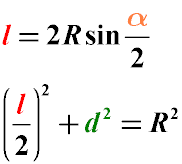Формула длины хорды окружности
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, (L):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
- Подробности
-
Автор: Administrator
-
Опубликовано: 16 октября 2011
-
Обновлено: 13 августа 2021
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
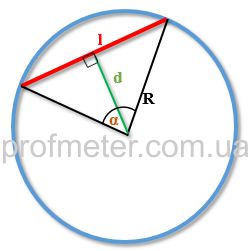
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
Определение хорды
Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
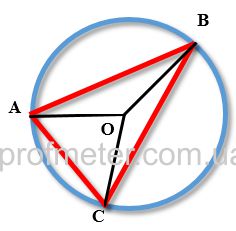
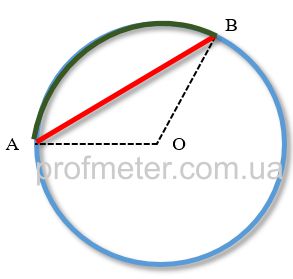
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности
Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .
Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.
Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.
Свойства хорды к окружности
- Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
- Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
- Наибольшая возможная хорда является диаметром
- Серединный перпендикуляр к хорде проходит через центр окружности
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
- Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.
Свойства хорды и вписанного угла
Свойства хорды и центрального угла
Формулы нахождения хорды
Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.
Решение задач
Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.
Задача.
Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.
Решение.
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x
Согласно свойству хорд AS x SB = CS x SD, тогда
2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10
Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10
Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то
3,5х + 5,5х + 3х = 360
12х = 360
х = 30
Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165
Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5
Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
http://www-formula.ru/circle-chord-l
http://profmeter.com.ua/communication/learning/course/course7/lesson318/
Хорда — под этим понятием понимается отрезок, который соединяет 2 любые точки, отмеченные на окружности.
Если хорда проходит через её центр, то она будет диаметром.
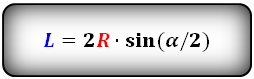
Для того, чтобы найти длину хорды l, можно воспользоваться следующей формулой:
l = 2R * sin(α/2).
Здесь: R — радиус окружности и α — центральный угол.
Кстати, диаметр как частный случай хорды, имеет самую максимальную длину.
Вообще, задача нахождения длины хорды нередко возникает перед инженерами, механиками или архитекторами.
Пример
Радиус окружности R равен 5 см.
Угол α равен 60 градусов.
Длина хорды будет равна: l = 2*5*sin(30°) = 2*5*0,5 = 5 см.
Секущая и хорда окружности
Зачем что-то знать о секущих и хордах в окружности?
Как обычно, знание свойств и закономерностей сильно облегчает жизнь.
Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ!
Поехали!
Секущая и хорда окружности — коротко о главном
Секущая окружности
Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Хорда окружности
Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.
Длина хорды
Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle AСB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB). Тогда:
( displaystyle AB=2Rsin alpha).
Произведение длин отрезков хорд и секущих
Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется:
( displaystyle ABcdot AC=ADcdot AE).
Теорема о секущей и касательной
Для любых секущей и касательной, проходящих через точку ( A), верно:
( displaystyle A{{C}^{2}}=ADcdot AE).
А теперь подробнее…
Определения секущей и хорды окружности
Давай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки.
Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.
Кстати, заметил ли ты, что на первом рисунке хорда ( displaystyle BC) является кусочком секущей ( displaystyle AC)?
Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас ( displaystyle AB) – она же снаружи, верно?
Что же мы должны знать о секущей и хорде окружности?
Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности.
Длина хорды окружности
Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle ACB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB).
Тогда ( Largefrac{AB}{sin alpha }=2R)
Узнал теорему синусов?
Значит, длину хорды окружности можно найти по формуле:
Произведение длин отрезков хорд и секущих
Сейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности.
Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами.
Произведение длин отрезков хорд окружности
Для любых двух хорд окружности, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)
Произведение длин отрезков секущих окружности
Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)
Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком?
Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом.
Вопрос второй: Как не перепутать, что на что умножать?
Произведение длин отрезков хорд окружности — доказательство
Повторим формулировку.
Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)
А теперь докажем.
Рассмотрим ( triangle ABD) и ( triangle AEC). У них углы ( displaystyle A) равны как вертикальные и ( angle DBC=angle DEC), потому что они опираются на одну дугу ( displaystyle DC).
Значит, ( displaystyle triangle ABDsim triangle AEC) по двум углам (вспоминаем признаки подобия треугольников).
Запишем, что же нам даёт это подобие (и откроем маленький секрет!).
Произведение длин отрезков секущих окружности — доказательство
Еще раз формулировку…
Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)
Снова рассмотрим ( displaystyle triangle ABD) и ( displaystyle triangle AEC).
- У них есть общий ( angle A);
- Четырехугольник ( BCED) — вписанный (срочно повторяем или читаем тему «Окружность. Вписанный угол»).
Значит, ( angle 1+angle 2=180{}^circ ) (сумма противоположных углов вписанного четырехугольника равна ( 180{}^circ )). Но ( angle 2+angle 3=180{}^circ ) — как смежные углы (смотри на картинку).
Что же получилось?
( left{ begin{array}{l}angle 1+angle 2=180{}^circ \angle 2+angle 3=180{}^circ end{array} right.Rightarrow angle 1=angle 3)
То есть ( underbrace{angle ACE}_{в triangle AEC}=underbrace{angle ADB}_{в triangle ABD }).
Из всего этого следует, что ( triangle AECsim triangle ABD) по двум углам (( angle A) – общий и ( angle ACE=angle ADB)).
Снова запишем отношение соответствующих сторон:
Теорема о секущей и касательной (секретное оружие)
А сейчас «секретное» оружие — теорема о секущей и касательной. Почему секретное?
Потому что множество задач ОГЭ и ЕГЭ можно решить с помощью этой теоремы. А акцент на ней в учебнике не делается. То есть ее как бы нет…
В предыдущем пункте мы выяснили, что ( ABcdot AC=ADcdot AE)
Но возникает вопрос: а что будет, если секущая ( AC) и «превратится» в касательную?
Видишь: осталось всего три зелёных точки? Оказывается, ничего страшного, всё почти так же. Формулируем:
Для любых секущей и касательной, проходящих через точку ( A), верно: ( Large A{{C}^{2}}=ADcdot AE).
Тут точки ( B) и ( C) как бы слились в одну – и на рисунке, и в формуле. Заметил?
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
| Учебный курс | Решаем задачи по геометрии |
Определение хорды Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Свойства хорды к окружности
Свойства хорды и вписанного углаНа рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности — AB
Свойства хорды и центрального углаНа рисунке [2] центральный угол обозначен как AOB, хорда как AB.
Формулы нахождения хорды Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задач Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда Ответ: 5√10 Задача. Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
Задачи про окружность | Описание курса | Треугольник (Трикутник) |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!


![Хорда к окружности вместе с вписанным [1] и центральными углами [2] Хорда к окружности вместе с вписанным [1] и центральными углами [2]](https://profmeter.com.ua/upload/medialibrary/b1c/horda2.jpg)