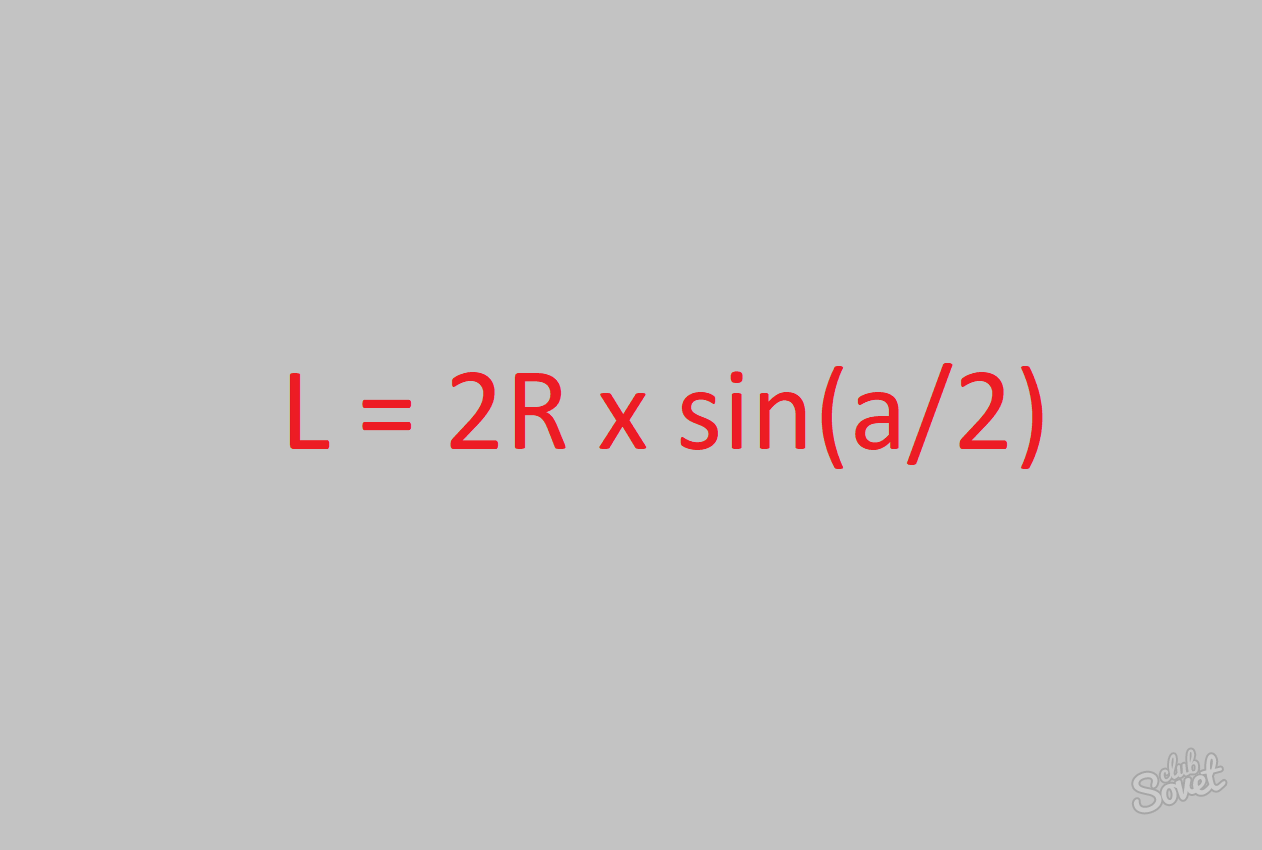Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
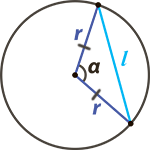
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Определение хорды
Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности
Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .
Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.
Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.
Свойства хорды к окружности
- Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
- Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
- Наибольшая возможная хорда является диаметром
- Серединный перпендикуляр к хорде проходит через центр окружности
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
- Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.
Свойства хорды и вписанного угла
Свойства хорды и центрального угла
Формулы нахождения хорды
Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.
Решение задач
Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.
Задача.
Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.
Решение.
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x
Согласно свойству хорд AS x SB = CS x SD, тогда
2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10
Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10
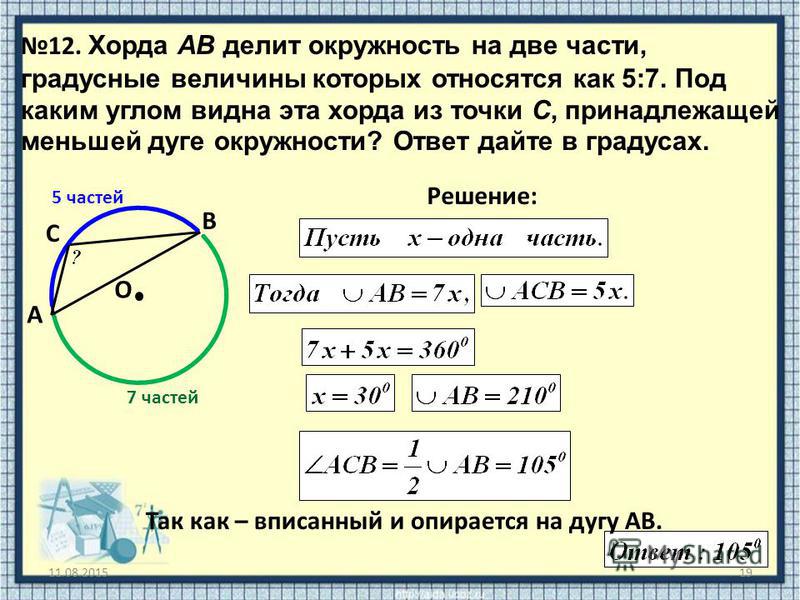
Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то
3,5х + 5,5х + 3х = 360
12х = 360
х = 30
Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165
Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5
Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
Как найти хорду окружности пример
Как посчитать хорду окружности
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
Хорда окружности — определение, свойства, теорема
Хорда в геометрии
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
- Это отрезок с наибольшей длиною в окружности это диаметр. Он обязательно будет проходить через центр круга.
- Если есть две равные дуги, то их отрезки, которые их стягивают, будут равны.
- Хорда, которая перпендикулярна диаметру, будет делить этот отрезок и его дугу на две одинаковые части (справедливо и обратное утверждение).
- Самый маленький отрезок в окружности это точка.
- Хорды будут равны, если они находятся на одном расстоянии от центра окружности (справедливо и обратное утверждение).
- При сравнении двух отрезков в кругу большая из них окажется ближе к центру окружности.
- Дуги, которые находятся между двумя параллельными хордами, равны.
Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
Касательная и секущая
Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Как найти хорду окружности пример
| Учебный курс | Решаем задачи по геометрии |
Определение хорды
Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности
Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .
Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.
Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.
Свойства хорды к окружности
- Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
- Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
- Наибольшая возможная хорда является диаметром
- Серединный перпендикуляр к хорде проходит через центр окружности
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
- Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.
Свойства хорды и вписанного угла
Свойства хорды и центрального угла
Формулы нахождения хорды
Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.
Решение задач
Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.
Задача.
Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.
Решение.
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x
Согласно свойству хорд AS x SB = CS x SD, тогда
2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10
Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10
Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то
3,5х + 5,5х + 3х = 360
12х = 360
х = 30
Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165
Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5
Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
http://profmeter.com.ua/communication/learning/course/course7/lesson318/
http://b4.cooksy.ru/articles/kak-nayti-hordu-okruzhnosti-primer
Как вычислить длину хорды
Хордой называется отрезок, соединяющий две любые точки одной окружности. Нахождение длины хорды, как и остальных элементов данной фигуры – одна из задач геометрического раздела математики. При вычислении хорды следует опираться на известные величины, свойства элементов и различных построений в окружности.
Инструкция
Пусть задана окружность с известным радиусом R, ее хорда L стягивает дугу φ, где φ определена в градусах или радианах. В этом случае вычислите длину хорды по следующей формуле: L = 2*R*sin(φ/2), подставив все известные значения.
Рассмотрим окружность с центром в точке О и заданным радиусом. Искомыми являются две одинаковые хорды АВ и АС, имеющие одну точку пересечения с окружностью (А). При этом известно, что угол, образуемый хордами, опирается на диаметр фигуры. Выполните графическое построение указанных элементов в окружности. Радиус из центра О опустите до точки пересечения хорд А. Хорды при этом будут образовывать треугольник АВС. Для определения длин одинаковых хорд используйте свойства полученного равнобедренного треугольника (АВ=АС). Отрезки ВО и ОС равны (АС по условию — диаметр) и являются радиусами фигуры, следовательно, АО представляет собой медиану треугольника АВС.
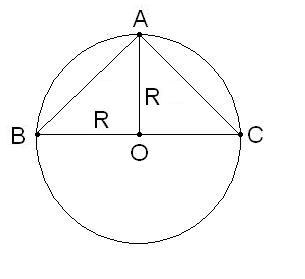
Согласно свойству равнобедренного треугольника, его медиана является одновременно и высотой, то есть, перпендикуляром к основанию. Рассмотрите полученный прямоугольный треугольник АОВ. Катет ОВ известен и равен половине диаметра, то есть, R. Второй катет АО также задан как радиус R. Отсюда, применив теорему Пифагора, выразите неизвестную сторону АВ, которая и является искомой хордой окружности. Вычислите окончательный результат АВ = √(АО² + ОВ²). По условию задачи, длина второй хорды АС равна АВ.
Допустим, задана окружность с диаметром D и хордой СЕ. При этом известен угол, образуемый хордой и диаметром. Вычислить длину хорды можно, используя следующие построения. Нарисуйте окружность с центром в точке О и хорду СЕ, проведите диаметр через центр и одну из точек хорды (С). Известно, что любая хорда соединяет две точки окружности. Опустите из второй точки ее пересечения с окружностью (Е) в центр О радиус ЕО. Таким образом, получается равнобедренный треугольник СЕО с основанием-хордой СЕ. При известном угле у основания ЕСО вычислите хорду с помощью формулы из теоремы о проекциях: СЕ = 2*ОС*cos
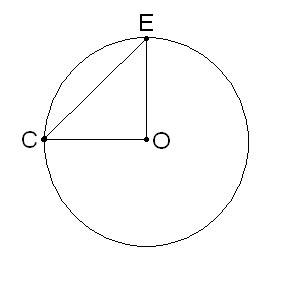
Полезный совет
Если хорда проходит через центр окружности, она является диаметром. Угол между пересекающимися хордами соответствует полусумме мер дуги, расположенной в углу, и дуги напротив нее. Если касательная к окружности и хорда образуют угол, то он равен половине градусного значения дуги, стягиваемой этой же хордой.
Источники:
- диаметр и хорда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти хорду окружности
Нахождение решений задач с хордами окружности – неотъемлемая часть геометрии. Многие задачи такого типа встречаются на экзаменах. Эта статья научит вас методам нахождения длины хорды окружности.
Как найти хорду окружности – формула
Если дана задача, где нам известен R и a, найти хорду можно одним простым вычислением. Формула нахождения выглядит следующим образом: L = 2R × sin(/2), где L – длина хорды, R – длина радиуса, a – угол между ними.
Пример:
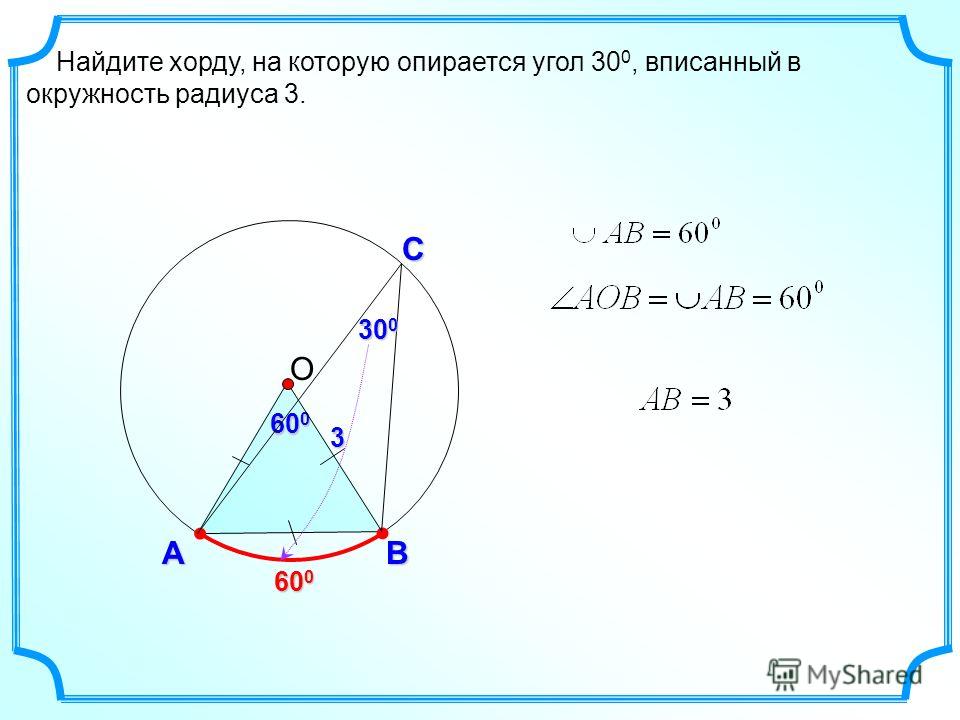
Найти L, если радиус = 5 см., а угол между ними = 90.
Решение:
Подставим значения в формулу: L = 2×5 × sin(90/2) = 2×5 × sin45 ≈ 7.1
Ответ: Хорда окружности равна 7.1
Анализ задачи: Треугольник, проведенный при помощи хорды и двух радиусов – равнобедренный. Равнобедренный он потому, что все радиусы окружности равны друг другу.
Если бы нам не было известно значение угла между радиусами, но было известно значение угла при бедре, можно было легко вычислить угол между радиусами.
Пример:
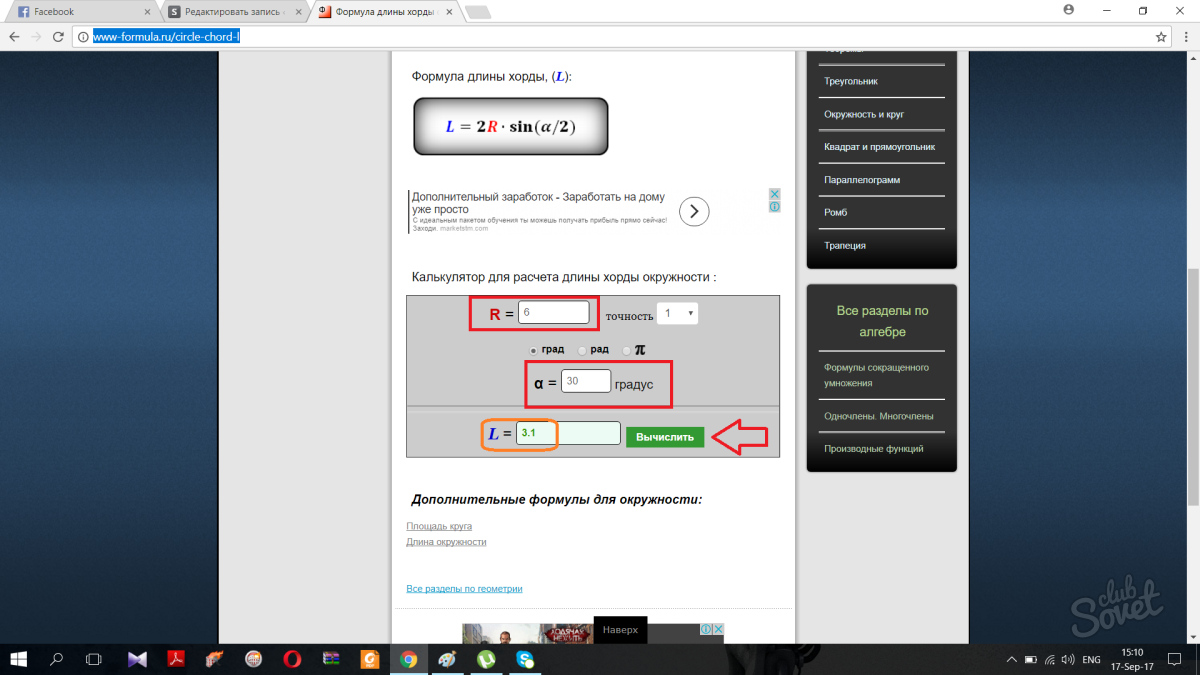
Найти длину хорды окружности, если радиус окружности = 6см, а угол при основании = 75.
Решение:
Вспомним формулу: L = 2R × sin(/2). Что нам известно? Радиус равен 5. Для решения задачи необходимо найти угол между радиусами. Мыслим следующим образом: Угол при основании треугольника (основание – хорда) равен 75. Это означает, что угол со второй стороны тоже будет равен 75. Так как сумма внутренних углов треугольника = 180, зная два угла, можно с легкостью найти третий. Угол = 180 – (75+75) = 180 – 150 = 30. Таким образом, a = 30.
Остается подставить значения в формулу: L = 2×6 × sin(30/2) = 12×sin15 ≈ 3.1 см.
Ответ: L = 3.1 см.
Как найти длину хорды окружности онлайн
Когда мы имеем дело с градусами, которых нет в тригонометрической таблице, крайне неудобно вычислять длину хорды окружности самостоятельно. Для этого можно воспользоваться онлайн ресурсом. Просто вставляете известные значения в соответствующие поля и мини-программа выдает вам правильный ответ.
Чтобы воспользоваться этим сервисом, кликните по ссылке.
Помните, несмотря на то, что сегодня можно решить практически любую задачу в Интернете, старайтесь вычислять все самостоятельно. На экзамене интернета не будет. Формула достаточно проста для запоминания, а градусное значение на экзамене или контрольной скорее всего будет таким, чтобы значение sin(a/2) было табличным. Это намного упростит решение.
Как посчитать хорду окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать хорду окружности
Чтобы посчитать хорду круга (окружности) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
угол α °
Ответ:
0
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
угол α рад
Ответ:
0
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
l = 2r⋅sinα/2
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
См. также
Длина хорды окружности при заданном вписанном угле Калькулятор
|
✖Радиус окружности — это длина любого отрезка, соединяющего центр и любую точку окружности.ⓘ Радиус круга [r] |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
|
✖Вписанный угол окружности — это угол, образованный внутри окружности при пересечении двух секущих на окружности. |
КругЦиклстепеньГонград, минута, секундамилМиллирадианминутМинуты дугиТочкаквадрантЧетверть кругаРадианРеволюцияПрямой уголВторойПолукругсекстанЗнакОчередь |
+10% -10% |
|
✖Длина хорды окружности — это длина отрезка, соединяющего любые две точки на окружности окружности.ⓘ Длина хорды окружности при заданном вписанном угле [lc] |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Длина хорды окружности при заданном вписанном угле Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Радиус круга: 5 метр —> 5 метр Конверсия не требуется
Вписанный угол окружности: 85 степень —> 1.4835298641949 Радиан (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
9.96194698091721 метр —> Конверсия не требуется
<
5 Длина хорды круга Калькуляторы
Длина хорды окружности при заданном вписанном угле формула
Длина хорды круга = 2*Радиус круга*(sin(Вписанный угол окружности))
lc = 2*r*(sin(∠Inscribed))
Что такое Круг?
Окружность — это базовая двумерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки.
Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.
Каковы свойства аккордов?
Если хорды параллельны друг другу, то длина дуги между ними будет одинаковой. Хорды одинаковой длины равноудалены от центра окружности. Чем больше длина хорды, тем ближе она к центру окружности.
Share
Copied!
Как найти радиус окружности зная хорду
Все основные формулы для определения длины радиуса окружности
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).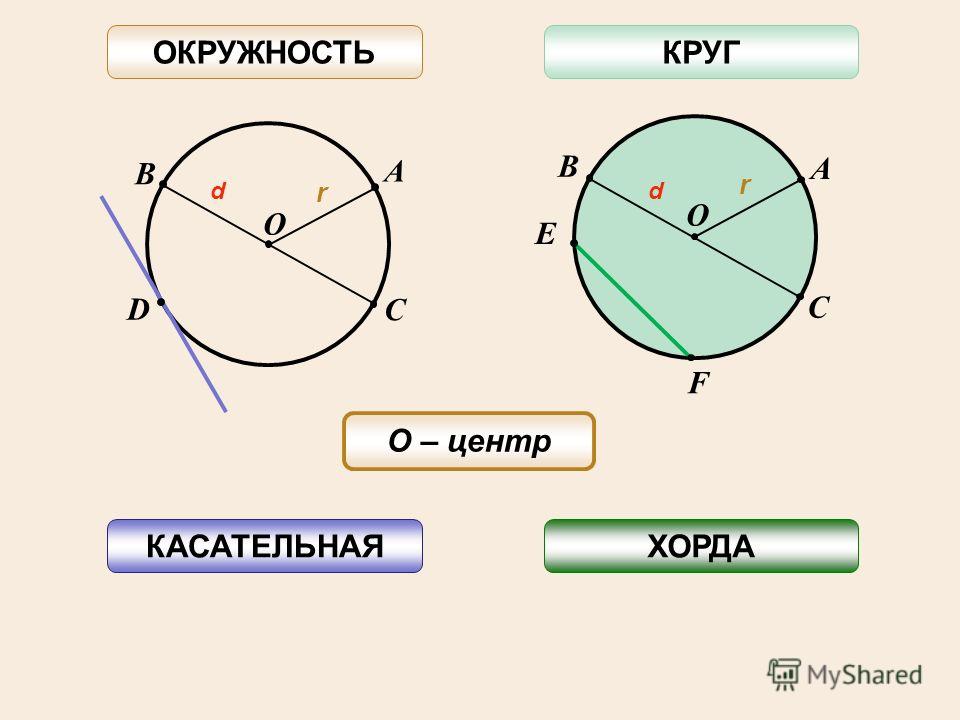
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Калькулятор для расчета длины радиуса через длину хорды
Подробности Автор: Сергей Кондратов Опубликовано: 07 сентября 2011 Обновлено: 13 августа 2021
Найти радиус
Здравствуйте! Можно ли найти радиус окружности по длине хорды и дуги? или нужны дополнительные данные?
Лучший ответ по мнению автора
Александр
ВОПРОС:
Здравствуйте! Можно ли найти радиус окружности по длине хорды и дуги? или нужны дополнительные данные?
ОТВЕТ:
Ничего дополнительного не нужно, решение задачи изложено ниже.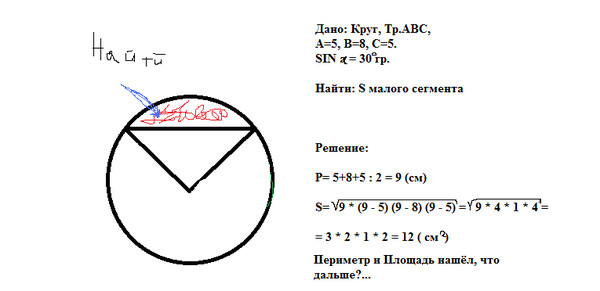
РЕШЕНИЕ:
Разделим исходный сектор круга, ограниченного центром круга и концами хорды, на два одинаковых, проведя биссектрису центрального угла. Будем рассматривать далее один из них (любой из двух полученных) и соответствующий прямоугольный треугольник (с вершинами в центре круга, одним из концов хорды и её серединой).
Пусть, далее, α – острый угол этого треугольника с вершиной в центре круга, a – длина противолежащей стороны (катета) этого треугольника, b — длины соответствующей дуги окружности, r – её радиус (искомый). Отметим также, что a и b – заданные величины, равные половине длин исходных хорды и дуги соответственно.
Тогда, очевидно (из чисто геометрического рассмотрения), имеем:
Это, по сути, запись двух определений: (1) – для длины дуги, (2) – для синуса угла. Таким образом, имеем систему двух уравнений с двумя неизвестными (α и r). Явного (аналитического) решения она не имеет – возможно лишь численное решение (которое существует и единственно).
Решать эту задачу в каждом конкретном случае – при заданных численных значениях a и b (точнее, как отмечено выше, – 2a и 2b) – можно двумя способами: «школьным» (геометрическим) и каким-либо численным методом.
«Школьный» метод:
После несложных преобразований уравнения (1) и (2) можно переписать, например, в виде:
где k = a/b. После этого строим графики функций f1(α) = kα, f2(α) = sin α и находим точку их пересечения, что соответствует решению уравнения (2′).
Отметим, что это пересечение (т.е. решение задачи) существует и единственно (и находится «недалеко» от начала координат): оба графика проходят через начало координат, причем второй (синусоида) выходит из начала координат под углом π/4 (=45o), первый (прямая) – под меньшим углом (поскольку k = a/b < 1, т.к. a < b – хорда должна быть короче дуги).
Таким образом, из графика находим α, а затем, используя уравнение (1′), и искомое значение радиуса r.
Численный метод:
Типичное численное решение такой задачи – каким-либо итерационным методом, например, методом Ньютона: дифференцируем и линеаризуем (по α) уравнение (2′), задаём какое-нибудь начальное приближение αo для α (наиболее логично и просто взять αo = 0) и дальше итерационно находим решение α = α* с любой наперед заданной точностью.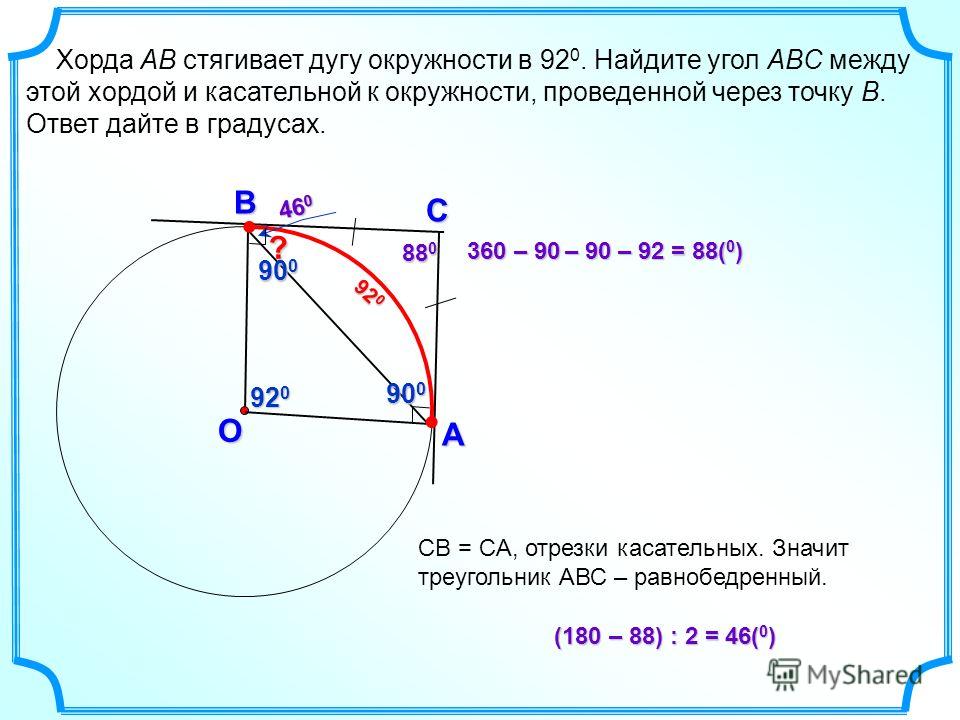
Далее, подставляя в уравнение (1′) найденное значение угла α*, находим искомое значение радиуса r.
Можно чуть по-другому – чтобы сразу решать уравнение (задачу) относительно радиуса r (без промежуточного нахождения угла α = α*). Для этого, например, просто подставляем из (1) (или из (1′)) выражение для угла α = b/r в уравнение (2′), получив тогда уравнение относительно переменной r.
Далее также как и выше дифференцируем, линеаризуем (но уже не по α, а по r) и решаем полученное уравнение и задачу в целом.
Научный форум dxdy
Найти радиус окружности по длине дуги и хорде
На одном из форумов попался вопрос, содржащий «школьную» задачку. Дано: Длина дуги части окружности , а длина хорды, на которую опирается эта дуга равна . Найти радиус окружности.
Вначале, все было хорошо и просто. Провел радиус из центра к концу дуги , а так же радиус, перпендикулярный хорде
, который пересек хорду в точке , образуя прямоугольный треугольник . Катет .
Угол при вершине O обозначил как .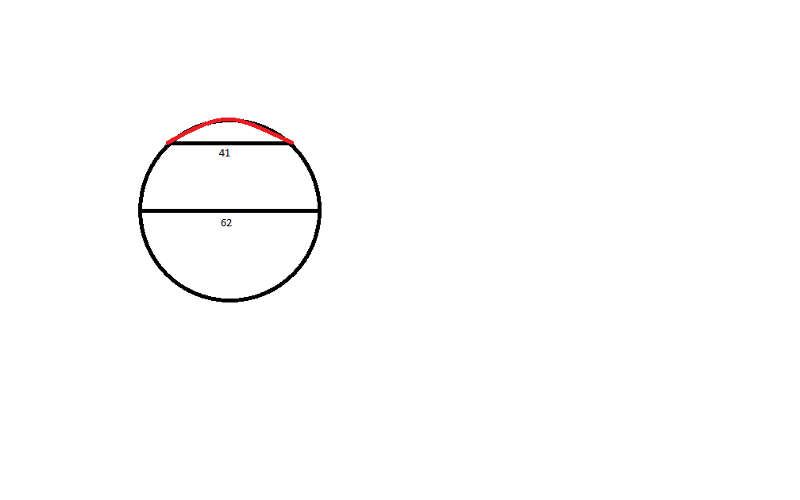
По определению синуса получил, что
или (1)
А из формулы длины дуги, получил или (2)
(2x потому, что — половина центрального угла рассматирваемой дуги).
Подстставляем в (1) вместо выражение, полученное из (2): или
, где
Ну, вот тут и заминочка вышла. Как найти по заданному ?
На практике, конечно нет проблем. В зависимости от точности либо найти значение графически, либо использовать один
из приближенных методов. Но возникает вопрос, есть ли аналитическое решение? Т.е. можно ли выразить через
элементарные функции от . Причем, функция интересует нас только при от 0 до пи.
Есть предположение, что это невозможно. Так ли это? Можно ли это доказать?
Хорда окружности ℹ️ определение, свойства, формула, теорема
Хорда в геометрии
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок.
Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
- Это отрезок с наибольшей длиною в окружности это диаметр. Он обязательно будет проходить через центр круга.
- Если есть две равные дуги, то их отрезки, которые их стягивают, будут равны.
- Хорда, которая перпендикулярна диаметру, будет делить этот отрезок и его дугу на две одинаковые части (справедливо и обратное утверждение).
- Самый маленький отрезок в окружности это точка.
- Хорды будут равны, если они находятся на одном расстоянии от центра окружности (справедливо и обратное утверждение).
- При сравнении двух отрезков в кругу большая из них окажется ближе к центру окружности.
- Дуги, которые находятся между двумя параллельными хордами, равны.
Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA.
Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
Касательная и секущая
Существует теорема о двух касательных, которые проведены с одной точки.
В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC.
Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180.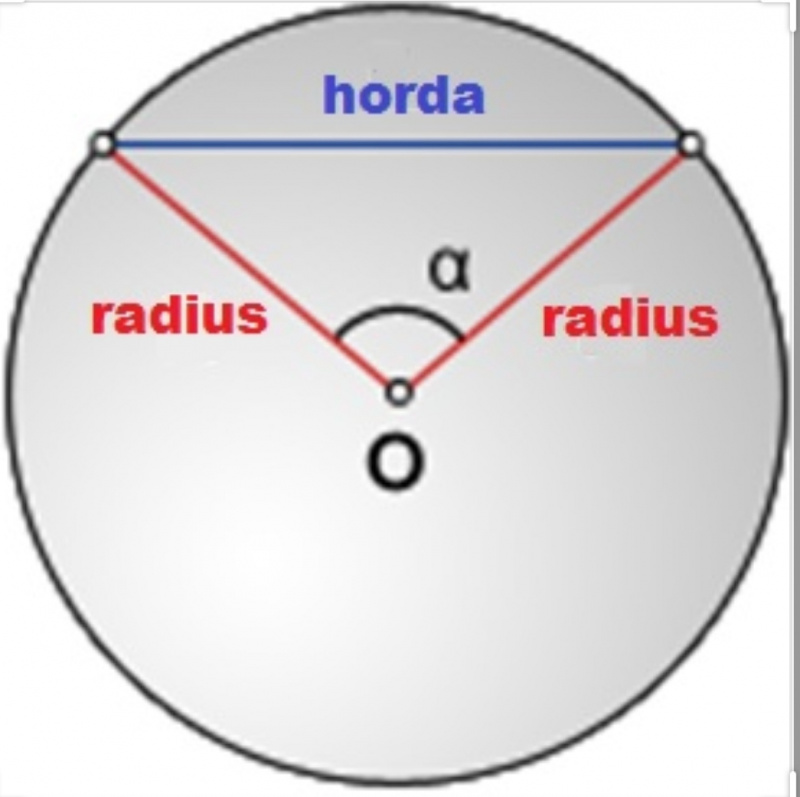
Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Как найти длину хорды
Все ресурсы по промежуточной геометрии
8 Диагностические тесты
250 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Справка по геометрии среднего уровня »
Плоская геометрия »
Круги »
Аккорды »
Как найти длину хорды
Радиус футов и .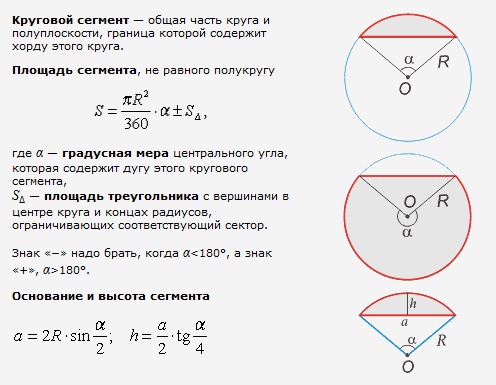
Найдите длину хорды.
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с трех радиусов: один к , один к и один перпендикулярно к с конечной точкой на нашей окружности.
Мы также должны помнить, что наш центральный угол имеет меру, равную дуге, на которую он опирается. Следовательно, . Наш перпендикулярный радиус фактически делится на два конгруэнтных треугольника. Следовательно, он также делит пополам наш центральный угол, а это означает, что
Следовательно, каждый из этих треугольников является треугольником 30-60-90, а это означает, что каждая половина нашей хорды равна половине длины гипотенузы (наш радиус равен 6). Следовательно, каждая половина равна 3, а вся хорда равна 6 футам.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам.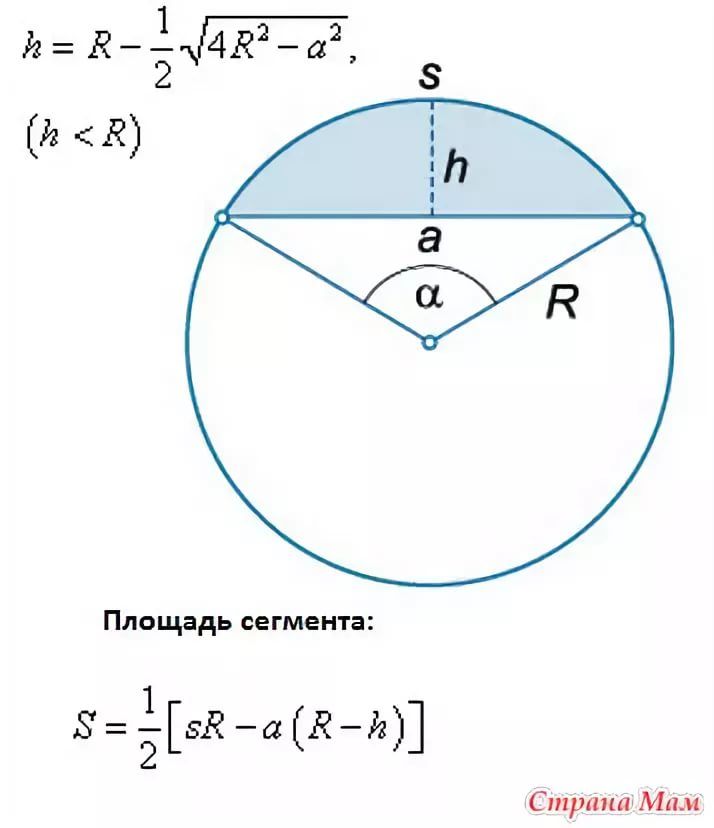
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 9,798.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 16.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам.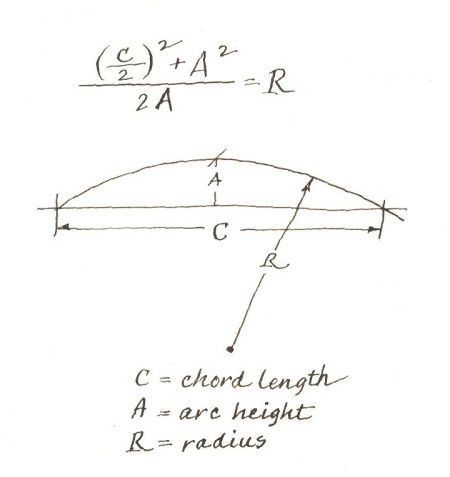
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 7,937.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 3,606.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам.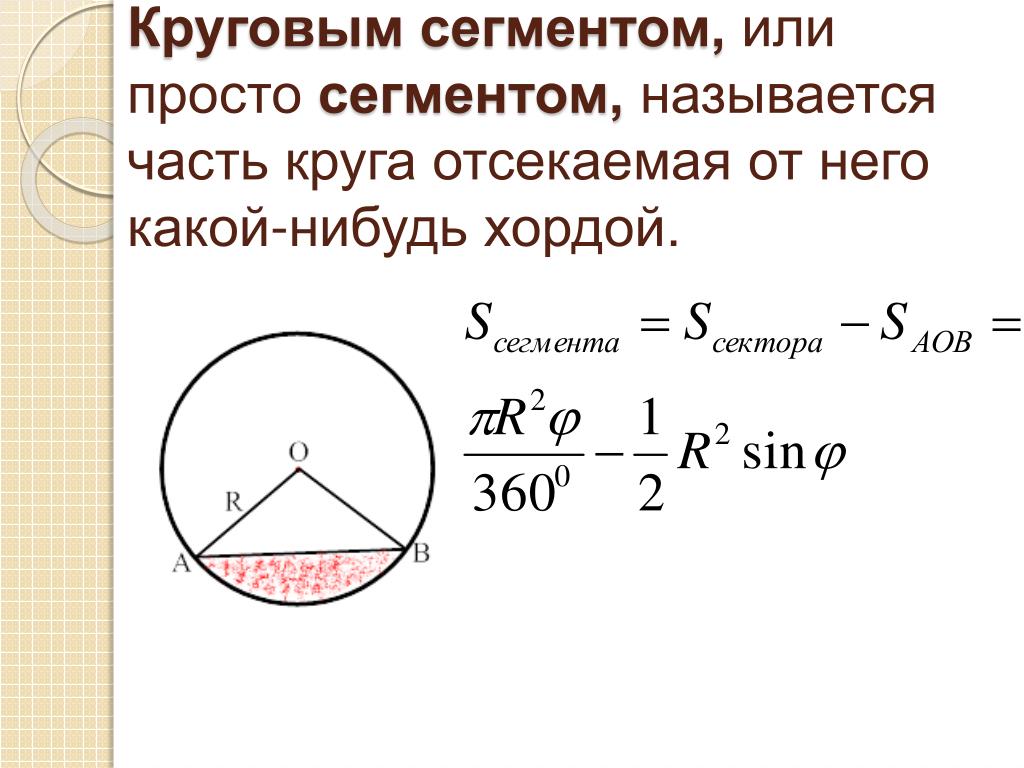
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше или в 6 раз больше.
Сообщить об ошибке
, какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 13,266.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам.
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 4,472.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 7,746.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам.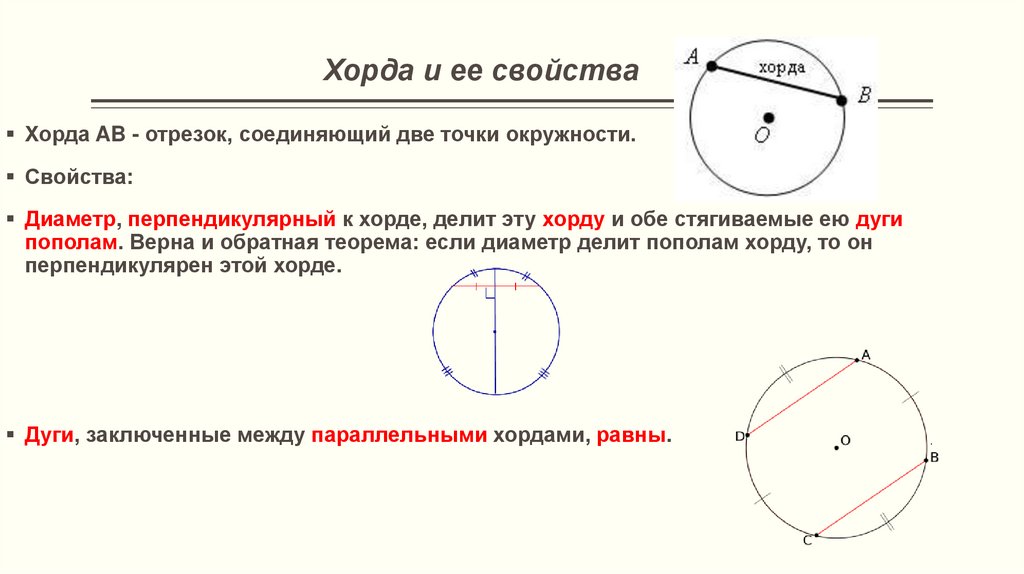
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 9,592.
Сообщить об ошибке
← Назад 1 2 3 4 Далее →
Уведомление об авторских правах
Все промежуточные ресурсы по геометрии
8 Диагностические тесты
250 практических тестов
Вопрос дня
Карточки
Learn by Concept
Расчет длины хорды
Все ресурсы по математике GMAT
22 диагностических теста
693 практических теста
Вопрос дня
Карточки
Learn by Concept
Помощь по математике GMAT »
Проблемные вопросы »
Геометрия »
Круги »
Аккорды »
Вычисление длины хорды
Какова длина хорды центрального угла окружности с площадью?
Возможные ответы:
Правильный ответ:
Объяснение:
Радиус круга с площадью можно найти следующим образом:
Окружность, центральный угол и хорда показаны ниже: Теорема треугольника, может быть доказана равносторонность, поэтому правильный ответ.
Сообщить об ошибке
Какова длина хорды центрального угла окружности с площадью?
Возможные ответы:
Правильный ответ:
Объяснение:
Радиус круга с площадью можно найти следующим образом:
Мы концентрируемся на треугольнике 30-60-90. По теореме 30-60-90
и
Хорда имеет вдвое большую длину, или
Сообщить об ошибке
Какова длина хорды центрального угла окружности с окружностью?
Возможные ответы:
Правильный ответ:
Объяснение:
Окружность с окружностью имеет радиус
.
Окружность, центральный угол и хорда показаны ниже вместе с , которая делит пополам равнобедренную :
Мы концентрируемся на треугольнике 30-60-90.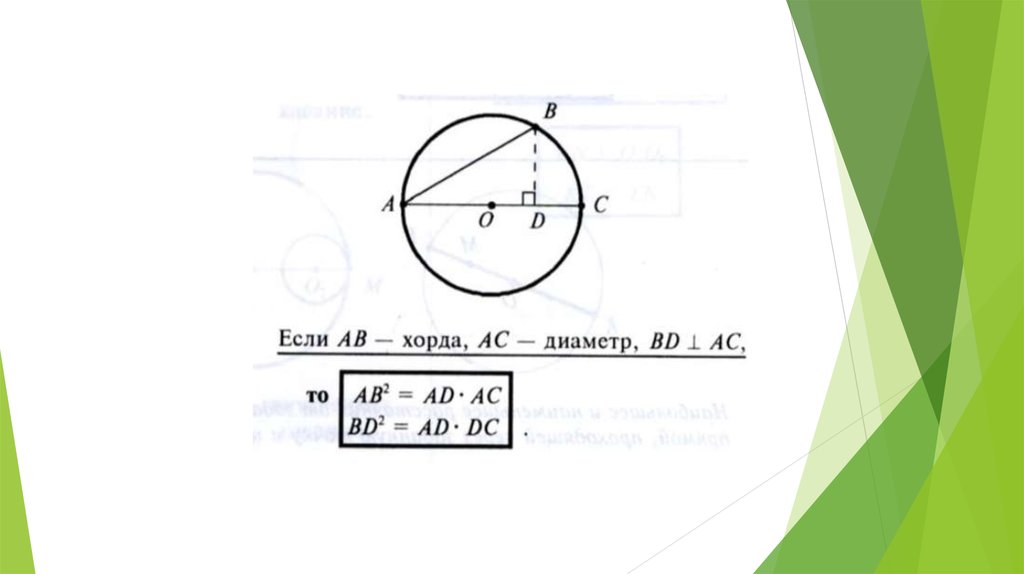
По теореме 30-60-90
имеет половину длины , поэтому
и
хорда имеет длину в два раза больше, или
Сообщить об ошибке
9000 центрального угла круг с площадью имеет какую длину?
Возможные ответы:
Правильный ответ:
Объяснение:
Радиус круга с площадью можно найти следующим образом:
Окружность, центральный угол и хорда показаны ниже: . Его гипотенуза имеет длину, умноженную на это, или
Это правильный ответ.
Сообщить об ошибке
Какова длина хорды центрального угла окружности с окружностью?
Возможные ответы:
Правильный ответ:
Объяснение:
Окружность с окружностью имеет радиус
.
Окружность, центральный угол и хорда показаны ниже:
С помощью теоремы о равнобедренном треугольнике можно доказать треугольник 45-45-90 с катетами длины 30. По теореме 45-45- 90 Теорема, его гипотенуза — хорда центрального угла — имеет длину, умноженную на это, или . Это правильный ответ.
Сообщить об ошибке
Рассмотрим круг:
(Рисунок не в масштабе.)
Если это угол, то какова мера сегмента?
Возможные ответы:
Правильный ответ:
Объяснение:
Это замаскированный треугольный вопрос. У нас есть девяностоградусный треугольник, две стороны которого состоят из радиусов окружности. Это означает, что два других угла ( и ) должны быть равны друг другу.
Используйте соотношения треугольников 45/45/90, чтобы найти окончательную сторону. Кроме того, вы можете использовать теорему Пифагора, чтобы найти недостающую сторону.
45/45/90 отношения длин сторон:
отрезок
Или, используя теорему Пифагора, переставляя его и находя гипотенузу, которая в данном случае представляет собой отрезок
Ошибка
Вычислите длину хорды в круге с радиусом , учитывая, что перпендикуляр расстояние от центра до хорды .
Возможные ответы:
Правильный ответ:
Пояснение:
Нам дан радиус окружности и расстояние по перпендикуляру от ее центра до хорды, и это все, что нам нужно для вычисления длины хорды. Используя формулу для длины хорды, которая включает эти две величины, мы находим решение следующим образом, где – длина хорды, – расстояние по перпендикуляру от центра окружности до хорды, а – радиус:
Сообщить об ошибке
Какова длина хорды центрального угла окружности с окружностью?
Возможные ответы:
Правильный ответ:
Объяснение:
Окружность с окружностью имеет радиус
.
Окружность, центральный угол и хорда показаны ниже:
С помощью теоремы о равнобедренном треугольнике можно доказать равносторонность, поэтому правильный ответ.
Сообщить об ошибке
Дуга окружности измеряет и имеет длину. Укажите длину хорды.
Возможные ответы:
Правильный ответ:
Объяснение:
Ссылка на рисунок приведена ниже.
Дуга окружности, поэтому длина окружности равна
.
Радиус — это длина окружности, деленная на , или
.
является, следовательно, гипотенузой равнобедренного прямоугольного треугольника с длиной катета ; по теореме о треугольнике 45-45-90 его длина умножается на эту, или
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по математике GMAT
22 диагностических теста
693 практических теста
Вопрос дня
Карточки
Learn by Concept
Определение хорды, формулы и различные теоремы
Окружность — это двумерная фигура, в которой множество всех точек равноотстоят от фиксированной точки на плоскости.
Неподвижная точка называется центром окружности. Еще одним важным термином в круге является его диаметр. Если вы образуете линию, которая пересекает две точки на краю круга и проходит через центр, это называется диаметром круга, а расстояние вокруг круга называется окружностью (c). Из этой статьи вы узнаете о том, что такое хорда окружности, а также о таких терминах, как длина хорды, формула длины хорды и многое другое. Что такое хорда окружности? Хорду окружности можно определить как отрезок, соединяющий любые две точки на окружности окружности. Таким образом, мы можем понять, что диаметр равен самая длинная хорда окружности, проходящая через центр окружности.
Хорда окружности: определение
Отрезок, соединяющий две точки на окружности, называется хордой окружности. Рассмотрим диаграмму ниже, где «O» — это центр, а AB и CD — хорда окружности. Здесь OE обозначает радиус окружности. AB является как диаметром, так и хордой на диаграмме.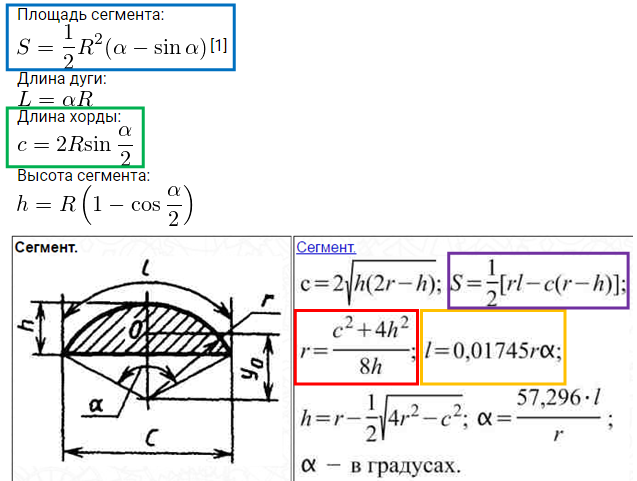
Это означает, что диаметр окружности является самой длинной хордой. Хорды, находящиеся на равном расстоянии от центра окружности, признаются равными хордами. Однако хорды, которые не находятся на одинаковом расстоянии от центра окружности, считаются неравными хордами. 92right)})
Как найти длину хорды:
Вот доказательство того, как найти длину хорды окружности.
На приведенной выше диаграмме r — радиус окружности, d — расстояние по перпендикуляру от хорды до центра окружности. Образуется треугольник, где r будет гипотенузой треугольника. Как известно, биссектриса, проведенная из хорды к центру окружности, делит хорду пополам.
Узнайте больше о линейных неравенствах здесь. 92right)}=2timessqrt{left(81−36right)}=2timessqrt{45})
(Хордадлина=13,416)
Если вы читая хорду круга, вы также должны прочитать о трехмерной геометрии здесь.
Длина хорды окружности по формуле с применением тригонометрии:
Рассмотрим приведенный выше рисунок, где r обозначает радиус окружности, а c — угол, опирающийся на центр.
(Хорда длина=2rsinleft(frac{c}{2}right))
Примечание: Стягиваемый угол
Рассмотрим окружность выше с CD в качестве хорды. Пусть P и Q — любые точки на окружности, кроме хорды, как показано на рисунке. Можно видеть, что концы хорды CD соединены с точкой P, тогда ∠CPD определяется как угол, образуемый хордой CD в положении P. Точно так же угол ∠CQD представляет собой угол, образуемый хордой CD на Q а угол ∠COD — это угол, образуемый хордой CD в центре O. 9{circ} )
(радиус окружности,r=24см)
(Тогда По формуле,)
(Хорда длина=2r sinleft(frac{c}{2}right))
(=2times24times Sineleft(frac{80}{2}right))
(= 2times24times Sine 40)
(=48times Sine 40)
(=30,853)
Узнайте о частях круга в этой статье!
Теоремы о хорде окружности
Теорема 1: Хорды, равные по мере, образуют равные углы в центре окружности.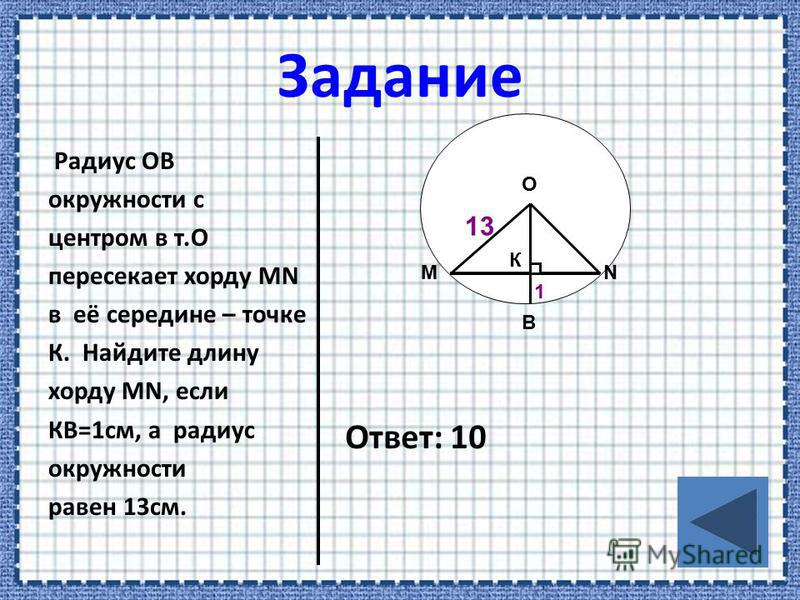
Это также известно как теорема о равных хордах и равных углах.
Теорема 2: Эта теорема утверждает, что если углы, образуемые хордами окружности, равны по мере, то длины хорд равны. Это также известно как теорема о равных углах и равных хордах или теорема, обратная теореме 1.
Теорема 3: Перпендикуляр, проведенный из центра окружности к хорде, делит ее пополам на равные половины.
Теорема 4 : Прямая, проходящая через центр окружности и делящая хорду, перпендикулярна хорде. Проще говоря, любая линия из центра, которая делит хорду пополам, перпендикулярна хорде. Это обратная теорема 3.9.0005
Теорема 5: Равные хорды окружности находятся на равном расстоянии от центра окружности.
Теорема 6: Эта теорема является обратной теореме 5. Она утверждает, что хорды, находящиеся на равном расстоянии от центра окружности, имеют одинаковую меру.
Теорема 7: Мера углов, опирающихся на любую точку окружности из одной и той же дуги, эквивалентна половине угла, опирающегося в центре на ту же дугу.
Другими словами, угол, образуемый дугой в центре окружности, в два раза больше угла, образуемого дугой в любом другом заданном месте на окружности.
Теорема 8: Углы, образуемые в одном и том же отрезке окружности, всегда равны по величине.
Теорема 9: Если отрезок, соединяющий любую пару точек, образует одинаковые углы в двух других точках, лежащих на соответствующей стороне, то они называются конциклическими. Это говорит о том, что все они покоятся в одном круге.
Теорема 10: Если есть 3 точки, не лежащие на одной прямой, то через них может пройти только одна окружность.
Узнайте больше о последовательностях и сериях здесь.
Связь между радиусом и хордой окружности
Радиус окружности определяется как любой отрезок, соединяющий центр окружности с любым местом на окружности. Однако хорда окружности — это отрезок, соединяющий любые две точки на окружности окружности.
Диаметр в два раза больше радиуса и также является хордой, проходящей через центр окружности.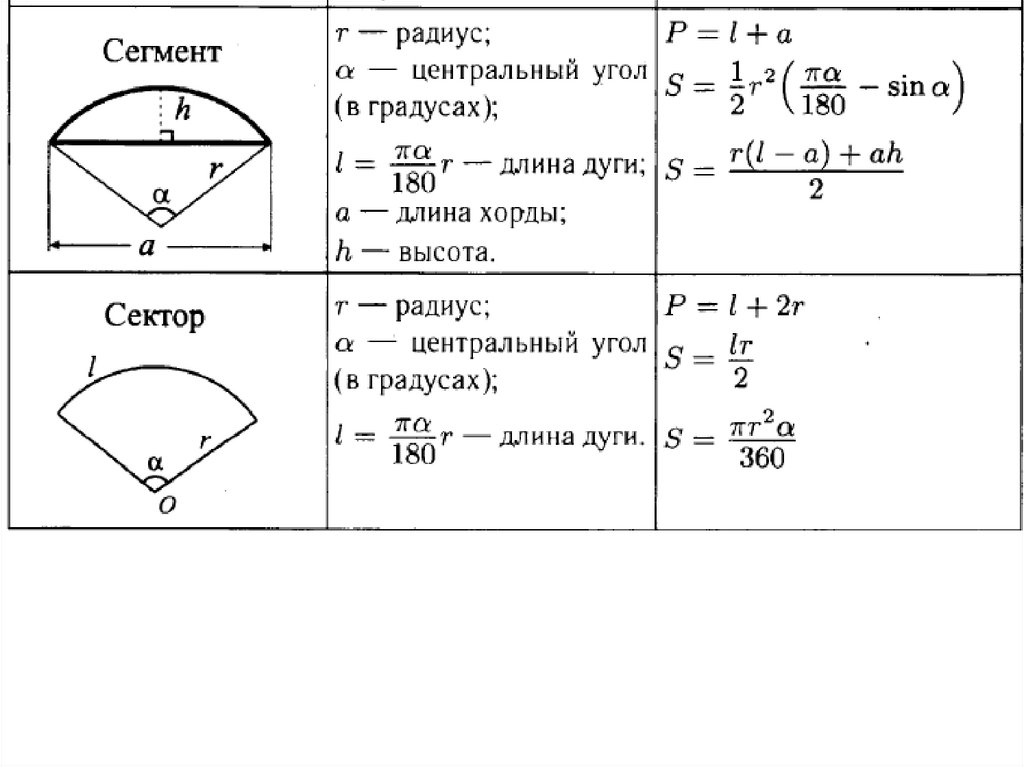
Также читайте об отношениях и функциях здесь.
Хордовые свойства окружности
- Радиус окружности работает как биссектриса хорды.
- Длина хорды увеличивается по мере уменьшения перпендикулярного расстояния от центра окружности до хорды и наоборот.
- Диаметр — это самая длинная хорда окружности, при этом длина перпендикуляра от центра к хорде равна нулю.
- Два радиуса, соединяющие концы хорды с центром окружности, образуют равнобедренный треугольник.
- Две хорды равны по длине, если они находятся на одинаковом расстоянии от центра окружности.
Узнайте о различных типах уравнений окружности в этой связанной статье
Мы надеемся, что приведенная выше статья об хорде окружности поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам.
Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы об аккорде окружности
В.1 Что такое аккорд в математике?
Ответ 1 Хорда — это отрезок, соединяющий две точки на окружности. Хорда включает только часть внутри круга.
Q.2 Как найти хорду окружности?
Ответ 2 Любой отрезок, концы которого лежат на окружности, называется хордой этой окружности.
Q.3 Является ли диаметр самой длинной хордой?
Ответ 3 Хорда, проходящая через центр окружности, называется диаметром, а диаметр также является самой длинной хордой этой конкретной окружности.
Q.4 Как найти радиус окружности с длиной хорды?
Ответ 4 Радиус окружности можно определить, если длина хорды определяется длиной хорды с использованием перпендикулярного расстояния или длины хорды формулы окружности с применением формулы тригонометрии, как описано в статье.