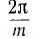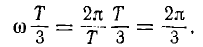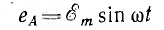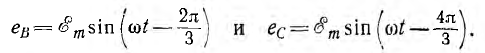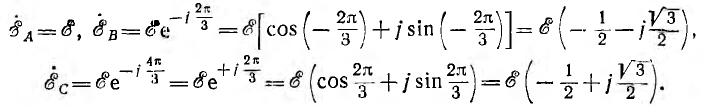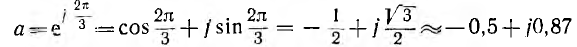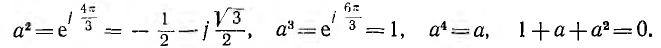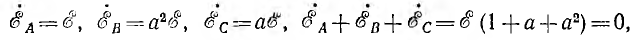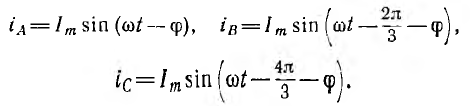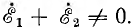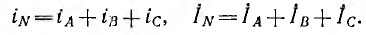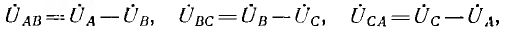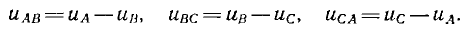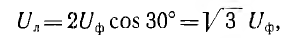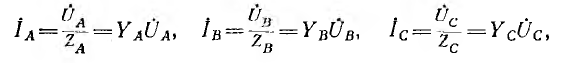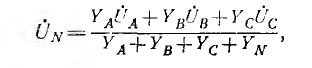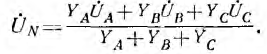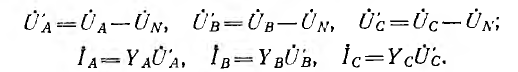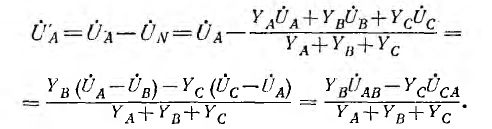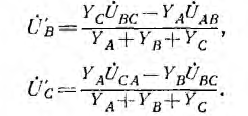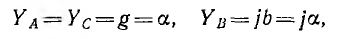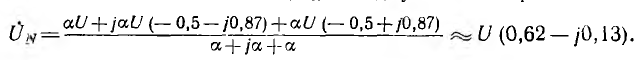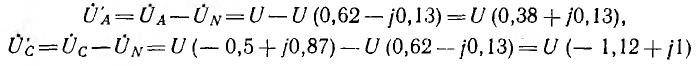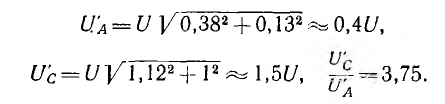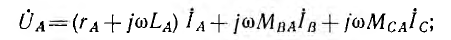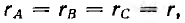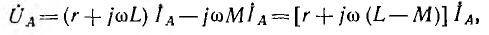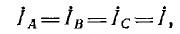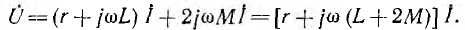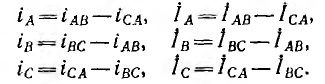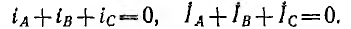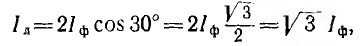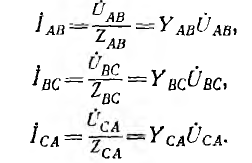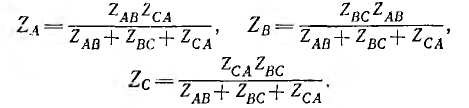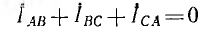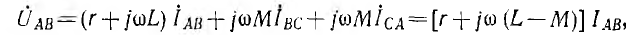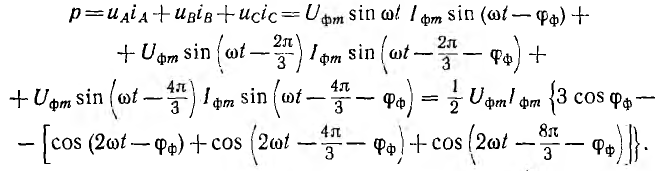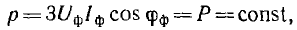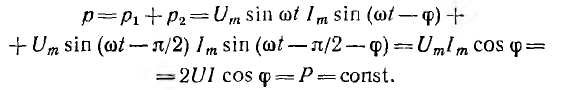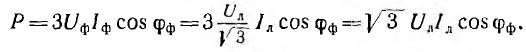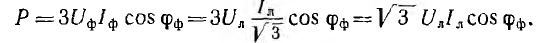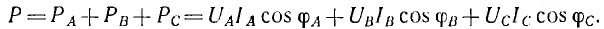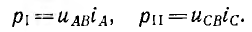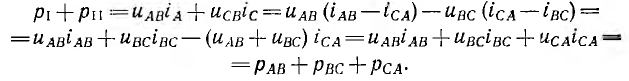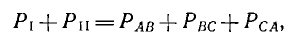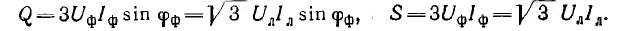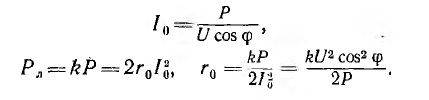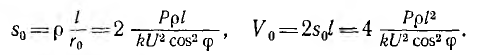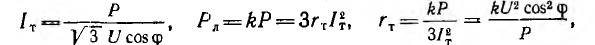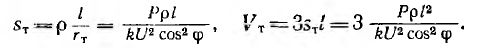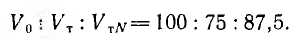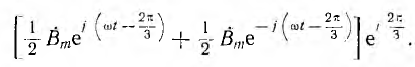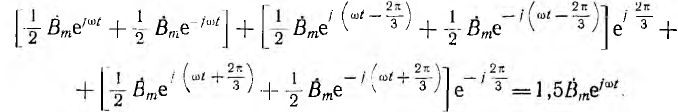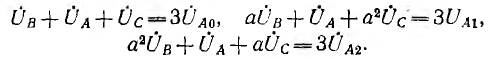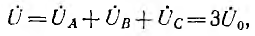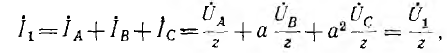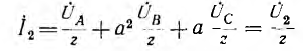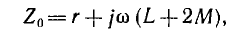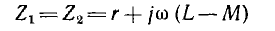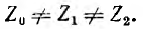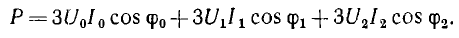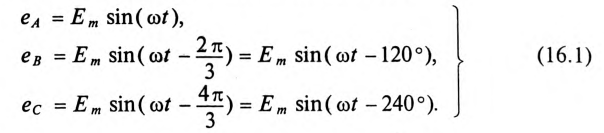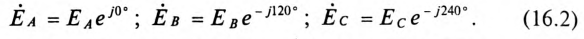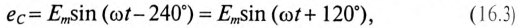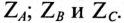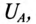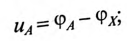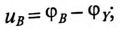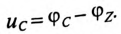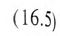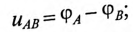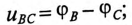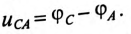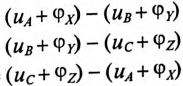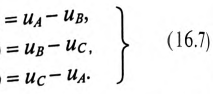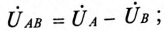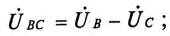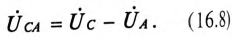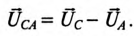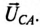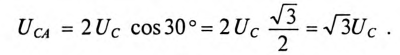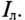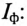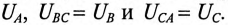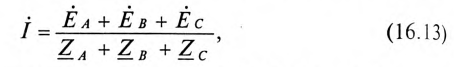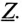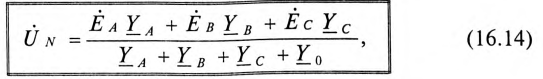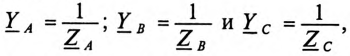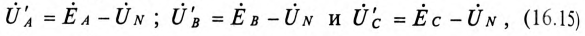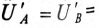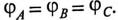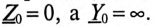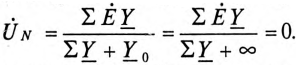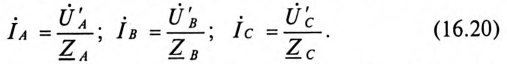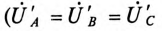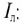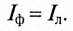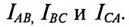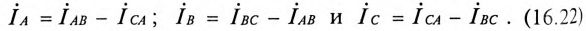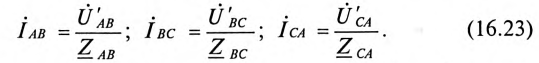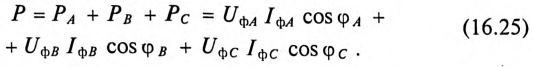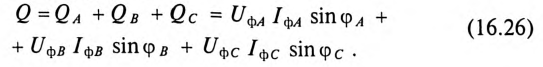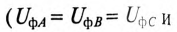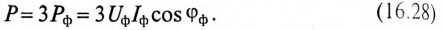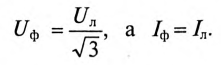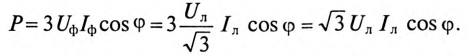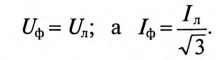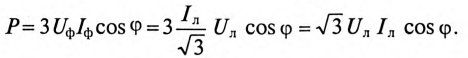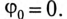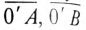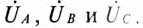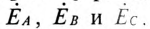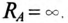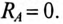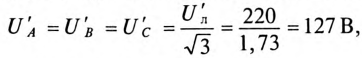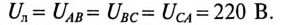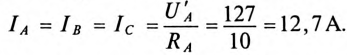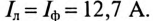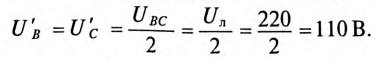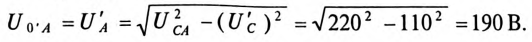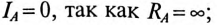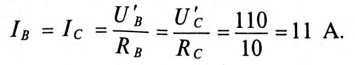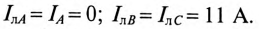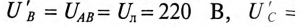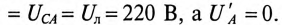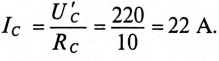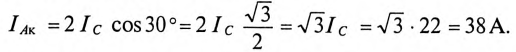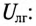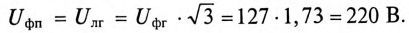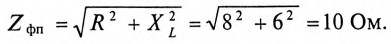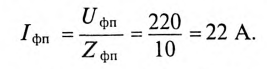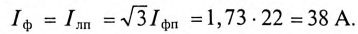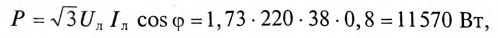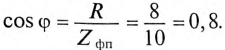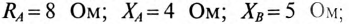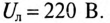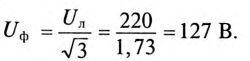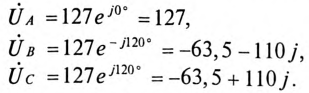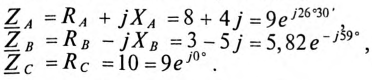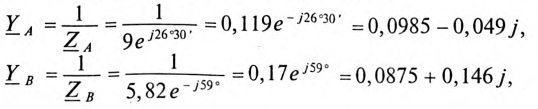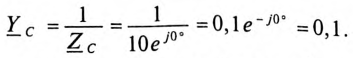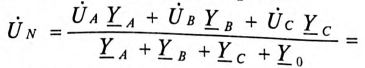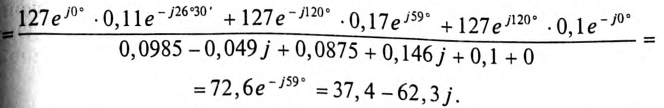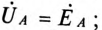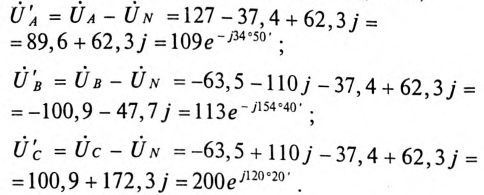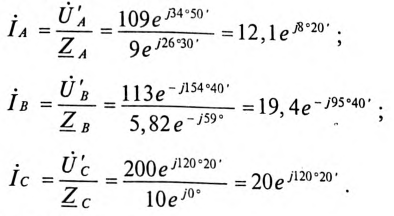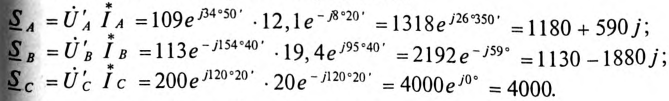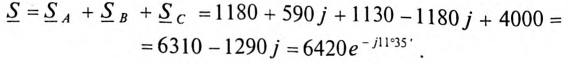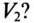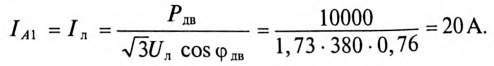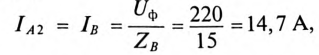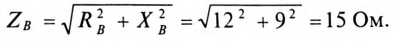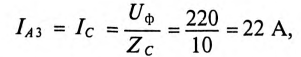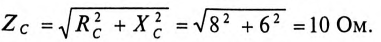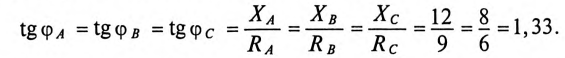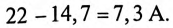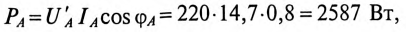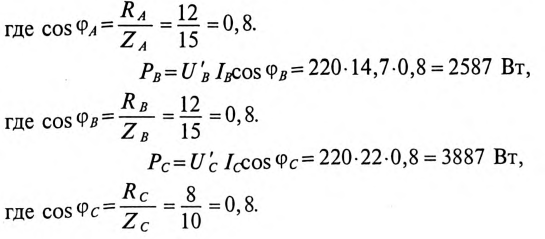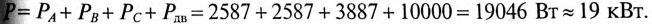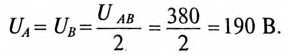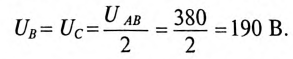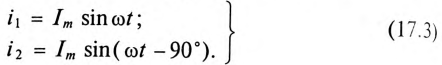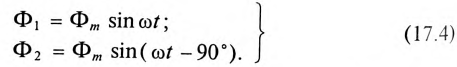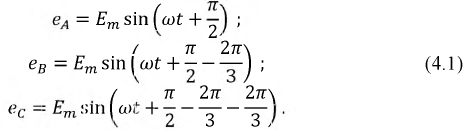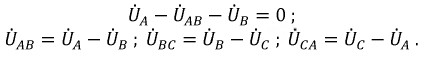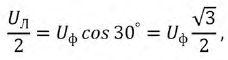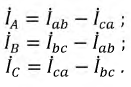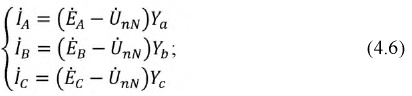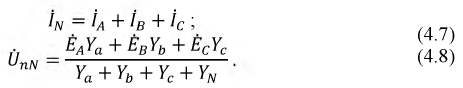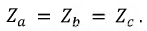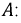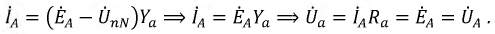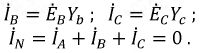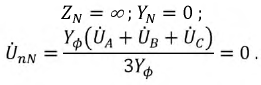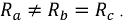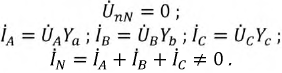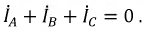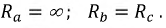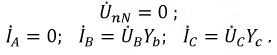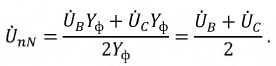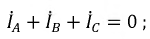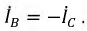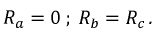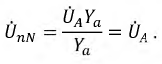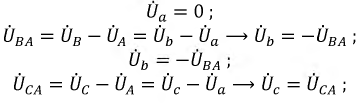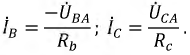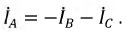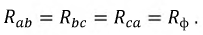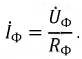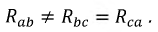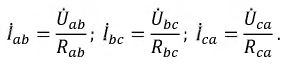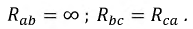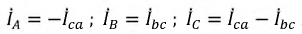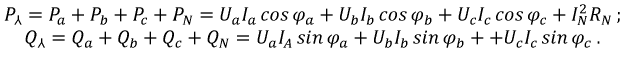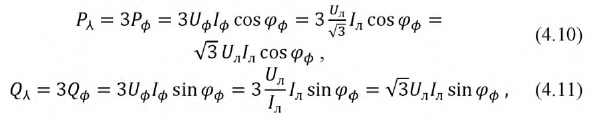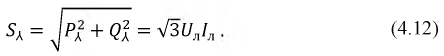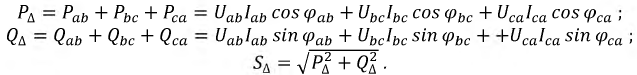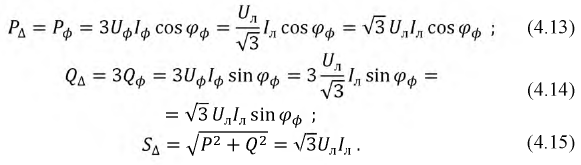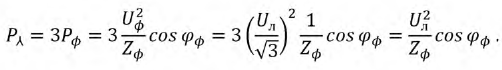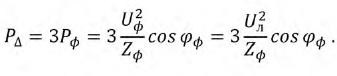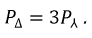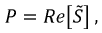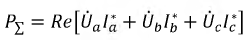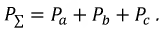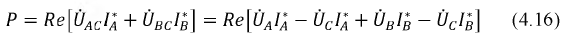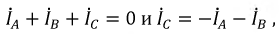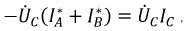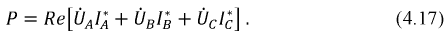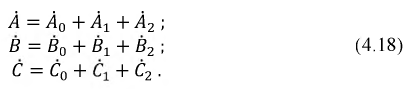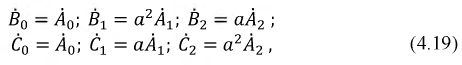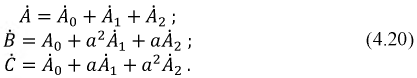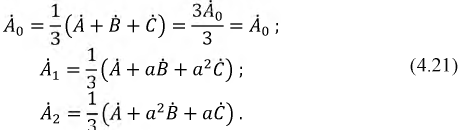Что такое фазный ток, как его найти и измерить
Содержание
- 1 Преимущества и недостатки трехфазных сетей
- 2 Что такое трехфазный генератор
- 3 Соединение обмоток генератора
- 3.1 Соединение звездой
- 3.2 Соединение треугольником
- 4 Видео по теме
В большинстве стран, в том числе и в России, используется трехфазная система электроснабжения. В ней действуют ЭДС синусоидального типа, которые образуются от единого генератора и имеют синхронную частоту. При подключении к трехфазной сети следует понимать, что такое фазные и линейные токи, а также напряжения.
Преимущества и недостатки трехфазных сетей
Основное преимущество трехфазных электросетей переменного тока — простота образования вращающегося магнитного поля. Это привело к созданию асинхронных короткозамкнутых двигателей как наиболее распространенных исполнительных электромоторов в мире.
Трехфазное питание двигателей с короткозамкнутым ротором легко обеспечивает следующие качества:
- легкий реверс. Изменяя чередование фаз на статоре при помощи пускателей можно менять направление вращения;
- снижение пусковых токов. Переключением звезда-треугольник обмоток статора снижается пусковой ток — фазный ток при выходе двигателя из состояния покоя;
- ступенчатое регулирование скорости. За счет переключения пар полюсов трехфазная система превращается в шестифазную у двухскоростных асинхронных двигателей;
- плавное регулирование оборотов. Изменяя частоту и амплитуду трехфазного питания, можно регулировать скорость короткозамкнутого двигателя в определенных пределах.
В системах трехфазного электроснабжения использование меньшего количества проводов и уменьшенного сечения нулевого провода на больших расстояниях дает существенную экономию цветных металлов. Магнитопровод и обмотки трехфазных трансформаторов при равных габаритах значительно мощнее однофазных, что тоже важно.
Использование трехфазных обогревателей позволяет иметь различный фазный ток нагрева при переключении звезда-треугольник. Это позволяет управлять скоростью нагрева объекта, что бывает полезным при включении и экономичным при поддержании заданной температуры.
Повсеместное использование люминесцентных и светодиодных светильников в промышленности при подключении их к разным фазам трехфазной системы снижает стробоскопический эффект. Сдвиг по фазе питающих токов снижает пульсации ламп.
Одно из основных требований к трехфазным нагрузкам — не допустить перекоса фаз. Для этого надо распределять однофазные устройства на группы и равномерно разносить их по трем фазам. Кроме того, при наличии двигателей переменного тока, установленных на механизмах, требуется следить за правильностью чередования фаз, чтобы при включении станки и агрегаты вращались в нужном направлении. В промышленности за этим следят электрики.
В частном домовладении распределение потребителей по группам ложится на владельца. Если не планируется в доме мощных трехфазных устройств типа котлов или варочных панелей, прокладывать такие сети внутри нет необходимости. Это дорого и, возможно, есть ограничение по мощности подключения от электросетей.
Что такое трехфазный генератор
Основой трехфазной сети является генератор, на якоре которого размещены три обмотки. Они разнесены по окружности относительно друг друга на 120 градусов. В каждой замкнутой катушке, вращающейся в однородном магнитном поле статора подобно замкнутой рамке, будет образовываться синусоидальная ЭДС, которая создаст ток той же частоты и формы.
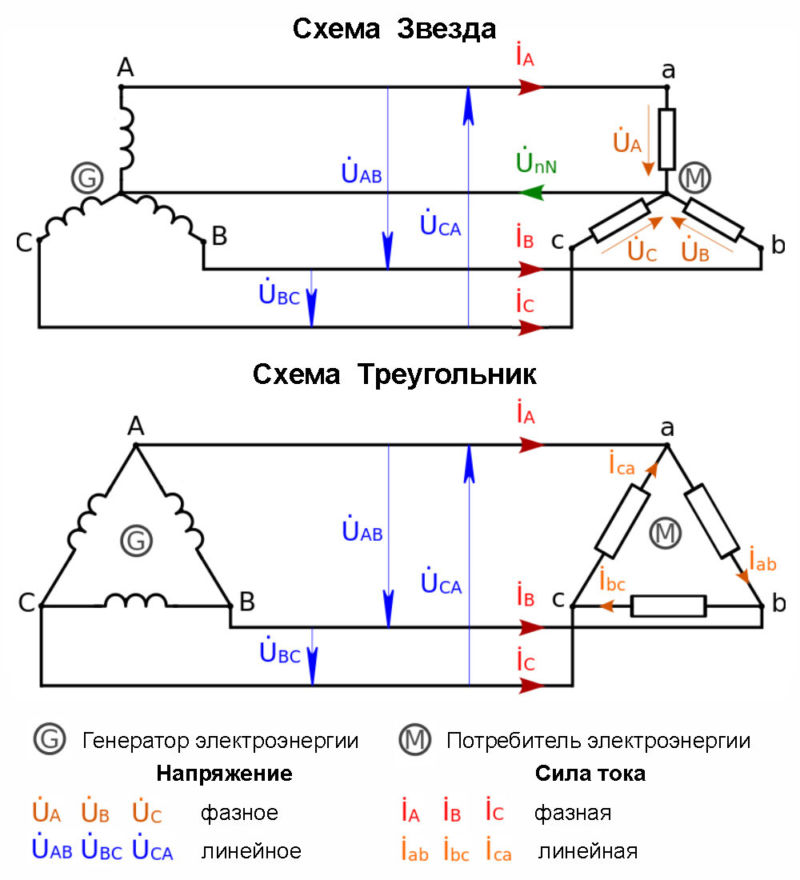
Чтобы катушки не действовали друг против друга, создавая ЭДС взаимоиндукции, они должны быть намотаны либо по часовой или против часовой стрелки, но все в одном направлении. Переменный ток снимается с контактных колец щетками и поступает на нагрузку. Каждая катушка — это фаза. Для их обозначения используются латинские буквы А, В, С. Переменные токи, присутствующие в фазах, называют фазными. Их обозначают IФ или для каждой фазы IА, IВ, IС. Токи, протекающие в ветвях нагрузки, принято называть линейными. Значение линейных токов зависит от величины фазных напряжений и типа нагрузки.
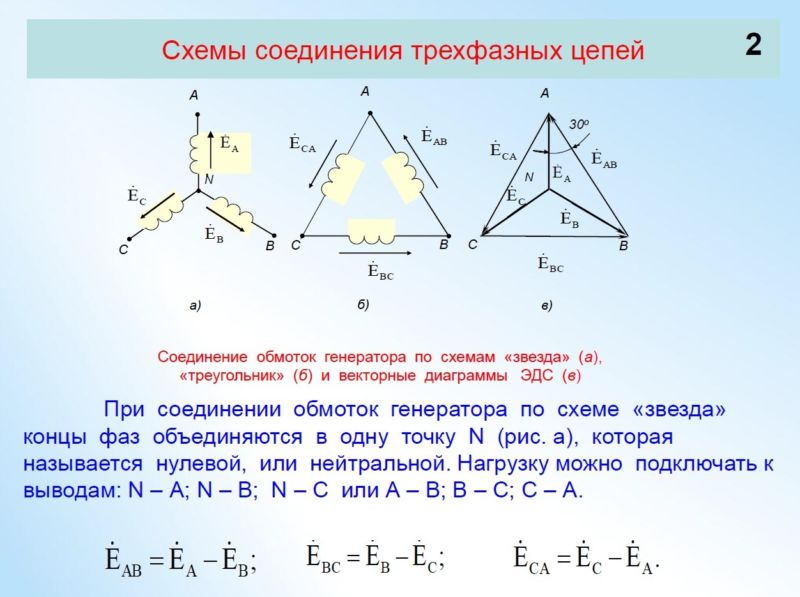
Формулы для определения значения ЭДС в каждой самостоятельной катушке генератора в зависимости от угла вращения будут иметь вид:
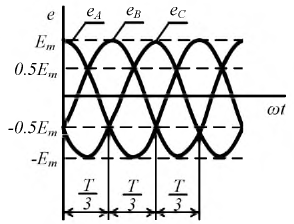
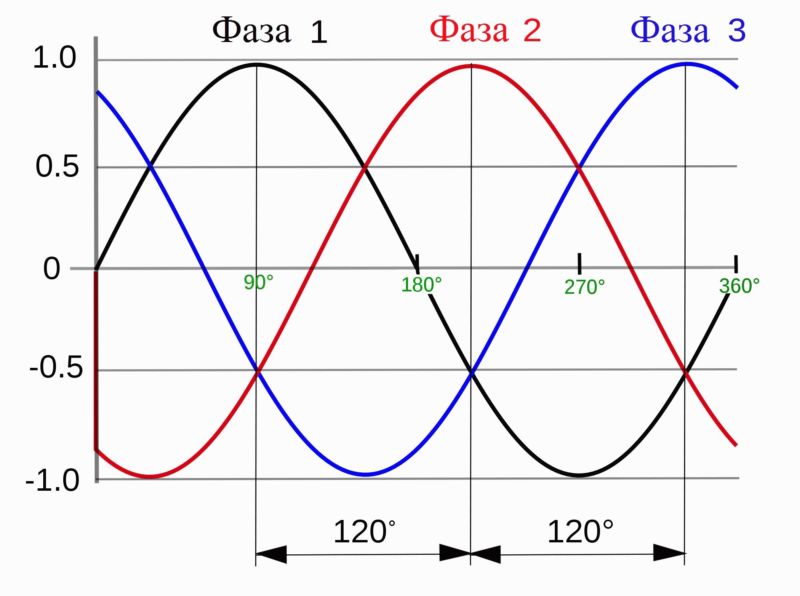
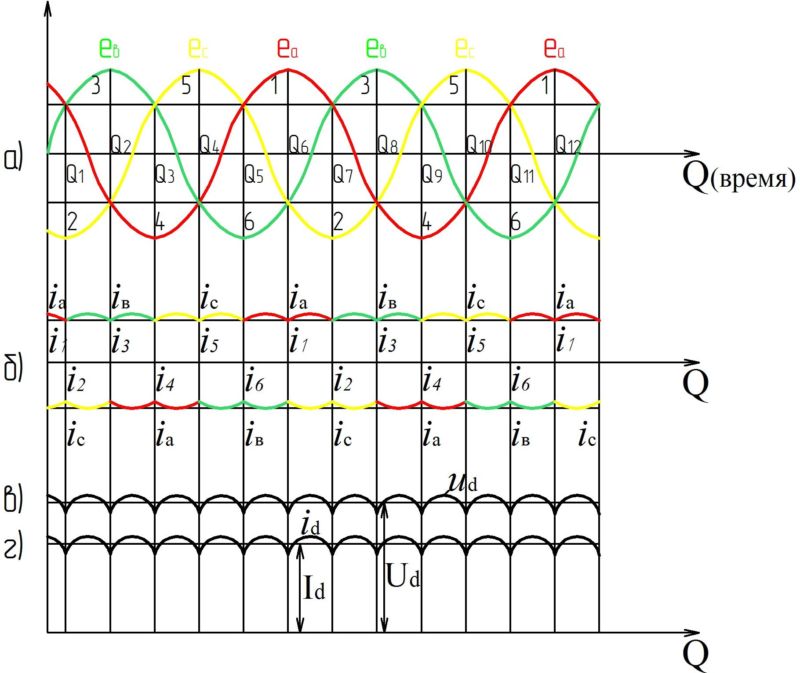
ЭДС можно представить графически в виде трех синусоид, сдвинутых на 1/3 периода.
Аналогично происходит образование токов, если разнесенные на угол 120 градусов (2π/3) обмотки размещены на статоре генератора, а вращается постоянный магнит — ротор электрической машины. Привод, обеспечивающий равномерное вращение ротора, может быть любым.
Соединение обмоток генератора
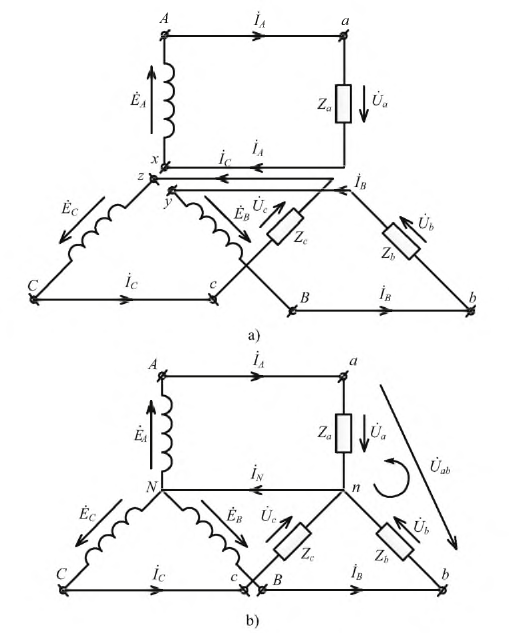
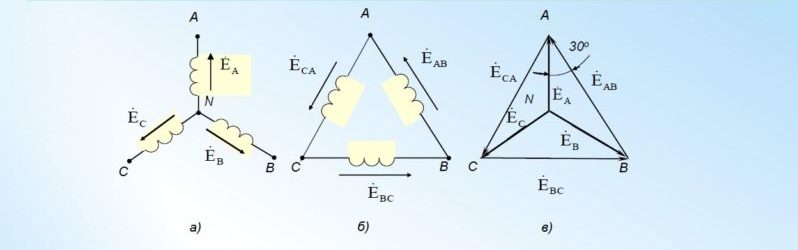
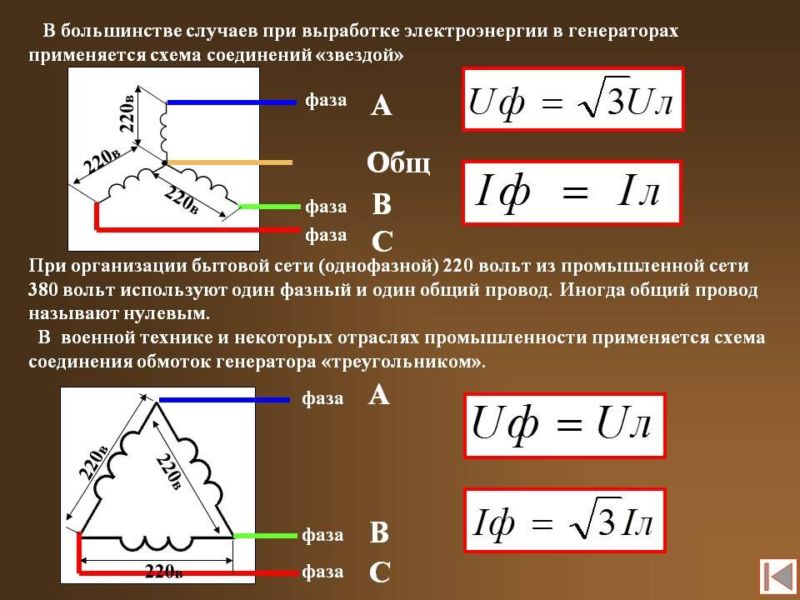
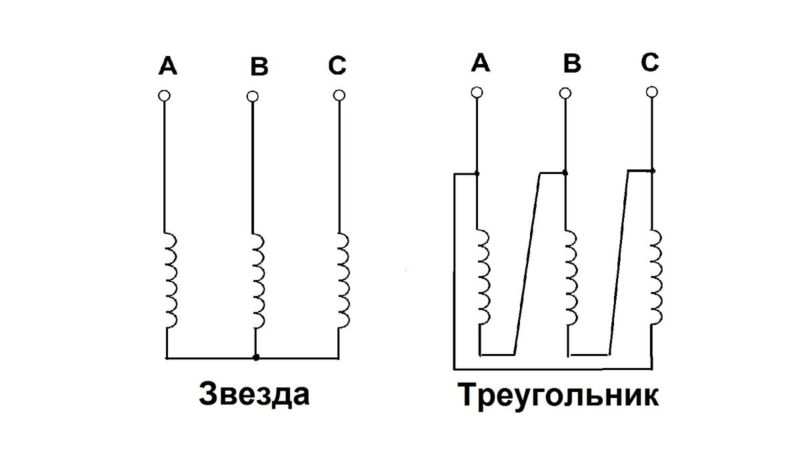
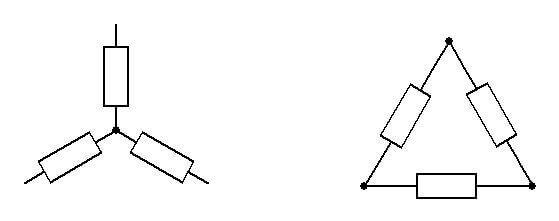
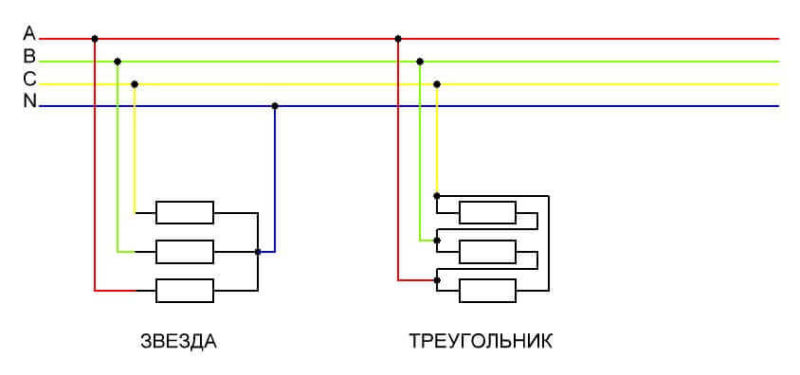
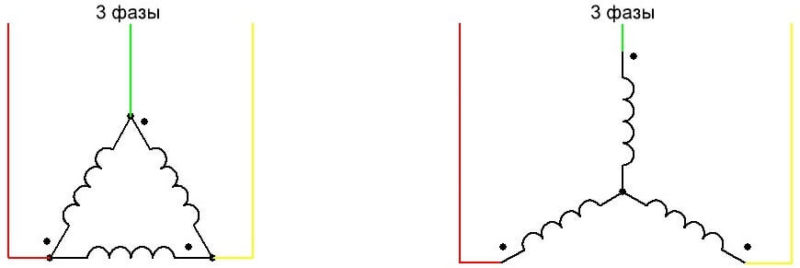
Обмотки генератора соединяют либо в звезду, либо в треугольник. В первом случае начала обмоток электрической машины соединены вместе (НА+НВ+НС), а концы КА, КВ, КС выводятся на нагрузку (концы вместе, а начала на нагрузку тоже правильно). При соединении в треугольник начало одной обмотки соединяется с концом другой (НА+КВ, НВ+КС, НС+КА), а на нагрузку выводятся места соединения.
Соединение звездой
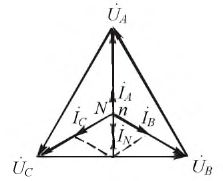
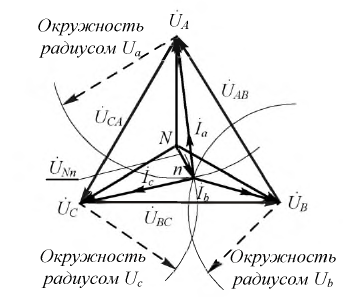
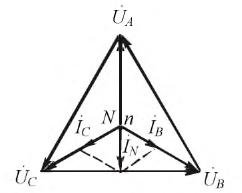
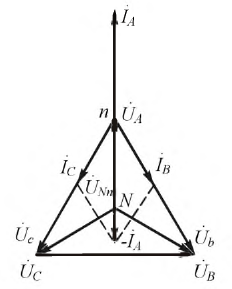
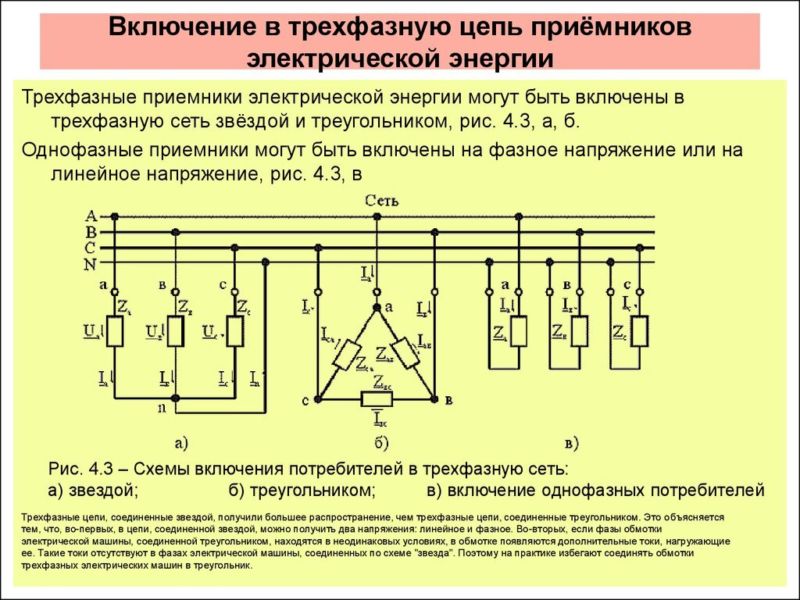
При соединении генератора переменного тока с нагрузкой по схеме звезда в несимметричных системах, когда фазы могут быть нагружены по-разному, применяется нулевой провод. С его помощью нейтраль генератора подключают к нейтрали приемника. Так можно устранить перекос фаз, если появляется разность между напряжениями точек N и n.
При разных сопротивлениях в приемнике фазные токи различны по величине. Ток в проводе, соединяющем нейтрали, определяется как сумма векторов всех фазных токов:
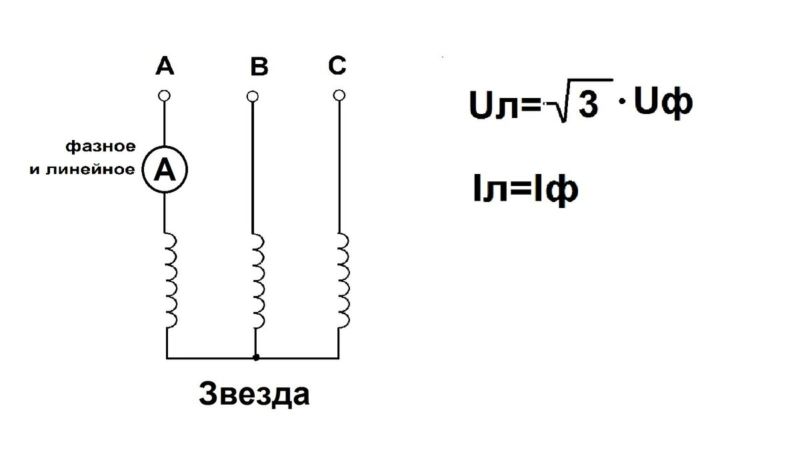
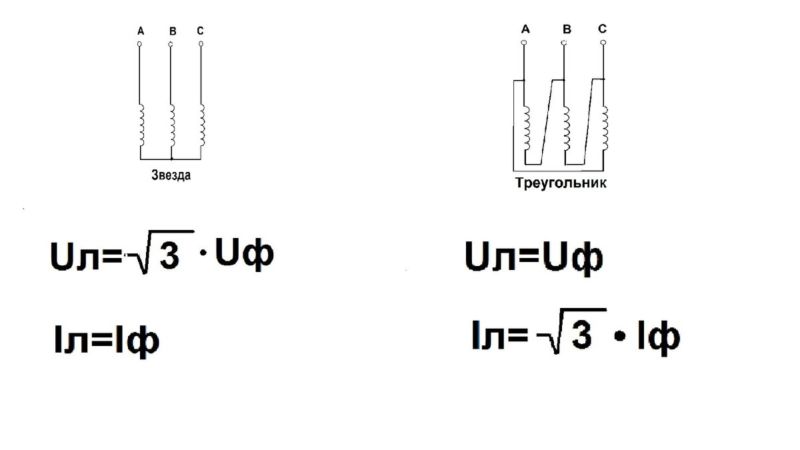
Разность потенциалов между проводниками, соединяющими обмотки генератора и приемника, называется линейным напряжением. При соединении звездой фазным напряжением становится потенциал на выходе из обмотки и нулевой точки звезды. Для определения соотношения между значениями линейного и фазного напряжения используется формула:
При соединении в звезду фазный и линейный ток имеют одинаковое значение в приемниках с одинаковыми сопротивлениями. Там, где сопротивления не равны, величина линейных и фазных токов будет определяться нагрузкой.
Соединение генератора и 3-х фазной нагрузки в звезду возможно без нейтрального провода при одинаковых сопротивлениях фаз приемника. Соотношения напряжений и токов при этом соответствуют варианту с симметричной нагрузкой. Трехфазный несимметричный приемник без провода, соединяющего нейтрали, создает аварийную ситуацию.
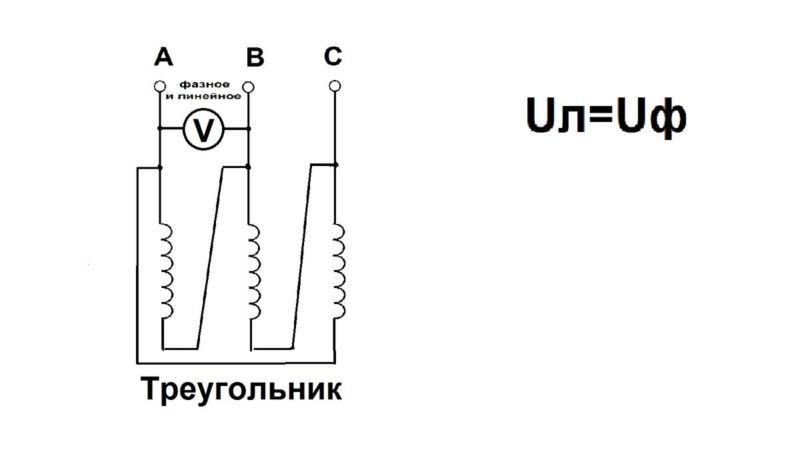
Соединение треугольником
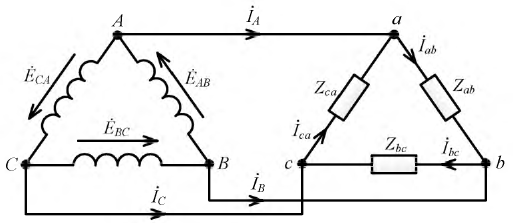
Подключение начала одной обмотки трехфазного генератора к концу другой образует треугольник — замкнутый контур, сумма ЭДС внутри которого равна 0.
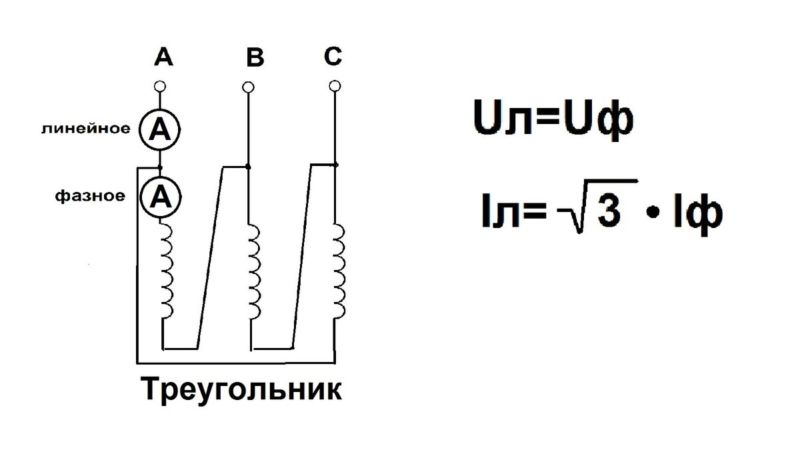
При соединении обмоток треугольником в случае симметричной нагрузки справедливым является соотношение между линейными и фазными токами и напряжениями:
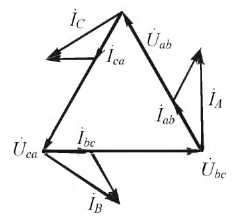
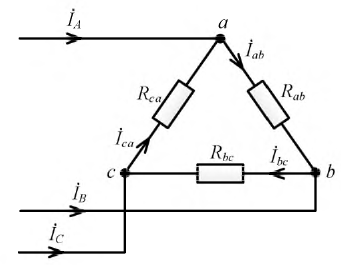
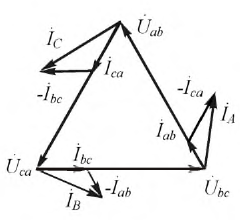
Согласно закону Кирхгофа, в вершинах треугольника приемника линейные токи можно определить по формулам:
Токи в фазах приемника можно найти, исходя из закона Ома:
При несимметричной нагрузке (различном сопротивлении фаз приемника) исходят из того, что она (не симметрия) никак не влияет на фазные напряжения и токи генератора, то есть, мощность источника бесконечно велика по сравнению с приемником. При таком допущении зависимость между фазными и линейными токами остается той же, что и при симметричной нагрузке.
Если необходимо узнать величину тока и напряжения в трехфазной цепи, зачастую выполняют измерение одного из линейных токов и одного из линейных напряжений. Измеряется параметр таким же способом, что и в однофазной цепи. Для этого используют вольтметры, амперметры и трансформаторы тока.
Видео по теме
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно,
все рассмотренные ранее методы расчета и анализа в символической форме в полной
мере распространяются на них. Анализ трехфазных систем удобно осуществлять с
использованием векторных диаграмм, позволяющих достаточно просто определять
фазовые сдвиги между переменными. Однако определенная специфика многофазных
цепей вносит характерные особенности в их расчет, что, в первую очередь, касается
анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными,
если в них комплексные сопротивления соответствующих фаз одинаковы, т.е.
если . В противном случае они являются
несимметричными. Равенство модулей указанных сопротивлений не является
достаточным условием симметрии цепи. Так, например трехфазный приемник на рис.
1,а является симметричным, а на рис. 1,б – нет даже при условии: .

Если к симметричной трехфазной цепи приложена симметричная трехфазная система
напряжений генератора, то в ней будет иметь место симметричная система токов.
Такой режим работы трехфазной цепи называется симметричным. В этом режиме
токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг
по отношению к другу на угол . Вследствие указанного расчет
таких цепей проводится для одной – базовой – фазы, в качестве которой
обычно принимают фазу А. При этом соответствующие величины в других фазах получают
формальным добавлением к аргументу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном
напряжении и сопротивлениях фаз можно записать

где
определяется характером нагрузки .
Тогда на основании вышесказанного
;
.

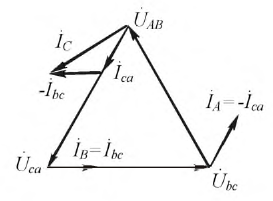
Комплексы линейных токов можно найти с использованием векторной диаграммы на
рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется
с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники
симметричны, то в соответствии с формулами преобразования «треугольник-звезда»

Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы
их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи
их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется
базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам
которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении необходимо определить линейные
токи и
в схеме на рис. 3, все сопротивления
в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена
на рис. 4. Здесь ,
.
Тогда для тока 

и соответственно .


Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет
место несимметричный режим работы. Такие режимы при наличии в цепи только статической
нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для
всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные
напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить,
что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес
также потенциалы узлов, чаще других для расчета сложных схем применяется метод
узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей
с электрическими машинами в основном применяется метод симметричных составляющих,
который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные
цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах
линейных напряжений в соответствии с законом Ома



По найденным фазным токам приемника на основании первого закона Кирхгофа определяются
линейные токи:
.
Обычно на практике известны не комплексы линейных напряжений, а их модули.
В этом случае необходимо предварительное определение начальных фаз этих напряжений,
что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений,
строим треугольник (см. рис.5), из которого (путем замера) определяем значения
углов a и b.
Тогда

Искомые углы a и b могут быть также найдены аналитически
на основании теоремы косинусов:

При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода
с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям
на фазах источника. В этом случае фазные токи легко определяются по закону Ома,
т.е. путем деления известных напряжений на фазах потребителя на соответствующие
сопротивления. Однако, если сопротивление нейтрального провода велико или он
отсутствует, требуется более сложный расчет.
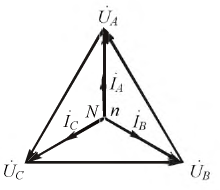
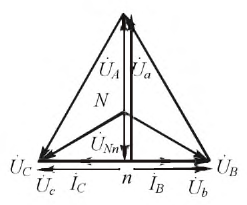
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной
нагрузке ей в общем случае будет соответствовать
векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные положения, т.е. .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением
смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения
нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке,
что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали.
Если оно известно, то напряжения на фазах нагрузки равны:
.

Тогда для искомых токов можно записать:
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода
узловых потенциалов, имеет вид
 . . |
(1) |
При наличии нейтрального провода с нулевым сопротивлением , и из (1)
. В случае отсутствия нейтрального
провода . При симметричной нагрузке
с учетом того, что
, из (1) вытекает
.
В качестве примера анализа несимметричного
режима работы цепи с использованием соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если
.
Запишем выражения комплексных сопротивлений фаз нагрузки:

Тогда для напряжения смещения нейтрали будем иметь

Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника
опускается)

Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения
(что обычно имеет место на практике), то с учетом того, что сумма последних
равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например,
и
. Тогда, поскольку при этом
, соотношение (1) трансформируется
в формулу
 . . |
(2) |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных
цепей? - С помощью каких приемов трехфазная симметричная схема сводится к расчетной
однофазной? - Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а
;
;
;
. Линейное напряжение равно 380
В. - В схеме предыдущей задачи
;
. Остальные параметры те же.
- В задаче 8 нейтральный провод оборван.
- В задаче 9 нейтральный провод оборван.
Определить ток в нейтральном проводе.
Ответ: .
Определить ток в нейтральном проводе.
Ответ: .
Определить фазные напряжения на нагрузке.
Ответ: ;
;
.
Определить фазные напряжения на нагрузке.
Ответ: ;
;
.
Содержание:
Трехфазные цепи:
Многофазной системой называется совокупность электрических цепей, называемых фазами, в которой действуют синусоидальные напряжения одной частоты, отличающиеся друг от друга по фазе. Чаще всего применяются симметричные многофазные системы, напряжения которых равны по величине и сдвинуты по фазе на угол
Трехфазная система
Наибольшее распространение имеет трехфазная система, созданная русским ученым М. О. Доливо-Добровольским (1891 г.); он изобрел и разработал все звенья этой системы — генераторы, трансформаторы, линии передачи и двигатели трехфазного тока.
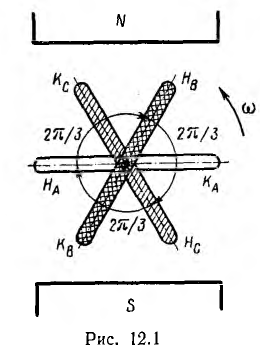
Простейший трехфазный генератор (рис. 12.1) подобен рассмотренному в источнику однофазного напряжения; он состоит из трех одинаковых плоских витков или катушек, называемых фазами генератора, вращающихся в однородном магнитном поле с равномерной угловой скоростью ω вокруг оси, перпендикулярной к направлению магнитных линий. В каждой фазе следует различать начало и конец. Считая, что все катушки намотаны в одном направлении, например по часовой стрелке, можно принять за начало начальный зажим катушки или, наоборот, конечный, но принятое условие должно быть одинаковым для всех фаз. Цепи нагрузки подключаются к генератору с помощью щеток, наложенных на кольца, соединенные с катушками аналогично рис. 6.1 (на рис. 12.1 они не показаны).
Три фазы трехфазного генератора расположены под углом 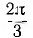
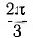
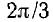
При вращении в фазах будут индуктироваться э. д. с.; период Т этих э. д. с. обороту. Катушки одинаковы, поэтому (амплитуды) э. д. с. фаз будут также одинаковы. Так как фазы сдвинуты друг относительно друга в пространстве на угол 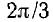
Если за начальный взять момент времени, когда плоскость первой катушки перпендикулярна линиям магнитной индукции (см. рис. 12.1), э. д. с. (отсчитываемая, например, от конца к началу)
и э. д. с. двух других катушек (отсчитываемые в том же направлении), отставая по фазе на углы 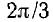
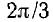
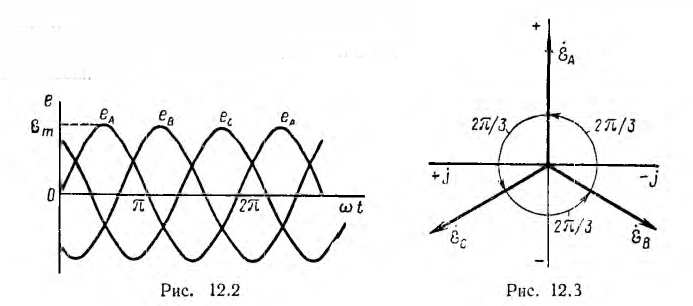
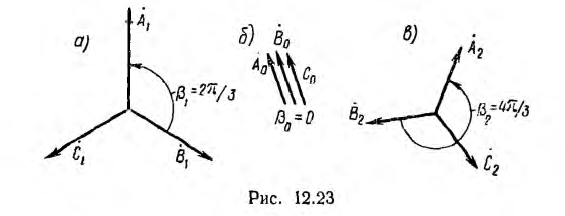
Временная диаграмма э. д. с. изображена на рис. 12.2. Если вектор э. д. с. первой фазы направить по оси вещественных комплексной плоскости (рис. 12.3), комплексы э. д. с. симметричной системы будут иметь вид:
Комплексный множитель
является оператором поворота вектора на угол 2π/3 в положительном направлении. Тогда
Следовательно,
т. е. сумма векторов симметричной системы равна нулю. Это значит, что равна нулю в любой момент времени и алгебраическая сумма мгновенных значений, что можно видеть и из рис. 12.2, если взять сумму ординат трех синусоид для любой абсциссы.
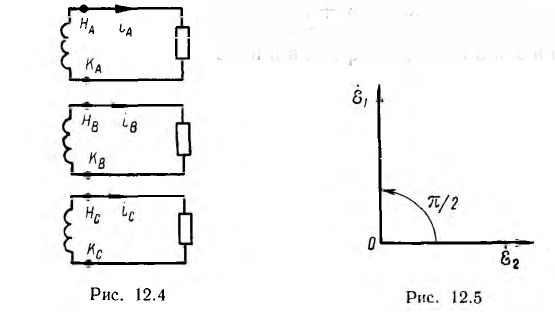
Если в цепь каждой фазы генератора включить одинаковые по величине и характеру сопротивления (рис. 12.4), то токи фаз будут равны по величине и сдвинуты по фазе относительно своих напряжений на один и тот же угол ϕ:
Они также образуют трехфазную симметричную систему векторов.
При неодинаковой нагрузке фаз максимальные значения токов и фазные сдвиги будут различны, и система токов будет несимметричной.
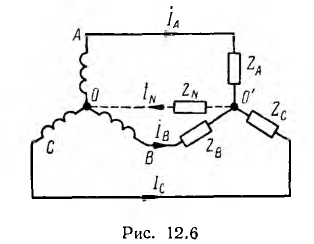
В электроизмерительной технике и автоматике применяется также двухфазная система, векторная диаграмма э д. с. которой показана на рис. 12.5. Хотя э. д. с. 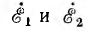
Показанная на рис. 12.4 несвязанная трехфазная система, при которой отдельные фазы не соединены между собой, на практике не применяется — генераторы и приемники связывают или в звезду, или в треугольник.
Соединение звездой
При соединении генератора звездой вместе соединяются концы фаз, образуя нулевую (нейтральную) точку 0. К началам фаз генератора с помощью трехпроводной линии передачи присоединяется приемник. Если последний также соединен звездой, нулевые точки генератора и приемника могут быть соединены нулевым (нейтральным) проводом (рис. 12.6).
Различают величины, относящиеся к фазам генератора и приемника — фазные напряжения и токи, и к линейным проводам — линейные напряжения и токи. Так как линейные провода соединены последовательно с фазами генератора и приемника, линейные токи в звезде равны соответствующим фазным токам.
Для получения симметричных соотношений между величинами следует выбирать положительные направления токов во всех фазах единообразно; обычно направляют токи от генератора к приемнику (см. рис. 12.6), т. е. в сторону движения энергии. В соответствии с аналогом закона Ома 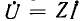
Если выбрать направление тока в нулевом проводе от нулевой очки приемника к нулевой точке генератора (см. рис. 12.6), мгновенное значение iN и комплекс IN этого тока в общем случае будут:
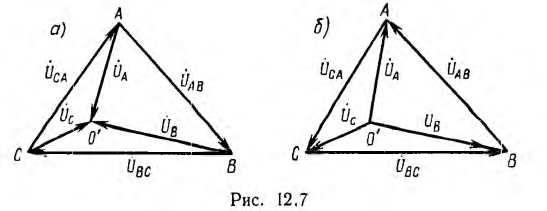
На рис. 12.7, а изображена диаграмма фазных напряжений на фиемнике в соответствии с принятым на рис. 12.6 направлением гоков, сходящихся в нулевой точке О’ приемника.
Эта диаграмма называется топографической, так как ее точкам А, В, С, О’ соответствуют одноименные точки цепи. Векторы и комплексные линейные напряжения 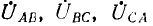
а их мгновенные значения
Из этих соотношений вытекает, что сумма линейных напряжений равна нулю.
Топографическая векторная диаграмма рис. 12.7, а, в которой векторы фазных напряжений сходятся в одной точке, соответствующей нулевой точке приемника, обычно заменяется диаграммой рис. 12.7, б, где эти векторы выходят из этой же точки; так как при этом все векторы фазных и линейных напряжений изменяют свои направления на обратные, приведенные выше соотношения между напряжениями сохраняются.
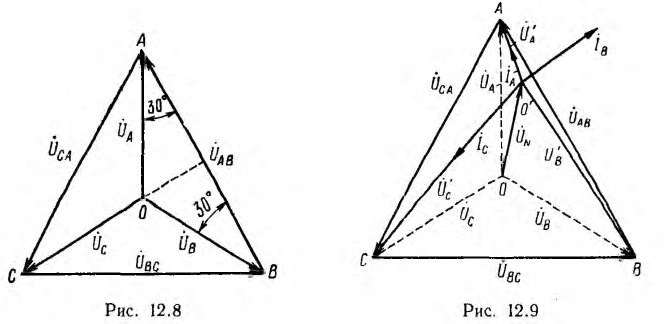
При симметричной системе фазных напряжений векторы линейных напряжений образуют равносторонний треугольник; нулевая точка совпадает с его центром тяжести (рис. 12.8) и линейное напряжение
г. е. по абсолютной величине линейные напряжения в 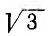
Далее сначала рассматриваются цепи без взаимной индукции между фазами и между фазами и нулевым проводом.
В звезде с нулевым проводом (см. рис. 12.6), если пренебречь его сопротивлением (ZN = 0), а также сопротивлением, линейных проводов, фазные напряжения приемника будут, очевидно равны фазным напряжениям генератора; их векторные диаграммы совпадут (см. рис. 12.7, б). Следовательно, фазные комплексные токи будут определяться фазными комплексными напряжениями генератора и комплексными сопротивлениями или проводимостями тех же фаз приемника:
т. е. соединение звездой с нулевым проводом без сопротивления обеспечивает независимую работу фаз.
При симметричной системе фазных напряжений и одинаковой нагрузке фаз система фазных токов будет симметричной и ток IN нулевого провода, равный сумме токов, будет также равен нулю независимо от величины сопротивления этого провода.
В звезде с нулевым проводом, имеющим сопротивление ZN в общем случае, когда 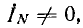
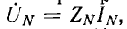
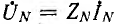
где 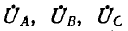
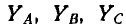
В звезде без нулевого провода YN =0 и
Фазные напряжения на приемнике и токи (см. рис. 12.9):
Выражения для узлового напряжения показывают, что 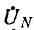
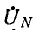
В случае звезды без нулевого провода фазные напряжения на приемнике могут быть выражены через линейные напряжения:
Выражения для 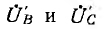
Приведенный вывод выражений для фазных напряжений на приемнике через фазные или линейные напряжения генератора справедлив для общего случая несимметричных систем фазных и линейных напряжений.
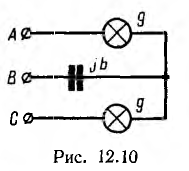
Примером неодинаковой нагрузки фаз может служить прибор для определения порядка следования фаз (рис. 12.10). Он представляет собой три одинаковые по величине проводимости, соединенные в звезду, — две лампы накаливания и конденсатор; тогда, считая, что проводимости ламп линейны,
где а — абсолютное значение проводимостей. При симметричной системе фазных напряжений генератора, если вектор UА направлен по оси вещественных величин (UA = U), узловое напряжение
Тогда комплексные напряжения на лампах будут:
На рис. 12.9 показана векторная диаграмма для рассматриваемой цепи. Векторы токов 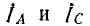
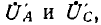
Действующие значения напряжений на лампах и их отношение будут:
Поэтому лампа, включенная в фазу С, будет светиться ярче лампы, включенной в фазу А, т. е. фазы следуют друг за другом в следующем порядке: яркая лампа, тусклая лампа, конденсатор.
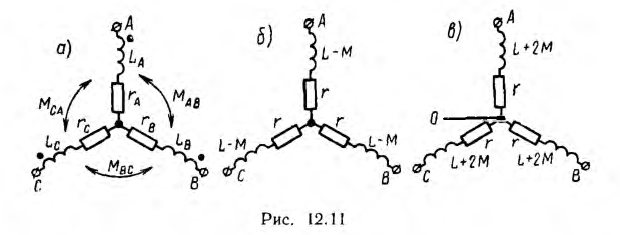
При индуктивных связях между фазами приемника и между его фазами и нулевым проводом должны быть учтены э. д. с. взаимной индукции. Так, например, для соединения звездой с нулевым проводом или без него по схеме рис. 12.11, а при взаимной индукции только между фазами уравнение по второму закону Кирхгофа для фазы А приемника будет иметь вид:
уравнения для второй и третьей фаз можно получить путем круговой перестановки индексов А, В, С.
Если нагрузка фаз одинакова, т. е.
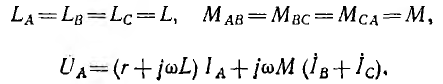
Если, кроме того, нулевой провод отсутствует или при его наличии система фазных напряжений симметрична, то сумма токов 1А + 1в + 1С=0, и уравнение (12.1) получит вид:
г. е. в этом случае цепь рис. 12.11, а эквивалентна схеме рис. 12.11, б без индуктивных связей, но с индуктивностью фаз приемника, равной L — М.
Для дальнейшего представляет интерес случай, когда есть нулевой провод, а все фазные напряжения генератора равны между собой и совпадают по фазе: 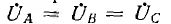
и уравнение (12.1) получит вид:
Это значит, что в данном случае цепь рис. 12.11, а эквивалентна схеме рис. 12.11, в без индуктивной связи, но с индуктивностью фаз приемника, равной L + 2М. Ток нулевого провода будет, очевидно, равен 3I.
Соединение треугольником
Чтобы соединить генератор в треугольник, нужно связать конец каждой фазы с началом следующей; в результате фазы генератора образуют замкнутый контур. При таком соединении симметричного генератора с отключенной нагрузкой (рис. 12.12) ток внутри него не возникает, так как сумма его э. д. c., образующих симметричную систему, равна нулю.
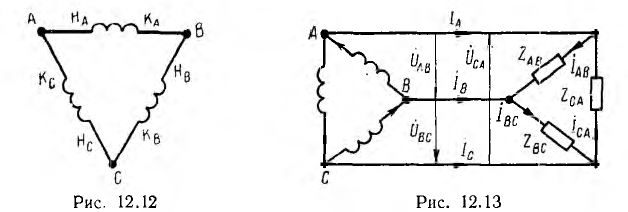
Соединив приемник также в треугольник (рис. 12.13), можно видеть, что фазные напряжения генератора и приемника одновременно являются и линейными, линейные же токи 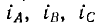
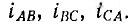
Для генератора соотношения между линейными и фазными токами аналогичны. Таким образом, линейные токи равны разностям соответствующих фазных токов.
Из полученных соотношений видно, что сумма линейных токов равна нулю:
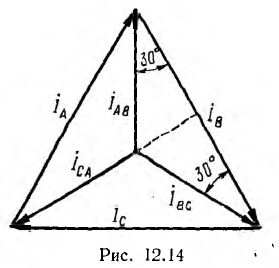
Для симметричной системы фазных токов (рис. 12.14)
т. е. по абсолютной величине линейные токи в 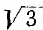
Токи в фазах приемника будут определяться линейными напряжениями и сопротивлениями или прово-димостями фаз приемника:
По приведенным соотношениям фазных токов могут быть определены линейные токи.
Если пренебречь сопротивлением проводов, напряжения генератора будут равны напряжениям приемника и фазы будут работать независимо друг от друга: всякое изменение сопротивления какой-либо фазы приемника вызовет изменение тока этой фазы и токов двух примыкающих к этой фазе линейных проводов, но никак не отразится на токах других фаз.
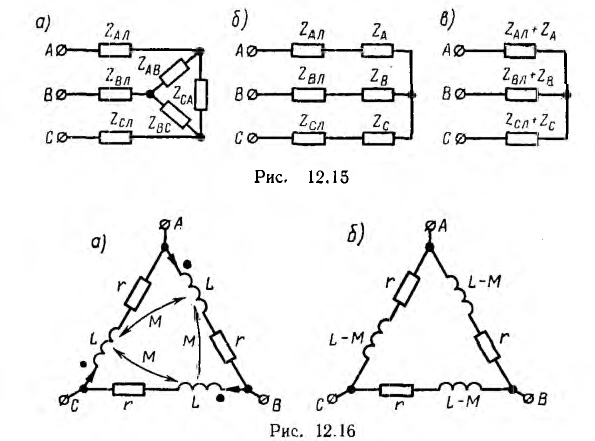
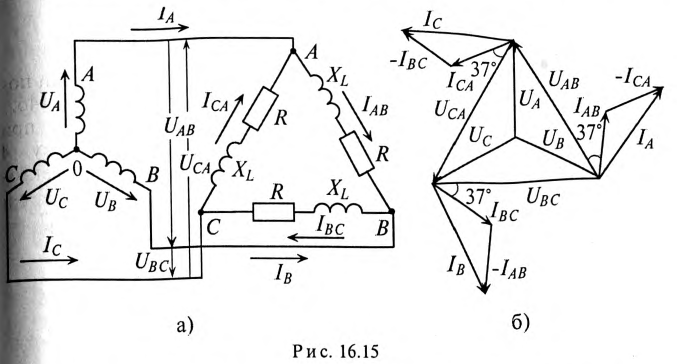
Если сопротивление линейных проводов не равно нулю (рис. 12.15, а), то из-за падения напряжения в них треугольник не обеспечивает независимой работы фаз. Изменение, например, сопротивления фазы АВ вызовет изменение фазного тока IAB, а следовательно, и линейных токов IА и IB. При этом изменятся падения напряжения в линейных проводах А и В, что при неизменных линейных напряжениях на зажимах генератора вызовет изменение напряжений на всех трех фазах приемника; следовательно, должны измениться также токи 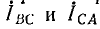
Для расчета цепи рис. 12.15, а при заданных линейных напряжениях, помимо методов уравнений Кирхгофа, наложения, контурных токов и узловых напряжений, при отсутствии взаимной индукции можно применить метод преобразования. Треугольник ZAB, ZBC. ZCA преобразуют в эквивалентную звезду ZA, ZB, Zc по формулам, соответствующим (рис. 12.15, б):
Объединяя в каждой фазе сопротивление линии и приемника, приводят схему к звезде (рис. 12.15, в), после определения токов которой возвращаются к цепи рис. 12.15, б, находя фазные и линейные напряжения на звезде ZA, ZB, Zc, а затем — к исходному треугольнику (см. рис. 12.15, а), чтобы найти его фазные токи.
Приведенные выше выражения для расчета соединения треугольником справедливы для общего случая несимметричной системы напряжений генератора.
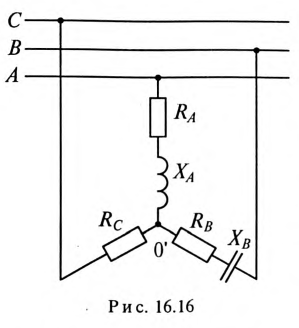
При наличии взаимной индукции, одинаковой нагрузке фаз и симметричной системе напряжений (рис. 12.16, а) система фазных токов будет также симметричной, тогда
и уравнение по второму закону Кирхгофа примет вид:
т. е. в этом случае цепь рис. 12.16, а эквивалентна схеме рис. 12.16, б без индуктивной связи, но с индуктивностью фаз приемника, равной L — М.
Мощность трехфазных систем и ее измерение
Мгновенная мощность трехфазной системы, как и всякой сложной цепи, равна сумме мощностей отдельных приемников, т. е. сумме мощностей фаз. Мгновенная мощность симметричной и одинакова нагруженной трехфазной системы
Сумма трех косинусоид, сдвинутых по фазе на угол 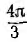
т. е. мгновенная мощность симметричной одинаково нагруженной трехфазной системы постоянна, тогда как мощность однофазной системы изменяется во времени с двойной частотой по сравнению с частотой напряжения и тока.
Многофазная система, мгновенная мощность которой постоянна, называется уравновешенной. Интересно отметить, что несимметричная двухфазная система с равными напряжениями (см. рис. 12.5) в случае одинаковой нагрузки фаз также является уравновешенной:
Из-за уравновешенности трехфазные и двухфазные двигатели имеют постоянный вращающий момент, тогда как момент однофазных двигателей пульсирует с двойной частотой.
Выражение для мощности уравновешенной трехфазной системы может быть преобразовано. В симметричной звезде
В симметричном треугольнике
В обоих случаях выражения для мощности получились одинаковыми.
Для измерения мощности трехфазной симметричной и одинаково нагруженной системы достаточен один ваттметр, включенный в одну из фаз и измеряющий ее мощность. Аналогично включается однофазный счетчик электрической энергии, Для получения мощности и, соответственно, энергии трехфазной системы показания этих приборов следует утроить.
В общем случае несимметричной системы и неодинаковой нагрузки мгновенная мощность р есть величина переменная, т. е. такая система является неуравновешенной. Средняя мощность этой системы равна сумме средних мощностей отдельных фаз:
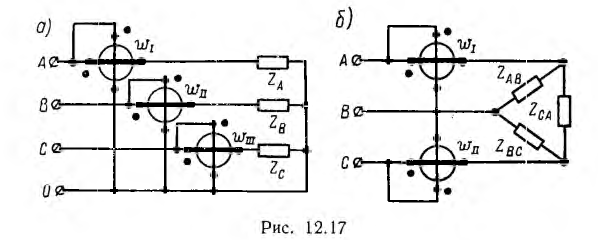
Следовательно, средняя мощность в данном случае может быть измерена тремя ваттметрами, включенными в каждую фазу, как это показано на рис. 12.17, а, для звезды с нулевым проводом (точками обозначены условные «начала» параллельных и последовательных цепей ваттметров).
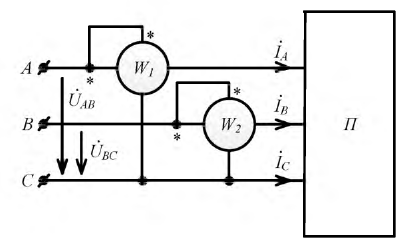
В случае трех проводной системы можно ограничиться двумя ваттметрами, включенными так, как показано на рис. 12.17, б для измерения средней мощности трехфазной системы, соединенной треугольником. Мгновенные мощности, усредняемые первым и вторым ваттметрами, соответственно равны:
Так как 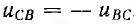
При переходе к средним мощностям получается, что сумма показаний ваттметров
т. е. равна мощности системы. Вывод справедлив и для звезды без нулевого провода, так как она может быть заменена эквивалентным треугольником.
Реактивная и полная мощности симметричной и одинаково нагруженной трехфазной системы равны суммам соответствующих мощностей всех фаз:
В общем случае несимметричной и неодинаково нагруженной трехфазной системы суммирование реактивных и полных мощностей фаз не дает величин, характерных для нагрузки генератора в целом, как это было в однофазной цепи с одним источником энергии. Предлагаемые в литературе определения реактивной и полной мощностей трехфазной несимметричной и неодинаково нагруженной системы чисто условны и потому здесь не рассматриваются.
Сравнение трехфазных и однофазной cиcтем
Сопротивление линейных и нулевого проводов, соединяющих генератор и приемник, обычно мало по сравнению с сопротивлением фаз приемника, и выводы, сделанные по поводу независимости работы фаз при соединении звездой и треугольником, можно обобщить следующим образом:
- в звезде с нулевым проводом и в треугольнике токи фаз практически мало зависят друг от друга и поэтому эти схемы следует применять при неодинаковой нагрузке фаз;
- звезда без нулевого провода может применяться только при одинаковой нагрузке фаз.
Необходимо отметить, что схема соединений генератора и приемника может быть различной, и один из них может быть соединен треугольником, другой — звездой без нулевого провода.
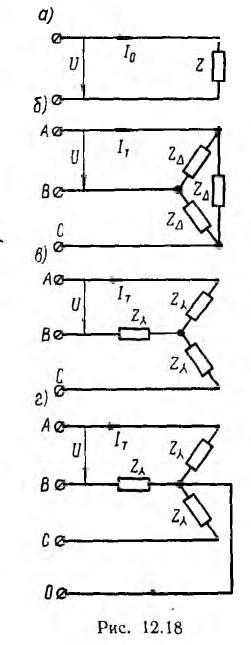
Представляет интерес сравнение расхода металла с удельным сопротивлением р на провода однофазной и трехфазной линий передачи (рис. 12.18) той же мощности Р на то же расстояние l при одинаковом cosϕ и том же к. п. д., т. е. тех же потерях в линии Рл = kP, где k — относительная потеря мощности, и одинаковом линейном напряжении U.
Для однофазной двухпроводной линии (рис. 12.18, а) Р = UI0 cosϕ; отсюда ток I0, потери Рл и сопротивление r0 одного провода:
Следовательно, сечение s0 и объем V0 проводов соответственно равны:
Отсюда видно, что формула для сечения двухпроводной линии переменного тока отличается от аналогичной формулы для линии постоянного тока наличием множителя 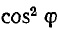
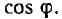
Для трехфазной трехпроводной линии (рис. 12.18, б и в) 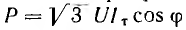
а сечение sT и объем VT проводов:
В знаменателе этих выражений также присутствует множитель 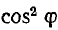
Из формул для s0 и sT видна эффективность высокого напряжения и большого коэффициента мощности — сечения обратно пропорциональны квадратам этих величин. Вместе с тем очевидно, что стоимость изоляции проводов растет с ростом напряжения. В результате экономически оптимальное напряжение U оказывается тем выше, чем больше передаваемая мощность Р и длина l линии.
Соотношение объемов металла линий: однофазной двухпроводной V0 и трехфазных —- трехпроводной Vr и четырехпроводной с нулевым проводом половинного сечения 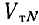
Таким образом, при одинаковом линейном напряжении звезда без нулевого провода и треугольник, очевидно, дают одинаковый расход металла на линию передачи и экономию в 25% по сравнению с однофазной линией, а нулевой провод половинного сечения вызывает перерасход металла, но все же система остается легче однофазной на 12,5%.
Соединение звездой с нулевым проводом имеет важное преимущество: помимо трехфазных приемников, рассчитанных на линейное напряжение, оно позволяет включать однофазные приемники и на линейное, и на фазное напряжение.
Если приемники работают при одинаковом фазном напряжении, линейное напряжение звезды будет в 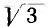
Основным преимуществом трехфазной системы по сравнению с однофазной является возможность легко создавать вращающееся магнитное поле, используемое, в частности, в трехфазных асинхронных двигателях, наиболее простых по конструкции и в эксплуатации.
Пульсирующее и вращающееся магнитные поля
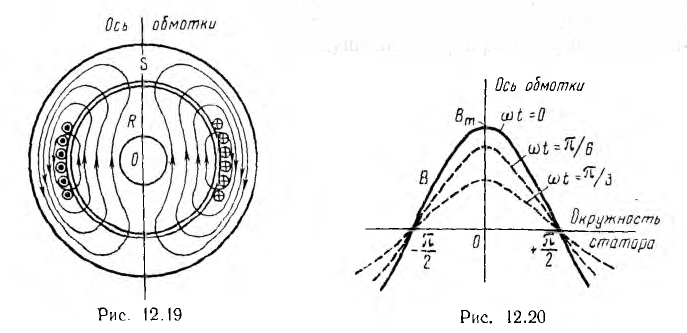
Электрические индуктивные машины переменного тока в большинстве случаев имеют магнитопровод в виде двух коаксиальных цилиндров, набранных из стальных листов и разделенных воздушным зазором (рис. 12 19). Внешний цилиндр S является статором, внутренний R — ротором.
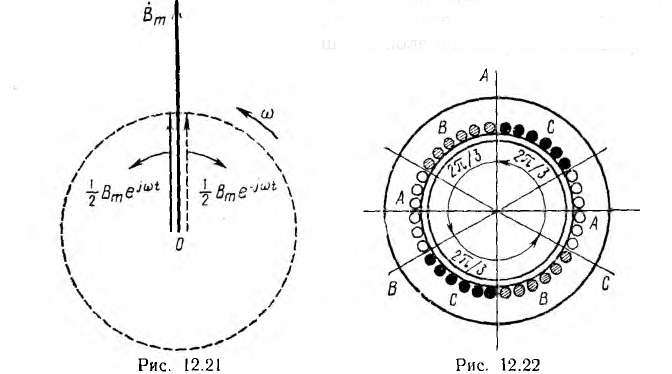
Если по обмотке статора, уложенной в его пазы н распределенной на части, например одной трети его окружности (рис. 12.19), будет проходить постоянный ток, магнитный поток, замыкающийся через статор, воздушный зазор и ротор будет постоянным. Приближенно магнитную индукцию можно считать распределенной по окружности статора по синусоидальному закону (сплошная линия на рис. 12.20); она имеет максимальные значения Вm по оси обмотки и равна нулю на нейтральной линии, перпендикулярной к оси обмотки. Такое синусоидально распределенное в зазоре машины поле можно условно изобразить постоянным вектором Вm (рис. 12.21), аналогично тому, как ранее это было сделано для величин, изменяющихся по синусоиде во времени.
Если по обмотке статора пропускать переменный ток, синусоидальное распределение магнитного поля сохранится, но поле будет пульсирующим, т. е. изменяющимся во времени по синусоидальному закону (см. рис. 12.20). Принимая за начало счета времени момент, когда индукция по оси обмотки максимальна, пульсирующее поле можно условно изобразить вектором 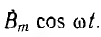
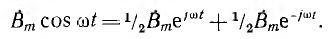
Это значит, что пульсирующее синусоидально распределенное поле может быть представлено в виде суммы двух также синусоидально распределенных полей 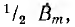
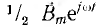
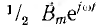
Разложение пульсирующего поля на два вращающихся используется, например, в однофазных двигателях, где прямое поле, воздействуя на ротор, приводит его во вращение, а обратное поле экранируется.
В трехфазных машинах на статор наложены три обмотки, показанные в разрезе на рис. 12.22, занимающие каждая треть его окружности; следовательно, эти обмотки и их оси сдвинуты в пространстве на угол 2π/3. Обмотки обтекаются токами, векторы которых образуют симметричную трехфазную систему. Тогда выражение для поля первой фазы А совпадает с выражением (12.2) при том же начале счета времени
Пусть обмотка, обтекаемая током второй фазы В, т. е. током, отстающим от тока первой фазы на угол 2π/3, сдвинута в пространстве вперед по направлению вращения прямого поля на тот же угол, что учитывается множителем 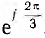
Аналогично записывается поле третьей фазы С, но так как она обтекается током, опережающим по фазе ток фазы А на угол 2π/3, и сдвинута в пространстве на тот же угол назад, знаки всех углов 2π/3 изменяются на обратные.
Результирующее поле определяется наложением полей всех трех фаз:
Отсюда видно, что все прямые поля трех обмоток арифметически складываются, тогда как обратные поля в сумме дают нуль и в машине возникает вращающееся поле, постоянное во времени. Амплитуда вращающегося поля в полтора раза превышает амплитуду пульсирующего поля отдельных обмоток, а фаза совпадает с фазой прямого поля обмотки первой фазы А.
В трехфазных двигателях вращающееся поле также используется для приведения во вращение ротора; из-за постоянства мощности в трехфазных системах и, следовательно, вращающего момента, а также отсутствия обратного поля эти двигатели имеют значительное преимущество перед однофазными.
Основы метода симметричных составляющих
Метод симметричных составляющих, предложенный Фортескью, позволяет сравнительно просто рассчитывать несимметричные, в частности, аварийные режимы в трехфазных системах и машинах. До предложения этого метода для таких расчетов надо было решать дифференциальные уравнения с переменными коэффициентами или оперировать с сопротивлениями, зависящими от токов.
В общем случае симметричной трехфазной системой векторов называется система, состоящая из трех равных по величине векторов, причем каждый вслед идущий вектор сдвинут относительно предыдущего на угол 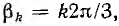
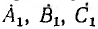
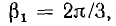
Симметричные системы линейных и фазных напряжений и токов, рассмотренные выше, были именно прямыми системами. Система 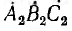
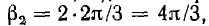
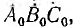
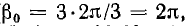
Система векторов, сдвинутых по фазе на угол 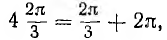
Пользуясь оператором 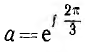
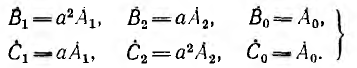
Пусть задана несимметричная система трех векторов А, В, С. Далее доказывается, что каждый вектор этой системы может быть представлен в виде суммы трех векторов, являющихся составляющими прямой, обратной и нулевой систем:
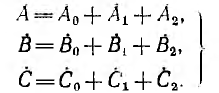
Подстановка уравнений (12.3) в уравнения (12.4) дает:
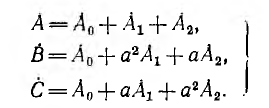
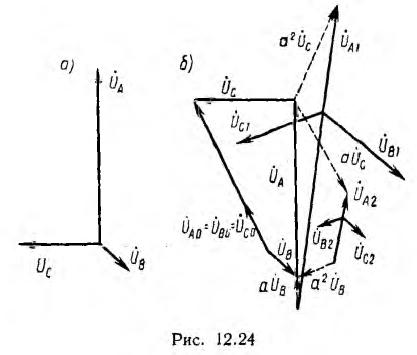
Система уравнений (12.5) решается относительно А0, А1, A2 однозначно:
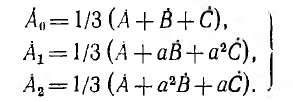
Отсюда и следует, что несимметричную систему векторов можно разложить на три симметричные системы.
Из первого уравнения системы (12.6) видно, что если сумма векторов несимметричной системы равна нулю, будут равны нулю и векторы нулевой системы. Следовательно, несимметричные системы линейных напряжений и линейных токов при отсутствии нулевого провода содержат только прямую и обратную составляющие.
Определение симметричных составляющих несимметричной системы векторов по выражениям (12.6) может быть выполнено также графически. Пусть задана несимметричная система векторов фазных напряжений 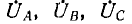
Далее очевидным построением определяются все векторы трех симметричных систем.
Аналогично производится разложение несимметричной системы токов.
Симметричные составляющие несимметричной трехфазной системы напряжений и токов могут быть определены экспериментально. Например, для измерения нулевой составляющей системы фазных напряжений надо однообразно включить на фазные напряжения трансформаторы малой мощности, вторичные обмотки которых и вольтметр соединяются последовательно (рис. 12.25). Тогда, считая для простоты, что у трансформаторов коэффициент трансформации напряжения равен единице, суммарное напряжение, измеряемое вольтметром,
т. е. пропорционально напряжению нулевой системы.
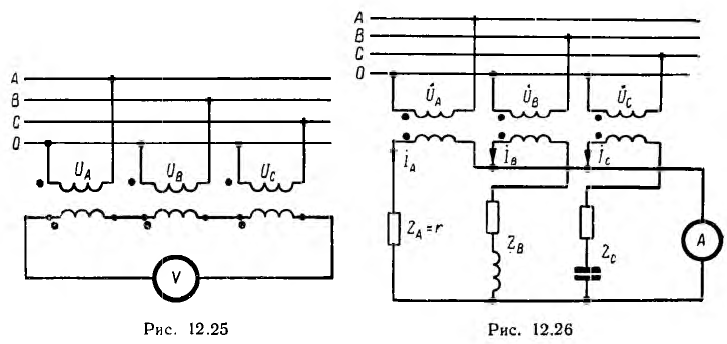
Для измерения напряжения прямой последовательности (рис. 12.26) трансформаторы включаются на одинаковые по величине полные сопротивления z — трансформатор фазы А на активное сопротивление ZA=r, фазы В на активно-индуктивное сопротивление 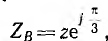
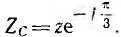
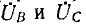
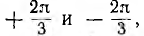
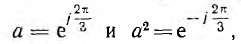
Цепи нагрузок всех трех трансформаторов соединяются параллельно и замыкаются на амперметр. Последний измеряет суммарный ток
пропорциональный напряжению U1 системы прямой последовательности.
Если поменять местами нагрузки фаз В и С, суммарный ток
будет пропорционален напряжению U2 системы обратной последовательности.
Рассмотренные схемы называются фильтрами симметричных составляющих. Они применяются в схемах защиты трехфазных энергетических систем от аварийных режимов, вызывающих несимметрию токов и напряжений отдельных фаз.
Разложение на симметричные составляющие позволяет весьма просто решать задачи на расчет трехфазных цепей при одинаковой нагрузке фаз с взаимной индукцией между ними при несимметричной системе напряжений, что широко используется в теории электрических машин. Система напряжений разлагается на симметричные составляющие, для каждой из них находят токи фаз и применяют метод наложения. При этом сопротивление фаз приемника для каждой составляющей может быть различным. Например, для цепи рис. 12.11, соединенной в звезду с нулевым проводом, сопротивление фаз для нулевой системы напряжений:
а для прямой и обратной составляющих, являющихся симметричными трехфазными системами, сопротивления
только для статических устройств, например для трансформаторов. Во вращающихся машинах прямая система токов создает магнитное поле, вращающееся в одном направлении с ротором, а обратная система токов — в противоположном; это приведет к неравенству 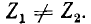
После определения комплексных токов каждой составляющей они пофазно суммируются и дают систему действительных токов фаз.
При неодинаковой нагрузке фаз приемника расчет усложняется, так как тогда каждая из симметричных составляющих системы такое зависит от всех составляющих систем напряжений. Эти задачи рассматриваются в литературе, посвященной расчету аварийных режимов в трехфазных электрических сетях и системах.
Можно показать, что в самом общем случае несимметрии средняя мощность всей цепи равна сумме средних мощностей нулевой, прямой и обратной составляющих:
Трехфазные цепи
Трехфазная система ЭДС:
Производство, передача и распределение электрической энергии осуществляется в основном трехфазным током в трехфазных цепях. Широкое распространение в качестве нагрузки в трехфазных цепях получили трехфазные потребители. В трехфазных цепях используются трехфазные трансформаторы. Электрическую энергию в трехфазных цепях производят трехфазные генераторы, создающие синусоидальные ЭДС одинаковой частоты, в трехфазных системах.
Трехфазной называется система трех ЭДС одинаковой частоты, Вдвинутых друг относительно друга по фазе так, что сумма углов сдвига равна 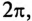
Трехфазная система ЭДС называется симметричной, если ЭДС трех фаз сдвинуты друг относительно друга на угол 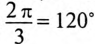
Комплексы этих ЭДС
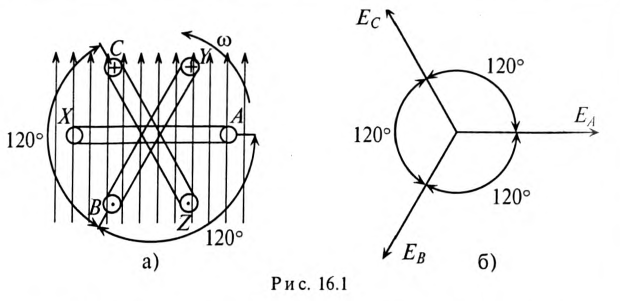
Получение симметричной трехфазной системы ЭДС осуществляется в трехфазном электромашинном генераторе (рис. 16.1а), в Котором три жестко скрепленные под углом 120° обмотки пересекают магнитное поле с частотой 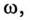
Начала обмоток трехфазного генератора обозначаются прописными буквами 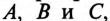
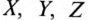
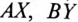
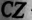
Таким образом, при вращении в магнитном поле жестко скрепленных обмоток в них индуктируются одинаковые ЭДС 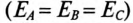
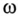
Векторная диаграмма такой симметричной системы ЭДС изображена на рис. 16.1б. Как видно из векторной диаграммы, мгновенное значение ЭДС в обмотке CZ можно записать в виде
а комплекс этой ЭДС
т. е. логично, чтобы начальная фаза 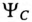
К каждой обмотке трехфазного генератора может быть подключена нагрузка с сопротивлениями
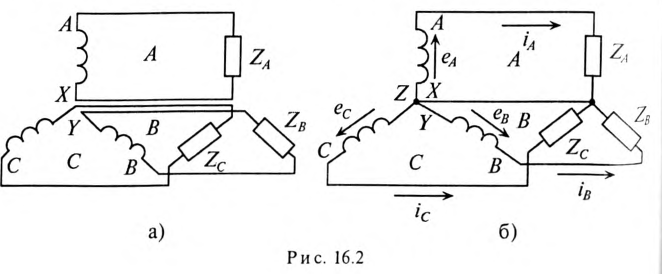
Если при этом три обмотки генератора электрически не соединены (рис. 16.2а), то такая трехфазная система называется несвязанной. Несвязанная трехфазная система практического применения не нашла.
Практическое применение нашла связанная трехфазная система (рис. 16.2б). Эта система экономически и энергетически более рациональна, так как используется три или четыре соединительных провода вместо шести и получить можно два различных напряжения, фазное и линейное, вместо одного.
Каждая обмотка трехфазного генератора со своей нагрузкой и соединительными проводами называется фазой (рис. 16.2). В трехфазной системе различают три фазы А, В и С (международные обозначения — прописные буквы).
Положительное направление ЭДС и токов в каждой фазе на рис. 16.26 указаны стрелками.
В связанных трехфазных системах применяется соединение обмоток генератора и потребителя звездой F или треугольником Е.
Соединение обмоток генератора звездой
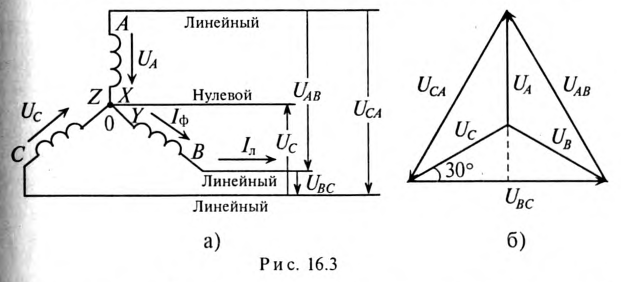
При соединении обмоток генератора звездой концы обмоток X, Yи Z элeктpичecки соединяются в одну точку 0 (рис. 16.3а), которая называется нулевой, или нейтральной. При этом генератор с потребителем соединяется тремя или четырьмя проводами.
Провода, подключенные к началам обмоток генератора (А, В и С, называют линейными проводами, а провод, подключенный к нулевой точке 0, называется нулевым, или нейтральным.
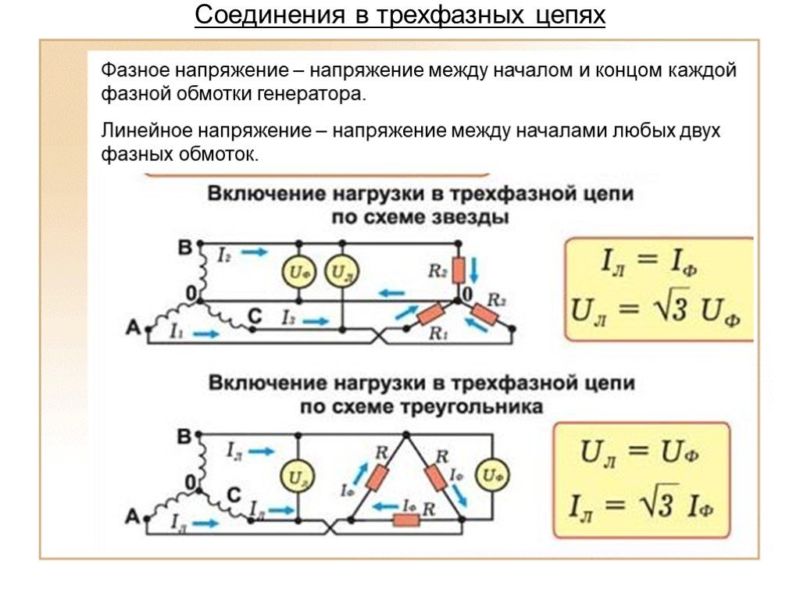
В связанных трехфазных системах различают фазные и линейные напряжения и токи.
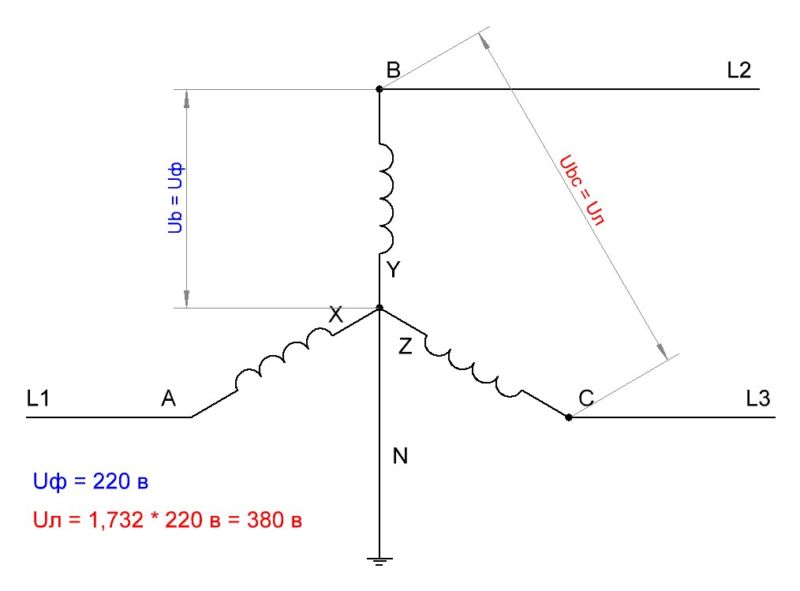
Фазным называется напряжение между началом и концом обмотки генератора или между нулевым и линейным проводом. Обозначаются фазные напряжения прописными буквами с индексами фаз 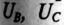
Линейным называется напряжение между началами обмоток генератора или между линейными проводами. Обозначаются линейные напряжения 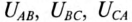
Можно определить зависимость между линейными и фазными напряжениями при соединении обмоток генератора звездой.
Мгновенные значения фазных напряжений равны разностям потенциалов между началами и концами соответствующих обмоток, т.е:
Мгновенные значения, линейных напряжений равны разностям потенциалов между началами соответствуют:
Потенциалы концов обмоток одинаковы 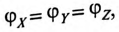
Тогда
То есть мгновенное значение линейных напряжений определяется разностью мгновенных значений двух соответствующих фазных напряжений.
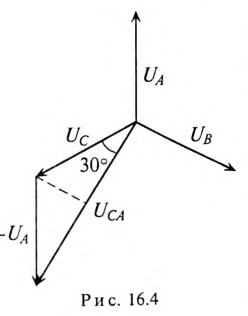
При соединении обмоток генератора звездой действующее значение линейного напряжения определяется геометрической разностью двух соответствующих фазных напряжений. На этом основании построена векторная диаграмма напряжений (рис. 16.3б) для соединения обмоток генератора звездой. К такому же результат) приводит определение комплексов линейных напряжений символическим методом:
При симметричной системе ЭДС фазные напряжения равны по величине 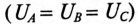
Линейное напряжение 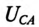
Из диаграммы (рис. 16.4) определяется вектор (комплекс)
При симметричной системе ЭДС линейное напряжение трехфазного генератора, обмотки которого соединены звездой, в 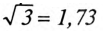
Если говорят о напряжении генератора 127/220 В, то имеется в виду, что фазное напряжение в трехфазной цепи 127 В, а линейное — 220 В. В сети с напряжением 220/380 В фазное напряжение 220 В, а линейное — 380 В. Очевидно, что обмотки генератора такой симметричной цепи соединены звездой и отношение напряжений получится равным
В связанных трехфазных системах фазным называется ток, провидящий по обмотке (фазе) генератора 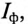
Как видно на рис. 16.3а, при соединении обмоток генератора звездой линейный ток 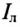
Соединение обмоток генератора треугольником
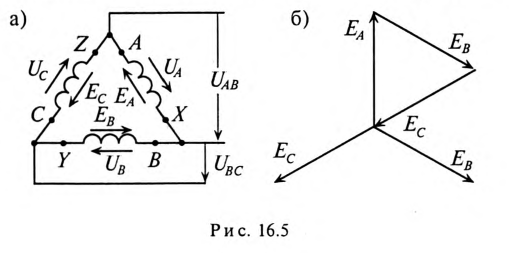
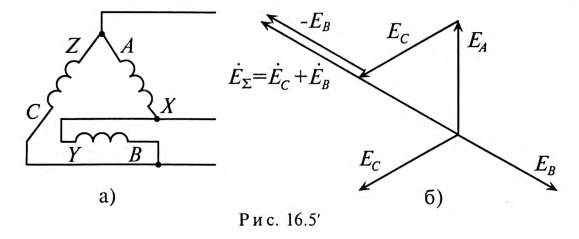
При соединении обмоток генератора треугольником (рис. 16.5а) конец обмотки фазы А соединяется с началом обмотки фазы В, конец обмотки фазы В соединяется к началом обмотки фазы С, конец обмотки фазы С соединяется с началом обмотки фазы А и к точкам соединения подключаются линейные провода.
При соединении обмоток генератора треугольником (рис. 16.5а) трехфазная цепь трехпроводная.
Как следует из схемы соединения обмоток треугольником (рис. 16.5а), линейное напряжение 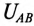
То есть
Из схемы (рис. 16.5а) следует, что три обмотки генератора, соединенные треугольником, образуют замкнутый контур, ток в котором при отсутствии нагрузки (холостой ход) определяется выражением
где 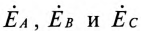
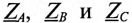
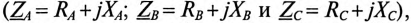
Так как сопротивления обмоток малы, падением напряжения на них можно пренебречь и считать, что напряжение на каждой обмотке генератора равно ее ЭДС.
При симметричной системе ЭДС и правильном соединении обмоток генератора треугольником (рис. 16.5а) геометрическая сумма ЭДС (комплексов) обмоток генератора, образующих замкнутый контур, равна нулю (рис. 16.5б). Следовательно, и ток в замкнутом контуре обмоток, соединенных треугольником, также равен нулю 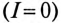
Если обмотки симметричного генератора соединены «неправильным» треугольником, т. е. неправильно подключить начало и конец хотя бы одной из обмоток, например 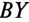
Соединение потребителей звездой
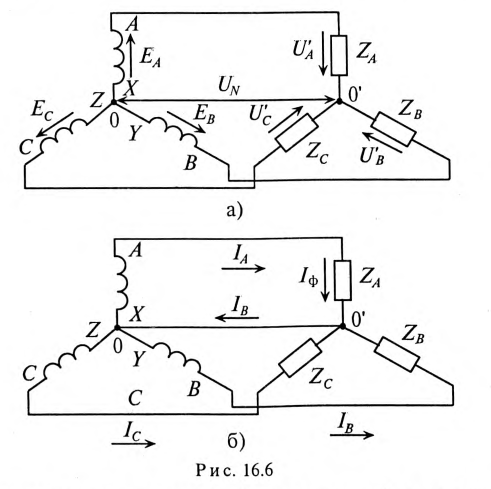
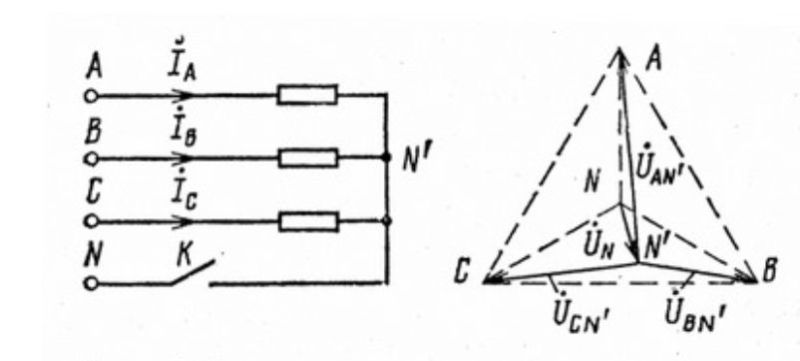
При соединении звездой потребителя и генератора (рис. 16.6) трехфазная система представляет собой сложную цепь с двумя узловыми точками 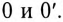
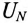
Соединение генератора и потребителя звездой может быть с нулевым проводом (рис. 16.6б), т.е. четырехпроводная цепь, и без нулевого провода (рис. 16.6а), т.е. трехпроводная цепь.
Величину напряжения смещения нейтрали 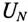
где 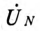
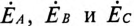
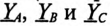
где 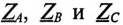
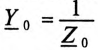
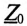
Напряжение U’ на каждой фазе потребителя, соединенного звездой (рис. 16.6а), с учетом напряжения смещения нейтрали, определяют следующим образом:
где 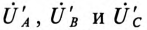
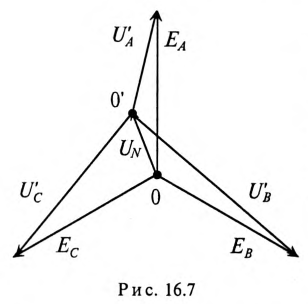
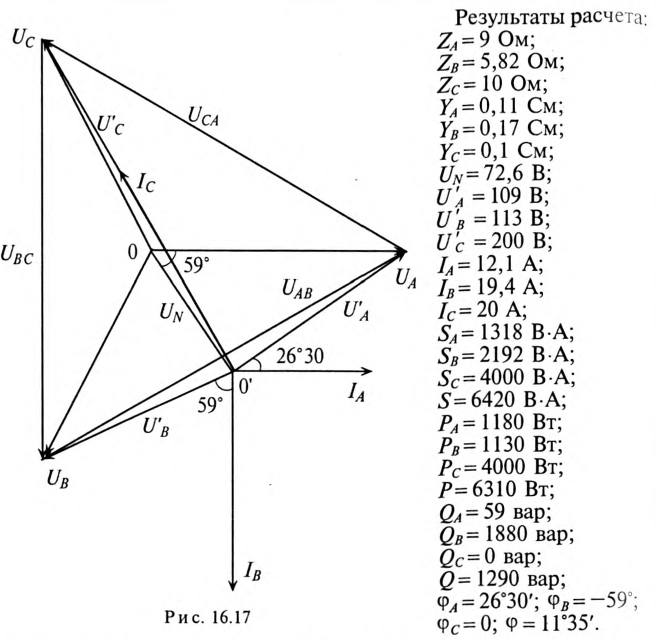
На основании (16.15) строится векторная диаграмма напряжений (рис. 16.7), на которой вектор напряжения смещения нейтрали взят произвольно. Из векторной диаграммы (рис. 16.7) следует, что при наличии напряжения смещения нейтрали напряжения на фазах потребителя, соединенного звездой, различны по величине и по начальной фазе даже при симметричной системе ЭДС в обмотках генератора.
Очевидно (рис. 16.7), что напряжения на фазах потребителя, соединенного звездой, будут одинаковыми по величине 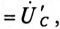
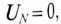
Напряжение смещения нейтрали отсутствует, т. е. 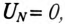
Рассмотрим эти условия:
1. Равномерная нагрузка фаз.
Равномерной называют нагрузку, при которой комплексы сопротивлений фаз равны между собой.
То есть
или
Тогда 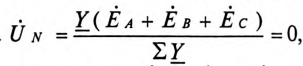
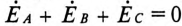
Так как комплекс сопротивления фазы 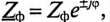
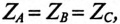
2. Наличие нулевого провода.
При наличии нулевого провода, соединяющего нейтральные точки 0 и 0′ (рис. 16.6б),
Тогда
В обоих случаях (1 и 2) напряжения на фазах потребителя, подключенного к трехфазному генератору с симметричной системой ЭДС, одинаковы по величине. При этом величина напряжения 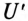
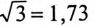
Ток в нулевом проводе 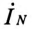
Токи в фазах потребителя определяются по формулам
Очевидно, что при равномерной нагрузке фаз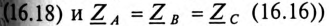
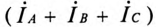
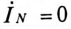
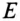
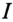
Таким образом, при равномерной нагрузке фаз нулевой провод не нужен.
При неравномерной нагрузке фаз отсутствие нулевого провода приводит к неодинаковым по величине напряжениям на каждой фазе потребителя (рис. 16.7). При этом на фазе с большим сопротивлением Z будет большее напряжение U’.
Так как отсутствие нулевого провода при неравномерной нагрузке фаз потребителя, соединенного звездой, нарушает режим работы потребителей U’, то предохранитель в нулевой провод не ставят.
Следовательно, нулевой провод служит для выравнивания напряжений на фазах потребителя при неравномерной нагрузке фаз.
При соединении потребителей звездой ток каждой фазы потребителя 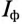
Соединение потребителей треугольником
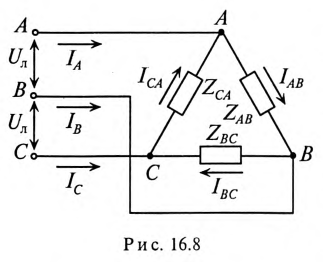
При соединении потребителя треугольником (рис. 16.8) к каждой фазе потребителя приложено линейное напряжение трехфазной цепи
Так как при симметричной системе ЭДС все линейные напряжения равны по величине и сдвинуты на угол 120° по фазе, то и напряжения на каждой фазе потребителя, соединенного треугольником, равны по величине 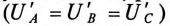
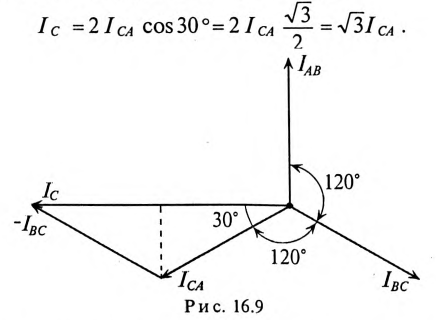
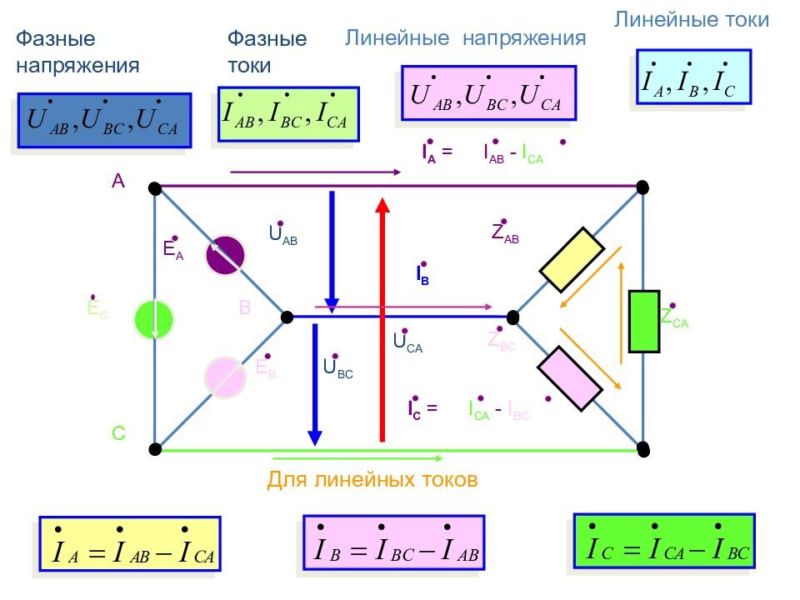
При соединении потребителей треугольником линейные токи обозначаются прописными буквами с индексами фаз, т. е. 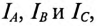
Воспользовавшись первым законом Кирхгофа, линейные токи можно определить выражениями (рис. 16.8)
Линейный ток при соединении потребителей треугольником определяется геометрической разностью двух фазных токов, сходящихся с линейным в одной узловой точке (рис. 16.8).
Фазные токи потребителя, соединенного треугольником, определяются:
При симметричной системе ЭДС генератора 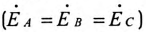
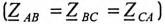
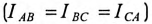
Таким образом, при равномерной нагрузке фаз и симметричной системе ЭДС при соединении потребителей треугольником линейный ток в трехфазной цепи в 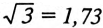
Мощность трехфазного тока
Активная мощность, отдаваемая трехфазным генератором и потребляемая трехфазным потребителем, определяется суммой активных мощностей каждой фазы потребителя:
Аналогичное определение можно отнести и к реактивной мощности трехфазного тока, т. е.
Полная, или кажущаяся, мощность трехфазного потребителя равна

Очевидно, что при равномерной нагрузке фаз 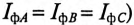
Однако на практике удобней оперировать линейными величинами, так как доступными являются линейные провода, а не обмотки генератора или двигателя.
При соединении потребителя звездой при равномерной нагрузке фаз
Тогда
При соединении потребителей треугольником при равномерной нагрузке фаз
Тогда
Таким образом, при равномерной нагрузке фаз при соединении потребителей звездой и треугольником мощности трехфазного тока определяются выражениями:
При неравномерной нагрузке фаз полная, или кажущаяся, мощность трехфазного тока может быть определена суммой полных мощностей каждой фазы, выраженной в комплексной форме, а именно
Равномерную нагрузку в трехфазных цепях обеспечивают электрические двигатели трехфазного тока, обмотки которых могут гь соединены или звездой, или треугольником.
Топографическая диаграмма
Напряжение между отдельными точками трехфазной цепи можно найти графически путем построения так называемой топографической диаграммы.
Топографическая диаграмма — это векторная диаграмма, поенная так, чтобы каждой точке цепи соответствовала определенная точка на диаграмме и чтобы вектор, проведенный в эту точку из начала координат, выражал по величине и фазе потенциал соответствующей точки цепи. Отрезок, соединяющий любые две точки на этой диаграмме, определяет напряжение между соответствующими точками цепи. Если топографическая диаграмма встроена в определенном масштабе, то по ней можно определить искомое напряжение и ток по величине и по фазе.
При построении топографической диаграммы для трехфазной цепи удобно принять за точку с нулевым потенциалом нулевую, или нейтральную, точку генератора. Этой точке генератора соответствует начало координат топографической диаграммы.
Топографическая диаграмма для трехфазной цепи, изображенной на рис. 16.6, построена при условии, что точка 0 на диаграмме (рис. 16.10) соответствует нулевой точке генератора, потенциал которой равен нулю, т. е.
Из точки 0 откладываются в определенном масштабе напряжений 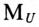
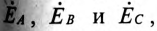
Отрезок 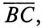
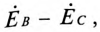
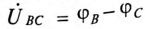
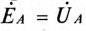
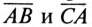
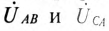
Отложив из точки 0 (начало координат) вектор напряжения смещения нейтрали 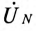
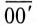
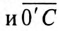
Если напряжение смешения нейтрали 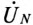
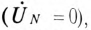
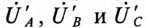
Применение топографической диаграммы для расчета трехфазной цепи рассмотрено в примере 16.1 настоящей главы.
Пример 16.1
К трехфазной трехпроводной сети с линейным напряжением 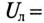
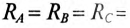
Определить напряжение и ток каждой фазы потребителя в каждом из трех режимов:
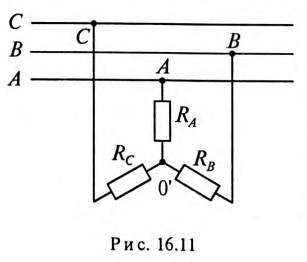
1. Потребители соединены звездой, как показано на рис. 16.11.
2. Обрыв в фазе А, т. е.
3. Короткое замыкание в фазе А, т. е.
Решение
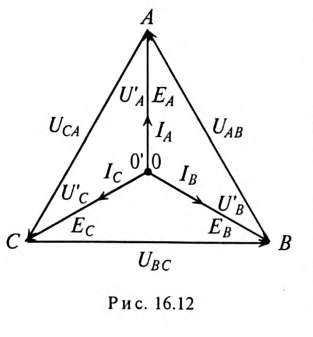
Решение этой задачи производится с помощью построения топографической диаграммы для каждого режима.
1. Так как в данном режиме имеет место равномерная нагрузка фаз 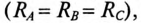
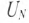
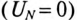
Пренебрегая внутренним сопротивлением обмоток генератора 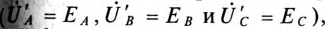
так как
Toк каждой фазы потребителя будет равен
Линейные токи в каждом линейном проводе также равны между собой и равны фазным токам каждой фазы, т.е.
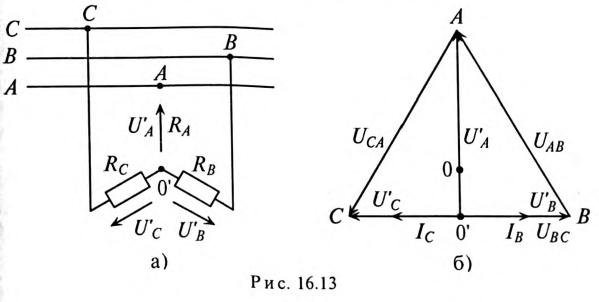
2. При обрыве в фазе А схема трехфазной цепи обретает следующий вид (рис. 16.13а), а топографическая диаграмма показана на рис. 16.13б.
Таким образом, точка 0′ на топографической диаграмме при обрыве в фазе А как бы опустилась на вектор линейного напряжения 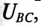
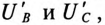
Напряжение на оборванной фазе А, т. е. напряжение между точками 0′ и А в схеме, как следует из топографической диаграммы рис. 16.13б), будет равно
Токи в фазах:
Токи в линейных проводах:
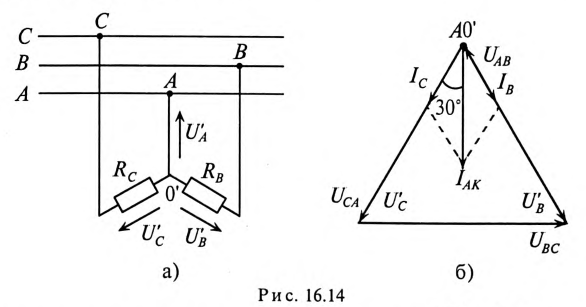
3. При коротком замыкании фазы А схема трехфазной цепи показана на рис. 16.14а, топографическая диаграмма на рис. 16.14б.
Таким образом, точка 0′ на топографической диаграмме при коротком замыкании фазы как бы поднялась в точку А 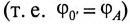
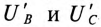
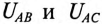
Токи в фазах будут равны 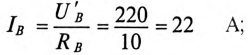
Ток в коротко замкнутой фазе 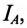
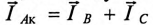
Напряжение 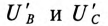
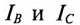
Пример 16.2
К соединенному звездой генератору с фазным напряжением 127 В подключен потребитель, соединенный треугольником. Активное сопротивление каждой фазы потребителя R = 8 Ом, индуктивное 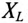
Определить ток в каждой фазе генератора, отдаваемую им мощность и построить векторную диаграмму.
Решение
Эту задачу можно решить, не прибегая к символическому методу и построению топографической диаграммы.
Напряжение на каждой фазе потребителя 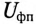
Сопротивление каждой фазы потребителя равно
Ток каждой фазы потребителя (нагрузка равномерная):
В каждой фазе генератора проходит линейный ток потребителя, единенного треугольником, т.е. (см. рис. 16.15а)
Отдаваемая генератором мощность (активная мощность) равна
Так как
Угол 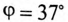
Таким образом, ток фазы потребителя отстает от напряжения на угол 37°, так как нагрузка индуктивного характера.
Вычисленные величины легли в основу построения векторной диаграммы (рис. 16.15б).
Пример 16.3
Параметры трехфазного потребителя, соединенного звездой, имеют следующие значения: 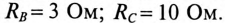
Определить:
1) напряжение на каждой фазе потребителя;
2) токи каждой фазы потребителя;
3) мощности 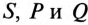
Решение
Допустим, что обмотки генератора соединены звездой, тогда напряжение каждой фазы генератора (при симметричной системе ЭДС)
Напряжение на каждой обмотке генератора в комплексной форме:
Сопротивление 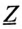
Проводимости 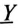
Напряжение смещения нейтрали 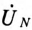
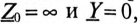
При вычислении 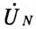
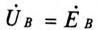
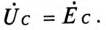
Токи в каждой фазе потребителя:
Мощности каждой фазы потребителя:
Мощность всей трехфазной нагрузки:
Векторная диаграмма рассматриваемой цепи изображена на рис. 16.17.
Пример 16.4
К трехфазной сети с линейным напряжением 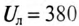
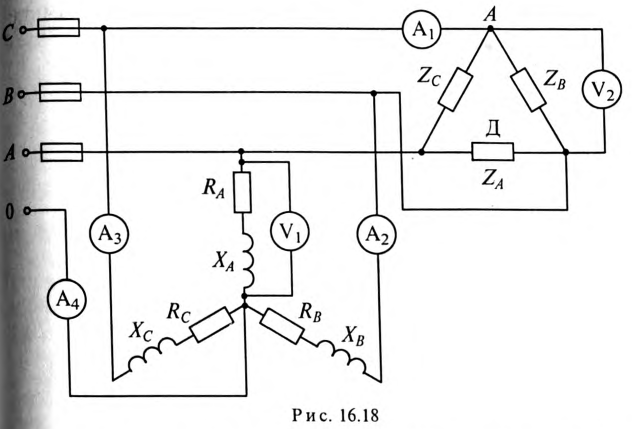
Обмотки трехфазного двигателя мощностью 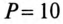
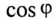
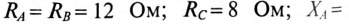
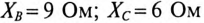
Определить: показания амперметров 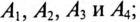
В линейном проводе С сгорел предохранитель (обрыв линейного провода С). Как при этом изменится показание вольтметpa 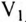
Решение
Расчет трехфазной цепи (рис. 16.18) можно осуществить, не прибегая к символическому методу и построению топографической диаграммы.
Амперметр 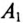
Амперметр 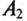
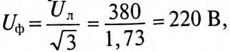
так как
Показания амперметра 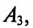
так как
Амперметр 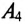
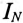
Для вычисления геометрической суммы токов фаз необходимо построить векторную диаграмму токов (рис. 16.19).
При наличии нулевого провода напряжения на фазах сдвинуты на угол 120°. Угол сдвига фаз между током и напряжением, исходя из условий, для всех трех фаз одинаков (это видно из заданных параметров силового потребителя):
Следовательно, фазные токи сдвинуты так же, как и напряжения, на угол 120°. Величины токов определены: 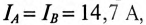
На векторной диаграмме складываются геометрически 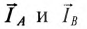
Поскольку этот суммарный ток находится в противофазе с током 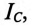
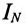
Следовательно, амперметр 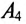
Для расчета мощности Р, потребляемой всей нагрузкой, вычисляется активная мощность каждого силового потребителя:
Тогда активная мощность, потребляемая всей нагрузкой, будет равна
При обрыве линейного провода С и нулевого провода две фазы силового потребителя А и В кажутся соединенными последовательно и подключенными к личному напряжению 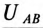
Таким образом, вольтметр 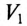
При обрыве линейного провода С фазы В и С двигателя окажутся соединенными последовательно и подключенными к линейному напряжению 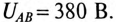
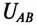
Таким образом, вольтметр 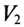
Вращающееся магнитное поле двухфазного тока
Двухфазным током называется совокупность двух однофазных токов, сдвинутых по фазе на угол 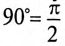
Эти токи создают в обмотках переменные магнитные потоки, сдвинутые по фазе также на угол 90°:
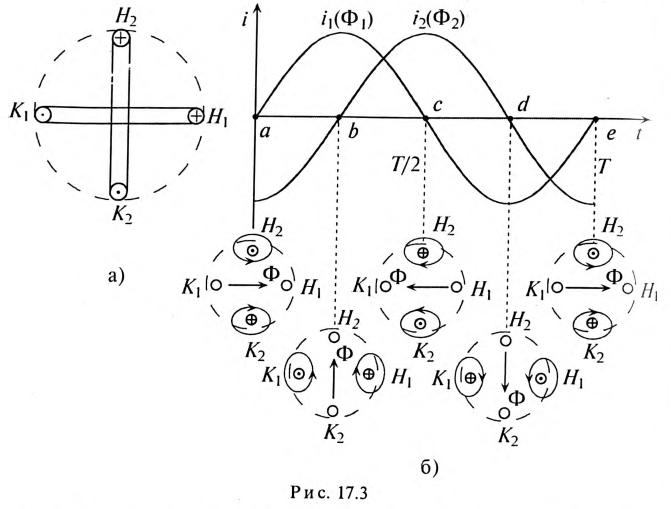
Таким образом, если по двум неподвижно скрепленным под углом 90° обмоткам пропустить двухфазный ток, то внутри этих обмоток (рис. 17.3а) создается вращающееся магнитное поле двухфазного тока.
Как видно (рис. 17.3б), постоянный магнитный поток 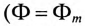
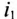
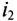
Нетрудно убедиться в том, что если бы второй ток 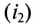
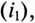
Пульсирующее магнитное поле
Если по неподвижной катушке (обмотке) машины пропустить синусоидальный ток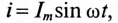
Пульсирующее магнитное поле, к видно из рис. 17.4, можно рассматривать как два магнитных поля, вращающихся в разные стогны. Поэтому в машинах, в которых используется пульсирующее магнитное поле, отсутствует пусковой момент. Для работы таких машин его необходимо создать. Пусковой момент в таких машинах создают или механически, или за счет пусковой обмотки, по которой в момент пуска пропускают импульс тока, сдвинутого по фазе относительно основного синусоидального тока, проходящего по катушке (обмотке) машины (аналогично двухфазному току).
Определение трёхфазных цепей
Наряду с однофазными источниками существуют источники энергии, содержащие две, три, четыре и т.д., характеризуемые тем, что их ЭДС, имея одинаковую частоту, сдвинуты друг относительно друга на некоторый угол. Такие генераторы называются многофазными, а электрические цепи с такими источниками — многофазными.
Трёхфазный генератор
Трёхфазные цепи получили наибольшее практическое применение. В связи с этим основные исследования многофазных цепей будем проводить на примере трёхфазных. Рассмотрим вопрос реализации трёхфазного источника, которым является трёхфазный генератор (рис. 4.1).
Рис. 4.1. Трёхфазный генератор
Для упрощения понимания принципа работы генератора обмотки (фазы) представлены одним витком. В качестве ротора генератора выбран постоянный магнит. Каждая из обмоток имеет начало — клеммы 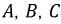
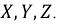
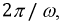
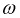
Последовательность, в которой ЭДС достигают максимума в соответствующих фазах, носит название порядка чередования фаз. Прямым порядком чередования фаз называют последовательность 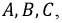
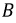
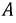
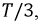
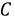
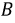
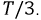
Рис. 4.2. Графики мгновенных значений ЭДС фаз
Запишем мгновенные значения ЭДС, индуктируемые в фазах при вращении ротора генератора:
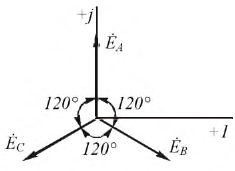
Поскольку ЭДС каждой фазы генератора синусоидальна, то их можно изобразить на комплексной плоскости в виде векторов соответствующих фазных ЭДС: 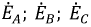
Рис. 4.3. Векторная диаграмма фазных ЭДС
Важным обстоятельством является то, что система векторов фазных ЭДС генератора на комплексной плоскости образует симметричную трехлучевую звезду и сумма этих векторов в любой момент времени равна нулю.
При подключении к каждой из фаз генератора нагрузки по ней будет протекать ток. Таким образом, реализуется трёхфазная система.
Способы соединения фаз генератора и нагрузки
Соединение фаз генератора и нагрузки четырехпроводной звездой:
При соединении фаз генератора звездой все концы или начала соединяют в одну общую точку. На рис. 4.4.а показана несвязанная трёхфазная система, в которой каждая фаза генератора и приемника образует отдельную электрическую цепь и поэтому для связи генератора и приемника требуется 6 проводов.
Рис. 4.4. Соединение звездой а) несвязанная трёхфазная система, b) четырехпроводная звезда
При соединении звездой количество проводов уменьшится до 4-х. Причем провод, соединяющий общие (нейтральные или нулевые) точки фаз генератора 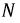
Токи, протекающие по фазам генератора или приемника, называются фазными токами, токи, протекающие по проводам, соединяющим фазы генератора и приемника, — линейными токам, ток, протекающий по нейтральному проводу — нейтральным.
Напряжение между началом и концом фазы генератора или приемника называется фазным, напряжение между двумя фазами или линиями — линейным.
Для этого способа соединения между линейными и фазными параметрами цепи существуют следующие соотношения:
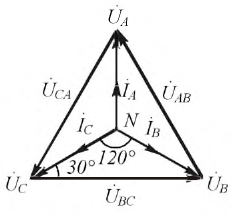
Установим взаимосвязь между комплексами линейных и фазных напряжений источника (рис. 4.5).
Рис. 4.5. Векторно-топографическая диаграмма трёхфазной цепи при соединении приёмников звездой при симметричной активной нагрузке
В дальнейших рассуждениях фазные ЭДС заменим напряжениями на фазах источника:
Выберем любой равнобедренный треугольник, образованный двумя фазными и линейным напряжениями и опустим перпендикуляр из вершины 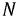
Из любого прямоугольного треугольника получим:
то есть:
Это второе важное соотношение для соединения звездой.
Частным случаем такого соединения является соединение «звезда-звезда» без нулевого провода.
Соединение фаз генератора и нагрузки треугольником
Вторым базовым способом соединения фаз генератора и нагрузки является соединение типа «треугольник-треугольник» (рис. 4.6).
Рис. 4.6. Соединение «треугольник-треугольник»
При соединении треугольником существует следующее соотношение:
Установим взаимосвязь между фазными и линейными токами:
Построим векторную диаграмму токов и напряжений приемника (рис. 4.7) для данного способа соединения.
Рис. 4.7. Векторно-топографическая диаграмма трёхфазной цепи при соединении
Рассмотрев любой треугольник токов, можно, аналогично напряжениям при соединении звездой, сделать вывод (только для симметричной нагрузки):
Помимо вышеназванных существуют и комбинированные способы соединения: «звезда-треугольник», «треугольник-звезда».
Режимы работы трёхфазных цепей
Различают симметричный и несимметричный режимы работы трехфазной цепи. При. симметричном режиме сопротивления трех фаз одинаковы и ЭДС образуют трехфазную. симметричную систему. В этом случае токи фаз а, в, с будут равны по величине и сдвинуты по угол 120 градусов.
Соединение «звезда-звезда» с нулевым проводом и без нулевого провода
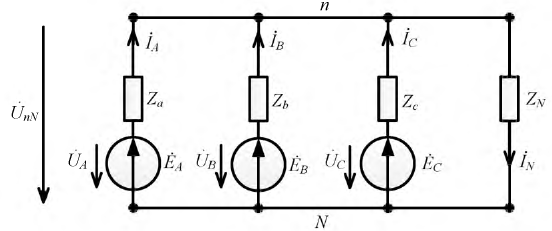
Поскольку трёхфазные цепи являются совокупностью однофазных цепей, то для их расчета используются все ранее рассмотренные специальные методы, в том числе и комплексный метод расчета. Следовательно, расчет трёхфазных цепей можно иллюстрировать построением векторных диаграмм токов нагрузки и топографических диаграмм напряжений.
Наиболее рациональным методом расчета такой цепи может считаться метод двух узлов. Для выбранных положительных направлений напряжений и токов на схеме (рис. 4.8) составим соответствующую систему уравнений для расчета токов. приемников треугольником и симметричной активной нагрузке
Рис. 4.8. Соединение фаз генератора и приемника по схеме «четырехпроводная звезда»
1. Симметричная нагрузка.
Нагрузка считается симметричной, если комплексные сопротивления ее фаз равны:
Четырехпроводная звезда.
Для простоты в качестве потребителей фаз нагрузки будем рассматривать активные сопротивления 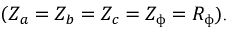
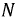
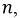
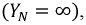
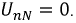
Аналогично для фаз 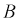
Исходя из сказанного, построим топографическую диаграмму фазных напряжений и векторную диаграмму токов (рис. 4.9).
Рис. 4.9. Векторно-топографическая диаграмма для симметричной нагрузки в трех- и четырехпроводной системах
Трехпроводная звезда.
При симметричной нагрузке, как и в четырехпроводной схеме, фазы приемника работают независимо друг от друга и нулевой провод не нужен. Диаграмма в данном случае будет абсолютно той же, что и для четырехпроводной звезды.
2. Несимметричная нагрузка.
Четырехпроводная звезда.
Пусть
На векторно-топографической диаграмме токов и напряжений (рис. 4.10) показано суммирование фазных токов.
Рис. 4.10. Векторно-топографическая диаграмма для несимметричной нагрузки
Трехпроводная звезда.
Пусть 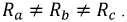
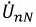
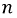
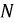
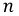
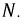
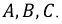
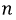
Рис. 4.11. Определение смещения нулевой точки
Соединив точки 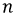
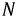
По результатам выполненных построений можно сделать главный вывод: если заведомо известно, что нагрузка несимметрична или может таковою стать, необходимо использовать четырехпроводную схему.
3. Обрыв фазы.
Четырёхпроводная звезда.
Векторная диаграмма (рис. 4.12) иллюстрирует работу четырехпроводной системы.
Рис. 4.12. Векторно-топографическая диаграмма для обрыва фазы в четырехпроводной системе
Трехпроводная звезда.
Напряжение смещения 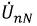
Рис. 4.13. Векторно-топографическая диаграмма для обрыва фазы в трехпроводной системе
По первому закону Кирхгофа:
Поскольку 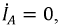
Токи в фазах 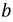
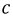
4. Короткое замыкание фазы.
Четырехпроводная звезда.
В четырехпроводной системе при коротком замыкании фазы приемника получаем короткое замыкание фазы источника.
Трехпроводная звезда:
Фазные напряжения приемника:
т.е. фазные напряжения увеличились до линейных напряжений, соответственно, токи в фазах:
возросли в 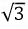
Построение векторно-топографической диаграммы для короткого замыкания показано на рис. 4.14.
5. Разнородная нагрузка.
Общий принцип построения векторных диаграмм токов и топографических диаграмм напряжений остается тем же. Единственное отличие будет состоять в появлении фазовых сдвигов между токами и напряжениями на фазах нагрузки в зависимости от ее характера.
Рис. 4.14. Векторно-топографическая диаграмма для короткого замыкания фазы 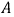
По схеме трехпроводной звезды включают трёхфазные симметричные приемники, например, трёхфазные асинхронные и синхронные двигатели.
Соединение потребителей треугольником
Рассмотрим различные режимы работы приемника при соединении его фаз треугольником (рис. 4.15).
Рис. 4.15. Соединение фаз приемника треугольником
Вновь будем считать, что в качестве потребителей в фазах включены активные сопротивления (для простоты построений).
Симметричный режим.
На рис. 4.7 построена векторная диаграмма для симметричной нагрузки при соединении фаз приемника треугольником.
Токи равны по модулю и отличаются только по фазе:
Линейные токи:
Несимметричный режим:
Фазы по-прежнему работают независимо друг от друга и поэтому токи будут:
Линейные токи определяются соответственно по формулам (4.9). Векторная диаграмма представлена на рис. 4.16.
Рис. 4.16. Векторно-топографическая диаграмма для несимметричной нагрузки приемников, соединенных треугольником
Обрыв фазы
На рис. 4.17 построена векторная диаграмма при соединении приемников треугольником для обрыва фазы.
Рис. 4.17. Векторно-топографическая диаграмма для обрыва фазы при соединении приемников треугольником
Соотношения для токов:
При разнородной нагрузке методика расчета не меняется.
Расчет мощности в трёхфазных цепях
Рассмотрим расчет мощности при соединении приемников по схеме четырехпроводной звезды и допустим, что нагрузка несимметрична. Если учесть, что сопротивление нейтрального провода не равно нулю и активное, имеем:
При симметричной нагрузке для трех- и четырехпроводной системы получим:
При соединении фаз приемника треугольником и несимметричной нагрузке имеем:
При симметричной нагрузке:
При этом необходимо учесть, что одинаковые формулы для расчета мощности при разном способе соединения фаз нагрузки (4.10-4.12) и (4.13- 4.15) не означают одинаковые численные значения.
Пример. Пусть трёхфазный приемник с сопротивлением фазы 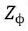
Теперь фазы того же приемника соединим «треугольником» и подключим к тому же трёхфазному источнику:
Итог очевиден:
Измерение мощности в трёхфазных цепях
Для измерения активной мощности в симметричной трехфазной цепи достаточно одного ваттметра, включенного на измерение мощности одной из фаз.
Соединение приемников по схеме четырехпроводной звезды
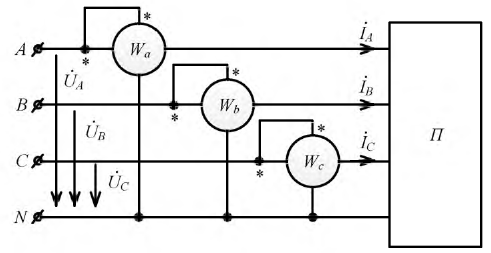
В схеме (рис. 4.18) однофазные ваттметры включаются в каждую фазу, причем через токовые катушки протекают линейные токи, а катушки напряжения ваттметров включены между нулевым проводом и соответствующими линейными проводами.
Рис. 4.18. Схема включения ваттметров для измерения мощности в четырехпроводной системе
Так как активная мощность — это вещественная часть полной мощности:
то суммарная мощность трех ваттметров может быть представлена выражением:
или
В случае симметричной нагрузки для измерения мощности, потребляемой ею, достаточно воспользоваться одним ваттметром, показание которого нужно утроить.
Соединение приемников по схеме трехпроводной звезды или треугольником
В этом случае измерить мощность трёхфазного приемника можно с помощью двух ваттметров (рис. 4.19).
Рис. 4.19. Схема измерения активной мощности двумя ваттметрами
Покажем это:
Если учесть, что:
получим:
Окончательно имеем:
Оба ваттметра выполняются в одном корпусе, и прибор имеет две пары выводов для токовых катушек и две пары выводов — для катушек напряжения. Включают трёхфазный ваттметр по приведенной на рис. 4.19 схеме или по любой схеме с циклической заменой фаз.
Метод симметричных составляющих
Любую несимметричную трёхфазную систему можно разложить на три симметричные трёхфазные системы: прямой, обратной и нулевой последовательностей фаз. Такое разложение широко применяется при анализе работы трёхфазных машин и, в особенности, при расчете токов короткого замыкания в трёхфазных системах.
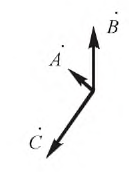
Пусть дана несимметричная трёхфазная система векторов 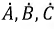
Рис. 4.20. Несимметричная трёхфазная система векторов
Каждый из векторов этой системы можно представить в виде суммы трех составляющих:
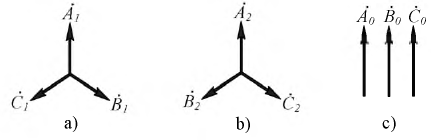
На рис. 4.21 изображены системы указанных выше последовательностей.
Рис. 4.21. Симметричные системы векторов прямой (a), обратной (b) и нулевой (с) последовательностей
Векторы прямой, обратной и нулевой последовательностей подчиняются следующим соотношениям:
где
Коэффициент 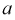
Подставим соотношения (4.19) в систему уравнений (4.18). Тогда получим:
Решение системы уравнений (4.20) относительно 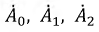
Симметричные составляющие можно определить графически, если на векторной диаграмме несимметричной системы векторов выполнить построения в соответствии с системой уравнений (4.21).
Фильтры симметричных составляющих
Симметричные составляющие несимметричных систем можно определить не только аналитически или графически, но и при помощи электрических схем, называемых фильтрами симметричных составляющих.
Эти фильтры применяются в схемах, защищающих электрические установки. Степень асимметрии системы токов и напряжений не должна превосходить известные пределы, т.е. составляющие нулевой и обратной последовательностей системы напряжений и токов при нормальных режимах должны быть меньше некоторых наперед заданных величин, определяемых для каждой конкретной установки индивидуально.
Возможность выделить при помощи электрических схем отдельные симметричные составляющие позволяет осуществить воздействие любой из них на приборы, защищающие установку, которые, будучи соответствующим образом отрегулированы, отключат или всю установку, или её часть, как только величина соответствующей составляющей превысит допустимый предел.
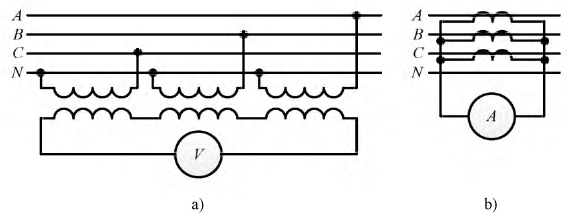
В качестве примера на рис. 4.22 приведены схемы фильтров нулевой последовательности линейных токов и фазных напряжений.
Рис. 4.22. Схемы фильтров нулевой последовательности
В схеме (рис. 4.22,a) вторичные обмотки трансформаторов напряжения включены последовательно и поэтому вольтметр определяет сумму фазных напряжений, т.е. утроенную составляющую нулевой последовательности системы фазных напряжений.
В схеме (рис. 4.22,b) вторичные обмотки трансформаторов тока включены параллельно и поэтому амперметр измеряет сумму линейных токов, то есть утроенную составляющую нулевой последовательности линейных токов.
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
- Переходные процессы
- Переходные процессы в линейных цепях
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Цепи с взаимной индукцией
Что такое фаза?
Фаза является значением тригонометрической функции, например определяющей вид или описывающей волновое или колебательное движение. Величина тождественна углу или аргументу периодической функции. Зависимость целой фазы от координат и времени не всегда бывает линейной и гармонической. Конец проводника, по которому ток поступает в цепь, или зажим представляет собой начало фазы. Изменение вольтажа цепи через временной промежуток является проекцией лучевого вектора на координатную ось.
Цепь представляет собой стандартные элементы — энергетический генератор, цепь передачи, приемник. Для понятия, что такое фазное, линейное напряжение, их взаимодействие требуется определение фазы. Положение фазы действует только для магистралей переменного тока. Понятие определятся в виде уравнения сектора векторного вращения с фиксацией одного конца в исходе координат.
Электрические линии отличаются числом фаз: одно-, двух-, трех- и многофазная.
В России популярна трехфазная сеть для питания потребителей, которые представлены бытовыми строениями или промышленными объектами. Подключение отличается преимуществами по сравнению с электроснабжающей однофазной цепью:
- экономичность из-за выгодного применения материалов;
- возможность транспортировки большого объема электричества;
- включение в рабочую цепь электрогенераторов и двигателей высокой мощности;
- создание разных показателей напряжения в зависимости от варианта включения потребляющей нагрузки в электрическую линию.
Работа в трехфазной цепи зависит от взаимного соотношения ее компонентов. Показатели напряжения зависят от фазы (угла наклона векторного луча к координатной плоскости оси). Вольтаж определяется по земельному потенциалу, который равен нулю. Из-за этого кабель с присутствующим вольтажом именуют фазным, а заземляющий провод — нулевым. Угол фазы единичного вектора не имеет особой значимости, т. к. в линии он делает полный оборот на 360° за 1/50 часть секунды. Во внимание берется междуфазный угол относительности 2 векторов.
В сети с применением реактивных деталей угол берется между векторными показателями электротока и вольтажа, он носит название сдвига фазы. Если значения подключенных нагрузок со временем не изменяются, то величина сдвига будет всегда постоянной. Неизменность показателя используется в расчете электрической линии и анализа работы.
При намотке на катушке множества оборотов провода номинальное напряжение увеличивается пропорционально числу витков. Явление привело к разработке генераторов, обеспечивающих потребителей электричеством. Для эффекта от применения магнитного поля иногда устанавливают несколько бобин. Статорное магнитное поле за поворот ротора пересекают одновременно 3 катушки, что ведет к увеличению мощности генератора. Это позволяет запитать сразу 3 пользователей.
Что такое фазное напряжение?
В трехфазных магистралях большинства государств размер напряжения равен 220 вольт. Фазный вольтаж измеряется в промежутке между фазами в начале и конце провода. Практически это величина посередине нулевого проводника и напряженного кабеля. При подсоединении по типу звезды значения линейных токов и фазного электричества не отличаются.
Фазное напряжение — это напряжение между нулевым проводом и одним из фазных (220 В).
Симметричная система исключает присутствие нейтральной жилы, при несимметричном способе нулевой кабель поддерживает соразмерность с источником. Во втором варианте часто в цепь включаются приборы освещения, и требуется независимое функционирование 3 рабочих кабелей, тогда выводы приемника объединяются по типу треугольника.
Межфазное напряжение используется в многоквартирном секторе с магазинами или офисами на первых этажах. Так можно запитать торговые площадки силовыми кабелями в целях обеспечения 380 вольт. В высотках подключение обеспечивает лифты, эскалаторы, промышленные холодильники. Разводка выполняется относительно просто, учитывая, что в жилье идет ноль и жила под нагрузкой, а на общественные помещения ответвляются 3 рабочих кабеля и нейтральная жила.
Отличие трехфазного тока от однофазного состоит в том, что показатель сети — это линейная мощность, а параметры, имеющие отношение к нагрузке, представляют собой фазный вольтаж. От станции к потребителю проводится линия, включающая рабочие жилы и нулевой провод. Для снижения утечек при прохождении по цепи в начале и конце сети ставятся преобразователи, но картина от этого не изменяется. Нейтральный провод фиксирует и транспортирует пользователю заявленный потенциал, полученный на выходе. Мощность в проводе под нагрузкой создается, исходя из значения в нейтрали.
Величина напряжения фазы выявляется и возникает относительно центра подключения обмоток — нейтрального провода. В симметричной относительно нагрузок схеме трехфазной цепи через ноль передается ток с минимальными показателями. На выводе такой линии провода под нагрузкой окрашиваются в общепринятые стандартные цвета:
- жила L1 — коричневый;
- провод L2 — черный;
- кабель L3 — серый;
- нулевая оплетка N — синий;
- желтый или зеленый — предусмотрен для заземления.
Такие мощные линии проводятся к крупным потребителям — целым микрорайонам, заводам. Для небольших приемников монтируется однофазная линия, включающая нагруженный провод и дополнительный ноль. При равномерном распределении мощности в однофазных ответвлениях появляется равновесие в трехфазной конструкции. Для прокладки составляющих ветвей принимается напряжение фазы одной жилы относительно нейтрали.
Что такое линейное напряжение?
В трехфазной магистрали можно выделить дополнительное напряжение, при подсоединении перемычку между 2 нагруженными кабелями. Значение его выше, т. к. является проекцией на плоскость координат 2 векторов, составляющих угол 120° между собой. Довесок к значению фазового напряжения составляет 73% или рассчитывается как √3-1. Общепринятое линейное напряжение в электролинии всегда составляет 380 вольт.
Линейное напряжение — это напряжение между двумя фазными проводами (380 В).
Напряжение вычисляется в промежутке фаз или между их выводами. При монтаже схемы появляются трудности, заключающиеся в неточности при расчете проводника, что иногда вызывает аварию. Схемы подключения различаются вариантами объединения нагруженных жил и источника электричества. Преимущества однофазной сети:
- безопасность эксплуатации оборудования, т. к. опасность в плане поражения исходит от 1 кабеля;
- схема применяется для осуществления эффективной разводки, выбора принципа эксплуатации, расчета параметров и выполнения измерений.
Расчеты в системе простые, выполняются с учетом стандартных физических формул. Для замеров показателей цепи используется мультиметр. Характеристики подключения к фазе определяются с помощью специальных вольтметров, токовых датчиков.
Линейное напряжение возникает при прохождении электрического тока в подводнике при объединении источника энергии и приемника. При понижении мощности на участке между выходом генератора и потребителем параметры фазного вольтажа также изменяются. Зная линейные показатели, нетрудно высчитать значение фазного напряжения.
Особенности сети:
- при разводке проводов профессиональных устройств не требуется, достаточно отвертки с встроенным индикатором;
- при соединении проводов не используется ноль — из-за нейтральной жилы нет опасности поражения током;
- схема применима для постоянных сетей и линий с переменным током;
- однофазное соединение выполняется в трехфазной линии, но не наоборот.
Соотношения фазного и линейного напряжения
Соотношение между напряжением линейным и фазным составляет 1,73. То есть при ста процентах мощности ЛН, напряжение фазы будет 58%. То есть, ЛН превышает ФН в 1,73 раза и при этом стабильно.
ФН и ЛН, отличие и соотношение
Напряжение в трёхфазной цепи оценивается по параметрам линейной составляющей. Обычно оно 380 вольт и тождественно 220 вольтам фазной компоненты сети трёхфазного электротока. В электрических сетях, где имеется четыре провода, напряжение 3-фазного тока обозначается 380/220В. Это позволяет подключить к подобной сети оборудование с 1-фазным потреблением электричества 220В и мощных приборов, которые могут работать от 380В.
Универсальной и приемлемой в большинстве случаев является трёхфазная цепь 380/220В 0-вым проводом. Электроприборы, которые функционируют от однофазного напряженья 220В, могут при подсоединении к паре проводов ФН питаться от ЛН.
Электрооборудование, которое запитывается от трёхфазной сети может работать, только если имеется подсоединение одновременно к 3-м выводам различных фаз. Тогда заземление не обязательно, но если изоляционный материал провода будет повреждён, то отсутствие 0-ого значительно увеличивает опасность удара электрическим током.
Важно! При понижении ЛН меняются величины ФН. При уже выясненном значении междуфазного напряжения определить величину ФН труда не составит.
Вычисление соотношения между фазным и линейным напряжением
Для расчёта соотношения следует знать линейные параметры. Все вычисления производятся по формуле: 12UAB=UA cos 30˚, либо UAB=2√3/2×UA=√3×UA. Таким образом, делаем вывод, что окончательная формула выглядит следующим образом – Uл=√3×UФ.
На первый взгляд может показаться, что формулы слишком сложны, однако это не так. С другой стороны, домашнему мастеру практически нет смысла заниматься подобными расчётами. Достаточно обычной проверки напряжения на каждой из фаз обычным мультиметром.
Типы соединения
Чтобы запустить генератор, часто используют именно линейное и фазное напряжение. Если говорить о запуске именно трехфазного генератора, то следует отметить один важный факт.
Состоит такой прибор не только из первичных, но и вторичных обмоток. Эти обмотки нужно правильно соединить и для этого существует два самых распространенных способа.
Только благодаря тому, что все обмотки будут правильно соединены, можно добиться определенных улучшений:
- Увеличение мощности передачи – это важнейшая задача, которую нужно решить, но сделать это следует без увеличения напряжения. И сделать это можно благодаря использованию определенных типов соединений.
- Снижение пульсаций напряжения – если в блоках питания наблюдаются постоянные колебания напряжения, это может стать причиной выхода из строя, подключенных к ней приборов. Поэтому устранение данного недочета с помощью разных соединений является первостепенной задачей.
- Уменьшение количества проводов – при подключении к сети нужно минимизировать количество соединений, чтобы улучшить качество работы приборов. Именно по этой причине использование двух упрощенных схем для подключения настолько важно.
Треугольник
Для выполнения соединения используют схему, отличную от той, которая была описана выше. Ведь нужно соединить одну обмотку с другой.
Свое название соединение получило из-за внешнего сходства с треугольником.
Его особенностью является то, что все обмотки соединяются в строгой последовательности. А поскольку общая точка соприкосновения отсутствует, такая система может быть только одного вида, а именно – трехпроводная.
Звезда
Сначала рассмотрим данный тип подключения. Чтобы его выполнить, нужно соединить начало всех мотков в одной точке.
Эту точку принято называть нулевой. В некоторых печатных руководствах упоминается другое обозначение – нейтральная точка.
Иногда встречается соединение нулевой точки и нулевым источником питания. И поэтому ошибочно юные и начинающие электрики считают его обязательным. Но это не так, такое соединение могут использовать в некоторых случаях, и оно не является обязательным.
Важно! Если такое соединение присутствует, то систему правильно называть 4-проводной. В том случае, если оно отсутствует, то соединение считается трехпроводным.
Комбинированный вариант соединения
В некоторых случаях используется комбинированный вариант «звезда-треугольник». Электродвигатель мягко запускается на соединении «звезда», а после того, как набирает необходимые обороты, реле переключает его на «треугольник». Однако не все двигатели можно подключить подобным образом. К примеру, существуют электромоторы, имеющие всего 3 вывода в контактной группе. Они изначально изготовлены под соединение «звезда» и подключить их «треугольником» невозможно.
Если объединить распространённые типы включения в трёхфазную сеть, можно увидеть следующую картину.
Отличие линейного от фазного напряжения
Если представить трехфазную цепь, то четко понятно, что в ней есть определенное напряжение между фазными контактами и фазным и нулевым проводом. Это происходит из-за того, что в этой схеме используется четырёхпроводная трехфазная цепь. Главные её характеристики – напряжение и частота. Напряжение, возникающее в цепи между двумя фазными проводами – это линейное, а то, что появляется между фазным и нулевым – фазным.
4-проводная сеть
Примечательной особенностью линейного напряжения является то, что именно по нему рассчитываются токи и другие параметры трехфазной цепи. Кроме того, к такой схеме можно подключать не только стандартные трехфазные контакты, но и однофазные (это различные бытовые приборы, приемники). Номинальное равняется 380 вольт, при этом оно может изменяться в зависимости от скачков или других перемен в локальной сети.
Существует несколько вариантов такого соединения, скажем, система с нейтралью под заземлением является самой популярной. Она характеризуется тем, что подключение к ней производится по особой схеме:
- Однофазные отводы подключаются к фазным проводам;
- Трехфазные – к трехфазным, соответственно.
Линейное напряжение имеет очень широкое использование благодаря своей безопасности и удобства разветвления сети. Электрические приборы подключаются только к одному- фазному проводу, опасность представляет он один. Расчет системы очень прост, в нем руководствуются стандартными формулами из физики. При этом, чтобы измерить этот параметр сети, достаточно воспользоваться простым мультиметром, для того, чтобы замерить характеристики фазового подключения потребуется несколько специальных устройств (датчики тока, вольтметры и прочие).
Некоторые особенности сети:
- При разводке такой проводки не требуется использовать профессиональные приборы- все измерения проводятся отвертками с индикаторами;
- При соединении проводников нет необходимости подключать нулевой провод, т. к. благодаря свободной нейтрали, риск поражения током крайне мал;
- Электротехника использует такую схему подключения для различных электродвигателей и других устройств, требующих высокую мощность для работы. Дело в том, что используя этот тип напряжения есть возможность повысить КПД на треть, что является весьма полезным свойством, в особенности, для асинхронного двигателя;
- Схема используется как для переменного тока, так и для постоянного;
- Нужно помнить, что однофазное соединение можно подключить к трехфазной сети, но не наоборот;
- Но, у такой цепи есть и определенные недостатки. В линейном соединении проводников очень сложно обнаружить повреждения. Это способствует повышенной пожарной опасности.
Соответственно, основная разница между фазовым и линейным напряжением заключается в разности подсоединяемых проводов обмоток.
Для контроля и выравнивания этого параметра часто используется специальный прибор – линейный стабилизатор напряжения. Он позволяет поддерживать показатель на определённом уровне, при этом нормализуя повышенное. Еще одно его определение – импульсный стабилизатор. Устройство может подключаться к розетке, контактам электрических приборов и т. д.
Измерение
Напряжение, возникающее между фазными проводниками, называется линейным. При этом между фазным и нулевым появляется фазное напряжение. Линейную разновидность применяют для определения токов и прочих показателей трехфазной цепи. При этом в такие схемы допустимо включать не только трехфазные контакты. Также разрешается использовать и однофазные – в частности, разные бытовые приборы.
Номинальный показатель линейного напряжения составляет 380 Вольт. Под влиянием ряда факторов, которые возникают в локальной сети, оно может меняться. Потому ключевые отличия между рассматриваемыми видами напряжений кроются в методах соединения обмоток.
Более распространенной считается линейная разновидность. Это обусловлено безопасным применением и удобством распределения сетей. Чтобы измерить этот параметр, стоит применять мультиметр. При этом для оценки показателей фазного напряжения потребуются датчики тока, вольтметры и прочие специальные устройства.
Контроль и выравнивание этого показателя производится линейным стабилизатором напряжения. Это устройство поддерживает параметр в норме. К тому же он помогает нормализовать высокое напряжение.
Величины измерения
Необходимо четко понимать, что даже установленные числа для фазного и линейного напряжения в 220 и 380 Вольт соответственно – это не конечные цифры. Важно понимать, что для каждого параметра установлена «диапазонная вилка», то есть тот интервал внутри которого изменения параметра считаются нормальными.
Поэтому, для фазного напряжения считается нормой колебания от 198 В до 242 В. Это говорит о том, что номинальному значению в 220 Вольт прибавляется и отнимается 10%, которые являются своеобразным стандартным отклонением.
Этот параметр установлен в соответствии с нормативным документом ГОСТ 13109.
Для расчета трехфазных цепей, чаще всего специалисты снимают параметр только линейного тока в сети, а также значение линейного напряжения.
Величину фазового напряжения определяют в момент падения линейного, то есть при образовании так называемого проседания.
Для определения величины ЛН используют формулы:
- Uл = Uф,
где
- Uл – напряжение линейное;
- Uф – напряжение фазовое.
В ситуации, когда необходимо установить значение реактивной мощности в трехфазной сети, использую формулу:
Q=Qa+Qb+Qc
Чаще всего подобную формулу использовать в том случае, когда необходимо подсчитать электрическую сеть, в которую будут включены различные промышленные приборы. А это значит, что она требует большей точности с точки зрения соответствия и недопущения различных перебоев в работе.
Если говорить о распространенности сетей, то стоит отметить, что наиболее часто встречается линейный вариант. Это обусловлено тем, что здесь безопасность находится на более высоком уровне. А разведение электропроводки достаточно просто осуществляется.
Все электрооборудование, которое необходимо включить в сеть, подсоединяться только к одному фазному проводу. Именно он запитывается электрическим током и представляет собой опасность с точки зрения поражения человека. Второй провод является заземлением.
Как измерить
Измерить подобную систему можно мультиметром или применив физические формулы.
Измерение подключения к сети
ЛН рассчитывается по формуле Кирхгофа: ∑ Ik = 0. Здесь сила тока равняется нулю во всех частях электроцепи, то есть к=1. Используется также закон Ома: I=U/R. Применив обе формулы можно высчитать параметры клейма или электросети.
В системе из несколько линий, потребуется найти напряжение между 0 и фазой IL = IF. Значения IL и IF непостоянные и меняются при разных вариациях подключения. Потому линейные параметры точно такие же, как и фазные.
Схемы подключения
Существует 2 схемы, по которым источники напряжения подключаются к сети:
- звездой;
- треугольником.
Каждый из вариантов отличается своими особенностями. При подключении звездой начала обмоток генератора соединяются в конкретной точке. Это препятствует повышению мощности. При использовании треугольника обмотки соединяются последовательно. При этом начало одной обмотки соединяется с концом другой. Это помогает втрое повысить напряжение.
Чтобы понимать схемы подключения, стоит ознакомиться с такими понятиями:
- линейным называют ток, который попадает в подводник между приемником и источником электроэнергии;
- фазным считается ток, текущий в каждой обмотке источника электроэнергии.
Эти виды токов важны при наличии несимметричной нагрузки на генератор. Это наблюдается довольно часто при подключении объектов к электросети. Все параметры, которые относятся к линии, представляют собой линейные токи и напряжения. Показатели, которые относятся фазе, считаются значениями фазных величин.
Соединение в виде звезды показывает, что все линейные токи отличаются теми же значениями, что и фазные. При симметричности системы потребность в нейтральном проводе пропадает. На практике он способствует поддержанию симметрии при асимметричности нагрузки.
В случае несимметричности используемой нагрузки важно, чтобы три фазы цепи функционировали независимо. Это удастся сделать и в трехпроводной линии, когда элементы приемника соединены в треугольник.
По мнению специалистов, снижение линейного напряжения приводит к изменению параметров фазного напряжения. Если знать показатель междуфазного напряжения, удастся без труда определить размер фазного.
Расчет
Сети с линейным током применяются довольно часто. Это обусловлено минимальными рисками и простотой разведения такой проводки. Все электроприборы в таком случае соединяются лишь с одним фазным проводом, по которому течет ток. При этом источником опасности считается только он.
Для расчета такой схемы будет достаточно обычных формул из курса физики. К тому же для измерения данного показателя сети хватит обыкновенного мультиметра. При этом для получения показаний фазного подключения потребуется целая система оборудования.
Чтобы подсчитать напряжение линейного тока, рекомендуется использовать формулу Кирхгофа и закон Ома. Благодаря применению этих понятий удастся быстро рассчитать характеристики определенного клейма или электрической сети.
Использование линейного и фазного напряжения
Электрические цепи бывают постоянного и переменного тока. Чаще для соединения источника электричества с потребителем используются трехфазные цепи переменного тока. Такой тип тока имеет ряд преимуществ:
- ниже затраты на передачу энергии;
- возможность создания электродвижущей силы для функционирования асинхронного оборудования (лифтов, подъемников);
- можно одновременно использовать линейное и фазное напряжение.
Для подключения генераторов в магистраль используют принцип треугольника или звезды. В первом варианте обмотки подсоединяются последовательно, начало фазы и конец другой фазы соединены. Схема позволяет повысить напряжение в несколько раз. Во втором случае начальные участки обмоток объединяются в общую точку, повышение мощности не происходит.
Классификация электросети по составу рабочих элементов:
- активная;
- пассивная;
- линейная;
- нелинейная.
Используя 4 кабеля в магистрали, можно, варьируя подключения, использовать одновременно линейные и фазные токи, что расширяет область применения. Трехфазные магистрали считаются универсальными, т. к. подключается большая нагрузка, например, к сети в 10 вольт. Если подсоединить к линии соответствующий приемник, например, трехфазный электрический двигатель, то его механическая мощность достигнет величин, в 3 раза превышающих показатели однофазного агрегата.
В многоквартирном секторе основными приемниками являются бытовые устройства и приборы, питающиеся от сети 220 В. Требуется равномерное разделение между проводами с нагрузкой, поэтому квартиры подключаются по шахматной схеме. В частном домостроении принята концепция рассредоточения нагрузки на каждый кабель от всех домашних приборов и оборудования. Учитываются проводниковые токи, передающиеся во время включения максимального числа устройств.
Включая в сеть с 1 или 3 фазами одинаковые электрические двигатели, можно получить разницу в мощности его работы. Если дополнительно выбрать эффективный способ подключения, то показатели на выходе повысятся втрое. Учитывая соотношение между фазными и линейными токами, следует рассчитывать обмотки на повышенные значения. Относительный показатель разницы зарядов между нагруженными проводами всегда больше аналогичного значения между фазой и нулем. Основное отличие линейных характеристик напряжения и мощности фазы состоит в параметрах получаемого вольтажа.
Классическим примером применения обоих видов напряжения является соединение при установке трехфазного генератора. Используются вторичные обмотки и первичные обвивки, соединяемые по одной из схем. Связь линейного напряжения и значения фазы при соединении по типу треугольника помогает выравнивать ток, и обе мощности становятся почти одинаковыми. Аналогично подсоединяются двигатели, преобразователи и трансформаторы.
Вариант звезды предполагает подсоединение контактов всех обмоток к одной цепи с применением перемычек. В проводниках проходит ток с показателями этой сети, а напряжение передается на активные выводы и контакты.
Плюсы и минусы
Для каждой из систем питания характерны определенные преимущества и недостатки. Однофазная сеть 220 Вольт отличается следующими плюсами:
- простота;
- доступная стоимость;
- опасное напряжение.
К недостаткам относятся:
- ограниченная мощность;
- невозможность функционирования асинхронных двигателей.
Для трехфазной сети 380 Вольт характерны такие преимущества:
- ограничение мощности лишь сечением проводов;
- экономия;
- возможность питания промышленного оборудования;
- возможность переключения однофазной нагрузки на другую фазу при снижении качества или отсутствии питания.
К недостаткам стоит отнести следующее:
- потребность в дорогостоящем оборудовании;
- высокое напряжение;
- ограничение мощности однофазных нагрузок.
Нюансы выбора типа соединения
В настоящее время оба типа соединения, звезда и треугольник, активно используются. Однако, подобное вовсе не означает, что можно по собственному усмотрению выбрать тот способ, который больше понравится.
Существуют определенные требования и общие рекомендации, следуя которым можно избежать ошибок.
Нужно запомнить, что при линейном напряжении в 220 вольт подключение двигателя по схеме звезда невозможно.
Для такого напряжения идеально подходит схема треугольник.
С другой стороны, если в сети напряжение выше 220 вольт, к примеру 380, то оптимальным вариантом станет использование именно звезды.
Если запомнить это простое правило, удастся в будущем избежать ошибок при подключении генераторов и других приборов.
Для чего требуется проверка напряжения фаз перед включением
При подключении оборудования, требующего напряжения 380 в (к примеру, асинхронного электродвигателя) следует проверить напряжение на каждой из трёх фаз и сравнить показатели. Особенно это касается частных секторов, где напряжение нестабильно или электромонтёры имеют недостаточную квалификацию. Дело в том, что в деревнях часто не обращают внимания на распределение нагрузки.
В результате подобных действий одна из фаз может быть перегружена при минимальной нагрузке на остальные. Вкупе с устаревшими трансформаторами это приводит к перекосу фаз. Получается, что на одной из фаз напряжение значительно снижается. Это приводит к перегреву трёхфазных двигателей или иного оборудования и выходу его из строя. Такой перекос явно не пойдёт на пользу оборудованию, работающему от трёх фаз
Система распределения электроэнергии
Исходно напряжение всегда является трехфазным. Под “исходно” я подразумеваю генератор на электростанции (тепловой, газовой, атомной), с которого напряжение в много тысяч вольт поступает на понижающие трансформаторы, которые образуют несколько ступеней напряжения. Последний трансформатор понижает напряжение до уровня 0,4 кВ и подаёт его конечным потребителям – нам с вами, в квартирные дома и в частный жилой сектор.
На крупных предприятиях с потреблением мощности более 100 кВт обычно существуют собственные подстанции 10/0,4 кВ.
С генератора G напряжение (везде речь идёт про трехфазное) 110 кВ (может быть 220 кВ, 330 кВ или другое) поступает на первую трансформаторную подстанцию ТП1, которая понижает напряжение в первый раз до 10 кВ. Одна такая ТП устанавливается для питания города или района и может иметь мощность порядка от единиц до сотен мегаватт (МВт).
Далее напряжение поступает на трансформатор ТП2 второй ступени, на выходе которого действует напряжение конечного потребителя 0,4 кВ (380В). Мощность трансформаторов ТП2 – от сотен до тысяч кВт. С ТП2 напряжение поступает к нам – на несколько многоквартирных домов, на частный сектор, и т.п.
Такие ступени преобразования уровня напряжения необходимы для того, чтобы уменьшить потери при транспортировке электроэнергии. Подробнее о потерях в кабельных линиях – в другой моей статье.
Схема упрощённая, ступеней может быть несколько, напряжения и мощности могут быть другие, но суть от этого не меняется. Только конечное напряжение потребителей одно – 380 В.
Что у нас на практике
Как получается два напряжения в трёхфазной сети мы разобрались, теперь давайте разберёмся, как это используется на практике.
В быту большая часть электроприборов питается однофазным напряжением. Напряжение в электросети стандартизировано — 230В с частотой 50 Гц, и вся бытовая техника рассчитана на питание именно этим напряжением. Если прибору необходимо пониженное напряжение, например, 5, 12, 19, 36 вольт или любая другая величина, то у него есть либо встроенный, либо выносной блок питания, который, собственно, и формирует нужное напряжение.
При необходимости подключения мощных приборов, например, электрических котлов и плит, сварочного оборудования, станков и прочего возникает проблема — большой ток. Например, обычная розетка рассчитана на ток до 16А, который длительно может проводить кабель с сечением токопроводящих жил 2.5 мм², через неё можно запитать приборы мощностью до 3.5 кВт.
Поэтому мощные приборы зачастую подключают отдельной линией напрямую к автоматическому выключателю или через силовые розетки на 32А. Но для такого тока нужно использовать кабель с сечением токопроводящих жил уже 6 мм² и более. При этом максимальная нагрузка в такой линии — 7 кВт.
При подключении нагрузки на линейное напряжение, то есть к двум проводам питающей сети между которыми 380В и потребляемом токе в те же 32А, мощность подключаемой нагрузки будет уже около 12 кВт. То есть кабель с таким же сечением жил сможет питать почти в 2 раза более мощную нагрузку. А у трёхфазного прибора при том же токе в 32А мощность будет уже 21 кВт.
И учтите, что для его подключения не понадобится прокладывать ЛЭП с более толстыми проводами, не придётся прокладывать от распределительного щита питающих кабелей с толстыми жилами и так далее… Тогда как в однофазной цепи прибор мощностью в 21 кВт будет потреблять ток около 95А, а для его питания нужно будет использовать кабель с жилами на 25 мм² против 6-8 мм² и 32А в трёхфазной цепи.
Для снижения питающего тока мощные электроприборы производят трёхфазными. Но не всегда прибор, рассчитанный на 380В, трёхфазный. Есть однофазные потребители с номинальным напряжением 380В, например, сварочные трансформаторы типа ТСМ-250 и другие подобные.
Из характеристик мы видим, что напряжение питающей сети 1х380. То есть его первичная обмотка подключается к двум фазам. Любопытно что многие называют подобные трансформаторы «двухфазными», но это в корне неверно. На первичную обмотку действует одна ЭДС, так же, как и в любом другом однофазном приборе.
Ничего выдающегося здесь нет, и такое напряжение первичной обмотки выбрано с той же целью – снизить ток питания, что позволит намотать обмотку проводом меньшего сечения и использовать кабели с меньшим сечением ТПЖ для подключения к сети.
Если бы он был рассчитан на питание от 220В, то в режиме максимальной нагрузки ток потребления составил бы 16 000/220 = 72А, а при питании от 380В ток будет не более: 16 000/380 = 42А.
Таким образом, наличие двух напряжений в трёхфазной сети позволяет подключать электрооборудование любой мощности и различной конфигурации. Что, безусловно, повышает гибкость и удобство использования этой системы питания.
Подведём итог
Из всего изложенного можно сделать вывод, что фазное напряжение в сети 0.4 кВ всегда равно 220 В, в то время как линейное 380 В. Однако не стоит считать, что если значения фазного напряжения ниже, оно становится менее опасным. Редакция Homius со всей ответственностью заявляет, что поражение электрическим током может привести к летальному исходу независимо от того, линейное напряжение в цепи или фазное. Ведь поражение тканям и органам наносит не само напряжение, а сила тока. К примеру, 220 В трансформированные в 36 В становятся даже опаснее. Ведь человек практически не чувствует столь низкого напряжения, а в это время ток поражает органы. Поэтому при электромонтажных работах не следует забывать о технике безопасности.
Надеемся, что изложенная информация будет полезна начинающим электромонтажникам и домашним мастерам. При возникновении вопросов можете смело излагать их в обсуждениях ниже. Редакция Homius с удовольствием ответит на них как можно более развёрнуто и быстро. Там же Вы можете изложить своё мнение о статье, оставить комментарий или поделиться личным опытом в подключении трёхфазного оборудования. Если понравилась статья, не забываем её оценивать. А мы напоследок предлагаем Вашему вниманию короткий видеоролик, который позволит более полно раскрыть сегодняшнюю тему.
Источники
- https://odinelectric.ru/elektrosnabzhenie/chto-takoe-faznoe-i-linejnoe-napryazhenie
- https://volt-race.ru/nachinayushchim/napryazhenie-mezhdu-fazami.html
- https://electric-220.ru/chem-otlichaetsya-faznoe-napryazhenie-ot-linejnogo
- https://kelmochka.ru/linejnoe-i-faznoe-napryazheniya
- https://homius.ru/faznoe-i-linejnoe-naprjazhenie.html
- https://www.asutpp.ru/linejnoe-napryazhenie.html
- https://otlichi.ru/nauka/estestvennye/linejnoe-i-faznoe-napryazhenie-razlichie
- https://kladochka.ru/linejnoe-napryazhenie
- https://SamElectric.ru/powersupply/chem-trehfaznoe-napryazhenie-otlichaetsya-ot-odnofaznogo.html
- https://ElectroInfo.net/raznoe/chto-takoe-faznoe-i-linejnoe-naprjazhenie-linejnoe-i-faznoe-naprjazhenija-razlichija-sootnoshenie-i-pojasnenija.html
[свернуть]
Линейное и фазное напряжения — определение, измерение, схемы и описание типов
Без электричества сегодня представить жизнь современного человека крайне сложно. Вот только в тонкостях, которые касаются непосредственно процесса снабжения городов, предприятий и домов, разбираются лишь единицы.
И это большое упущение. Поскольку в жизни может возникнет ситуация, когда подобные знания действительно пригодятся. Поэтому попробуем разобраться в данном вопросе.
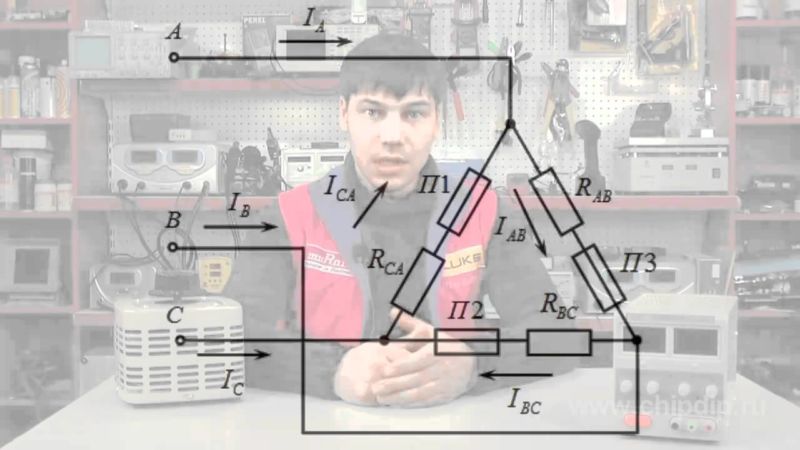
Содержание
Особенности напряжения в трехфазных сетях
Для того чтобы снабдить объекты электричеством, используются сети из 3-х фаз. Конечно, существуют и другие генераторы. Например, шестифазные. Но их применяют крайне редко.
Объясняется подобное необходимостью минимизировать затраты, которые возникают в процессе создания вращающегося магнитного поля. Эти затраты в любом случае возникают во время генерации электричества.
Хотя избежать их невозможно, но свести к минимуму вполне реально. И поэтому предпочтение отдается именно сетям с 3-х фазных напряжением.
В трехфазной сети выделяют три основных элемента:
- генератор;
- линии электропередач;
- нагрузка.
Под термином «нагрузка» принято подразумевать непосредственно потребителя. Фаза же представляет собой одну электрическую цепь в многофазной системе электрических цепей.
Важно! Данный вид подключения предоставляет возможность использовать сразу два вида напряжения.
Теперь поговорим о том, что представляют собой фазное и линейное напряжение. Ведь именно эти два термина в данном случае играют ключевую роль.
Итак, фазное напряжение должно определяться непосредственно между началом и концом фазы. Линейное напряжение измеряют между 2-мя фазами. То есть, между выводами разных фаз.
В этом заключается основное отличие этих двух понятий. И о нем ни в коем случае нельзя забывать. Особенно тем, кто в будущем все-таки планирует устроиться на работу по специальности электрик.
Поскольку фазное и линейное напряжения отличаются на 60%, то появляется возможность при линейном напряжении в 380 вольт, получить 220 вольт фазного напряжения. Именно по этой причине делать разводку сетей достаточно просто.
Необходимость сделать это часто возникает в случае, когда на первых этажах многоквартирных домов компания начинает оборудовать собственные офисы. Ведь тогда напряжения, доступного для рядовых потребителей, оказывается недостаточно.
Соотношение линейного и фазного напряжения
Универсальным и приемлемым соотношением этих двух видов напряжения является такая цепь – 380/220 вольт нулевым проводом.
Если приборам для нормального функционирования требуется напряжение 220 вольт, то их необходимо подсоединить к двум проводам фазного напряжения, которые будут питаться от линейного напряжения.
Следует отметить тот факт, что приборы, которые запитываются от 3-х фазной сети, могут функционировать исключительно в том случае, если они были подсоединены к трем выводам разных фаз.
Важно! Использовать заземление в таком случае вовсе необязательно. Однако, если изоляционный материал, покрывающий провод, будет поврежден, то вероятность удара током возрастет.
Как определить линейное и фазное напряжение
Чтобы правильно определить эти два вида напряжения, нужно вспомнить о некоторых тонкостях.
Ведь зачастую эти два понятия многие попросту путают. И поэтому правильно определить их величину становятся сложно.
Во-первых, линейное напряжение следует определять исключительно между двумя фазами.
Во-вторых, фазное напряжение по определению нужно вычислять непосредственно между фазой и нулем. Поэтому нельзя пытаться определить фазное напряжение между двумя фазами.
Типы соединения
Чтобы запустить генератор, часто используют именно линейное и фазное напряжение. Если говорить о запуске именно трехфазного генератора, то следует отметить один важный факт.
Состоит такой прибор не только из первичных, но и вторичных обмоток. Эти обмотки нужно правильно соединить и для этого существует два самых распространенных способа.
Только благодаря тому, что все обмотки будут правильно соединены, можно добиться определенных улучшений:
- Увеличение мощности передачи – это важнейшая задача, которую нужно решить, но сделать это следует без увеличения напряжения. И сделать это можно благодаря использованию определенных типов соединений.
- Снижение пульсаций напряжения – если в блоках питания наблюдаются постоянные колебания напряжения, это может стать причиной выхода из строя, подключенных к ней приборов. Поэтому устранение данного недочета с помощью разных соединений является первостепенной задачей.
- Уменьшение количества проводов – при подключении к сети нужно минимизировать количество соединений, чтобы улучшить качество работы приборов. Именно по этой причине использование двух упрощенных схем для подключения настолько важно.
Звезда
Сначала рассмотрим данный тип подключения. Чтобы его выполнить, нужно соединить начало всех мотков в одной точке.
Эту точку принято называть нулевой. В некоторых печатных руководствах упоминается другое обозначение – нейтральная точка.
Иногда встречается соединение нулевой точки и нулевым источником питания. И поэтому ошибочно юные и начинающие электрики считают его обязательным. Но это не так, такое соединение могут использовать в некоторых случаях, и оно не является обязательным.
Важно! Если такое соединение присутствует, то систему правильно называть 4-проводной. В том случае, если оно отсутствует, то соединение считается трехпроводным.
Треугольник
Для выполнения соединения используют схему, отличную от той, которая была описана выше. Ведь нужно соединить одну обмотку с другой.
Свое название соединение получило из-за внешнего сходства с треугольником.
Его особенностью является то, что все обмотки соединяются в строгой последовательности. А поскольку общая точка соприкосновения отсутствует, такая система может быть только одного вида, а именно – трехпроводная.
Нюансы выбора типа соединения
В настоящее время оба типа соединения, звезда и треугольник, активно используются. Однако, подобное вовсе не означает, что можно по собственному усмотрению выбрать тот способ, который больше понравится.
Существуют определенные требования и общие рекомендации, следуя которым можно избежать ошибок.
Нужно запомнить, что при линейном напряжении в 220 вольт подключение двигателя по схеме звезда невозможно.
Для такого напряжения идеально подходит схема треугольник.
С другой стороны, если в сети напряжение выше 220 вольт, к примеру 380, то оптимальным вариантом станет использование именно звезды.
Если запомнить это простое правило, удастся в будущем избежать ошибок при подключении генераторов и других приборов.
Фото схем и формул измерения линейного и фазного напряжения

Об авторе: эксперт в области электроники и деревообработки
Задать вопрос