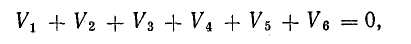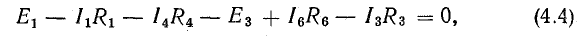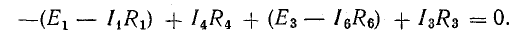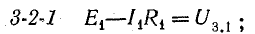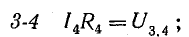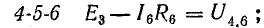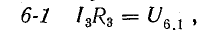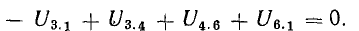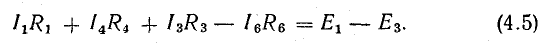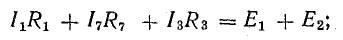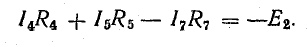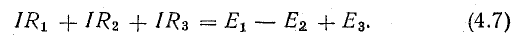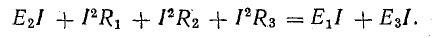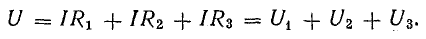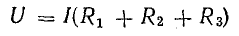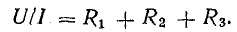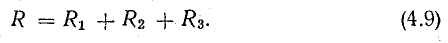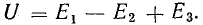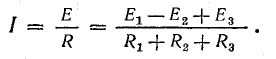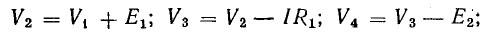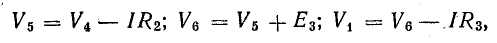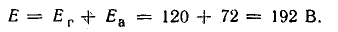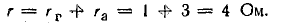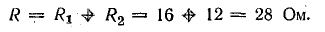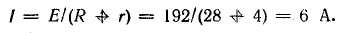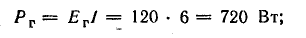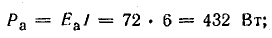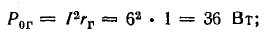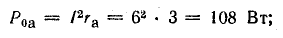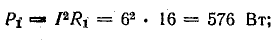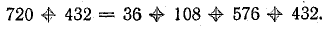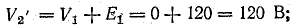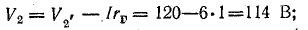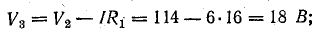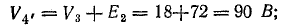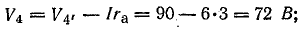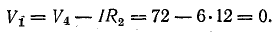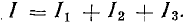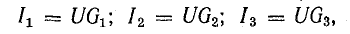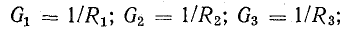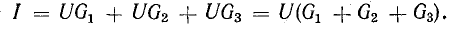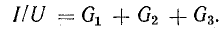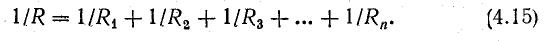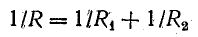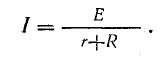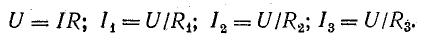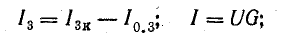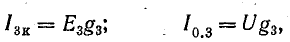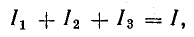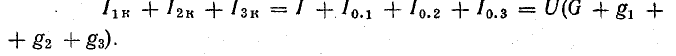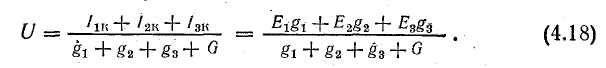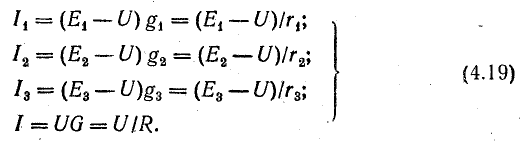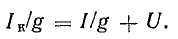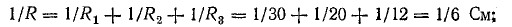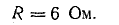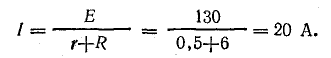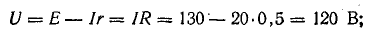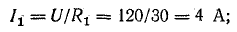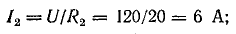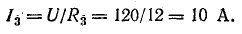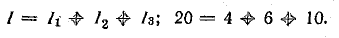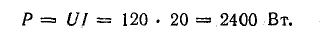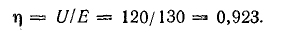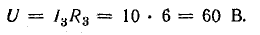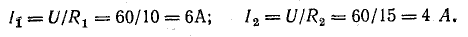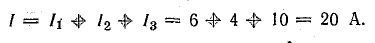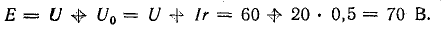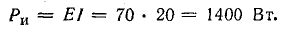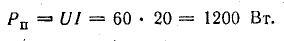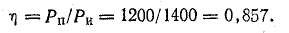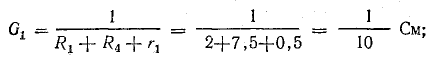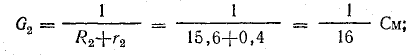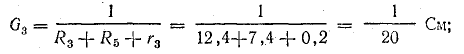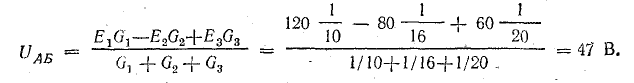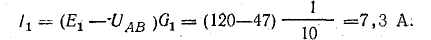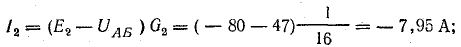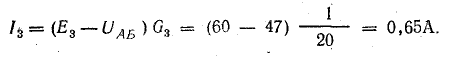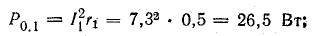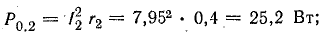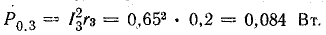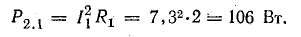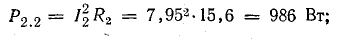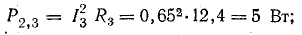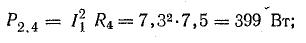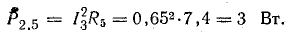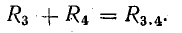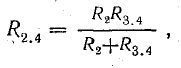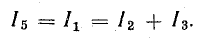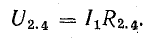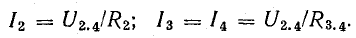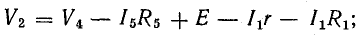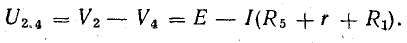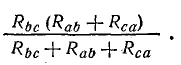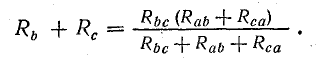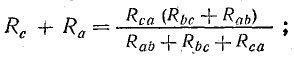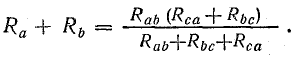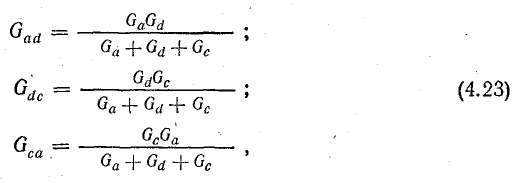Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
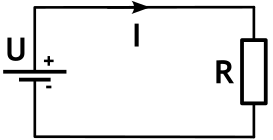
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.
Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I2R, откуда
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.
Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:
Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.
Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.
Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.
При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.
Мультиметром
Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.
Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.
Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.
Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.
Задача 1.
На участке цепи имеются три параллельно включенных резистора (см. рис. 5). Значения сопротивлений резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и на всём участке, если на нем поддерживается постоянное напряжение 100 В.
Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
- I1 = U/R1 =100/5 = 20 А;
- I2 = U/R2 =100/25 ≈ 4 А;
- I3 = U/R3 =100/50 = 2 А.
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:
Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
Ответ:
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Задача 2.
Мощность электрочайника 2 кВт. Чайник работает от городской сети под напряжением 220 В. Сколько электричества потребляет этот электроприбор?
Решение:
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Задача 3.
Вычислить силу тока в цепи, если известно, что сопротивление составляет 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление составляет 1 Ом.
Решение.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
I = 6 В / (5 Ом + 1 Ом) = 1 А.
Ответ: сила тока 1 А.
Задача 4.
Сколько энергии потребляет электроплита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?
Решение:
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U2/R)*t или
A = ((220 В)2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.

{I = dfrac{U}{R}}
На этой странице вы можете рассчитать силу тока, напряжение и сопротивление по закону Ома для участка цепи с помощью удобного калькулятора онлайн
Закон Ома — один из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Он был открыт эмпирическим путем Георгом Омом в 1826 году.
Содержание:
- калькулятор закона Ома
- закон Ома для участка цепи
- формула силы тока
- формула напряжения
- формула сопротивления
- примеры задач
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи I= dfrac{U}{R}
Формула силы тока
Формула позволяет найти силу тока I через напряжение U и сопротивление R по закону Ома для участка цепи.
{I = dfrac{U}{R}}
I — сила тока
U — напряжение
R — сопротивление
Сила тока (I) в проводнике прямо пропорциональна напряжению (U) на его концах и обратно пропорциональна его сопротивлению (R).
Формула напряжения
Формула позволяет найти напряжение U через силу тока I и сопротивление R по закону Ома для участка цепи.
{U = I cdot R}
U — напряжение
I — сила тока
R — сопротивление
Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем.
Формула сопротивления
Формула позволяет найти сопротивление R через силу тока I и напряжение U по закону Ома для участка цепи.
{R = dfrac{U}{I}}
R — сопротивление
U — напряжение
I — сила тока
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него.
Примеры задач на нахождение силы тока, напряжения и сопротивления по закону Ома
Задача 1
Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В.
Решение
Воспользуемся формулой силы тока. Подставим в нее значения напряжения и сопротивления, после чего останется произвести простейший математический расчет.
I = dfrac{U}{R} = dfrac{4}{40} = 0.1 А
Ответ: 0.1 А
На этой странице есть калькулятор, который поможет проверить полученный ответ.
Задача 2
Найдите напряжение на концах нагревательного элемента, если его сопротивление 40 Ом, а сила тока 2А.
Решение
Для решения этой задачи нам пригодится формула напряжения.
U = I cdot R = 2 cdot 40 = 80 В
Ответ: 80 В
Проверим получившийся результат с помощью калькулятора .
Задача 3
Найдите сопротивление спирали, сила тока в которой 0.5 А, а напряжение на ее концах 120 В.
Решение
Чтобы найти сопротивление спирали нам потребуется формула сопротивления.
R = dfrac{U}{I} = dfrac{120}{0.5} = 240 Ом
Ответ: 240 Ом
Проверка .
Формулы, примеры решения задач: ТОЭ | Электрические машины | Высшая математика | Теоретическая механика
- Электрический ток, плотность тока, электрическое напряжение, энергия при протекании тока, мощность электрического тока
- Электрический ток
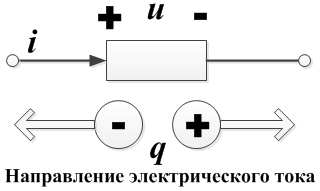
Электрический ток — это явление упорядоченного движения электрических зарядов. За направление электрического тока принимается направление движения положительных зарядов.
Формула электрического тока:
Электрический ток измеряется в амперах. СИ: А.
Электрический ток обозначается латинскими буквами i или I. Символом i(t) обозначается «мгновенное» значение тока, т.е. ток произвольного вида в любой момент времени. В частном случае он может быть постоянным или переменным.
Прописной латинской буквой I обозначается, как правило, постоянное значение тока.
В любом участке неразветвленной электрической цепи протекает одинаковый по величине ток, который прямо пропорционален напряжению на концах участка и обратно пропорционален его сопротивлению. Величина тока определяется по закону Ома:
1) для цепи постоянного тока
2) для цепи переменного тока,
где U — напряжение, В;
R — омическое сопротивление, Ом;
Z — полное сопротивление, Ом.
Омическое сопротивление проводника:
,
где l — длина проводника, м;
s — поперечное сечение, мм2;
ρ — удельное сопротивление, (Ом · мм2) / м.
Зависимость омического сопротивления от температуры:
Rt = R20 [1 + α(t — 20°)],
где R20 — сопротивление при 20°C, Ом;
Rt — сопротивление при t°C, Ом;
α — температурный коэффициент сопротивления.
Полное сопротивление цепи переменного тока:
,
где— активное сопротивление, Ом;
— индуктивное сопротивление, Ом;
— индуктивность, Гн;
— емкостное сопротивление, Ом;
— ёмкость, Ф.
Активное сопротивление больше омического сопротивления R:
,
где— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
При промышленной частоте, для нестальных проводников, принимаюти считают
.
- Плотность тока
Плотность тока (j) — это сила тока, рассчитанная на единицу площади поперечного сечения (s).
Для равномерного распределения плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, формула плотности тока принимает вид:,
где I — сила тока через поперечное сечение проводника площадью s.
СИ: А/м2 - Электрическое напряжение
При протекании тока, как и при всяком перемещении зарядов, происходит процесс преобразования энергии. Электрическое напряжение — количество энергии, которое необходимо затратить на перемещение единицы заряда из одной точки в другую.
Формула электрического напряжения:
Электрическое напряжение обозначается латинской буквой u. Символом u(t) обозначается «мгновенное» значение напряжения, а прописной латинской буквой U обозначается, как правило, постоянное напряжение.
Электрическое напряжение измеряется в вольтах. СИ: В. - Энергия при протекании электрического тока
Формула энергии, при протекании электрического тока:
СИ: Дж - Мощность при протекании электрического тока
Формула мощности, при протекании электрического тока:
СИ: Вт.
- Электрическая цепь
- Электрическая цепь — это совокупность устройств, предназначенных для протекания по ним электрического тока.
Эти устройства называются элементами цепи. - Источники электрической энергии — устройства, преобразующие различные виды энергии, например механическую или химическую, в энергию электрического тока.
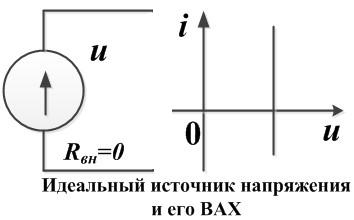
- Идеальный источник напряжения — источник, напряжение на зажимах которого не зависит от величины протекающего через него тока.
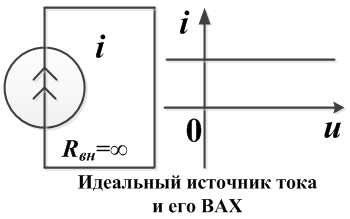
Внутреннее сопротивление идеального источника напряжения можно условно принять равным нулю. - Идеальный источник тока — источник, величина протекающего тока через который не зависит от напряжения на его зажимах.
Внутреннее сопротивление такого источника можно условно принять равным бесконечности. - Приемник — это устройство, потребляющее энергию или преобразующее электрическую энергию в другие виды энергии.
- Двухполюсник — это цепь, имеющая два зажима для подключения (полюса).
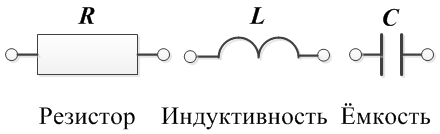
- Идеальный R-элемент (резистивный элемент, резистор) — это такой пассивный элемент цепи, в котором происходит необратимый процесс преобразования электрической энергии в тепловую.
Основной параметр резистора — это его сопротивление.
Сопротивление измеряется в омах. СИ: Ом
Проводимость — это обратная величина по отношению к сопротивлению..
Измеряется проводимость в сименсах. СИ: См.
Формула мощности R-элемента:.
Формула энергии R-элемента:
.
- Идеальный С-элемент (емкостной элемент, или конденсатор) — это такой пассивный элемент цепи, в котором происходит процесс преобразования энергии электрического тока в энергию электрического поля и наоборот. В идеальном C-элементе потери энергии отсутствуют.
Формула ёмкости:
. Примеры: задача 1, задача 2.
Ток в ёмкости:
Напряжения на ёмкости:
.
Закон коммутации для емкостного элемента. При токе конечной амплитуды заряд на C-элементе не может измениться скачком:.
.
При неизменной ёмкости, напряжение на емкостном элементе не может измениться скачком:.
Мощность C-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия C-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Емкость измеряется в фарадах. СИ: Ф. - Идеальный L-элемент (индуктивный элемент или катушка индуктивности) — это такой пассивный элемент цени, в котором происходит процесс преобразования энергии электрического тока в энергию магнитного поля и наоборот. В идеальном L-элементе потери энергии отсутствуют.
Для линейного L-элемента формула индуктивности (L) имеет вид:
,
где— потокосцепление.
Индуктивность обозначается буквойи играет роль коэффициента пропорциональности между потоком
и током
.
Напряжение на индуктивном элементе:
.
Ток в индуктивном элементе:
.
Закон коммутации для индуктивного элемента. При напряжении конечной амплитуды, потокосцепление не может измениться скачком:.
.
При неизменной индуктивности ток в индуктивном элементе не может измениться скачком:.
Мощность L-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия L-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Индуктивность измеряется в генри. СИ: Гн
Пример: задача 3. - R, L, C — основные пассивные двухполюсные элементы электрических цепей.
- Основные законы электрических цепей
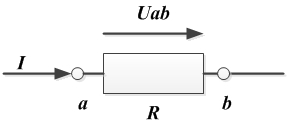
- Закон Ома для участка цепи, не содержащего источник ЭДС.
Закон Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке.
Применительно к данному рисунку, математическое выражение закона Ома имеет вид:
, или
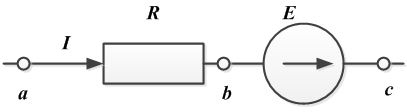
Формулируется это равенство так: при неизменном сопротивлении проводника напряжение на нем пропорционально току в проводнике. - Закон Ома для участка цепи, содержащего источник ЭДС
Для схемы
.
Для схемы
.
В общем случае
.
- Закон Джоуля-Ленца. Энергия, выделяемая на сопротивлении R при протекании по нему тока I, пропорциональна произведению квадрата силы тока и величины сопротивления:
- Законы Кирхгофа.
Топология (строение) цепи.
Электрическая схема — графическое изображение электрической цепи.
Ветвь ‐ участок цепи, содержащий один или несколько последовательно соединенных элементов и заключенный между двумя узлами.
Узел ‐ точка цепи, где сходится не менее трех ветвей. Узлы нумеруют произвольно, как правило, арабской цифрой. На схеме узел может быть обозначен точкой, а может и не быть обозначен. Как правило, не обозначают те узлы, расположение которых очевидно (т‐образные соединения). Если пересекающиеся ветви образуют узел, то он обозначается точкой. Если в месте пересечения ветвей точки нет, то и узла нет (провода лежат друг на друге).
Контур – замкнутый путь, проходящий по нескольким ветвям. Контуры независимы, если отличаются хотя бы одной ветвью. Контура обозначают стрелкой с указанным направлением обхода и римской цифрой. Направление обхода выбирают произвольно. Независимых контуров в схеме может быть много, при этом не все эти контура необходимы для составления достаточного для решения задачи количества уравнений.
Первый закон Кирхгофа:
1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
;
2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
. Пример 1. Первый закон Кирхгофа.
Второй закон Кирхгофа:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
. Пример 2. Второй закон Кирхгофа.
- Матричная форма записи уравнений Кирхгофа:
,
где А, В — квадратные матрицы коэффициентов при токах и напряжениях порядка p х p (p — число ветвей схемы; q — число узлов схемы);
I, E — матрицы-столбцы неизвестных токов и заданных ЭДС
Элементами матрицы А являются коэффициенты при токах в левой части уравнений, составленных по первому и второму законам Кирхгофа. Первыестроки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
Элементы следующихстрок матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строки матрицы имеют нулевые элементы, так как ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные
строки содержат элементы +1, -1 в зависимости от того, с каким знаком входит ЭДС в уравнение, и 0, если ЭДС в уравнения не входит.
Общее решение уравнений, составленных по законам Кирхгофа:
,
где— матрица проводимостей.
.
Токи в каждой ветви:
;
;
.
- Режимы работы электрических цепей
- Номинальный режим работы элемента электрической цепи — это режим, при котором он работает с номинальными параметрами.
- Согласованный режим — это режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Такое значение получается при определенном соотношении (согласовании) параметров электрической цепи.
- Режим холостого хода — это такой режим, при котором через источник или приемник не протекает электрический ток. При этом источник не отдает энергию во внешнюю часть цепи, а приемник не потребляет ее. Для двигателя это будет режим без механической нагрузки навалу.
- Режим короткого замыкания — это режим, возникающий при соединении между собой разноименных зажимов источника или пассивного элемента, а также участка электрической цепи, находящегося под напряжением.
- Электрические цепи постоянного тока
- Если ток постоянный, то отсутствует явление самоиндукции и напряжение на катушке индуктивности равно нулю:
, так как
- Постоянный ток через емкость не проходит.
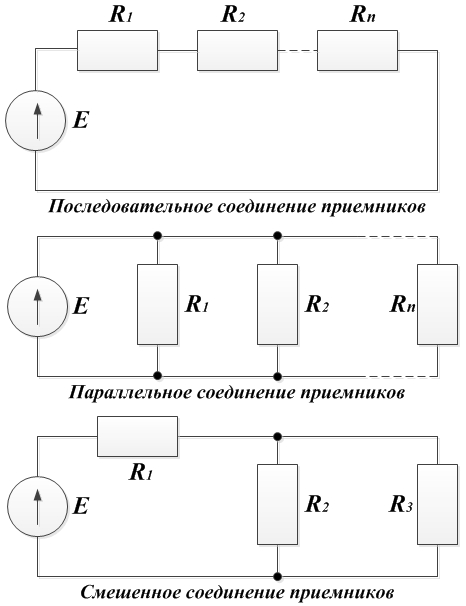
- Простая цепь постоянного тока — это цепь с одним источником при последовательном, параллельном или смешанном соединение приемников.
При последовательном соединении приемников:
I×Rэкв;
Rэкв=ΣRi.
При параллельном соединении приемников напряжение на всех приемниках одинаково.
По закону Ома токи в каждой ветви:
.
По первому закону Кирхгофа общий ток:
E×Gэкв;
Gэкв=G1+G2+…+Gn; Rэкв=1/Gэкв.
При смешанном соединении:
Rэкв=.
- Метод контурных токов.
Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений.
Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура.
Контурные токи, в отличие от токов ветвей, имеют следующие индексы:или
Уравнения составляют по второму закону Кирхгофа для контурных токов.
Токи ветвей выражают через контурные токи по первому закону Кирхгофа.
Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа:.
Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура, имеет следующие индексы:или
Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входят в уравнение со знаком плюс, если направления ЭДС и направление тока контура совпадают. Пример 3. Метод контурных токов. - Метод узловых потенциалов.
Метод основан на применении первого закона Кирхгофа и позволяет сократить число решаемых уравнений при нахождении неизвестных токов до. При составлении уравнений потенциал одного из узлов схемы принимают равным нулю, а токи ветвей выражают через неизвестные потенциалы остальных
узлов схемы и для них записывают уравнения по первому закону Кирхгофа. Решение системы
уравнений позволяет определить неизвестные потенциалы, а через них найти токи ветвей.
Приследует отдавать предпочтение методу узловых потенциалов.
- Формула двух узлов:
.
Пример 4. Метод узловых потенциалов. - Метод пропорциональных величии.
Метод применяют для нахождения неизвестных токов при цепочечном соединении резистивных элементов в электрических цепях с одним источником. Токи и напряжения, а также и известную ЭДС цепи выражают через ток самой удаленной от источника ветви. Задача сводится к решению одного уравнения с одним неизвестным. - Баланс мощностей
На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии:
.
— сумма мощностей, развиваемых источниками;
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
Баланс мощностей составляют, чтобы проверить правильность найденного решения. При этом сравнивают мощность, внесенную в цепь источниками энергии с мощностью, затрачиваемой потребителями.
Формула мощности для одного резистора:
Суммарная мощность потребителей:
PП=
Мощность источников:
Pист = PE + PJ,
где PE = ±EI — мощность источника ЭДС (определятся умножением его ЭДС на ток, протекающий в данной ветви. Ток берут со знаком, полученным в результате расчета. Минус перед произведением ставят, если направление тока и ЭДС не совпадают на схеме);
PJ = JUJ — мощность источника тока (определятся умножением тока источника на падение напряжения на нем).
Для определения UJ выбирают любой контур, который включал бы в себя источник тока. Обозначают падение UJ на схеме против тока источника, и записывают контурное уравнение. Все величины, кроме UJ, в данном уравнении уже известны, что позволяет рассчитать падение напряжения UJ.
Сравнение мощностей: Pист = PП. Если равенство соблюдено, значит, баланс сошелся и расчет токов верен. - Алгоритм расчета цепи по законам Кирхгофа
- Топология цепи.
- Определяем общее число ветвей p*.
- Определяем число ветвей с источниками тока pит. Токи в данных ветвях считаем известными и равными токам источников.
- Определяем число ветвей с неизвестными токами: p*‐pит
- Находим количество узлов q.
- Находим число уравнений, составляемых по первому закону Кирхгофа:
.
- Находим число уравнений, составляемых по второму закону Кирхгофа:
.
- Произвольно наносим на схему номера и направления неизвестных токов.
- Произвольно наносим на схему номера узлов.
- Составляем узловые уравнения для произвольно выбранных узлов (по первому закону).
- Обозначаем на схеме контура и выбираем направления их обхода.
- Количество обозначаемых контуров равно количеству уравнений, составляемых по второму закону Кирхгофа. При этом ни один из контуров не должен включать в себя ветвь с источником тока.
- Составляем контурные уравнения для выбранных контуров (по второму закону).
- Объединяем составленные уравнения в систему. Известные величины переносим в правую часть уравнений. Коэффициенты при искомых токах вносим в матрицу А (левые части уравнений)(о матрицах читаем здесь). Заполняем матрицу F, занося в нее правые части уравнений.
- Решаем полученную систему уравнений (примеры решения систем уравнений).
- Проверяем правильность решения составлением баланса мощностей.
Пример: задача 4.
- Электрические цепи переменного тока
- Электрическая цепь синусоидального тока — это электрическая цепь, в которой ЭДС, напряжения и и токи, изменяющиеся по синусоидальному закону:
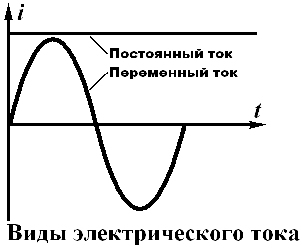
- Переменный ток — это ток, периодически меняющийся по величине и направлению и характеризующийся амплитудой, периодом, частотой и фазой.
- Амплитуда переменного тока — это наибольшее значение, положительное или отрицательное, принимаемое переменным током.
- Период — это время, в течение которого происходит полное колебание тока в проводнике.
- Частота — это величина, обратная периоду.
- Фаза — это угол
или
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
- Периодический режим:
. К такому режиму может быть отнесен и синусоидальный:
,
где— амплитуда;
— начальная фаза;
— угловая скорость вращения ротора генератора.
При f = 50 Гцрад/с.
- Синусоидальный ток — это ток изменяющийся во времени по синусоидальному закону:
.
- Среднее значение синусоидального тока (ЭДС, напряжение), формула:
,
то есть среднее значение синусоидального тока составляетот амплитудного. Аналогично,
.
- Действующее значение синусоидального тока (ЭДС, напряжение), формула:
. Аналогично,
.
- Количество теплоты, выделенное за один период синусоидальным током, формула:
.
Действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты,что и синусоидальный ток.
=R×Iпост2×T или Iпост=I=
- Коэффициент амплитуды синусоидального тока (κa) — это отношение амплитуды синусоидального тока к действующему значению синусоидального тока:
.
- Коэффициент формы синусоидального тока (κф) — это отношение действующего значения синусоидального тока к среднему за пол периода значению синусоидального тока:
κф=.
Для несинусоидальных периодических токов κa≠, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
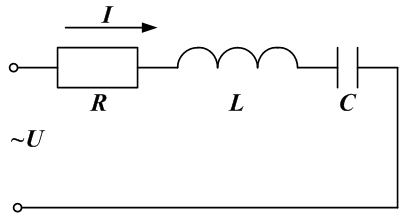
- Резонансные явления в электрических цепях
- Резонанс напряжений.
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю.
Режим резонанса может быть получен при изменении частоты ω питающего напряжения или изменением параметров L и C.
При последовательном соединении возникает резонанс напряжения.
Ток в схеме равен:
При совпадении вектора тока с вектором напряжения по фазе:
где— резонансная частота напряжения, определяемая из условия
Тогда
Волновое или характеристическое сопротивление последовательного контура:
Добротность контура — это отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса:
Добротность контура представляет собой коэффициент усиления по напряжению:
ULрез=IрезXрез=
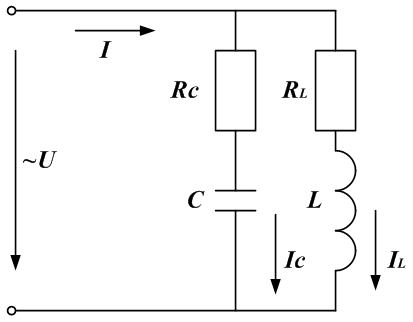
В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции. - Резонанс токов.
Резонанс токов может возникнуть при параллельном соединении реактивных элементов в цепях переменного тока. В этом случае:где
тогда
При резонансной частоте реактивные составляющие проводимости могут сравниться по модулю и суммарная проводимость будет минимальной. При этом общее сопротивление становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость:.
При g << bL ток в ветви с индуктивностью значительно больше общего тока, поэтому такое явление называется резонансом токов.
Резонансная частота:
ω*=
Из формулы следует:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если RL и RC больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс не возможен;
3) если RL = RC = ρ, то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при RL = RC << ρ резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам при резонансе напряжений.
Реактивная мощность при резонансе токов равна нулю. Подробно, реактивная мощность рассмотрена здесь.
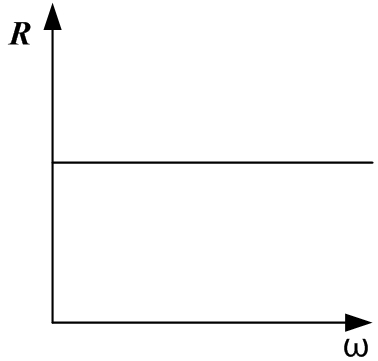
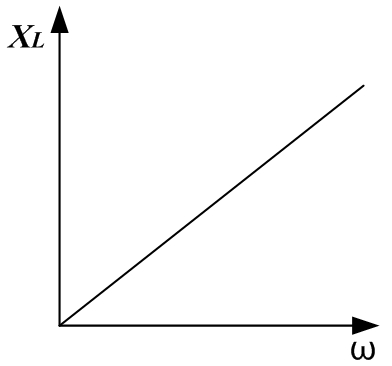
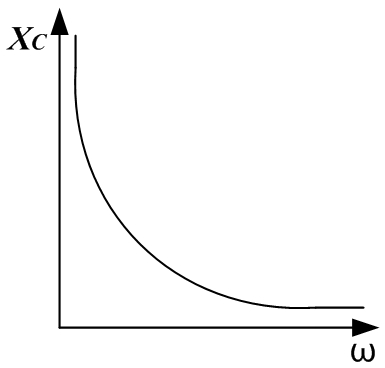
Идеальное активное сопротивление не зависит от частоты, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:

Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:
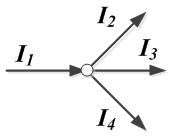
В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:
Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре
или
В этом уравнении напряжения ветвей
поэтому
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:
Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1
для 3-4-6-3
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
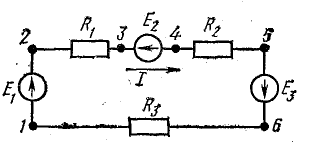
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
Ток в цепи
При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.
Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть:
Получим уравнение баланса мощности — для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
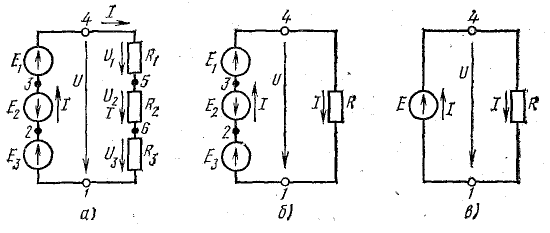
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].
Вынеся I за скобку, получим
или
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:
т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)
и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле
где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в),
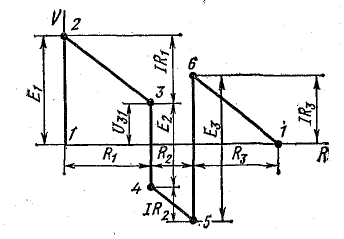
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2.
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
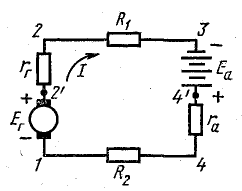
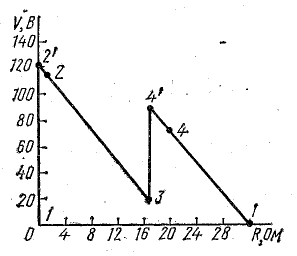
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи
Эквивалентное внутреннее сопротивление
Эквивалентное сопротивление нагрузки
Ток в цепи
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора
аккумуляторной батареи
потерь внутри генератора
потерь внутри аккумуляторной батареи
потребления в резисторе R1
потребления в резисторе R2
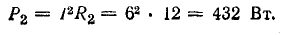
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
Потенциальная диаграмма показана на рис. 4.5.
Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.
Рис. 4.7. Преобразование схемы с параллельным соединением приемников
Параллельное соединение пассивных элементов
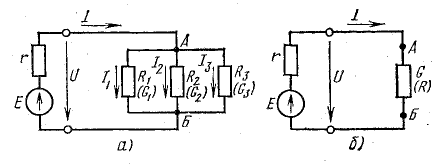
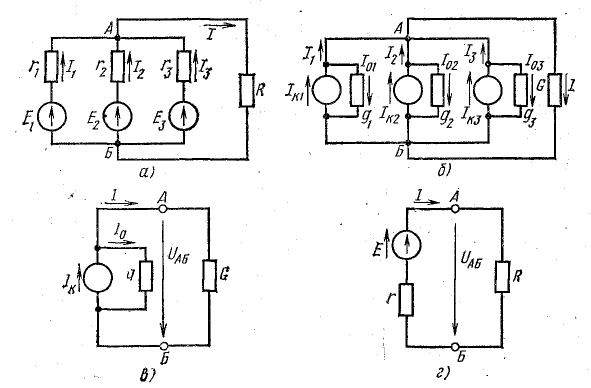
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа:
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:
где
Разделим это уравнение на U:
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:
Этот вывод можно распространить на любое число n параллельно соединенных приемников:
При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле
или
Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:
Параллельное соединение источников энергии
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).
Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А
или
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
и внутренней проводимостью
Для схемы рис. 4.8, в
Напряжение между узлами
Токи в ветвях можно определить по следующим формулам:
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников:
Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
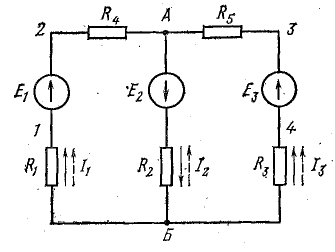
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид
Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:
Ток в неразветвленной части цепи
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:
Проверим правильность определения токов по уравнению (4.1):
Мощность передачи энергии приемникам
К. п. д. источника
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:
Ток в неразветвленной части цепи
Э. д. с. источника
Мощность источника
Мощность потребления энергии приемниками
К. п. д. источника
Задача 4.12.
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:
Токи в ветвях:
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников:
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
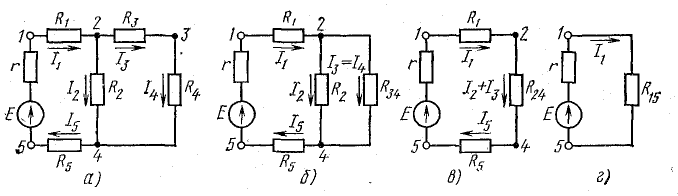
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
и получить более простую схему (рис. 4.10, в).
Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что
Кроме того, напряжение между точками 2 и 4
Зная это напряжение, легко определить токи I2 и I3 = I4:
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5:
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
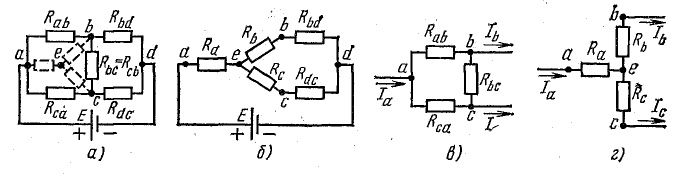
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.
Полагая Ib =0, а затем Ic = 0, получим:
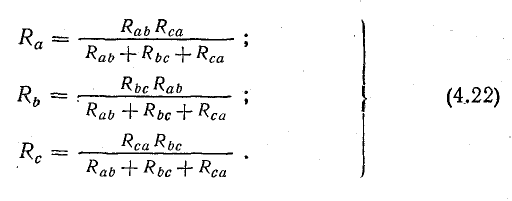
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:
Преобразование звезды сопротивлений в эквивалентный треугольник
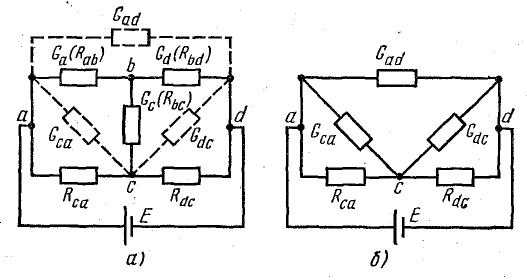
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток









 ,
, ,
, ,
, — активное сопротивление, Ом;
— активное сопротивление, Ом; — индуктивное сопротивление, Ом;
— индуктивное сопротивление, Ом; — индуктивность, Гн;
— индуктивность, Гн; — емкостное сопротивление, Ом;
— емкостное сопротивление, Ом; — ёмкость, Ф.
— ёмкость, Ф. ,
, — коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника. и считают
и считают  .
. .
. ,
,



 .
. .
. .
. . Примеры: задача 1, задача 2.
. Примеры: задача 1, задача 2.
 .
. .
. .
. .
. .
. , или
, или .
. , энергия равна 0, то
, энергия равна 0, то
 ,
, — потокосцепление.
— потокосцепление. .
. .
. .
. .
. .
. .
.
 , или
, или 
 .
.
 .
. .
.
 ;
;
 . Пример 1. Первый закон Кирхгофа.
. Пример 1. Первый закон Кирхгофа.
 . Пример 2. Второй закон Кирхгофа.
. Пример 2. Второй закон Кирхгофа. ,
, строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение. строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые  ,
, — матрица проводимостей.
— матрица проводимостей. .
. ;
; ;
;
 .
. , так как
, так как 
 I×Rэкв;
I×Rэкв; .
. E×Gэкв;
E×Gэкв; .
. или
или 
 .
. или
или 
 следует отдавать предпочтение методу узловых потенциалов.
следует отдавать предпочтение методу узловых потенциалов. .
. .
. — сумма мощностей, развиваемых источниками;
— сумма мощностей, развиваемых источниками; — сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.

 .
.
 или
или  , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной. . К такому режиму может быть отнесен и синусоидальный:
. К такому режиму может быть отнесен и синусоидальный: ,
, — амплитуда;
— амплитуда; — начальная фаза;
— начальная фаза; — угловая скорость вращения ротора генератора.
— угловая скорость вращения ротора генератора. рад/с.
рад/с. .
. ,
, от амплитудного. Аналогично,
от амплитудного. Аналогично, .
. . Аналогично,
. Аналогично, .
. .
. =R×Iпост2×T или Iпост=I=
=R×Iпост2×T или Iпост=I=
 .
. .
. , κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального. .
.




 — резонансная частота напряжения, определяемая из условия
— резонансная частота напряжения, определяемая из условия




 где
где


 .
.