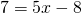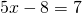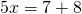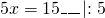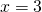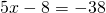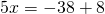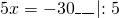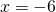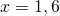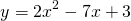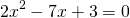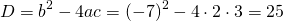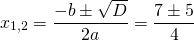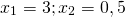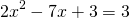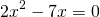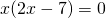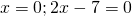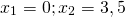Как найти игрик при икс 5

Примеры функций

Простой пример функции

y = x + 5

Где здесь функция?

Игрек – это функция, икс – это аргумент функции, математический закон в данном примере состоит в том, что к иксу надо прибавить пять.

Как найти значение функции? Надо вместо аргумента, т.е. икса, подставить его значение и вычислить чему равен игрек.

Игрек и есть значение функции.

Итак, пусть икс = 5. Найдем значение функции, т.е. значение игрека: 5 + 5 = 10.

Значит значение функции при икс = 5 будет 10.

Пример функции.

Площадь квадрата равна квадрату стороны:

S = a²

Где здесь функция? S – это функция, «a» – это аргумент функции, математический закон в данном примере состоит в том, что «a» нужно возвести в квадрат.

Как найти значение функции?

Надо вместо аргумента, т.е. “а” подставить его значение и вычислить чему равена площадь S. S и есть значение функции.

Итак, пусть a = 5. Найдем значение функции, т.е. значение S. Имеем 5 * 5 = 25. Значит значение функции при a = 5 будет 25.

Составим небольшую таблицу соответствия значений “а” значениям площадей S:

Площадь S	0	1	4	9	16
Сторона a	0	1	2	3	4

Используя математический закон, в данном случае это возведение в квадрат, мы каждому значению длины стороны а поставили в соответствие значение площади S.

В нашем выражении

S = a²

S – это зависимая переменная или функция, ведь её значение зависит от значения длины стороны а;
длина стороны а – это независимая переменная или аргумент функции.

• Функция
• График функции
• Построитель графиков
• Виды функций

• Понятие функции
• Примеры функций
• Определение функции
• Аргумент функции
• Значение функции
• Область определения функции
• Множество значений функции
• Сложная функция
• Четные функции
• Нечетные функции
• Ни четные и ни нечетные функции

Что такое функция? Что такое функция математическая? Рассмотрим простой пример функции. Пусть дано уравнение:

y = 2x

Если вместо x подставить 1, то y будет равен 2. Вычислив это, мы иксу, равному 1, поставили в соответствие y, равный 2. Соответствие определяется математическим законом. И каков здесь закон? В данном примере математический закон таков: два умножить на икс, т.е. любое значение икс надо умножить на два. Если икс равен 2, то какое значение игрека ему будет соотвестствовать? Применим к иксу наш математический закон, т.е. умножим его на 2 и получим: y = 4.

И где же здесь функция? Функцией здесь является y. Игрек – это функция от икс. Если мы изменим икс, изменится и игрек, игрек зависит от икс, игрек есть функция от икс.

Итак, игрек здесь является функцией от икс.

Икс называют аргументом или независимой переменной. Значение игрека зависит от икс, поэтому игрек называют зависимой переменной или функцией от икс.

Простой пример:

y = x + 5

Где здесь функция? Игрек – это функция, икс – это аргумент функции, математический закон в данном примере состоит в том, что к иксу надо прибавить пять. Как найти значение функции? Надо вместо аргумента, т.е. икса, подставить его значение и вычислить чему равен игрек. Игрек и есть значение функции. Итак, пусть икс = 5. Найдем значение функции, т.е. значение игрека: 5 + 5 = 10. Значит значение функции при икс = 5 будет 10.

Другой пример. Площадь квадрата равна квадрату стороны:

S = a²

Где здесь функция? S – это функция, «a» – это аргумент функции, математический закон в данном примере состоит в том, что «a» нужно возвести в квадрат. Как найти значение функции? Надо вместо аргумента, т.е. “а” подставить его значение и вычислить чему равена площадь S. S и есть значение функции. Итак, пусть a = 5. Найдем значение функции, т.е. значение S. Имеем 5 * 5 = 25. Значит значение функции при a = 5 будет 25.

Составим небольшую таблицу соответствия значений “а” значениям площадей S:

Площадь S	0	1	4	9	16
Сторона a	0	1	2	3	4

Используя математический закон, в данном случае это возведение в квадрат, мы каждому значению длины стороны а поставили в соответствие значение площади S.

В нашем выражении

S = a²

S – это зависимая переменная или функция, ведь её значение зависит от значения длины стороны а;
длина стороны а – это независимая переменная или аргумент функции.

Определение функции: пусть каждому числу икс из множества А поставлено в соответствие одно число игрек, тогда игрек есть функция от икс.

Главное слово в определении функции – это “соответствие”. Если мы определили это соответствие, то определили и функцию.

Когда говорят о функции обычно пишут выражение:

y = f(x)

здесь y – это функция или зависимая переменная,
x – это аргумент функции или независимая переменная,
f – это обозначение математического закона, по которому каждому значению икс ставится в соответствие одно значение игрека.

Примеры функций смотрите выше.

Вот пример функции:

y = 2x – 1

икс в данном примере называется аргументом функции или независимой перемнной.

А где аргумент в такой функции:

S = 20 / t

здесь аргумент – это t. А функция – это S.

Примеры функций и их аргументов смотрите выше.

Значение функции – это то, чему равна функция. Пример. Пусть дана функция:

y = 5x

Функцией здесь является игрек. Чтоб найти значение функции, т.е. значение игрека, нужно подставить допустимое значение аргумента x. Так и сделаем. Пусть икс равен 4, тогда

y = 5 * 4

откуда получаем, что значение функции при икс = 4 будет равно 20-ти.

Область определения функции – это множество допустимых значений аргумента функции. Как это понимать? Вот пример функции:

y = 2x

Чтоб ответить на вопрос какова здесь область определения функции надо понять при каких значениях аргумента икс эта функция имеет смысл. И при каких? При любых. Значит область определения данной функции является вся числовая прямая от минус бесконечности до плюс бесконечности.

Вот другой пример функции:

y = 2/x

при каких значениях аргумента икс эта функция имеет смысл? При любых, кроме нуля. Ведь на ноль делить нельзя. Итак, в для этой функции областью определения является вся числовая прямая, кроме нуля.

Итак, область определения функции – это множество допустимых значений аргумента функции.

Рассмотрим простые примеры, как находить область определения функции.

Найдем область определения функции

y = 2 / (x + 2)

Область определения функции — это множество значений аргумента, при которых функция имеет смысл. В данном примере область определения функции составляют все числа, кроме тех, при которых знаменатель равен нулю. Ведь на ноль делить нельзя. Значит мы должны найти значения икс, при которых знаменатель обратится в ноль и исключить их из области определения функции. Для решения этой задачи приравняем знаменатель к нулю:

x + 2 = 0

Решим это уравнение:

x = -2

Итак, при x = -2 знаменатель будет равен нулю. На ноль делить нельзя, а значит при этом значении икс функция теряет смысл. Теперь мы можем найти область определения функции

y = 2 / (x + 2)

Областью определения функции является вся числовая прямая, кроме числа -2.

Ещё пример. Найти область определения функции

y = 2 / (4x² — 4x +1)

Мы уже знаем, как находить область определения функции: надо указать значения аргумента, при которых она имеет смысл. Здесь перед нами дробное выражение. Знаменатель не должен быть равен нулю. Значит, область определения функции в данном случае — это все числа, кроме тех, которые обращают знаменатель в ноль. Как найти такие числа? Приравнять знаменатель нулю:

4x² — 4x +1 = 0

и решить это квадратное уравнение. Решаем и находим,что корень уравнения x = 0,5. Теперь можно указать область определения функции — это вся числовая прямая, кроме числа 0,5. А что значит указать область определения функции? Это значит указать все значения аргумента (т.е. икса), при которых функция имеет смысл. В нашем случае это все числа, кроме 0,5.

Множество значений функции – это все значения, котороые принимает функция на своей области определения. Рассмотрим функцию:

y = 2x

Множество значений функции в данном случае есть вся числоая прямая.

Другой пример функции:

y = x²

Множество значений функции в данном случае есть интервал от нуля до плюс бесконечности, ведь любое число в квадрате даёт положительное число или ноль.

Чем множество значений функции отличается от области значений функции? Ничем.

Сложная функция. Что такое сложная функция? Это когда одна функция находится внутри другой функции, т.е. аргументом функции является другая функция. Пример сложной функции:

y = (x + 2)⁵

выражение x + 2 – это функция. Но эта функция в нашем примере возводится в 5-ю степень, т.е. над функцией есть ещё одна функция. Чтоб увидеть вот эту внешнюю функцию обозначим x + 2 через t, получаем:

y = t⁵

вот так выглядит внешняя функция. Но t само является функцией, т.е. у нас функция оказалась под знаком другой функции.

Сложную функцию обычно представляют так:

y = g(f(x))

здесь икс находится под знаком функции f, а функция f находится под знаком функции g. Одна функция оказалась внутри другой, стала аргументом другой функции, это и есть сложная функция.

Итак, если аргументом функции является другая функция, то мы имеем дело со сложной функцией.

График функции. Как построить график функции? Построение графиков функций обычно начинают с заполнения таблицы, в первой строке который укажем значения функции, а во второй – значения аргумента. Рассмотрим простой пример построения графика функции

y = 2x

Чертим таблицу, в нижней строке указываем значения аргумента функции, т.е. “х”, а в верхней строке укажим соответствующие значения функции, т.е. “y”. Пример: икс равно -2, тогда

y = 2 * (-2) = -4

Y	-4	0	2	4	6
X	-2	0	1	2	3

Таблица готова. Теперь чертим прямоугольную систему координат и найдём на ней точки, соответствуюшие найденым парам координат. Пример: найдём точку с координатами x = -2; y = -4:

Найдём положение остальных точек и построим график по этим точкам:

Конечно, этот график можно было построить и по двум точкам, ведь прямая определяется двумя точками.

Если для функции f(x) выполняется равенство:

f(x) = f(-x)

то такая функция называется четной.

График четной функции симметричен относительно оси ординат. Пример функция y = x². Это — парабола:

Если для функции f(x) выполняется равенство:

f(-x) = -f(x)

то такая функция называется нечетной.

График нечетной функции симметричен относительно начала координат. Пример функция y = x³. Это — кубическая парабола:

Если даже для одного значения х функции y = f(x) не выполняется условие четности функции и даже для одного значения х функции y = f(x) не выполняется условие нечетности функции, то данная функция не является четной и не является нечетной.

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.

Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.

1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.

Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):

Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):

Обе части уравнения делим на число, стоящее перед иксом:

2) При каком значении аргумента значение функции

Решаем квадратное уравнение.

При y=0 x=3 и x=0,5.

Это — неполное квадратное уравнение. Общий множитель x выносим за скобки

При y=3 x=0 и x=3,5.

Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.

В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.

Рассмотрим, как по данному графику функции найти y по x.

1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.

Аргумент — это x, функция — y.

Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.

Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.

От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).

Следовательно, при x=1 y=2.

Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.

Получаем, что при x=3 y=4.

Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.

При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.

Записываем: при x=-1 y=0.

При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.

2) На рисунке 2 изображен график функции y=f(x).

Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.

Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.

При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.

Пишем: при x=1 y=2.

При x равном -1 и -5 идем сначала вверх, затем — вправо.

При иксах равных 3; 5 и 7 идём вниз и влево.

Обратите внимание: различным значениям икса может соответствовать одно значение y:

Дана следующая функция y=f(x) :
y = 2x – 10, если x > 0
y = 0, если x = 0
y = 2 * |x| – 1, если x

Требуется найти значение функции по переданному x .

1. Получить с клавиатуры значение x .
2. Если x больше 0, то вычислить выражение 2*x-10 , результат присвоить переменной y .

1. Иначе если x равен 0, то присвоить y значение 0.

1. Иначе присвоить y результат выражения 2*|x|-1 .

Вывести значение y на экран.

var x , y : integer ;
begin
readln ( x ) ;
if x > 0 then y : = 2 * x – 10
else
if x = 0 then y : = 0
else y : = 2 * abs ( x ) – 1 ;

writeln ( y ) ;
end .

main ( ) <
int x , y ;
scanf ( «%d» , & x ) ;
if ( x > 0 ) y = 2 * x – 10 ;
else
if ( x == 0 ) y = 0 ;
else
y = 2 * abs ( x ) – 1 ;

printf ( «%d
» , y ) ;
>

x = input ( )
x = int ( x )

if x > 0 :
y = 2 *x – 10
elif x == 0 :
y = 0
else :
y = 2 * abs ( x ) – 1

В КуМир функция взятия модуля от числа возвращает вещественное значение. Поэтому используется функция int(), чтобы привести к целому, иначе присвоение невозможно.

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

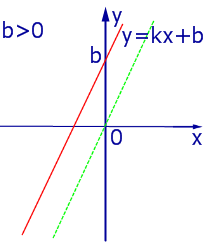
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

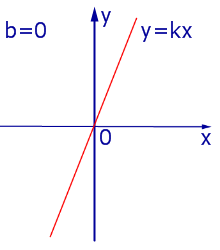
b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

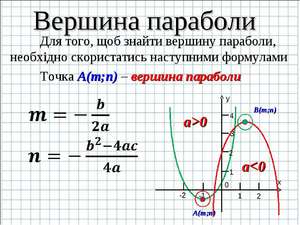
Как найти вершину параболы: три формулы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

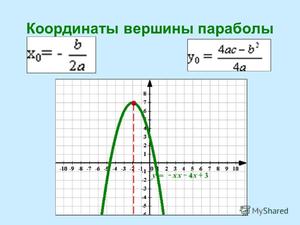
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x 2 –8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x 2 –6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b 2 –4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 — первый корень;
• 5 — второй корень.

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

Прямые на координатной плоскости

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

Рис.1

Рис.2

Рис.3

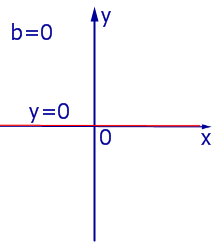
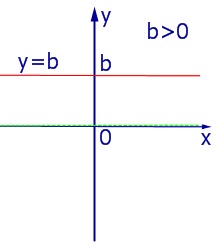
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

Рис.4

Рис.5

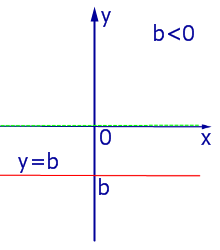Рис.6

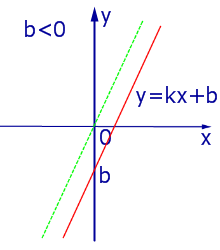
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b₁ и y = kx + b₂ ,

имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны .

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).

Рис.10

Рис.11

Рис.12

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат

Прямые, параллельные оси Oy , задаются формулой

где c – произвольное число, и изображены на рис. 13, 14, 15.

Рис.13

Рис.14

Рис.15

Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

что и требовалось.

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2 . При любом значении r₁ , не совпадающем с r прямая линия, заданная уравнением

параллельна прямой, заданной уравнением (4) .

Замечание 3 . При любом значении r₂ прямая линия, заданная уравнением

перпендикулярна прямой, заданной уравнением (4) .

Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

1. параллельной к прямой
2. перпендикулярной к прямой (8).

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

Итак, уравнение прямой, параллельной к прямой

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство

источники:

http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly

http://www.resolventa.ru/spr/algebra/degree1.htm