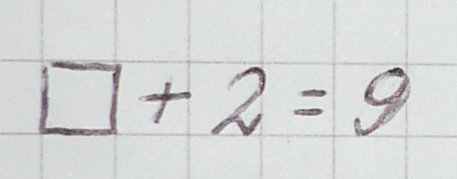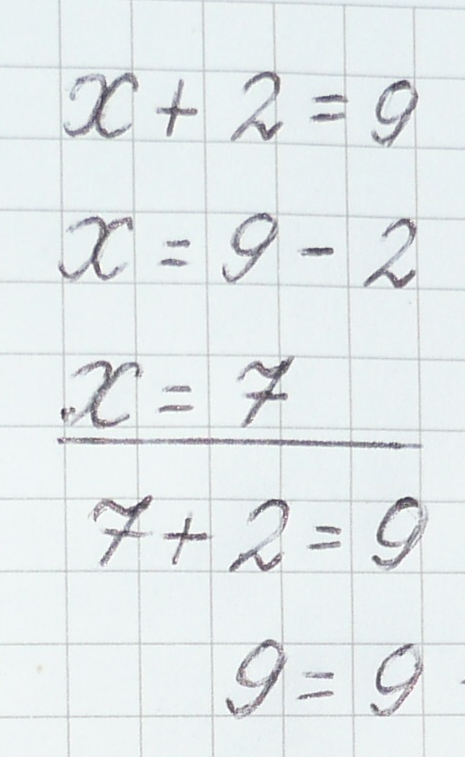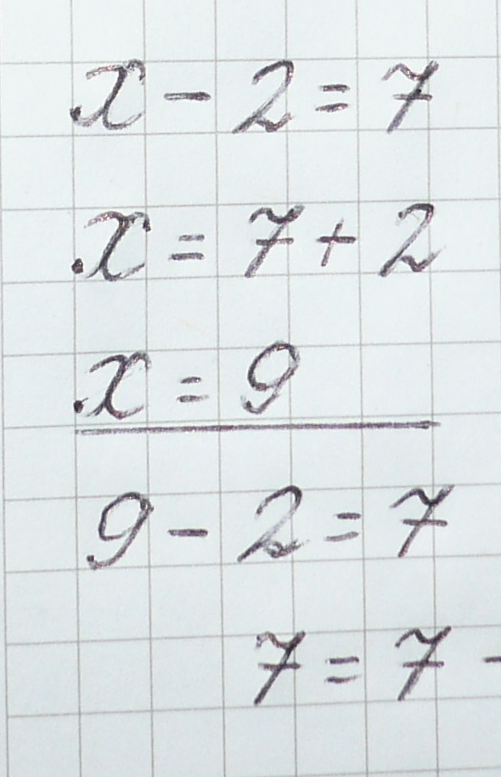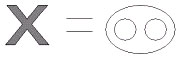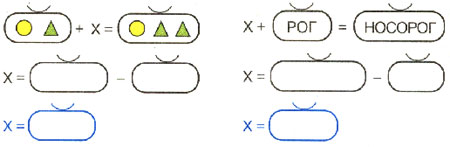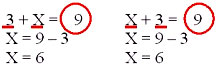Памятка составлена для отработки умения решать простые уравнения. В памятку включен пошаговый алгоритм рассуждения при нахождении неизвестного слагаемого, неизвестного уменьшаемого, неизвестного вычитаемого. Для более детального усвоения темы определены понятия «целое» и «части»Даны понятия «уравнение», «переменная». Каллиграфическим почерком написан способ записи примерных уравнений, на основе, который выполняются все остальные.
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Начальные классы. Уравнения.
С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:
И одно число решили спрятать:
Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.
В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.
Неизвестное число обозначают маленькими латинскими буквами
или любой другой буквой.
И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.
При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.
Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.
Решение записывается так:
Корень пишем на следующей строке и подчеркиваем прямой линией.
Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.
Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:
Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 66
Урок математики в 1 классе по теме: «Уравнения»
Цели. Ввести понятие уравнения, научить решать уравнения с неизвестными компонентами-слагаемыми на основе взаимосвязи между частью и целым; обрабатывать навыки быстрого и стабильного счета в пределах 9; развивать логическое мышление, внимание, память, аналитические способности.
Оборудование. Учебник “Математика. 1 класс” (сост. Л.Г. Петерсон). Издательство “С-инфо”.
I. Организационный момент
Учитель: Прочитайте, что написано?
На доске: “Если не лениться…”
У. Как бы вы продолжили? (Ответы детей). Вот как продолжила я: “Можно многого добиться”. Вы готовы не лениться?
II. Актуализация знаний и мотивация.
Проверка устного счета. Учитель диктует числовые выражения:
Дети устно считают, ответ говорят вслух. Учитель на доске записывает ответы.
У. Составьте с помощью чисел 2, 7, 5 четыре равенства. Обозначьте в них целое и части.
Проверка: один ученик на доске записывает суммы (2 + 5 = 7, 5 + 2 =7), другой – разности (7 –5 =2, 7 – 2 =5).
У. Назовите, где целое и части. Почему?
Д. 2 и 5 – это части, т.к. складывать мы можем только части. 7 – это целое, т.к. вычитать мы можем только из целого.
У. Что записано на доске?
Д. Равенства с неизвестным числом.
У. Каким образом будем считать?
Д. Методом подбора.
У. Найдите ошибки. Почему?
III. Постановка проблемы.
У. Рассмотрите вот эту запись. Что это на ваш взгляд?
На доске: Х + 2 = 5
Д. Равенство, в котором есть неизвестный компонент.
У. Такие равенства в математике называются уравнениями. (Учитель на доске вывешивает табличку с надписью “Уравнение”).
Неизвестное число в уравнениях можно обозначить по-разному, но чаще всего используют латинские буквы, например Х.
Давайте решим наше уравнение. Чему равен Х?
Д. Х равен 3.
У. Значение Х называют корнем уравнения.
У. Почему Х равен 3? Как нашли?
Д. 5 – это 2 и 3. Подобрали число.
У. Итак, мы решили уравнение с помощью подбора корней.
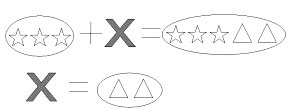
У. Чем это уравнение отличается от предыдущего? Сравните их.
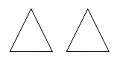
Д. В этом уравнении даны геометрические фигуры.
У. Решим уравнение. Чему равен Х?
Д.
У. Как нашли корень уравнения?
Д. Способом подбора.
У. У вас на карточках дано уравнение. Решите его самостоятельно. Каким способом вы будете решать?
Д. Способом подбора.
У. Легко ли найти Х – корень уравнения способом подбора?
Д. Трудно.
У. Удобно подбирать геометрическую фигуру?
Д. Нет.
IV. Поиск решения.
У. Что же нам нужно сделать сегодня на уроке?
Д. Найти новый способ решения уравнения.
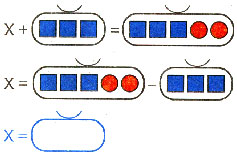
У. Есть такой “секрет”, который как “волшебный ключик”, поможет решить любое уравнение. Подумайте, какое действие с “мешками” нужно сделать, чтобы найти Х?
Д. Вычитание.
У. Почему?
Д. Потому, что Х – это часть.
У. А как найти часть?
Д. Из целого вычесть другую часть.
У. Зачеркните в сумме известную часть. Какие фигурки остались? Удобно так считать? Какое правило нам помогло?
Д. Чтобы найти часть, надо из целого вычесть другую часть.
У. Давайте проверим по учебнику.
с. 20 (Дети читают по учебнику правило и убеждаются в правильности своего вывода.)
Чтобы найти часть, надо из целого вычесть другую часть
V. Закрепление изученного материала с проговариванием.
У. Прочитайте уравнение. Что неизвестно?
Д. Из целого вычесть другую часть.
Уравнения можно составлять не только с геометрическими фигурами, но и с буквами.
- Прочитайте уравнение.
- Что неизвестно?
- Как найти?
- Чему равен Х?
Дети отвечают на вопросы.
VI. Самостоятельная работа по выбору.
с. 20, № 3, 4. Проверка в парах.
VII. Включение нового способа действия в систему знаний.
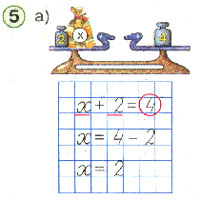
У. Давайте рассмотрим рисунок. Что видите?
Д. Весы в равновесии.
У. Что обозначено за Х?
Д. Масса мешка с крупой.
У. Давайте составим уравнение.
Д. Х + 2 = 4
У. Объясните по образцу как решали уравнение. (Составление алгоритма на доске).
Д.
1. Выделить части и целое.
2. Определить, что неизвестно.
3. Применить правило (как найти).
4. Найти корень уравнения.
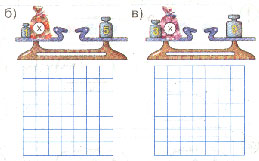
№5 (б) – с комментированием (рассмотреть рисунок, составить уравнение, решить по алгоритму);
№5 (в) – самостоятельно с проверкой на доске:
У. Встаньте те ребята, у кого решено уравнение так, как у меня на доске.
VIII. Итог урока. Рефлексия деятельности.
У. Мы начали урок со слов: “Если не лениться, можно многого добиться”.
Кто сегодня не ленился? А чего же вы добились? Что узнали нового? Какое “открытие” сделали?
А вы хотите составить свои уравнения? У вас на столах лежат листочки. Попробуйте сейчас придумать свои уравнения. Они могут быть любые: числовые, буквенные, с использованием геометрических фигур. Пофантазируйте, как можно изобразить неизвестный компонент.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
источники:
http://urok.1sept.ru/articles/213382
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:
И одно число решили спрятать:
Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.
В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.
Неизвестное число обозначают маленькими латинскими буквами
или любой другой буквой.
И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.
При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.
Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.
Решение записывается так:
Корень пишем на следующей строке и подчеркиваем прямой линией.
Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.
Решим еще одно уравнение:
Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:
Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Похожие статьи
Цели. Ввести понятие уравнения,
научить решать уравнения с неизвестными
компонентами-слагаемыми на основе взаимосвязи
между частью и целым; обрабатывать навыки
быстрого и стабильного счета в пределах 9;
развивать логическое мышление, внимание, память,
аналитические способности.
Оборудование. Учебник “Математика. 1
класс” (сост. Л.Г. Петерсон). Издательство
“С-инфо”.
ХОД УРОКА
I. Организационный момент
Учитель: Прочитайте, что написано?
На доске: “Если не лениться…”
У. Как бы вы продолжили? (Ответы
детей). Вот как продолжила я: “Можно многого
добиться”. Вы готовы не лениться?
II. Актуализация знаний и мотивация.
Проверка устного счета. Учитель диктует
числовые выражения:
9-2-3+1-3+0
1+6-4+2-5+7
8-4+2-3-1+3
Дети устно считают, ответ говорят вслух.
Учитель на доске записывает ответы.
У. Составьте с помощью чисел 2, 7, 5
четыре равенства. Обозначьте в них целое и части.
Проверка: один ученик на доске записывает суммы
(2 + 5 = 7, 5 + 2 =7), другой – разности (7 –5 =2, 7 – 2 =5).
У. Назовите, где целое и части. Почему?
Д. 2 и 5 – это части, т.к. складывать мы
можем только части. 7 – это целое, т.к. вычитать мы
можем только из целого.
У. Что записано на доске?
На доске:
_ + 3 = 7
2 + _ = 9
Д. Равенства с неизвестным числом.
У. Каким образом будем считать?
Д. Методом подбора.
На доске:
6 + 1 = 8
2 + 5 = 6
У. Найдите ошибки. Почему?
III. Постановка проблемы.
У. Рассмотрите вот эту запись. Что
это на ваш взгляд?
На доске: Х + 2 = 5
Д. Равенство, в котором есть
неизвестный компонент.
У. Такие равенства в математике
называются уравнениями. (Учитель на доске
вывешивает табличку с надписью “Уравнение”).
Неизвестное число в уравнениях можно
обозначить по-разному, но чаще всего используют
латинские буквы, например Х.
Давайте решим наше уравнение. Чему равен Х?
Д. Х равен 3.
У. Значение Х называют корнем
уравнения.
На доске:
Х=3
КОРЕНЬ УРАВНЕНИЯ
У. Почему Х равен 3? Как нашли?
Д. 5 – это 2 и 3. Подобрали число.
У. Итак, мы решили уравнение с помощью
подбора корней.
На доске:
У. Чем это уравнение отличается от
предыдущего? Сравните их.
Д. В этом уравнении даны
геометрические фигуры.
У. Решим уравнение. Чему равен Х?
Д.
У. Как нашли корень уравнения?
Д. Способом подбора.
У. У вас на карточках дано уравнение.
Решите его самостоятельно. Каким способом вы
будете решать?
Д. Способом подбора.
У. Легко ли найти Х – корень уравнения
способом подбора?
Д. Трудно.
У. Удобно подбирать геометрическую
фигуру?
Д. Нет.
IV. Поиск решения.
У. Что же нам нужно сделать сегодня
на уроке?
Д. Найти новый способ решения
уравнения.
У. Есть такой “секрет”, который как
“волшебный ключик”, поможет решить любое
уравнение. Подумайте, какое действие с
“мешками” нужно сделать, чтобы найти Х?
Д. Вычитание.
У. Почему?
Д. Потому, что Х – это часть.
У. А как найти часть?
Д. Из целого вычесть другую часть.
У. Зачеркните в сумме известную часть.
Какие фигурки остались? Удобно так считать? Какое
правило нам помогло?
Д. Чтобы найти часть, надо из целого
вычесть другую часть.
У. Давайте проверим по учебнику.
с. 20 (Дети читают по учебнику правило и
убеждаются в правильности своего вывода.)
Чтобы найти часть, надо из
целого вычесть другую часть
V. Закрепление изученного материала с
проговариванием.
У. с. 20, №3 (а)
У. Прочитайте уравнение. Что
неизвестно?
Д. Часть.
У. Как найти?
Д. Из целого вычесть другую часть.
У. Чему равен Х?
Д.
У. с. 20, №4 (а)
Уравнения можно составлять не только с
геометрическими фигурами, но и с буквами.
- Прочитайте уравнение.
- Что неизвестно?
- Как найти?
- Чему равен Х?
Дети отвечают на вопросы.
VI. Самостоятельная работа по выбору.
с. 20, № 3, 4. Проверка в парах.
Физминутка.
VII. Включение нового способа действия в
систему знаний.
с. 21, №5
У. Давайте рассмотрим рисунок. Что
видите?
Д. Весы в равновесии.
У. Что обозначено за Х?
Д. Масса мешка с крупой.
У. Давайте составим уравнение.
Д. Х + 2 = 4
У. Объясните по образцу как решали
уравнение. (Составление алгоритма на доске).
Д.
1. Выделить части и целое.
2. Определить, что неизвестно.
3. Применить правило (как найти).
4. Найти корень уравнения.
У доски ученик:
№5 (б) – с комментированием (рассмотреть
рисунок, составить уравнение, решить по
алгоритму);
№5 (в) – самостоятельно с проверкой на доске:
У. Встаньте те ребята, у кого решено
уравнение так, как у меня на доске.
На доске:
VIII. Итог урока. Рефлексия деятельности.
У. Мы начали урок со слов: “Если не лениться,
можно многого добиться”.
Кто сегодня не ленился? А чего же вы добились?
Что узнали нового? Какое “открытие” сделали?
А вы хотите составить свои уравнения? У вас на
столах лежат листочки. Попробуйте сейчас
придумать свои уравнения. Они могут быть любые:
числовые, буквенные, с использованием
геометрических фигур. Пофантазируйте, как можно
изобразить неизвестный компонент.
ПАМЯТКА
Решение уравнений. 1 класс
-
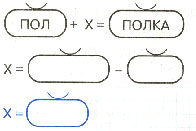
Уравнения с неизвестным слагаемым.
6 + x = 8 у + 5 = 10 Чтобы найти неизвестное
x = 8 – 6 у = 10 – 5 слагаемое, нужно из
x = 2 у = 5 суммы вычесть
6 + 2 = 8 5 + 5 = 10 известное слагаемое.
8 = 8 10 = 10
Ответ: х=2 Ответ: у=5
-
Уравнения с неизвестным вычитаемым.
7 – y = 4 Чтобы найти неизвестное
y = 7 – 4 вычитаемое, нужно из
y = 3 уменьшаемого вычесть разность.
7 – 3 = 4
4 = 4
Ответ: у=3
-
Уравнения с неизвестным уменьшаемым.
x – 2 = 7 Чтобы найти неизвестное
x = 7 + 2 уменьшаемое, нужно к
x= 9 разности прибавить вычитаемое.
9 – 2 = 7
7 = 7
Ответ: х=9
ПАМЯТКА
Решение уравнений. 1 класс
-
Уравнения с неизвестным слагаемым.
6 + x = 8 у + 5 = 10 Чтобы найти неизвестное
x = 8 – 6 у = 10 – 5 слагаемое, нужно из
x = 2 у = 5 суммы вычесть
6 + 2 = 8 5 + 5 = 10 известное слагаемое.
8 = 8 10 = 10
Ответ: х=2 Ответ: у=5
-
Уравнения с неизвестным вычитаемым.
7 – y = 4 Чтобы найти неизвестное
y = 7 – 4 вычитаемое, нужно из
y = 3 уменьшаемого вычесть разность.
7 – 3 = 4
4 = 4
Ответ: у=3
-
Уравнения с неизвестным уменьшаемым.
x – 2 = 7 Чтобы найти неизвестное
x = 7 + 2 уменьшаемое, нужно к
x= 9 разности прибавить вычитаемое.
9 – 2 = 7
7 = 7
Ответ: х=9