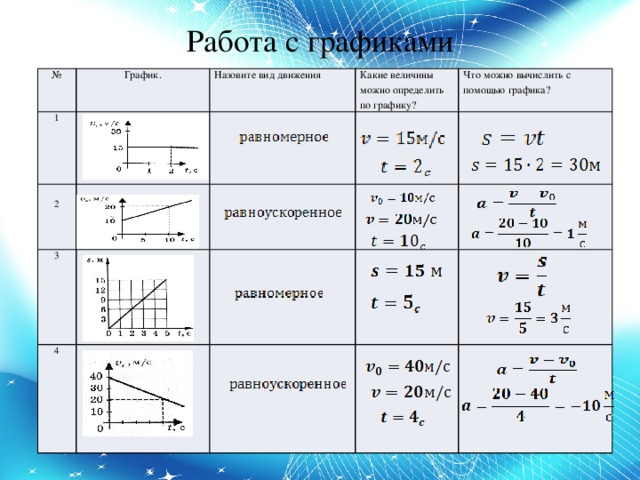
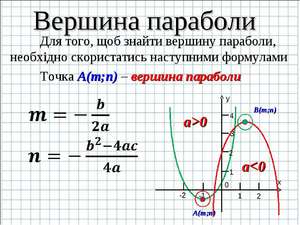
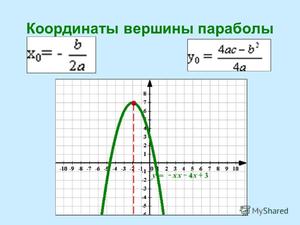
Как найти икс нулевое
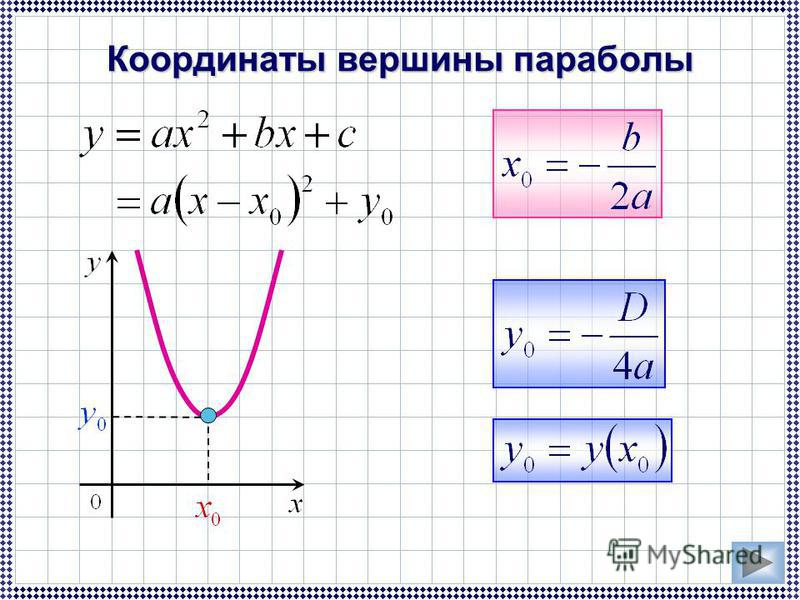
В качестве «икс нулевое» обозначается координата вершины параболы по оси абсцисс. В этой точке функция принимает наибольшее или наименьшее значение, поэтому x0 − точка экстремума функции.
Инструкция
Если имеется аналитическое задание функции, приведите ее к стандартному виду: A*x²+B*x+C=y(x), где A − старший коэффициент при x², B − средний коэффициент при x, C − свободный член. Обратите внимание, чтобы коэффициент при x² не равнялся нулю, иначе это будет уже не квадратичная функция.
Координата вершины параболы x0 по оси абсцисс находится по формуле: x0=-B/2A. В случае приведенного квадратного уравнения, то есть, когда A=1, формула упрощается: x0=-B/2. Если в уравнении нет «икса» в первой степени, значит, коэффициент B=0, и тогда x0 тоже обращается в нуль.
Чтобы найти координату вершины параболы по оси ординат, подставьте полученное значение для x0 в уравнение. Когда вы упростите выражение, с одной стороны у вас останется «игрек», с другой − некоторое число Q. Оно и показывает ординату вершины параболы: y0=Q.
Итак, исследование аналитически заданной функции дало вам точку на графике с координатами (x0;y0). Если старший коэффициент A > 0, то ветви параболы направлены вверх, и в вершине промежуток убывания будет сменяться промежутком возрастания. Если же A
Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.
Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.
Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.
Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
Разбор примера
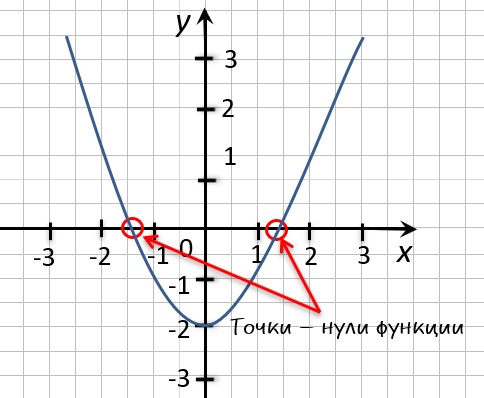
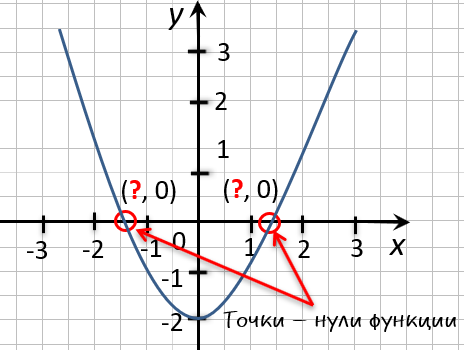
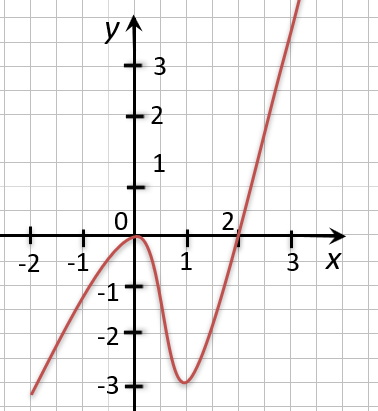
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
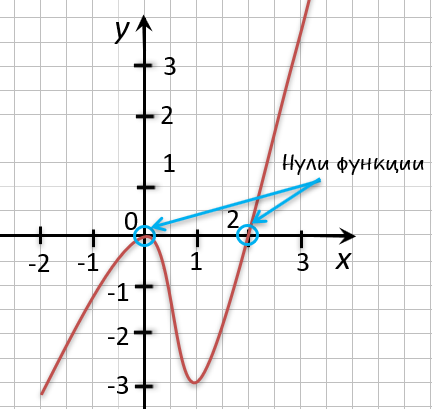
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
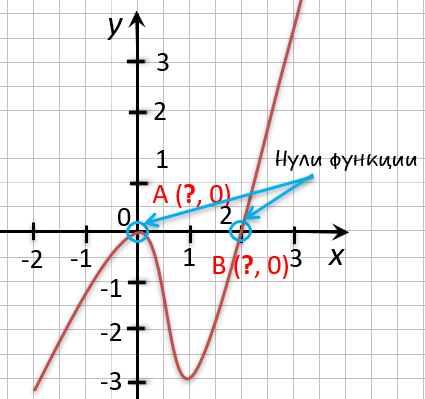
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
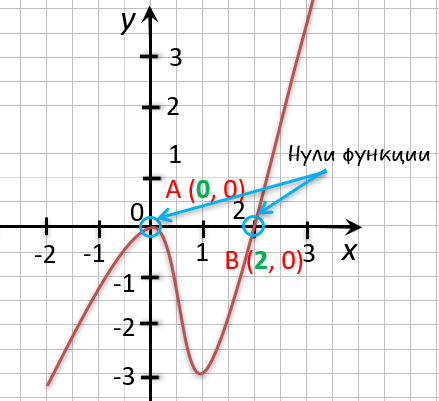
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Уравнения квадратичной функции
Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:
- Каноническая.
- Квадратичная.
- Общая.
В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).
Рисунок 2. Директриса и фокус.
Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y 2 ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y 2 ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax 2 + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax 2 . В этом случае формула нахождения вершины параболы выглядит таким образом:
- Абсцисса вершины параболы: xa = -b / 2a.
- Координата «игрек» по оси ординат: yb = — D / 2a.
В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.
Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).
В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.
Видео
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2+11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Алгоритм построения
В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:
- Если вершина не задана, то нужно найти ее любым из методов.
- Определить точки пересечения с осями декартовой системы координат.
- Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
- Выполнить построение, соединив точки.
Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x 2 + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.
Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.
Теги
Понимание нулевой гипотезы для логистической регрессии
Логистическая регрессия — это тип регрессионной модели, которую мы можем использовать для понимания взаимосвязи между одной или несколькими переменными-предикторами и переменной ответа, когда переменная ответа является двоичной.
Если у нас есть только одна предикторная переменная и одна переменная отклика, мы можем использовать простую логистическую регрессию , которая использует следующую формулу для оценки взаимосвязи между переменными:
log[p(X)/(1-p(X))] = β 0 + β 1 X
Формула в правой части уравнения предсказывает логарифмические шансы переменной ответа, принимающей значение 1.
Простая логистическая регрессия использует следующие нулевые и альтернативные гипотезы:
- Н 0 : β 1 = 0
- Н А : β 1 ≠ 0
Нулевая гипотеза утверждает, что коэффициент β 1 равен нулю. Другими словами, нет статистически значимой связи между предикторной переменной x и переменной ответа y.
Альтернативная гипотеза утверждает, что β 1 не равно нулю. Другими словами, существует статистически значимая связь между x и y.
Если у нас есть несколько переменных-предикторов и одна переменная ответа, мы можем использовать множественную логистическую регрессию , которая использует следующую формулу для оценки взаимосвязи между переменными:
log[p(X) / (1-p(X))] = β 0 + β 1 x 1 + β 2 x 2 + … + β k x k
Множественная логистическая регрессия использует следующие нулевые и альтернативные гипотезы:
- Н 0 : β 1 = β 2 = … = β k = 0
- H А : β 1 = β 2 = … = β k ≠ 0
Нулевая гипотеза утверждает, что все коэффициенты в модели равны нулю. Другими словами, ни одна из переменных-предикторов не имеет статистически значимой связи с переменной отклика y.
Альтернативная гипотеза утверждает, что не каждый коэффициент одновременно равен нулю.
В следующих примерах показано, как принять решение об отклонении или отказе от отклонения нулевой гипотезы как в моделях простой логистической регрессии, так и в моделях множественной логистической регрессии.
Пример 1: простая логистическая регрессия
Предположим, профессор хотел бы использовать количество часов обучения, чтобы предсказать экзаменационные баллы, которые получат студенты в его классе. Он собирает данные по 20 учащимся и использует простую модель логистической регрессии.
Мы можем использовать следующий код в R, чтобы соответствовать простой модели логистической регрессии:
#create data df <- data.frame(result=c(0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1), hours=c(1, 5, 5, 1, 2, 1, 3, 2, 2, 1, 2, 1, 3, 4, 4, 2, 1, 1, 4, 3)) #fit simple logistic regression model model <- glm(result~hours, family='binomial', data=df) #view summary of model fit summary(model) Call: glm(formula = result ~ hours, family = "binomial", data = df) Deviance Residuals: Min 1Q Median 3Q Max -1.8244 -1.1738 0.7701 0.9460 1.2236 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -0.4987 0.9490 -0.526 0.599 hours 0.3906 0.3714 1.052 0.293 (Dispersion parameter for binomial family taken to be 1) Null deviance: 26.920 on 19 degrees of freedom Residual deviance: 25.712 on 18 degrees of freedom AIC: 29.712 Number of Fisher Scoring iterations: 4 #calculate p-value of overall Chi-Square statistic 1-pchisq(26.920-25.712, 19-18) [1] 0.2717286
Чтобы определить, существует ли статистически значимая связь между учебными часами и экзаменационным баллом, нам необходимо проанализировать общее значение хи-квадрата модели и соответствующее значение p.
Мы можем использовать следующую формулу для расчета общего значения хи-квадрата модели:
X 2 = (Нулевое отклонение – Остаточное отклонение) / (Нулевое df – Остаточное df)
Значение p оказывается равным 0,2717286 .
Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Другими словами, не существует статистически значимой связи между количеством часов обучения и полученными экзаменационными баллами.
Пример 2: Множественная логистическая регрессия
Предположим, профессор хотел бы использовать количество часов обучения и количество сданных подготовительных экзаменов, чтобы предсказать экзаменационный балл, который студенты получат в его классе. Он собирает данные по 20 учащимся и использует модель множественной логистической регрессии.
Мы можем использовать следующий код в R, чтобы соответствовать модели множественной логистической регрессии:
#create data df <- data.frame(result=c(0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1), hours=c(1, 5, 5, 1, 2, 1, 3, 2, 2, 1, 2, 1, 3, 4, 4, 2, 1, 1, 4, 3), exams=c(1, 2, 2, 1, 2, 1, 1, 3, 2, 4, 3, 2, 2, 4, 4, 5, 4, 4, 3, 5)) #fit simple logistic regression model model <- glm(result~hours+exams, family='binomial', data=df) #view summary of model fit summary(model) Call: glm(formula = result ~ hours + exams, family = "binomial", data = df) Deviance Residuals: Min 1Q Median 3Q Max -1.5061 -0.6395 0.3347 0.6300 1.7014 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -3.4873 1.8557 -1.879 0.0602 . hours 0.3844 0.4145 0.927 0.3538 exams 1.1549 0.5493 2.103 0.0355 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 26.920 on 19 degrees of freedom Residual deviance: 19.067 on 17 degrees of freedom AIC: 25.067 Number of Fisher Scoring iterations: 5 #calculate p-value of overall Chi-Square statistic 1-pchisq(26.920-19.067, 19-17) [1] 0.01971255
Значение p для общей статистики хи-квадрат модели оказывается равным 0,01971255 .
Поскольку это p-значение меньше 0,05, мы отвергаем нулевую гипотезу. Другими словами, существует статистически значимая взаимосвязь между суммой часов обучения и сданных подготовительных экзаменов и полученной итоговой оценкой экзамена.
Дополнительные ресурсы
Следующие руководства предлагают дополнительную информацию о логистической регрессии:
Введение в логистическую регрессию
Как сообщить о результатах логистической регрессии
Логистическая регрессия против линейной регрессии: ключевые отличия
Что такое «сигма»? • Физика элементарных частиц • LHC на «Элементах»
Сигмой (σ) в статистическом анализе обозначают стандартное отклонение.
Зачем всё это нужно: сигмы и вероятности
При обсуждении погрешностей мы уже говорили, что фраза «измеренная масса равна 100 ± 5 грамм» вовсе не означает, что истинная масса гарантированно лежит в интервале от 95 до 105 грамм. Она может оказаться и за пределами этого интервала «± 1σ», но, как правило, недалеко. В небольшом проценте случаев может даже случиться, что она выходит за пределы интервала «± 2σ», и уж совсем редко она оказывается за пределами «± 3σ». В общем, тенденция ясна: количество сигм связано с вероятностью того, что истинное значение будет настолько отличаться от измеренного.
Пропустим все математические подробности и покажем результат для самого простого и распространенного случая, который называется «нормальное распределение» (см. рисунок). Вероятность попасть в интервал ± 1σ — примерно 68%, в интервал ± 2σ — примерно 95%, в интервал ± 3σ — примерно 99,8%, и т. д. Итак, можно сформулировать некую договоренность:
Договоренность: выражение какого-то отличия в количестве сигм — это сообщение о том, какова вероятность, что такое или еще более сильное отличие могло произойти за счет случайного стечения обстоятельств при измерении.
Использовать эту договоренность можно разными способами. Если вы просто сообщаете результат измерения (100 ± 5 грамм) и уверены в том, что нормальное распределение применимо, то вы можете сказать, что истинное значение массы с вероятностью 68% лежит в этом интервале, с вероятностью 95% лежит в интервале от 90 до 110 грамм, и т. д.
Вы можете также сравнивать результат вашего измерения с чужим измерением той же самой величины или с теоретическими расчетами.
- Если отличие составляет меньше 1σ, то вероятность того, что два числа согласуются друг с другом, больше 32%. В таком случае просто говорят, что два результата совпадают в пределах погрешностей.
- Если отличие составляет меньше 3σ, то вероятность того, что два числа согласуются друг с другом, больше 0,2%. В физике элементарных частиц такой вероятности недостаточно для каких-либо серьезных выводов, и принято говорить: различие между двумя результатами не является статистически значимым.
- Если отличие от 3σ до 5σ, то это повод подозревать что-то серьезное. Впрочем, даже в этом случае физики говорят осторожно: данные указывают на существование различия между двумя результатами.
- И только если два результата отличаются на 5σ или больше, физики четко заявляют: два результата отличаются друг от друга.
Эти выражения особенно стандартны, когда речь идет о поиске новой частицы. Вы сравниваете экспериментальные данные с теоретическим предсказанием, сделанным без новой частицы, и, если видите отличие от 3 до 5 сигм, вы говорите: получено указание на существование новой частицы (по-английски, evidence). Если же отличие превышает 5 сигм, вы говорите: мы открыли новую частицу (discovery).
«Уверенность» против «статистической значимости»
Заметьте, что в приведенных выше примерах нас интересовали вопросы, на которые можно ответить «да» или «нет». Проступает ли в полученных данных какая-то новая частица? Согласуется ли распределение по импульсу с теоретическими расчетами? Зависит ли сечение процесса от энергии столкновений? Совпадает ли масса у частицы и ее античастицы? Попытка ответить на эти вопросы с помощью данных называется на научном языке проверкой гипотез.
В простейшем приближении результат экспериментальной проверки гипотезы выглядит так: ответ «да» с вероятностью p и ответ «нет» с вероятностью 1 – p. Эти вероятности очень важны для сообщения результата; физики обычно избегают абсолютных утверждений («мы открыли» или «мы опровергли») без указания вероятностей.
Но тут сразу же надо сделать важное уточнение. Если его четко осознать, то станет понятным, почему такие стандартные для научно-популярных новостей фразы, как «Ученые на 99% уверены, что открыли что-то новое», — обманчивы.
Точная формулировка, которую обычно используют ученые, такова:
При проверке гипотезы получен ответ «да» на уровне статистической значимости p.
При этом величина p часто выражается в виде количества сигм. В англоязычной литературе используется словосочетание confidence level, CL (доверительный уровень).
Отличие «популярной» фразы от истинного утверждения вот в чём. Во всяком измерении есть не только статистические, но и систематические погрешности. Описанные выше правила связи вероятностей и количества сигм работают только для статистических погрешностей — и то если к ним применимо нормальное распределение. Если статистические погрешности всегда можно обсчитать аккуратно, то систематические погрешности — это немножко искусство. Более того, из многолетнего опыта известно, что сильные систематические отклонения уж точно не описываются нормальным распределением, и потому для них эти правила пересчета не справедливы. Так что даже если экспериментаторы всё перепроверили много раз и указали систематическую погрешность, всегда остается риск, что они что-то упустили из виду. Корректно оценить этот риск невозможно, поэтому вы на самом деле не знаете, с какой истинной вероятностью ваш ответ верен.
Конечно, по умолчанию систематическим погрешностям стоит доверять, особенно если они исходят от опытных экспериментальных групп. Но вековой опыт изучения элементарных частиц показывает, что несмотря на все предосторожности регулярно случаются проколы. Бывает, что коллаборация получает результат, сильно противоречащий какой-то гипотезе, перепроверяет анализ много раз и никаких ошибок у себя не находит. Однако этот результат затем не подтверждается другими — порой намного более точными! — экспериментами. Почему первый эксперимент дал такой странный результат, что в нём было не то, где там ошибка или неучтенная погрешность — всё это зачастую так и остается непонятым (впрочем, иногда источник ошибки быстро вскрывается, как это случилось со «сверхсветовыми» нейтрино в эксперименте OPERA).
Физики к таким оборотам событий уже привыкли, поэтому каждый экспериментальный результат, сильно отличающийся от всей сложившейся к тому времени картины, вызывает оправданный скепсис. Физики так консервативны в своем отношении вовсе не потому, что они ретрограды и намертво уверовали в какую-то одну теорию, как это хотят представить опровергатели физики.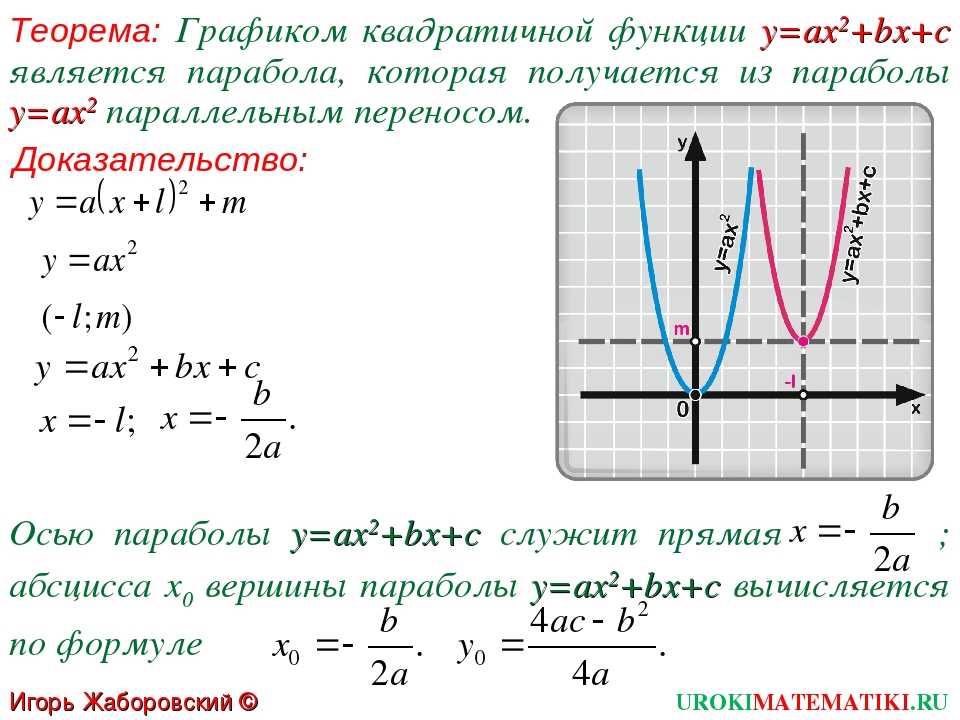
ФЭЧ в сравнении с другими науками
Надо сказать, что сформулированные выше жесткие критерии статистической достоверности характерны именно для физики элементарных частиц и некоторых смежных разделов. Во многих других разделах физики, а тем более в других дисциплинах (в особенности, в биомедицинских науках) критерии намного слабее.
Предположим, вы измерили некие данные и хотите узнать, какова вероятность того, что они «вписываются в норму». Вы проводите статистический тест, который дает вам вероятность того, что «нормальная ситуация» без какого-либо реального отклонения только за счет статистической флуктуации даст вот такое или еще более сильное отклонение. Эта вероятность называется p-значение. В биологии пороговое p-значение, ниже которого уже уверенно говорят про реальное отличие, составляет один или даже несколько процентов.
Нули многочлена — формулы, уравнения, примеры, сумма и произведение
Нули многочлена — это точки, в которых многочлен в целом равен нулю. Проще говоря, можно сказать, что нули полинома — это такие значения переменной, что полином равен 0 в этой точке. Нули полинома также называют корнями уравнения и часто обозначают как α, β, γ соответственно.
Некоторые из методов, используемых для нахождения нулей многочлена, включают группировку, факторизацию и использование алгебраических выражений.
Кроме того, нули полинома помогают составить исходное полиномиальное уравнение. Здесь мы узнаем, как найти нули многочлена, сумму и произведение нулей многочлена. Мы решим несколько связанных с ним примеров для лучшего понимания концепции.
| 1. | Что такое нули многочлена? |
| 2. | Как найти нули многочлена? |
| 3. | Нули полиномиальной формулы |
| 4. | Сумма и произведение нулей многочлена |
| 5. | Составление уравнения из нулей многочлена |
| 6. | Представление нулей многочлена на графике |
| 7. | Часто задаваемые вопросы о нулях многочлена |
Что такое нули многочлена?
Нули многочлена f(x) — это значения x, которые удовлетворяют уравнению f(x) = 0.
Графически нули многочлена представляют собой точки, в которых график y = f(x) пересекает ось x. Мы узнаем больше об этом в приведенном ниже содержании представления нулей многочлена на графике.
Как найти ноль многочлена?
Существует множество способов найти нули многочлена. Количество нулей многочлена зависит от степени уравнения полинома. Различные уравнения были классифицированы как линейные уравнения, квадратные уравнения, кубические уравнения и многочлены более высокой степени, и каждое из уравнений анализируется отдельно, чтобы найти нули многочлена. Различные типы уравнений и методы нахождения их нулей полинома следующие.
Линейное уравнение: Линейное уравнение имеет форму y = ax + b.
Квадратное уравнение: Существует два метода факторизации квадратного уравнения. Квадратное уравнение вида x 2 + x(a + b) + ab = 0 можно разложить на множители как (x + a)(x + b) = 0, и мы имеем x = -a и x = — b как нули полинома. А для квадратного уравнения вида ах 2 + bx + c = 0, которое нельзя разложить на множители, нули можно вычислить по формульному методу, и формула x = [- b ± √(b 2
— 2ac) ] / 2a.
Кубическое уравнение: Кубическое уравнение вида y = ax 3 + bx 2 + cx + d можно разложить на множители, применяя теорему об остатках. В соответствии с теоремой об остатках мы можем подставлять любые меньшие значения для переменной x = α, и если значение y равно нулю, y = 0, то (x — α) является одним корнем уравнения. Кроме того, мы можем разделить кубическое уравнение с (x — α), используя длинное деление, чтобы получить квадратное уравнение.
Полином высшей степени: Уравнение полинома высшей степени имеет вид y = ax n + bx n — 1 +cx n — 2 + ….. px + q. Эти многочлены более высокой степени можно разложить на множители, используя теорему об остатках, чтобы получить квадратное уравнение. И квадратное уравнение можно разложить на множители, чтобы получить последние два необходимых множителя.
Нули полиномиальной формулы
Как обсуждалось в предыдущем разделе, мы можем найти нули многочленов разных типов разными способами. Для многочленов более высоких степеней мы используем теорему об остатках и в конечном итоге приходим к квадратичному многочлену, для которого мы используем квадратичную формулу для нахождения нулей. Итак, формула, которую мы используем для нахождения нулей квадратного многочлена ах 2 + bx + c = 0 равно:
x = [- b ± √(b 2 — 2ac) ] / 2a
Сумма и произведение нулей многочлена
Нули многочлена можно легко вычислить с помощью:
Сумма и произведение нулей многочлена для квадратного уравнения
Сумма и произведение нулей многочлена могут быть вычислены непосредственно из переменных квадратного уравнения , и не находя нулей многочлена.
Сумма нулей полинома = α + β = -b/a = — коэффициент x/коэффициент x 2
Произведение нулей полинома = αβ = c/a = постоянный член/коэффициент x 2
Сумма и произведение нулей многочлена для кубического уравнения
Кубический многочлен имеет форму ax 3 + bx 2 + cx + d = 0 постоянный член, а α, β, γ — корни кубического полиномиального уравнения.
α + β + γ = -b/a = — коэффициент при x 2 /коэффициент при x 3
αβ + βγ + γα = c/a = коэффициент при x/коэффициент при x 3
αβγ = -d/a = -константа/коэффициент x 3
Составление уравнения из нулей многочлена
Нули многочлена используются для формирования уравнения полинома.
Кубическое уравнение: Возьмем корни полиномиального уравнения как α, β, γ. Множителями уравнения являются (x — α), (x — β), (x — γ), а требуемое уравнение имеет вид (x — α)(x — β)(x — γ) = 0,
Квадратное уравнение: Для квадратного уравнения, имеющего два нуля уравнения как α, β, коэффициентами являются (x — α) и (x — β). И искомое квадратное уравнение имеет вид x 2 — x(α+ β) + α.β = 0,
Также мы можем найти уравнение полинома более высокой степени, составив требуемые множители и взяв произведение факторы, чтобы составить требуемое уравнение.
Представление нулей многочлена на графике
Полиномиальное выражение вида y = f(x) может быть представлено на графике по оси координат. Значение x представлено на оси x, а значение f(x) или значение y представлено на оси y. Полиномиальное выражение может быть линейным выражением, квадратичным выражением или кубическим выражением, основанным на степени полиномов. Линейное выражение представляет собой линию, квадратное уравнение представляет собой кривую, а полином более высокой степени представляет собой кривую с неровными изгибами.
Нули полинома можно найти на графике, наблюдая точки, в которых линия графика пересекает ось x. Координаты x точек, где график пересекает ось x, являются нулями многочлена.
Важные замечания по нулям полинома
- Нули полинома — это значения переменной, для которых полином равен 0.
- Мы можем найти нули многочлена, определив точки пересечения по оси x.
- Чтобы найти нули квадратного многочлена, мы используем квадратичную формулу.
☛Статьи по теме
- Полиномиальные функции
- Полиномиальные выражения
- Полиномиальные уравнения
Часто задаваемые вопросы о нулях многочлена
Что понимают под нулями многочлена?
нуля полинома относятся к значениям переменных, присутствующих в полиномиальном уравнении, для которых полином равен 0. Количество значений или нулей полинома равно степени полиномиального выражения. Для полиномиального выражения вида ax n + bx n — 1 + cx n — 2 +…. px + q , всего до n нулей многочлена. Нули многочлена также называют корнями уравнения.
Как найти нули многочлена?
Существует несколько способов найти нули многочлена. Метод, используемый для нахождения нулей полинома, зависит от степени уравнения. Полиномиальное выражение решается с помощью факторизации, группировки, алгебраических тождеств и получаются множители. Факторы индивидуально решаются, чтобы найти нули многочлена. Квадратное уравнение вида x 2 + x(a + b) + ab = 0 имеет множители (x + a)(x + b) = 0, а нули квадратного уравнения равны -a, -b.
Как найти нули многочлена графически?
Нули многочлена можно легко найти графически, найдя точки, в которых график многочлена пересекает ось x. Для всех точек, где линия уравнения пересекает ось x, координата x точки представляет собой нули многочлена.
Как найти комплексные нули полиномиальной функции?
Комплексные нули многочленов можно вычислить по формуле комплексных чисел i 2 = -1. Отрицательные корни также можно упростить, используя значение i из комплексных чисел. Для уравнения вида (x + 3) 2 = -25 нахождение квадратного корня из отрицательного числа невозможно. Здесь мы используем i 2 = -1, чтобы записать (x + 3) 2 = 25i 2 , и при упрощении имеем (x + 3) = + 5i, а нули полинома равны -3 + 5i и -3 -5i.
Что такое сумма нулей многочлена?
Сумма нулей многочлена квадратного уравнения вида ax 2 + bx + c = 0, имеющего корнями α, β, равна коэффициент x 2 . А сумма нулей многочлена кубического уравнения ах 3 + bx 2 + cx + d = 0, имеющего корни α, β, γ, равна α + β + γ = -b/a = -коэффициенту x 2 /коэффициент x 3
Что такое произведение нулей многочлена?
Произведение нулей многочлена квадратного уравнения формы ax 2 + bx + c = 0, имеющего α, β в качестве корней, равно αβ = c/a = постоянный член/коэффициент при x 2 . А произведение нулей многочлена для кубического уравнения ax 3 + bx 2 + cx + d = 0, имеющего корни α, β, γ, равно αβγ = -d/a = -постоянный член/коэффициент x 3
Сколько нулей многочлена у = f(x)?
Количество нулей полинома зависит от степени выражения полинома y = f(x). Для линейного уравнения с одной переменной у нас есть только один корень. Для квадратичного и кубического многочлена у нас есть два и три нуля многочлена соответственно.
Какое количество нулей полинома имеет линейный многочлен?
Линейный многочлен имеет только один нуль. Линейное выражение формы ax + b = 0 имеет только одно значение x = -b/a, которое является нулем этого линейного полинома
Как найти нули квадратичной функции 4 лучших метода
Как найти найти нули квадратной функции?
В предыдущем уроке мы обсуждали, как найти нули функции. 9{2} .
Как найти нули квадратичной функции – 4 лучших метода
Существуют разные методы нахождения нулей квадратичной функции.
Мы увидим лучшие 4 метода из них
- Заполнение квадрата,
- Факторинг,
- Квадратичная формула,
- График.
Нахождение нулей квадратичной функции путем заполнения квадрата
Существуют некоторые квадратичные полиномиальные функции, нули которых можно найти, превратив их в полный квадрат. 9{2} + 1 = 0 являются x = + i, — i, и оба они комплексные (не вещественные).
Как найти нули квадратичной функции на графике
Чтобы найти ноль на графике, нам нужно посмотреть, где график функции пересекает или касается оси X, и эти точки будут ноль этой функции, так как в этих точках y равен нулю.
Здесь возникнут 3 случая:
- Когда график пересекает ось x,
- Когда график касается оси x, 9{2} = — 2
или, x = pm sqrt{- 2}
или, x = pm sqrt{2} i
или, x = + sqrt{2} i, — sqrt{2} i
Для лучшего понимания вы можете посмотреть это видео (продолжительность: 5 минут 29 секунд), в котором Марти Брандл объяснил процесс поиска нулей на графике
Как найти нули квадратичной функции на график
Источник – Youtube, видео Марти БрандлаЧасто задаваемые вопросы по нахождению нулей квадратичной функции
-
Сколько нулей может быть у квадратичной функции?
Квадратичная функция имеет 2 действительных или комплексных нуля.
2 – 16x – 15? 92-48 это х = +4, -4.
-
3x+1/x-8=0 является квадратным уравнением или нет
Мы знаем, что степень квадратичной функции равна 2.
Но степень функции frac{3x+1}{x-8} не равна 2.
Следовательно, данная функция frac{3x+1} {x-8} не является квадратичной функцией.
Следовательно, 3x+1/x-8=0 не является квадратным уравнением. -
Найдите квадратный многочлен, сумма корней которого равна 0, а произведение корней равно 1.
Пусть корни квадратного многочлена равны «a» и «b». 9{2}+1, а нули квадратного многочлена равны x= +sqrt{-1}, -sqrt{-1} .
Надеемся, вы понимаете, как находить нули квадратной функции.
Если у вас есть какие-либо сомнения или предложения по теме, как найти нули квадратичной функции, не стесняйтесь спрашивать в разделе комментариев. Мы рады услышать от вас.
Дополнительно можно прочитать:
- Что такое функция? — Определение, пример и график.
-
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
- Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
- Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три формулы неполных квадратных уравнений:
- ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax² + c = 0, при b = 0;
- ax² + bx = 0, при c = 0.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как решить уравнение ax² = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.
Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.
Пример 1. Решить −5x² = 0.
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!
Как решить уравнение ax² + с = 0
Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
- перенесем c в правую часть: ax² = — c,
- разделим обе части на a: x² = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.
В двух словах
Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
- не имеет корней при — c/а 0.
Пример 1. Найти решение уравнения 9x² + 4 = 0.
-
Перенесем свободный член в правую часть:
Разделим обе части на 9:
Ответ: уравнение 9x² + 4 = 0 не имеет корней.
Пример 2. Решить -x² + 9 = 0.
-
Перенесем свободный член в правую часть:
Разделим обе части на -1:
Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.
Как решить уравнение ax² + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.
Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:
Пример 1. Решить уравнение 2x² — 32x = 0
-
Вынести х за скобки
Ответ: х = 0 и х = 16.
Пример 2. Решить уравнение 3x² — 12x = 0
Разложить левую часть уравнения на множители и найти корни:
Как найти х нулевое ?
Физика | 5 — 9 классы
Как найти х нулевое ?
Если есть уравнение вида x(t) = 3 + 5t + 2t² то число без t есть Хо = 3, начальная скорость 5 ускорение 4.
Скажите пожалуйста формулу как найти нулевую скорость при равноускоренном движении?
Скажите пожалуйста формулу как найти нулевую скорость при равноускоренном движении?
G нулевое что это такое?
G нулевое что это такое?
Тела брошено со скоростью V (нулевое), под углом к горизонту Продолжительность полета t = 2, 2с?
Тела брошено со скоростью V (нулевое), под углом к горизонту Продолжительность полета t = 2, 2с.
Найти наибольшую высоту поднятия этого тела.
Сопротивления воздуха не учитывать.
Скажите пожалуйста формулу как найти нулевую скорость?
Скажите пожалуйста формулу как найти нулевую скорость.
Дано масса = 3кг?
Дано масса = 3кг.
, скорость = 5м / с.
, скорость нулевая = 2м / с.
Помогите пожалуйста решить очень надо.
Нулевая скорость = 0, время = 4сек, путь = 40 м, найти ускорение?
Нулевая скорость = 0, время = 4сек, путь = 40 м, найти ускорение.
Помогите решить задави по физике Дано : Скорость = 2 + 4t t = 2c Найти : Скорость нулевая , скорость , ускорение?
Помогите решить задави по физике Дано : Скорость = 2 + 4t t = 2c Найти : Скорость нулевая , скорость , ускорение.
Где находится нулевой меридиан?
Где находится нулевой меридиан.
Дано : h — 20 м t — 1 сек найти V(нулевой) — ?
Дано : h — 20 м t — 1 сек найти V(нулевой) — ?
Дано : S = 800 м а = 5 м / с V нулевое = 0 Найти : V — ?
Дано : S = 800 м а = 5 м / с V нулевое = 0 Найти : V — ?
Вы открыли страницу вопроса Как найти х нулевое ?. Он относится к категории Физика. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Физика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
Формула = > Q = mc( t2 — t1) Подставляем данные : 4 * 880 ( 30 — 15) = 4 * 880 * 15 = 52 800 Джоулей, переводим в кДж ( килоДжоули), получаем 52, 8 кДж Ответ : 52, 8 кДж.
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 — первый корень;
- 5 — второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
http://fizika.my-dict.ru/q/3332857_kak-najti-h-nulevoe/
http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly


 3714 1.052 0.293
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 26.920 on 19 degrees of freedom
Residual deviance: 25.712 on 18 degrees of freedom
AIC: 29.712
Number of Fisher Scoring iterations: 4
#calculate p-value of overall Chi-Square statistic
1-pchisq(26.920-25.712, 19-18)
[1] 0.2717286
3714 1.052 0.293
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 26.920 on 19 degrees of freedom
Residual deviance: 25.712 on 18 degrees of freedom
AIC: 29.712
Number of Fisher Scoring iterations: 4
#calculate p-value of overall Chi-Square statistic
1-pchisq(26.920-25.712, 19-18)
[1] 0.2717286
 5061 -0.6395 0.3347 0.6300 1.7014
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.4873 1.8557 -1.879 0.0602 .
hours 0.3844 0.4145 0.927 0.3538
exams 1.1549 0.5493 2.103 0.0355 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 26.920 on 19 degrees of freedom
Residual deviance: 19.067 on 17 degrees of freedom
AIC: 25.067
Number of Fisher Scoring iterations: 5
#calculate p-value of overall Chi-Square statistic
1-pchisq(26.920-19.067, 19-17)
[1] 0.01971255
5061 -0.6395 0.3347 0.6300 1.7014
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.4873 1.8557 -1.879 0.0602 .
hours 0.3844 0.4145 0.927 0.3538
exams 1.1549 0.5493 2.103 0.0355 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 26.920 on 19 degrees of freedom
Residual deviance: 19.067 on 17 degrees of freedom
AIC: 25.067
Number of Fisher Scoring iterations: 5
#calculate p-value of overall Chi-Square statistic
1-pchisq(26.920-19.067, 19-17)
[1] 0.01971255