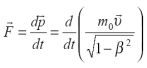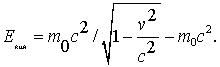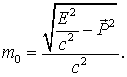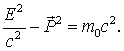1.17.
ОСНОВЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ
Релятивистский
импульс. Уравнение движения частицы в
специальной теории относительности.
Работа и энергия. Полная энергия
тела. Взаимосвязь энергии и массы,
энергии и импульса.
Релятивистская
динамика строится на основе постулатов
Эйнштейна и их следствий — преобразований
Лоренца, которые математически
аккумулируют в себе метрические свойства
пространства и времени.
Релятивистский
импульс частицы
В
релятивистской физике для описания
механического движения вводятся
4-вектора положения частицы
,
перемещения
и скорости

Вводим импульс по аналогии с ньютоновой
механикой — как произведение инвариантной
массы (массы покоя), одинаковой в
инерциальных системах отсчета I
и II,
на 4-скорость. Итак, четырехмерным
импульсом называется величина
.
|
|
(17.1) |
Сокращенно
пишем
,
где пространственная и временная
компоненты 4-импульса имеют вид
|
|
(17.2) |
Здесь
—
так называемый релятивистский
3-импулъс.
Очевидно, 4-импульсу отвечает его
инвариант
|
|
(17.3) |
Масса
покоя —
—
инвариант преобразований Лоренца. При
небольших скоростях, когда
,
он переходит в инвариант преобразований
Галилея.
Основное
уравнение релятивистской динамики
В ньютоновой
механике обычная трехмерная 3-сила
определяется как скорость изменения
во времени количества движения,
переносимого на данное тело от окружающих
тел и полей (равенство
Ньютона
является одновременно и определением
силы, и законом движения). Аналогично в
релятивистской механике будем определять
силу как производную от релятивиского
3-импулься
|
|
(17.4) |
Это
равенство обобщает ньютонову трактовку
3-силы. В то же время оно представляет
основной закон движения частицы
(материальной точки) в инерциальной
системе отсчета при любых
возможных
скоростях меньших с. Законы
классической динамики получаются из
законов релятивистской динамики в
предельном случае υ
<<
c.
Энергия
свободной частицы. Связь между массой
и энергией
В ньютоновой
механике работа силы равна приращению
кинетической энергии:

В СТО понятие силы обобщено, и работу
релятивистской силы нужно заново
вычислить. Найдем работу релятивистской
силы
на
элементарном перемещении
частицы

(17.5)
Здесь
использовано правило дифференцирования
произведения функций; учтено что
и
.
Объединяя оба слагаемые под одним
дифференциалом, окончательно получаем
|
|
(17.6) |
Найденное
равенство показывает, что работа силы
равна приращению величины

Поэтому последнюю следует истолковать
как энергию
движущегося
тела (частицы):
|
|
(17.7) |
Эта
формула, установленная Эйнштейном в
1905 г., в начале прошлого столетия вызывала
сомнение, а позже обеспечила полный
триумф теории относительности. Формула
(17.7)
устанавливает связь между массой (покоя)
и энергией тела при его скорости
.
Из формулы
Эйнштейна вытекает важное открытие 20
века: любое тело в состоянии покоя
обладает колоссальной энергией, которая
называется
энергией покоя
и равна
|
|
(17.8) |
Например,
тело массой m0
=
l
кг обладает энергией
Дж,
т.е. оно обладает энергией, которую,
например, Днепровская ГЭС вырабатывает
за 8 лет, давая в год 3 млрд. квт.-ч. энергии.
Соотношение
носит универсальный характер, оно
применимо ко всем формам энергии,
т.е.можно утверждать, что с энергией,
какой бы формы она не была, связана масса
и, наоборот, со всякой массой связана
энергия.
Дадим
определение: кинетической
энергией
тела
называется разность
,
откуда
или
|
|
(17.9) |
Формула
(17.7)
для энергии определяет сумму двух
энергий: энергии покоя (она относится
в внутренней энергии)
и
кинетической
.
Связь
между энергией и импульсом частицы
Учитывая
значения временной компоненты 4-импульса
P0
(формула (17.2))
и полной энергии Е (формула (17.7)),
4-импульс
(формула
(17.1))
можно представить в виде
|
|
(17.10) |
Как
видим, в 4-импульсе объединились энергия
Е и релятивистский 3-импульс
,
что означает глубокую внутреннюю связь
между релятивистской энергией

релятивистским импульсом

При переходе из одной инерциальной
системы отсчета в другую значение каждой
из четырех компонент 4-импульса
определяется
по формулам Лоренца через все четыре
компоненты в исходной системе I.
Например, значение энергии в системе
II
определяется не только через энергию
в системе I,
но и через все компоненты импульса
.
Полезными
являются также очевидные формулы для
релятивистского импульса
и
его модуля в виде:
|
|
(17.11) |
Релятивистские
инварианты. Закон сохранения
энергии-импульса
Определим
величины, сохраняющиеся при переходе
из одной системы отсчета в другую. Их
обычно называются инвариантами. Как
отмечалось, 4-импульсу
соответствует
инвариант
Подставляя
значение
получаем
|
|
(17.12) |
Это
соотношение между релятивистской
энергией и релятивистским импульсом
выполняется как для частицы» так и
для тела, и даже для сложной системы,
так как при его выводе нигде не
использовалась неделимость объекта. И
общем случае в (17.12)
под Е следует понимать полную энергию
системы, а под
—
геометрическую
сумму импульсов всех
частей системы. Равенство (17.12)
можно рассматривать так же как определение
инвариантной массы (массы покоя) любой
физической системы
|
|
(17.13) |
В частном
случае системы отсчета, в которой импульс
равен нулю (),
имеем
|
|
(17.14) |
Следовательно, масса
покоя тела определяет его энергию покоя
(во всех ее видах). В релятивистской
механике, в отличие от классической,
энергия тела всегда положительна.
В другом
частном случае, когда масса покоя равна
нулю,
соотношение
(17.12)
дает связь между релятивистским импульсом
и энергией следующего вида
В частности, для для
фотона с нулевой массой покоя эта формула
преобразуется к виду
Вернемся
к рассмотрению 4-импульса
.
Он объединяет релятивистскую энергию

релятивистским импульсом

значит представляет собой некоторую
новую (одну единую!) величину, которую
можно определить термином энергия-импульс.
4-вектору энергия-импульс соответствует
инвариант (17.12),
играющий важную роль в атомной и ядерной
физике
В случае
изолированной физической системы эта
величина сохраняется не только при
переходе от системы отсчета I
к системе II,
но также сохраняется ее значение как
до, так и после реакции, происходящей в
физической системе.
5
Соседние файлы в папке физика лекцыи_1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Если скорость релятивистской частицы меньше скорости света, то она называется массовой. Её собственная энергия, то есть энергия при (v=0):
(boxed{E_0=m_0cdot c^2}), ((1))
где (m_0) — масса покоя частицы, (E_0) — энергия покоя частицы.
Масса движущейся релятивистской частицы:
(boxed{m=frac{m_0}{sqrt{1-frac{v^2}{c^2}}}}). ((2))
Полная (релятивистская) энергия, или энергия свободной (невзаимодействующей) движущейся релятивистской частицы (сформулировал А. Эйнштейн):
(boxed{E=frac{m_0 c^2}{sqrt{1-frac{v^2}{c^2}}}}). ((3))
Кинетическая энергия массовой частицы:
(boxed{E_k=E-E_0}). ((4))
Импульс частицы:
(boxed{vec{p}=frac{m_0 vec{v}}{sqrt{1-frac{v^2}{c^2}}}}). ((5))
Если скорость частицы равна скорости света, то такую частицу называют безмассовой (фотон и нейтрино). В таком случае энергия и импульс свободной частицы связаны соотношением:
(boxed{E^2-p^2c^2=0}). ((6))
Таким образом, для всех свободных частиц в любой инерциальной системе можно записать:
(boxed{E^2-p^2c^2=m_0^2c^4}). ((7))
Физика, 11 класс
Урок №21. Релятивистские эффекты
На уроке рассматриваются понятия: энергия покоя, полная энергия частиц; связь массы и энергии в специальной теории относительности; релятивистский импульс частицы, релятивистская кинетическая энергия; принцип соответствия.
Глоссарий урока:
Релятивистская механика — раздел физики, где описывается движение частиц со скоростями близкими к скорости света.
Закон взаимосвязи энергии и массы — тело обладает энергией и при нулевой скорости, такую энергию называют энергией покоя.
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии.
Безмассовыми называют частицы массы, которых в состоянии покоя равны нулю, они существуют только в движении, при этом во всех инерциальных системах отсчёта их импульс и энергия не равны нулю.
Массовыми называют частицы, для которых масса является важной характеристикой, мерой инертности тела.
Принцип соответствия – это подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматриваются как частный случай релятивистских законов при скоростях намного меньших скорость света.
Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай.
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 239 – 241.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 149
Дополнительная литература:
- Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 253-260.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 311-315.
- Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.144-157
Основное содержание темы
«Основы физики претерпели неожиданные и радикальные изменения благодаря смелости молодого и революционно мыслящего гения.»
Вернер Гейзенберг
Эти слова и множество других восхищённых эпитетов будут высказаны в адрес гениального учёного Альберта Эйнштейна. Эйнштейн не боялся опровергать общепринятые утверждения. Он разрушил представление об абсолютном времени и незыблемости пространства. Его теория утверждала, что есть движущиеся системы координат со своим относительным временем. А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости — опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.
Альберт (Einstein) Эйнштейн
14 марта 1879 г. – 18 апреля 1955 г.
Физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист.
По законам классической физики: масса – это мера инертности тела. Но Эйнштейн утверждает другое: масса – это мера энергии, содержащейся в теле.
Любое тело обладает энергией уже в силу своего существования. Альбертом Эйнштейном была установлена пропорциональность между энергией и массой:
На первый взгляд, простая формула, является фундаментальным законом природы, законом взаимосвязи энергии и массы.
Согласно этой формуле тело обладает энергией даже при нулевой скорости, в таком случае энергию называют E энергией покоя. А массу, которая входит в формулу Эйнштейна назовём m0 массой покоя.
Как же будет выглядеть закон взаимосвязи массы и энергии для движущегося тела? К нему добавляем радикал 
Такую формулу называют релятивистской энергией или полной энергией движущегося тела.
Релятивистская механика — раздел физики, где описываются движения тел и частиц со скоростями близкими к скорости света, где используются преобразования Лоренца, перехода из одной инерциальной системы в другую, когда одна система движется относительно другой со скоростью вдоль оси ОХ.
Любые изменения физических величин, связанные с сокращением размеров:
эффект замедления времени:
изменение массы тела при изменении энергии:
закон сложения скоростей:
в специальной теории относительности называют релятивистскими изменениями.
По законам классической физики полная энергия равна сумме кинетической и потенциальной энергий тела или частицы
Отсюда выразим кинетическую энергию тела
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии
В классической физике кинетическая энергия вычисляется по формуле
Получим ещё одно выражение
Выразим кинетическую энергию из формулы релятивистской энергии:
Поставим релятивистский радикал
Или другой способ выражения кинетической энергии, если использовать классическую кинетическую энергию, то получим
— выражение для определения релятивистской кинетической энергии.
Путём не сложных математических вычислений можно доказать, что формула определения кинетической энергии в классической физике
Давайте проверим работают ли главные законы механики — законы Ньютона в релятивистской физике.
Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.
Первый постулат СТО Эйнштейна: все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.
Внимание! Они не противоречат друг другу!
Третий закон Ньютона: силы с которыми тела действуют друг на друга равны по модулю и направлены вдоль одной прямой в противоположные стороны. Этот закон тоже работает в релятивистской физике (смотрите первый постулат СТО).
А что же со вторым законом классической механики? Второй закон Ньютона: ускорение тела прямо пропорционально силе и обратно пропорционально его массе.
Рассмотрим предельный случай: если на тело долгое время t
Отсюда 

Но давайте рассмотрим другую формулировку второго закона Ньютона, когда сила прямо пропорциональна изменению импульсов тела ко времени этого изменения:
В классической механике импульс равен произведению массы тела или частицы на его скорость: 
В релятивистской механике выражение импульса можно записать, используя преобразования Лоренца:
При скоростях намного меньших, чем скорость света 𝟅
Эти проявления — подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматривают как частный случай релятивистских законов при скоростях намного меньших скорости света и называют принципом соответствия. Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.
В природе существуют такие частицы (фотоны, мюоны, нейтрино), скорость которых равна или близка к скорости света. Массы таких частиц в состоянии покоя равны нулю, эти частицы называют безмассовыми. Они существуют только в движении, но во всех инерциальных системах отсчёта их импульс и энергия не равны нулю. Тогда подтверждается утверждение Эйнштейна, что масса – это мера энергии тела. Частицы, для которых масса является важной характеристикой — мерой инертности, называют массовыми.
Найдём соотношение между энергией и импульсом:
Взаимно уничтожаются подкоренные выражения, сокращается произведение массы на скорость света, и мы получим простое соотношение энергии и импульса, где нет зависимости от массы.
Энергия и импульс связаны соотношением
Поэтому во всех инерциальных системах отсчёта импульс и энергия не равны нулю. При превращениях элементарных частиц, обладающих массой покоя 

Во всех инерциальных системах отсчёта импульс частицы и её энергия связаны соотношением:
или
— эта формула является фундаментальным соотношением энергии и импульса для массовых частиц релятивистской механики. Эти соотношения экспериментально подтверждены.
Следовательно, для безмассовых частиц, где 

Основное выражение энергии через её импульс записывают так:
Отсюда, масса, движущейся частицы, будет равна
Если частица покоится, то её значение можно определить из основной формулы Эйнштейна взаимосвязи массы и энергии:
В обычных условиях, при нагревании тела или его охлаждении, при химической реакции, эти приращения массы происходят, их можно вычислить, но изменения массы не так заметны. Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.
Рассмотрим задачи тренировочного блока урока:
1. Чтобы выработать количество энергии, которой обладает тело массой 1 кг, Красноярской ГЭС потребуется времени _________ суток (1,5·107; 173,6; 182,3). Мощность Красноярской ГЭС 6000МВт.
Дано:
m = 1 кг
P = 6000 МВт = 6·109 Вт
t — ? (сутки)
Воспользуемся выражением, описывающим зависимость энергии тела от массы:
И зависимостью мощности от работы и времени:
Выразим секунды в часах, а затем в сутках:
Ответ: 173,6 суток.
2. Чему равен импульс протона, летящего со скоростью 8,3·107 м/с? На сколько будет допущена ошибка, если пользоваться формулами классической физики? Данные поученных вычислений занесите в таблицу:
|
Физические величины |
Показатели |
|
Масса покоя протона, m |
1,67·10-27 кг |
|
Скорость света, с |
3·108 м/с |
|
Скорость движения протона, 𝟅 |
8,3·107 м/с |
|
Импульс протона по классическим законам, рк |
? |
|
Импульс протона по релятивистским законам, рр |
? |
|
Разница в вычислениях импульса протона, |
? |
Воспользуемся формулами для определения импульса релятивистским и классическим способами:
Вычислим разницу показаний:
|
Физические величины |
Показатели |
|
Масса покоя протона, m |
1,67·10-27кг |
|
Скорость света, с |
3·108 м/с |
|
Скорость движения протона, 𝟅 |
8,3·107 м/с |
|
Импульс протона по классическим законам, рк |
1,38·10-19кг·м/с |
|
Импульс протона по релятивистским законам, рр |
5,2·10-19 кг·м/с |
|
Разница в вычислениях импульса протона, |
в 3,8 раза |
Многие задачи на движение в классической механике могут быть решены с использованием понятия импульса частицы или всей механической системы. Рассмотрим подробнее концепцию импульса, а также покажем, как полученные знания можно использовать для решения физических задач.
Главная характеристика движения
В XVII веке при изучении перемещения небесных тел в пространстве (вращение планет в нашей Солнечной системе) Исаак Ньютон использовал концепцию количества движения. Справедливости ради отметим, что несколькими десятками лет ранее подобную характеристику уже применял Галилео Галилей при описании тел в движении. Однако только Ньютон смог ее лаконично встроить в разработанную им классическую теорию перемещения небесных тел.
Все знают, что одной из важных величин, характеризующих быстроту изменения координат тела в пространстве, является скорость. Если ее умножить на массу движущегося объекта, то мы получим упомянутое количество движения, то есть справедлива следующая формула:
p¯ = m*v¯
Как видно, p¯ — это векторная величина, направление которой совпадает с таковым для скорости v¯. Измеряется она в кг*м/с.
Физический смысл p¯ можно понять на следующем простом примере: с одинаковыми скоростями едет грузовик и летит муха, ясно, что остановить грузовик человек не сможет, а вот муху сможет без проблем. То есть количество движения прямо пропорционально не только скорости, но и массе тела (зависит от инерционных свойств).
Движение материальной точки или частицы
При рассмотрении многих задач на движение размеры и форма перемещающегося объекта часто не играют существенной роли для их решения. В этом случае вводят одно из самых распространенных приближений — тело считают частицей или материальной точкой. Она представляет собой безмерный объект, вся масса которого сосредоточена в центре тела. Это удобное приближение справедливо, когда размеры тела намного меньше проходимых им расстояний. Яркий пример — движение автомобиля между городами, вращение нашей планеты по своей орбите.
Таким образом, состояние рассматриваемой частицы характеризуется массой и скоростью ее перемещения (заметим, что скорость может зависеть от времени, то есть не быть постоянной).
Что это — импульс частицы?
Часто под этими словами понимают количество движения материальной точки, то есть величину p¯. Это не совсем правильно. Разберемся в этом вопросе подробнее, для этого запишем второй закон Исаака Ньютона, который проходят уже в 7 классе школы, имеем:
F¯ = m*a¯
Зная, что ускорение — это скорость изменения величины v¯ во времени, перепишем ее следующим образом:
F¯ = m*dv¯/dt => F¯*dt = m*dv¯
Если действующая сила не будет меняться со временем, тогда для интервала Δt будет справедливо равенство:
F¯*Δt = m*Δv¯ = Δp¯
Левая часть этого равенства (F¯*Δt) называется импульсом силы, правая часть (Δp¯) — изменение количества движения. Поскольку рассматривается случай движения материальной точки, то можно это выражение назвать формулой импульса частицы. Она показывает, на сколько изменится ее полное количество движения за время Δt при действии соответствующего импульса силы.
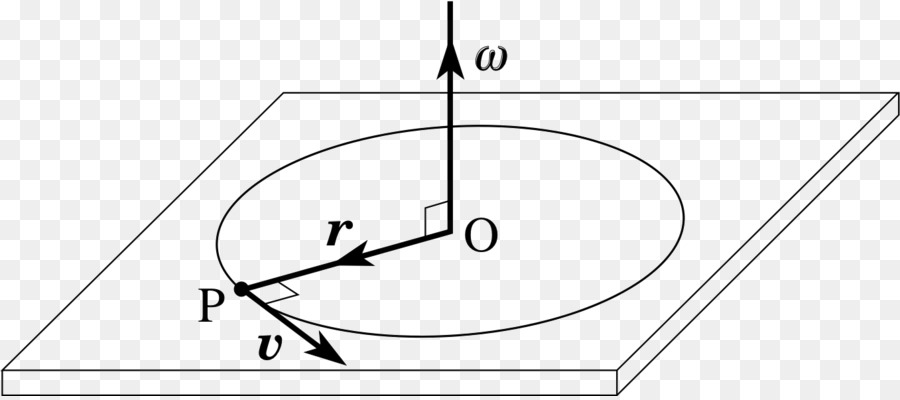
Момент импульса
Разобравшись с понятием импульса частицы массой m для линейного движения, перейдем к рассмотрению аналогичной характеристики для кругового перемещения. Если материальная точка, имея импульс p¯, вращается вокруг оси O на расстоянии от нее r¯, тогда можно записать такое выражение:
L¯ = r¯*p¯
Это выражение представляет собой момент импульса частицы, который так же, как и p¯, является величиной векторной (L¯ направлен согласно правилу правой руки перпендикулярно плоскости, построенной на отрезках r¯ и p¯).
Если импульс p¯ характеризует интенсивность линейного перемещения тела, то L¯ имеет аналогичный физический смысл только для круговой траектории (вращение вокруг оси).
Формула для момента импульса частицы, записанная выше, в этом виде не используется для решения задач. Путем несложных математических преобразований можно прийти к следующему выражению:
L¯ = I*ω¯
Где ω¯ — угловая скорость, I — момент инерции. Эта запись подобна таковой для линейного импульса частицы (аналогия между ω¯ и v¯ и между I и m).
Законы сохранения величин p¯ и L¯
В третьем пункте статьи было введено понятие импульса внешней силы. Если такие силы не действуют на систему (она является закрытой, и в ней имеют место лишь внутренние силы), то суммарный импульс частиц, принадлежащих системе, остается величиной постоянной, то есть:
p¯ = const
Заметим, что в результате внутренних взаимодействий сохраняется каждая координата импульса:
px = const.; py = const.; pz = const
Обычно этот закон используют для решения проблем со столкновением твердых тел, например шаров. Важно знать, что какой бы характер не имело столкновение (абсолютно упругое или пластическое), общее количество движения всегда будет оставаться одним и тем же до удара и после него.
Проводя полную аналогию с линейным движением точки, закон сохранения для момента импульса запишем так:
L¯ = const. или I1*ω1¯ = I2*ω2¯
То есть любые внутренние изменения момента инерции системы ведут к пропорциональному изменению угловой скорости ее вращения.
Пожалуй, одним из распространенных явлений, демонстрирующих этот закон, является вращение фигуриста на льду, когда он группирует по разному свое тело, изменяя при этом свою угловую скорость.
Задача на столкновение двух липких шаров
Рассмотрим пример решения задачи на сохранение линейного импульса частиц, движущихся друг навстречу другу. Пусть этими частицами будут шары, имеющие липкую поверхность (в данном случае шар можно считать материальной точкой, поскольку его размеры не влияют на решение поставленной проблемы). Итак, один шар движется вдоль положительного направления оси X со скоростью 5 м/с, он имеет массу 3 кг. Второй шар движется вдоль отрицательного направления оси X, его скорость и масса равны 2 м/с и 5 кг соответственно. Необходимо определить, в каком направлении и с какой скоростью будет перемещаться система после столкновения шаров и их прилипания друг к другу.
Импульс системы до столкновения определяется разностью количества движения для каждого шара (разность берется потому, что тела направлены в разные стороны). После же столкновения импульс p¯ выражен лишь одной частицей, масса которой равна m1 + m2. Поскольку шары движутся только вдоль оси X, имеем выражение:
m1*v1 — m2*v2 = (m1+m2)*u
Откуда неизвестная скорость находится по формуле:
u = (m1*v1 — m2*v2)/(m1+m2)
Подставляя данные из условия, получаем ответ: u = 0,625 м/c. Положительное значение скорости говорит о том, что система после удара будет двигаться по направлению оси X, а не против него.
Видеоурок 1: Основы специальной теории относительности. Часть 1
Видеоурок 2: Основы специальной теории относительности. Часть 2
Лекция: Энергия свободной частицы. Импульс частицы

Когда тела начинают двигаться с высокими скоростями, все знания классической механики перестают работать. В том числе речь идет и об одновременности событий между телами, что двигаются быстро и медленно.
Существует некий парадокс близнецов. В его основе лежит рассмотрение процессов человека, что двигается на космическом корабле высоких скоростей, и человека, находящегося на Земле. Считается, что процессы старения, а также другие возможные изменения организма на корабле происходят с меньшей скоростью. Существует предположение, что если на космическом корабле пройдет время равное году, то для человека на Земле оно будет исчисляться десятками лет.
Определить время, которое проходит для тела, двигающегося с высокими скоростями, относительно земного, можно по формуле:
Если, например, тело будет двигаться со скоростью близкой скоростью света, то для него пройдет 1 год, а для наблюдателя с Земли более 20 лет.
Если же два тела двигаются с высокими скоростями, то определить их относительные скорости можно по формуле:
При использовании данной формулы, относительная скорость не может получиться больше скорости света.

Для определения энергии тела, двигающегося со скоростью, близкой к свету, используют основную и всеми известную формулу:
С помощью нее можно определить энергию тела, что покоится.
Однако, если тело начинает быстро двигаться, то её энергия увеличивается на величину релятивистского корня:

Для определения импульса тела используют аналогичную формулу с релятивистским корнем:

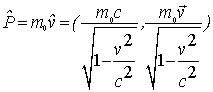
 .
.