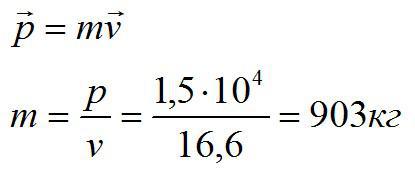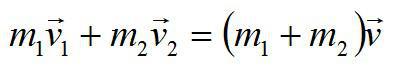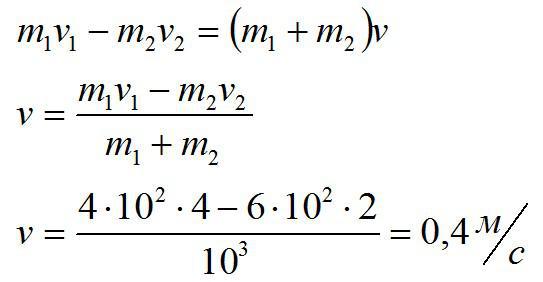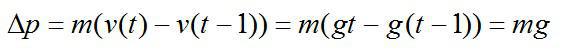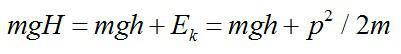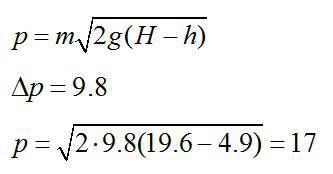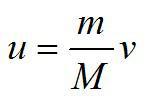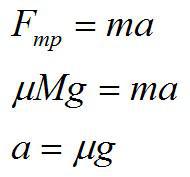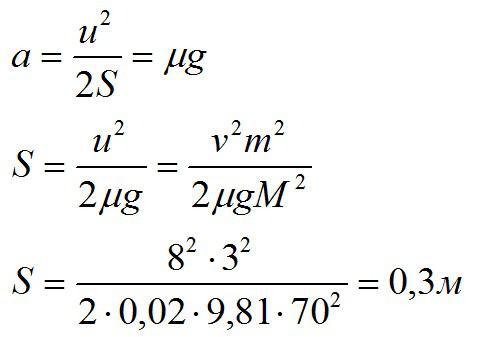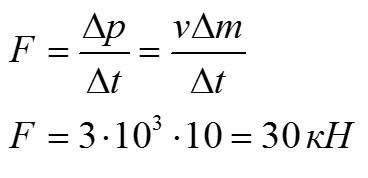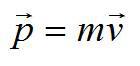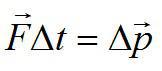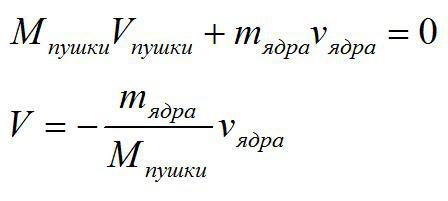Как найти импульс через высоту - Исправление недочетов и поиск решений вместе с Examum.ru

Сегодня в рубрике «Физика для чайников» занимаемся решением и разбором задач на закон сохранения импульса. И не говорите, что вы этого не ждали.

Полезные лайфхаки и новости для студентов – ежедневно на нашем телеграм-канале. Подписывайтесь!

Задачи на закон сохранения импульса с решением

Задача №1 на нахождение импульса

Условие

Небольшой автомобиль движется со скоростью 60 км/ч, его импульс равен 1,5*10^4 кг*м/с. Какова масса автомобиля?

Решение

По формуле для импульса найдем:

Ответ: 903 кг.

Задача №2 на закон сохранения импульса

Условие

Дрезина массой 400 кг движется со скоростью 4 м/с, а навстречу ей со скоростью 2 м/с едет дрезина массой 60 кг. После неупругого соударения дрезины движутся вместе. В каком направлении и с какой скоростью будут двигаться дрезины?

Решение

Общий импульс системы до и после соударения должен остаться неизменным:

Запишем закон сохранения импульса в проекции на горизонтальную ось:

Движение будет происходить в сторону первой дрезины. Именно она изначальна имела больший импульс.

Ответ: 0,4 м/с.

Задача №3 на нахождение импульса

Условие

Тело массой m=1 кг упало с высоты H=19,6 м. Определить изменение импульса тела за последнюю секунду движения и импульс тела на высоте h=4,9 м.

Решение

Изменение импульса тела за последнюю секунду движения равно:

Импульс тела на заданной высоте найдем по закону сохранения энергии, который имеет вид для двух состояний:

Отсюда получим:

Ответ: Изменение импульса равно 9,8 кг*мс2; р=17 кг*мс2.

Задача №4 на применение закона сохранения импульса и второго закона Ньютона

Условие

Хоккеист массой М = 70 кг стоит на льду и бросает в горизонтальном направлении шайбу массой m = 3 кг со скоростью v = 8 м/с относительно льда. На какое расстояние S откатится при этом конькобежец, если коэффициент трения равен 0,02.

Решение

По закону сохранения импульса найдем скорость u, с которой хоккеист откатиться назад:

По второму закону Ньютона для хоккеиста:

С другой стороны:

Ответ: 0,3 м.

Задача №5 на реактивное движение

Условие

Реактивный двигатель каждую секунду выбрасывает 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты. Какую силу тяги он развивает?

Решение

Запишем второй закон Ньютона в импульсной форме и найдем силу, которая действует на выбрасываемые продукты сгорания топлива:

По третьему закону Ньютона сила тяги будет равна найденной силе.

Ответ: 30 кН.

Вопросы на закон сохранения импульса

Вопрос 1. Что такое замкнутая система?

Ответ. Замкнутая система – такая система, на которую не действуют внешние силы со стороны других тел.

Вопрос 2. Что такое импульс силы?

Ответ. Импульс силы – физическая величина, равная произведению силы на время ее действия.

Вопрос 3. Как направлен импульс тела?

Ответ. Направление импульса совпадает с направлением вектора скорости тела.

Вопрос 4. Что такое реактивное движение?

Ответ. Реактивное движение – движение, основанное на принципе отдачи. По аналогии с системой «пушка-ядро», систему «ракета-выхлопные газы» также можно считать замкнутой.

Вопрос 5. Два тела разной массы движутся с одинаковой скоростью. Импульс какого тела больше?

Ответ. Тело с большей массой обладает большим импульсом.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Импульс и закон сохранения импульса

Что такое импульс в механике

Импульс, или количество движения – векторная физическая величина, равная произведению массы тела на его скорость.

Обозначается латинской буквой p и измеряется в килограммах на метр в секунду.

Второй закон Ньютона с применением импульса можно записать следующим образом:

Здесь дельта p – изменение импульса тела за время дельта t под действием равнодействующей силы F.

Закон сохранения импульса

Этот фундаментальный закон природы и гласит:

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Закон сохранения импульса является следствием второго и третьего законов Ньютона.

Более подробную теорию по этой и другим темам вы найдете в нашем справочнике.

Пример действия закона сохранения импульса

Представим себе пушку, которая стреляет ядрами. Систему «пушка-ядро» можно считать замкнутой. При стрельбе из пушки действует закон сохранения импульса. Ядро летит в одну сторону, а пушка под действием отдачи откатывается назад. При этом скорость, приобретенная пушкой, зависит от соотношения масс орудие/ядро и скорости ядра.

Знак минус указывает на то, что пушка и ядро движутся в разные стороны.

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис.

Источник

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p₀ – p = m(v₀ – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p = 2mv₀
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁+ m₂)v

Отсюда скорость равна:

Задание EF17556

Импульс частицы до столкновения равен −p₁, а после столкновения равен −p₂, причём p₁= p, p₂= 2p, −p₁⊥−p₂. Изменение импульса частицы при столкновении Δ−p равняется по модулю:

а) p

б) p√3

в) 3p

г) p√5

Алгоритм решения

1.Записать исходные данные.

2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.

3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.

4.Подставить известные значения и вычислить.

Решение

Запишем исходные данные:

• Модуль импульса частицы до столкновения равен: p₁= p.

• Модуль импульса частицы после столкновения равен: p₂= 2p.

• Угол между вектором начального и вектором конечного импульса: α = 90^о.

Построим чертеж:

Так как угол α = 90^о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δp=√p21+p22

Подставим известные данные:

Δp=√p2+(2p)2=√5p2=p√5

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17695

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Алгоритм решения

1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.

2.Сделать вывод о том, как зависит характер движения от импульса.

3.На основании вывода и анализа графика установить характер движения тела на интервалах.

Решение

Импульс тела есть произведение массы тела на его скорость:

p = mv

Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.

На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.

Верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22730

Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.

Алгоритм решения

1.Записать исходные данные.

2.Записать закон сохранения импульса применительно к задаче.

3.Записать формулу кинетической энергии тела.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса камня: m₁ = 3 кг.

• Масса тележки с песком: m₂ = 15 кг.

• Кинетическая энергия тележки с камнем: E_k = 2,25 Дж.

Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:

m1v1+m2v2=(m1+m2)v

Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:

m1v1cosα=(m1+m2)v

Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:

Ek=(m1+m2)v22

Отсюда скорость равна:

v=√2Ekm1+m2

Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:

v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2

Подставим известные данные и произведем вычисления:

v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)

Ответ: 6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22520

Снаряд, имеющий в точке О траектории импульсp₀, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:

а) −−→AB

б) −−→BC

в) −−→CO

г) −−→OD

Алгоритм решения

1.Сформулировать закон сохранения импульса и записать его в векторной форме.

2.Применить закон сохранения импульса к задаче.

3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:

−p1+−p2=−p′
1+−p′2

Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:

−p0=−p1+−p2

Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:

−p2=−p0−−p1

Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18122

Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?

Ответ:

а) 27 г

б) 64 г

в) 81 г

г) 100 г

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.

3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса пластилиновой пули: m = 9 г.

• Скорость пластилиновой пули: v = 20 м/с.

• Максимальный угол отклонения нити: α = 60°.

Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.

После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:

mv=(m+M)V

После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.

Закон сохранения энергии для точки В:

(m+M)V22=(m+M)gh

V22=gh

Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:

V=√2glcosα

Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 20.2k

Источник

Импульсом тела называется произведение его массы на скорость. Также импульс называют количеством движения. Импульс является векторной величиной. Направление его совпадает с направлением скорости.

Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует:

Здесь — изменение импульса за время . Произведение силы на время ее действия называют импульсом силы. Сила здесь может быть и равнодействующей всех сил, действующих на тело.

Закон сохранения импульса – следствие второго и третьего законов Ньютона. Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.

В замкнутой системе суммарный импульс системы тел остается постоянным при любых взаимодействиях тел в системе между собой.

Система тел может быть не замкнута вдоль одной из осей, а вдоль другой – замкнута. Тогда закон сохранения импульса будет работать в такой системе вдоль этой оси. Например, если рассматривать столкновение лодок на озере и не принимать в расчет трение, то такая система может считаться замкнутой вдоль горизонтальной оси, и вдоль этой оси работает закон сохранения импульса. Вдоль вертикальной оси действует сила тяжести, и система не замкнута.

Также при решении задач, связанных с импульсом, очень важны такие понятия, как абсолютно упругий и абсолютно неупругий удары. При абсолютно упругом ударе тело отскакивает от другого тела, сохраняя модуль импульса, и «угол падения равен углу отражения». При абсолютно неупругом ударе тела слипаются, образуя новое тело, масса которого равна сумме их масс. То, что удар был неупругим можно понять, например, если тело отскочило под углом, не равным углу падения, если о неупругом ударе специально не сказано в задаче.

Рассмотрим сначала простые задачи, где движение тел происходит вдоль одной прямой.

Задача 1.

Тело массой кг движется равномерно по окружности, со скоростью м/с. Определить изменение импульса тела после того, как оно пройдет четверть окружности, половину окружности.

Изменение импульса

После того, как тело пройдет четверть окружности, вектор его скорости повернется на 90 градусов, как показано на рисунке — . Изменение скорости можно определить как , поэтому разворачиваем вектор скорости , чтобы получить вектор , и складываем его с по правилу параллелограмма. Зеленым показан вектор изменения скорости . По теореме Пифагора можно найти его длину – он будет равен м/с, тогда изменение импульса тела в этом случае кг*м/с.

Вектора импульсов тел системы

Вектора импульсов и их сложение

Когда тело пройдет половину окружности, вектор его скорости развернется в противоположную сторону — . Точно так же изменение скорости можно определить как , поэтому разворачиваем вектор скорости , чтобы получить вектор , и складываем его с по правилу многоугольника. Зеленым показан вектор изменения скорости . Видно, что м/с.

Изменение импульса тела в этом случае кг*м/с.

Ответ: кг*м/с, кг*м/с.

Задача 2.

Снаряд массой кг вылетает из ствола орудия со скоростью м/с. Зная, что время движения снаряда внутри ствола равно с, определить среднюю силу давления пороховых газов.

На вылете из ствола пушки снаряд обладает импульсом, равным кг*м/с. Так как на систему не действуют никакие внешние силы, то импульс системы сохраняется, а до выстрела он был нулевым. После выстрела суммарный импульс системы также нулевой, а это значит, что импульс снаряда равен по модулю и противоположен по направлению изменению импульса пороховых газов в стволе. Таким образом, газы будут давить с силой кН

Ответ: 1000 кН

Задача 3.

На тело в течение времени с действовала сила Н. Найти массу тела, если изменение скорости тела в результате действия силы равно м/с.

Изменение импульса равно произведению изменения скорости на массу тела. Импульс силы равен , масса тела тогда кг.

Ответ: 100 кг

Задача 4.

Скорость реактивного самолета равна км/ч. На пути самолета оказалась птица массой кг. Определить среднюю силу удара птицы о стекло кабины летчика, если длительность удара с. Каково среднее давление на стекло при ударе, если площадь соприкосновения птицы со стеклом см?

Среднюю силу удара можно определить так:

Скорость самолета выразим в единицах СИ – метрах в секунду. км/ч м/с

Или 500 кН. Можно теперь определить среднее давление на стекло при ударе, только прежде представить площадь в м:

см м

Паскалей или 50 атмосфер.

Ответ: Па или 50 атмосфер.

Задача 5.

Падающий вертикально шарик массой кг ударился о пол и подпрыгнул на высоту 0,4 м. Найти среднюю силу, действующую со стороны пола на шарик, если длительность удара с, к моменту удара о пол скорость шарика м/с.

Шарик двигается равноускоренно, поэтому, когда он соприкоснется с полом, его вес будет больше силы тяжести. А его вес – это, собственно, и есть сила его давления на пол.

При равноускоренном движении вес можно вычислить:

Определим ускорение шарика. Здесь — мера изменения скорости шарика,

Так как шарик взлетел на высоту 0,4 метра, то определим его скорость при отрыве от пола по формуле:

Скорость шарика в наивысшей точке равна 0, поэтому:

Тогда изменение скорости

Ответ: 158 Н

Задача 6.

Шарик летит навстречу стенке со скоростью . Стенка движется навстречу шарику со скоростью . Какой станет скорость шарика после упругого удара о стенку?

Сначала рассмотрим полет шарика относительно стенки. Тогда (если мы представим себе, что смотрим от стенки, и вместе с ней двигаемся со скоростью , не замечая этого) нам будет казаться, что шарик летит на нас со скоростью . Тогда после отскока шарик изменит свою скорость на такую же по модулю, но противоположную по направлению: — это мы его от стенки наблюдаем. А вот теперь мы покинули движущуюся стенку и смотрим с неподвижной земли – и тогда шарик летит уже со скоростью — минус показывает противоположное, относительно первоначального, направление полета.

Задача 7.

Мальчик массой 22 кг, бегущий со скоростью 2,5 м/c, вскакивает сзади на платформу массой 12 кг. Чему равна скорость платформы с мальчиком?

Импульс системы тел будет сохраняться вдоль горизонтальной оси. Поэтому суммарный импульс тележки (0) и мальчика () будет равен суммарному импульсу тележки с мальчиком на ней после прыжка:

Ответ: 1, 62 м/с

Задача 8.

Два неупругих шара с массами 4 и 6 кг движутся со скоростями 8 м/с и 3 м/с соответственно, направленными вдоль одной прямой. С какой скоростью они будут двигаться после абсолютно неупругого удара, если первый догоняет второй? Если они двигаются навстречу?

Запишем закон сохранения в первом случае:

Все слагаемые с плюсами, так как тела движутся в одну сторону.

Теперь тела двигаются навстречу друг другу:

Ответ: 5 м/с, 1,4 м/с

Задача 9.

Тележка с песком катится со скоростью 1 м/с по горизонтальному пути без трения. Навстречу тележке летит шар массой 2 кг с горизонтальной скоростью 7 м/с. Шар после попадания в песок застревает в нем. В какую сторону и с какой скоростью покатится тележка после столкновения с шаром? Масса тележки 10 кг.

Записываем уравнение сохранения импульса системы тел вдоль горизонтальной оси: примем — масса камня, — скорость камня, — масса тележки, — скорость тележки.

За положительное направление примем направление полета камня, тогда скорость тележки будет со знаком «минус»

Получили скорость тележки с камнем со знаком «плюс» — это значит, что она после «поимки» камня поедет в противоположную сторону.

Ответ: 2 м/c

Задача 10.

Средневековая пушка массой 200 кг установлена у края плоской крыши высокой башни. Пушка выпускает ядро массой 5 кг горизонтально, оно приземляется на расстоянии 300 м от стены башни. Пушка, двигаясь без трения, откатывается назад и падает на землю. На каком расстоянии от основания башни она упадет?

Предположим, что высота стены башни . Ядро пушка выпустила горизонтально, и его полет подобен телу, брошенному горизонтально: по горизонтали ядро перемещается с постоянной скоростью, а по вертикали падает, то есть движется равноускоренно.

Тогда ядро будет падать с этой высоты в течение времени, которое можно установить из формулы:

Все это время ядро летит горизонтально с постоянной скоростью, и пролетает 300 метров. Тогда его скорость по горизонтали равна:

Импульс ядра равен импульсу пушки, поэтому пушка откатится назад со скоростью:

Здесь — масса ядра, — его скорость, — масса пушки, — ее скорость.

Найдем горизонтальную скорость пушки:

Пушка падает ровно столько же времени, как и ядро, так как все тела на Земле падают вниз с одним и тем же ускорением, поэтому пушка пролетит за время расстояние от стены до места падения, равное: м

Ответ: 7,5 м

Источник

Импульсом
материальной точки называют вектор p,
равный произведению массы m
точки на ее скорость v
в данной системе отсчета.

(12.1)

Импульс
материальной точки является одной из
важнейших ее динамических характеристик,
зависящих как от скорости движения
точки, так и от ее инертности (массы).

Второй
закон Ньютона для материальной точки
т
(7.1) можно записать в виде:

.
(12.2)

Выражение
(12.2) является более общей записью этого
закона, который можно трактовать
следующим образом: «Скорость
изменения импульса p
материальной точки равна сумме сил,
действующих на эту точку».
В такой форме второй закон Ньютона можно
применять для тел и в случае их переменной
массы.

Импульсом
P
системы материальных точек называют
геометрическую
сумму импульсов всех материальных точек
системы.

.
(12.3)

Импульс
P
тела массой m,
состоящего из материальных точек, в
случае его поступательного движения
со скоростью v
равен:

В
этом случае импульс тела является мерой
его движения. Однако эта характеристика
не может служить универсальной мерой
для всех форм движения. Поясним это
следующими примерами.

Например,
если однородное тело правильной формы
(шар или куб) равномерно вращается
вокруг неподвижной оси, проходящей
через центр симметрии, то легко проверить,
что векторная сумма (12.3) импульсов всех
материальных точек равна нулю при любой
угловой скорости тела. Следовательно,
импульс тела не может служить мерой
его вращательного
движения
.
Два
тела массой 1кг и 2кг, соответственно,
свободно падая с высот 20м и 5м, имеют
у поверхности Земли одинаковые импульсы.
Однако, как показывают опыты, при ударе
о Землю первое тело способно сжать две
одинаковые пружины на столько же,
насколько второе тело может сжать
только одну из этих пружин. Таким
образом, импульс тела не может полностью
количественно охарактеризовать
динамические свойства тел даже при
поступательном движении.

Единой
мерой различных форм движения служит
физическая величина, называемая энергией.

§13. Энергия

Установлено,
что все формы движения превращаются
друг в друга в строго определенных
количественных соотношениях. Именно
это обстоятельство и позволило ввести
понятие об энергии, т.е. позволило
измерять различные формы движения и
взаимодействия единой мерой.

Энергия
механической системы количественно
характеризует ее с точки зрения возможных
в ней превращений движения. Эти превращения
обусловлены взаимодействием тел системы,
как между собой, так и с внешними телами.

Важность
понятия энергии определяется еще и тем,
что энергия подчиняется закону сохранения.
Это означает, что если взаимодействием
данной системы с окружающим миром можно
пренебречь, то в этой системе при любых
процессах энергия может только
превращаться из одной формы в другую,
сохраняя свое значение. Понятие энергии
связывает воедино все явления природы.
Поэтому вводят понятия механической
энергии (механика), внутренняя энергия
(термодинамика), электромагнитная
энергия (электричество и магнетизм),
ядерная энергия (ядерная физика) и др.

Механическую
энергию разделяют на два вида: кинетическую
и потенциальную энергии.

Кинетическая
энергия

Кинетическая
энергия Е_к
материальной точки является мерой ее
механического движения.

Пусть
на материальную точку массой m,
движущуюся со скоростью v
действует сила F.
На малом участке dr
эта сила совершает работу A,
равную
Fdr,
а скорость материальной точки изменяется
от v
до значения v+dv.

Из
второго закона Ньютона для материальной
точки m
следует:

Отсюда,
.

Работа,
совершаемая силой F
при
возрастании скорости материальной
точки от v₁
до v₂,
равна:

Здесь
учтено, что
.
(см.2.6)

Величина
называется кинетической энергией
материальной точкит.

Таким
образом, можно сказать, что работа,
совершаемая над материальной точкой
произвольной силой, равна изменению
кинетической энергии этой точки:

.
(13.1)

Если
работа силы положительна, то кинетическая
энергия частицы возрастает, если
отрицательна, то убывает.

Это
позволяет интерпретировать кинетическую
энергию частицы как запас работы, которую
совершили над ней внешние силы. Этот
запас может расходоваться (кинетическая
энергия убывает), и тогда внешние силы
совершают отрицательную работу. Говорят,
что кинетическая энергия израсходована
на работу против
внешних сил.

Кинетическая
энергия – величина аддитивная. Это
означает, что кинетическая энергия Е_к_
системы N
материальных точек равна сумме
кинетических энергий всех точек, входящих
в эту систему.

,
(13.2)

где

—
масса и скорость i-ой
материальной точки.

Полученные
результаты можно обобщить на случай
произвольной системы материальных
точек.

Если
записать соотношение (13.1) для каждой
материальной точки и затем все уравнения
сложить, то мы получим:

А_{всех

сил}
=
–= (Е_к_)_кон
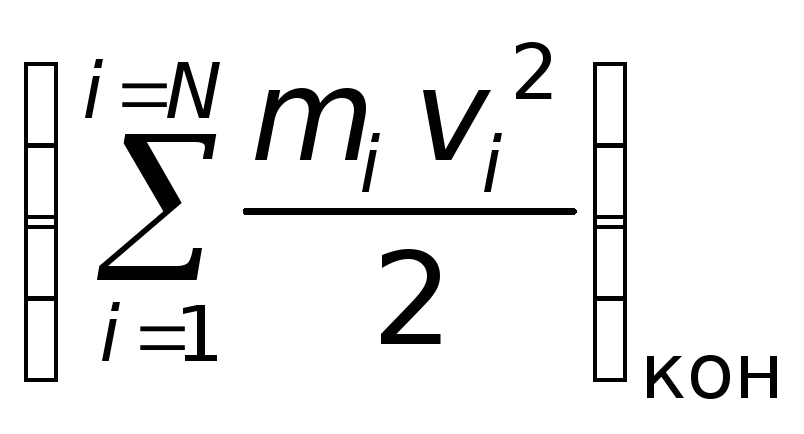
– (Е_к_)_нач.
(13.3)

Таким
образом, работа
всех сил, действующих на систему
материальных точек, равна приращению
кинетической энергии этой системы.

Полученное
выражение выражает теорему
об изменении кинетической энергии:
приращение
кинетической энергии системы материальных
точек равно сумме работ всех приложенных
к системе внешних и внутренних сил.

Важность
полученного результата заключается в
том, что приращение кинетической энергии
системы определяется работой не только
внешних
сил (сил со стороны тел, не включенных
в рассматриваемую систему), но и работой
внутренних
сил, т.е. силами взаимодействия между
материальными точками системы.

Как
мы увидим в дальнейшем, внутренние силы
не могут изменить импульс всей системы
материальных точек.

Потенциальная
энергия частицы во внешнем силовом
поле.

Введем
понятие силового поля.

Если
в каждой точке данного пространства
известны величина направление силы,
действующей на рассматриваемую частицу,
то говорят, что в этом пространстве
задано поле сил
или силовое поле.

Мы
ограничимся рассмотрением полей сил,
не зависящих от времени,
т.е. стационарных
полей.

Например,
в каждой точке пространства данной
аудитории на частицу массой m
действует сила гравитации со стороны
Земли, равная mg
и направленная к центру Земли. Можно
сказать, что в данной аудитории действует
гравитационное поле сил.

Другой
пример: при движении материальной точки
по поверхности стола на нее со стороны
поверхности действует сила трения,
равная μN
и направленная противоположно скорости
ее движения. Говорят, что на поверхности
стола действует поле сил трения.

Вводя
понятие работы, мы говорим, что действие
силы на каком-либо участке характеризуется
работой, т.е. сила совершает работу на
данном участке. Например, при движении
тела из точки 1 в точку 2 по поверхности
стола силы трения будут совершать
работу. Очевидно, что работа сил трения
будет зависеть от того, по какому пути
будет двигаться тело из точки 1 в точку
2. Чем длиннее путь, пройденный телом,
тем больше работа сил трения, хотя при
этом отправная и конечные точки пути
одни и те же.

Однако,
можно выделить класс сил, которые
обладают замечательным свойством –
работа,
совершаемая силой при перемещении
частицы из точки 1 в точку 2, не
зависит от формы пути,
по которому частица перемещается из
т.1 в т.2 ( рис. 13.1).

Это
означает, что
,

где
—
работа при перемещении частицы из 1 в 2
по траектории 1-а-2;

—
работа при перемещении частицы из 1 в 2
по траектории 1-b-2.

Рис.13.1.
Работа
консервативных сил

не
зависит от формы траектории, по

которой
частица перемещается из т.1 в т.2.

акие силы называютсяконсервативными.
Если такое свойство сохраняется и для
силовых полей, меняющихся со временем
(не стационарных полей), то такие силы
называются потенциальными.
Консервативные силы – это частный
случай потенциальных сил.

Изменение
направления движения частицы на
противоположное вызывает изменение
знака работы консервативной силы, так
как
меняет свой знак. Поэтому, при перемещении
частицы по любому замкнутому контуруL,
например, 1-а-2-b-1,
работа консервативной силы тождественно
равна 0. Это обстоятельство позволяет
записать условие консервативности сил
в следующей математической форме:

.
(13.4)

Кружок
на знаке интеграла означает суммирование
по замкнутому контуру. Тождество (13.4)
является необходимым
условием консервативности сил F_кон.
Условие (13.4) не может быть достаточным
условием консервативности сил данного
поля. Для этого нужно доказать, что это
условие выполняется для любого
замкнутого контура. Как это сделать, мы
узнаем позже, когда познакомимся с
понятием ротора векторной функции.

К
неконсервативным
силам относятся диссипативные
(силы трения) и
гироскопические
силы, с которыми мы познакомимся попозже.

Введем
понятие потенциальной энергии. Допустим,
что на частицу в пространстве действуют
консервативные силы. В этом случае
говорят, что задано потенциальное поле
сил. Из определения консервативных сил
ясно, что работа, совершаемая силами
потенциального поля над частицей,
зависит только от взаимного расположения
начальной 1 и конечной 2 точек пути. Это
означает, что работу в этом случае можно
выразить в виде:

,
(13.5)

где

—
некоторые значения функции состояния
частицы, зависящие только от ее координат.
Эту функцию и называютпотенциальной
энергией.

Из
соотношения (13.5) следует, что работа
сил потенциального поля равна убыли
потенциальной энергии частицы:

.
(13.6)

Выражение
(13.5) позволяет найти зависимость
потенциальной энергии частиц от координат
только с точностью до постоянного
слагаемого С,
не влияющего величину разности
.
Поэтому в каждой конкретной задаче для
получения однозначной зависимостиU_пот
от
координат выбирают точку, для которой
потенциальную энергию частицы (или
системы) условно считают равной нулю.

Используя
выражение (13.5), можно дать определение
потенциальной энергии. Потенциальная
энергия системы в произвольном состоянии
равна работе, которую должны совершить
потенциальные силы при переводе системы
из этого состояния в состояние, где U_п2
равна нулю.

В
качестве примера рассмотрим однородное
силовое поле и поле центральных сил.

а)
Однородное поле.

Если
во всех точках рассматриваемого
пространства силы поля равны и по
величине и по направлению, то такое поле
называется однородным.

Работа,
совершаемая постоянной силой F,
равна (11.4):

Очевидно,
что эта работа не зависит от формы
траектории, а зависит только от начального
и конечного положения точек движения
r₁и
r₂.
Следовательно, однородное силовое поле
потенциально.

Например,
гравитационное поле вблизи поверхности
Земли в пределах небольшой области
(r<<R_Земли)
можно считать однородным: F=mg=
const.
Тогда работа сил тяжести будет равна:
А
= mg(r₂
–
r₁)
= mgr
= mgrcos(g,r)
= mg(h₂
– h₁)
= –U_пот.

Итак,
работа сил тяжести будет равна: А
= –(U_кон
– U_нач).

Следовательно,
потенциальная энергия в однородном
поле сил тяжести равна:

U(h)
= mgh
+ C.
(13.8)

Константу
С
удобнее всего выбрать равной нулю. Это
означает, что на высоте h
равной нулю потенциальная энергия U(0)
будет считаться тоже равной нулю. Начало
отсчета высоты h
выбирается произвольно из соображений
удобства решения задачи. Таким образом,
потенциальная энергия материальной
точки, поднятой на высоту h,
возрастает на величину mgh.

б)
Поле центральных
сил

Аналогичным
образом вычисляется потенциальная
энергия для различных потенциальных
полей: сначала доказывается, что данное
поле сил потенциально и затем вычисляется
работа этих сил при переходе системы
из начального положения в конечное,
причем по наиболее удобной траектории.
Подобным образом получают выражение
для потенциальной энергии данного поля.

Рассмотрим
поле центральных сил. Если все
силы данного поля направлены к одной
точке (или от нее), а их величина зависит
только от расстояния до этой точки,
называемой силовым
центром,
то такое поле называется центральным
полем сил. Это определение можно записать
в математической форме:

F
=
f(r)
e_r,
(13.9)

где
e_r
– единичный вектор, задающий направление
радиус-вектора точки поля относительно
силового центра, т.е.
r
= re_r.
Элементарная работа такой силы будет
равна А
= f(r)e_rdr.
С учетом соотношения (2.6) произведение
e_rdr
равно:

.
Следовательно, dА
= f(r)×dr.
Работа этой силы на произвольном пути
от точки 1 до точки 2 равна:

.
(13.10)

Полученное
выражение зависит только от вида функции
f(r)
и от значений r₁
и r₂,
и никак не зависит от формы траектории
движения и поэтому является потенциальным.

Рассмотрим
гравитационное взаимодействие двух
материальных точек М
и
т. По
закону всемирного тяготения сила
взаимодействия по модулю равна:
.
Если рассматривать силу, действующую
на точку т,
то можно сказать, что гравитационное
силовое поле, создаваемое материальной
точкой М,
действует на точку т
с силой F.

Другими
словами, материальная точка М
создает поле центральных сил с силовым
центром в точке М.

Поместим
начало отсчета в точку М.

Тогда
в векторном виде сила гравитации,
действующая на точку т,
примет следующий вид:

(13.11)

При
перемещении точки т
из r₁
в точку r₂
силы гравитации совершат работу:

.
(13.12)

Сравнивая
полученное выражение с (13.6), получим,
что потенциальная энергия частицы т
в гравитационном поле точки М
равна:

.
(13.13)

При
большом удалении точек друг от друга
(),
сила их гравитационного взаимодействия
стремится к нулю, и, следовательно,
должна стремиться к нулю и потенциальная
энергия. Поэтому в данном случае константуС
можно положить равной нулю.

Выражение
(13.13) является точным для расчета
потенциальной энергии частицы т
в гравитационном поле точки М.
Выражение (13.8) является приближенным
расчетным соотношением для вычисления
потенциальной энергии частицы в
гравитационном поле. Покажем это.

Можно
доказать, что тело сферической формы
массой М
создает вне себя точно такое же
гравитационное поле, как материальная
точка такой же массы, помещенная в центр
шара. Следовательно, при поднятии тела
массой т
с поверхности, например, Земли на высоту
h
ее потенциальная энергия меняется на
величину

.
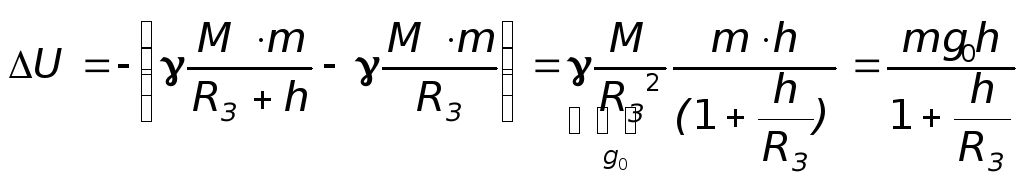
(13.14)

Если
h<<R_Земли,
то это выражение переходит в (13.8).

Таким
образом, если все перемещения происходят
вблизи поверхности Земли, то можно
пользоваться выражением (13.8), если нет
– то надо использовать более точное
выражение (13.14).

Если
в силовом потенциальном поле находится
система невзаимодействующих
между собою материальных точек, то
потенциальная энергия такой системы в
этом силовом поле будет равна сумме
потенциальных энергий каждой точки в
отдельности: U_сист
= U_i

Если
частицы системы взаимодействуют между
собой, то для того чтобы найти потенциальную
энергию всей системы, нужно к потенциальной
энергии частиц во внешнем силовом поле
добавить потенциальную энергию их
взаимодействия.

Соседние файлы в папке Лекции по физике

Источник

Содержание:

Импульс
Сохранение импульса
Центр инерции
Соударения
Явления отдачи

Импульс — это векторная физическая величина, являющаяся мерой механического движения тела.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Импульс

Импульс – векторная величина, направлен он всегда в ту сторону, в которую направлена скорость. Само слово «импульс» латинское и переводится на русский язык как «толкать», «двигать».

Сохранение импульса

Импульсом тела или материальной точки называют произведение массы точки на вектор скорости, (другой термин для этой величины — количество движения). Импульс является, таким образом, векторной величиной. Если речь идет о системе тел или системе точек, то импульс такой системы равен геометрической сумме импульсов точек, составляющих систему:

Основная особенность, делающая эту векторную величину интересной для физика, заключается в том, что в замкнутой системе вектор не изменяется, какие бы движения ни происходили внутри системы. Это положение носит название закона сохранения импульса.

Закон сохранения импульса следует непосредственно из законов Ньютона. Для каждого из тел, входящих в замкнутую систему, справедливо уравнение

Подумаем, что будет, если сложить такие уравнения, записанные для всех тел. В правой части равенств стоят силы, действующие на данное тело со стороны остальных. Скажем, сила, действующая на первое тело, равна сумме сил, действующих на него со стороны второго, третьего и т. д. тел. Пользуясь двойными индексами, это можно записать так: Совершенно аналогично можно записать выражение силы, действующей на второе тело: на третье: и т. д. Нетрудно сообразить, что при сложении правые части равенств дают нуль. Каждому слагаемому одной строки всегда найдется в другой строке ему равное и противоположное по знаку в соответствии с правилом действия и противодействия. Так, сила даст нуль в сложении сила — в сложении с и т. д. Поэтому в замкнутой системе имеет место равенство

Это и есть закон сохранения импульса. Величины и направления импульсов отдельных тел могут меняться, но их геометрическая сумма для замкнутой системы не меняется.

Значения некоторых импульсов: импульс электрона с энергией винтовочной пули товарного поезда

Центр инерции

Известны способы нахождения центра тяжести любого тела. Если тело закреплено в центре тяжести, то оно находится в положении безразличного равновесия. Если имеется система материальных точек или если сплошное тело условно разбить на элементарные объемы, рассматривая каждый как материальную точку, то можно дать аналитическое выражение для положения центра тяжести.

Используя правило сложения параллельных сил (рис. 19), мы можем найти для случая, когда материальные точки расположены вдоль одной линии, скажем, вдоль оси х, следующее выражение для положения центра тяжести:

Здесь —координаты материальных точек, а .— их массы. Массы появляются вместо весов, так как ускорение силы тяжести сокращается.

В теоретической мбх нике показывается, что при произвольном расположении материальных точек выражение для положения центра тяжести имеет вид

где — радиус-вектор центра, а — радиусы-векторы точек.

То, что ускорение силы тяжести сократилось в этих формулах, позволяет нам считать, что найденная точка имеет объективный смысл и в том случае, когда тело будет перенесено в другие гравитационные условия и даже если будет находиться в условиях невесомости в межпланетном пространстве. Поэтому целесообразно распространенное название «центр тяжести» заменить на название, имеющее прямое отношение к существу дела, а именно, говорить не о центре тяжести, а о центре инерции тела.

Сейчас же мы увидим глубокий смысл этого названия. Рассмотрим скорость движения центра инерции

Пользуясь формулой местонахождения центра инерции, получим

В числителе стоит суммарный импульс, который сохраняется в замкнутой системе; значит, в правой части равенства находится постоянная величина. Отсюда вывод: вектор скорости центра инерции не меняется ни по величине, ни по направлению. Или, иначе говоря, центр инерции замкнутой системы материальных точек совершает инерционное движение.-

Как мы знаем, все инерциальные системы координат равноправны. Можно поэтому всегда перейти к системе координат, связанной с центром инерции изучаемой системы, и считать эту интересную точку покоящейся. В атомной физике часто рассматриваются соударения частиц между собой. Для этой цели используются две системы координат: лабораторная (естественная координатная система наблюдателя) и система, связанная с центром инерции соударяющихся частиц. Удобство последней системы отсчета очевидно: суммарный импульс частиц равен нулю.

Соударения

Слово «соударение» надо понимать в несколько более широком смысле, чем это принято в житейской практике. Для механических задач, которые нас серчас интересуют, к соударениям относятся любые встречи двух или более тел, при которых взаимодействие длится короткий срок. Таким образом, кроме явлений, которые можно отнести к соударениям во всех смыслах этого слова,— удара биллиардных ша-ров, столкновений атомов или атомных ядер,— сюда можно отнести и такие события, как прыжок человека с трамвая или на трамвай или попадание пули в стенку. При таких коротких взаимодействиях возникают столь большие силы, что роль всех постоянно действующих сил можно считать ничтожной. Это дает нам право рассматривать соударяющиеся тела как замкнутую систему и применять к ним закон сохранения импульса.

Во многих соударениях длительность взаимодействия измеряется тысячными долями секунды. За это время сила доходит до своего максимального значения, затем падает до нуля. Типичная кривая силы при ударе показана на рис. 20. В каждое мгновение удара соотношение между силой, действующей на любое из тел, и импульсом этого тела дается вторым законом Ньютона:

Переписывая его в виде мы можем сказать, что произведение среднего значения силы на время ее действия должно равняться изменению импульса. Более точное утверждение мы получим, проинтегрировав написанное уравнение от начального времени удара до окончания взаимодействия. Очевидно,

Интеграл в левой части называют иногда импульсом силы. Геометрический смысл этой величины на графике — площадь под кривой удара (см. рис. 20).

В зависимости от упругих свойств тел соударения могут протекать весьма различно. Принято выделять два крайних случая: идеально упругий и абсолютно неупругий удары.

Остановимся сначала на втором из них. Под неупругим ударом понимают такую встречу двух тел, в результате которой эти тела объединяются. К неупругим ударам относятся столкновение глиняных шаров, прыжок человека на движущуюся вагонетку, столкновение двух разноименных ионов с образованием молекулы, захват электрона положительным ионом и т. д.

Пусть до встречи тела двигались со скоростями суммарный импульс равнялся После встречи тела имеют общую массу, равную и движутся с какой-то скоростью Импульс системы после встречи равен Закон сохранения импульса требует равенства

откуда скорость тел после неупругого удара представится формулой

Вектор импульса после встречи тел должен равняться сумме векторов импульса тел до удара.

Если встречное движение происходит вдоль одной прямой, то после удара тела будут двигаться в том направлении, куда ранее шло тело с большим импульсом. Если импульсы тел равняются по величине, то значит, равно нулю — столкнувшиеся тела остановятся.

Неупругий удар сопровождается энергетическим превращением. Из только что приведенного примера видно, что кинетическая энергия может даже обратиться в нуль. Нетрудно подсчитать величину, на которую возрастает внутренняя энергия встретившихся тел в том или ином случае; для этого лишь надо составить разность

Рассмотрим теперь идеально упругие столкновения, т. е. такие, при которых тела полностью восстанавливают свою форму. Это значит, что в состоянии этих тел не происходят какие-либо изменения, их потенциальная и внутренняя энергия до и после удара неизменна и, следовательно, кинетическая энергия должна сохраняться. Для двух тел, соударяющихся таким образом, можно составить два уравнения: закон сохранения импульса и закон сохранения кинетической энергии. Обозначим массы тел через Всегда можно выбрать начало координат совпадающим с одним из тел. Это упрощает задачу, нисколько не уменьшая общности рассмотрения. Мы положим поэтому тело с массой М покоящимся до удара. Указанные два закона сохранения дадут тогда такие равенства:

здесь — скорости шара до и после удара, — скорость шара М после удара.

Рассмотрим несколько примеров применения этих уравнений. Прежде всего, изучим нецентральное *) соударение двух шаров равной массы (рис. 21). Тогда массы сокращаются в обоих уравнениях и мы получим

Из векторного равенства ясно, что вектор является замыкающей треугольника, построенного на векторах Из правого уравнения следует, что треугольник, в котором — гипотенуза, должен быть прямоугольным; отсюда следует, что скорости после столкновения двух частиц равной массы должны быть направлены под прямым углом друг к другу. Этот интересный вывод легко проследить для биллиардной игры: направления движений шара, который подвергся удару, и «своего» шара образуют угол в 90°. В остальном характер изменения вектора скорости не определяется нашими уравнениями, в которых не учитывается отклонение линии удара от линии, проходящей через центры шаров.

Полные сведения о движении шаров после удара мы получим, если ограничим себя случаем центрального удара. Движение столкнувшихся шаров будет тогда и после удара происходить вдоль той же прямой. Поэтому можно не пользоваться векторными символами, помня, однако, что изменение знака скорости будет означать изменение направления движения. В этом случае нам нет зато нужды рассматривать упрощенный случай равных масс. Уравнения центрального соударения имеют вид

Преобразовывая эти уравнения к виду

и деля их друг на друга, найдем: или Мы замечаем, что относительная скорость движения шара по отношению к шару М до удара (мы ее обозначили через равна с обратным знаком той же относительной скорости после удара.

Интересная формула возникает при подстановке в формулу закона сохранения импульса. Находим выражение скорости шара т после удара через скорость этого же шара до удара:

Если массы шаров равны, то скорость V обращается в нуль. Это явление можно очень эффектно демонстрировать на стальных или костяных шариках. Шары как бы обмениваются скоростями при таком ударе (рис. 22). В остальных случаях шар т замедляется. Чем ближе массы соударяющихся шаров, тем эффектнее замедление. Нетрудно прикинуть, что нейтрон (масса 1) отскочит от ядра атома углерода (масса 12), потеряв своей скорости, а от ядра атома урана (масса 235) — потеряв всего лишь своей скорости.

Для макроскопических тел законы упругого удара неплохо выполняются для таких материалов как слоновая кость, сталь, резина и т. д. Эти материалы обладают способностью превосходно восстанавливать свою форму, что видно из интересной фотографии, приводимой на рис. 23, где при помощи так называемой «лупы времени» снят момент удара хоккейного мяча о препятствие. За секунды мяч сжимается почти на один сантиметр, такое же время затрачивается на восстановительную фазу удара. В первой фазе кинетическая энергия удара превращается в потенциальную энергию упругого сжатия. Во второй фазе потенциальная энергия переходит в кинетическую. При идеально упругом ударе этот обратный переход должен был бы полностью восстановить значение кинетической энергии, затраченной в первой фазе удара.

Нашими формулами не охватывается важный случай упругого удара шара о стенку (рис. 24). Так как кинетическая энергия должна сохраняться, то скорость шара не может измениться по величине. Что же касается направления движения шара после удара, то оно должно образовывать тот же угол с нормалью, что и вектор скорости до удара. Действительно, в случае удара о гладкую стенку тангенциальная (касательная) составляющая скорости остается неизменной, так как отсутствуют тангенциальные силы сцепления со стенкой. Как видно из рисунка, приращение импульса численно равно и направлено вдоль нормали к стенке. Согласно основному закону механики, в момент удара сила, действующая на шар со стороны стенки, должна быть направлена туда же, куда направлен вектор изменения импульса. Поэтому-то и угол падения шара равен углу отражения.

Рассмотрим неупругий удар на примере баллистического маятника (прибор для измерения скорости пули). Ящик с песком массой М подвешен на тросе. Пуля влетает в ящик и застревает в песке. Импульс пули до удара ти, импульс системы после удара Имеем

Приобретя кинетическую энергию ящик израсходует ее, поднявшись на высоту удовлетворяющую условию

Пусть

Если бы мы не пользовались законом сохранения импульса, а определили бы основываясь на полном переходе кинетической энергии пули в потенциальную энергию маятника, то получили быЭто означает, что в нашем примере 3920 Дж механической энергии (99,9% общего запаса) «исчезло» (пошло на нагревание системы). Так как абсолютно упругих тел не существует, то при каждом «упругом» ударе механическая энергия не сохраняется, часть ее переходит в энергию теплового движения молекул и рассеивается. Мы еще вернемся к этому в гл. 11 (стр. 159).

Теперь на примере соударений мы проиллюстрируем достоинства системы координат, связанной с центром инерции.

Пусть на шарик с массой покоящийся в лабораторной системе координат, налетает другой такой же шарик со скоростью Если удар неупругий, то какая-то часть кинетической энергии системы перейдет в тепло. В иных системах координат кинетическая энергия этой пары шариков выразится другими числами. Что же касается выделяемого тепла, то оно будет одним и тем же для данной пары шариков и будет определяться скоростью их относительного движения. Поэтому, вместо того чтобы с помощью закона сохранения импульса искать переходящую в тепло долю кинетической энергии, вычисленной для лабораторной системы координат, достаточно рассчитать кинетическую энергию для системы, связанной с центром инерции. Так как в этой системе координат суммарный импульс тел равен нулю, то после неупругого соударения шары останавливаются: вся кинетическая энергия переходит в тепло. Кинетическая энергия для системы, связанной с центром инерции, будет иметь минимальное значение.

В системе координат, связанной с центром инерции, шары движутся навстречу друг другу со скоростями Кинетическая энергия каждого шарика равна а полная энергия системы

Таково будет количество тепла, выделяемое при неупругом соударении. Какой бы ни был удар, выделение тепла (или другой формы энергии) за счет кинетической энергии тел может произойти в количестве, не превышающем кинетическую энергию, подсчитанную для системы, связанной с центром инерции. И наоборот, для выделения заданного количества тепла нужно эквивалентное количество кинетической энергии, подсчитанное для системы центра инерции.

Пример. Ядерная реакция бомбардировки азота протекает согласно уравнению

и идет с поглощением энергии 1,13 МэВ. Какой кинетической энергией влабора-торной системе координат должна обладать а-частица, чтобы реакция пошла? На первый взгляд кажется, что для этого достаточно энергии 1,13 МэВ. Номы уже знаем, что это не так. В системе координат, связанной с центром инерции, нужна энергия 1,13 МэВ, однако в лабораторной системе координат нужна большая энергия.
Действительно, скорость центра инерции где импульс первой частицы,второй. Скорость первой частицы в системе координат центра инерции для второй частицы можно написать

Отсюда кинетическая энергия системы в системе координат центра инерции будет

— так называемая приведенная масса обеих частиц. Будем считать ядра неподвижными Это предположение справедливо, так как всегда можно пренебречь медленным тепловым движением ядер-мишеней по сравнению с огромными скоростями налетающих частиц. Тогда кинетическая энергия в лабораторной системе координат следовательно,Реакция идет, если Учитывая, что получим

Явления отдачи

Закон сохранения импульса помогает легко разобраться в основных чертах явления отдачи при выстреле, реактивном движении и при рассмотрении других аналогичных проблем.

Рассмотрим, прежде всего, явление отдачи, происходящее в системе отсчета, где в начальный момент тела покоились. В случае выстрела из орудия такое рассмотрение вполне естественно. Если в начальный момент система, состоящая из двух или более тел, покоится, то суммарный импульс ее равен нулю. Какие бы события далее ни произошли, равенство нулю суммарного импульса продолжает иметь место. Если поэтому в какое-то мгновение происходит взрыв, в результате которого система делится на части с массами которые разлетаются со скоростями то сумма импульсов разлетающихся тел должна по-прежнему равняться нулю.

Если речь идет о выстреле из орудия (система делится на две части), то условие равенства нулю импульса этой системы из двух тел имеет вид здесь малые буквы относятся к одному телу, скажем снаряду, а большие — к другому, к орудию. Разделение системы на две части может происходить при разлете частей только вдоль общей прямой линии. Поэтому векторные значки можно отбросить и записать условие в виде Скорости орудия и снаряда должны быть обратно пропорциональны их массам. Итак, явление отдачи будет ощущаться тем резче, чем больше масса снаряда по отношению к массе орудия.

Чрезвычайно большой интерес представляют явления «непрерывной отдачи», имеющие место в реактивном движении. Подобные явления составляют своеобразную главу механики, которую можно назвать механикой переменной массы. Они’ осуществляются не только в реактивном самолете. Напротив, можно указать ряд обыденных явлений, в которых мы имеем дело с подобным движением. В качестве примера достаточно указать рулон разматывающейся бумаги или падение непрерывно конденсирующейся в атмосфере капли (см. пример в конце параграфа). Основания механики переменной массы были заложены в конце XIX в. профессором И. В. Мещерским. Не имея возможности останавливаться на его работе, мы рассмотрим лишь одну-единственную проблему этой области, касающуюся возможной скорости движения ракеты.

Ракета движется со скоростью и в какое-то мгновение выбрасывает некоторую порцию горючего газа с массой Масса ракеты естественно уменьшится на эту величину. Если скорость истечения газов обозначить через (это скорость не по отношению к ракете, а по отношению к той же инерциальной системе отсчета, в которой описывается скорость движения ракеты), то импульс отделившегося от ракеты вещества будет равен Ракета уменьшит свою массу и увеличит свою скорость на величину йи. Импульс ракеты после выброса горючего будет равен В соответствии с законом сохранения импульса мы можем приравнять импульс ракеты до выброса порции горючего и импульс системы после истечения порции газа. Последний будет равен разности импульса ракеты и массы горючего. Итак,

откуда с точностью до бесконечно малых второго порядка

Но есть относительная скорость истечения горючих газов (по отношению к ракете). Обозначая эту скорость через мы приходим к следующему уравнению для приращения скорости ракеты:

Знак минус поставлен, чтобы учесть возрастание скорости при убывании массы. Мы видим, что прирост скорости равен доле потерянной массы, умноженной на относительную скорость истечения горючего.

Считая скорость истечения газов по отношению к ракете величиной постоянной, мы легко проинтегрируем написанное уравнение. Если масса ракеты была когда скорость ракеты была и стала равной М тогда, когда скорость ракеты изменилась до и, то интегрирование дает

Последняя формула была впервые получена первым создателем конструкции ракеты и исследователем теории межпланетного сообщения К- Э. Циолковским.

Переходя к десятичным логарифмам и вводя для разности масс ракеты, т. е. для массы отброшенного горючего, обозначение получим формулу Циолковского в виде

(начальную скорость полагаем равной нулю).

Для скорости истечения газов 2000 м/с расчет по формуле дает такие характерные цифры:

Как видно из этой таблицы, скорость ракеты возрастает много медленнее с количеством выброшенного горючего, чем хотелось бы. Для придания ракете значительной скорости необходимо выбросить огромное количество горючего по отношению к начальной массе ракеты. Так, для придания скорости 7 км/с от массы ракеты должна остаться меньше чем часть.

Чтобы ракета вышла за пределы земного тяготения, ей нужно придать скорость, равную примерно 11 км/с. Эта цифра получается следующим простым рассуждением. Для отрыва от Земли ракета должна обладать такой кинетической энергией, которой хватило бы для производства работы перемещения тела с земной поверхности в бесконечность. Но эта работа против сил тяжести равна разности потенциальных энергий ракеты на поверхности Земли и в бесконечности. Так как в бесконечности потенциальная энергия равна нулю, то условие отрыва от Земли имеет следующий простой вид:

где — масса и радиус Земли. Умножив числитель и знаменатель правой части равенства навспоминая формулу ускорения силы тяжести на поверхности Земли сокращая на массу ракеты, находим условие отрыва от Земли: что и дает цифру около 11 км/с.

Если считать, что скорость истечения газов 2000 м/с*), то можно найти по формуле Циолковского отношение Оно будет равно 244. Желая оторвать ракету от Земли, мы должны придать ей такую конструкцию, чтобы в межпланетное путешествие отправить всего лишь долю той массы, которой обладала покоящаяся ракета. Если бы эту скорость удалось повысить в три раза, т. е. довести до 6 км/с, то отношение упало бы до 5,3. Но это, видимо, пока нереально, судя хотя бы по сообщению прессы в декабре 1968 г. о рейде «Аполлона-8» вокруг Луны: «в земную атмосферу вернется отсек весом 5,3 тонны — все что останется от корабля в 3100 тонн».

Меньшие трудности приходится преодолеть при выведении на орбиту спутника Земли. Для создания искусственного спутника требуется меньшая начальная скорость. Если полагать, что ускорение силы тяжести на тех высотах, где мы желаем создать орбиту спутника, примерно то же, что и на земной поверхности, то закон механики, записанный для искусственной планеты, будет иметь вид а так как спутник движется по окружности, то центростремительное ускорение Отсюда находим значение скорости обращения спутника т. е. 8 км/с. Если такая скорость будет придана ракете, то она превратится в земного спутника. Из приведенной выше таблицы, рассчитанной для скорости истечения газа в 2000 м/с, мы видим, что значение нужное для придания ракете скорости 8 км/’с, равно 54.

Пример движения тела с переменной ма с с о й. Пусть водяная капля падает в насыщенной водяными парами атмосфере. В момент времени капля имеет массу и радиус За время объем капли, а следовательно, и масса (при плотности, равной 1) увеличатся на величину Следовательно, скорость возрастания массы — В то же время из физических соображений ясно,что скорость конденсации водяного пара должна быть пропорциональной конденсирующей поверхности Отсюда где — некоторый коэффициент пропорциональности.

Составим уравнение движения этой капли в поле тяготения Земли. Нас интересует изменение импульса которое по основному закону механики равно Имеем Подставляя сюда выражения для получим Интегрирование этого уравнения показывает, что т. е. капля падает с постоянным ускорением Сопротивление воздуха в расчет не принималось.