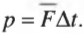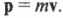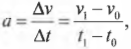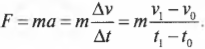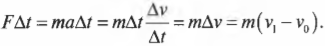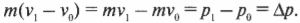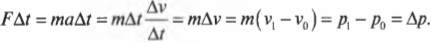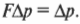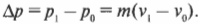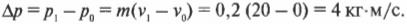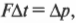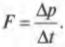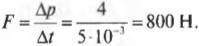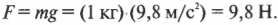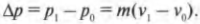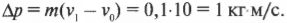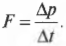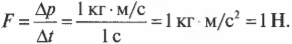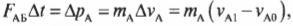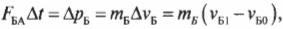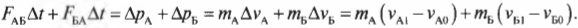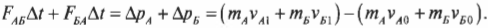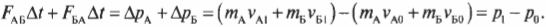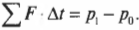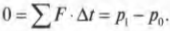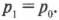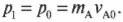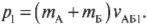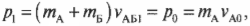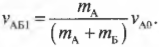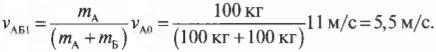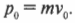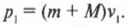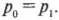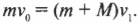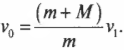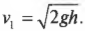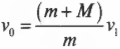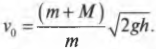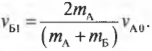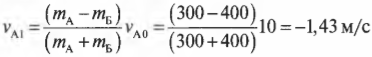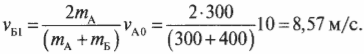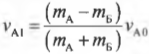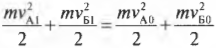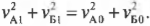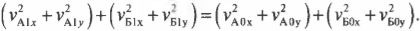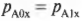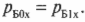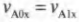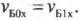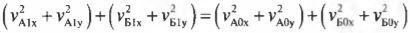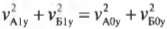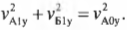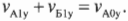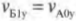In English
Preprints
2017, 2017040150. http://dx.doi.org/10.20944/preprints201704.0150.v1
УДК 53.02+530.131:531.62+531.26+531.61+531.422++
537.8+537.213
Энергия, импульс, масса и скорость движущегося тела
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
e—mail intelli@list.ru
В приближении слабого поля в ковариантной теории гравитации формулируется
проблема 4/3 для внешнего и внутреннего гравитационного поля тела в виде
однородного шара. Описывается
зависимость энергии и массы движущегося вещества от энергии поля, сопровождающего
вещество, а также зависимость от характерного размера объёма, занимаемого
веществом. В явном виде вычислены добавки в энергию и импульс тела,
определяемые энергией и импульсом гравитационного и электромагнитного полей,
связанных с данным телом. Обосновывается вывод о том, что энергия и масса тела
могут быть описаны через энергии обычной и сильной гравитации, и через энергии
электромагнитных полей частиц, из которых составлено тело.
Ключевые слова: энергия; импульс; теория относительности; гравитация; потенциалы поля.
Energy, Momentum, Mass and Velocity
of a Moving Body
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
In the weak-field approximation of
covariant theory of gravitation the problem of 4/3 is formulated for internal
and external gravitational fields of a body in the form of a ball. The
dependence of the energy and the mass of the moving substance on the energy of
field accompanying the substance, as well as the dependence on the
characteristic size of the volume occupied by the substance are described.
Additives in the energy and the momentum of the body, defined by energy and
momentum of the gravitational and electromagnetic fields associated with the
body are explicitly calculated. The conclusion is made that the energy and the
mass of the body can be described by the energy of ordinary and strong
gravitation, and through the energies of electromagnetic fields of particles
that compose the body.
Keywords: energy; momentum; theory of
relativity; gravitation; field potentials.
Введение
В релятивистской механике существуют стандартные формулы,
описывающие зависимость полной энергии и импульса частицы с некоторой массой от скорости
её движения:
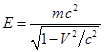
. (1)
Зная энергию и импульс
, из (1) вычисляют массу и скорость частицы:
,
. (2)
В (1) и (2) входит скорость света . Для неподвижной частицы скорость и импульс равны нулю, а
полная энергия частицы равна энергии покоя:
.
(3)
Соотношение (3) отражает принцип пропорциональности массы и
энергии. В физике элементарных частиц измеряемыми параметрами являются обычно
энергия и импульс, а масса и скорость находятся из (2) и оказываются вторичными
параметрами.
Предположим теперь, что измеряемыми параметрами являются
энергия и скорость частицы. В таком случае из (1) можно вычислить массу и
импульс:
,
. (4)
Возможен также случай, когда измеряемыми параметрами являются
импульс и скорость частицы, а вычисляемыми величинами становятся масса и
энергия:
,
. (5)
Если скорость частицы задана, то
массу можно найти либо через энергию согласно (4), либо через импульс согласно
(5), в обоих случаях масса должна быть одинакова.
Имеются ещё две возможности сочетания параметров, когда
известны энергия и масса, либо импульс и масса. Это позволяет вычислять модуль
импульса и скорость, либо энергию и скорость соответственно:
,
,
,
.
Из вышеуказанных формул не видно, содержат ли они в себе
энергию и импульс полей, которые присущи частицам и пробным телам. В частности,
пробные тела всегда обладают собственным гравитационным полем и могут ещё нести
электрический заряд и соответствующее электромагнитное поле. В общей теории
относительности (ОТО) считается, что релятивистские энергия и масса тела
уменьшаются за счёт вклада гравитационной энергии. Хотя в ОТО нет однозначного
определения гравитационной энергии и её вклада в общую энергию [1], в
приближении слабого поля предполагается следующее [2]:
,
. (6)
где – релятивистская энергия в
гравитационном поле, – энергия в отсутствие
поля, – потенциальная
гравитационная энергия тела.
Поскольку энергия отрицательна, то
согласно ОТО масса тела должна уменьшаться по
мере усиления поля.
Основной целью данной
статьи является включение в явном виде в релятивистские формулы для энергии и
импульса добавок, возникающих от энергии и импульса полей, связанных с пробными
телами. Все последующие расчёты будут производиться в рамках ковариантной
теории гравитации (КТГ) [3]. Мы будем применять приближение слабого поля, когда
КТГ переходит в лоренц-инвариантную теорию гравитации (ЛИТГ), и становится
возможным сравнить наши результаты с формулами ОТО (6).
Внешнее
гравитационное поле. Проблема 4/3
Предположим, что соотношения (1) – (5) записаны для малой
частицы и через массу учитывают энергию её собственного гравитационного поля.
Если частиц в объёме тела много, то их энергия взаимодействия приводит к
заметному вкладу энергии поля в полную энергию тела. В слабом поле можно
считать, что либо метрика пространства-времени мало отличается от метрики
пространства-времени Минковского, либо гравитационные эффекты замедления
времени и сокращения размеров значительно меньше, чем аналогичные эффекты
вследствие движения тела. В таком приближении ОТО переходит в гравитомагнетизм, а КТГ – в ЛИТГ.
Гравитационные потенциалы от элемента вещества точечных
размеров, находящегося при в точке пространства
и двигающегося вдоль
оси с постоянной скоростью
, согласно [4] имеют вид:
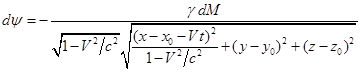
, (7)
здесь – скалярный потенциал,
– гравитационная
постоянная,
– масса элемента
вещества,
– скорость
распространения гравитации, которую далее для упрощения расчётов будем считать
равной скорости света ,
– координаты точки, в
которой определяется потенциал в момент времени ,
– векторный потенциал.
Согласно (7), гравитационный потенциал в момент времени
от точечной массы
при её движении вдоль
оси зависит от начального
положения этой массы при
. После интегрирования (7) по всем точечным массам внутри
шара на основе принципа суперпозиции получаются стандартные формулы для потенциалов гравитационного поля вокруг движущегося
шара с учётом запаздывания гравитационного
взаимодействия:
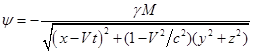
,
(8)
где – общий скалярный
потенциал движущегося шара,
– масса шара,
– координаты точки, в
которой определяется потенциал в момент времени (с условием, что при
центр шара находился в
начале координат системы отсчёта),
– векторный потенциал.
В (8) предполагается, что шар двигается вдоль оси с постоянной скоростью
, так что
,
,
. С помощью потенциалов поля можно
вычислить напряжённости поля вокруг шара по формулам [5]:
,
, (9)
где есть гравитационное
ускорение,
– гравитационное
кручение в ЛИТГ (гравитомагнитное поле в гравитомагнетизме).
С учётом (8) и (9) находим:
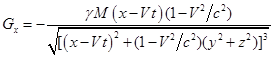
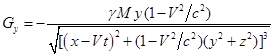
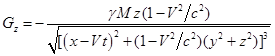
, (10)
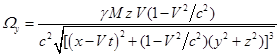
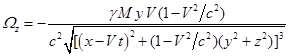
Плотность энергии гравитационного поля определяется формулой
[5]:
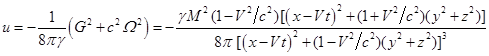
Полная энергия поля за пределами шара при постоянной скорости
движения не должна зависеть от момента времени. Положим в (11) и проинтегрируем
плотность энергии поля по всему внешнему объёму пространства. Для этого введём
новые координаты:
,
,
. (12)
Элемент объёма определяется
формулой , где:
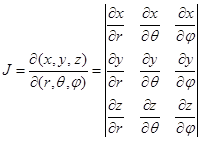
Отсюда следует, что . Интеграл по пространству от плотности энергии (11) будет
равен:
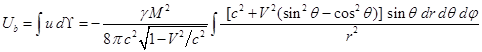
Учтём, что за счёт лоренцевского
сокращения при движении вдоль оси шар должен
представляться эллипсоидом, уравнение поверхности которого при следующее:
.
(14)
После подстановки (12) в (14) становится видно, что радиус при интегрировании в
(13) должен меняться от до
, а углы
и
меняются так же, как и
в сферических координатах (от 0 до для угла
, и от 0 до
для угла
). Для энергии гравитационного поля за пределами движущегося
шара находим:
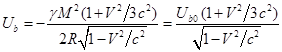
где есть энергия поля
вокруг неподвижного шара.
Предположим, что формула (4) для связи массы и энергии
частицы справедлива также и для гравитационного поля. Тогда можно ввести
эффективную массу поля, связанную с энергией:
. (16)
Рассмотрим теперь вопрос о плотности импульса гравитационного
поля:
,
(17)
где есть вектор плотности
потока энергии поля [5].
Подставляя в (17) компоненты напряжённостей поля (10),
находим:
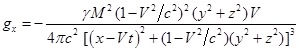
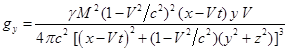
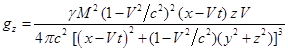
Можно видеть, что компоненты плотности импульса гравитационного
поля (18) выглядят приблизительно так же, как если бы на шар со стороны оси набегала жидкость, перенося
аналогичную плотность импульса – при встрече с шаром жидкость растекается в
стороны, чтобы слиться вновь на противоположной стороне шара. Интегрируя
компоненты плотности импульса гравитационного поля (18) по объёму за пределами
движущегося шара при аналогично (13),
получаем:
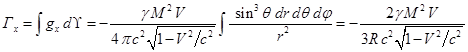
,
.
В (19) суммарный импульс поля имеет лишь компоненту вдоль оси
. По аналогии с (5) коэффициент перед скоростью
в (19) можно
интерпретировать как эффективную массу внешнего, передвигающегося вместе с
шаром гравитационного поля:
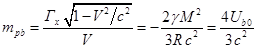
где есть энергия внешнего
статического поля в системе покоя шара.
Сравнение (20) с (16) даёт:
.
(21)
Несовпадение масс и
в (21) составляет суть
так называемой проблемы 4/3, согласно которой масса поля , вычисляемая через импульс поля, при малых скоростях
приблизительно в 4/3 больше, чем масса поля , находимая через энергию поля. Характерной чертой
фундаментальных полей, к которым относятся гравитационное и электромагнитное
поля, является подобие их уравнений для потенциалов и напряжённостей поля.
Проблема 4/3 известна довольно давно в отношении массы электромагнитного поля
движущегося заряда. О ней писали в конце 19 века Д.Д. Томсон, Д.Ф. Фицджеральд,
О. Хевисайд [6], Сирл (George Frederick Charles Searle) и многие
другие. Мы также рассматривали эту проблему ранее, в отношении гравитационного
поля движущегося шара [7]. Сейчас же мы представляем точное решение задачи, не
ограничиваясь приближением малых скоростей.
Гравитационное
поле внутри движущегося шара
Согласно [4] для шара с плотностью вещества (измеренной в
сопутствующей системе отсчёта), движущегося вдоль оси , потенциалы внутри шара (обозначенные индексом i ) зависят от времени и имеют следующий вид:
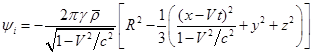
. (22)
С учётом (9) вычисляем внутренние напряжённости поля:
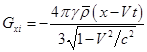
,
,
,
,
. (23)
Аналогично (11) для плотности энергии поля находим:
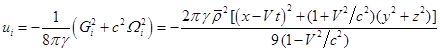
Из (24) вытекает, что минимальная плотность энергии внутри
движущегося шара достигается на его поверхности, а в самом центре при она равна нулю.
Интеграл от (24) по объёму шара при в координатах (12) с
элементом объёма даёт:
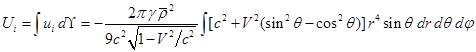
Движущийся шар выглядит как эллипсоид с уравнением (14), и в
координатах (12) радиус при интегрировании в (25) изменяется от 0 до. С учётом этого для энергии гравитационного поля внутри
движущегося шара имеем:
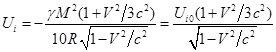
где есть энергия поля
внутри неподвижного шара радиуса .
Эффективная масса поля, связанная с энергией, получается
аналогично (4):
. (27)
Подставляя в (17) компоненты напряжённостей поля (23),
находим компоненты вектора плотности импульса гравитационного поля:
,
,
.
(28)
Вектор, соединяющий начало координат и центр шара, зависит от
времени и имеет компоненты . Отсюда в точке, совпадающей с центром шара, компоненты
вектора плотности импульса гравитационного поля всегда равны нулю. При центр шара проходит
через начало координат, и в этот момент из (28) следует, что максимальная плотность
импульса поля
достигается на поверхности шара, на окружности радиуса в плоскости
, перпендикулярной линии
движения шара. Это же следует и из (18).
Интегрируем компоненты плотности импульса гравитационного
поля (28) по объёму внутри движущегося шара при в координатах (12)
аналогично (19):
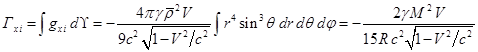
,
.
Как и в (19), суммарный импульс поля (29) имеет лишь
компоненту вдоль оси . По аналогии с (5) коэффициент перед скоростью
в (29) интерпретируем
как эффективную массу внутреннего, передвигающегося вместе с шаром
гравитационного поля:
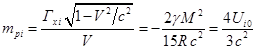
где есть энергия поля
внутри неподвижного шара.
Сравнение (27) и (30) даёт:
.
(31)
Связь (31) между массами поля внутри шара такая же, как и в
(21) для масс внешнего поля, то есть внутри шара тоже имеется проблема 4/3.
Учёт вклада
гравитационного поля в энергию и импульс движущегося тела
Попробуем включить найденные выше соотношения для энергии и
импульса гравитационного поля движущегося пробного тела в виде шара в формулы
(1). Будем считать, что в покое вместо (3) выполняется соотношение:
,
(32)
где – полная статическая энергия гравитационного поля снаружи и внутри шара при однородной
плотности его вещества,
– энергия покоя вещества, находимая
таким образом, что она не зависит от энергии гравитационного поля. Для
определения энергии вещество тела следует
разделить на части и разнести их на бесконечность.
Выбор знака минус перед в (32) будет обоснован
в последнем разделе. Будем далее анализировать хорошо известный мысленный
эксперимент. Предположим, что вещество шара состоит из материи и антиматерии,
которые в некоторый момент времени начинают аннигилировать и излучать фотоны.
Пусть фотоны летят в противоположные стороны вдоль оси в количестве
штук в каждую сторону,
так что в конце концов вся масса шара превращается в электромагнитное
излучение. В процессе излучения вследствие равенства импульсов всех фотонов и
симметрии излучения вдоль оси шар остаётся
неподвижным. Чтобы процесс не зависел от изменения радиуса шара, полагаем
радиус шара постоянным независимо от изменения массы. Энергия шара из (32) должна
превратиться в энергию фотонов:
,
(33)
где – постоянная Планка,
– частота излучения.
Рассмотрим эту же ситуацию в системе отсчёта , в которой шар двигается с постоянной скоростью
вдоль оси
и находится при
в начале координат.
Считаем, что скорость шара не меняется, несмотря на излучение фотонов. В
системе отсчёта частота фотонов будет
зависеть от того, летят ли они вдоль оси или в противоположную
сторону. Учитывая релятивистский эффект Доплера и (32), для энергии фотонов
вместо (33) будет:
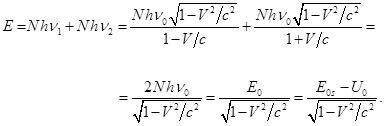
(34)
С другой стороны, полная энергия гравитационного поля
снаружи и внутри шара с учётом (15) и (26) равна:
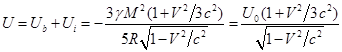
(35)
Для энергии вещества и поля движущегося шара имеем:
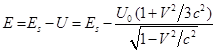
(36)
Из (34) и (36) следует:
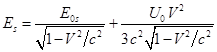
(37)
Так как энергия статического поля отрицательна: , то в (37) в энергии
вещества движущегося шара
появляется отрицательная добавка от энергии поля, при этом энергия от
не зависит.
Рассмотрим теперь закон сохранения импульса. До излучения
фотонов импульс движущегося шара состоит из импульса вещества шара и импульса
гравитационного поля, причём с учётом (19) для импульса поля за пределами шара,
и (29) для импульса поля внутри шара, суммарный импульс поля равен:
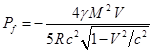
Тогда для импульса движущегося шара можно записать:
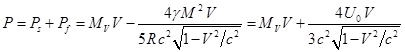
где есть масса вещества
шара как некоторая функция от скорости движения .
После излучения фотонов весь импульс шара и его
гравитационного поля переходит в импульс фотонов:
, (39)
где есть энергия (32)
покоящегося шара, равная разности энергии покоя вещества и энергии
гравитационного поля ; кроме этого
есть энергия фотонов
согласно (33). Из сравнения (38) и (39) следует:
.
(40)
Предположим, что для массы движущегося вещества шара
справедлива формула:
, где
– наблюдаемая масса
покоящегося тела, – некоторая функция.
Здесь мы считаем, что наблюдаемая масса тела, и та масса,
через которую определяется энергия и импульс
гравитационного поля,
является одной и той массой. Тогда
вместо (40) будет:
.
(41)
Но энергия покоящегося вещества не должна зависеть от
скорости движения, а также в силу (32) от энергии поля неподвижного шара . Поэтому в (41) должно быть
, откуда с учётом (40) вытекает следующее:
,
, (42)
где масса задаёт энергию покоя
вещества в (32).
Подставим из (42) в (37):
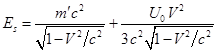
(43)
Из (43) следует, что в покое при энергия вещества не
включает энергию поля, но при движении в энергии вещества появляется добавка,
связанная с энергий поля . Энергия поля
делает также вклад в
массу движущегося вещества в (42). Полная энергия
движущегося вещества и поля (36) с учётом (43) будет равна:
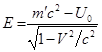
(44)
где в случае однородной плотности вещества шара .
Из (44) вытекает, что энергия тела увеличивается за счёт
вклада отрицательной гравитационной энергии .
Подставим теперь из (42) в (38), либо
из (42) в (39). Это
даёт следующее:
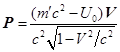
(45)
Из сравнения (44) и (45) с (1) видно, что при учёте
гравитационного поля роль суммарной массы вещества и поля играет величина . Мы считаем, что
, то есть суммарная масса вещества и поля есть не что иное,
как наблюдаемая масса , которая также определяет гравитационное поле и инертные
свойства тела.
Если нам известна энергия в (44) и импульс
в (45), то из этих
соотношений можно выразить массу вещества и скорость движения
тела . В случае однородного шара радиуса
при вычислении массы
движущегося вещества шара можно записать:
,
.
(46)
Согласно (46), масса вещества тела определяется не только энергией и
импульсом, но зависит также от среднего размера тела за счёт вклада массы
гравитационного поля в постоянную по величине массу .
Заметим ещё, что проблема 4/3 для гравитационного поля (неравенство массы
поля, находимой из энергии, и массы поля, вычисляемой через импульс поля)
оказалась скомпенсированной зависимостью энергии в (37) и массы
в (42) движущегося
вещества от энергии поля . В результате в формулах (44) и (45) энергия поля
входит симметрично как
в полную энергию, так и в полный импульс тела.
Анализ
компонент массы и энергии тела
До сих пор мы не уточняли, из каких компонент состоит масса вещества тела, вносят
ли в неё вклад другие энергии, кроме гравитационного поля? Например, что произойдёт,
если тело нагреть? С точки зрения кинетической теории, рост температуры
приводит в первую очередь к увеличению средней скорости движения частиц,
составляющих тело. В таком случае согласно (1) увеличится средняя энергия
каждой частицы тела, а в силу аддитивности энергии
должна измениться и суммарная энергия покоящегося тела . Для случая вещества и гравитационного поля
, и (44) – (45) можно записать так:
,
. (47)
Нагревание
тела приводит к изменению в (47), причём теплота
как некоторый вид энергии распределяется между кинетической энергией вещества и
энергией гравитационного поля.
Массу однородного шара можно определить через массу из соотношений:
,
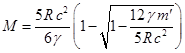
Любое
взаимодействие частиц тела между собой или с окружающей средой, которое
изменяет энергию частиц, изменяет суммарную
энергию покоящегося тела . При этом согласно (48) масса
вещества шара зависит
не только от , но и от радиуса шара
.
Ввиду подобия
уравнений электромагнитного и гравитационного полей, в энергии должен быть ещё
вклад от полной энергии электромагнитного поля
тела:
.
(49)
Для однородно заряженного по объёму и неподвижного шара с зарядом полная энергия
электрического поля равна:
.
Вклад в может давать и энергия
магнитного поля, если шар является намагниченным, либо если имеются
электрические токи. Мы предполагаем, что другие виды энергии (например, теплота
при нагревании) могут изменить массу тела, но не могут изменить заряд тела,
поскольку для этого нужно перенести на тело (или удалить с него) заряженные
частицы. В этом одно из отличий электромагнитного поля от гравитационного, в
дополнение к однополярности гравитационных зарядов
(которыми являются массы) и двуполярности
электромагнитных зарядов.
Массу
вещества в (49) можно разбить
на две части, одна из которых есть масса вещества
при нуле температуры по шкале Кельвина, а другая часть представляет собой дополнительную
массу от внутренней кинетической энергии , включающей в себя кинетическую энергию движения атомов и
молекул, и энергию турбулентного движения потоков вещества [8]. Если есть средняя скорость
частиц тела, то выполняются приблизительные соотношения: ,
. Как и энергии поля, мы включаем энергию
в (49) с отрицательным
знаком:
.
(50)
Для тел,
находящихся лишь под действием собственных гравитационных и электромагнитных
полей, выполняется теорема вириала, согласно которой модуль потенциальной
энергии поля в среднем в два раза больше кинетической энергии вещества:
,
, (51)
здесь есть полная энергия
без учёта энергии покоя частиц тела.
Подстановка
(51) в (50) даёт приблизительное равенство:
. (52)
Рассмотрим
теперь сущность массы , относящейся к массе вещества тела без учёта вклада массы от
внутренней кинетической энергии и энергии макроскопических полей. В массу делают вклад массы от
различных видов энергии, связанных с атомами и молекулами вблизи абсолютного
нуля температуры: сильное взаимодействие, скрепляющее вещество элементарных
частиц и удерживающее нуклоны в атомных ядрах; электромагнитное взаимодействие
частиц; энергия движения электронов в атомах; энергия вращения атомов и
молекул; энергия колебаний атомов в молекулах, и т.д. В стандартной модели
предполагается, что сильное взаимодействие возникает благодаря действию глюонного поля между кварками, находящимися в адронах
(мезонах и барионах), а на лептоны сильное взаимодействие не распространяется.
Существует
также гипотеза о том, что сильное взаимодействие есть проявление сильной гравитации
на уровне элементарных частиц и атомов [9]. Поскольку гравитация имеет две
компоненты, в виде поля ускорения и поля кручения
, то устойчивость нуклонов в атомных ядрах может быть описана
как баланс сил от притяжения нуклонов друг к другу за счёт , и отталкивания нуклонов за счёт поля кручения
[3]. Эта же идея
применяется для описания структуры и устойчивости ряда адронов, рассматриваемых
как композиции из нуклонов и мезонов [4]. Сильная гравитация отличается от
обычной гравитации заменой гравитационной постоянной на постоянную сильной
гравитации , и действует между всеми частицами, включая лептоны. Оценку
величины можно получить из
баланса четырёх сил, действующих на электрон в атоме водорода: 1. Сила
электрического притяжения между электроном и ядром атома. 2. Сила
электрического отталкивания заряженного вещества электрона самого от себя
(электрон представляется в виде облака вокруг ядра). 3. Центростремительная
сила от вращения электрона вокруг ядра. 4. Притяжение электрона к ядру под
действием сильной гравитации. Указанные силы приблизительно равны друг другу,
так что выполняются соотношения для сил притяжения от сильной гравитации и
электрической силы [5]:
,
м3∙кг
–1∙с –2 , (53)
где и
– массы протона и
электрона соответственно,
– радиус вращения
электронного облака,
– элементарный
электрический заряд как заряд протона, равный модулю отрицательного заряда
электрона,
– электрическая
постоянная.
Другой способ
оценки основан на теории
подобия уровней материи и использовании коэффициентов подобия. Данные
коэффициенты определяются следующим образом: – коэффициент подобия
по массе (отношение массы нейтронной звезды к массе протона); – коэффициент подобия
по размерам (отношение радиуса нейтронной звезды к радиусу протона); – коэффициент подобия по
скоростям (отношение характерной скорости частиц нейтронной звезды к скорости
света как к характерной скорости вещества протона). Для постоянной сильной
гравитации получается формула: , причём степени коэффициентов подобия в данном равенстве соответствуют размерности
гравитационной постоянной согласно теории размерностей.
Если сильное
взаимодействие рассматривать как результат сильной гравитации, то основной
вклад в энергию покоя протона должна вносить положительная кинетическая энергия
его вещества и отрицательная энергия сильной гравитации (электрической энергией
протона можно пренебречь ввиду её малости). Сумма этих энергий даёт полную
энергию протона, причём в силу теоремы вириала (51) данная сумма энергий
приблизительно равна половине энергии сильной гравитации. Так как энергия
сильной гравитации отрицательна, то отрицательна и полная энергия протона.
Полную энергию протона с точностью до знака можно рассматривать как энергию
связи его вещества; энергия связи равна работе, которую надо совершить, чтобы
разнести вещество на бесконечность так, чтобы там полная энергия вещества
(потенциальная и кинетическая) стала равной нулю. По своему смыслу
положительная энергия покоя протона должна равняться энергии связи или модулю
полной энергии протона. Это даёт равенство между энергией покоя и модулем
половины энергии сильной гравитации:
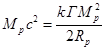
(54)
где для случая, если бы
протон был однородным по плотности шаром радиуса .
Если в (54)
подставить (53), получится ещё одно равенство, позволяющее оценить радиус
протона:
,
,
где есть классический
радиус электрона.
В
самосогласованной модели протона [10] находится, что в (54) радиус протона м, причём коэффициент
вследствие небольшого
увеличения плотности вещества в центре протона. Одновременно с этим в
предположении, что положительный заряд распределён по объёму протона аналогично
массе, а максимальная угловая скорость вращения протона ограничена условием его
целостности в поле сильной гравитации, находится магнитный момент протона как
результат вращения заряженного вещества:
,
(55)
где Дж/Тл есть магнитный
момент протона,
(в случае однородной
плотности вещества и заряда протона должно быть ).
Постоянная
сильной гравитации (53) объясняет не только энергию (54) и магнитный момент
(55) протона, но и даёт оценку константы взаимодействия двух нуклонов
посредством сильной гравитации:
,
где для
взаимодействия двух нуклонов, и стремится к 1 для частиц с меньшей плотностью
вещества, – постоянная Дирака,
– скорость света.
Для энергии
взаимодействия двух нуклонов посредством псевдоскалярного пион-нуклонного взаимодействия,
находящихся на расстоянии друг от друга, и для
соответствующей константы взаимодействия при малых энергиях справедливы
формулы:
,
,
где – эффективный заряд
сильного взаимодействия, – масса пиона.
Как видно,
константа взаимодействия близка к константе
псевдоскалярного пион-нуклонного сильного взаимодействия.
То, что
энергия покоя протона связана с сильной гравитацией, вытекает также из модернизированной
теории гравитации Фатио-Лесажа [11]. В этой теории на
основе поглощения потоков гравитонов в веществе тел с передачей импульса
гравитонов веществу выводится точная формула гравитационной силы Ньютона (закон
обратных квадратов), находится плотность энергии потока гравитонов ( Дж/м3 ), сечение их взаимодействия с веществом
( м2 ) и
другие параметры.
В теории бесконечной
вложенности материи [3], [5] показывается, что на
каждом основном уровне материи появляется соответствующий вид гравитации, на
уровне элементарных частиц это сильная гравитация, а на уровне звёзд – обычная
гравитация. Гравитация достигает максимума в самых плотных объектах – в
нуклонах и в нейтронных звёздах. В веществе земной плотности диапазон действия
сильной гравитации не превышает долей метра, и при таких размерах тел
происходит замена сильной гравитации на обычную. Это соответствует тому, что
массы и размеры объектов на различных уровнях материи нарастают в
геометрической прогрессии, причём точка замены сильной гравитации на обычную
гравитацию лежит вблизи середины диапазона масс от нуклонов до звёзд на оси
масс, взятой в логарифмическом масштабе.
Причиной
гравитации и электрических сил в рамках теории Фатио-Лесажа
полагаются потоки гравитонов, состоящие из частичек наподобие нейтрино, фотонов
и заряженных частиц. Данные потоки гравитонов, порождаемые веществом низших
уровней материи, управляют телами с помощью гравитационных и электромагнитных
сил и создают массивные объекты на более высоких уровнях материи. Эти объекты в
свою очередь на определённых стадиях своей эволюции излучают порции нейтрино,
фотонов, заряженных частиц, становящихся основой других потоков гравитонов,
действующих уже на более высоких уровнях материи. Так поля и массивные объекты
взаимно порождают друг друга на разных уровнях материи.
В описанной
картине энергия покоя протона (54) приблизительно равна модулю полной энергии
протона в собственном поле сильной гравитации (для увеличения точности следует
учесть ещё электромагнитную энергию протона), а энергия в (52) складывается из
энергий покоя нуклонов и электронов вещества тела с добавкой от энергии их
гравитационного и электромагнитного взаимодействия в составе вещества и
механического движения в атомах и молекулах. Следовательно, энергия тела с учётом теоремы вириала
(51) может быть сведена к половине модуля суммы энергии сильной гравитации и электромагнитной
энергии нуклонов, электронов,
атомов и молекул, участвующих в образовании энергии связи. В результате для
суммарной энергии вещества и поля некоторого покоящегося тела вместо (52) можно
записать:
.
(56)
Чтобы лучше понять смысл энергии , рассмотрим баланс энергии в процессе слияния вещества
вначале в элементарные частицы, затем в процессе слияния элементарных частиц в
атомы и наконец в процессе образования тела из множества атомов. Вначале
вещество находится неподвижно на бесконечности и его части друг с другом не
взаимодействуют, так что полная энергия системы равна нулю (мы не учитываем
здесь энергию покоя вещества в том его состоянии, когда оно является
раздробленным и ещё не вошло в состав элементарных частиц). Если вещество будет
сближаться под действием сильной, а также обычной гравитации, то появится
отрицательная энергия гравитационного поля и положительная
кинетическая энергия движения вещества , причём в силу закона сохранения энергии полная энергия не
должна меняться, оставаясь равной нулю. В балансе энергий следует учесть ещё
электромагнитную энергию и энергию
, уходящую из системы за счёт излучения квантов поля типа
фотонов и нейтрино:
,
. (57)
В (57) использована теорема вириала (51) для компонент полной энергии
системы . Согласно (57), энергия ушедшего из системы излучения
с точностью до знака
равна полной энергии , то есть энергия излучения
равна энергии связи
системы. Из сравнения (57) и (56) теперь видно, что суммарная энергия
вещества и поля некоторого покоящегося тела есть не что иное, как
энергия, извлекаемая из этого тела при его образовании, путём различного
излучения. Как правило в энергии учитываются только те
компоненты, которые связаны с образованием элементарных частиц, атомов и
молекулярного макроскопического вещества, а энергии связи частиц, из которых
построено вещество самих элементарных частиц, не учитываются и считаются
постоянными. Нагревание тела под действием гравитации в соответствии с (57) и
(56) приводит к увеличению энергии тела . Данный вывод обусловлен тем, что хотя внутренняя
кинетическая энергия тела входит в (57) с
отрицательным знаком, но изменение потенциальной энергии по теореме вириала
компенсирует вклад от энергии . Примером здесь является звезда, которая в процессе сжатия
гравитацией разогревается и ускоряет своё вращение, причём модуль гравитационной
энергии звезды увеличивается.
Согласно (56), суммарная энергия покоящегося тела , с помощью которой по формулам (47) вычисляются энергия и импульс
движущегося тела, состоит в основном из энергий двух фундаментальных полей –
гравитационного и электромагнитного, ответственных как за целостность частиц тела, так и за составленность самого тела из отдельных частиц. При этом
сильное взаимодействие частиц учитывается энергией сильной гравитации и электромагнитной
энергией .
Что касается
слабого взаимодействия, то оно полагается результатом трансформации вещества,
длительное время находящегося под воздействием фундаментальных полей. Примером
является долговременная эволюция достаточно массивной звезды с образованием
нейтронной звезды во вспышке сверхновой, когда излучается нейтринный импульс с
энергией порядка полной энергии звезды (энергия гравитации при сжатии вещества
в малую по размерам нейтронную звезду конвертируется в энергию нейтрино, в
энергию фотонного излучения и в кинетическую энергию и нагрев сбрасываемой
оболочки). На уровне элементарных частиц это соответствует процессу образования
нейтрона с излучением нейтрино.
Если от
покоящегося тела в ходе слабого взаимодействия излучаются (поглощаются телом)
нейтрино, фотоны и другие частицы, то это приводит и к изменению суммарной энергии тела . В общем случае энергия
тела является функцией
времени и скорости, с которой отдельные частицы или элементы вещества
излучаются от тела или поглощаются им. В силу законов сохранения энергии и
импульса, если некоторые частицы приносят в систему энергию и импульс, то через
некоторое время они распределятся в системе и с учётом теоремы вириала могут
быть учтены через энергию и импульс фундаментальных полей. Поэтому можно
утверждать, что согласно (56) источником суммарной энергии тела, а также его
массы как меры инерции
являются гравитационные и электромагнитные поля, связанные с массой и с зарядами
(а также с токами) в веществе. В теории гравитации Фатио-Лесажа
предполагается, что поля, связанные с массой и с зарядами, являются следствием
взаимодействия вещества и зарядов с потоками гравитонов и мельчайших заряженных
частиц, пронизывающих пространство. Если определить суммарную массу тела в виде
, то (47) становится таким:
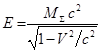
. (58)
Заключение
Соотношения (58) выглядят точно так же, как (1) для малой пробной
частицы. Однако масса тела в (58) в полной мере
учитывает энергии полей, тогда как для массы малой частицы в (1) это только
предполагалось. Появление в массе вклада от энергии
полей произошло оттого, что мы учли энергию взаимодействия множества малых
частиц при их композиции в массивном теле. Отсюда по индукции следует
предполагать, что не только масса тела, но и масса любой изолированной малой
частицы должна определяться с учётом вклада от энергий собственных
фундаментальных полей этой частицы. Описанная концепция массы в ковариантной
теории гравитации (КТГ) подтверждается анализом функции Гамильтона [12] и
функции Лагранжа в принципе наименьшего действия [13].
Следует отметить различие результатов КТГ и общей теории относительности
(ОТО) в отношении массы и энергии. В КТГ масса
покоящегося однородного сферического тела радиуса выражается формулами
(46) – (49):
, (59)
где масса задаёт массу частей
тела без учёта потенциальной энергии полей. В результате релятивистская и
гравитационная масса тела при объединении частей
тела в одно целое растёт за счёт энергии поля гравитации , и уменьшается за счёт электрической энергии
.
В ОТО масса тела в приближении слабого
поля согласно (6) определяется суммированием всех энергий с последующим
делением результата на квадрат скорости света:
. (60)
В отличие от (59), в (60) используется не масса , а масса
, входящая в формулу для энергии покоя и в лагранжиан. Как
было показано в [12], для трёх масс, связанных с телом, выполняется следующее соотношение: . При этом
, что так же следует из (59) и (60). На наш взгляд, причина несовпадения
(59) и (60) связана с различием позиций обеих теорий: в КТГ явным образом
существует тензор энергии-импульса гравитационного поля, входящий в лагранжиан
и вносящий свой вклад в метрику пространства-времени и в энергию-импульс
рассматриваемой системы. Это позволяет определить все три массы и найти их смысл,
причём масса связывается с
космологической постоянной в уравнении для метрики системы. Вместо этого в ОТО используется принцип эквивалентности,
гравитационное поле сводится к метрическому полю, соответственно, энергия и
импульс не образуют тензора и могут быть найдены лишь косвенно, через метрику
пространства-времени. В ОТО имеют смысл лишь две массы, и
.
Равенство означает, что релятивистская и гравитационная масса
тела находится посередине
между массами и
, и отличается от них на величину модуля потенциальной
энергии полей. Отсюда следует непротиворечивость позиций КТГ и ОТО, так как эти
теории определяют массу и энергию с различных точек зрения.
Список использованных источников
1.
Misner, Charles W.; Kip. S. Thorne
& John A. Wheeler (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0.
2.
Okun L. B.
Photons, Clocks, Gravity and the Concept of Mass. Nucl.
Phys. B (Proc. Suppl.) 110 (2002) 151–155.
3.
Федосин С.Г. Физические теории и бесконечная вложенность материи.
Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
4.
Федосин С.Г. Комментарии к книге: Физические
теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21,
Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
5.
Федосин С.Г. Физика и философия
подобия от преонов до метагалактик. Пермь,
Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
6. Heaviside, Oliver (1888/1894), «Electromagnetic
waves, the propagation of potential, and the electromagnetic effects of a
moving charge«, Electrical papers, 2, pp. 490–499.
7. Fedosin S.G. Mass, Momentum and Energy of Gravitational Field. Journal of Vectorial Relativity, Vol. 3, No. 3, September
2008, P. 30–35.
8. Fedosin
S.G. The Principle
of Proportionality of Mass and Energy: New Version. Caspian
Journal of Applied Sciences Research, 2012, Vol. 1, No 13, P. 1–15.
9. Sivaram,
C. and Sinha, K.P. Strong gravity, black holes, and hadrons. Physical Review D,
1977, Vol. 16, Issue 6, P. 1975–1978.
10. Fedosin
S.G. The radius of
the proton in the self-consistent model. vixra.org, 03 August 2012.
Accepted by Hadronic Journal.
11. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of
Vectorial Relativity, Vol. 4, No. 1, March 2009, P. 1–24.
12. Fedosin S.G. The
Hamiltonian in covariant theory of gravitation.
Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.
13. Fedosin S.G. The
Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, February 2012, Vol. 35, No. 1, P. 35–70.
Источник:
http://sergf.ru/dt.htm
На
научный сайт
Релятивистская динамика
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: полная энергия, связь массы и энергии, энергия покоя.
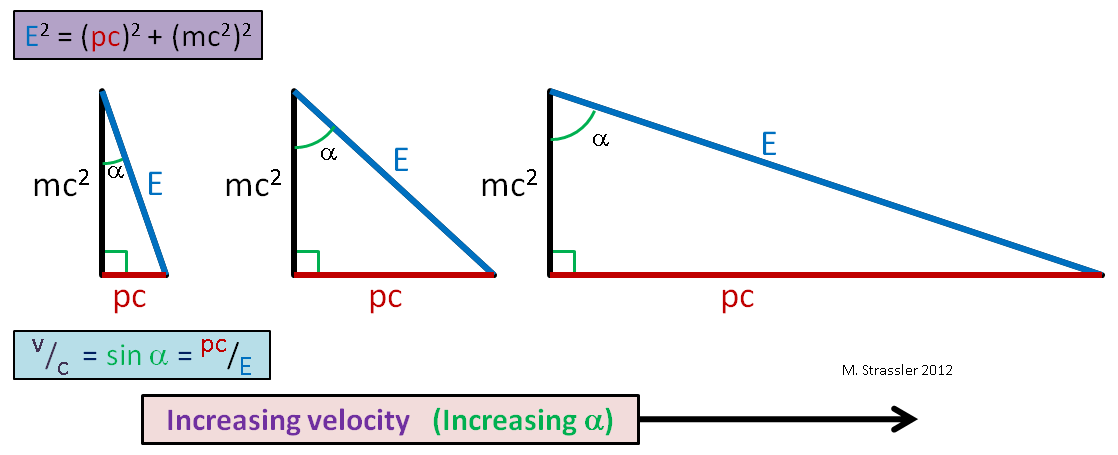
В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.
Релятивистская энергия
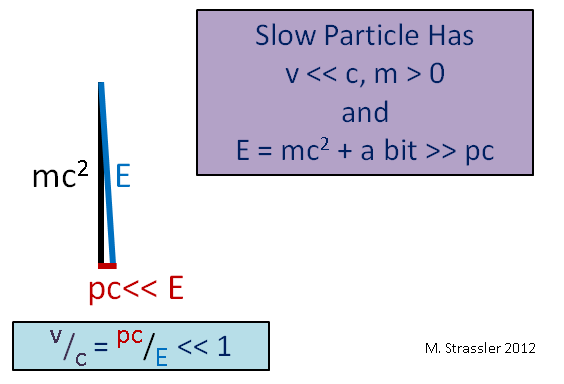
Предположим, что изолированное тело массы покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:
(1)
Здесь — энергия тела,
— скорость света в вакууме. Поскольку тело покоится, энергия
, вычиляемая по формуле (1), называется энергией покоя.
Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия
Дж.
Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна Дж/кг, поэтому находим:
кг. Это девять миллионов тонн!
Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.
Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.
Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину приводит к изменению массы тела на
.
Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой кг на
(удельная теплоёмкость воды равна
) ей нужно передать количество теплоты:
Дж.
Увеличение массы воды будет равно:
кг.
Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.
Формула ( 1) даёт энергию покоящегося тела. Что изменится, если тело движется?
Снова рассмотрим неподвижную систему отсчёта и систему
, движущуюся относительно
со скоростью
. Пусть тело массы
покоится в системе
; тогда энергия тела в системе
есть энергия покоя, вычисляемая по формуле ( 1). Оказывается, при переходе в систему
энергия преобразуется так же, как и время — а именно, энергия тела в системе
, в которой тело движется со скоростью
, равна:
( 2)
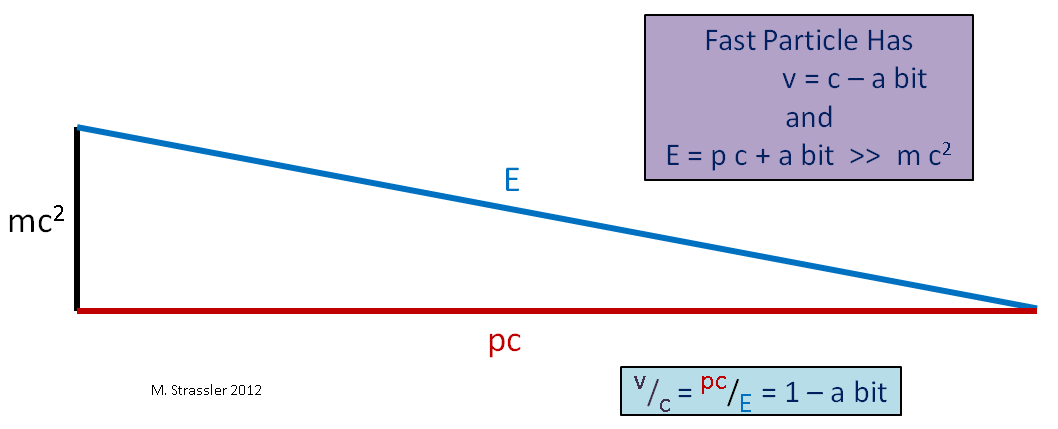
Формула ( 2) была также установлена Эйнштейном. Величина — это полная энергия движущегося тела. Поскольку в данной формуле
делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при
.
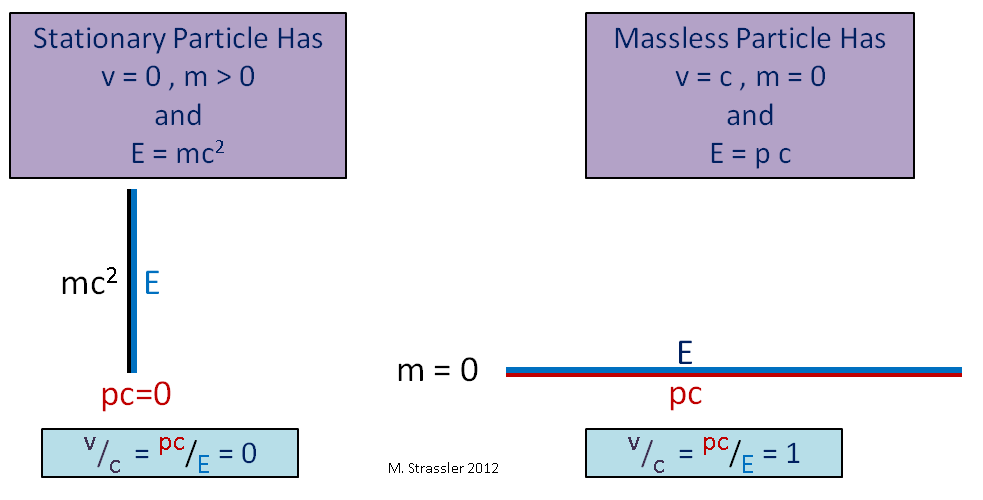
Выражение для полной энергии ( 2) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.
1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства
.
Оно означает, что : скорость массивного тела всегда меньше скорости света.
2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке в формулу ( 2) её числитель обращается в нуль. Но энергия-то фотона ненулевая!
Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула ( 2) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.
Интуитивно чувствуется, что полная энергия ( 2) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при :
( 3)
( 4)
С помощью этих формул последовательно получаем из ( 2):
( 5)
Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:
. ( 6)
При формула ( 6) переходит в нерелятивистское выражение
.
Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из ( 5), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!
Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана суммарная масса продуктов распада примерно на
меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.
При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!
Рассмотрим в качестве примера два тела массы , летящих навстречу друг другу с одинаковой скоростью
. В результате неупругого столкновения образуется тело массы
, скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:
,
,
,
.
Мы видим, что, — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный
, возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.
Релятивистский импульс.
Классическое выражение для импульса не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.
Пусть система движется относительно системы
со скоростью
(рис. 1). Два тела массы
в системе
летят навстречу друг другу с одинаковой скоростью
. Происходит неупругое столкновение.
 |
| Рис. 1. К закону сохранения импульса |
В системе тела после столкновения останавливаются. Давайте, как и выше, найдём массу
образовавшегося тела:
,
откуда
.
Теперь посмотрим на процесс столкновения с точки зрения системы . До столкновения левое тело имеет скорость:
.
Правое тело имеет скорость:
.
Нерелятивистский импульс нашей системы до столкновения равен:
.
После столкновения получившееся тело массы двигается со скоростью
.
Его нерелятивистский импульс равен:
.
Как видим, , то есть нерелятивистский импульс не сохраняется.
Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы , двигающегося со скоростью
, равен:
. 7
Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.
Импульс системы до столкновения:
.
Импульс после столкновения:
Вот теперь всё правильно: !
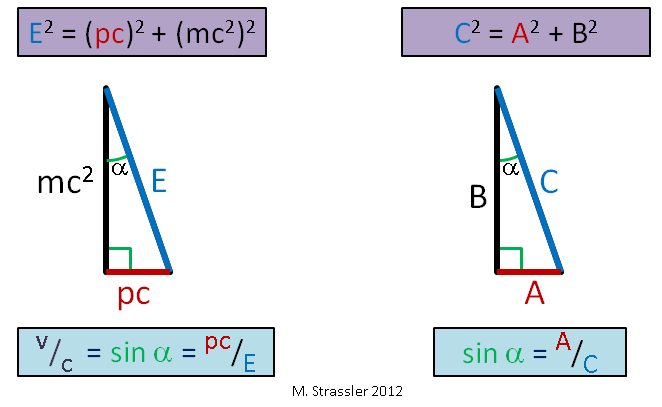
Связь энергии и импульса.
Из формул ( 2) и ( 7) можно получить замечательное соотношение между энергией и импульсом в теории относительности. Возводим обе части этих формул в квадрат:
,
Преобразуем разность:
Это и есть искомое соотношение:
. ( 8)
Данная формула позволяет выявить простую связь между энергией и импульсом фотона. Фотон имеет нулевую массу и движется со скоростью света. Как уже было замечено выше, сами по себе энергия и импульс фотона в СТО найдены быть не могут: при подстановке в формулы ( 2) и ( 7) значений и
мы получим нули в числителе и знаменателе. Но зато с помощью ( 8) легко находим:
, или
( 9)
В квантовой физике устанавливается выражение для энергии фотона, после чего с помощью формулы ( 9) находится его импульс.
Релятивистское уравнение движения.
Рассмотрим тело массы , движущееся вдоль оси
под действием силы
. Уравнение движения тела в классической механике — это второй закон Ньютона:
. Если за бесконечно малое время
приращение скорости тела равно
, то
, и уравнение движения запишется в виде:
. ( 10)
Теперь заметим, что — изменение нерелятивистского импульса тела. В результате получим «импульсную» форму записи второго закона Ньютона — производная импульса тела по времени равна силе, приложенной к телу:
. ( 11)
Все эти вещи вам знакомы, но повторить никогда не помешает 
Классическое уравнение движения — второй закон Ньютона — является инвариантным относительно преобразований Галилея, которые в классической механике описывают переход из одной инерциальной системы отсчёта в другую (это означает, напомним, что при указанном переходе второй закон Ньютона сохраняет свой вид). Однако в СТО переход между инерциальными системами отсчёта описывается преобразованиями Лоренца, а относительно них второй закон Ньютона уже не является инвариантным. Следовательно, классическое уравнение движения должно быть заменено релятивистским, которое сохраняет свой вид под действием преобразований Лоренца.
То, что второй закон Ньютона ( 10) не может быть верным в СТО, хорошо видно на следующем простом примере. Допустим, что к телу приложена постоянная сила. Тогда согласно классической механике тело будет двигаться с постоянным ускорением; скорость тела будет линейно возрастать и с течением времени превысит скорость света. Но мы знаем, что на самом
деле это невозможно.
Правильное уравнение движения в теории относительности оказывается совсем не сложным.
Релятивистское уравнение движения имеет вид ( 11), где p — релятивистский импульс:
. ( 12)
Производная релятивистского импульса по времени равна силе, приложенной к телу.
В теории относительности уравнение ( 12) приходит на смену второму закону Ньютона.
Давайте выясним, как же в действительности будет двигаться тело массы m под действием постоянной силы . При условии
из формулы ( 12) получаем:
.
Остаётся выразить отсюда скорость:
. ( 13)
Посмотрим, что даёт эта формула при малых и при больших временах движения.
Пользуемся приближёнными соотношениями при :
, ( 14)
. ( 15)
Формулы ( 14) и ( 15) отличаются от формул ( 3) и ( 4) только лишь знаком в левых частях. Очень рекомендую вам запомнить все эти четыре приближённых равенства — они часто используются в физике.
Итак, начинаем с малых времён движения. Преобразуем выражение ( 13) следующим образом:
.
При малых имеем:
.
Последовательно пользуясь нашими приближёнными формулами, получим:
.
Выражение в скобках почти не отличается от единицы, поэтому при малых имеем:
.
Здесь — ускорение тела. Мы получили результат, хорошо известный нам из классической механики: скорость тела линейно растёт со временем. Это и не удивительно — при малых временах движения скорость тела также невелика, поэтому мы можем пренебречь релятивистскими эффектами и пользоваться обычной механикой Ньютона.
Теперь переходим к большим временам. Преобразуем формулу ( 13) по-другому:
.
При больших значениях имеем:
,
и тогда:
.
Хорошо видно, что при скорость тела
неуклонно приближается к скорости света
, но всегда остаётся меньше
— как того и требует теория относительности.
Зависимость скорости тела от времени, даваемая формулой ( 13), графически представлена на рис. 2.
 |
| Рис. 2. Разгон тела под действием постоянной силы |
Начальный участок графика — почти линейный; здесь пока работает классическая механика. Впоследствии сказываются релятивистские поправки, график искривляется, и при больших временах наша кривая асимптотически приближается к прямой .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Релятивистская динамика» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
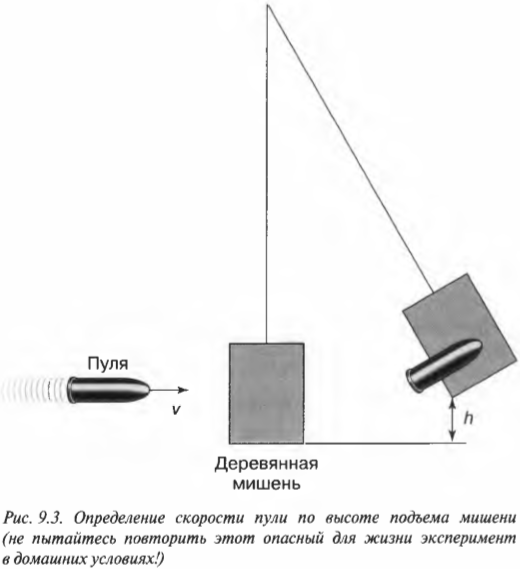
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.2k
В этой главе…
- Измеряем количество движения
- Вычисляем импульс
- Выясняем связь между силой и изменением импульса
- Разбираемся с законом сохранения импульса
- Знакомимся с разными типами столкновений
Эта глава посвящена понятиям, которые следует учитывать при изучении движения объектов, а именно с импульсом и моментом импульса. Оба эти понятия играют большую роль в двух разделах механики: кинематике, посвященной изучению движения объектов, и динамике, посвященной изучению взаимодействия объектов. Владея этими понятиями, можно легко описывать поведение объектов при столкновениях: с какой скоростью продолжат движение сталкивающиеся объекты (не хотелось бы, чтобы на их месте были ваш автомобиль или велосипед), в каком направлении продолжит движение теннисный мячик после столкновения с ракеткой, насколько глубоко дротик для игры в дартс вонзится в мишень и т.п. Чтобы получить ответы на эти и многие другие вопросы, нужно очень хорошо представлять себе, что такое импульс и момент импульса. Описанию именно этих понятий и посвящается данная глава.
Содержание
- Изучаем количество движения
- Получаем импульс
- Связываем работу силы и изменение импульса
- Пример: вычисляем импульс бильярдного шара
- Пример: определяем импульс капель дождя
- Изучаем закон сохранения импульса
- Измеряем скорость с помощью закона сохранения импульса
- Измеряем начальную скорость пули с помощью закона сохранения импульса
- Упругие и неупругие столкновения
- Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
- Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
- Упругие столкновение на прямой
- Упругое столкновение с более тяжелым объектом
- Упругое столкновение с более легким объектом
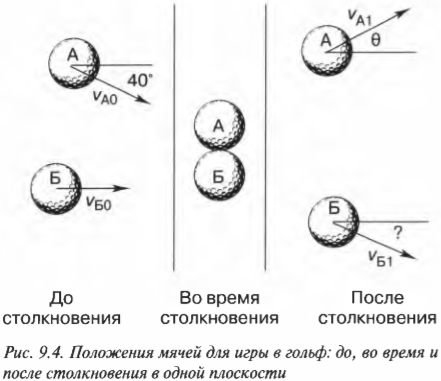
- Упругие столкновения в одной плоскости
Изучаем количество движения
В физике импульсом называется количество движения, которое приобретает тело под действием заданной силы за определенное время. Играя в бильярд, нетрудно убедиться в разнообразных проявлениях импульса. Чем сильнее и быстрее удар кия по шару, тем интенсивнее движется шар. Чем больше столкновений испытает шар, тем менее интенсивным становится его движение.
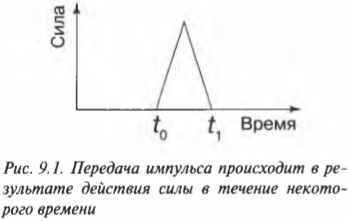
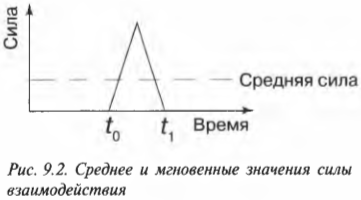
В повседневных ситуациях мы привыкли говорить, что тому или иному объекту или событию придают импульс. Рассмотрим процесс передачи импульса более подробно на примере бильярдного кия и шара. Процесс передачи импульса начинается в момент ( t_0 ) первого соприкосновения кия с шаром и заканчивается в момент ( t_1 ) утраты контакта между кием и шаром. В общем зависимость силы воздействия кия на шар от времени имеет сложный характер. Однако доя простоты можно положить, что она линейно возрастает от нулевого значения в момент ( t_0 ) первого соприкосновения, достигает максимального значения в момент наибольшего контакта, а потом снижается до нуля в момент ( t_1 ) утраты контакта между кием и шаром. Эта идеализированная зависимость силы взаимодействия кия и шара от времени графически показана на рис. 9.1.
Время взаимодействия кия и шара очень мало (несколько долей секунды), и зафиксировать характер изменения силы можно только с помощью очень точного оборудования. Обычно физики используют не точные мгновенные значения, а усредненные величины. Например, в данном примере приобретенный шаром импульс ( mathbf{p} ) равен произведению средней силы взаимодействия ( mathbf{overline{F}} ) и времени взаимодействия ( Delta{t}=t_1-t_0 ):
Обратите внимание, что эта формула связывает векторы силы и импульса. Действительно, импульс — это вектор, обладающий некоторой величиной и направлением, совпадающим с направлением силы, например результирующей векторной суммы всех действующих на объект сил.
Из этой формулы ясно, что изменение импульса измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Получаем импульс
Изменение импульса (т.е. определенного количества движения) объекта означает изменение характера его движения. Причем это изменение зависит от массы и скорости объекта, поскольку импульс равен произведению скорости и массы объекта. Импульс является очень важной физической концепцией, которая используется не только в начальном курсе физики, но и в некоторых очень сложных разделах физики, например в физике элементарных частиц, где компоненты атомов носятся с огромными скоростями. Именно на основании анализа импульсов до и после столкновения элементарных частиц ученые могут делать выводы о поведении субатомного мира.
Общая идея импульса понятна даже тем, кому незнакомо это понятие. Не так уж легко остановить тележку, которая катится по склону горы. Дело в том, что тележка массивна и обладает большой скоростью. Еще труднее остановить огромный нефтяной танкер. Порой для полной остановки крупного танкера требуется около 30 км тормозного пути! И все это из-за огромного импульса, которым он обладает.
Чем больше масса движущегося объекта (представьте себе огромный танкер) и чем больше скорость объекта (представьте себе быстро плывущий танкер), тем больше импульс объекта.
Итак, импульс объекта равен:
Как видите, импульс — это вектор с определенной величиной и направлением (о векторах подробнее рассказывается в главе 4). Импульс, как и количество движения, измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Связываем работу силы и изменение импульса
Придать объекту импульс так же просто, как ударить клюшкой для гольфа по мячу. Достаточно применить элементарные алгебраические преобразования ко второму закону Ньютона и мы получим связь между работой силы и изменением импульса. С чего начать? Начнем со связи силы и скорости. Как известно, ускорение определяется следующей формулой:
где ( Delta{v} ) — это изменение скорости за промежуток времени ( Delta{t} ), ( v_0 ) — это начальная скорость в момент времени ( t_0 ), a ( v_1 ) — это конечная скорость в момент времени ( t_1 ). Теперь, если умножить обе части этой формулы на массу объекта ( m ), то слева получим:
Теперь, чтобы получить связь силы с импульсом объекта, умножим эту формулу на промежуток времени ( Delta{t} ) и получим:
Посмотрите повнимательнее на правую часть формулы ( m(v_1-v_0) ). Поскольку импульс объекта с массой ( m ) равен ( p=mv ), то эта часть формулы выражает разницу конечного ( p_1=mv_1 ) и начального ( p_0=mv_0 ) импульса, т.е.:
Следовательно, в итоге получим:
Итак, справа имеем силу, умноженную на промежуток времени ее действия, т.е. ( FDelta{t} ), а слева — изменение импульса ( Delta{p} ). Убирая промежуточные выкладки, получим искомую формулу связи силы и изменения импульса объекта:
Произведение силы на время ее действия называется импульсом силы за то же время. (Его не следует путать с понятием импульс объекта ( p=mv ). Применение обоих этих понятий часто приводит к путанице, и потому понятие импульс силы используется довольно редко. — Примеч. ред.)
Пример: вычисляем импульс бильярдного шара
С помощью приведенных выше уравнений можно связать действующую на объект силу и приобретенный им импульс. Попробуем применить полученные знания при игре в бильярд. Допустим, что время контакта кия с бильярдным шаром приблизительно равно 5 мс (1 миллисекунда, или сокращенно 1 мс, равна 10-3 с). Насколько нужно изменить импульс неподвижного бильярдного шара, чтобы загнать его в лузу с отскоком от боковой стенки?
Пусть шар имеет массу 200 г (т.е. 0,2 кг). Допустим, что путем тщательных замеров и вычислений стало известно, что для попадания в лузу с отскоком от боковой стенки шару нужно приобрести скорость 20 м/с. Какую силу нужно приложить к кию для выполнения этой задачи?
Итак, в начальный момент времени шар покоится, т.е. начальная скорость ( v_0 ) = 0, а его конечная скорость ( v_1 ) должна быть равна 20 м/с. Вычислим необходимое изменение импульса по уже известной нам формуле:
Подставив значения получим:
Итак, необходимо изменить импульс шара на 4 кг·м/с. Вычислим, какую силу нужно для этого приложить за промежуток времени 5 мс по известной формуле:
откуда
Подставив значения, получим:
Итак, чтобы загнать бильярдный шар в лузу с отскоком от боковой стенки нужно прилагать к кию силу 800 Н в течение 5 мс.
Пример: определяем импульс капель дождя
После триумфальной демонстрации своих физических познаний в бильярдной попробуем использовать их в более привычной ситуации. Предположим, что на обратном пути домой внезапно начался дождь. Не беда, ведь под рукой есть зонт. Допустим, что на раскрытый зонт ежесекундно со средней скоростью около 10 м/с падает приблизительно 100 г капель воды. Вопрос: с какой силой нужно удерживать зонт массой 1 кг, чтобы удержать его под таким дождем?
Чтобы удержать зонт даже в отсутствие дождя, потребуется сила, равная весу зонта, то есть:
А как же подсчитать воздействие капель дождя? Предположим, что капли после падения на зонт почти мгновенно стекают по его почти горизонтальной поверхности. Даже в этом случае нам нужно учесть не только их массу, но и уменьшение скорости из-за встречи с зонтом. Действительно, летящие капли имеют начальную скорость 10 м/с, а после падения на зонт останавливаются, т.е. приобретают нулевую конечную скорость. Итак, имеем изменение импульса капель дождя, вызванное взаимодействием с зонтом. Попробуем оценить это изменение с помощью известной формулы:
Подставляя значения, получим:
Такое изменение импульса капель происходит ежесекундно. Свяжем теперь его с известной нам формулой:
Подставив значения, получим:
Итак, помимо силы 9,8 Н для удержания сухого зонта потребуется еще дополнительная сила 1 Н для компенсации торможения капель, т.е. всего потребуется сила 10,8 Н.
Наибольшую трудность при вычислениях изменения импульса под действием силы вызывает оценка времени действия этой силы. Поэтому при решении задач, связанных с изменением импульса, при столкновениях объектов обычно стремятся использовать другие параметры процесса, например скорость до и после столкновения, избегая оценок трудновычислимых параметров.
Изучаем закон сохранения импульса
Согласно этому закону, в изолированной системе без внешних сил общий импульс всех объектов системы до столкновений между ними равен общему импульсу всех объектов системы после столкновений между ними.
Если для анализа импульсов взаимодействующих объектов использовать приведенные выше формулировки с указанием силы и времени ее действия, то на это придется затратить чрезвычайно много усилий. Закон сохранения импульса позволяет избежать этих сложностей. Дело в том, что, применяя этот закон, можно полностью исключить из рассмотрения силы и время их действия.
Допустим, что два беспечных пилота космических кораблей А и Б не смогли избежать лобового столкновения своих машин. Во время столкновения корабль Б воздействовал на корабль А со средней силой ( F_{АБ} ). Согласно известной формуле о связи между силой и изменением импульса, получим для корабля А:
где ( m_{А} ) — это масса корабля A, ( v_{А1} ) — скорость корабля А после столкновения и ( v_{А0} ) — скорость корабля А до столкновения.
Аналогично, во время столкновения корабль А воздействовал на корабль Б со средней силой ( F_{БА} ). Опять по известной формуле о связи между силой и изменением импульса, получим для корабля Б:
где ( m_{Б} ) — это масса корабля Б, ( v_{Б1} ) — скорость корабля Б после столкновения и ( v_{Б0} ) — скорость корабля Б до столкновения.
Сложим оба последних равенства и получим следующее уравнение:
Опустим промежуточные выкладки и оставим только крайние левую и правую части этого равенства. Причем в правой части соберем отдельно члены начального и конечного состояний и получим:
Сумма ( m_Av_{A1}+m_Бv_{Б1} ) означает суммарный конечный импульс ( p_{1}=p_{A1}+p_{Б1} ) двух кораблей после столкновения, а сумма ( m_Av_{A0}+m_Бv_{Б0} ) — суммарный начальный импульс ( p_{0}=p_{A0}+p_{Б0} ) двух кораблей до столкновения. Следовательно, последнее уравнение можно переписать в следующем виде:
Если теперь ввести обозначение ( sum!{F} ) для суммы этих двух сил ( F_{АБ}+F_{БА} ), то получим:
При работе с изолированной, или замкнутой, системой объектов внешних сил нет. Именно такая ситуация рассматривается в данном примере.
Если два космических корабля столкнутся при отсутствии внешних сил, то согласно третьему закону Ньютона, ( F_{АБ}=-F_{БА} ). Иначе говоря, в замкнутой системе имеем:
А это означает, что:
Это равенство означает, что в изолированной системе без внешних сил начальный импульс двух сталкивающихся объектов до их столкновения равняется конечному импульсу после столкновения, что соответствует закону сохранения импульса.
Извлекаем тепло из суммарного импульса.
Всегда ли сохраняется суммарный импульс объектов при их лобовом столкновении и сцеплении? В реальном мире далеко не всегда. Дело в том, что часто при столкновениях объектов они необратимо деформируются и часть их кинетической энергии расходуется на необратимую деформацию и рассеивается в виде тепловой энергии. Однако для точного расчета такого преобразования кинетической энергии в тепловую требуется учесть много других сложных физических процессов. Эти процессы обычно не рассматриваются в начальном курсе физики, а тем более в этом курсе.
Измеряем скорость с помощью закона сохранения импульса
Попробуем применить закон сохранения импульса для расчета некоторых параметров движения. Предположим, что при игре в хоккей игрок А с массой 100 кг решил применить силовой прием против другого неподвижного игрока Б тоже с массой 100 кг (который оказался его братом-близнецом). Для этого игрок А разогнался до скорости 11 м/с, грубо толкнул игрока Б и, схватив его руками, устроил потасовку. С какой скоростью будут двигаться оба сцепившихся руками игрока после столкновения?
Будем считать, что в данном примере мы имеем дело с замкнутой системой (см. предыдущий раздел), поскольку мы пренебрегаем всеми внешними силами, включая силу трения. Хотя в вертикальном направлении на хоккеистов со стороны ледяного катка действует нормальная сила (подробнее о ней см. в главе 6), но она равна по величине весу игроков и противоположна по направлению и в сумме дает нуль.
Итак, рассмотрим горизонтальные проекции импульсов игроков. Согласно закону сохранения импульса, имеем:
Подставим в эту формулу массу и начальную скорость игроков (на самом деле нужно подставить массу ( m_А ) и начальную скорость ( v_{А0} ) только игрока А, поскольку игрок Б имел нулевую начальную скорость):
Конечный импульс ( p_1 ) должен быть равен произведению общей массы ( m_А+m_Б ) игроков на их конечную скорость ( v_{АБ1} ), т.е. получаем:
Из двух последних уравнений получаем:
откуда легко можно выразить конечную скорость ( v_{АБ1} ):
Подставляя значения, получим:
Конечная скорость двух игроков равна половине начальной скорости одного игрока. Этого следовало ожидать, ведь масса движущихся объектов увеличилась вдвое, а поскольку импульс сохраняется, то скорость должна уменьшиться во столько же раз.
Измеряем начальную скорость пули с помощью закона сохранения импульса
Закон сохранения импульса очень удобно использовать для определения скорости объекта, если ее нельзя или очень трудно измерить с помощью секундомера. Предположим, что изготовитель пуль хочет знать, какой будет начальная скорость новой пули. Как ему поступить? Для решения этой задачи ему предложили использовать приспособление, показанное на рис. 9.3.
Как оно может помочь? Оказывается, что если выстрелить пулей с массой ( m ) в массивную деревянную мишень с массой ( M ) и пуля застрянет в мишени, то, как и в примере с хоккеистами, конечная скорость мишени с пулей ( v_1 ) будет зависеть от начальной скорости пули ( v_0 ). Как именно? Для конкретного ответа на этот вопрос попробуем использовать закон сохранения импульса.
Итак, начальный суммарный импульс пули и мишени равен:
Поскольку пуля застряла в мишени, то конечный суммарный импульс пули и мишени равен:
Если пренебречь потерями энергии на преодоление трения при попадании пули в мишень, то согласно закону сохранения импульса, эти два импульса должны быть равны:
Тогда:
и искомая начальная скорость равна:
Итак, остается только определить конечную скорость ( v_1 ) мишени с застрявшей в ней пулей. Для этого нужно вспомнить закон сохранения энергии, который описывается в главе 8. Ведь после попадания пули мишень отклонится и поднимется на некоторую максимальную высоту ( h ), на которой ее скорость станет равной нулю. В этой точке ее кинетическая энергия ( frac{(m+M)v^2_1}{2} ) преобразуется в потенциальную ( (m+M)gh ). Итак, согласно закону сохранения энергии получим:
Откуда легко вывести формулу для конечной скорости мишени с застрявшей в ней пулей ( v_1 ):
Подставим эту формулу в прежнее выражение для искомой начальной скорости пули:
и получим:
Пусть пуля имеет массу 50 г, деревянная мишень — 10 кг, а после попадания пули в нее мишень отклонилась и поднялась на максимальную высоту 0,5 м. Подставляя значения в приведенную выше формулу, получим:
Таким образом, мы определили начальную скорость пули. Изготовитель пуль будет просто в восторге от такого простого и удобного способа.
Упругие и неупругие столкновения
Изучение физики на примере столкновений разных тел — это очень интересное и увлекательное занятие. Во многом это объясняется тем, что многие вычисления значительно упрощаются благодаря закону сохранения импульса (более подробно он рассматривается в предыдущих разделах этой главы). Однако, как мы уже убедились в предыдущих примерах, в некоторых столкновениях одного этого закона недостаточно и нужно применять закон сохранения энергии. Это особенно полезно для анализа столкновений объектов со скоростями, векторы которых направлены не вдоль одной прямой (как в предыдущих примерах), а лежат в одной плоскости.
В реальной жизни такие ситуации происходят сплошь и рядом. Например, при изучении причин дорожно-транспортного происшествия часто требуется проанализировать начальные и конечные скорости столкнувшихся автомобилей. При сортировке вагонов нужно учитывать начальные и конечные скорости сталкивающихся вагонов и составов.
Что происходит в таких столкновениях, если столкнувшиеся объекты не “слипаются” друг с другом? Рассмотрим более общий пример: пусть два бильярдных шара сталкиваются дуг с другом с разными скоростями, направленными друг к другу под произвольным углом. Как определить их величину и направление их скоростей после столкновения? Для этого потребуется не только закон сохранения импульса, но и закон сохранения энергии.
Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
В реальном мире при столкновении тел всегда наблюдаются потери энергии на деформацию и рассеивание тепла. В некоторых случаях эти потери столь малы, что ими можно пренебречь, как, например, при столкновении двух бильярдных шаров. В физике такие столкновения с сохранением кинетической энергии сталкивающихся объектов называют упругими столкновениями. Итак, в упругом столкновении сохраняется общая кинетическая энергия замкнутой системы объектов, т.е. суммарная кинетическая энергия после столкновения равна суммарной кинетической энергии до столкновения.
Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
Если во время столкновения объектов какая-то часть энергии тратится на работу каких-то неконсервативных сил (например, на преодоление силы трения, деформацию и т.п.), то кинетическая энергия системы не сохраняется. Она частично преобразуется в другие формы энергии. Такие столкновения в физике называют неупругими столкновениями. Итак, в неупругом столкновении общая кинетическая энергия замкнутой системы объектов не сохраняется, т.е. суммарная кинетическая энергия после столкновения не равна суммарной кинетической энергии до столкновения. Примеры неупругих столкновений можно наблюдать в дорожно-транспортных происшествиях, когда столкнувшиеся машины деформируют друг друга или даже сцепляются и движутся как единое целое.
Совсем не обязательно, чтобы после неупругого столкновения объекты сцеплялись друг с другом. Достаточно, чтобы часть кинетической энергии “утрачивалась”, т.е. переходила в другую форму, например в тепловую энергию. Неупругое столкновение внешне может быть очень похоже на упругое столкновение, например при касательном столкновении двух машин с образованием легких повреждений. На образование этих повреждений необратимо тратится часть кинетической энергии, но машины могут независимо продолжить движение.
Упругие столкновение на прямой
Итак, мы уже выяснили, что при упругом столкновении кинетическая энергия сталкивающихся объектов сохраняется. Проще всего изучать особенности упругого столкновения, когда векторы скоростей находятся на одной прямой. Рассмотрим идеализированный пример столкновения двух машин с совершенно упругими (т.е. недеформирую- щимися) бамперами, которые движутся по прямой.
Упругое столкновение с более тяжелым объектом
Предположим, что вы решили прокатиться на автомобиле А с массой 300 кг и на скорости около 10 м/с столкнулись с внезапно остановившимся перед вами другим автомобилем Б с массой 400 кг. Какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой ( m_А ) = 300 кг имел начальную скорость ( v_{А0} ) = 10 м/с, а автомобиль Б с массой ( m_Б ) = 400 кг — начальную скорость ( v_{Б0} ) = 0. Если считать систему двух автомобилей замкнутой, то их общий импульс должен сохраняться, то есть:
где ( v_{А1} ) — это конечная скорость автомобиля А после столкновения, a ( v_{Б1} ) — это конечная скорость автомобиля Б после столкновения.
У нас есть одно уравнение с двумя неизвестными ( v_{А1} ) и ( v_{Б1} ). Чтобы их найти, нужно иметь еще одно уравнение, связывающее эти неизвестные. Как насчет кинетической энергии? Действительно, поскольку столкновение было упругим, то кинетическая энергия объектов должна сохраняться, т.е. должно выполняться равенство:
Теперь у нас есть два уравнения и две неизвестных величины. С помощью простых алгебраических операций можно легко получить выражения для неизвестных скоростей ( v_{А1} ) и ( v_{Б1} ):
и
Подставляя значения в обе эти формулы, получим:
и
Анализируя полученные значения, можно легко восстановить ход событий. Итак, автомобиль А на скорости 10 м/с столкнулся с неподвижным автомобилем Б. После столкновения автомобиль А отскочил назад (об этом свидетельствует отрицательный знак конечной скорости ( v_{А1} )) со скоростью 1,43 м/с, а автомобиль Б начал движение вперед со скоростью 8,57 м/с. Автомобиль А легче автомобиля Б, а что если бы было наоборот?
Упругое столкновение с более легким объектом
Предположим, что в предыдущем примере движущийся автомобиль А тяжелее неподвижного автомобиля Б. Пусть автомобиль А с массой 400 кг на скорости около 10 м/с сталкивается с внезапно остановившимся перед вами другим автомобилем Б с массой 300 кг. Вопрос остается прежним: какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой ( m_А ) = 400 кг имеет начальную скорость ( v_{А0} ) = 10 м/с, а автомобиль Б с массой ( m_Б ) = 300 кг — начальную скорость ( v_{Б0} ) = 0. Используем уже известные нам формулы скоростей ( v_{А1} ) и ( v_{Б1} ):
и
Подставим в них новые значения и получим:
и
Как видите, более тяжелый движущийся автомобиль А после столкновения с более легким автомобилем Б смог продолжить движение в том же направлении, но с меньшей скоростью. Причем часть своего импульса он передал более легкому автомобилю Б.
Упругие столкновения в одной плоскости
Столкновения объектов не всегда происходят по прямой линии. Например, бильярдные шары сталкиваются так, что векторы их скоростей могут быть направлены не вдоль одной прямой, а находится в одной плоскости под произвольным углом друг к другу. В этом случае нужно учитывать не только величину, но и направление скорости. Пусть во время игры в гольф два игрока одновременно (простим им это нарушение правил) ударяют по разным мячам А и Б, мячи упруго сталкиваются и продолжают движение, как показано на рис. 9.4. Какими будут скорости мячей после столкновения?
Попробуем решить эту задачу, учитывая, что мячи имеют одинаковую массу ( m ) = 46 г. Мяч А имеет начальную скорость ( v_{А0} ) = 1,0 м/с, а мяч Б — начальную скорость ( v_{Б0} ) = 2,0 м/с. Кроме того, пусть нам известны направления векторов начальных скоростей обоих мячей (см. рис. 9.4).
Для решения задачи нам потребуются закон сохранения импульса и закон сохранения энергии. Поскольку столкновение считается упругим, то кинетическая энергия системы сохраняется, т.е. согласно закону сохранения энергии, имеем:
или в более простой форме:
Если подставить вместо скоростей их компоненты по осям X и Y, то получим:
Так как трение здесь не учитывается, то в процессе столкновения внутренние силы упругого взаимодействия мячей направлены только по вертикальной оси Y. Эти силы не изменяют компоненты импульсов мячей по горизонтальной оси X:
и
Отсюда следует, что компоненты скоростей мячей по горизонтальной оси X после столкновения тоже не изменяются:
и
(То есть компоненты скоростей мячей по горизонтальной оси X в результате столкновения не изменились.)
Соотношение, полученное ранее из закона сохранения энергии:
с учетом постоянства компонент скоростей по оси X теперь будет иметь следующий вид:
или (поскольку ( v_{Б0у} ) = 0);
Согласно закону сохранения импульса, для компонент импульса по вертикальной оси Y имеем( mv_{А1у}+mv_{Б1у}=mv_{А0у}+mv_{Б0у} ) или в более простой форме (поскольку ( v_{Б0у} ) = 0):
Из двух последних равенств нетрудно получить выражения для компонент скоростей по вертикальной оси Y:
и
Как видите, при таком упругом столкновении у мячей остались прежними их компоненты скоростей по горизонтальной оси X, и они “обменялись” компонентами скоростей по вертикальной оси Y. Это значит, что мяч А продолжит движение с нулевой компонентой ( v_{А1у} ), т.е. по горизонтали, а мяч Б продолжит движение под углом ( alpha ), который легко вычислить по формуле:
где знак “минус” перед значением угла означает, что на рис. 9.4 угол откладывается в направлении против часовой стрелки.
А скорости мячей после столкновения будут равны
и:
Подставив значения, получим:
и
Глава 9. Двигаем объекты: количество движения и импульс
3 (60%) 5 votes
Множество непонятных свойств мира связаны с природой массы и энергии (а также импульса). Все мы слышали эти слова и у многих из нас есть туманное представление об их значении. Конечно, значений у слов «масса» и «энергия» в английском и других языках довольно много. К сожалению, ни одно из них не совпадает с теми, что имеют в виду физики. Попробуйте отставить в сторону эти значения слов и поработать с точными физическими понятиями – иначе вы полностью запутаетесь.
Необходимо отметить, что не стоит при словосочетании «масса и энергия» вспоминать другую популярную пару, «вещество и энергия». Многие люди упоминают последнее словосочетания так, будто вещество и энергия – это две стороны одной медали. Но это не так. Вещество и энергия относятся к разным категориям, как яблоки и орангутанги. Вещество, не важно, как его определять – это класс объектов, существующих во Вселенной, а масса и энергия – это не объекты, а свойства, которыми эти объекты обладают. Масса и энергия глубоко переплетены друг с другом, и заслуживают общего объяснения.
Чтобы понять массу и энергию, необходимо добавить к ним импульс и обсудить различия и связи этих величин.
Энергия
У слова «энергия» есть множество значений. Когда мы заболеваем, то говорим о том, что у нас не осталось энергии, имея в виду силу и мотивацию. Когда мы говорим, что у кого-то полно энергии, мы имеем в виду его высокую активность. Мы жалуемся на рост цен на энергию, имея в виду топливо. Мы говорим о духовной энергии как о чём-то неизмеримом, но важном, возможно, о некоей форме харизмы. И все эти понятия перекликаются друг с другом, поэтому мы и выбираем одно слово для их описания. Но в физике энергия – это совсем другое. С точки зрения физики ошибочно будет смешивать одно из этих определений с физическим. В физике нужно придерживаться физического термина, чтобы не получить неправильные ответы и не запутаться вконец.
К несчастью, понятие «энергии» в физике очень сложно описать так, как это делают словари – короткой содержательной фразой. Но не подумайте плохого – всё дело в несовершенстве естественного языка, а не в том, что понятие энергии в физике расплывчато. В любой заданной физической системе совершенно понятно, какова её энергия, как в смысле её экспериментального измерения, так и в смысле расчётов (при наличии описывающих систему уравнений).
Одна из причин, по которым энергию так сложно описать – она может принимать множество форм, и не все из них просто понять. Вот три наиболее часто встречающихся разновидности:
1. Энергия может быть заключена в массе объекта. Здесь я называю такой вариант «энергией массы» (благодаря известному уравнению E=mc2 энергия связывается с массой. Также она называется «энергия покоя», поскольку это энергия объекта, находящегося в покое, то есть, без движения).
2. Во-вторых, энергия бывает связанной с движением объекта. Здесь я называю её «энергией движения», а технический термин для этого – кинетическая энергия. Этот вариант интуитивно легко воспринять, поскольку у быстро движущихся объектов энергия больше, чем у медленно движущихся. Кроме того, у тяжёлого объекта энергия движения больше, чем у лёгкого, движущегося с той же скоростью.
3. Энергия может храниться во взаимоотношении объектов (и обычно называется «потенциальной»). Она хранится в растянутой пружине, в воде за дамбой, в гравитационном взаимодействии Земли и Солнца, во взаимодействиях атомов в молекуле. Существует множество способов хранения энергии. Звучит расплывчато, но в этом виноват язык. В любом из перечисленных случаев существуют точные формулы, описывающие сохранённую в системе энергию и хорошо определённые пути её измерения.
С третьим типом энергии связано то, что я буду называть энергией взаимодействия, и это наиболее запутанное понятие из всех. В отличие от энергии массы и энергии движения, которые всегда больше или равны нулю, энергия взаимодействий может быть положительной и отрицательной. Пока я оставлю эту тему, но мы к ней ещё вернёмся.
Энергия – это особая величина огромной важности для физики. Причина такой важности – в том, что она «сохраняется». Что же это означает?
Если вы начнёте наблюдение с объекта или с набора объектов – назовём их «системой объектов» – обладающих определённым количеством энергии в начальный момент (не забудьте подсчитать всю энергию – массы, движения, сохранённую энергию всех типов, и т.п.), а затем части системы будут взаимодействовать только друг с другом и более ни с чем, тогда в конце наблюдения общее количество энергии, которым обладают эти объекты, будет тем же, что и в начале. Общая энергия системы сохраняется – её общее количество не меняется. Она может менять форму, но если отслеживать все разновидности, то в конце её будет столько же, сколько и в начале.
Это правило работает, даже если некоторые объекты будут исчезать и уступать место другим, к примеру, если одна частица в системе распадётся на две других, вливающихся в систему.
Почему энергия сохраняется? Из-за математического принципа, соотносящего тот факт, что законы природы со временем не меняются, с существованием сохраняющейся величины, которую мы по определению называем «энергией».
Самым известным и общим определением этого принципа мы обязаны Эмми Нётер, одной из величайших математических физиков предыдущего столетия, современнице Эйнштейна. Некоторые члены физического и математического сообщества относились к ней с глубоким уважением, но в то время в своей родной Германии она страдала от дискриминации по половому и национальному признаку (там блокировали попытки присвоить ей звание профессора в Гёттингене, и оттуда ей пришлось бежать после того, как к власти пришли нацисты). Эмигрировав в США, всего после двух лет преподаваний в колледже Брин-Мар (который по сию пору принимает для обучения только женщин), она умерла от онкологического заболевания.
Знаменитая теорема Нётер (реально это две тесно связанных теоремы) говорит нам, что если в законах природы существует симметрия – в нашем случае это значит, что законы природы одинаковы в любой момент времени – то из этого следует сохранение некоей величины – в нашем случае, энергии.
Более того, теорема в точности сообщает нам, что это за величина – каковы различные формы энергии, для заданной системы объектов, которые необходимо сложить, чтобы получить общую энергию. Именно поэтому физики всегда точно знают, что такое энергия, и почему её легче получить при помощи уравнений, чем определить словами.
Импульс
С импульсом дело обстоит примерно таким же образом, что и с энергией. Законы природы везде одинаковые. Грубо говоря, эксперименты дают одни и те же ответы, проводите ли вы их к северу или к югу отсюда, к западу или востоку, на вершине здания или в глубокой шахте. Выберите любое направление в пространстве. Тогда, согласно Нётер, импульс вдоль этого направления сохраняется. Поскольку в пространстве есть три измерения, то можно двигаться в трёх разных независимых направлениях и существуют три независимых закона сохранения. Выбрать можно три любых направления, при условии, что они разные. К примеру, можно выбрать в качестве трёх законов сохранения импульсы в направлениях север-юг, запад-восток и вверх-вниз. Или можно выбрать три других – по направлению к и от Солнца, вдоль орбиты Земли в обе стороны, и вверх и вниз по отношению к плоскости Солнечной системы. Ваш выбор не имеет значения, ибо импульс сохраняется вдоль любого направления.
Простейшая форма импульса возникает благодаря простому движению объектов, и это примерно то, что можно представить себе интуитивно: если объект двигается в определённом направлении, то у него есть импульс в этом направлении, и чем быстрее он двигается, тем больше этот импульс. А у более тяжёлого объекта импульс больше, чем у лёгкого, если они двигаются с одинаковыми скоростями.
Одно из интересных следствий этого сохранения: если у вас имеется неподвижная система из объектов (то есть, система в целом не двигается, если усреднить все движения составляющих её объектов), тогда она будет оставаться неподвижной, если только ей не придаст движение какое-либо внешнее воздействие. Причина в том, что у неподвижной системы суммарный импульс равен нулю, и поскольку импульс сохраняется, он останется равным нулю навсегда, если только не вмешается что-либо извне системы.
Масса, и её связь с энергией и импульсом
Теперь обратимся к массе
К сожалению, с массой связано много путаницы – после выхода работы Эйнштейна по теории относительности некоторое время существовало два понятия массы. И только одно из них (то, на котором остановился сам Эйнштейн, и которое иногда называют «инвариантной массой» или «массой покоя», чтобы отличить её от уже ставшего архаичным термина «релятивистская масса»), до сих пор используют в физике частиц. В отдельной статье я поясню это более подробно.
Рис. 1
Под массой m, которую я использую в статьях, подразумевается та масса, что непосредственно связывает энергию и импульс. Для объекта, двигающегося без воздействия внешних сил (не взаимодействующего значительно с другими объектами), Эйнштейн предположил (и это было подтверждено экспериментами), что его энергия E, импульс p и масса m удовлетворяют простому пифагорову равенству:
Помните старика Пифагора, утверждавшего, что для прямоугольного треугольника со сторонами A и B и гипотенузой C выполняется равенство
? Это связь того же типа – см. рис. 1. У нас с – постоянная скорость, которая, как мы увидим, служит универсальным пределом скорости. Также мы увидим, почему её называют «скоростью света».
Согласно уравнениям Эйнштейна, скорость объекта, делённая на предел скорости с, это просто отношение pc к Е:
То есть отношение горизонтального катета к гипотенузе. Оно также равно синусу угла α на рис. 1. Вот так вот, граждане. А поскольку катеты прямоугольного треугольника всегда короче гипотенузы (синус любого угла всегда меньше или равен 1), скорость любого объекта не может превышать с, универсальный предел скорости. С увеличением скорости объекта фиксированной массы p и E становятся очень большими (рис. 2), но E всегда больше pc, поэтому v всегда меньше c!
Рис. 2
Теперь обратите внимание, что если объект не двигается, то его импульс p равен нулю, и отношение в уравнении 1 сводится к:
Знаменитая формула Эйнштейна, связь массы с фиксированным количеством энергии (то, что я называю энергией массы), это просто утверждение, соответствующее тому, что когда треугольник вырождается в вертикальную линию, как на рис. 3 слева, его гипотенуза становится такой же длины, как вертикальный катет. При этом оно не означает, что энергия всегда равна массе, помноженной на квадрат с. Это работает только для покоящегося объекта с нулевым импульсом.
Рис. 3
Ещё одно интересное наблюдение: для безмассовой частицы вертикальный катет треугольника нулевой, а гипотенуза и горизонтальный катет совпадают, как на рис. 3. В таком случае E равняется pc, что означает, что v/c = 1, или v = c. Видно, что безмассовая частица (к примеру, фотон, частица света) неизбежно перемещается со скоростью с. Поэтому скорость света такая же, как универсальный предел скорости, с.
С другой стороны, если взять обладающую массой частицу, как на рис. 4, то неважно, насколько большим вы делаете импульс и энергию, E всегда будет немного больше, чем p*c, поэтому скорость всегда будет меньше с. Безмассовые частицы обязаны перемещаться с максимальной скоростью. Скорость массивных частиц должна быть меньше.
Рис. 4. Здесь «>>» означает «гораздо больше»
Представьте себе другой пограничный случай, медленно (по сравнению со скоростью света) движущийся массивный объект, к примеру, автомобиль. Поскольку его скорость v гораздо меньше с, его импульс p умноженный на c будет гораздо меньше E, и, как видно из рис. 5, E будет немногим больше, чем mc2. Поэтому энергия движения медленного объекта E — mc2 гораздо меньше, чем энергия его массы mc2, а у быстрого объекта энергию движения можно сделать сколь угодно большой, как мы видели на рис. 4.
Один тонкий момент: импульс – это не только число, но и вектор. У него есть величина и направление. Он направлен в сторону движения частицы. Когда я пишу «p», я указываю только величину. Во многих случаях необходимо отслеживать и направление импульса, хотя в уравнении №1, связывающем импульс с энергией и массой, этого делать не нужно.
Рис. 5
Ещё один тонкий момент: я использовал треугольники и простейшую тригонометрию, поскольку она известна всем из школы. Экспертам же нужно быть осторожнее – правильно понять уравнения Эйнштейна можно, используя гиперболические функции, обычно не встречающиеся дилетантам, но крайне важные для понимания структуры теории, и делающие более понятными такие вещи, как сложение скоростей, сжатие расстояний и т.п. Не претендующие на экспертизу люди могут это игнорировать.
Но скорость же относительна?..
Если вы внимательно читали текст, вас уже может кое-что удивить. Вы знаете, что скорость частицы – или чего угодно, движущегося медленнее света – зависит от точки зрения.
Если вы сидите дома и читаете книгу, вы скажете, что скорость книги нулевая (и относительно вас она действительно покоится), следовательно, у неё нет импульса и энергии движения, только энергия массы. Но если бы я стоял на Луне, то я напомнил бы вам, что Земля вертится, поэтому это вращение увлекает и вас, и двигает вас относительно меня со скоростью в сотни километров в час. Так что вы с вашей книгой обладали бы импульсом с моей точки зрения.
Кто же прав?
Вариант относительности согласно Галилею – первый принцип относительности – утверждает, что правы мы оба. Вариант относительности Эйнштейна соглашается с точкой зрения Галилея в том, что правы оба, но вносит важные корректировки в то, как обозначили бы последователи Галилея энергию, импульс и массу книги, помещая эти величины в пифагорово соотношение уравнения №1.
Но если правы все, какую E и какой p мне нужно подставить в соотношение энергии/импульса/массы,
? Подставить E и p, измеренные вами, читающим книгу, то есть E = mc2 и p = 0? Или подставить E и p, которыми обладает книга с моей точки зрения, когда вы двигаетесь вместе с Землёй?
В ответе на этот вопрос содержится вся суть уравнения Эйнштейна №1. Каждый наблюдатель измерит разные величины E и p для книги, в зависимости от того, как быстро книга будет двигаться относительно него. Но для всех наблюдателей уравнение
будет верным!
Магия! А на самом деле, гениальность – мысль, пришедшая в 1905 году, о том, как можно заменить набор уравнений, предложенных Ньютоном и его последователями, новым удивительным набором уравнений, всё ещё совпадающим со всеми предыдущими экспериментами, но оказавшимся более точным представлением реальности. Сложно представить, как сильно нужно было изменить образ мышления, чтобы додуматься до этого, пока не разберёшься с тем, сколько всего во время формирования новой теории могло пойти не так, и сколько других различных уравнений, содержащих противоречия с математикой или с предыдущими экспериментами, можно было бы предложить (а люди их предлагали). Мне, к примеру, постоянно приходят работы начинающих физиков, пытающихся «исправить» уравнения Эйнштейна, но я никогда не видел, чтобы кто-нибудь из них проверил свои уравнения на внутреннюю непротиворечивость. Это очень сложная задача и причина неудачи большинства теорий.
Но как тогда могут сохраняться энергия и импульс?
Погодите-ка, – скажете вы, когда ваша голова уже готова будет взорваться и забрызгать всё вокруг мозгами (я и сам помню это ощущение), – но энергия и импульс должны сохраняться! Так как же могут разные наблюдатели не соглашаться с тем, что они собой представляют?
Тут есть ещё больше магии, которая, кстати, была ещё до Эйнштейна. Поверьте мне, Вселенная – очень, очень хитроумный бухгалтер, и, несмотря на то, что разные наблюдатели не будут соглашаться по поводу энергии, имеющейся у объекта или системы объектов, они все согласятся, что эта энергия не меняется со временем. То же касается и импульса.
А вот масса очень сильно отличается от энергии и импульса. Во-первых, масса не сохраняется. В природе есть множество процессов, изменяющих общую массу системы: к примеру, массивная частица Хиггса может распадаться на два безмассовых фотона. С массой не связана симметрия, и поэтому у Нётер нет для нас закона сохранения. Во-вторых, в отличие от энергии и импульса, чьи величины зависят от наблюдателя (в частности, от его скорости по отношению к измеряемым объектам), все наблюдатели согласятся с величиной массы m объекта. А это вовсе не очевидно, и происходит так оттого, как ужасно хитроумно работают уравнения Эйнштейна.
Итак, что мы имеем
На текущий момент у нас несколько, на первый взгляд, противоречивых знаний. Мы знаем, что:
• Энергия и импульс изолированной физической системы сохраняются (общая энергия и общий импульс изолированной системы не меняются со временем) с точки зрения любого наблюдателя.
• Разные наблюдатели, движущиеся относительно друг друга, по-разному оценят величины энергии и импульса системы!
• Сумма масс объектов, составляющих систему, не сохраняется, она может меняться.
• Но все наблюдатели согласятся с величиной массы объекта.
К этому списку нужно добавить ещё два факта и два вывода:
Масса физической системы объектов не равна сумме масс объектов, составляющих эту систему.
Вместо этого масса физической системы, по поводу которой согласятся все наблюдатели, определяется её энергией и импульсом, и удовлетворяет своему варианту уравнения №1:
Получается, что дополнительный закон сохранения не нужен, и что хотя сумма масс объектов, составляющих систему, не сохраняется, масса системы сохраняется, поскольку она связана через уравнение №1′ с энергией и импульсом системы, которые сохраняются.
Масса системы объектов – это единственный пункт нашего списка, одновременно и сохраняющийся, и не являющийся предметом споров наблюдателей.
Нужно лишь помнить, что масса системы объектов – это не сумма масс объектов, составляющих систему, а то, что задано уравнением №1′.
Чем пытаться объяснить это, просто посмотрим, как это работает. Яркий пример стоит тысячи слов. Давайте в качестве примера системы рассмотрим самую модную штуку, а именно, частицу Хиггса (обладающую массой в 126 ГэВ/с2), и посмотрим, как различные утверждения, сделанные выше, работают при её распаде на два фотона.
Одна частица Хиггса, два фотона и три наблюдателя
Рис. 6. Три наблюдателя смотрят на частицу Хиггса. По отношению к ней Петя (Peter) не двигается, Маша (Marie) двигается вниз, а Костя (Chris) двигается влево.
Давайте посмотрим на то, как частица Хиггса распадается на два фотона, с точки зрения трёх разных наблюдателей. Они изображены на рис. 6 вместе с частицей Хиггса, на которую они смотрят. Конечно, они не могут увидеть её глазами, ибо она существует слишком малый отрезок времени и она слишком мала. Им необходимо использовать какое-либо научное оборудование. Для Пети частица Хиггса не двигается. Маша двигается вниз относительно Пети. Костя двигается влево относительно Пети. Значит, для Маши частица Хиггса двигается вверх, а для Кости – вправо. Три наблюдателя видят, как частица распадается согласно рис. 7. Петя видит, что Хиггс распадается на два фотона одинаковых энергий, один из которых двигается вверх, а другой – вниз. Маша видит, что Хиггс распадается на два фотона различных энергий, и у двигающегося вверх энергии больше, чем у двигающегося вниз. Костя видит, как Хиггс распадается на два фотона, направляющихся вправо вверх и вправо вниз. Давайте посчитаем, какие энергии и импульсы присвоят Хиггсу и двум фотонам наблюдатели, и как каждый из них придёт к выводу о сохранении энергии и импульса в процессе распада.
Распад неподвижной частицы Хиггса
Для начала разберём частицу Хиггса с точки зрения Пети. Петя смотрит (при помощи измерительных приборов) на частицу Хиггса, и что же он видит? (Я буду ставить чёрточку над всем, что видит Петя, и потом мы сравним это с наблюдениями Маши и Кости). Хиггс не двигается, значит, его импульс
равен нулю, и согласно уравнению №1 у него, с его массой m = 126 ГэВ/c2 энергия будет
Теперь, согласно сохранению энергии и импульса, система, состоящая из частицы Хиггса, сохранит всю энергию и импульс после распада. И это будет так, пока никакая внешняя сила не будет воздействовать на Хиггса. Вы можете спросить, нужно ли нам волноваться по поводу земного притяжения, ведь гравитация и будет внешним воздействием, способным менять импульс. Отвечу, что за то краткое время, которое нужно Хиггсу на распад, влияние гравитации будет столько малым, что если бы я рассказал вам, какое оно на самом деле мелкое, вы бы захихикали. Забудьте об этом.
Итак, когда Хиггс распадается, энергии частиц, составляющих его остатки, должны в сумме дать 126 ГэВ, а импульс частиц (учитывая, что импульс – это не только величина, но и направление — вектор) в сумме даст ноль.
Два безмассовых фотона, на которые распадается Хиггс, могут разлететься в любых направлениях, но чтобы упростить пример, представим, что они разлетятся вертикально – один вверх, а другой, отскочив от него, вниз. (Чуть позже обсудим, почему они должны разлетаться в противоположных направлениях).
Каким импульсом обладают фотоны? Это просто. Во-первых, общий импульс системы – сумма импульсов двух фотонов – должен быть нулевым, поскольку у Хиггса до распада был нулевой импульс (с точки зрения Пети). Теперь у каждого из фотонов есть импульс определённой величины и направления. В сумме они могут давать ноль только одним способом – если они равной величины и противоположного направления. Если один идёт вверх, другой должен идти вниз, и величина их должна быть одинаковой.
Рис. 8: что видит Петя
Во-вторых, общая энергия системы – это сумма энергий двух фотонов. Это происходит потому, что между ними нет никакой энергии взаимодействия (кроме крайне малого гравитационного притяжения, о котором можно забыть). Конечно, раз у них нет масс, то вся их энергия заключается в энергии движения. Кроме того, в случае для безмассовой частицы уравнение №1 говорит о том, что E = p c, где p – величина импульса. Из-за этого два фотона с одинаковыми импульсами должны обладать и одинаковыми энергиями. А поскольку две эти энергии в сумме должны дать энергию частицы Хиггса, то энергия каждого фотона должна равняться половине энергии частицы Хиггса.
А поскольку для безмассовой частицы p = E/c, то
И это отображено на рис. 8.
Энергия и импульс сохраняются, а масса – нет, поскольку у фотонов нет массы, а у Хиггса была. А что по поводу массы системы? Какова масса системы из двух фотонов? Ненулевая. Очевидно, какая она. Точно так же, как и для самого Хиггса (из которого и состояла изначально вся система), система из двух фотонов обладает той же энергией и импульсом, что были у Хиггса:
А поскольку для Пети
,
Что и есть масса Хиггса. Масса системы не изменилась за время распада, как и ожидалось.
Наблюдатель, для которого Хиггс движется вверх
Маша движется вниз по отношению к Пете, так что с её точки зрения Петя и Хиггс двигаются вверх. Допустим, что Хиггс двигается со скоростью v = 0,8 c, то есть 4/5 скорости света, относительно неё. В отличие от Пети, с точки зрения Маши Хиггс обладает ненулевым импульсом, а импульсы у фотонов оказываются разными по величине, но по-прежнему разнонаправленными – в результате чего сумма их импульсов будет ненулевой.
Рис. 9: как Маша видит распад частицы Хиггса
Как посчитать, какими импульсом и энергией обладает Хиггса и два фотона, на которые он распадается, с точки зрения Маши? Для этого нам понадобится ещё один набор простых уравнений Эйнштейна. Допустим, с точки зрения некоего наблюдателя объект обладает импульсом p и энергией E. Тогда с точки зрения другого наблюдателя, движущегося со скоростью v по направлению движения объекта (или против него), импульс и энергия объекта будут выражаться следующим образом:
Где γ удовлетворяет ещё одному пифагорову уравнению:
согласно Эйнштейну. Это позволяет нам выполнять преобразования между тем, что видит Петя, и тем, что видит Маша (или любой другой наблюдатель, двигающийся со скоростью v). То, что мы обнаружим, показано на рис. 9.
Чтобы сравнить наблюдения Маши с наблюдениями Пети, нам понадобятся v и γ. Я утверждаю, что если v=4/5 c, то γ = 5/3.
Проверим, используя уравнение №5: 1 = (4/5)2 + (3/5)2 = 16/25 + 9/25 = 25/25
Петя говорит, что у Хиггса
. Что насчёт Маши? Она говорит, что:
Петя утверждает, что у двух фотонов
, и для каждого из них E = p c. Теперь мы можем подсчитать, что видит Маша, используя уравнения №4 и №4.
Работает! Энергия сохраняется и с точки зрения Марии, ибо
Импульс тоже сохраняется:
Масса системы совпадает с массой Хиггса до и после распада, поскольку до и после распада
Что, согласно уравнению №1′, приводит массу системы вновь к
, как и у Пети, поскольку
Наблюдатель, с точки зрения которого Хиггс движется вправо
Что у нас с Костей? Костя двигается влево относительно Пети, допустим, со скоростью v=4/5 c, так что относительно Кости Хиггс (и Петя) двигаются вправо со скоростью v=4/5 c. Те же расчёты, что мы делали для Маши, показывают, что энергия Хиггса
, но, в отличие от Маши, для которой Хиггс двигается вверх, для Кости импульс Хиггса направлен вправо. Это изображено на рис. 10.
Рис. 10
Хиггс распадается на два фотона. Если с точки зрения Пети фотоны двигаются вверх и вниз, то для Кости, наблюдающего, как Хиггс и Петя двигаются вправо, один из фотонов двигается вправо вверх, а другой – вправо вниз. Какие у них тогда будут импульс и энергия?
Через уравнения №4 и №5 нам этого не узнать, поскольку они предназначаются для случаев, когда частица и наблюдатель двигаются в одном направлении. Для нашего случая уравнения будут такими:
Эти уравнения будут проще, чем кажутся, поскольку с точки зрения Пети, у p нет компоненты, двигающейся слева направо, и весь импульс идёт вверх или вниз. Так что Костя наблюдает следующие величины для Хиггса:
А у фотона, идущего вверх
Для второго фотона формулы те же, только его вертикальная составляющая направлена вниз. Заметьте, что для обоих фотонов E = p c, согласно теореме Пифагора для размера p у каждого из импульсов – согласно врезке на рис. 10
И вновь Костя наблюдает другие величины энергии и импульса, по сравнению с Петей и Машей. Но и для Кости энергия и импульс всё равно сохраняются. Также Костя наблюдает, что у системы с двумя фотонами масса совпадает с массой Хиггса. Почему? Общая вертикальная часть импульса системы нулевая, она взаимно уничтожается. Горизонтальная часть импульса системы равна 168 ГэВ/с. Общая энергия системы 210 ГэВ. Это то же, что наблюдала Маша, за исключением того, что у неё импульс системы шёл вверх, а не вправо. Но направление импульса не влияет на уравнение №1′. Там играет роль только его величина. Так что, как и Маша, Костя видит, что масса системы из двух протонов получается
, равной массе первичной частицы Хиггса.
Итог
Итак, мы видим, что наблюдают три разных наблюдателя. Их наблюдения:
• разнятся по поводу того, какие у Хиггса энергия и импульс,
• разнятся в части энергии и импульса обоих фотонов,
• согласуются по поводу сохранения энергии и импульса при распаде,
• следовательно, они согласны, что при этом сохраняется масса системы,
• соглашаются, что масса системы равна 126 ГэВ/c2,
• и более того, что сумма масс объектов системы не сохраняется, а уменьшается с 126 ГэВ/c2 до нуля.
И это не случайно. Эйнштейн из предыдущих экспериментов знал, что энергия и импульс сохраняются, поэтому он искал и нашёл уравнения, сохраняющие эту особенность мира. Также в процессе он обнаружил, что масса системы должна удовлетворять уравнению №1′.
Бонус: как это используется в поисках частицы Хиггса
Учёные:
• наблюдают столкновения протонов, в результате которых рождается два фотона;
• подсчитывают массу системы из двух фотонов (на техническом жаргоне это называется инвариантная масса пары фотонов).
Когда в результате эксперимента получается частица Хиггса, распадающаяся на два фотона, то вне зависимости от того, в каком направлении и с какой скоростью двигается частица по отношению к лаборатории, система из двух фотонов, на которую она распадётся, всегда будет обладать массой, равной массе частицы Хиггса, произведшей их на свет! Поэтому, в отличие от случайных процессов, в результате которых получается система из двух фотонов случайной массы, частицы Хиггса всегда будут порождать систему из двух фотонов одной и той же массы. Поэтому, если в результатах эксперимента появятся частицы Хиггса, и если они иногда будут распадаться на два фотона, то мы увидим пик от распадов Хиггса, возвышающийся над гладким фоном из других случайных процессов. Так и произошло в эксперименте на БАК!