2017-12-17
Тело массой $m = 0,2 кг$ брошено с начальной скоростью $v_{1} = 50 м/с$ под углом $alpha = 30^{ circ}$ к горизонту. Найти приращение импульса тела: 1) за время от начала полета до падения на землю; 2) за половину этого времени. Сопротивление воздуха не учитывать.
Решение:
Приращение импульса
$Delta vec{p} = m vec{v}_{2} — m vec{v}_{1}$,
где $vec{v}_{1}$ — скорость в начальной точке; $vec{v}_{2}$ — скорость в конечной точке. Имеем очевидно (рис.)
$begin{cases} | Delta vec{p}| = 2mv_{1} sin alpha = 10 кг cdot м/с, \ | Delta vec{p}^{ prime}| = mv_{1} sin alpha = 5 кг cdot м/с, end{cases}$
где $| Delta vec{p}|$ — модуль приращения импульса за все время полета; $| Delta vec{p}^{ prime}|$ — модуль приращения импульса за половину времени полета.
Эти же результаты полезно получить иным путем. Приращение импульса тела за малый промежуток времени
$Delta vec{p} = vec{F} Delta t$, (2)
где $vec{F}$ — сила, действующая на тело. В данном случае $vec{F} = m vec{g}$ есть постоянная по модулю и направлению сила тяжести, поэтому равенство (2) справедливо для любого промежутка времени.
За время полета $tau$ тела его импульс изменяется под действием силы тяжести $vec{F} = m vec{g}$ на величину $Delta vec{p} = m vec{g} tau.$ Это время
$tau = (2 v_{1} sin alpha)/g$,
и для приращения импульса снова получаем выражение (1).
Примечание. Напомним, что приращением $Delta u$ или $Delta vec{u}$ некоторой величины (скалярной или векторной), произошедшим за время $Delta t = t_{2} — t_{1}$, называется разность между ее значениями в конечный $t_{2}$ и начальный $t_{1}$ моменты времени $Delta u = u_{2} — u_{1}$ или $Delta vec{u} = vec{u}_{2} — vec{u}_{1}$.
§2. Законы Ньютона. Импульс или количество движения материальной точки
В основе динамики материальной точки лежат законы (аксиомы) Ньютона. Напомним ключевые определения и законы.
Система отсчёта, в которой любая материальная точка, не взаимодействующая с другими телами (такая точка называется свободной), движется равномерно и прямолинейно или покоится, называется инерциальной.
инерциальные системы отсчёта (ИСО) существуют
в ИСО приращение импульса материальной точки пропорционально силе и происходит по направлению силы:
`Delta vec p = vec F * Delta t` (1)
Импульсом (или количеством движения) материальной точки называют физическую величину, определяемую произведением её массы на вектор скорости в данной системе отсчёта:
`vec p = m * vec v`.
`vec F` — сумма сил, действующих на материальную точку. Величину `vec F * Delta t` называют импульсом силы за время от `t` до `t + Delta t`, в течение которого силу можно считать неизменной по величине и направлению. Величину `Delta vec p = vec p (t + Delta t) — vec p (t)` называют приращением импульса материальной точки за время от `t` до `t + Delta t`. Поэтому второй закон Ньютона для материальной точки можно сформулировать так:
в ИСО приращение импульса материальной точки равно импульсу силы.
Отметим, что при изучении динамики второй закон Ньютона часто формулируют следующим образом:
в ИСО ускорение материальной точки прямо пропорционально сумме сил, действующих на неё, и обратно пропорционально её массе:
`vec a = vec F/m` (2)
Если масса тела остаётся неизменной, то `Delta vec p = Delta (m vec v) = m Delta vec v`, и соотношение (1) принимает вид `m Delta vec v = vec F Delta t`. С учётом `vec a = (Delta vec v)/(Delta t)` приходим к эквивалентности соотношений (1) и (2) в рассматриваемом случае.
В настоящем Задании представлены задачи, для решения которых привлекается второй закон Ньютона (см.(1)), устанавливающий равенство приращений импульса материальной точки и импульса силы.
при взаимодействии двух материальных точек сила `vecF_(12)`, действующая на первую материальную точку со стороны второй, равна по величине и противоположна по направлению силе `vecF_(21)`, действующей со стороны первой материальной точки на вторую:
`vecF_(12) = — vecF_(21)`.
1) силы возникают парами и имеют одинаковую природу, они приложены к разным материальным точкам,
2) эти силы равны по величине,
3) они действуют вдоль одной прямой в противоположных направлениях.
Заметим, что согласно третьему закону Ньютона обе силы должны быть равны по величине в любой момент времени независимо от движения взаимодействующих тел. Другими словами, если в системе двух взаимодействующих тел изменить положение одного из тел, то это изменение мгновенно скажется на другом теле, как бы далеко оно ни находилось. На самом деле скорость распространения взаимодействий конечная; она не может превзойти скорость света в вакууме. Поэтому третий закон Ньютона имеет определённые пределы применимости. Однако в классической механике при малых скоростях взаимодействующих тел он выполняется с большой точностью.
Второй закон Ньютона (уравнение движения) можно представить в виде теоремы об изменении импульса материальной точки:
`(Delta vec p)/(Delta t) = vec(F)` (3)
Скорость изменения импульса материальной точки в инерциальной системе отсчёта равна сумме сил, действующих на эту точку.
Напомним, что для решения задач динамики материальной точки следует:
привести «моментальную фотографию» движущегося тела, указать приложенные к нему силы;
выбрать инерциальную систему отсчёта;
составить уравнение (3);
перейти к проекциям приращения импульса и сил на те или иные направления;
решить полученную систему.
Рассмотрим характерные примеры.
К телу, первоначально покоившемуся на шероховатой горизонтальной поверхности, прикладывают в течение времени t1=10 сt_1=10;mathrm с горизонтальную силу величиной F=5 HF=5;mathrm H. После прекращения действия силы тело движется до остановки t2=40 ct_2=40;mathrm c. Определите величину $$ {F}_{mathrm{тр}}$$ силы трения скольжения, считая её постоянной.
На рис. 1 показаны ИСО и силы, действующие на тело в процессе разгона. По второму закону Ньютона
`(Delta vec p)/(Delta t) = M vec g + vec N + vecF_(«тр») + vec F`.
Переходя к проекциям на горизонтальную ось, находим элементарные приращения импульса в процессе разгона
$$ ∆{p}_{x}=left(F-{F}_{mathrm{тр}}right)∆t$$
и в процессе торможения `(F = 0)`
$$ ∆{p}_{x}=-{F}_{mathrm{тр}}∆t$$.
Просуммируем все приращения импульса тела от старта до остановки:
`sum Delta p_x = sum_(0 <= t <= t_1) (F — F_sf»тр») Delta t + sum_(t_1 <= t <= t_1 + t_2) (-F_sf»тр» ) Delta t`.
Напомним, что для любой физической величины сумма приращений равна разности конечного и начального значений. Тогда
px конечн-px начальн=F-Fтрt1+-Fтрt2p_{x;mathrm{конечн}}-p_{x;mathrm{начальн}}=left(F-F_mathrm{тр}right)t_1+left(-F_mathrm{тр}right)t_2.
С учётом равенств px конеч=0p_{x;mathrm{конеч}}=0, px начальн=0p_{x;mathrm{начальн}}=0 и независимости сил от времени приходим к ответу на вопрос задачи:
Fтр=t1t1+t2F=1010+40·5=1 HF_mathrm{тр}=dfrac{t_1}{t_1+t_2}F=dfrac{10}{10+40}cdot5=1;mathrm H.
Далее рассмотрим пример, в котором одна из сил зависит от времени.
На какое максимальное расстояние `L_max` улетит мяч, если в процессе удара футболист действует на мяч постоянной по направлению силой, величина которой изменяется по закону, представленному на рис. 2. Длительность удара τ=8·10-3 ctau=8cdot10^{-3};mathrm c, максимальная сила Fmax=3,5·103 HF_max=3,5cdot10^3;mathrm H, масса мяча m=0,5 кгm=0,5;mathrm{кг}. Здесь и далее ускорение свободного падения g=10 м/с2g=10;mathrm м/mathrm с^2. Сопротивление воздуха не учитывайте.
В процессе удара на мяч действуют две силы: mg=0,5·10=5 Hmg=0,5cdot10=5;mathrm H — тяжести и сила `vec F`, с которой футболист действует на мяч,
F≤Fmax=3,5·103 HFleq F_max=3,5cdot10^3;mathrm H.
Так как `mg < < F_max`, силой тяжести пренебрежём. Из кинематики известно, что максимальная дальность полёта наблюдается при старте под углом `alpha = pi/4`. Процесс удара показан на рис. 3.
По второму закону Ньютона приращение импульса равно импульсу силы `Delta vec p = vec F * Delta t`. Переходя к проекциям приращения импульса и силы на ось `Ox`, получаем
`Delta p_x = F Delta t`.
Просуммируем элементарные приращения импульса мяча за время удара
`sum Delta p_x = mv — 0 = sum_(0 <= t <= tau) F Delta t`.
Импульс силы `sum_(0 <= t <= tau) F(t) Delta t` за время удара численно равен площади под графиком зависимости этой силы от времени (каждое слагаемое `F(t) Delta t` в импульсе силы можно интерпретировать как площадь элементарного прямоугольника со сторонами `F(t)` и `Delta t` на графике зависимости `F(t)`). Тогда импульс силы `F` за время удара равен
`sum_(0 <= t <= tau) F Delta t = (F_max tau)/2`
и в рассматриваемом случае не зависит от того, в какой именно момент времени сила достигает максимального значения (площадь треугольника равна половине произведения основания на высоту!). Далее находим импульс мяча в момент окончания действия силы
`mv = 1/2 F_max * tau`.
Отсюда находим начальную скорость полёта мяча
`v = (F_max * tau)/(2m) = (3,5 * 10^3 * 8 * 10^-3)/(2 * 0,5) = 28 sf»м/с»`
и максимальную дальность (старт под углом `alpha = pi/4`) полёта
`L_max = (v^2)/g = (28^2)/(10) ~~ 78 sf»м»`.
В рассматриваемом модельном примере получен несколько завышенный по сравнению с наблюдениями результат.
На вступительных испытаниях и олимпиадах в вузах России регулярно предлагаются задачи динамики, в которых наряду с «традиционными» силами: силой тяжести, силой Архимеда и т. д., на тело действует сила лобового сопротивления. Такая сила возникает, например, при движении тел в жидкостях и газах. Вопрос о движении тел в жидкостях и газах имеет большое практическое значение. Знакомство с действием такого рода сил уместно начинать, как это принято в физике, с простейших модельных зависимостей, в которых сила сопротивления принимается пропорциональной скорости или её квадрату.
Мяч, брошенный с горизонтальной поверхности земли под углом `alpha = 60^@` к горизонту со скоростью `v = 10 sf»м/с»`, упал на землю, имея вертикальную составляющую скорости по абсолютной величине на `delta = 30 %` меньшую, чем при бросании. Найдите время полёта мяча. Считать, что сила сопротивления движению мяча пропорциональна его скорости.
Согласно второму закону Ньютона приращение импульса пропорционально силе и происходит по направлению силы:
`m * Delta vec v = (m vec g — k vec v) * Delta t`.
Переходя к проекциям сил и приращения скорости на вертикальную ось, получаем
`m * Delta v_y = — mg * Delta t — k * v_y * Delta t`.
Заметим, что элементарное перемещение мяча по вертикали равно `Delta y = v_y * Delta t`, и перепишем последнее соотношение в виде:
`m * Delta v_y = — mg * Delta t — k * Delta y`.
Просуммируем все приращения вертикальной проекции импульса по всему времени полёта, т. е. от `t = 0` до `t = T`:
`m * (sum Delta v_y) = — mg * (sum Delta t) — k* (sum Delta y)`.
Переходя к конечным приращениям, получаем
`m (v_y (T) — v_y (0)) = — mg (T — 0) — k (y (T) — y (0))`.
Точки старта и финиша находятся в одной горизонтальной плоскости, поэтому перемещение мяча по вертикали за время полёта нулевое
`y (T) — y (0) = 0`.
Тогда `- (1 — delta) mv_0 sin alpha — mv_0 sin alpha = — mgT`. Отсюда находим продолжительность полёта мяча:
`T = (v_0 sin alpha)/(g) (2 — delta) = (10 * sin 60^@)/(10) (2,0 — 0,3) ~~ 1,5 sf»с»`.
В следующем примере рассматривается удар, в ходе которого две очень большие силы, «согласованно» действуют во взаимно перпендикулярных направлениях.
Кубик, движущийся поступательно со скоростью `v` (рис. 4) по гладкой горизонтальной поверхности, испытывает соударение с шероховатой вертикальной стенкой.
Коэффициент трения `mu` скольжения кубика по стенке и угол `alpha` известны. Одна из граней кубика параллельна стенке. Под каким углом `beta` кубик отскочит от стенки? Считайте, что перпендикулярная стенке составляющая скорости кубика в результате соударения не изменяется по величине.
Силы, действующие на кубик в процессе соударения, показаны на рис. 5.
По второму закону Ньютона
`Delta vec p = (m vec g + vecN_(«г») + vecF_(«тр») + vecN_(«в») ) * Delta t`.
Переходя к проекциям на горизонтальные оси `Ox` и `Oy`, получаем
`Delta p_x = — F_sf»тр» Delta t`, `Delta p_y = N_sf»в» Delta t`.
Просуммируем приращения `Delta p_y = N_sf»в» Delta t` по всему времени `tau` соударения, получим:
`sum Delta p_y = p_y (tau) — p_y (0) = mv sin alpha — (- mv sin alpha) = sum_(0 <= t <= tau) N_sf»в» Delta t`.
В процессе удара в любой момент времени `F_sf»тр» = mu N_sf»в»`, следовательно, во столько же раз отличаются импульсы этих сил за время соударения
`sum_(0 <= t <= tau) F_sf»тр» Delta t = mu sum_(0 <= t <= tau) N_sf»в» Delta t = mu 2 mv sin alpha`.
Тогда легко вычислить проекцию `v_x (tau)` скорости кубика после соударения. Для этого просуммируем приращения
`Delta p_x = — F_sf»тр» Delta t = — mu N_sf»в» Delta t`
по всему времени `tau` соударения, получим:
`sum Delta p_x = p_x (tau) — p_x (0) = mv_x (tau) — mv cos alpha = — sum _(0 <= t<= tau) F_sf»тр» Delta t =- mu 2 mv sin alpha`.
Отсюда `v_x (tau) = v (cos alpha — 2 mu sin alpha)`. Далее, считая `v_x (tau) > 0`, получаем
`bbb»tg» beta = (v_y (tau))/(v_x (tau)) = (sin alpha)/(cos alpha — 2 mu sin alpha)`.
dnepr1
9 лет назад
Светило науки — 9801 ответ — 46531 помощь
Импульс P = m*V.
Для определения скорости надо сначала найти время:=
=(50*1/2+√(50²*1/4)) / 9.81 =
5,09684 c.
М =
0,2
кг
Скорость в момент
t =
2,548
c
Импульс
Р =
8,66
кг*м/с
V =
43,30
m/c
t =
5,097
c
М =
0,2
кг
V =
50,00
m/c
Импульс
Р =
10,00
кг*м/с
(6 оценок)
Здесь я собрала еще несколько задач на закон сохранения импульса.
Задача 1. С высоты см на горизонтальную поверхность сыпется песок. Массовый расход песка равен
г/с. Найти силу давления песка на поверхность через
с после касания поверхности первыми песчинками. Ответ выразить в Н, округлив до десятых. Ускорение свободного падения принять равным
м/c
.
Решение.
Сила, с которой песок действует на поверхность, складывается из двух составляющих — во-первых, давит неподвижно лежащий песок, который упал раньше, во-вторых, давит песок, который, падая, тормозит о данную поверхность. Первая равна по модулю силе тяжести выпавшего песка
Вторая определяется скоростью подлетающих песчинок и массовым расходом
. По второму закону Ньютона
Таким образом, сила давления песка на поверхность в момент равна
Ответ: 3,8 Н.
Задача 2.
По длинному склону, образующему угол с горизонтом, съезжают сани, на которых установлен бак с водой. Через отверстие площадью
м
в задней стенке бака вытекает струя воды со скоростью
м/с относительно бака. Поверхность воды в баке установилась параллельно склону. Найти коэффициент трения
. Ответ округлить до десятых. Масса саней с баком равна
кг. За время спуска вытекает лишь небольшая часть воды. Ускорение свободного падения принять равным
м/c
. Плотность воды
кг/м
.
К задаче 2
Решение.
Поверхность жидкости устанавливается перпендикулярно вектору эффективного ускорения свободного падения. Этот вектор — результат сложения ускорения свободного падения с ускорением, с которым бак съезжает с горы. Так как по условию поверхность жидкости имеет постоянный угол наклона к горизонту, сани движутся с постоянным ускорением, равным
Запишем второй закон Ньютона для саней в проекции на поверхность склона.
здесь — реактивная сила со стороны вытекающей воды. Для некоторой малой массы вытекшей воды можно записать
— площадь отверстия,
— длина столбика этой элементарной массы.
Относительно бака импульс этой массы воды меняется, отсюда можно найти реактивную силу:
Теперь можно найти коэффициент трения
Ответ: 0,1.
Задача 3.
Под каким углом к горизонту необходимо бросить камень, чтобы модуль изменения импульса за всё время полёта был равен модулю начального импульса? Ответ выразить в градусах, округлив до целых. Считать, что начальная и конечная точка находятся на одной высоте. Сопротивлением воздуха пренебречь.
К задаче 3
Решение.
За время полёта тела, брошенного под углом к горизонту, его горизонтальная проекция скорости остается постоянной, а значит, горизонтальная проекция импульса сохраняется, а вертикальная — изменяется на противоположную. Таким образом, модуль изменения импульса за всё время полёта
. По условию, модуль изменения импульса за всё время полёта равен модулю начального импульса
, следовательно,
, откуда получаем, что искомый угол равен
Ответ: 30
Задача 4.
Катер с водомётным двигателем движется с постоянной скоростью, забирая забортную воду и выбрасывая назад струю со скоростью м/с относительно катера. Площадь поперечного сечения струи
м
. Найти скорость катера
, если действующая на него сила сопротивления пропорциональна квадрату скорости по формуле
, причём
Н
c
/м
. Ответ выразить в м/с, округлив до десятых. Плотность воды
кг/м
Решение.
В системе отсчёта, связанной с катером, набегающая на катер вода изменяет свою скорость от до
. За интервал времени
изменение импульса воды равно импульсу силы, действующей на неё со стороны катера. Таким образом, можно записать
где — масса изменившей скорость воды, равная
.
Решая квадратное уравнение
получаем, что скорость катера равна
Ответ: 13,3 м/с.
Задача 5.
На гладком льду лежит цилиндрическое однородное бревно длиной м. Один из его концов стали медленно поднимать с помощью верёвки. Когда угол между бревном и поверхностью льда стал равным
, вертикально натянутая верёвка оборвалась. На какое расстояние сместится при падении бревна его нижний конец? Ответ выразить в см, округлив до целых.
Решение.
Центр масс бревна при подъеме перемещался по дуге окружности, поэтому в момент обрыва веревки он сместился по горизонтали на расстояние
После обрыва веревки центр масс просто «падает» — движется по вертикали. Поэтому на такое же расстояние , на какое переместился центр масс, должен переместиться и конец бревна — ведь мы считаем его жестким.
Ответ: 25 см.
2 комментария
Алексей
✉️
07.05.2019 19:16:32
Можно пояснить как появилось выражение для реактивной силы во второй задаче? И можно сделать рисунки ко 2 и 3 задачам, а то из вашего решения не совсем всё понятно?
Анна Валерьевна
✨
08.05.2019 12:34:36
С картинками лучше. Согласна.
Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса
Классическое определение импульса тела
Определение
Векторную величину ($overline{p}$), служащую мерой механического движения равную произведению массы ($m$) этой точки на скорость ($overline{v}$) ее перемещения:
[overline{p}=moverline{v}left(1right)]
называют импульсом материальной точки.
Вектор импульса имеет такое же направление как вектор скорости, так как масса является положительной величиной.
В Международной системе единиц (СИ) единицей измерения импульса считают килограмм — метр в секунду ($frac{кгcdot м}{с}$):
[left[pright]=left[mright]left[vright]=кгcdot frac{м}{с}.]
Определение
Импульсом тела называют импульс системы материальных точек, которые составляют данное тело:
[overline{p}=sumlimits^N_{i=1}{m_i{overline{v}}_ileft(2right),}]
где $m_i$ — масса элемента тела (материальной тоски системы); ${overline{v}}_i$ — скорость данного элемента тела; $N$ — число материальных точек. Суммирование импульсов точек проводят с учетом их направлений.
Импульс и уравнение движения
Если на тело действуют другие тела, то мерой этого воздействия можно считать величину $frac{doverline{p}}{dt}$. Эта производная зависит от положения материальной точки по отношению к окружающим телам, иногда даже от ее скорости: $frac{doverline{p}}{dt}(overline{r},overline{v}{rm )}$. Такой функцией является сила ($overline{F}$($overline{r},overline{v}$)). Второй закон Ньютона в данной трактовке записывают как:
[overline{F}=frac{doverline{p}}{dt}left(3right),]
где $overline{F}$ — можно считать векторной суммой всех внешних сил, которые действуют на тело.
Содержание второго закона Ньютона заключается в том, что сила зависит только от координат и скорости материальной точки. Уравнение (3) называют уравнением движения материальной точки. Конкретное содержание этот закон Ньютона получает, когда определена функция $overline{F}$($overline{r},overline{v}$). К установлению вида этой функции сводится основная задача механики для каждого конкретного случая.
Из формулы (3) получим, что:
[Delta overline{p}=intlimits^{t_2}_{t_1}{overline{F}dt}left(4right),]
$Delta overline{p}$ — изменение импульса тела.
Если сила, действующая на материальную точку постоянна, то второй закон Ньютона можно представить в форме:
[overline{F}Delta t=Delta overline{p}left(5right).]
Формула (5) означает, что изменение импульса материальной тела прямо пропорционально силе, которая на нее воздействует и сонаправлено с этой силой. Величину $overline{F}Delta t$ называют импульсом силы. Из уравнения (5) следует, что равные изменения импульса точки могут быть получены в результате действия большой по модулю силы за маленький промежуток времени или воздействуя на точку небольшой силой длительное время.
Закон сохранения импульса
Если на тело не действуют внешние силы ($overline{F}=0$) или их действие взаимно компенсируется, то из уравнения движения (3), мы видим, что:
[frac{doverline{p}}{dt}=0to overline{p}=constleft(6right).]
Для системы тел закон сохранения импульса тоже выполняется, только формулу (6) следует читать так: векторная сумма импульсов всех тел изолированной системы не изменяется при любых взаимодействиях, которые происходят внутри рассматриваемой системы. Это не значит, что какие — то тела системы не могут изменять свой импульс, но суммарный импульс системы остается неизменным.
Для материальной точки закон сохранения импульса закон сохранения импульса означает, что при отсутствии внешних сил, она перемещается прямолинейно и равномерно. Для системы материальных точек в нерелятивистском случае закон говорит о том, что центр масс системы движется равномерно и прямолинейно.
Закон сохранения импульса выполняется и в релятивистском случае и нерелятивистском. Но в релятивистском случае нельзя говорить о равномерном и прямолинейном движении центра масс, так как в этом случае центра масс не существует. Но существует система центра масс, в которой закон сохранения импульса сводится к равенству $overline{p}=0$, и это означает, что данная система при любых процессах внутри нее остается системой центра масс.
Примеры задач на импульс тела и закон сохранения импульса
Пример 1
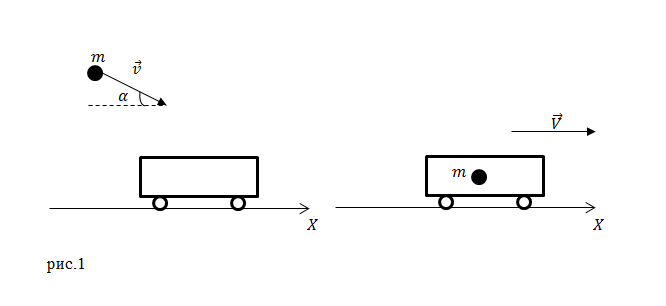
Задание. Контейнер с песком массой $M$ стоит на рельсах на горизонтальном участке дороги. В песок падает тело массой $m,$ и остается в нем. С какой скоростью станет двигаться контейнер, если в момент попадания скорость тела была равна $v$, ее направление было сверху вниз под углом $alpha $ к горизонту (рис.1)? Силу трения не учитывать.
Решение. Задачу будем решать на основе закона сохранения импульса, так как в отсутствии сил трения систему из двух тел (контейнер — тело) можно считать изолированной. Тогда закон сохранения импульса запишем в виде:
[sum{{overline{p}}_1=sum{{overline{p}}_2}left(1.1right),}]
где ${overline{p}}_1$ — импульс системы до попадания тела в песок контейнера. Этот импульс будет равен импульсу движущегося тела, так как скорость контейнера равна нулю:
[{overline{p}}_1=moverline{v }left(1.2right).]
Импульс системы после того, как тело застряло в песке, равен:
[{overline{p}}_2=left(m+Mright)overline{V}left(1.3right).]
Согласно закону сохранения импульса имеем:
[moverline{v }=left(m+Mright)overline{V}left(1.4right).]
Запишем проекцию уравнения (1.4) на ось X, имеем:
[mv{cos alpha =left(m+Mright)Vleft(1.5right). }]
Из уравнения (1.5) выразим искомую скорость:
[V=frac{mv {rm cos}alpha }{m+M}.]
Ответ. $V=frac{mv {rm cos}alpha }{m+M}$
Пример 2
Задание. Каково приращение импульса тела ($Delta overline{p}$) за время полета $tau $, которое бросили под углом к горизонту с начальной скоростью ${overline{v}}_0$? Сопротивление воздуха не учитывать.
Решение. Изменение импульса будем искать, используя формулу:
[Delta overline{p}=intlimits^{tau }_0{overline{F}dt}left(2.1right),]
где $tau $ — время полета тела. Тело при заданных условиях движется в поле тяжести Земли:
[overline{F}=moverline{g }left(2.2right).]
Из (2.2) очевидно, что сила не изменяется при движении тела. Подставим (2.2) в интеграл, получим:
[Delta overline{p}=intlimits^{tau }_0{moverline{g }dt}=moverline{g }tau .]
Ответ. $Delta overline{p}=moverline{g }tau $
Читать дальше: колебательное движение.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!