Импульсный
отклик системы.
По определению,
импульсными характеристиками систем
(второй широко используемый термин —
импульсный отклик систем) называются
функции h(t) для аналоговых и h(kt)
для цифровых систем, которые является
реакцией (откликом) систем на единичные
входные сигналы: дельта-функцию (t)
для аналоговых и импульс Кронекера
(kt)
для цифровых систем, поступающие на
вход систем соответственно при t=0 и k=0.
Эта реакция однозначно определяется
оператором преобразования:
y(t)
= T[(t)]
h(t).
(11.2.1)
y(kt)
= T[(kt)]
h(kt).
(11.2.1′)
Импульсный отклик
аналоговой системы, как результат
операции над дельта-функцией, в
определенной степени представляет
собой математическую абстракцию
идеального преобразования. С практической
точки зрения под импульсным откликом
аналоговой системы можно понимать
математическое отображение реакции
системы на импульсный входной сигнал
произвольной формы с площадью, равной
1, если длительность сигнала пренебрежимо
мала по сравнению со временем реакции
системы или с периодом ее собственных
колебаний. Под временем (длиной) реакции
системы обычно понимают интервал, на
котором значения функции h(t) существенно
отличаются от нуля после прекращения
действия единичного сигнала на ее входе.
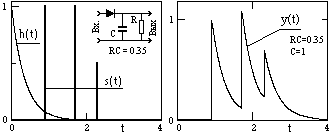
Рис. 11.2.1. Импульсный отклик системы
h(t),
входной сигнал s(t) и выходная реакция
системы y(t).
Для цифровых систем импульсный
отклик однозначно определяется реакцией
системы на импульс Кронекера (kt)=1
при k=0.
Функцию импульсного
отклика называют также весовой функцией
системы.
На рисунке 11.2.1
приведен пример импульсного отклика
h(t) интегрирующей RC-цепи. При подаче на
вход RC-цепи импульса заряда q
емкость С заряжается до напряжения Vо
= q/C
и начинает разряжаться через сопротивление
R, при этом напряжение на ней изменяется
по закону v(t) = Voe-t/RC
= (q/C)e-t/RC.
Отсюда, отклик RC-цепи по выходному
напряжению на входной сигнал q
= 1: h(t) = (1/C)e-t/RC.
По существу, импульсным откликом системы
h(t) определяется доля входного сигнала,
которая действует на выходе системы по
истечении времени t после поступления
сигнала на вход (запаздывающая реакция
системы).
Реакция
системы на произвольный сигнал.
Если функция
импульсного отклика системы известна,
то, с учетом принципа суперпозиции
сигналов в линейной системе, можно
выполнить расчет реакции системы в
любой произвольный момент времени на
любое количество входных сигналов с
любыми моментами времени их прихода
путем суммирования запаздывающих
реакций системы на эти входные сигналы,
как это показано на рис. 11.2.1 для трех
входных импульсов. В общем случае
произвольный сигнал на входе системы
может быть разложен в линейную
последовательность взвешенных единичных
импульсов:
y(t) = T[s(t)]
T[s()(t-)
d
На
основании принципа суперпозиции линейный
оператор Т может быть внесен под знак
интеграла, т.к. последний представляет
собой предельное значение суммы. При
этом операция преобразования действует
только по переменной t:
y(t) =s()
Т[(t-)]
ds()
h(t-)
d
Это выражение
представляет собой интеграл Дюамеля
или свертку (конволюцию) входного сигнала
с импульсной характеристикой системы.
Заменой переменных t-=
можно
убедиться в том, что эта операция, как
и положено свертке, коммутативна:
s()
h(t-)
d
h()
s(t-)
d.
Аналогично, для
дискретных сигналов:
y(kt)
=
h(kt-nt)

s(kt-nt).
(11.2.3′)
В символической
форме математического представления:
y(t) = s()
*
h(t-)
s(t-)
*
h()
s(t)
*
h(t).
В реальных физических
системах импульсный отклик h(t) равен
нулю при t<0 (реакция на выходе системы
не может опережать входной сигнал) и,
как правило, отличен от нуля только на
определенном интервале r, по которому
и ведется интегрирование или суммирование
в выражениях свертки. При обработке
данных на ЭВМ требований по односторонности
импульсного отклика не предъявляется,
равно как и по его размерам вперед и
назад от нуля по координатам.
Усиление
постоянной составляющей сигнала.
Подадим на
вход системы постоянный сигнал s(t) = A.
При этом сигнал на выходе системы:
y(t) = h()
s(t-)
d
= Аh()
dАКпс,
(11.2.4)
т.е. площадь
импульсного отклика (для цифровой
системы соответственно сумма коэффициентов
импульсного отклика) является коэффициентом
Кпс
усиления постоянной составляющей
входного сигнала. Если при обработке
сигналов должны изменяться только
динамические характеристики их формы
без изменения постоянной составляющей,
а равно и различных постоянных уровней
(фона, пьедесталов, региональных трендов
и т.п.), то площадь импульсного отклика
(сумма коэффициентов) должна нормироваться
к единице.
Рис. 11.2.2.
На рис. 11.2.2 приведен пример
выполнения свертки рассмотренной нами
выше RC-цепью при нормированной к 1 площади
импульсного отклика h().
Входной сигнал s(t) находится на постоянном
фоновом значении, в данном случае —
нулевом, при этом, как и следовало
ожидать, площадь выходного сигнала y(t)
равна площади входного сигнала.
Усиление
шумов.
Критерием
качества системы при использовании
любого метода обработки информации
можно считать выполнение целевого
назначения с минимальным усилением
шумов (максимальным их подавлением).
Допустим, что система имеет нормированный
к 1 импульсный отклик h(k). Обозначим через
(k)
аддитивный шум с математическим ожиданием
M{(k)}=
= 0 и дисперсией D2,
который в сумме с сигналом поступает
на вход системы. Значения (k)
статистически независимы и некоррелированы
с сигналом. С учетом помехи во входном
сигнале значение сигнала на выходе
системы:
y(k) =
h(n)[x(k-n)+(k-n)].
Математическое
ожидание значений выходного сигнала:
M{y(k)}
=
h(n)[x(k-n)+M{(k-n)}]
=
h(n) x(k-n).
Вычислим дисперсию
распределения отсчетов выходного
сигнала:
D{y(k)}
=
M{[h(n)[x(k-n)+(k-n)]-M{y(k)}]2}
= M{[h(n)
(k-n)]2}.
Если правую часть
последнего выражения представить в
виде
M{[h(n)
(k-n)][
h(m) (k-m)]},
то в этом выражении
математические ожидания всех членов
произведения с сомножителями (n)(m)
при n
m равны 0 в силу статистической независимости
значений шума. Остаются только члены с
n = m, т.е.:
M{h2(n)2(n)}
=
h2(n)
M{2(n)}
= D
h2(n)
= 2
h2(n).
(11.2.5)
Отсюда следует,
что сумма квадратов значений нормированного
импульсного отклика системы представляет
собой коэффициент усиления аддитивных
шумов во входном сигнале.
Пример.
Сглаживающий фильтр: y(k) = 0.2x(k-n).
Коэффициент
усиления шумов: 5 (0.22)
= 0.2. Дисперсия шумов уменьшается в
1/0.2 = 5 раз.
Для систем с m
входами и n выходами аналогично
определяются парциальные импульсные
отклики hij(t),
i = {1,2, … ,n}, j = {1,2, … ,m}, каждым из которых
отображается сигнал на i-м выходе при
поступлении сигнала t)
на j-й вход. Полная совокупность импульсных
откликов образует матрицу:

а выражение свертки
приобретает вид:
=
d
Определение
импульсной реакциитребуется,
как правило, для рекурсивных систем,
так как импульсная реакция для НЦС
специального определения не требует:
h(k)
=b(n)(k-n)
b(k).
Если выражение
для системы известно в общей форме
(11.1.2), определение импульсной реакции
производится подстановкой в уравнение
системы импульса Кронекера с координатой
k = 0 при нулевых начальных условиях, при
этом сигнал на выходе системы будет
представлять собой импульсную реакцию
системы: y(k)
h(k).
Пример. Уравнение
РЦС: yk =
xk
+ 0.5yk-1.
Входной сигнал: xk=
o=
{1,0,0,0,…}.
Расчет выходного
сигнала при нулевых начальных условиях:
yo
=
xo+0.5
y-1
=
1+0 = 1 = ho.
y1
=
x1+0.5
yo
=
0+0.5 = 0.5 = h1.
y2
=
x2+0.5
y1
=
0+0.25 = 0.25= h2
y3
=
x3+0.5
y2
=
0.125 = h3.
y4
=
x4+0.5
y3
=
0.0625 = h4,
т.д.
Импульсный
отклик
системы:
hk
=
{1, 0.5, 0.25, 0.125,
… }
(O.5)k,
k = 0,1,2….
Определение
импульсной реакции физических систем
обычно производится подачей на вход
систем ступенчатой функции uo(k)
= 1 при k
0, и uo(k)
= 0 при k < 0:
g(k) =h(n)
uo(k-n)
=h(n).
h(k)
= g(k) — g(k-1), k=0,1,2,…
Функция g(k) получила
название переходной характеристики
системы (перехода из одного статического
состояния в другое).
В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g(t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (d-функции) (7.21). Обозначается импульсная характеристика h(t). Причем, g(t) и h(t) определяются при нулевых начальных условиях в цепи. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А.
Использование понятий переходной и импульсной характеристик цепи позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1(t) или d(t).
Между переходной g(t) и импульсной h(t) характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/t, сдвинутых друг относительно друга на время t (см. рис. 7.4):
т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи
т. е. импульсная характеристика является производной от переходной характеристики цепи.
Уравнение (8.2) справедливо для случая, когда g(0) = 0 (нулевые начальны е условия для цепи). Если же g(0) ¹ 0, то представив g(t) в виде g(t) = 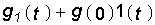
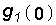
Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы. Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной d(t) функции. Обычно классическим методом удобно определять переходную характеристику g(t), а импульсную характеристику h(t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.
Пример. Найдем классическим методом переходную характеристику по напряжению для цепи, изображенной на рис. 8.1. Численно gu(t) для данной цепи совпадает с напряжением на емкости при подключении ее в момент t= 0 к источнику напряжения U1 = l В:
Закон изменения напряжения uC(t) определяется уравнением (6.27), где необходимо положить U= l В:
При нахождении характеристик g(t) и h(t) операторным методом пользуются изображениями функций 1(t), d(t) и методикой расчета переходных процессов, изложенных в гл. 7.
Пример. Определим операторным методом переходную характеристику gu(t) RС-цепи (см. рис. 8.1). Для данной цепи в соответствии с законом Ома в операторной форме (7.35) можем записать:
где
Окончательно получаем
Отсюда по теореме разложения (7.31) находим
т. е. то же значение, что и полученное классическим методом.
Следует отметить, что величина I(р) в уравнении (8.4) численно равна изображению переходной проводимости. Аналогичное изображение импульсной характеристики численно равно операторной проводимости цепи
Например, для RС-цепи (см. рис. 8.1) имеем:
Применив к Y(p) теорему разложения (7.30), получим:
Следует отметить, что формула (8.5) определяет свободную составляющую реакции цепи при единичном импульсном воздействии. В общем случае в реакции цепи, кроме экспоненциальных составляющих свободного режима при t > 0 присутствует импульсное слагаемое, отображающее воздействие при t = 0 единичного импульса. Действительно, если учесть, что для RС-контура (см. рис. 8.1) переходная характеристика по току при U= 1(t) согласно (6.28) будет
то после дифференцирования (8.6) согласно (8.2) получаем импульсную характеристику RС-цепи hi(t) в виде
т. е. реакция hi(t) содержит два слагаемых — импульсное и экспоненциальное.
Физический смысл первого слагаемого в (8.7) означает, что при t = 0 в результате воздействия на цепь импульсного напряжения d(t) зарядный ток мгновенно достигает бесконечно большого значения, при этом за время от 0– до 0+ элементу емкости передается конечный заряд и она скачком заряжается до напряжения I/RC. Второе слагаемое определяет свободный процесс в цепи при t> 0 и обусловлено разрядом конденсатора через короткозамкнутый вход (так как при t> 0 d(t) = 0, что равносильно КЗ входа) с постоянной времени t = RC. Из этого следует, что при d(t)-импульсном воздействии на RС-цепь нарушается непрерывность заряда на емкости (второй закон коммутации). Аналогично нарушается и условие непрерывности тока в индуктивности (первый закон коммутации), если к цепи, содержащей элемент индуктивности воздействовать напряжением в виде d(t).
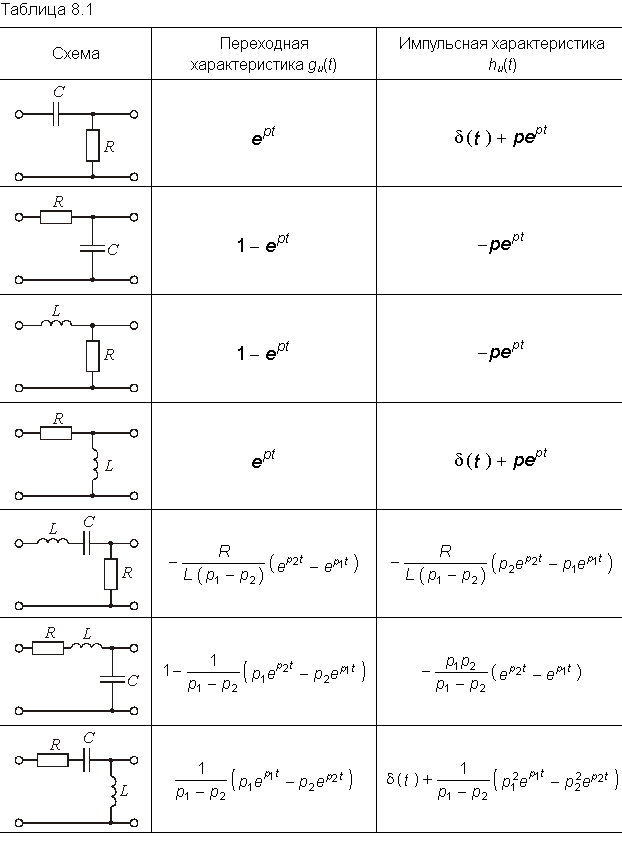
В табл. 8.1 сведены значения переходной и импульсных характеристик по току и напряжению для некоторых цепей первого и второго порядка.
Домашнее задание № 3.2
-
Определить переходную и импульсную характеристику цепи. Входное напряжение
подключено к зажимам 1-1’. Выходное напряжение
снимается с зажимов 2-2’.
-
Пользуясь любой из найденных характеристик, определить реакцию цепи
на заданное входное воздействие
.
: длительность импульса
следует выбрать равной постоянной времени цепи,
-
Построить временную зависимость
. Рассчитать значения
,
,
,
|
R1 |
R2 |
C2 |
|
10 Ом |
10 Ом |
20 мкФ |
-
Определим переходную и импульсную характеристики цепи.
Входное сопротивление цепи:
Ток равняется:
Выходное напряжение найдём по второму закону Кирхгофа:
Тогда передаточная функция цепи:
Подставляя числовые значения, получим:
Переходная характеристика цепи — это реакция цепи на единичное входное воздействие:
Изображение единичной функции , поэтому мы можем найти изображение выходного напряжение при таком воздействии на входе цепи:
Теперь найдём оригинал этого изображения выходного напряжения – это и будет переходная характеристика цепи. Изображение имеет вид дроби , где корни уравнения
равняются
и
. Повторяющихся корней нет. Производная знаменателя:
Так как дробь мы можем представить в виде дроби:
То в нашем случае:
Таким образом:
Оригинал , который и будет переходной функцией, имеет вид:
Импульсная характеристика четырёхполюсника определяется как реакция на входное воздействие, представляющее собой дельта-функцию . Изображение дельта-функции равняется 1, поэтому изображение выходного напряжения имеет вид:
Оригинал этого напряжения будет импульсной характеристикой цепи:
Импульсная характеристика — это производная от переходной характеристики:
-
Определим реакцию цепи
на заданное входное воздействие.
Входное воздействие имеет вид:
Где — постоянная времени цепи. Постоянная времени цепи определяет время, в течении которого напряжение на выходе уменьшается в
раз. В нашем случае
Это входное воздействие можно рассматривать как 3 следующих друг за другом этапа:
— скачок входного напряжения в момент времени от 0 до
— постоянное значение при
— скачок входного напряжения в момент времени от
до 0
Воспользуемся для определения реакции цепи (нахождения ) интегралом Дюамеля:
при :
Первое слагаемое обусловлено скачком в момент времени , второе слагаемое — постоянным значением напряжения на входе цепи в период времени
, равняется 0, так как
.
при
Третье слагаемое обусловлено скачком напряжения в момент . Воспользовавшись единичной функцией
, можем записать для
:
Входной сигнал имеет вид:
Найдём изображение входного напряжения :
Определим реакцию цепи на такое входное воздействие. Изображение выходного напряжения :
Рассмотрим дробь:
Корни уравнения , откуда
и
. Первая производная
. Таким образом:
Таким образом:
Оригинал выходного напряжения имеет вид:
Что совпадает с выходным напряжением, полученным с использованием переходной характеристики цепи.
-
Построим графически зависимость
. Рассчитаем значения
,
,
,
График напряжения :
Рассчитаем значения в моменты времени
. Для этого воспользуемся аналитическим выражением для
.
Для :
Так как выходное напряжение – это напряжение на конденсаторе, поэтому согласно законам коммутации оно не может измениться скачком, а для оно было равно нулю, так как входное напряжение было равно нулю. Таким образом,
.
Для моментов времени и
также
, потому что выходное напряжение – это напряжение на конденсаторе, и оно не может измениться скачком, согласно законам коммутации.
Заметим, что, если бы входное напряжение представляло собой единичный скачок амплитудой бесконечной длительности, то напряжение на конденсаторе для
равнялось бы напряжению на резисторе
в установившемся процессе:
. Но так как длительность единичного импульса ограниченно временем
, равным постоянной времени цепи, то конденсатор не успевает зарядиться до этого значения, и успевает зарядиться только до значения, на
меньшее, а при
разряжается через резистор
.
Для :
При входное напряжение равняется нулю, поэтому при
конденсатор разряжается через резистор
и напряжение на нем, которое равняется выходному, стремится к нулю.
Ответ:
Переходная характеристика цепи:
Импульсная характеристика цепи:
Реакция цепи на заданное входное воздействие:
Сайт управляется системой uCoz


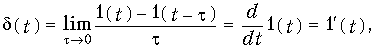
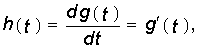
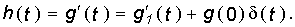
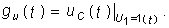
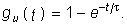
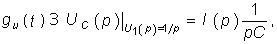
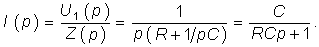
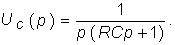
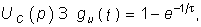
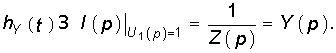
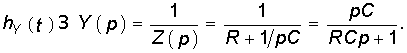
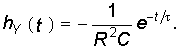
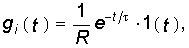
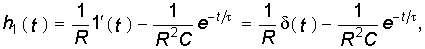
![toe3_2-12.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-12.jpg)
![toe3_2-13.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-13.jpg)
![toe3_2-14.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-14.jpg)
![toe3_2-17.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-17.jpg)
![toe3_2-31.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-31.jpg)
![toe3_2-40.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-40.jpg)
![toe3_2-52.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-52.jpg)
![toe3_2-57.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-57.jpg)
![toe3_2-62.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-62.jpg)
![toe3_2-67.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-67.jpg)
![toe3_2-76.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-76.jpg)
![toe3_2-77.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-77.jpg)
![toe3_2-85.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-85.jpg)