Функция отклика.Если на вход нерекурсивного фильтра
подать импульс Кронекера, расположенный
в точке k = 0, то на выходе фильтра мы
получим его реакцию на единичный входной
сигнал (формула 2.1.3), которая определяется
весовыми коэффициентамиbnоператора фильтра:
y(k) = TL[(0)] = bn
③(k-n)
= h(k) ≡ bn. (2.2.1)
Для рекурсивных фильтров реакция на
импульс Кронекера зависит как от
коэффициентов bnфильтра, так и от
коэффициентов обратной связи am.
С использованием формулы (2.1.2):
y(k) =bn
(k-n)
–am
y(k-m)
=hk.
(2.2.1′)
Функция h(k), которая связывает вход и
выход фильтра по реакции на единичный
входной сигнал и однозначно определяется
оператором преобразования фильтра,
получила название импульсного отклика
фильтра (функции отклика). Для рекурсивных
фильтров длина импульсного отклика, в
принципе, может быть бесконечной.
Если
произвольный сигнал на входе фильтра
представить в виде линейной комбинации
взвешенных импульсов Кронекера
x(k) =(n)
x(k-n),
то сигнал на выходе фильтра можно
рассматривать как суперпозицию
запаздывающих импульсных реакций на
входную последовательность взвешенных
импульсов:
y(k) = h(n)(n) x(k-n))
h(n)
x(k-n).
Для нерекурсивных фильтров пределы
суммирования в последнем выражении
устанавливаются непосредственно по
длине импульсного отклика h(n).
Определение импульсной
реакциина практике требуется,
как правило, только для рекурсивных
фильтров, так как импульсная реакция
для НЦФ при известных значениях
коэффициентов b(n), как это следует из
выражения (2.2.1), специального определения
не требует: h(n) ≡ b(n).
Если выражение для системы известно в
общей форме (2.1.2), определение импульсной
реакции производится подстановкой в
уравнение системы импульса Кронекера
с координатой k = 0 при нулевых начальных
условиях. В соответствии с выражением
(2.2.1) сигнал на выходе системы будет
представлять собой импульсную реакцию
системы.
Пример. Уравнение РЦФ: yk =
xk+ 0.5yk-1.
Входной сигнал: xk=o=
{1,0,0,0,…}.
Расчет выходного сигнала при нулевых
начальных условиях:
yo =
xo+0.5
y-1 =
1+0 = 1 = ho.
y1 =
x1+0.5
yo =
0+0.5 = 0.5 = h1.
y2 =
x2+0.5
y1 =
0+0.25 = 0.25 = h2.
y3 =
x3+0.5
y2 =
0.125 = h3.
y4 =
x4+0.5
y3 =
0.0625 = h4,
и т.д.
Импульсный отклик
фильтра: hk
= (O.5)k,
k = 0, 1, 2….
Определение импульсной реакции физической
системы обычно производится подачей
на вход системы ступенчатой функции
Хевисайда, которая равна u(k)= 1 при k0,
и u(k)= 0 при k<0:
g(k) =h(n)u(k-n)
=h(n).
Отсюда:
h(k) =g(k)
-g(k-1).
Функция g(k) получила название переходной
характеристики системы (из одного
статического состояния в другое). Форму
реакции фильтра на функцию Хевисайда
можно видеть на рис. 2.1.4 (с точки k = 10 и
далее) в сопоставлении с реакцией на
импульс Кронекера в точке k=2.
2.3. Передаточные функции фильтров /7/.
Z-преобразование.Удобным методом решения разностных
уравнений линейных систем является
z-преобразование.
Напоминание.
yn↔ynzn =Y(z).
Аргумент zиспользуется
в двух вариантах:znилиz—n.
В данном курсе по умолчанию используем
аргумент zn.
Применяя z-преобразование к обеим частям
равенства (2.1.1), c учетом сдвига функций
(y(k-m) zmY(z)),
получаем:
Y(z)amzm
= X(z)bnzn,
(2.3.1)
где X(z),Y(z)- соответствующие z-образы
входного и выходного сигнала. Отсюда,
полагая ao= 1, получаем в общей
форме уравнение передаточной функции
системы в z-области:
H(z) = Y(z)/X(z) =bnzn
(1+
amzm).
(2.3.2)
Для НЦФ, при нулевых коэффициентах am:
H(z) =bnzn.
(2.3.3)
При проектировании фильтров исходной,
как правило, является частотная
передаточная функция фильтра H(ω), по
которой вычисляется ее Z-образ H(z) и
обратным переходом в пространство
сигналов определяется алгоритм обработки
данных. В общей форме для выходных
сигналов фильтра:
Y(z) = H(z)·X(z).
Y(z)·(1+am
zm) =
X(z)bn
zn
Y(z) = X(z)bn
zn –
Y(z)am
zm.
(2.3.4)
После обратного Z-преобразования
выражения (2.3.4):
y(k) =bnx(k-n)
–amy(k-m).
(2.3.5)
При подаче на вход фильтра импульса
Кронекера о,
имеющего z-образ(z)
= zn = 1, сигнал на выходе фильтра
будет представлять собой импульсную
реакцию фильтра y(k) ≡ h(k), при этом:
H(z) = Y(z)/(z) = Y(z) =
TZ[y(k)] =h(k)
zk, (2.3.6)
т.е. передаточная функция фильтра
является z-образом его импульсной
реакции. При обратном z-преобразовании
передаточной функции получаем импульсную
характеристику фильтра:
h(k) H(z).
(2.3.7)
Если функция H(z) представлена конечным
степенным полиномом, что характерно
для НЦФ, являющихся КИХ-фильтрами, то
обратное z-преобразование осуществляется
элементарно — идентификацией коэффициентов
по степеням z. Передаточная функция РЦФ
также может быть представлена степенным
полиномом прямым делением числителя
на знаменатель правой части выражения
(2.3.2), однако результат при этом может
оказаться как конечным, так и бесконечным,
т.е. система может иметь либо конечную,
либо бесконечную импульсную характеристику.
Практически используемые рекурсивные
фильтры обычно имеют бесконечную
импульсную характеристику (БИХ-фильтры)
при конечном числе членов алгоритма
фильтрации (2.3.5).
Примеры.
1. Передаточная функция РЦФ: H(z) =
(1-z5)/(1-z).
Прямым делением числителя на
знаменатель получаем: H(z) = 1+z+z2+z3+z4.
H(z) h(n) =
{1,1,1,1,1}. Фильтр РЦФ является КИХ-фильтром.
2. Передаточная функция: H(z) = 1/(1-2z).
Методом обратного z-преобразования:
h(n) = 2n. Фильтр РЦФ является
БИХ-фильтром.
Устойчивость фильтров.Фильтр называется устойчивым, если при
любых начальных условиях реакция фильтра
на любое ограниченное воздействие также
ограничена. Критерием устойчивости
фильтра является абсолютная сходимость
отсчетов его импульсного отклика:
|h(n)|
<.
(2.3.8)
Анализ устойчивости может быть проведен
по передаточной функции. В устойчивой
системе значение H(z) должно быть конечным
во всех точках z-плоскости, где |z| 1, а, следовательно, передаточная функция
не должна иметь особых точек (полюсов)
на и внутри единичного круга на
z-плоскости. Полюсы H(z) определяются
корнями знаменателя передаточной
функции (2.3.2).
Пример.
Передаточная функция фильтра рис.
2.1.4: H(z) = b0/(1-a1z). При а1=
0.5 полюс знаменателя: zр= 2. |zр|>1.
Фильтр устойчив.
Передаточная функция фильтра рис.
2.1.5: H(z) = b0/(1+a1z). При а1=
1.1 полюс знаменателя: zр= -0.909. |zр|
< 1. Фильтр неустойчив, что и подтверждает
пример фильтрации.
Передаточная функция фильтра рис.
2.1.6: H(z) = 0.5(1+z)/(1-z). Полюс знаменателя: zр=
1. В принципе, фильтр неустойчив, но эта
неустойчивость проявляется только при
k = ∞. Импульсный отклик фильтра h(n) =
{0.5,1,1,1, ….}, сумма которого равна ∞ только
при n = ∞, т.е. при интегрировании бесконечно
больших массивов. При интегрировании
конечных массивов результат всегда
конечен.
Приведенный критерий устойчивости
относится к несократимой дроби, т.к. в
противном случае возможна компенсация
полюса нулем передаточной функции, и
следует проверить наличие однозначных
нулей и полюсов.
Проверка на устойчивость требуется
только для рекурсивных цифровых фильтров
(систем с обратной связью), нерекурсивные
системы всегда устойчивы.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g(t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (d-функции) (7.21). Обозначается импульсная характеристика h(t). Причем, g(t) и h(t) определяются при нулевых начальных условиях в цепи. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А.
Использование понятий переходной и импульсной характеристик цепи позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1(t) или d(t).
Между переходной g(t) и импульсной h(t) характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/t, сдвинутых друг относительно друга на время t (см. рис. 7.4):
т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи
т. е. импульсная характеристика является производной от переходной характеристики цепи.
Уравнение (8.2) справедливо для случая, когда g(0) = 0 (нулевые начальны е условия для цепи). Если же g(0) ¹ 0, то представив g(t) в виде g(t) = 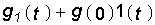
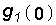
Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы. Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной d(t) функции. Обычно классическим методом удобно определять переходную характеристику g(t), а импульсную характеристику h(t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.
Пример. Найдем классическим методом переходную характеристику по напряжению для цепи, изображенной на рис. 8.1. Численно gu(t) для данной цепи совпадает с напряжением на емкости при подключении ее в момент t= 0 к источнику напряжения U1 = l В:
Закон изменения напряжения uC(t) определяется уравнением (6.27), где необходимо положить U= l В:
При нахождении характеристик g(t) и h(t) операторным методом пользуются изображениями функций 1(t), d(t) и методикой расчета переходных процессов, изложенных в гл. 7.
Пример. Определим операторным методом переходную характеристику gu(t) RС-цепи (см. рис. 8.1). Для данной цепи в соответствии с законом Ома в операторной форме (7.35) можем записать:
где
Окончательно получаем
Отсюда по теореме разложения (7.31) находим
т. е. то же значение, что и полученное классическим методом.
Следует отметить, что величина I(р) в уравнении (8.4) численно равна изображению переходной проводимости. Аналогичное изображение импульсной характеристики численно равно операторной проводимости цепи
Например, для RС-цепи (см. рис. 8.1) имеем:
Применив к Y(p) теорему разложения (7.30), получим:
Следует отметить, что формула (8.5) определяет свободную составляющую реакции цепи при единичном импульсном воздействии. В общем случае в реакции цепи, кроме экспоненциальных составляющих свободного режима при t > 0 присутствует импульсное слагаемое, отображающее воздействие при t = 0 единичного импульса. Действительно, если учесть, что для RС-контура (см. рис. 8.1) переходная характеристика по току при U= 1(t) согласно (6.28) будет
то после дифференцирования (8.6) согласно (8.2) получаем импульсную характеристику RС-цепи hi(t) в виде
т. е. реакция hi(t) содержит два слагаемых — импульсное и экспоненциальное.
Физический смысл первого слагаемого в (8.7) означает, что при t = 0 в результате воздействия на цепь импульсного напряжения d(t) зарядный ток мгновенно достигает бесконечно большого значения, при этом за время от 0– до 0+ элементу емкости передается конечный заряд и она скачком заряжается до напряжения I/RC. Второе слагаемое определяет свободный процесс в цепи при t> 0 и обусловлено разрядом конденсатора через короткозамкнутый вход (так как при t> 0 d(t) = 0, что равносильно КЗ входа) с постоянной времени t = RC. Из этого следует, что при d(t)-импульсном воздействии на RС-цепь нарушается непрерывность заряда на емкости (второй закон коммутации). Аналогично нарушается и условие непрерывности тока в индуктивности (первый закон коммутации), если к цепи, содержащей элемент индуктивности воздействовать напряжением в виде d(t).
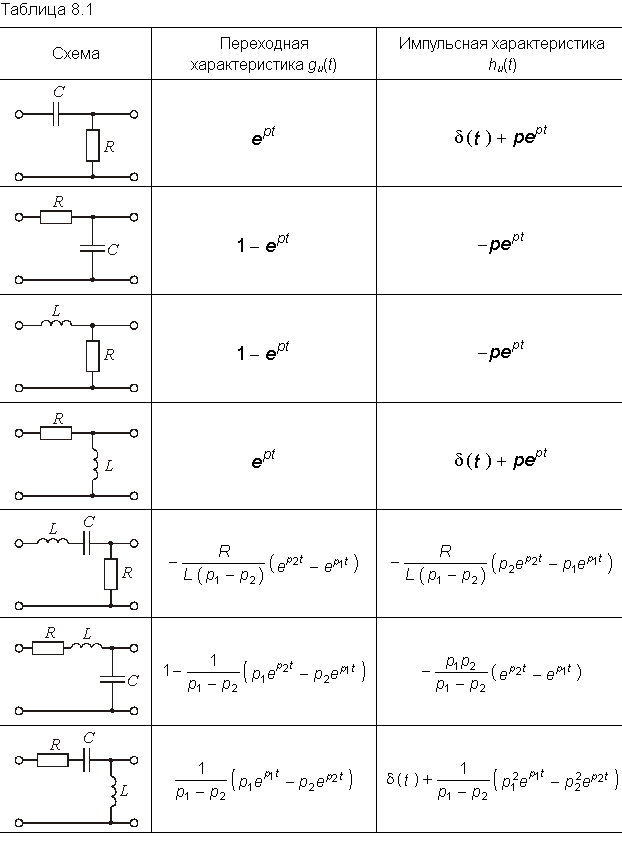
В табл. 8.1 сведены значения переходной и импульсных характеристик по току и напряжению для некоторых цепей первого и второго порядка.
Домашнее задание № 3.2
-
Определить переходную и импульсную характеристику цепи. Входное напряжение
подключено к зажимам 1-1’. Выходное напряжение
снимается с зажимов 2-2’.
-
Пользуясь любой из найденных характеристик, определить реакцию цепи
на заданное входное воздействие
.
: длительность импульса
следует выбрать равной постоянной времени цепи,
-
Построить временную зависимость
. Рассчитать значения
,
,
,
|
R1 |
R2 |
C2 |
|
10 Ом |
10 Ом |
20 мкФ |
-
Определим переходную и импульсную характеристики цепи.
Входное сопротивление цепи:
Ток равняется:
Выходное напряжение найдём по второму закону Кирхгофа:
Тогда передаточная функция цепи:
Подставляя числовые значения, получим:
Переходная характеристика цепи — это реакция цепи на единичное входное воздействие:
Изображение единичной функции , поэтому мы можем найти изображение выходного напряжение при таком воздействии на входе цепи:
Теперь найдём оригинал этого изображения выходного напряжения – это и будет переходная характеристика цепи. Изображение имеет вид дроби , где корни уравнения
равняются
и
. Повторяющихся корней нет. Производная знаменателя:
Так как дробь мы можем представить в виде дроби:
То в нашем случае:
Таким образом:
Оригинал , который и будет переходной функцией, имеет вид:
Импульсная характеристика четырёхполюсника определяется как реакция на входное воздействие, представляющее собой дельта-функцию . Изображение дельта-функции равняется 1, поэтому изображение выходного напряжения имеет вид:
Оригинал этого напряжения будет импульсной характеристикой цепи:
Импульсная характеристика — это производная от переходной характеристики:
-
Определим реакцию цепи
на заданное входное воздействие.
Входное воздействие имеет вид:
Где — постоянная времени цепи. Постоянная времени цепи определяет время, в течении которого напряжение на выходе уменьшается в
раз. В нашем случае
Это входное воздействие можно рассматривать как 3 следующих друг за другом этапа:
— скачок входного напряжения в момент времени от 0 до
— постоянное значение при
— скачок входного напряжения в момент времени от
до 0
Воспользуемся для определения реакции цепи (нахождения ) интегралом Дюамеля:
при :
Первое слагаемое обусловлено скачком в момент времени , второе слагаемое — постоянным значением напряжения на входе цепи в период времени
, равняется 0, так как
.
при
Третье слагаемое обусловлено скачком напряжения в момент . Воспользовавшись единичной функцией
, можем записать для
:
Входной сигнал имеет вид:
Найдём изображение входного напряжения :
Определим реакцию цепи на такое входное воздействие. Изображение выходного напряжения :
Рассмотрим дробь:
Корни уравнения , откуда
и
. Первая производная
. Таким образом:
Таким образом:
Оригинал выходного напряжения имеет вид:
Что совпадает с выходным напряжением, полученным с использованием переходной характеристики цепи.
-
Построим графически зависимость
. Рассчитаем значения
,
,
,
График напряжения :
Рассчитаем значения в моменты времени
. Для этого воспользуемся аналитическим выражением для
.
Для :
Так как выходное напряжение – это напряжение на конденсаторе, поэтому согласно законам коммутации оно не может измениться скачком, а для оно было равно нулю, так как входное напряжение было равно нулю. Таким образом,
.
Для моментов времени и
также
, потому что выходное напряжение – это напряжение на конденсаторе, и оно не может измениться скачком, согласно законам коммутации.
Заметим, что, если бы входное напряжение представляло собой единичный скачок амплитудой бесконечной длительности, то напряжение на конденсаторе для
равнялось бы напряжению на резисторе
в установившемся процессе:
. Но так как длительность единичного импульса ограниченно временем
, равным постоянной времени цепи, то конденсатор не успевает зарядиться до этого значения, и успевает зарядиться только до значения, на
меньшее, а при
разряжается через резистор
.
Для :
При входное напряжение равняется нулю, поэтому при
конденсатор разряжается через резистор
и напряжение на нем, которое равняется выходному, стремится к нулю.
Ответ:
Переходная характеристика цепи:
Импульсная характеристика цепи:
Реакция цепи на заданное входное воздействие:
Сайт управляется системой uCoz

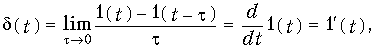
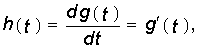
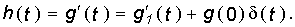
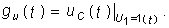
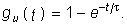
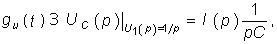
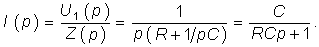
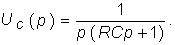
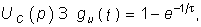
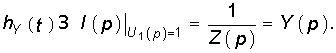
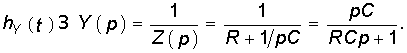
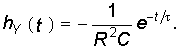
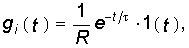
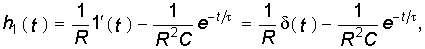
![toe3_2-12.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-12.jpg)
![toe3_2-13.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-13.jpg)
![toe3_2-14.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-14.jpg)
![toe3_2-17.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-17.jpg)
![toe3_2-31.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-31.jpg)
![toe3_2-40.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-40.jpg)
![toe3_2-52.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-52.jpg)
![toe3_2-57.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-57.jpg)
![toe3_2-62.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-62.jpg)
![toe3_2-67.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-67.jpg)
![toe3_2-76.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-76.jpg)
![toe3_2-77.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-77.jpg)
![toe3_2-85.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-85.jpg)