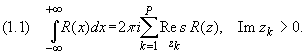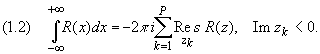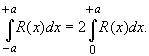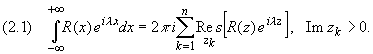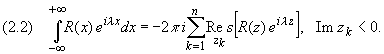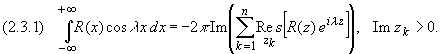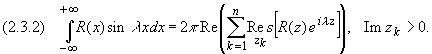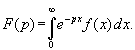Определение. Число вида z = х + iy, где х, , a i – так называемая мнимая единица, называется комплексным числом. Мнимая единица определяется равенством:
(2.1)
Действительные числа x и y называются соответственно действительной и мнимой частью комплексного числа z и обозначаются:
x = Rez; y = Imz (2.2)
Множество комплексных чисел обозначают буквой С.
Например, – комплексное число, где Rez = 5 – действительная часть; Imz = 8 – мнимая часть.
Определение. Два комплексных числа считают равными тогда и только тогда, когда у них равны соответственно действительные и мнимые части. В частности, комплексное число z = х + iy равно нулю тогда и только тогда, когда х =0 и у =0 .
Определение. Числа z = х + iy и z = х – iy называются (комплексно) сопряженными.
Записать сопряженное число для .
Решение
Сопряженное число: .
Выбираем на плоскости систему декартовых координат xОy (рис. 2.1) , тогда каждому z = х + iy будет соответствовать вектор плоскости, начало которого совпадает с началом координат, и, наоборот, каждому вектору
плоскости xОy будет отвечать определённое комплексное число z = х + iy (последнее следует из основной формулы векторного исчисления), где x и y – компоненты (координаты)
.
Таким образом, между множеством C и множеством векторов (и точек!) плоскости xOy устанавливается взаимно однозначное соответствие.
Определения. Плоскость xОy называется плоскостью комплексных чисел (или просто комплексной плоскостью), будем её обозначать Z. Ось Ox – действительная ось; ось Oy – мнимая ось.
Поскольку – вектор, то он имеет длину и характеризуется направлением.
Длину вектора называют модулем комплексного числа z = х + iy, а величину угла наклона вектора
по отношению к оси Ox – аргументом z. Их обозначают символами:
и
. (2.3)
Модуль комплексного числа есть однозначная функция:
. (*)
Из рисунка 2.1 видно, что:
,
. (2.4)
Аргумент есть функция многозначная. Все значения аргумента
удовлетворяют соотношению:
(2.5)
При аргумент не определен. Из множества значений
(z
0) выделяют одно, лежащее в интервале
, которое обозначают argz и называют главным значением аргумента:
(2.6)
Очевидно, что
(2.7)
Из формул (2.5) и (2.6) следует:
(2.8)

Дано комплексное число .
Необходимо: найти модуль комплексного числа, изобразить число на комплексной плоскости, найти главное значение аргумента комплексного числа.
Решение
Используем формулу (*) и находим модуль комплексного числа:
Изобразим число на комплексной плоскости (рис. 2.2).
Определим главное значение аргумента комплексного числа , используя формулу (2.8), так как
т.е.
, то
Модуль и аргумент комплексного числа
Пусть задано комплексное число $ z = a+bi $.
| Формула |
| Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$ |
Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.
Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.
| Формула |
Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$:
|
Введите комплексное число
Пример 1 Пример 2 Правила ввода
| Пример 1 |
| Найти модуль и аргумент комплексного числа $ z = 3 — 4i $. |
| Решение |
|
Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$ |
| Ответ |
| $$ |z| = 5, varphi = -arctg frac{4}{3} $$ |
| Пример 2 |
| Найти модуль и аргумент комплексного числа $ z = 3i $ |
| Решение |
|
В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$ |
| Ответ |
| $$ |z| = 3, varphi = frac{pi}{2} $$ |
| Пример 3 |
| Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$ |
| Решение |
|
Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ varphi = frac{pi}{3}, |z| = 2 $$ |
| Пример 4 |
| Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$ |
| Решение |
|
Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi — arctg(sqrt{3}) = pi — frac{pi}{3} = frac{2pi}{3}. $$ |
| Ответ |
| $$ varphi = frac{2pi}{3} $$ |
Определение комплексного числа.
Комплексным
числом z
называют символ x+yi,
где
х
и
у—
действительные числа. При этом х
называется
действительной
частью комплексного
числа, у
—
мнимой
частью, i
—
мнимой
единицей.
Действительная
часть комплексного числа обозначается
ReZ
(ReZ=x),
а мнимая часть обозначается символом
ImZ
(ImZ=y).
Следовательно, комплексное число можно
записать
.
Запись
комплексного числа
называется алгебраической формой
записи.
Комплексное
число
называется сопряженным с комплексным
числоми обозначается
.
Комплексные
числа
и
называютсяравными,
если
соответственно равны их действительные
и мнимые части:
.
(1)
Если
у = 0, то комплексное число имеет вид
.
Будем его сокращенно записыватьz=x
и
называть действительным
числом.
Если x=0
и y=0,
то комплексное число z=0+i0
сокращенно записывается в виде z=0
и называется нулем.
Если
х=0, у≠0,
то комплексное число имеет вид z=0+yi
или, короче, z
= yi.
Его называют
мнимым числом.
В частности, если х=0,
y=1,
получаем
комплексное число
0+1i=i
— мнимую единицу. Всякое число z
=
x+yi,
где
y≠0,
называют
мнимым
числом.
Два
комплексных числа x+yi
и x-yi
— называются комплексно-сопряженными.
Если
z=x+yi,
то
сопряженное число x-yi
—
принято
обозначать
.
Операции
над комплексными числами.
Суммой
комплексных
чисел
называют комплексное число
Его
обозначают
.
Таким образом,
(2)
При сложении
комплексных чисел складываются их
действительные и мнимые части.
Комплексное
число
называется разностью двух комплексных
чисел,
если.
Разность комплексных чисел
обозначается
.
Из определения
следует, что
.
(3)
При вычитании из
действительной и мнимой части уменьшаемого
соответственно вычитается действительная
и мнимая часть вычитаемого.
Умножение
двух
комплексных чисел
вводится равенством
.
(4)
Равенство (4)
следует, из
(5)
Действительно,
Если
при умножении двух комплексных чисел
получится некоторое число
,
то
при умножении сопряженных им чисел
получится число сопряженное, т. е.
.
Деление
вводится
как действие, обратное умножению. Частным
от деления числа
называют число
,
такое, что,
т.
е.
.
(6)
Отсюда, на основании
равенства (4), получаем:
(7)
Решая
систему (7) относительно
находим:
(8)
(где
,
так как по условию).
Таким образом,
(9)
Нетрудно
заметить, что равенство (9) может быть
получено путем умножения числителя и
знаменателя дроби
на число, комплексно сопряженное
знаменателю.
Возведение
комплексного
числа z
в натуральную степень п рассматривается
как частный случай умножения комплексных
чисел:
Комплексные
числа можно рассматривать как расширение
множества действительных чисел. В самом
деле, алгебраические операции над
комплексными числами введены так, что
совокупность всех «действительных»
комплексных чисел (т. е. чисел вида
или, короче,
z
= x
с
указанными операциями над ними совпадает
с совокупностью действительных чисел
и известными действиями над этими
числами.
Тригонометрическая
форма комплексного числа.
Выберем на плоскости XOY
полярную
систему координат (рис. 1) так, чтобы
полюс совпал с началом координат, а
полярная ось пошла бы по положительному
направлению действительной оси. Обозначим
полярный радиус точки
через
ρ, а полярный угол через φ. Полярный
радиус ρ называется модулем
комплексного
числа и обозначается
.
Полярный
угол φ называется аргументом
комплексного
числа и обозначается arg
z,
если берется главное значение угла
,
иArgz,
если берется общее значение угла. Таким
образом,
,
где k
—
произвольное целое число, а φ — любое
из значений аргумента z.
Так
как
,
а,
то
(*)
Выражение
(*) называется тригонометрической
формой записи
комплексного числа. Очевидно, что
Например,
Геометрическая
интерпретация сложения комплексных
чисел.
Пусть плоскости комплексной переменной
даются два числа
(рис. 2).
Рис.
2.
Проведя
радиусы-векторы точек
получим два вектора
,
которые соответствуют комплексным
числам.
При сложении комплексных чисел
складываются их действительные и мнимые
части, а при сложении векторов складываются
соответствующие координаты. Это позволяет
сложение комплексных чисел представлять
в виде сложения векторов. Вектор,
являющийся
диагональю параллелограмма, построенного
на векторах
и
представляет комплексное число:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Небольшой теоретический курс по теории функций комплексного переменного.
1. Различные формы представления комплексных чисел. Арифметические операции с комплексными числами.
2. Элементарные функции комплексного переменного.
3. Дифференцирование функций комплексного переменного.
4. Интегралы в комплексной области.
5. Нули аналитической функции.
6. Изолированные особые точки функции комплексного переменного.
7. Ряд Тейлора функций комплексного переменного.
8. Ряды Лорана.
9. Вычеты.
10. Вычисление интегралов по замкнутому контуру.
11. Вычисление несобственных интегралов.
12. Преобразование Лапласа. Решение задачи Коши операционным методом.
Наверх
Различные формы представления комплексных чисел. Арифметические операции с комплексными числами
Комплексным числом z называется упорядоченная пара действительных чисел x и y.
Первое из них x называется действительной частью комплексного числа z и обозначается Rez, x = Rez;
второе число y называется мнимой частью комплексного числа z и обозначается Imz, y = Imz.
Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:
Алгебраическая форма записи комплексного числа
Число
, где
называется комплексно сопряженным числу
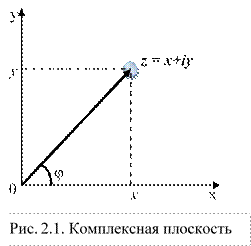
Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).
Если x и y — декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью
x = rcosj, y = rsinj
получим тригонометрическую форму записи комплексного числа:
z = r (cosj + isinj) .
При этом число r называют модулем комплексного числа, |z| = r, а число j — аргументом комплексного числа,
Arg z = arg z+2kp= j.
При решении задач для вычисления аргумента удобно пользовааться схемой, приведенной ниже:
Справедливы соотношения:
Используя формулу Эйлера
получим показательную форму записи комплексного числа:
Арифметические операции c комплексными числами определяются следующим образом:
если
то
Наверх
Элементарные функции комплексного переменного
Значение целой положительной степени комплексного аргумента, значение функции f(z) = z n , проще всего вычислять в тригонометрической форме.
Если z = x + iy = r (cosj + isinj ), то для любого целого положительного числа n имеет место формула:
w = f(z) = z n = r n (cos nj + isin nj ).
Если w = f (z) = f (x + iy) = u(x, y) + iv(x, y), то
u(x, y) = r ncos nj , u(x, y) = r nsin nj.
Корнем n-й степени из комплексного числа z называется число
такое, что wn = z.
Для любого комплексного числа z существует n комплексных чисел w таких, что wn = z.
Значение корня, т.е. значение функции
проще всего вычислять в тригнометрической форме.
Если z = x + iy = r (cosj + isinj), то для любого целого положительного числа n имеет место формула:
Т.е. функция
является многозначной функцией _ каждому значению аргумента отвечает n различных значений корня.
Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то
Если z = x + iy = r (cosj + isinj ), то значения функции f(z) = exp(z) вычисляются по формуле
f(z) = ez = ex+iy = e xe iy = ex (cosy + isiny).
Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то
u(x,y) = ex cosy , v(x,y) = ex siny.
Тригонометрические функции комплексного аргумента определяются формулами:
Гиперболические функции комплексного переменного определяются совершенно так же, как функции в действительной области:
Логарифмом комплексного числа z называется такое число w, что
exp(w) = z.
Значения логарифмической функции f(z) = Ln(z) вычисляются по формуле
Ln(z) = ln(|z|) + iArg z = ln(|z|) + iarg z + 2kp i, k = 0,1,2,…
Величину ln(|z|) + iarg z называют главным значением логарифма.
Функция f(z) = Ln(z) является многозначной функцией _ каждому значению аргумента отвечает бесконечное множестворазличных значений логарифма.
Показательная (f(z) = az) и степенная (f(z) = za) функции комплексного переменного определяются с помощью логарифма — для любых комплексных чисел a и z справедливо:
f(z) = az = ezLna;
f(z) = za= eaLnz.
Значения обратных тригонометрических функций комплексного переменного вычисляются по формулам:
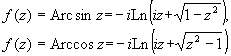
Наверх
Дифференцирование функций комплексного переменного
Производная функции комплексного переменного определяется, как и производная в действительной области:
Здесь
z0, Dz _ комплексные и Df(z0) = f(z0+Dz) — f(z).
Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.
1. Сумма и произведение дифференцируемых в точке функций, есть функция и справедливы равенства:
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :
3. Сложная функция f(j (z)) дифференцируема в точке z0, если в этой точке дифференцируема функция j (z), а функция f(u) дифференцируема в точке u0,
где u0 = j (z0) и u = j (z). При этом в точке z0 имеет место формула:
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.
Например, рассмотрим функцию f(z) = z3.
По определению производной для любой точки z, принадлежащей комплексной области, записываем:
Предел существует для любой точки z, принадлежащей комплексной области и
(z3)’ =3z2.
Аналогично можно получить:
(zn)’ = nzn-1 (n — действительное число).
Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z),
то справедливы следующие утверждения:
1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей
u(x, y) = Re f(z), v(x, y) = Im f(z)
и выполняется условие Коши-Римана:
2. Если u(x, y) и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция f(z) = f(x+iy) = u(x, y) + iv(x, y) дифференцируема в точке z0 = x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из формул:
Наверх
Интегралы в комплексной области.
Интегралом от функции комплексного переменного называется предел последовательности интегральных сумм; функция при этом определена на некоторой кривой l, кривая предполагается гладкой или кусочно-гладкой:
где — точка, произвольно выбранная на дуге
разбиения кривой,
— приращение аргумента функции на этом участке разбиения,
— шаг разбиения,
— длина хорды, соединяющей концы дуги
,
кривая l разбивается произвольным образом на n частей , k=1,2…n.
На кривой выбрано направление, т.е. указаны начальная и конечная точки.
В случае замкнутой кривой l = C
интегрирование происходит в положительном направлении, т.е. в направлении обхода, оставляющем слева конечную область, ограниченную контуром С.
Существует несколько способов вычисления интегралов в комплексной области.
1 способ. Интеграл вычисляется сведением к криволинейным интегралам от функций действительных переменных — примененяются формулы:
где f(z) = u + iv, u = Re f(z), v = Im f(z).
2 способ. Интеграл вычисляется сведением к определенному интегралу (путь интегрирования l задается в параметрической форме z = z(t)) — применяется формула:
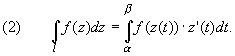
3 способ. Вычисление интегралов от аналитической функции в односвязных областях — примененяеется формула:
где F(z) — первообразная для f(z).
Наверх
Нули аналитической функции.
Пусть функция f (z) является аналитической в точке z0. Точка z0 называется нулем функции f (z), если ее значение в этой точке равно нулю, т.е. f (z0) = 0.
В разложении функции в ряд Тейлора в окрестности нуля этой функции (т. z0) отсутствует свободный член: С0 = f(z0) = 0.
Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности (z-z0) до n-ой степени, т.е. разложение имеет вид:
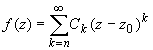
то точка z0 называется нулем порядка nфункции f(z).
Нуль первого порядка (n = 1) называется простым нулем.
Следующие условия являются необходимым и достаточным условиями нуля порядка n функции f (z) в точке z0:
a).
b). представление функции в виде произведения:
Порядок нуля в точке z0 функции, полученной в результате перемножения аналитических функций
f (z) = f1(z) f2(z) равен сумме порядков нуля (n1 + n2) в этой точке функций сомножителей
( n1 — порядок нуля в точке z0 функции f1(z), n2 — порядок нуля в точке z0 функции f2(z) ).
Наверх
Изолированные особые точки функции комплексного переменного.
Точка z0, принадлежащая области комплексных чисел, называется изолированной особой точкой функции f(z), если такая, что f(z) является однозначной аналитической функцией в
(в самой точке аналитичность f(z) нарушается).
Изолированная особая точка z0 функции f(z) называется:
-
устранимой особой точкой, если
существует и конечен;
-
полюсом, если
;
-
существенно особой точкой, если
не существует.
Для того чтобы особая точка функции f(z) была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если z0 — устранимая особая точка, то ряд Лорана функции f(z) имеет вид: 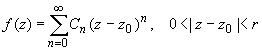
для z0 — конечной точки, принадлежащей области комплексных чисел.
Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов.
Ряд Лорана функции f(z) в случае z0-полюс имеет вид:
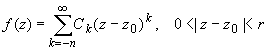
если z0 принадлежит области комплексных чисел.
Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка z0 является полюсом порядка n функции f(z), если в разложении (2) , Ck = 0 при k < -n.
Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции f(z) в случае z0 — существенно особой точки имеет вид: 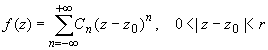
если z0 принадлежит области комплексных чисел.
Наверх
Ряд Тейлора функций комплексного переменного.
Теорема Тейлора (о разложении функции в степенной ряд).
Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z0 этой области представляется в виде степенного ряда:
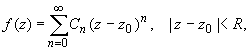
радиус сходимости R которого не меньше, чем расстояние от точки z0 до границы области D.
Такой степенной ряд называется рядом Тейлора.
Коэффициенты ряда Тейлора вычисляются по формуле:
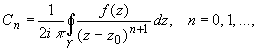
где — произвольный контур, принадлежащий области D и охватывающий точку z0 (в частности,
— окружность
), или по формуле:
(3)
Радиус сходимости ряда Тейлора равен расстоянию от точки z0 до ближайшей особой точки функции.
Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:
Основные разложения.
(z принадлежит области комплексных чисел);
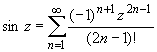
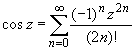
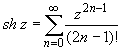
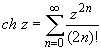
Наверх
Ряды Лорана.
Теорема Лорана (о разложении функции в ряд по целым степеням).
Функция f(z), аналитическая в кольце
r < | z — z0 | < R,
представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство:
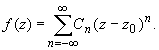
Коэффициенты ряда вычисляются по формуле: 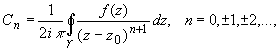
где — произвольный контур, принадлежащий кольцу и охватывающий точку z0; в частности,
— окружность
Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f(z).
Совокупность членов ряда с неотрицательными степенями 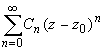
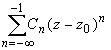
Для коэффициентов ряда имеет место формула оценки коэффициентов — неравенство Коши:
где
r — радиус контура интегрирования в формуле (2).
На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f(z) — его суммы.
Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z0 (r = 0) и в окрестности бесконечно удаленной точки (z0 = 0, ).
При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами.
Наверх
Вычеты.
Вычетом функции f(z) в изолированной особой точке z0 (точка принадлежит области комплексных чисел) называется интеграл вида:
где — контур, принадлежащий окрестности точки z0 и охватывающий ее. Обход контура — положительный, т.е. область ограниченная им и принадлежащая окрестности z0 при обходе расположена слева: обход против часовой стрелки.
Обозначается вычет
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z-z0) для z0, принадлежащей области комплексных чисел:
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то
Если z0 — полюс порядка n функции f(z), z0 принадлежит области комплексных чисел, то
Если z0 — простой полюс функции ,
где аналитические функции в точке z0 и
,
то
Наверх
Вычисление интегралов по замкнутому контуру.
Теорема (Основная теорема о вычетах).
Если функция f(z — аналитична в за исключением конечного числа особых точек
, то справедливо равенство
где D — односвязная область в комплексной плоскости, — граница D,
— вычет функции f(z) в точке zk.
Наверх
Вычисление несобственных интегралов
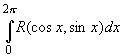
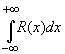
Утверждение. Пусть R(x, y) — рациональная функция двух действительных переменных. Тогда справедливы равенства
Действительно, замена z = eix переводит отрезок в окружность |z| = 1,
.
При этом:
В результате имеем формулу, сопоставляющую интеграл от действительной переменной с интегралом по замкнутой кривой от функции комплексного переменного:
Замечание. Для вычисления таких интегралов в математическом анализе в общем случае, за исключением некоторых частных случаев, применяется замена tg(1/2)= t («универсальная» подстановка) и интеграл приводится к интегралу от рациональной дроби.
Утверждение. Пусть функция
где Pn(x) и Qm(x) — многочлены степени n и m (n = const, m = const), удовлетворяет условиям:
1. (m — n) больше или равно 2.
2. Qm(x) не равна 0 при x, принадлежащим области действительных чисел.
Тогда справедливы равенства:
Здесь zk, k = 1,2,…, p — все особые точки функции R(z), расположенные выше оси Ох (Im zk> 0) в случае формулы (1) и ниже оси Ох (Im zk< 0) в случае формулы (1.2).
Замечание. Если R(z) — четная функция, то можно, используя формулы (1.1) и (1.2), вычислить интеграл вида
т.к. для четной функции имеет место равенство:
Утверждение. Пусть R(x) — рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, — нуль порядка не ниже первого (т.е. (m — n) больше или равно 1). Тогда справедливы формулы:
Наверх
Преобразование Лапласа. Решение задачи Коши операционным методом
Операционное исчисление — один из наиболее эффективных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. При решении операционным методом задача интегрирования линейного дифференциального уравнения с постоянными коэффициентами сводится к задаче о решении алгебраического уравнения.
Функцией-оригиналом называется функция f (x) для которой справедливо:
f (x) непрерывна при неотрицательных x, за исключением, быть может конечного числа точек, f (x) = 0 при x<0, существуют такие постоянные M и a, что при всех неотрицательных x.
Преобразованием Лапласа функции f (x) называется функция
Функция F (p) называется изображением функции f (x), а функция f (x) — оригиналом для F (p).
Основные свойства преобразования Лапласа, используемые при решении дифференциальных уравнений следующие:
-
оригинал восстанавливется по изображению единственным образом, с точностью до значений в точках разрыва — теорема единственности;
-
если F (p) и G (p) — изображения соответственно для f (x) и g (x), то изображением для af (x) + bg (x) является aF (p) + bG (p) — линейность преобразования Лапласа;
-
изображением для производной f (n)(x) является функция pnF(p) — pn-1f (0) — pn-2f ‘(0) -…- pf (n-2)(0) — f (n-1)(0) — изображение производных;
-
если F (p) изображения для f (x), то для любого a>0 изображением для f (x-a) является
— теорема запаздывания.
Рассмотри задачу Коши:
a1, a2, …, an — постоянные.
Алгоритм решения задачи Коши для уравнений операционным методом состоит в следующем. Обрзначим Y (p) и F (p) изображения для y (x) и f (x).
Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
или, A (p)Y (p) + B (p) = F (p), где A (p) и B (p) — многочлены.
Отсюда:
и искомое решение задачи Коши y (x) является оригиналом для Y (p).
Совершенно аналогично операционное исчисление применяется к решению задачи Коши для систем линейных дифференциальных уравнений с постоянными коэффициентами. Рассмотри задачу Коши:
A- постоянна матрица размерности n.n.
Алгоритм решения задачи Коши для систем операционным методом состоит в следующем.
Обозначим изображения для
— компонентами вектор-функций
являются изображения соответствующих компонент вектор-функций
. Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
,
где E — единичная матрица, — обратная матрица к матрице
. Тогда искомое решение задачи Коши
является оригиналом для
.


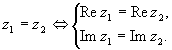
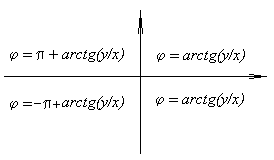
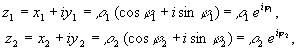
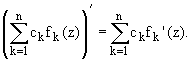
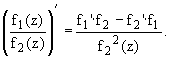
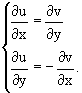
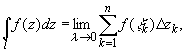
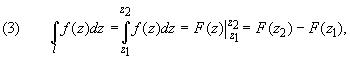
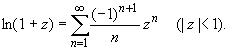
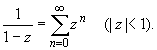
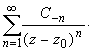
.gif)
.gif)
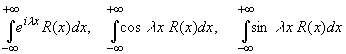
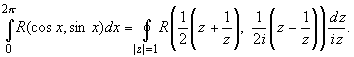
.gif)