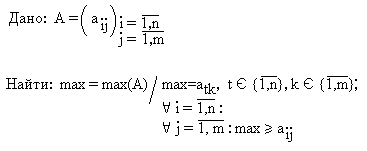Как найти индекс наибольшего значения матрицы

Matrices in MATLAB are 2-dimensional arrays that store mostly numeric data at different indices. Now, to find the indices of maximum and minimum values of a given matrix, MATLAB does not provide any direct functionality however, we can do the same by using two other functionalities. Firstly, we will find the maximum or minimum value of a given matrix and then, we will find the indices of those two values. In this scenario, MATLAB does offer simple functions to perform the former tasks. In this article, we shall see how to do the same for a magic square.

Maximum and Minimum Values in a Matrix:

The max() and min() functions find the maximum and minimum values respectively in an array, along a given dimension. The output of these commands will be a row vector(default) which will have max/min values of each column in that array/matrix. Then we can apply the max()/min() function again to find the max/min values from that 1D vector. 

Syntax:

To get row vectors with extreme values

max-row = max(matrix)

min-row = min(matrix)

To get extreme value from a given row vector of extreme values

max(max-row)

min(min-row)

Now let us see the same in action.

Maximum Value:

We will create a 5×5 magic square and find its maximum value, which should be 25.

Example 1:

Output:

Minimum Value:

Similarly, we will now find the minimum value of the same magic square, which should be 1.

Example 2:

Output:

Finding Indices of Max/Min Values in the Same Magic Square:

Now we will use the find() function to get the indices of the max/min values.

Syntax:

max-index = find(matrix==max_val)

min-index = find(matrix==min_val)

Example 3:

Output:

Finding Max/Min Values With Multiple Occurrences:

We can also find the indices of all occurrences of the max/min value of a matrix in a similar way. See the following code for understanding the same.

Example 4:

Output:

As can be seen, the minimum value 1 occurs at (1,1) and (2,1), and the maximum value 23 occurs at (2,2) and (3,2) indices. The same results are given by the above code.

Last Updated :
21 Nov, 2022

Like Article

Save Article

Замените li на Ваш список:

import random

li = [[random.randint(10, 99) for i in range(6)] for j in range(5)]

print('Список:', *li, sep='n', end='nn')

max_el = li[0][0]
max_i = (0, 0)
for i in range(len(li)):
    for j in range(len(li[i])):
        x = li[i][j]
        if x > max_el:
            max_el = x
            max_i = (i, j)

print('Максимальный элемент: {}  # {}'.format(max_i, li[max_i[0]][max_i[1]]), end='')

Один из возможных stdout:

Список:
[64, 84, 44, 77, 50, 71]
[49, 28, 99, 97, 21, 38]
[21, 89, 40, 91, 15, 17]
[97, 28, 20, 84, 34, 32]
[69, 62, 51, 31, 91, 83]

Максимальный элемент: (1, 2)  # 99

Алгоритм нахождения максимального значения в матрице

Постановка задачи

Найти
максимальное значение в двумерном
массиве вещественных чисел.

Математическая модель

Метод решения

Применяем
общий алгоритм поиска экстремального
значения: первое значение берем за
максимальное, перебираем все остальные
значения, среди которых ищем максимальное.
Если очередное значение больше
максимального, то это очередное значение
берем за максимальное.

1)
max:=A_1,1

2)

i:=1..n :

 j:=1..n
:

если
A_i,j
>
max
max:=
A_i,j

Примечание:
индексы изменяются от 1, так как иначе
пропускаются элементы матрицы. Поэтому
элемент с индексами 1, 1 сравнивается
сам с собой.

Информационная модель

Таблица 18.1.
Информационная
модель

Статус	Назначение	Имя	Тип
Вход	исходная матрица	A	TMatr
Выход	максимальное значение	max	Real
Промеж.	индексы по строкам и столбцам	i,j	Integer

Type
Tmatr=array[1..n,1..m]of real;

Const
n=3; m=4;

Программная
модель

program
poisk_max_matr;

const
n=3;

m=4;

type
TMatr=array[1..n,1..m] of real;

var
A:TMatr;

max:Real;

i,j:Integer;

begin

{построчный ввод
матрицы}

for
i:=1 to n do

begin

{ввод
i-ой строки}

for
j:=1 to m do

read(A[i,j]);

{обработка нажатия
клавиши Enter}

readln

end;

{построчный вывод
матрицы}

writeln(‘Исходная
матрица:’);

for
i:=1 to n do

begin

{вывод i-ой строки}

for j:=1 to m
do

write(A[i,j]:10:2); {одно
число занимает 10 позиций,

из них 2
позиции в дробной части}

{переход на новую
строку экрана}

writeln

end;

{реализация метода
решения — поиск максимума}

max:=A[1,1];

for
i:=1 to n do

for
j:=1 to m do

if
A[i,j]>max then max:=A[i,j];

{вывод результата}

writeln(‘Максимальное
значение=’,max:10:2)

end.

18.5. Алгоритмы сортировки

Под
сортировкой понимают упорядочение
данных в массиве по какому-либо признаку.
Обычно числовые массивы сортируются
по возрастанию или убыванию значений,
а литерные и строковые по алфавиту.
Существует огромное количество методов
сортировки. Методы отличаются друг от
друга числом перестановок при выполнении
сортировки, это число принципиально
зависит от размеров исходного массива
и от начального заполнения.

Так
как сортировка массивов используется
в различных задачах, то оформим ее в
виде библиотечных подпрограмм. При
создании библиотеки будем использовать
только 2 метода.

1-ый метод сортировки
“Выбор с перестановкой”

В
этом методе сортируется массив либо по
возрастанию, либо по убыванию значений,
результат сортировки располагается на
месте исходных данных, т.е. исходная
информация портится.

Метод
заключается в следующем:

1. формируются
   все элементы массива с первого по
   предпоследний;

2. для
   каждого формируемого места решаются
   две задачи:

а)
Ищется экстремальное значение и его
местоположение, начиная с формируемого
места до конца массива. (при сортировке
по возрастанию ищется минимальное
значение, по убыванию – максимальное)

б)
Осуществляется перестановка значения,
расположенного на формируемом месте,
с экстремальным значением.

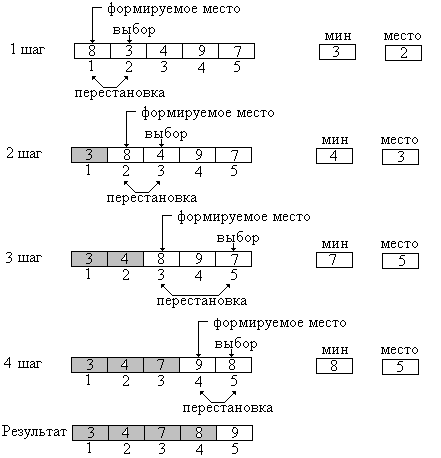
Проиллюстрируем
метод рисунком 18.10. Исходный массив
сортируется по возрастанию и состоит
из пяти целочисленных элементов: 8, 3, 4,
9, 7

Рис.
18.10. – Сортировка
выбором с перестановкой

Соседние файлы в папке Лекции по Паскалю

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

var arr = [ 1, 3, 2, 3, 6, 2 ];
var maxIndex = arr.indexOf( Math.max.apply(null, arr)); // 4, считается от 0

1. Math.max() возвращает наибольшее значение из аргументов.
2. чтобы передать массив вместо списка, используется apply()
3. получив само наибольшее значение, остаётся найти его индекс в массиве через метод массива indexOf().

Не очень эффективно, т.к. фактически массив перебирается дважды: в поиске максимума и в поиске индекса. Можно сделать за один проход, запоминая вместе с найденным максимальным значением его позицию:

var arr = [ 1, 3, 2, 3, 6, 2 ];

function index_max(arr) {
  var i, maxV, maxP;
  for( i = 0; i < arr.length; i++) {
    if( typeof maxV === "undefined" || arr[i] > maxV ) {
      maxV = arr[i];
      maxP = i;
    }
  }
  
  return maxP;
}

index_max(arr) // 4