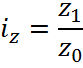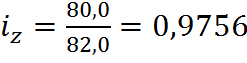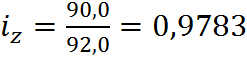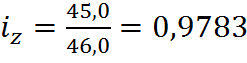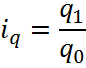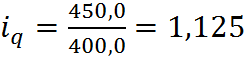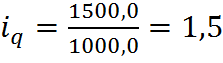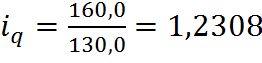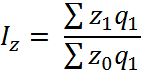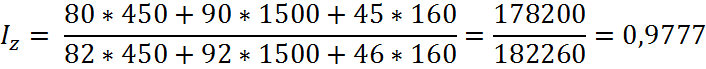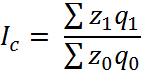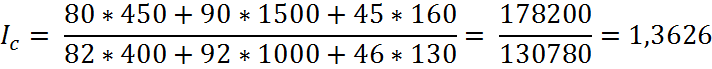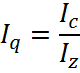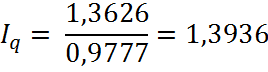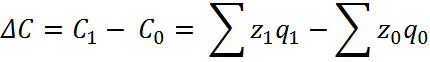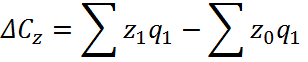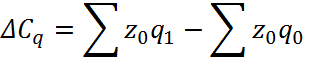Индексный
метод — один из самых распространенных методов статистического анализа
экономических явлений. С помощью индексов изучаются народное хозяйство в целом
и его отдельные отрасли, а также деятельность предприятий, объединений, фирм,
хозяйств и др.; выявляется динамика развития социально-экономических явлений,
анализируется выполнение планов или норм; определяется влияние отдельных
факторов на общий результат, вскрываются резервы производства; проводятся
территориальные и международные сопоставления экономических показателей.
Индексом
в статистике называется относительный показатель, характеризующий соотношение
во времени, по сравнению с планом или в пространстве уровней социально-экономических
явлений. Так как индекс — относительный показатель, то он всегда получается при
соотношении двух величии: отчетной (или текущей), т. е. сравниваемой, и
базисной, т. е. той, с уровнем которой сравнивается отчетная величина. Если за
базу сравнения берется уровень явления за какой-то прошлый период времени,
получают динамические индексы; если за базу сравнения берется уровень явления
на другой территории, получают территориальные индексы, а если за базу
сравнения берется какой-либо нормативный уровень, получают индексы выполнения
плана, индексы выполнения норм и т. д.
В
формулах, системах уравнений, экономико-математических моделях текущие данные
помечаются единицей, стоящей чуть ниже буквенного обозначения величины.
Как
и всякая относительная величина, индексы выражаются в виде коэффициентов, если
за основание принимается единица, или в виде процентов, если за основание
принимается сто.
Социально-экономические
явления, изучаемые статистикой, обычно состоят из многих элементов. Так,
валовой выпуск продуктов и услуг включает стоимость конечных товаров и услуг,
созданных всеми общественно организованными видами экономической деятельности и
во всех отраслях экономики. Другими словами, валовой выпуск продуктов и услуг
состоит из многих отдельных видов продуктов и услуг.
Индексы
рассчитываются как для отдельных элементов сложного явления, так и для всего
сложного явления в целом. В первом случае они называются индивидуальными и
обозначаются латинской буквой
, а во второй —
общими и обозначаются
. К индивидуальным
индексам относятся индексы, характеризующие изменение выпуска одного
какого-либо вида продукции (индексы выплавки стали, добычи калийных удобрений,
производства телевизоров и др.), индексы, характеризующие изменение цены
какого-либо товара (велосипедов, цемента, говядины и др.), себестоимости
отдельного изделия и т.д.
К
индексам, исчисленным для всего сложного явления, то есть к общим, относятся
индексы, характеризующие динамику выпуска всей продукции предприятия, отрасли и
др., динамику цен группы товаров, или всех товаров, или набора
продовольственных и непродовольственных товаров и услуг, входящих в «потребительскую
корзинку», динамику себестоимости ряда изделий и т. д.
Общие
индексы используются для сопоставления непосредственно несоизмеримых,
разнородных явлений. Например, с помощью общих индексов можно охарактеризовать
динамику выпуска продукции всей промышленности или динамику объемов всей
выпускаемой продукции на мебельной фабрике, изготавливающей различные виды
продукции: столы, кресла, диваны, шкафы. Однако нельзя просто сложить объемы
продукции различных видов за два периода и отнести эти суммы одну к другой.
Такое суммирование бессмысленно не только из-за различных единиц измерения
(тонны, штуки, метры и др.), но также из-за того, что каждый вид продукции
имеет свое назначение и произведен с разными затратами средств и общественно
необходимого времени.
Чтобы
сделать сопоставимыми несоизмеримые явления (или их элементы), нужно выразить
их общей мерой; стоимостью, трудовыми затратами и т. д. Эта задача решается
построением и расчетом общих индексов. Основной формой общих индексов являются
агрегатные индексы.
Агрегатный
индекс состоит из двух элементов: индексируемых величин, изменение которых
должен отразить индекс, и показателей, которые служат соизмерителями (весами).
Произведение
каждой индексируемой величины на соизмеритель (вес) должно давать определенную
экономическую категорию.
Значение
индексируемой величины всегда изменяется: отчетное значение сопоставляется с
базисным. Конкретное название индекса дается всегда по индексируемой величине.
Например, если индексируется цена, то получают индекс цен, если индексируется физический объем,
получают индекс физического объема и т. д.
Показатель-соизмеритель
(вес) выполняет функцию веса по отношению к индексируемой величине. Значение
соизмерителя (веса) в конкретном индексе принимается одинаковым в числителе и
знаменателе, чтобы исключить влияние соизмерителя на изменение индексируемого
показателя. Веса индексов могут быть выражены в стоимостных, трудовых и других
единицах измерения, а также в виде относительных величин структуры. При
построении агрегатных индексов важно правильно выбрать веса индексов. Они
должны выбираться с учетом сущности исследуемого социально-экономического
явления, чтобы сохранить экономический смысл индекса и получить возможность на
его основе исчислять абсолютные суммы экономического эффекта.
В
зависимости от содержания и характера индексируемой величины различают индексы
количественных (объемных) показателей и индексы качественных показателей.
Количественные (экстенсивные) показатели характеризуют общий, суммарный размер
того или иного явления, например, количество (физический объем) продукции в
натуральном выражении, численность работников, общие затраты времени на
произведенную продукцию, размер посевной площади и т. д. Качественные
(интенсивные) показатели характеризуют размер признака в расчете на единицу
совокупности: цена единицы продукции (товара), себестоимость единицы продукции,
затраты рабочего времени па единицу продукции (трудоемкость единицы продукции),
выработка продукции на одного работающего, расход материала (топлива) на
единицу продукции, урожайность культуры в расчете на один гектар и т. п. Как
правило, качественные показатели представляют собой либо средние значения, либо
относительные величины.
Существует
правило построения агрегатных факторных индексов, в соответствии с которым в
индексах качественных показателей весами выступают показатели отчетного
периода, а в индексах количественных показателей — базисного периода.
Соответствующие
количественные (объемные) и качественные показатели тесно связаны друг с другом.
В общем виде эта взаимосвязь выражается в том, что произведение качественного
показателя на связанный с ним количественный показатель дает новый показатель,
другую экономическую категорию. Например, если перемножить цену одного изделия
(
, качественный
показатель) на количество этих изделий (
, количественный
показатель), то получим общую стоимость данных изделий или товарооборот (
, новый
показатель); произведение удельного расхода материала
на количество единиц продукции
представляет собой
общий расход материала (
, новый
показатель); произведение урожайности культуры на ее посевную площадь дает
валовой сбор этой культуры (новый показатель) и т. д. Эта взаимосвязь между
количественными и качественными показателями справедлива при построении и
исчислении их агрегатных индексов.
Например,
произведение агрегатного индекса цен
на агрегатный индекс физического объема
равно агрегатному индексу стоимости продукции
(товарооборота)
.
Агрегатный
индекс цен
определяется по формуле:
Агрегатный
индекс цен характеризует, как изменились в среднем цены на различные виды
продукции, включенные в расчет общего индекса цен.
Агрегатный
индекс физического объема
характеризует, как изменился в среднем общий
объем продукции по анализируемому перечню. Он определяется по формуле:
Индекс
стоимости продукции (товарооборота) определяется по формуле:
Индекс
стоимости продукции характеризует изменение фактической стоимости произведенной
или реализованной продукции или же размера товарооборота по анализируемой
совокупности.
Взаимосвязь
индексов может быть представлена выражением:
Используя
эти формулы, можно по двум известным индексам определить третий.
Агрегатный
индекс является основной, но не единственной формой общего индекса. Общий
индекс может быть исчислен и как средняя величина индивидуальных индексов. Эта
средняя может быть рассчитана как средняя арифметическая и как средпяя
гармоническая. Как одна, так и другая средняя выводятся из агрегатных индексов
и дают результаты, тождественные этим индексам. Выбор формы индекса зависит от
характера исходных данных. Если известны значения индексируемого показателя и
веса в отчетном (текущем) и базисном периодах, то пользуются агрегатной формой
индексов. Если отсутствуют значения индексируемого показателя или веса в
отчетном или базисном периодах, по известны изменения индексируемого показателя
или веса по отдельным единицам изучаемой совокупности, то пользуются формой
средних индексов.
При сравнении уровней
средних величин отчетного и базисного периодов получают индекс, который в
статистике называют индексом переменного состава. Так, например, индекс
себестоимости переменного состава исчисляется по формуле:
На индекс переменного
состава (динамику средних величин) оказывают влияние два фактора: во-первых,
изменение уровней осредняемого признака (в нашем
примере изменение уровней себестоимости продукции по каждому из предприятий) и,
во-вторых, изменение долей единиц совокупности с различными значениями признака
(структурные сдвиги).
Индекс переменного состава
вычисляют и по такой формуле:
где
Индекс себестоимости
постоянного фиксированного состава рассчитывают по формуле:
или
Индекс
структурных сдвигов исчисляют по формуле:
или
Взаимосвязь индексов:
Вычитая из числителя
каждого из индексов приведенной системы знаменатель, получим разложение
абсолютного изменения (прироста) среднего уровня признака за счет
непосредственного изменения уровней осредняемого
признака (индивидуальных уровней себестоимости), так и за счет изменения
удельных весов (структурных сдвигов):
Задача 1
Динамика средних цен и
объема продажи на колхозных рынках города характеризуется следующими данными:
| Продукция | Продано продукции, тыс. кг | Средняя цена за 1 кг, тыс. р. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Колхозный рынок №1 | ||||
| Картофель | 4.0 | 4.2 | 6.4 | 7.6 |
| Капуста | 2.5 | 2.4 | 7.2 | 8.4 |
| Колхозный рынок №2 | ||||
| Картофель | 10.0 | 12.0 | 7.6 | 7.0 |
На основании имеющихся данных вычислите:
- Для колхозного рынка №1 (по двум видам продукции):
- а) индивидуальные индексы цен, физического объема и стоимости;
- б) общий индекс товарооборота;
- в) общий индекс цен;
- г) общий индекс физического объема товарооборота;
- Определите в отчетном периоде абсолютный прирост товарооборота и разложите по
факторам ( за счет изменения цен и объема продаж товаров). - Покажите взаимосвязь между исчисленными индексами.
- Для колхозных рынков вместе (по картофелю):
- а) индекс цен переменного состава
- б) индекс цен постоянного состава
- в) индекс влияния изменения структуры объема продаж картофеля на динамику средней цены
- Объясните разницу между величинами индексов постоянного и переменного состава.
- Определите общее абсолютное изменение средней цены картофеля в отчетном периоде
по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней
цен и за счет изменения структуры продаж картофеля. - Сформулируйте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Вычисление индивидуальных индексов товарооборота, цен и физического объема
Вычислим индивидуальные индексы цен:
Картофель:
Капуста:
Цены на картофель увеличились на 18,8%, а на капусту на 16,7%
Вычислим индивидуальные индексы физического объема:
Картофель:
Капуста:
Физический объем продаж картофеля увеличился на 5%, а физический
объем продаж капусты снизился на 4%.
Вычислим индивидуальные индексы стоимости продаж:
Картофель:
Капуста:
Стоимость продаж картофеля увеличилась на 24,7%, а капусты на 12%.
Вычисление общих индексов товарооборота, цен и физического объема
Общий индекс товарооборота можно вычислить по формуле:
где
— цена,
-количество проданной продукции
Общий индекс цен вычисляем по формуле:
Общий индекс физического объема
товарооборота:
Эти индексы связаны между собой формулой:
Таким образом, товарооборот увеличился на 19,4%, в том числе за счет
увеличения цен на 17,9%, за счет увеличения физического объема товарооборота на
1,3%
Разложение на факторы абсолютного прироста товарооборота
Абсолютный прирост товарооборота:
В том числе за счет изменения цены:
В том числе за счет изменения продажи товаров:
Абсолютные приросты связаны между собой формулами:
Таким образом, товарооборот
увеличился на 8,48 млн.р., в том числе за счет увеличения цен на 7,92 млн.р.,
за счет увеличения физического объема товарооборота на 0,56 млн.р.
Вычисление индесов средней цены переменного состава, постоянного состава и структурных сдвигов
Вычислим для 2-х колхозных
рынков по картофелю индекс цен переменного состава:
Вычислим индекс цен постоянного состава:
Вычислим индекс влияния изменения структуры объема продаж картофеля на
динамику средней цены:
Разница между индексами
переменного и постоянного состава заключается в том, что индекс переменного
состава равен соотношению средних уровней
цены, а постоянного характеризует изменение средней
цены за счет изменения только цен на каждом рынке.
Таким образом, средняя цена на рынках уменьшилась на 1.4%. Если бы на
обоих рынках структура продаж была одна и та же, средняя цена бы уменьшилась на 1.9% Увеличение доли более дорогого рынка в
структуре продаж увеличило среднюю цену на 0,4%.
Разложение на факторы абсолютного прироста средней цены
Определим общее абсолютное изменение цены картофеля:
Общее абсолютное изменение
цены за непосредственного изменения уровней цен картофеля:
Общее абсолютное изменение цены за счет изменения структуры продажи
картофеля:
Таким образом, средняя цена на
картофель снизилась на 0,11 тыс.р., в том числе за счет непосредственного
изменения уровней цен на 0,14 тыс.р. Увеличение доли рынка с более дорогим
картофелем увеличило результативный показатель на 0,03 тыс.р.
Задача 3
Имеются
следующие данные о выпуске одноименной продукции по трем цехам предприятия:
| Цех |
Произведено продукции, тыс.шт. |
Себестоимость производства единицы продукции, руб. |
||
| базисный период | отчетный период | базисный период | отчетный период | |
| 1 | 86 | 56 | 34.0 | 39.0 |
| 2 | 152 | 146 | 52.0 | 56.0 |
| 3 | 134 | 132 | 48.0 | 46.0 |
Определите:
- Индексы себестоимости переменного состава, постоянного состава и индекс
структурных сдвигов. - Абсолютное изменение средней себестоимости производства единицы продукции в
отчетном периоде по сравнению с базисным: а) общее; б) за счет изменения
себестоимости производства единицы продукции в отдельных цехах; в) за счет
изменения структуры произведенной продукции. - Установите
и проверьте взаимосвязи: а) между рассчитанными индексами; б) между
рассчитанными абсолютными изменениями. Поясните, в чем состоит структурный
сдвиг в производстве продукции в отчетном периоде по сравнению с базисным. - Сделайте
выводы.
Решение
Индексы себестоимости постоянного и переменного состава
Вычислим индекс себестоимости
переменного состава:
Вычислим индекс себестоимости постоянного состава:
Таким образом, средняя себестоимость в отчетном периоде увеличилась на
6%, при условии одинаковой структуры производства в цехах, себестоимость
увеличилась на 3,8%.
Индекс структурных сдвигов
Вычислим индекс влияния изменения структуры производства продукции на
динамику средней себестоимости:
Разница между индексами
переменного и постоянного состава заключается в том, что индекс переменного
состава равен соотношению средних уровней
себестоимости, а постоянного
характеризует изменение средней себестоимости за счет изменения только
себестоимости в каждом цеху. Структурный сдвиг состоит в изменение доли цехов с
более высокой (более низкой) себестоимостью.
Взаимосвязь между рассчитанными индексами будет следующая:
Индексы средней себестоимости в разностной форме
Определим общее абсолютное изменение себестоимости:
Общее абсолютное изменение
себестоимости за счет
непосредственного изменения уровня
себестоимости:
Общее абсолютное изменение себестоимости за счет изменения структуры
производства продукции:
Проверка:
Вывод к задаче
Средняя себестоимость изделия в отчетном периоде увеличилась на 2,8
руб., в том числе за счет изменения уровня себестоимости на 1,8 руб.,
увеличение доли продукции с более высокой себестоимостью увеличило
результативный показатель на 1 руб.
Индексы себестоимости переменного состава, постоянного (фиксированного) состава, структурных сдвигов
Имеются следующие данные о производстве однородной продукции по двум заводам:
Таблица– Показатели производства продукции и ее себестоимости
|
Завод |
Выработано продукции «А», тыс. шт. |
Себестоимость единицы продукции, руб. |
||
|
2001 г., q0 |
2002 г., q1 |
2001 г. z0 |
2002 г., z1 |
|
|
1 |
12 |
20 |
148,2 |
160,5 |
|
2 |
16 |
17 |
80,5 |
68,0 |
|
Сумма |
28 |
37 |
Вычислить: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов;
Покажите взаимосвязь исчисленных индексов. Поясните полученные результаты.
1) Индекс себестоимости переменного состава определяется по формуле
2) Индекс себестоимости постоянного (фиксированного) состава определяется по формуле
3) Индекс структурных сдвигов определяется по формуле
|
Завод |
Вспомогательные расчеты |
||
|
z0q1 |
z1q1 |
z0q0 |
|
|
1 |
2964 |
3210 |
1778,4 |
|
2 |
1368,5 |
1156 |
1288 |
|
Сумма |
4332,5 |
4366 |
3066,4 |
Покажем взаимосвязь исчисленных индексов
1,077 = 1,0077*1,069 — равенство выполняется
Решение другие задач по статистике смотрите тут.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Определение индивидуальных индексов себестоимости и физического объема продукции. Определение общего индекса себестоимости ед. продукции. Определение индекса себестоимости переменного и постоянного составов
Страницы работы
Содержание работы
Задача 3.
Имеются следующие данные по предприятию:
|
Вид |
Количество |
Себестоимость |
||
|
Базисный |
Отчетный |
Базисный |
Отчетный |
|
|
А |
400 |
450 |
82,0 |
80,0 |
|
Б |
1000 |
1500 |
92,0 |
90,0 |
|
В |
130 |
160 |
46,0 |
45,0 |
Определить:
1)
индивидуальные
индексы себестоимости и физического объема продукции;
2)
общий
индекс себестоимости ед. продукции;
3)
общий
индекс затрат на производство продукции;
4)
выполните
факторный анализ;
5)
используя
взаимосвязь индексов, определите индекс физического объема продукции.
Решение.
z –
себестоимость единицы продукции
q – объем
производства
c – затраты.
|
Вид |
Количество |
Себестоимость |
||
|
q0 |
q1 |
z0 |
z1 |
|
|
А |
400 |
450 |
82,0 |
80,0 |
|
Б |
1000 |
1500 |
92,0 |
90,0 |
|
В |
130 |
160 |
46,0 |
45,0 |
1)
Индивидуальный
индекс себестоимости:
Для товара А:
Для товара Б:
Для товара В:
Индивидуальный
индекс физического объема продукции:
Для товара А:
Для товара Б:
Для товара В:
2)
общий индекс себестоимости продукции:
3)
общий индекс затрат на производство продукции:
4)
взаимосвязь между исчисленными индексами:
Общий индекс физического объема производства продукции составит:
5)
Факторный анализ влияния себестоимости и объема выпуска на
изменение общих затрат на производство.
Выводы: в отчетном
периоде по сравнению с базовым увеличился объем выпуска продукции (объем выпуска
товара А повысился на 12,5%; объем выпуска товара Б – на 50%; объем выпуска товара В – на 23,1%); произошло
снижение себестоимости единицы продукции (для товара А себестоимость единицы
товара снизилась на 2,44%; для товара Б – 2,17%; для товара В – 2,17%). Общий
уровень затрат на производство продукции вырос на 36,26%, увеличился объем
выпуска (на 39,36%), себестоимость снизилась на 2,23%. Общее увеличение затрат
составило 47420 тыс. руб., что было обусловлено увеличением объема выпуска.
Задача 4.
Динамика
себестоимости и объема продукции А на двух предприятиях характеризуется
следующими данными:
|
№ предпр. |
Себестоимость тыс. руб. |
Выработано продукции, |
||
|
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
|
|
1 |
120 |
100 |
2,0 |
2,0 |
|
2 |
200 |
180 |
4,0 |
6,0 |
Определить:
1) индекс
себестоимости переменного состава;
2) индекс
себестоимости постоянного состава;
3) индекс структурных
сдвигов;
4) изменение
средней себестоимости (в абсолютных величинах) в целом и за счет действия
отдельных факторов;
5) покажите
взаимосвязь индексов.
Решение.
|
№ предпр. |
Себестоимость тыс. руб. |
Выработано |
Показатель структуры |
|||
|
z0 |
z1 |
q0 |
q1 |
d0 |
d1 |
|
|
1 |
120 |
100 |
2,0 |
2,0 |
0,33 |
0,25 |
|
2 |
200 |
180 |
4,0 |
6,0 |
0,67 |
0,75 |
|
Итого: |
6,0 |
8,0 |
1 |
1 |
Показатель структуры
рассчитывается следующим образом:
1) индекс
себестоимости переменного состава:
2) индекс
себестоимости постоянного состава:
3) индекс структурных
сдвигов
4) Факторный
анализ.
Изменение
средней себестоимости в целом:
Изменение
средней себестоимости за счет снижения себестоимости на отдельных
предприятиях:
Изменение
средней себестоимости за счет структурных сдвигов в составе
продукции каждого предприятия:
5)
взаимосвязь индексов:
Выводы: в текущем периоде по сравнению с
базисным средняя себестоимость снизилась на 7,69%. Снижение средней
себестоимости из-за снижения себестоимости на отдельных предприятиях составило 11,11%.
Повышение средней себестоимости из-за структурных сдвигов в составе
продукции каждого предприятия составило 3,85%.
Похожие материалы
- Сводка и группировка, средние величины, показатели вариации. Индексы
- Сводка и группировка, средние величины, показатели вариации. Ряды динамики. Индексы
- Статистика продукции. Статистика издержек. Статистика основных фондов и материальных оборотных средств. Статистика трудовых ресурсов и использования рабочего времени
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
В
качестве примера рассмотрим индекс
себестоимости.
Предположим,
что определенный вид продукции
производится на нескольких предприятиях.
Если обозначить себестоимость единицы
продукции через с
(раньше обозначали через х),
а выпуск продукции отдельных предприятий
как веса через q
(раньше – f),
можно записать формулы индексов
себестоимости.
Индекс
себестоимости переменного состава:
=
=
:
.
(25)
Индекс
себестоимости фиксированного состава:
=
:
,
т.е. (25,а)
=
.
(25,б)
Индекс
структурных сдвигов себестоимости:
=
:
.
(26)
Пример.
Имеются данные о выпуске и себестоимости
одноименного продукта по трем предприятиям
(табл. 4). Требуется определить изменение
себестоимости единицы продукции на
каждом предприятии, а также в целом по
всем предприятиям с помощью индексов:
а) переменного состава, б) фиксированного
состава, в) структурных сдвигов.
Таблица
11.4
|
Номер предприятия |
Базисный |
Отчетный |
||||
|
Выпуск |
Себестоимость |
Выпуск |
Себестоимость |
|||
|
тыс. единиц |
в |
тыс. |
в |
|||
|
1 |
10 |
0,50 |
15 |
10 |
0,40 |
14,2 |
|
2 |
6 |
0,30 |
13 |
7 |
0,28 |
12,5 |
|
3 |
4 |
0,20 |
10 |
8 |
0,32 |
9,5 |
|
|
20 |
1,00 |
( |
25 |
1,00 |
( |
1)
Расчет
индивидуальных
индексов
себестоимости продукции по каждому
предприятию дает следующие результаты:
По
1-му предприятию
= 0,947 (или 94,7%);
По
2-му предприятию
= 0,961 (или 96,1%);
По
3-му предприятию
= 0,95 (или 95%);
2)
Для расчета
индекса
себестоимости переменного состава
рассчитаем:
а)
среднюю себестоимость в базисном
периоде:
руб.;
а)
среднюю себестоимость в отчетном
периоде:
руб.,
тогда
по формуле (11.23)
=
,
т.о.=
= 12,22 : 13,4 = 0,912 (или 91,2%),
т.е.
средняя себестоимость единицы продукции
снизилась
на 8,8%.
Пояснения.
-
Если
бы продукции по отдельным предприятиям
оставался без
изменения
или изменился всюду пропорционально,
т.е. если удельный вес каждого предприятия
в выпуске продукции оставался неизменным,
то тогда, очевидно, снижение средней
себестоимости на 8,8% можно было бы
объяснить только снижением себестоимости
на каждом предприятии. Фактически же
в рассматриваемом примере менялась не
только себестоимость на каждом
предприятии, но и удельный вес каждого
предприятия в общем выпуске продукции.
Следовательно, снижение
средней себестоимости на 8,8% достигнуто
за счет изменения двух факторов (с
и q). -
В
примере общий индекс переменного
состава меньше, чем каждый из индивидуальных
индексов, т.е. снижение средней
себестоимости (8,8%) оказалось больше,
чем снижение себестоимости на отдельных
предприятиях (5,3: 3,9 и 5%), Очевидно, что
это можно объяснить изменением структуры
выпуска, в частности увеличением доли
3-го предприятия, имеющего самую низкую
себестоимость.
3)
Чтобы исключить влияние изменения
структуры совокупности на динамику
средних величин, рассчитаем индекс
себестоимости фиксированного состава
по формуле (25,а) (приняв в качестве
фиксированной
структуру выпуска отчетного периода
):
=
:
= 1,22 :
= = 1,22 : 1,84 – 0,952 (или 95,2%).
Пояснение.
-
,
характеризуя среднее изменение
себестоимости на всех
трех
предприятиях, не может выходить за
пределы значений
(см. замечание 3), т.е для данного примера
не может быть меньше 94,1% и не может быть
больше 96,1%, что и подтверждается.
(Вычислите
по (25,б) и сопоставьте результаты.)
4)
Влияние структурного фактора отразим
с помощью индекса
структурных сдвигов
(см. 26):
=
:
= 12,8 : 13,4 = 0,958 = 0,958 (или 98,8%).
Пояснение.
-
Данный
результат означает, что на 4,2% (95,8-100)
средняя себестоимость снизилась за
счет структурного фактора, в частности,
за счет увеличения
доли продукции на 3-м предприятии
с более низкой себестоимостью и за счет
уменьшения
доли выпуска на 1-м предприятии
с более высокой себестоимостью.
(Вычислите
по (24) и сопоставьте результаты.)
5)
Значения
,
и
можно получить, используя в качестве
весовдоли
по предприятиям
d
(см. графы 3 и 6 в табл. 4) вместо q,
т.е.
=
;
=
;
=
.
Вычислите
по этим формулам
,
и сопоставьте результаты.
Индексы переменного, постоянного состава и структурных сдвигов являются
общими индексами. Они показывают изменение среднего значения индексируемого
показателя.
Приведены формулы
для расчета индексов:
Средней себестоимости
Средней цены
Средней
производительности труда
Средней заработной
платы
Средней фондоотдачи
Изменение средней себестоимости.
1)
индекс себестоимости переменного состава
–объем производства продукции в отчетном и базисном
периодах, соответственно
– себестоимость продукции в отчетном и базисном
периодах, соответственно.
С помощью индекса переменного состава находится общее
изменение средней себестоимости
2)
индекс себестоимости постоянного состава
С помощью индекса постоянного состава находится изменение
средней себестоимости за счет изменения себестоимости в каждой из групп.
3)
индекс структурных сдвигов.
С помощью индекса структурных сдвигов находится изменение
средней себестоимости за счет изменения структуры производства.
Общее абсолютное изменение средней себестоимости
Изменение себестоимости за счет изменения себестоимости
За счет изменения структуры производства
Индексы
средней цены
Индекс цен
переменного состава
– цена продукции в отчетном и базисном периодах,
соответственно
– количество продукции в отчетном и базисном периодах,
соответственно
Индекс цен
постоянного состава
Индекс структурных сдвигов
Абсолютное изменение средней цены

В том числе за счет изменения цен

За счет изменения структуры продаж
Пример:
Динамика себестоимости и объема
производства продукции заводов характеризуется следующими данными:
|
Продукция |
Выработано продукции, тыс. ед. |
Себестоимость единицы продукции, |
|||
|
базисный период |
отчетный период |
базисный период |
отчетный период |
||
|
Завод №1 |
|||||
|
КТ-5 |
26 |
28 |
4,0 |
4,4 |
|
|
БЛ-20 |
12 |
14 |
5,5 |
5,8 |
|
|
Завод №2 |
|||||
|
КТ-5 |
30 |
35 |
5,2 |
5,6 |
На основании имеющихся данных
вычислите:
Для двух заводов вместе (по продукции КТ-5):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства
продукции на динамику средней себестоимости.
Объясните различие между полученными
величинами индексов постоянного и переменного состава.
Определите общее
абсолютное изменение средней себестоимости единицы продукции в отчетном периоде
по сравнению с базисным и разложите его по факторам: за счет непосредственного
изменения себестоимости единицы продукции и изменения структуры производства. Сформулируйте выводы.
Решение.
для обоих
заводов (по продукции КТ-5)
а) индекс
себестоимости переменного состава
–объем производства продукции в отчетном и базисном
периодах, соответственно
– себестоимость продукции в отчетном и базисном
периодах, соответственно.
б) индекс
себестоимости постоянного состава
В) индекс структурных сдвигов
Индекс
постоянного состава показывает изменение средней стоимости товара в зависимости
от уровня стоимости товара, а индекс же переменного состава также учитывает
изменение и изменение структуры продаж.
Общее
абсолютное изменение средней цены
Δ=

В том числе
за счет изменения уровня себестоимости
Δz=

За счет
изменения структуры производства
Δстр=

В отчетном
периоде по сравнению с базисным затраты на производство выросли на 34,4 млрд. руб. или на 20,2%, в
том числе за счет изменения себестоимости на 15,4 млрд. руб. или на 8,1%, за
счет изменения физического объема производства увеличилась на 19 млрд. руб. или
на 11,2%.
Средняя себестоимость продукции КТ-5 в отчетном периоде выросла по
сравнению с базисным на 0,393 млн. руб. или на 8,8% и составила 4,867 млн. руб., рост
себестоимости за счет изменения уровня себестоимости на двух заводах составил
0,367 млн. руб. или на 8,2%, за счет изменения структуры производства средняя
себестоимость КТ-5 выросла на 0,026 млн. руб. или на 0,6%