Как найти индуцированную в проводнике эдс

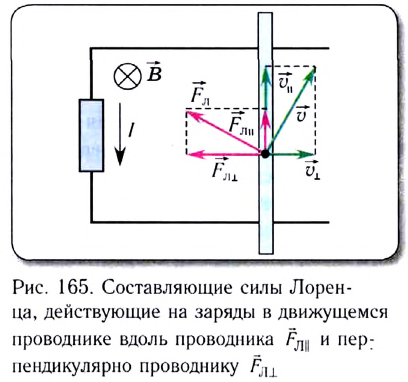
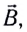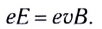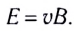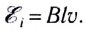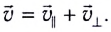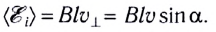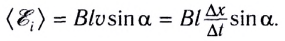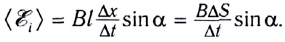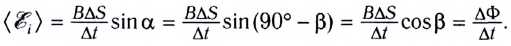ЭДС индукции в движущихся проводниках

ЭДС – это аббревиатура трех слов: электродвижущая сила. ЭДС индукции () появляется в проводящем теле, которое находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.

Закон Фарадея для электромагнитной индукции

Основным законом, который используют при расчетах, связанных с электромагнитной индукцией является закон Фарадея. Он говорит о том, что электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока () сквозь поверхность, которую ограничивает рассматриваемый контур:

   

Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Если изменение потока происходит равномерно, то ЭДС индукции находят как:

   

Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.

ЭДС индукции в движущемся проводнике

Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, результирующая ЭДС, появляющаяся в контуре будет равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.

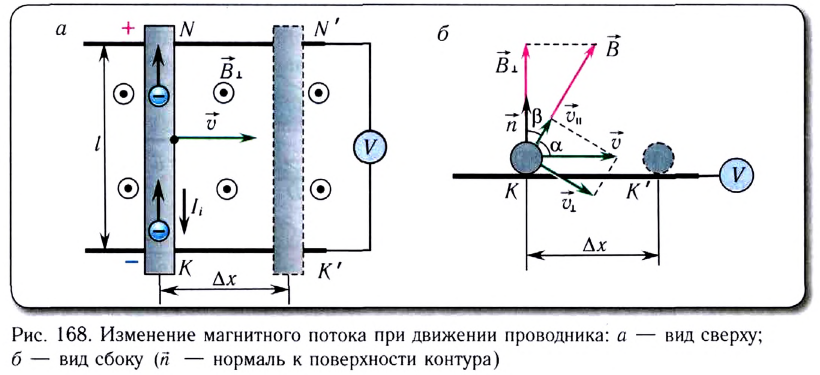
Рассмотри случай, когда в однородном магнитном поле находится прямоугольная проводящая рамка (рис.1). Одна сторона рамки может двигаться. Длина этой стороны равна l. Это и будет наш движущийся проводник. Определим, как можно вычислить ЭДС индукции, в нашем проводнике, если он перемещается со скоростью v. Величина индукции магнитного поля равна B. Плоскость рамки перпендикулярна вектору магнитной индукции. Выполняется условие .

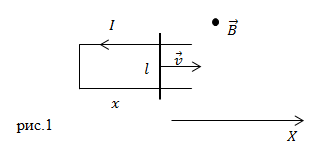
ЭДС индукции в рассматриваемом нами контуре будет равна ЭДС, которая возникает только в подвижной его части. В стационарных частях контура в постоянном магнитном поле индукции нет.

Для нахождения ЭДС индукции в рамке воспользуемся основным законом (1). Но для начала определимся с магнитным потоком. По определению поток магнитной индукции равен:

   

где , так как по условию плоскость рамки перпендикулярна направлению вектора индукции поля, следовательно, нормаль к рамке и вектор индукции параллельны. Площадь, которую ограничивает рамка, выразим следующим образом:

   

где – расстояние, на которое перемещается движущийся проводник. Подставим выражение (2), с учетом (3) в закон Фарадея, получим:

   

где v – скорость движения подвижной стороны рамки по оси X.

Если угол между направлением вектора магнитной индукции () и вектором скорости движения проводника () составляет угол , то модуль ЭДС в проводнике можно вычислить при помощи формулы:

   

Примеры решения задач

В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.

Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.

Магнитный поток

Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.

При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.

ЭДС индукции

Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.

Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.

Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.

Законы Фарадея и Ленца

Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.

Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.

Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.

Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:

Е = — dФ/dt.

Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.

Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.

Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.

Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.

Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.

Движение провода в магнитном поле

Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.

Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.

Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.

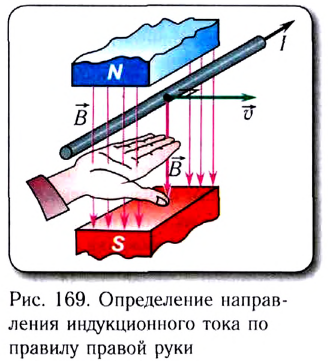
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.

Вращающаяся катушка

Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).

Согласно формуле, на Ф воздействуют изменения в ситуациях:

• при изменении магнитного потока меняется вектор направления;
• изменяется площадь, заключенная в контур;
• меняется угол.

Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.

На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.

ЭДС самоиндукции

При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.

В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:

Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.

Взаимоиндукция

При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.

Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.

Значение взаимоиндуктивности второй катушки в отношении первой:

М21 = (N2 x F21)/I1.

Значение магнитного потока:

Ф21 = (М21/N2) x I1.

Индуцированная ЭДС вычисляется по формуле:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt.

В первой катушке значение индуцируемой ЭДС:

Е1 = — M12 x dI2/dt.

Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.

Тогда взаимоиндуктивность считается равной:

М12 = М21 = М.

Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.

Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.

Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.

---

According to principle of electromagnetic induction, when the magnetic flux linking to a conductor or coil changes, an EMF is induced in the conductor or coil. In practice, the following two ways are used to bring the change in the magnetic flux linkage.

Method 1 − Conductor is moving in a stationary magnetic field

We can move a conductor or coil in a stationary magnetic field in such a way that the magnetic flux linking to the conductor or coil changes in magnitude. Consequently, an EMF is induced in the conductor. This induced EMF is known as dynamically induced EMF. It is so called because the EMF induced in a conductor which is in motion. Example of dynamically induced EMF is the EMF generated in the AC and DC generators.

Method 2 − A stationary conductor is placed in a changing magnetic field

When a stationary conductor or coil is placed in a moving or changing magnetic field, an EMF is induced in the conductor or coil. The EMF induced in this way is known as statically induced EMF. It is so called because the EMF is induced in a conductor which is stationary. The EMF induced in a transformer is an example of statically induced EMF.

Therefore, from the discussion, it is clear that the induced EMF can be classified into two major types namely,

• Dynamically Induced EMF

• Statically Induced EMF

Dynamically Induced EMF

As discussed in the above section that the dynamically induced EMF is one which induced in a moving conductor or coil placed in a stationary magnetic field. The expression for the dynamically induced EMF can be derived as follows −

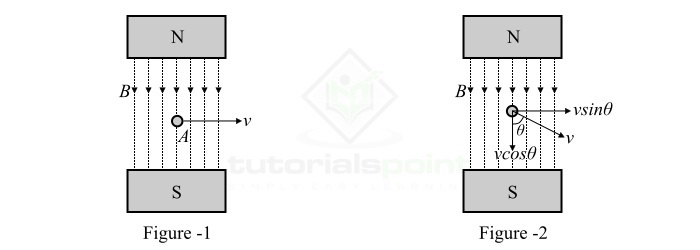
Consider a single conductor of length l meters located in a uniform magnetic field of magnetic flux density B Wb/m² as shown in Figure-1. This conductor is moving at right angles relative to the magnetic field with a velocity of v m/s.

Now, if the conductor moves through a small distance dx in time dt seconds, then the area swept by the conductor is given by,

$$mathrm{mathit{A:=:ltimes dx:}mathrm{m^{mathrm{2}}}}$$

Therefore, the magnetic flux cut by the conductor is given by,

$$mathrm{mathit{dphi }:=:mathrm{Flux:densitytimes Area: swept}}$$

$$mathrm{Rightarrow mathit{dphi }:=:mathit{Btimes ltimes dx}:mathrm{Wb}}$$

According to Faraday’s law of electromagnetic induction, the EMF induced in the conductor is given by,

$$mathrm{mathit{e}:=:mathit{N}frac{mathit{dphi }}{mathit{dt}}:=:mathit{N}frac{mathit{Bldx}}{mathit{dt}}}$$

Since, we have taken only a single conductor, thus N = 1.

$$mathrm{mathit{e}:=:mathit{Blv}:mathrm{volts}cdot cdot cdot (1)}$$

Where, v = dx/dt, velocity of the conductor in the magnetic field.

If there is angular motion of the conductor in the magnetic field and the conductor moves at an angle θ relative to the magnetic field as shown in Figure-2. Then, the velocity at which the conductor moves across the magnetic field is equal to «vsinθ». Thus, the induced EMF is given by,

$$mathrm{mathit{e}:=:mathit{B:l:v}:mathrm{sinmathit{theta }}:mathrm{volts}cdot cdot cdot (2)}$$

Statically Induced EMF

When a stationary conductor is placed in a changing magnetic field, the induced EMF in the conductor is known as statically induced EMF. The statically induced EMF is further classified into following two types −

• Self-Induced EMF

• Mutually Induced EMF

Self Induced EMF

When EMF is induced in a conductor or coil due to change of its own magnetic flux linkage, it is known as self-induced EMF.

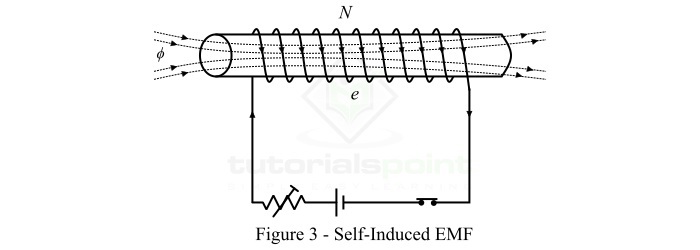
Consider a coil of N turn as shown in Figure-3. The current flowing through the coil establishes a magnetic field in the coil. If the current in the coil changes, then the magnetic flux linking the coil also changes. This changing magnetic field induces an EMF in the coil according to the Faraday’s law of electromagnetic induction. This EMF is known as self-induced EMF and the magnitude of the self-induced EMF is given by,

$$mathrm{mathit{e}:=:mathit{N}frac{mathit{dphi }}{mathit{dt}}}$$

Mutually Induced EMF

The EMF induced in a coil due to the changing magnetic field of a neighboring coil is known as mutually induced EMF.

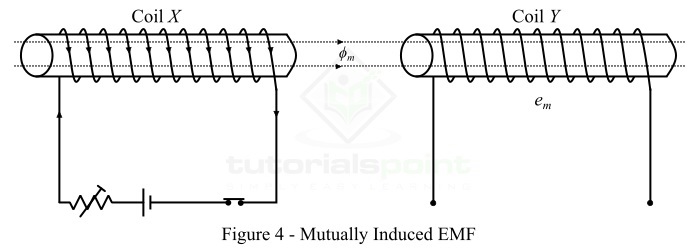
Consider two coils X and Y placed adjacent to each other as shown in Figure-4. Here, a fraction of the magnetic flux produced by the coil X links with the coil Y. This magnetic flux of coil X which is common to both coils X and Y is known as mutual flux ($mathit{phi _{m}}$).

If the current in coil X is changed, then the mutual flux also changes and hence EMF is induced in both the coils. Where, the EMF induced in coil X is known as self-induced EMF and the EMF induced in coil Y is called mutually induced EMF.

According to Faraday’s law, the magnitude of the mutually induced EMF is given by,

$$mathrm{mathit{e_{m}}:=:mathit{N_{Y}}frac{mathit{dphi _{m}}}{mathit{dt}}}$$

Where,$mathit{N_{Y}}$ is the number of turns in coil Y and $frac{mathit{dphi _{m}}}{mathit{dt}}$ is rate of change of mutual flux.

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

ЭДС индукции в движущемся проводнике:

На заряженную частицу, движущуюся в магнитном поле индукцией

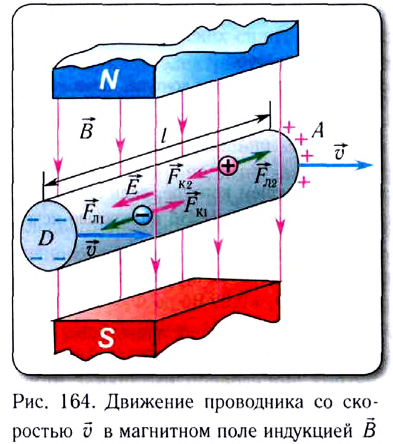
Рассмотрим проводник, находящийся в магнитном поле. Свободные заряды внутри проводника участвуют в тепловом движении. Вследствие хаотичности
теплового движения средняя скорость перемещения и среднее смещение частиц равны нулю. Следовательно, при тепловом движении заряженных частиц внутри проводника среднее значение силы Лоренца также равно нулю. При поступательном движении проводника как целого ситуация меняется, поскольку наряду с тепловым (беспорядочным) движением свободные заряды участвуют в направленном движении вместе с проводником.

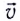
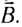
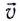
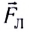
Рассмотрим движение проводника длиной l со скоростью перпендикулярно магнитному полю индукцией Поскольку свободные электроны движутся вместе с проводником со скоростью (рис. 164), то под действием силы Лоренца они будут смещаться вдоль проводника к его концу D. Направление силы Лоренца можно определить по правилу левой руки с учетом знака заряда электрона.

Вследствие этого на торцах D и А проводника появятся, соответственно, отрицательные и положительные заряды, которые создадут электрическое поле, а значит, и некоторую разность потенциалов между торцами проводника.

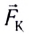
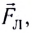
Процесс разделения зарядов (поляризации проводника) будет продолжаться до тех пор, пока сила, действующая на любой свободный электрон со стороны электрического поля (см. рис. 164), не уравновесит силу Лоренца действующую на электрон со стороны магнитного поля.

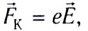
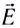
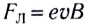
С учетом выражения для силы Кулона, действующей на каждый электрон где — напряженность созданного электрического поля, и силы Лоренца можно записать:

Откуда

Под действием сил Кулона и Лоренца заряды будут находиться в равновесии, и дальнейшее их разделение прекратится. По всей длине проводника установится однородное электрическое поле. Между концами проводника (в разомкнутой цепи) длиной l появится разность потенциалов
 которая является частным случаем возникновения ЭДС электромагнитной индукции.

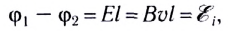
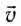
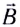
Таким образом, при движении проводника длиной l со скоростью в постоянном магнитном поле индукцией в нем возникает ЭДС индукции

Причиной появления этой ЭДС является сила Лоренца, действующая на свободные электроны в движущемся проводнике.

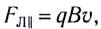
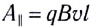
Подчеркнем, что полная работа силы Лоренца в движущемся проводнике равна нулю. Продольная составляющая силы Лоренца действующая на заряды, совершает работу по их разделению (рис. 165).

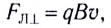
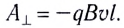
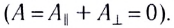
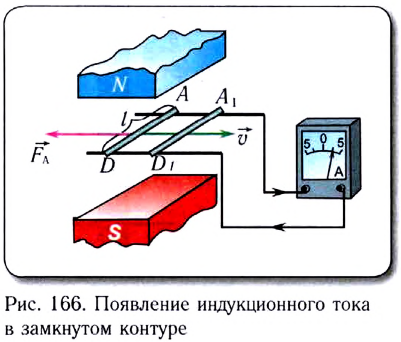
Поперечная составляющая направленная противоположно скорости движения проводника, совершает работу Полная работа силы Лоренца (сумма этих работ) равна нулю Вследствие того что работа поперечной составляющей силы Лоренца отрицательна, при движении проводника в магнитном поле происходит его торможение. Поэтому для движения проводника с постоянной скоростью на него необходимо действовать постоянной внешней силой, равной по модулю поперечной составляющей силы Лоренца.

Если проводник замкнуть расположенным вне магнитного поля проводом (рис. 166), то по этому проводу от точки D к точке А электроны будут перемещаться под действием ЭДС электромагнитной индукции.

Существование ЭДС индукции приводит к появлению в замкнутом контуре индукционного тока. Таким образом, электроны в проводнике движутся от точки А к точке D против сил электрического поля под действием силы Лоренца, а от точки D к точке А по проводу (во внешней цепи) их движение происходит под действием сил электрического поля.

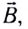
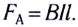
Когда проводник длиной l с индукционным током силой I движется в магнитном поле индукцией то на него со стороны поля действует сила Ампера, модуль которой Для определения направления этой силы применим правило левой руки (рис. 167).

Направление силы противоположно направлению движения про
водника. Следовательно, индукционный ток, взаимодействуя с магнитным полем, создает силу, тормозящую движение проводника. Таким образом, для движения проводника необходима внешняя сила, совершающая работу против силы Ампера. Индукционный ток нагревает проводник, по которому он проходит. Выделяющаяся в виде тепла энергия поступает в цепь благодаря работе, которую совершает внешняя сила, двигая проводник против сил поля.

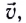
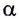
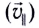
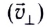
Если проводник, расположенный перпендикулярно линиям индукции магнитного поля, движется со скоростью направленной под углом к линиям индукции (рис. 168, а), то ее можно разложить на две составляющие — параллельную и перпендикулярную  направлению магнитного поля (рис. 168, б):

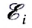
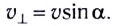
При движении проводника вдоль линии индукции в нем не возникает ЭДС индукции, поэтому вклад в  вносит только перпендикулярная составляющая скорости Вследствие этого выражение для ЭДС индукции в общем виде представляется соотношением

Таким образом, в общем случае необходимо учитывать угол между направлением скорости движения проводника (скорости электронов) и вектором индукции магнитного поля (как это делалось для силы Лоренца).
Вернемся к рассмотрению ЭДС электромагнитной индукции, возникающей в проводнике, движущемся равномерно и прямолинейно в магнитном поле. Поскольку скорость определяется, как 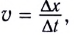то выражение для ЭДС можно представить в виде

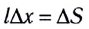
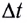
Учитывая, что — площадь прямоугольника KNN’K’, охватываемая проводником за промежуток времени (см. рис. 168, а), можем записать:

С учетом определения магнитного потока полученное выражение для ЭДС индукции можно представить в виде (см. рис. 168, б):

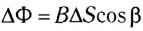
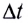
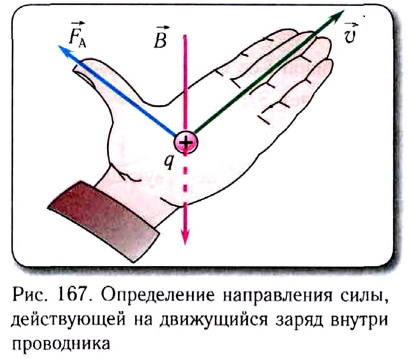
Здесь — изменение магнитного потока через контур за промежуток времени (число пересеченных проводником линий индукции магнитного поля).

Направление индукционного тока в контуре с перемещающимся проводником может быть установлено с помощью правила правой руки (рис. 169):
если ладонь правой руки расположить так, чтобы вектор индукции 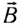магнитного поля входил в ладонь, а отставленный на 90° большой палец совпадал с направлением скорости движения проводника, то четыре вытянутых пальца укажут направление индукционного тока.

Таким образом, явление электромагнитной индукции связано с изменением магнитного потока через контур вне зависимости от характера причин, обусловливающих это изменение. ЭДС электромагнитной индукции прямо пропорциональна скорости изменения магнитного потока, т. е. изменению магнитного потока через контур в единицу времени.

Подчеркнем еще раз, что изменение магнитного потока через контур возникает при изменении: