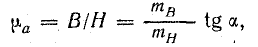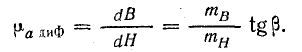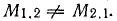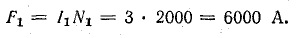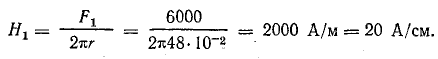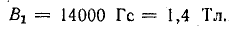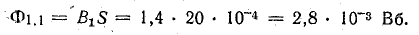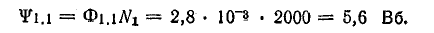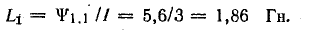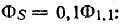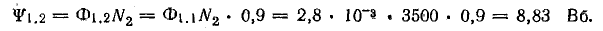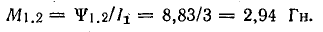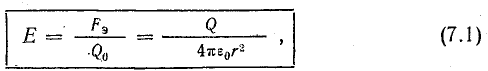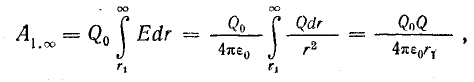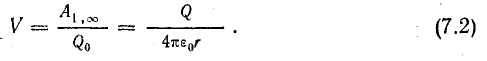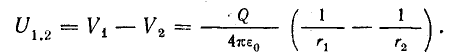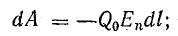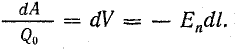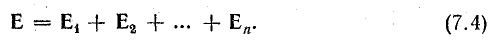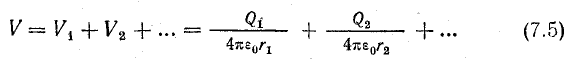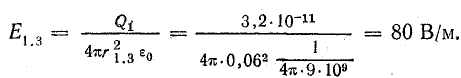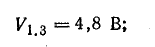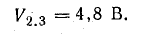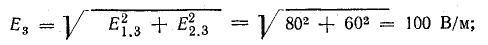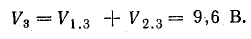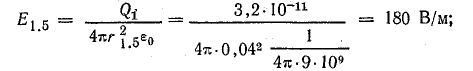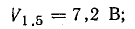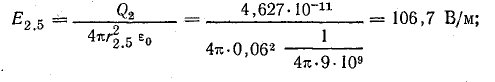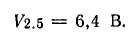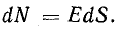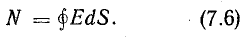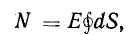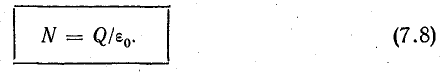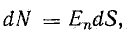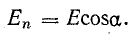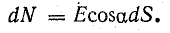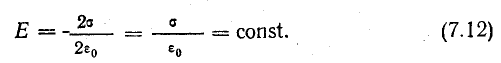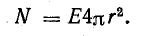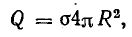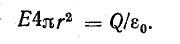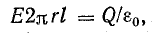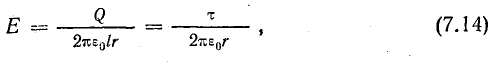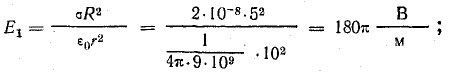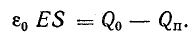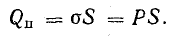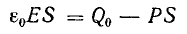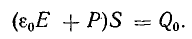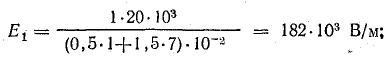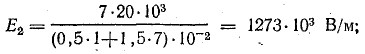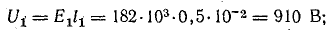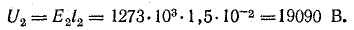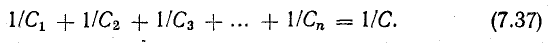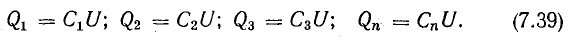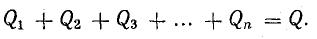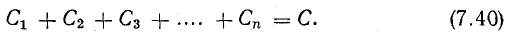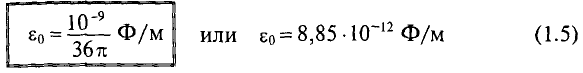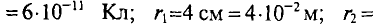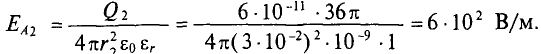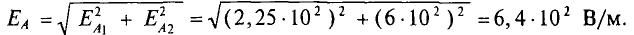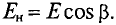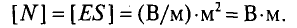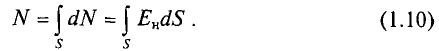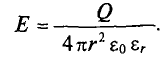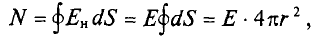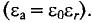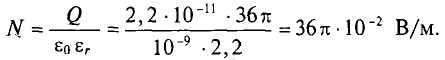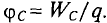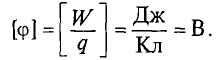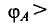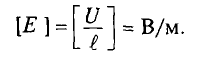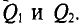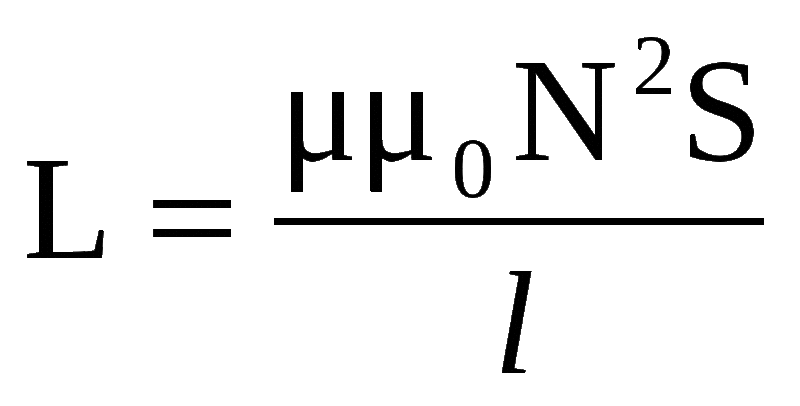Электромагнитная индукция
Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.1 (62.16%) 111 votes
-
Индукция магнитного поля на оси соленоида
конечной длины (рис 2.1)
,
где – плотность витков; α1 и
α2 – углы, под которыми видны
края соленоида из точки А, где определяется
магнитная индукция.
-
Индукция магнитного поля на оси длинного
соленоида
.
-
Индукция поля тороида
,
где r – радиус выбранного
контура.
Если тороид имеет неограниченное число
витков, а его радиус R
стремится к бесконечности, то в пределе
получается выражение аналогичное
магнитному полю бесконечно длинного
соленоида
.
Примеры решения задач
1. Катушка длиною 2 см и радиусом
3 см состоит из 1000 витков. Ток,
проходящий по катушке равен 200 мА.
Найти магнитную индукцию на оси катушки
в точке:
а) равностоящей от торцов; б) на одном
из торцов; в) отстоящей от торца на
расстоянии 2см.
Решение.
Воспользуемся
формулой для расчета магнитной индукции
соленоида конечной длины ,
где
.
Согласно рис. 2.2.а ,
,
,
.
Согласно
рис. 2.2.б
,
,
,
.
В
соответствии с рис. 2.2 в
,
Рис. 2.2 в
,
.
2.
Чему должно быть равно отношение длина
катушки к ее диаметру L/D,
чтобы магнитную индукцию в центре
катушки можно было найти по формуле для
поля бесконечно длинного соленоида?
Ошибка при таком допущении не должна
превышать 1%.
Р
ешение.
Относительная
ошибка ищется по следующей формуле
,
где
,
Рис. 2.3
—
магнитная индукция бесконечно длинного
соленоида.
—
магнитная индукция соленоида конечной
длины, где α
1
и α2
–
обозначены на рис. 2.3
,
,
.
Следовательно
.
После упрощения
,
,
,
.
3
.
Очень длинный прямой соленоид имеет
радиус сечения R
и n
витков на единицу длины. По соленоиду
течет постоянный ток I.
Пусть x
– расстояние, отсчитываемое вдоль оси
соленоида от его торца. Найти:
а)
индукцию магнитного поля на оси как
функцию x;
б
Рис. 2.4
) расстояние х0
до точки на оси, в которой индукция поля
отличается от В
в глубине соленоида на η=1%.
Решение.
а) Относительная
погрешность определяется по формуле
,
где
;
,
так как
.
,
где
.
Таким образом,
.
б) Воспользовавшись
соотношением для относительной
погрешности, получим:
;
.
;
;
;
.
;
,
.
4.
Однослойная катушка (соленоид) имеет
длину
и радиус сечения R.
Число витков на единицу длины равно n.
Найти индукцию магнитного поля в центре
катушки, если ток через нее равен I.
Решение.
Воспользуемся
формулой для расчета магнитной индукции
на оси витка с током
,
где
,
;
.
Знак
“-” показывает, что с увеличением угла
α dx
возрастает в отрицательном направлении
оси х (см. рис.2.5).
,
,
,
,
.
5.
Обмоткой длинного прямого соленоида с
радиусом сечения R=2,5
см служит
тонкая лента-проводник шириной h=5
см, намотанная
в один слой практически вплотную. По
ленте течет ток I=5
А. Найти
индукцию магнитного поля внутри и вне
соленоида как функцию расстояния r
от его оси.
Решение.
Изобразим
схематически
отрезок
ленты, образующий один виток (рис.2.6а).
Разложим ток текущий по ленте на две
составляющие – параллельную оси
соленоида I║
и
перпендикулярную I┴
(рис. 2.6 б).
Поле
внутри соленоида создается перпендикулярной
составляющей тока I┴,
а снаружи параллельной составляющей
I║.
Поле внутри соленоида рассчитывается
по известной формуле
,
где
— линейная плотность перпендикулярной
составляющей тока.
(рис.3.6 б), где
.
;
.
Для
нахождения индукции магнитного поля
вне соленоида необходимо использовать
теорему о циркуляции вектора магнитной
индукции ,
где
,
-линейная
плотность параллельной составляющей
тока.
(рис.2.6
б) =>
.
Следовательно
и
,
где
(рис. 2.6 а).
,
где
.
Таким
образом
.
6
.
На деревянный
тороид малого поперечного сечения
намотано равномерно N=2,5∙103
витков провода, по которому течет ток
I.
Найти отношение η индукции магнитного
поля внутри тороида к индукции в центре
тороида (рис.2.7).
Р
Рис. 2.7
ешение.
Индукция
магнитного поля внутри тороида рис. 2.7
ищется с использованием теоремы о
циркуляции вектора индукции
,
где
N
– число витков тороида; R
– радиус тороида.
Расчет индукции
в центре тороида производится по формуле
для кругового проводника с током.
,
.
7.
Имеется
очень длинный прямой соленоид с током
I.
Площадь поперечного сечения соленоида
S,
число витков на единицу длины n.
Найти поток вектора
через
торец соленоида.
Решение.
Поток
магнитной индукции в центре соленоида
определяется по формуле
.
На
концах соленоида
.
8.
Вычислить магнитный момент тонкого
проводника с током I=0,8
A,
плотно навитого на половину тора (рис.
2.8). Диаметр сечения тора d=5
см, число
витков N=500.
Решение.
Суммарный
магнитный момент формируется параллельными
составляющими
(рис. 2.8 б).
,
где
— число витков на 1 радиан,
–
число витков,
приходящихся на угловой интервал
.
В результате
интегрирования получим
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Магнитное поле окружает движущиеся элементарные частицы, обладающие электрическим зарядом, и связано с ними. В проводнике с током и пространстве вокруг него магнитное поле создается этим током, а внутри и вне намагниченного тела (постоянного магнита) — внутриатомным и внутримолекулярным движением элементарных заряженных частиц (например, вращением электронов вокруг собственной оси и ядра атома).
Магнитное поле характеризуется воздействием на движущуюся электрически заряженную частицу с силой, пропорциональной заряду частицы и ее скорости.
Закон ампера и магнитная индукция
Магнитное поле обнаруживается благодаря магнитным явлениям: притяжению и отталкиванию проводов с токами или намагниченных тел, действию проводника с током на магнитную стрелку, электромагнитной индукции.
В основе этих явлений лежит характерное свойство магнитного поля — силовое действие на движущиеся заряженные частицы. Силы взаимодействия магнитного поля с движущимися заряженными частицами (токами) называются электромагнитными.
Изучение магнитных явлений и расчеты, связанные с их использованием, невозможны без количественной оценки магнитного поля.
Выбирая необходимую для этого величину, можно исходить из силового взаимодействия двух проводов с токами.
Закон Ампера
Опыт показывает, что на каждый из двух проводов действуют силы, притягивающие друг к другу провода с одинаковым направлением токов и отталкивающие провода с противоположными направлениями токов (рис. 8.1).
Магнитные поля, обусловленные каждым из токов, распределены в одной и той же области пространства. Поэтому в соответствии с принципом наложения можно полагать, что оба провода окружены общим магнитным полем, которое получается в результате наложения двух полей. Каждое поле связано со своим током, когда соответствующий провод уединен.
Рис. 8.1. К закону Ампера
В таком случае притяжение или отталкивание проводов нужно рассматривать как результат силового действия общего магнитного ноля на заряженные частицы, образующие ток в каждом из проводов. Количественные соотношения для этого случая определены законом Ампера, согласно которому силовое действие магнитного поля на движущиеся заряженные частицы рассматривается как взаимодействие двух элементов линейного тока.
Величина силы взаимодействия между двумя элементами линейных токов в вакууме пропорциональна произведению элементов линейных токов и обратно пропорциональна квадрату расстояния между ними.
Элементом линейного тока называется произведение Idl, где dl — длина участка провода с током I, весьма малая (так же как и диаметр провода) по сравнению с расстоянием от него до точек, в которых рассматривается магнитное поле тока I.
Если элементы линейных токов расположены параллельно, то сила взаимодействия между ними
В Международной системе единиц (СИ) магнитная постоянная
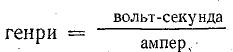
Заметим, что формула (8.1) и последующие формулы, относящиеся к магнитному полю в вакууме, справедливы и для магнитного поля в воздухе.
Магнитная индукция
Предположим, что элемент линейного тока I2dl2 столь мал, что его поле практически не изменяет поле тока I1. Тогда этот элемент линейного тока можно рассматривать как пробный, служащий лишь для регистрации электромагнитной силы, которая в этом случае является результатом действия магнитного поля первого тока на пробный элемент линейного тока.
Величина тока I1 определяет интенсивность магнитного поля: чем больше ток, тем «сильнее» его магнитное поле.
Для оценки интенсивности магнитного поля введено понятие магнитной индукции В.
Магнитная индукция — векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля.
В численном выражении магнитная индукция равна отношению силы, действующей на заряженную частицу, к произведению заряда Q и скорости частицы υ, направленной так, что эта сила максимальна:
Направление вектора магнитной индукции перпендикулярно векторам силы и скорости и совпадает с поступательным перемещением правого винта (или буравчика), если вращать его в направлении от вектора силы к вектору скорости частицы с положительным зарядом.
За некоторое время dt, согласно (2.2), заряд 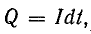
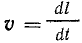
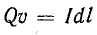
Из формулы (8.1) следует
Магнитное поле в окружающем проводник пространстве создается не только выбранным элементом линейного тока, но и другими элементами, на которые может быть разделен реальный проводник (рис. 8.2).
Рис. 8.2. К закону Био — Савара
Магнитная индукция В в данной точке является векторной суммой элементарных векторов dВ.
Формула (8.3), по которой определяется элементарная магнитная индукция, является математическим выражением закона Био — Савара.
Из нее следует единица измерения магнитной индукции:
В расчетах применяется также единица магнитной индукции — гаусс (Гс) (1 Гс = 10-4 Тл).
Линии магнитной индукции
Графически магнитное поле можно изобразить с помощью линий магнитной индукции.
Линию магнитной индукции проводят так, чтобы в каждой точке этой линии касательная к ней совпадала с вектором магнитной индукции.
Пользуясь этим правилом, можно изобразить магнитное поле для различных случаев.
Магнитное поле тока прямолинейного провода имеет линии магнитной индукции в виде окружностей, лежащих в плоскостях, перпендикулярных направлению тока, с центром на оси провода (рис. 8.3).
Направление магнитной индукции в этом случае определяется с помощью правила буравчика: если направление поступательного движения буравчика совместить с направлением тока в проводе, то вращение рукоятки покажет направление линий магнитной индукции.
Большой практический интерес представляет картина магнитного поля тока катушек, так как во многих электротехнических устройствах (трансформаторы, электрические машины, электромагнитные реле и т. д.) магнитное поле создается токами в катушках различной формы.
Магнитное поле тока цилиндрической катушки изображено на рис. 8.4. Если длина катушки значительно больше ее диаметра, то линии магнитной индукции имеют внутри катушки одинаковое направление (вдоль оси катушки) и величина магнитной индукции во всех точках одинакова, за исключением точек, расположенных у краев.
Рис. 8.3. Магнитное поле прямого тока
Рис. 8.4. Магнитное поле тока в цилиндрической катушке
Магнитное поле, имеющее во всех точках одинаковую по величине и направлению магнитную индукцию, называется однородным (равномерным).
По форме магнитного поля цилиндрическая катушка подобна постоянному магниту кругового сечения (рис. 8.5). На конце катушки, где линии магнитной индукции выходят из нее, образуется северный полюс, а на противоположном конце — южный.
Кольцевая катушка с обмоткой на тороидальном сердечнике (рис. 8.6) создает магнитное поле только внутри витков. Направление линий индукции магнитного поля тока катушки или контура тоже определяется правилом буравчика, но в другой формулировке: если рукоятку буравчика вращать по направлению тока в витках, то поступательное перемещение буравчика совпадает с направлением линий магнитной индукции внутри катушки.
Рис. 8.5. Магнитное поле прямого постоянного магнита
Рис. 8.6. Кольцевая катушка
С помощью линий магнитной индукции можно выразить не только направление магнитного поля, но и величину магнитной индукции, подобно тому, как это делается при исследовании электрического поля.
Неравномерное магнитное поле изображается замкнутыми линиями, проведенными с неодинаковой плотностью в различных областях.
В отличие от линий напряженности электростатического ноля, которые начинаются на положительных, а оканчиваются на отрицательных заряженных телах или уходят в бесконечность, линии индукции магнитного поля всегда замкнуты на себя, т. е. не имеют ни начала, ни конца.
Проводник с током в магнитном поле
Большой практический интерес представляет выражение силы, действующей на проводник с током в равномерном магнитном поле. На рис. 8.7 показан прямолинейный провод в пространстве между полюсами постоянного магнита или электромагнита (катушки, со стальным сердечником), расположенный так, что между направлениями вектора магнитной индукции В и тока в проводе I угол α = 90°.
В равномерном магнитном поле на элемент длины провода в любом месте действует одинаковая электромагнитная сила, поэтому на основании формул (8.2) и (8.3) можно записать выражение силы, действующей на часть провода, расположенную в пределах магнитного поля:
где В — магнитная индукция, Тл; I —ток в проводе, А; l — длина части провода, расположенной в магнитном поле, м; Fм — величина электромагнитной силы, Н.
Рис. 8.7. Прямой провод с током в магнитном поле
Если провод располагается так, что между направлениями вектора магнитной индукции поля и тока в проводе угол а ≠ 90°, то электромагнитная сила определяется той же формулой (8.4), но вместо полной длины провода берется ее проекция на направление, перпендикулярное направлению поля:
На провод с током, расположенный вдоль линий магнитной индукции, магнитное поле не действует.
Сила Fм направлена всегда перпендикулярно плоскости, в которой лежит провод и находятся линии магнитной индукции. Направление электромагнитной силы наиболее удобно определять по правилу левой руки: если расположить левую руку так, чтобы вытянутые четыре пальца (кроме большого) показывали направление тока в проводе, а линии магнитной индукции «входили» в ладонь, то большой палец, отогнутый перпендикулярно остальным четырем, покажет направление электромагнитной силы.
Задача 8.3.
В равномерное магнитное поле с индукцией В = 1,2 Тл помешен прямолинейный проводник длиной l = 80 см с током I = 20 А. Определить силу, действующую на проводник, если он расположен перпендикулярно направлению линий магнитной индукции.
Решение. Подставим в формулу (8.5) заданные величины, от которых зависит сила:
Примеры расчета магнитных полей с помощью закона Био — Савара
Определим с помощью закона Био — Савара магнитную индукцию и напряженность магнитного поля в ряде конкретных случаев.
Поле кругового тока
На рис. 8. 10 изображен кольцевой провод (виток) с током I. Требуется определить индукцию магнитного поля в центре этого витка (точка О).
Рис. 8.10. К определению магнитной индукции поля кругового тока
Согласно закону Био — Савара [см. формулу (8.3)], каждый элемент тока создает в точке О магнитную индукцию
При этом имеется в виду, что угол α = 90° и составляющие результирующей магнитной индукции В в центре витка от каждого элемента имеют одно и то же направление, перпендикулярное плоскости витка.
Поэтому
Постоянные величины вынесем, за знак интеграла:
где 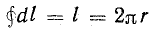
Следовательно,
или
Рис. 8.11. К определению магнитной индукции поля прямого тока
Поле прямого тока
Определим индукцию магнитного поля в точке А (рис. 8.11), если оно создается током I прямолинейного провода конечной длины.
Элемент длины провода dl создает в точке А элементарный вектор магнитной индукции dВ [см. формулу (8.3)]. Для того чтобы найти полную величину магнитной индукции, следует сложить элементарные векторы dВ от всех элементов dl, из которых складывается длина провода.
Учитывая, что провод и отрезки r, проведенные от любого элемента провода в точку А, лежат в одной плоскости, можно заключить, что все векторы dВ в точке А направлены по одной прямой перпендикулярно этой плоскости, в данном случае за чертеж.
Поэтому полную величину магнитной индукции можно найти интегрированием:
Из рис. 8.11 видно, что 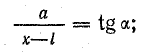
Отсюда
Кроме того,
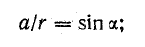
Полная величина магнитной индукции в точке А
Задача 8.4.
В витке, имеющем форму прямоугольника со сторонами b = 10 см и c = 20 см, ток I = 10 А. Определить магнитную индукцию в точке пересечения диагоналей прямоугольника (точка А на рис. 8.12, а).
Решение. Магнитную индукцию поля прямолинейного провода конечной длины определяют по формуле (8.7).
Подставив в эту формулу обозначения величин по рис. 8.12, а, получим выражения для составляющих магнитной индукции. От участков провода, расположенных по сторонам b,
В данном случае α1 = α2 = α, поэтому
Аналогично, от участков провода, расположенных по сторонам с, при γ1 = γ2 = γ
Рис. 8.12. К задачам: а —8.4; б —8.5; в — 8.6
Магнитная индукция в точке А(ВА) складывается из составляющих В1 (от двух сторон b) и В2 (от двух сторон c): 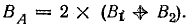
Из чертежа следует, что
Учитывая эти выражения, после преобразования получим:
Расчет симметричных магнитных полей
Связь тока с его магнитным полем ранее выражена формулой закона Био — Савара, который можно применять для определения основных характеристик магнитного поля в любом случае. Подобные задачи решаются более просто на основе понятий о циркуляции вектора магнитной индукции и полном токе.
Циркуляция вектора магнитной индукции и полный ток
Для выяснения смысла этих понятий в магнитном поле системы токов выберем произвольный замкнутый контур (рис. 8.13).
В каждой точке этого контура вектор магнитной индукции В может иметь любое направление. Обозначим через Вl проекцию этого вектора на направление элемента длины dl около выбранной точки контура.
Выражение 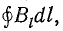
Алгебраическую сумму токов 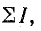
На основе закона Био — Савара можно доказать, что циркуляция вектора магнитной индукции по произвольному замкнутому контуру пропорциональна полному току, пронизывающему поверхность, ограниченную этим контуром (рис. 8.13):
Для магнитного поля в вакууме коэффициентом пропорциональности между циркуляцией вектора магнитной индукции и полным током является магнитная постоянная μ0.
При составлении уравнения (8.8) для конкретного случая знак произведения Вldl берется положительным, если в данной точке направление Вl совпадает с направлением обхода контура; знак тока принимается положительным, если направление линий индукции магнитного поля данного тока, определенное по правилу буравчика, совпадает с направлением обхода.
Выражение 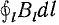
Рис. 8.13. К вопросу о циркуляции вектора магнитной индукции
Для рис. 8.13
Если выбрать контур, совпадающий с линией магнитной индукции, то вместо проекции вектора магнитной индукции Вl в формулу (8.8) можно подставить полную его величину В. .
В отдельных случаях магнитное поле обладает симметрией, при которой магнитная индукция во всех точках такого контура имеет одинаковую величину. Для этих случаев формула (8.8) имеет более простое выражение.

где 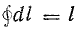
тогда
Формула (8.8) справедлива для магнитного поля, созданного замкнутыми токами. Ее нельзя применить для определения составляющей магнитной индукции поля, образуемого током на участке провода конечной длины, как это сделано при выводе формулы (8.7) на основании закона Био — Савара.
Поле прямого тока
Наметим на произвольном расстоянии а от оси провода точку А (рис. 8.14, а) и проведем через нее замкнутый контур, совпадающий с линией магнитной индукции. Как известно, эта линия — окружность с центром на оси провода. Все точки контура находятся на одинаковом расстоянии от оси провода, поэтому магнитная индукция поля в них имеет одинаковую величину.
Согласно формуле (8.8),
Формула (8.10) совпадает с выводами, полученными из закона Био — Савара [см. формулу (8.7)] при α1 и α2, равных нулю.
Для определения магнитной индукции поля внутри провода выберем произвольный контур радиуса r и будем полагать плотность тока во всех точках сечения провода одинаковой и равной
где r0 — радиус провода.
Рис. 8.14. К определению магнитной индукции поля прямого тока
Полный ток, пронизывающий часть сечения, ограниченную выбранным контуром, имеет величину
отсюда
На рис. 8.14, б показан график изменения магнитной индукции внутри и вне линейного провода большой протяженности, построенный по формулам (8.10) и (8.11).
Поле тока кольцевой катушки
Выберем замкнутый контур, совпадающий с линией магнитной индукции в центре сечения сердечника (см. рис. 8.6). Предполагая намотку витков равномерной, по соображениям симметрии применим формулу (8.9).
Поверхность, ограниченная выбранным контуром, пронизывается током I столько раз, сколько витков N имеет катушка, поэтому
магнитная индукция
Эта формула пригодна для определения магнитной индукции и в других точках, расположенных внутри катушки дальше или ближе к центру, если в них подставить соответствующий радиус.
Поле тока цилиндрической катушки
Если витки катушки навиты вплотную друг к другу, то при бесконечной ее протяженности все точки на любой линии, параллельной оси, находятся в одинаковых условиях (рис. 8.15).
Магнитная индукция поля внутри катушки во всех точках этой линии одинакова и направлена вдоль оси катушки. Вне катушки магнитного поля нет.
Выделим замкнутый контур а-6-в-г прямоугольной формы и применим к нему формулу (8.8). При обходе контура нужно учитывать, что на участке б-в поля нет (В = 0); на участках а-б и в-г вне катушки поля нет, а внутри катушки магнитная индукция направлена перпендикулярно направлению обхода, поэтому проекция вектора В на направление обхода равна нулю. На участке г-а Вl = В.
Таким образом, циркуляция вектора магнитной индукции имеет величину
Полный ток контура а-б-в-г
где N — число витков, уложенных на участке длиной l.
Согласно выражению (8.9),
Из этой формулы следует, что магнитное поле внутри бесконечно длинной катушки равномерно.
Рис. 8.15. К определению магнитной индукции поля цилиндрической катушки с током
Формулу (8.13) можно применить, допуская некоторую погрешность, для определения магнитной индукции цилиндрической катушки конечной длины lк, если она значительно больше диаметра витка
Применение закона Био — Савара к цилиндрической катушке конечной длины дает для определения В в любой точке М на оси катушки выражение
Формулы (8.12)—(8.15), определяющие магнитное поле катушек, имеют в числителе произведение тока и числа витков IN. Магнитное поле данной интенсивности можно получить при относительно малом числе витков, но большом токе, или при малом токе, но относительно большом числе витков.
Это дает основание при расчете магнитных полей пользоваться произведением IN как единой величиной, которая называется намагничивающей силой. В практике эту величину называют также ампер-витками.
Магнитный поток и потокосцепление
Понятие о магнитном потоке как характеристике магнитного поля имеет в электротехнике большое значение. Его применяют при рассмотрении принципов работы и расчетах электромагнитных устройств {электрических машин, трансформаторов, электромагнитов различного назначения).
Магнитный поток
Любой проводник с током создает магнитное поле. Рассмотрим для примера в качестве источника магнитного поля виток провода кольцевой формы с током l (рис. 8.16).
Линии магнитной индукции этого неравномерного поля сцеплены с самим витком и часть их пронизывает некоторую поверхность S.
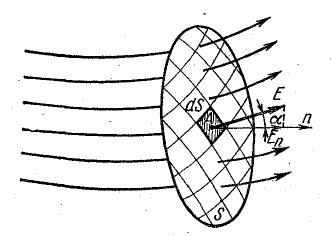
Выделим на этой поверхности элемент площади dS, в пределах которой магнитную индукцию В можно считать одинаковой. Вектор магнитной индукции в общем случае направлен под некоторым углом β к нормали n этой поверхности. Проекция вектора В на направление нормали дает вектор Вn, направленный перпендикулярно выделенной элементарной площадке dS.
Величина 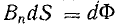
Сложив элементарные потоки по всей поверхности, получим выражение полного потока вектора магнитной индукции или магнитного потока через заданную поверхность S:
Рис. 8.16. К определению магнитного потока
Рис. 8.17. К определению магнитного потока
Аналогично можно выразить магнитный поток через любую другую поверхность, в том числе и через поверхность, ограниченную самим витком, т. е. магнитный поток, сцепленный с ним.
В практике бывают случаи, когда магнитное поле можно считать равномерным, а поверхность, через которую определяется магнитный поток, — плоскостью (рис. 8.17).
В этих величинах В и Вn остаются одинаковыми для всех точек плоскости, поэтому
где Sn — проекция площади S на плоскость, перпендикулярную направлению вектора магнитной индукции.
Если плоскость S расположена перпендикулярно линиям магнитной индукции, то магнитный поток
Согласно формулам (8.18) и (8.16), магнитная индукция В является плотностью магнитного потока в данной точке поля.
Единица измерения магнитного потока — вебер:
[Ф] = [ВS] = тесла • метр2 = вольт • секунда = вебер (Вб).
Работа при перемещении проводника с током в магнитном попе
Рассмотрим проводящий контур прямоугольной формы, одна сторона которого находится в равномерном магнитном поле. При токе I в магнитном контуре на провод действует электромагнитная сила Fм (рис. 8.18).
Незакрепленный контур перемещается в направлении действия силы; при этом на пути b сторона его описывает плоскую поверхность S, перпендикулярную линиям магнитной индукции S = bl.
Произведение магнитной индукции и площади этой поверхности выражает магнитный поток Ф равномерного поля через данную площадь S [см. (8.18)].
При движении контура с током в магнитном поле электромагнитная сила Fм на пути b совершает работу
В этом случае работа считается положительной. При движении провода против силы (при наличии внешней механической силы) работа отрицательна.
Рис. 8.18. Замкнутый виток с током в магнитном поле
Учитывая формулу (8.18), работу, совершенную в результате взаимодействия магнитного поля и тока в проводнике, движущемся в магнитном поле, можно определить произведением тока в проводнике и магнитного потока сквозь поверхность, очерченную проводником при его движении: А = ФI.
Магнитный поток через поверхность, очерченную проводником, является разностью потоков, пронизывающих проводящий контур в конечном и начальном положениях, т. е. положительным приращением магнитного потока, сцепленного с контуром:
где
Работа, затраченная на перемещение контура,
На основании рассмотренного примера можно сделать следующие выводы, справедливые для любой электромагнитной системы (см. также задачу 8.10).
- Работа электромагнитных сил, затраченная на перемещение контура с током, равна произведению тока в контуре на изменение магнитного потока, сцепленного с контуром.
- Всякий контур с током в магнитном поле стремится занять положение, при котором магнитный поток, пронизывающий контур, оказывается положительным и наибольшим (положительным считается магнитный поток, совпадающий внутри контура с потоком, созданным током этого контура).
Приведем такой пример. Стальной .сердечник втягивается внутрь катушки с током. При этом магнитный поток катушки увеличивается, так как добавляется действие контуров тока внутри стального сердечника, которые образуются внутриатомным и внутримолекулярным движением заряженных частиц. Если перемещение сердечника ничем не ограничено, то он втягивается до тех пор, пока поток не увеличится до максимальной величины для этой системы.
Сказанное относится к любым электромагнитным устройствам с подвижным стальным якорем (реле, тяговые электромагниты и т. п.).
Магнитное потокосцепление
При определении работы, совершаемой электромагнитными силами, была взята рамка, имеющая один виток. Но на рамку можно намотать несколько витков, тогда работа электромагнитных сил при перемещении рамки увеличится.
Если предположить, что все N витков сцеплены с одним и тем же потоком, то работа электромагнитных сил увеличится в N раз: А = NΔФI.
Произведение числа витков и сцепленного с этими витками магнитного потока называют потокосцеплением:
Следовательно, работа электромагнитных сил выражается произведением тока в витках и приращения магнитного потокосцепления:
В общем случае витки катушки могут быть сцеплены с разными потоками, тогда общее потокосцепление определяется алгебраической суммой потоков, сцепленных с каждым витком:
При этом имеется в виду, что потокосцепление одного витка численно равно потоку через поверхность, ограниченную этим витком.
Рис. 8.19. Потокосцепление цилиндрической катушки
Отдельные потоки (Ф1, Ф2 и т. д.) могут быть сцеплены с несколькими витками (рис. 8.19), тогда потокосцепление будет выражено алгебраической суммой следующего вида:
Если в уединенном контуре любой формы имеется ток, то его магнитное поле сцеплено с самим контуром. Потокосцепление такого контура называется собственным (потокосцеплением самоиндукции). Собственное потокосцепление характеризует связь тока с собственным магнитным полем.
Потокосцепление имеет ту же размерность, что и магнитный поток.
Задача 8.10.
Прямоугольная рамка с током I расположена в магнитном поле, как показано на рис. 8.20. Найти выражение для работы, совершенной при повороте рамки из положения I в положение II.
Рис. 8.20. Прямоугольная рамка с током в магнитном поле
Решение. По правилу левой руки найдем направления сил, действующих на стороны рамки в положении I.
На стороны аб и вг рамки действуют силы F1м и F2м, на две другие стороны силы не действуют, так как ток в них направлен вдоль линий магнитной индукции. Силы F1м и F2м образуют вращающий момент, под действием которого рамка поворачивается из положения I в положение II.
В положении II вращающий момент равен нулю, так как силы F1м и F2м направлены противоположно вдоль линии, проходящей через ось вращения рамки.
Стороны рамки аб и вг переместились в направлении действия силы на d/2, где d — ширина рамки.
Работа по перемещению каждой стороны рамки составляет
а всей рамки —
где ld — площадь рамки; ВS = Фm — наибольшая величина магнитного потока, пронизывающего рамку.
Величина Фm в данном случае определяет изменение потока, сцепленного с рамкой при повороте ее из положения I (Ф1 = 0) в положение II (ФII = Фm).
Изменение потока в зависимости от угла поворота рамки происходит по закону
так как в любом промежуточном положении проекция площади рамки на плоскость, перпендикулярную направлению линий магнитной индукции, равна Ssinα.
Задача 8.11.
В обмотке тороидальной катушки, имеющей длину lк = 40 см, площадь поперечного сечения S = 6 см2, число витков N = 400, ток I = 20 А, определить магнитный поток внутри катушки.
Решение. Магнитную индукцию внутри катушки определим по формуле (8.12), учитывая, что длина катушки 2πr = lk:
Магнитный поток определим приближенно, полагая поле внутри катушки равномерным:
Индуктивность собственная и взаимная
При изменении тока в контуре или катушке изменяется потокосцепление самоиндукции или собственное потокосцепление, обусловленное током в этом контуре (катушке), а также взаимное потокосцепление с другим контуром или катушкой.
Опыт показывает, что одинаковое изменение тока в двух контурах или катушках приводит в общем случае к различному изменению их потокосцепления. Особенности данного контура или катушки в отношении образования потокосцепления характеризуются индуктивностью собственной и взаимной.
Индуктивность собственная
На зависимость между потокосцеплением и током уединенного контура влияют форма, размеры контура и среда, в которой создается его магнитное поле, т. е. факторы, обусловленные конструкцией контура или катушки.
Для выражения этого влияния введено понятие индуктивности контура или катушки.
Собственная индуктивность уединенного контура (или катушки) есть величина, характеризующая связь потокосцепления самоиндукции и тока, численно равная отношению потокосцепления самоиндукции контура к току в нем:
В вакууме и неферромагнитных веществах это отношение для данного контура (катушки) остается неизменным независимо от величин тока и потокосцепления.
Единица индуктивности
В практических расчетах индуктивность часто выражается в долях генри: миллигенри (мГн) и микрогенри (мкГн); 1 Гн = 103 мГн = = 106 мкГн.
Индуктивность взаимная
Рассмотрим магнитную связь двух катушек с токами, расположенных друг от друга так, что магнитный поток, вызванный током первой катушки I1 сцеплен с витками обеих катушек.
Предположим, что потоков магнитного рассеяния нет, т. е. все магнитные линии одной катушки сцеплены с другой катушкой (рис. 8.21, а).
Собственное потокосцепление первой катушки
где N1 — число витков первой катушки.
Магнитный поток, созданный током первой катушки, сцеплен с витками второй катушки.
Взаимное потокосцепление, как и собственное, пропорционально току, создающему поток:
Рис. 8.21. Магнитная связь двух катушек
Коэффициент пропорциональности М1.2 — величина постоянная (в неферромагнитных средах), зависит от конструктивных особенностей рассматриваемой системы катушек и называется взаимоиндуктивностью.
Из уравнений (8.24) и (8.25) следует, что
Магнитная связь может осуществляться потоком второй катушки, имеющей ток I2.
По аналогии с первой катушкой, собственное потокосцепление второй катушки
взаимное потокосцепление
Отношение индуктивности L2 к взаимоиндуктивности М2.1
Из отношений индуктивностей катушек к взаимоиндуктивности находим
Нетрудно доказать, что коэффициенты М1.2 и М2.1 одинаковы.
Для этого предположим, что вторая катушка с током I2 удаляется в бесконечность. Потокосцепление этой катушки изменяется на величину взаимного потокосцепления. Работа, совершаемая при удалении катушки, согласно формуле (8.21), определяется произведением 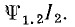
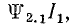
Отсюда
или
Взаимоиндуктивность выражается через индуктивности катушек:
Коэффициент связи
Формула (8.26) справедлива при отсутствии рассеяния магнитных потоков, т. е. когда между катушками существует наибольшая магнитная связь. В действительности некоторая часть линий магнитной индукции поля данной катушки сцеплена только с собственными витками (на рис. 8.21, б это относится к первой катушке). Этими линиями определяется магнитный поток рассеяния Фs, который не образует магнитной связи катушек; поэтому в реальных устройствах, где используется магнитная связь, поток рассеяния должен быть по возможности уменьшен.
Из-за потоков рассеяния магнитная связь катушек оказывается неполной (Ф1.2<Ф1). При этом взаимоиндуктивность будет меньше величины 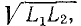
Коэффициент связи 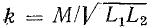
Потоки рассеяния уменьшить до нуля практически невозможно, поэтому коэффициент связи k всегда меньше единицы.
В системе магнитносвязанных контуров или катушек различают согласное и встречное включение.
Рис. 8.22. Согласное и встречное включение катушек
Если направления намагничивающих сил двух катушек, определенные по правилу буравчика, совпадают, то включение катушек называется согласным (рис. 8.22, а). При несовпадении этих направлений включение называется встречным (рис. 8.22, б).
Для изменения направления намагничивающей силы катушки можно, согласно правилу буравчика, изменить направление тока или направление хода витков (правая или левая намотка).
Изменяя направление тока или направление намотки одной из катушек, получают согласное или встречное включение.
При встречном включении катушек можно добиться такого положения, когда потоки обеих катушек, определенные порознь, равны, а результирующий поток в соответствии с принципом наложения равен нулю.
Если требуется получить катушку без индуктивности, можно применить бифилярную намотку, которая выполняется проводом, сложенным вдвое.
Магнитный поток, а следовательно, и индуктивность бифилярно намотанной катушки равны нулю, так как каждый виток ее состоит из двух проводников с противоположным направлением тока.
Вычисление индуктивностей
Проводящие контуры, катушки — наиболее распространенные элементы электротехнических устройств, а индуктивность является конструктивной характеристикой этих элементов и применяется при расчетах. Поэтому важно не только само понятие об индуктивности, но и вычисление ее для различных случаев.
Индуктивность катушки
Определим индуктивность участка l бесконечно длинной цилиндрической катушки, имеющей на этом участке N витков диаметром D (см. рис. 8.15).
Магнитное поле такой катушки равномерное. В этом случае по формуле (8.13)
Если витки катушки плотно прилегают друг к другу, можно считать поток всех витков одинаковым:
где S = πD2/4 — площадь поперечного сечения катушки.
Согласно формуле (8.23), индуктивность
Выражение (8.28) можно использовать для приближенного вычисления индуктивности цилиндрической катушки конечной длины, если 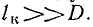
Точность результата тем больше, чем больше отношение 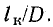
В практике (например, радиотехнической) применяются катушки различной формы, для которых условие 
Индуктивность двухпроводной линии
Для определения индуктивности участка двухпроводной линии (рис. 8.23) нужно применить формулу (8.23), для чего предварительно следует подсчитать потокосцепление.
Поток, сцепленный с контуром, образованным прямым и обратным проводами линии, нужно подсчитать по формуле (8.16), учитывая, что магнитное поле линейного тока неравномерное.
Выделим между проводами элемент площади dS = ldx, в пределах которой магнитную индукцию можно считать постоянной:
или
Рис. 8.23. К определению индуктивности двухпроводной линии
Поток, образованный током прямого провода, определим суммированием элементарных потоков на всем расстоянии между проводами в свету:
Учитывая, что 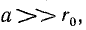
Точно такой же поток и в том же направлении создается током обратного провода, поэтому общий поток
Двухпроводная линия, имея прямой и обратный провода, образует один виток; поэтому потокосцепление численно равно определенному магнитному потоку:
Индуктивность
Подсчет по формуле (8.29) дает неточный результат, так как не была учтена внутренняя индуктивность, образованная магнитным потоком внутри проводов.
Задача 8.17.
Определить индуктивность кольцевой катушки прямоугольного поперечного сечения S = 6 см2, имеющей наружный радиус r2 = 11 см, внутренний r1 = 9 см, а число витков N = 500 (см. рис. 8.6).
Решение. Магнитная индукция по формуле (8.12)
При плотной намотке тонким проводом магнитный поток можно считать одинаковым для всех витков, поэтому потокосцепление
Индуктивность катушки
Магнитные свойства вещества
Ранее магнитное поле рассматривалось в вакууме, где из-за отсутствия вещества оно не испытывает на себя его влияния и определяется только токами в проводах. Эти токи будем называть внешними.
Если магнитное поле внешних токов создается в веществе, то поле воздействует на него, а вещество определенным образом изменяет магнитное поле.
Намагничивание вещества
Любое вещество, находящееся в магнитном поле внешних токов, приходит в особое состояние намагниченности, характеризующееся возникновением в нем добавочного магнитного поля.
Движение заряженных частиц внутри атома можно рассматривать как элементарные внутриатомные токи, поэтому добавочное магнитное поле, возникшее в результате намагничивания, будем называть полем элементарных (внутренних) токов.
Магнитные свойства элементарного кругового тока (рис. 8.24, а) можно характеризовать магнитным моментом, величина которого определяется произведением элементарного кругового тока и площади описанного им круга, а направление — по правилу буравчика:
Рис. 8.24. Магнитный момент элементарных токов
При отсутствии магнитного поля внешних токов элементарные токи внутри вещества ориентированы беспорядочно, поэтому общий магнитный момент даже малых объемов вещества оказывается равным нулю, а магнитное поле элементарных токов не обнаруживается.
Влияние магнитного поля внешних токов на круговые элементарные токи в веществе состоит в том, что изменяется ориентация осей вращения частиц так, что их магнитные моменты оказываются направленными в одну сторону.
Интенсивность и характер намагничивания у различных веществ в одинаковом магнитном поле внешних токов значительно отличаются. Поэтому все вещества делятся на три группы.
К первой группе относятся диамагнитные вещества, в которых магнитное поле элементарных токов направлено против вызвавшего его поля внешних токов. Иначе говоря, результирующее магнитное поле в веществах этой группы слабее магнитного поля внешних токов. К диамагнитным веществам относятся вода, водород, кварц, серебро, медь и др.
Ко второй и третьей группам относятся соответственно парамагнитные (алюминий, кислород, воздух и т. д.) и ферромагнитные вещества (железо, никель, кобальт и Некоторые их сплавы). Общим для веществ этих групп является то, что при намагничивании магнитные моменты элементарных токов в них ориентируются в направлении ноля внешних токов. В результате магнитное поле усиливается.
Ферромагнитные вещества имеют особое значение в электротехнике, поэтому их магнитные свойства. Здесь отметим лишь, что магнитная индукция в ферромагнитном веществе во много (сотни и тысячи) раз больше, чем в парамагнитном, при одинаковой намагничивающей силе внешних токов.
Намагниченность вещества
Из сказанного ранее ясно, что результирующее магнитное поле в веществе складывается из двух полей: поля внешних токов (токов в проводах) и поля элементарных внутренних токов.
В связи с этим для равномерного магнитного поля катушки (рис. 8.24, б) при наличии внутри ее какого-либо сердечника, например стального, можно записать уравнение, аналогичное уравнению (8.9) (это можно сделать и при неравномерном поле; равномерное поле взято для упрощения рассуждения):
где Iв — полный элементарный ток, сцепленный с контуром а-6-в-г.
Сравнивая (8.31) с (8.13), видим, что магнитная индукция в веществе (парамагнитном или ферромагнитном) больше, чем в вакууме, в связи с действием элементарных токов, т. е. благодаря намагничиванию вещества.
Степень намагничивания вещества оценивается вектором намагниченности М.
Для однородного по всем направлениям вещества величина вектора намагниченности равна геометрической сумме магнитных моментов элементарных токов в единице объема вещества:
Напряженность магнитного поля
Найдем величину общего магнитного момента элементарных токов, сцепленных с контуром а-б-в-г, учитывая, что при одинаковой ориентации токи с контуром сцеплены только на участке а-г длиной l (рис. 8.24, б):
где iв — элементарный ток, сцепленный с контуром а-б-в-г; S — площадь, ограниченная контуром элементарного тока. Подставив 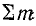
откуда
Равенство (8.31) можно представить в виде
или
Из формулы (8.33) следует, что магнитное поле в веществе можно рассматривать как результат действия только токов в проводах (в витках катушки), если в качестве характеристики поля принять новую векторную величину Н, которая называется напряженностью магнитного поля:
С введением этого понятия формула (8.33) примет вид
Это уравнение подобно уравнению (8.13), полученному на основе представления о циркуляции вектора магнитной индукции в поле тока бесконечно длинной катушки.
Напряженность Н как характеристика магнитного поля не зависит от свойств среды, а определяется только величиной токов в проводах, что значительно облегчает расчеты магнитных полей.
Магнитная проницаемость вещества
Из уравнения (8.34) можно выразить величину магнитной индукции в веществе:
Намагниченность вещества является результатом действия внешнего магнитного поля токов. Коэффициент пропорциональности между напряженностью поля Н и намагниченностью М называется магнитной восприимчивостью
Магнитная восприимчивость выражает способность вещества намагничиваться под действием внешнего магнитного ноля. Учитывая выражение (8.35), запишем
В этой формуле величина μ0Н характеризует только магнитное поле в вакууме, обозначается В0, а называется магнитной индукцией в вакууме:
Магнитную индукцию в веществе можно выразить формулой
Величина
характеризует магнитные свойства вещества, в котором существует магнитное поле, и называется абсолютной магнитной проницаемостью,
На основе формулы (8.37) абсолютную магнитную проницаемость можно определить отношением модуля магнитной индукции к модулю напряженности магнитного поля.
В практике удобно пользоваться отношением абсолютной магнитной проницаемости вещества μa к магнитной постоянной μ0:
Величина 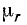
Магнитная восприимчивость ферромагнитных веществ велика, поэтому их величина 
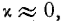
Задача 8.21.
На кольцевой неферромагнитный сердечник, средний радиус которого r = 48 см, намотана обмотка, имеющая N1 = 2000 витков. На эту обмотку концентрично наложена вторая обмотка с числом витков N2 = 3500. Площадь поперечного сечения сердечника S = 20 см2. Определить взаимную индуктивность обмоток, если коэффициент магнитной связи между ними k = 0,9. При последовательном соединении обмоток и токе I = 3 А определить магнитный поток в сердечнике в двух случаях: а) обмотки включены согласно; б) обмотки включены встречно.
Решение. Для определения взаимной индуктивности воспользуемся формулой (8.27). Но предварительно найдем индуктивность каждой катушки.
Индуктивность первой катушки
Индуктивность второй катушки
Взаимная индуктивность
Для определения магнитного потока найдем намагничивающую силу:
а) при согласном включении
б) при встречном включении
Напряженность магнитного поля
Магнитная индукция
Магнитный поток
Закон полного тока и его применение
Введение понятия о магнитной проницаемости вещества позволяет все формулы, полученные ранее для магнитного поля в вакууме, применить и для магнитного поля в веществе, заменив в них магнитную постоянную магнитной проницаемостью μa. О такой возможности свидетельствует полная аналогия формул (8.36) и (8.37).
Это обстоятельство вместе с понятием о напряженности магнитного поля является основой для формулировки закона полного тока.
Закон полного тока
В формуле (8.8)
вместо μ0 запишем μa, а вместо магнитной индукции подставим равную ей величину 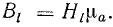
Уравнение (8.40) выражает закон полного тока:
циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему поверхность, ограниченную этим контуром.
В тех случаях, когда напряженность магнитного поля имеет одинаковую величину по всему контуру, а выбранный контур совпадает с линией магнитной индукции, уравнение (8.40) оказывается более простым: 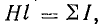
Если контур содержит несколько участков с различными величинами напряженности поля (Н1, Н2, .., Нn), но в пределах каждого участка напряженность не меняется, то уравнение (8.40) можно записать так:
где n — номер участка контура.
В таком выражении закон полного тока напоминает второй закон Кирхгофа и применяется при расчете магнитных цепей.
Рис. 8.25. Изменение характеристик магнитного поля на границе двух сред
Изменение магнитного поля на границе двух сред
Выделим на границе двух сред, имеющих относительные магнитные проницаемости μr1 и μr2, замкнутый контур а-б-в-г-д-е-а (рис. 8.25) около некоторой точки А.
Магнитная индукция и напряженность магнитного поля в этой точке характеризуются векторами B1 и Н1, в первой и В2 и Н2 во второй среде.
Разложим векторы В и Н в обеих средах на нормальные Вn, Нn и тангенциальные Вt и Ht составляющие.
При отсутствии на поверхности раздела сред токов проводимости по закону полного тока для указанного контура
Учитывая равенство соответствующих отрезков контура, получим Н1t = H2t или
На границе двух сред тангенциальная составляющая напряженности магнитного поля не изменяется.
Магнитный поток сквозь поверхность раздела сред создают только нормальные составляющие магнитной индукции. Учитывая же непрерывность линий магнитной индукции, можно заключить, что магнитный поток на границе двух сред не изменяется. Таким образом,
где ΔS — любой элемент площади на границе раздела сред.
Сокращая на ΔS, получим B1n = B2n или
Разделим равенство (8.43) на (8.44):
Отсюда
Равенство (8.45) выражает закон преломления линий магнитной индукции на границе двух сред.
В частном случае, когда линии магнитной индукции перпендикулярны плоскости раздела, тангенциальные составляющие напряженности и индукции равны нулю. Магнитная индукция на границе двух сред в этом случае не изменяется [см. формулу (8.44)]: B1 = B2.
Напряженность магнитного поля изменяется скачком:
или
и оказывается больше в среде с меньшей магнитной проницаемостью.
Задача 8.24.
Определить изменение направления линий магнитной индукции на границе стали с воздухом, если известны для стали μr1 = 1000; α1 = 89°.
Решение. По формуле (8.45),
Случай изменения магнитного поля на границе ферромагнитной среды и воздуха часто встречается в электромагнитных устройствах, где магнитный поток замыкается по стальным участкам, чередующимся с воздушными зазорами.
Магнитная проницаемость стали во много раз больше магнитной проницаемости воздуха, поэтому при значениях α1 даже близких к 90°, α2 получается близким к нулю.
Практически можно считать, что линии магнитной индукции в воздухе у границы со сталью перпендикулярны поверхности раздела.
Свойства и применение ферромагнитных материалов
Ферромагнитные вещества широко применяются в электротехнике благодаря их способности намагничиваться и значительно усиливать внешнее магнитное поле. Для практики большое значение имеют особые свойства ферромагнитных веществ, выявляющиеся в процессе намагничивания. Эти свойства можно проследить на опыте, измеряя напряженность поля Н и магнитную индукцию В катушки со стальным сердечником (рис. 8.26).
Рис. 8.26. Схема для намагничивания ферромагнитного сердечника
Намагничивание ферромагнитных материалов
С ростом напряженности поля Н магнитная индукция В увеличивается по закону
График В(Н), соответствующий первоначальному намагничиванию и показанный на рис. 8.27, называется кривой первоначального намагничивания. Там же даны зависимости от напряженности поля обоих слагаемых μ0М и μ0Н, из которых складывается магнитная индукция в ферромагнитной среде.
Получив состояние магнитного насыщения, уменьшим напряженность внешнего магнитного поля Н. Магнитная индукция уменьшается по кривой 1-2 (рис. 8.28), которая не совпадает с кривой первоначального намагничивания (кривая 0-1). При Н = 0 магнитная индукция имеет остаточное значение Вr.
Рис. 8.27. Зависимость магнитной индукции и намагниченности от напряженности поля
Рис. 8.28. График циклического перемагничивания ферромагнитного сердечника
Размагничивание сердечника как бы запаздывает по сравнению с уменьшением напряженности поля. Это явление называют магнитным гистерезисом.
Особенностью ферромагнитных веществ является наличие сильных магнитных связей молекул, вследствие чего в них образуются весьма малые (микроскопические) области, внутри которых магнитные моменты молекул ориентированы в одну сторону. Такие области имеют значительный общий магнитный момент и называются самопроизвольно намагниченными.
В отсутствие внешнего магнитного поля ферромагнитные вещества не проявляют своих магнитных свойств, так как магнитные моменты самопроизвольно намагниченных областей направлены беспорядочно. Общий магнитный момент всего объема тела оказывается равным нулю.
Усиление магнитного поля в ферромагнитной среде, а также явления магнитного насыщения и остаточного магнетизма хорошо объясняются изменением ориентации магнитных моментов областей самопроизвольной намагниченности под действием внешнего поля.
В образовании внутреннего магнитного поля участвуют не отдельные молекулы, как в диамагнитных и парамагнитных веществах, а целые области, обладающие магнитным моментом.
Магнитное насыщение означает, что все магнитные моменты ориентированы по направлению внешнего поля. Остаточный магнетизм объясняется тем, что при снятии внешнего поля определенная часть магнитных моментов сохраняет приобретенное при намагничивании направление, так что результирующий магнитный момент объема сердечника не уменьшается до нуля.
Магнитный гистерезис
Изменив направление тока в катушке и, следовательно, направление внешнего поля в сердечнике, увеличим напряженность поля (вектор Н изменил направление). Магнитная индукция уменьшается до нуля (отрезок кривой 2-3), а затем изменит направление на обратное.
Величину напряженности поля Н, необходимую для уничтожения поля в сердечнике, называют коэрцитивной (задерживающей) силой. В точке 3 внешнее поле скомпенсировало остаточное поле намагниченности сердечника (—Нс = М). В дальнейшем результирующее поле в сердечнике изменяет направление и усиливается, пока не наступает насыщение (участок 3-4). Аналогично можно получить данные и начертить нижнюю часть графика 4-5-6-1. Полученную замкнутую кривую В(Н) называют петлей магнитного гистерезиса.
Циклическое перемагничивание вещества в области значений В и Н, меньших тех, которые соответствуют полному насыщению, тоже образует петлю гистерезиса, полностью заключенную внутри предельной петли.
Ряд таких петель гистерезиса показан на рис. 8.29. Кривую 0-1- 2-3-4, проведенную через вершины всех петель гистерезиса, называют основной кривой намагничивания. Она проходит близко к кривой первоначального намагничивания, но не совпадает с ней.
Основную кривую намагничивания используют при технических расчетах магнитных систем. На рис. 8.30 изображены основные кривые намагничивания некоторых ферромагнитных материалов.
Рис. 8.29. Петли магнитного гистерезиса
Рис. 8.30. Основные кривые намагничивания некоторых ферромагнитных материалов
Свойства ферромагнитных материалов
На основе опыта намагничивания и перемагничивания ферромагнитных материалов можно сформулировать основные их свойства.
- Ферромагнитные вещества относительно легко и сильно намагничиваются. Относительная магнитная проницаемость μr для некоторых ферромагнитных материалов достигает значений 105 и выше.
- С ростом напряженности внешнего магнитного поля намагниченность и магнитная индукция увеличиваются; однако намагниченность и магнитная индукция не пропорциональны напряженности поля (см. рис. 8.27). Это значит, что магнитная восприимчивость
и магнитная проницаемость μr — не постоянные величины, а зависят от намагниченности М.
- Начиная с некоторой напряженности поля Н при ее увеличении происходит магнитное насыщение, т. е. такое состояние ферромагнитных веществ, при котором рост напряженности поля не влечет за собой увеличения намагниченности.
- При уменьшении напряженности поля Н после достижения состояния насыщения намагниченность и магнитная индукция уменьшаются. Однако величины М и В отличаются от тех, которые были зафиксированы для одинаковых Н при увеличении напряженности.
- При устранении внешнего поля (Н = 0) обнаруживается остаточная намагниченность (М и В не равны нулю).
- При увеличении напряженности поля Н в обратном направлении происходит сначала размагничивание намагниченного образца, а затем намагничивание в обратном направлении (М и В меняют знак) до насыщения.
- При циклическом перемагничивании с определенной частотой ферромагнитное вещество нагревается, что свидетельствует о затрате энергии на перемагничивание.
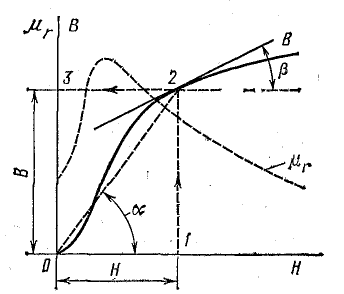
Абсолютная магнитная проницаемость ферромагнитного вещества определяется в каждой точке основной кривой намагничивания (рис. 8.31) отношением
где mВ и mН — масштабы по осям координат.
Рис. 8.31. К определению магнитной проницаемости
Магнитная проницаемость, определяемая этим отношением, называется статической.
Как видим, с ростом напряженности поля магнитная проницаемость вначале увеличивается, а при переходе в область насыщения уменьшается.
Кроме статической магнитной проницаемости μa определяется дифференциальная магнитная проницаемость μaдиф. Последняя пропорциональна тангенсу угла наклона касательной к основной кривой намагничивания в каждой точке:
Что касается затрат энергии на перемагничивание, то, как будет показано дальше, величина их пропорциональна площади, ограниченной петлей магнитного гистерезиса.
Магнитно-мягкие и магнитно-твердые материалы
Для всех ферромагнитных материалов отмеченные свойства являются общими, однако проявляются они по-разному в зависимости от их химического состава.
В связи с этим различают две основные группы ферромагнитных материалов: магнитно-твердые и магнитно-мягкие.
Магнитно-твердые материалы имеют большие величины остаточной магнитной индукции и коэрцитивной силы, широкую петлю магнитного гистерезиса. Магнитно-твердыми являются хромовольфрамовые, хромомолибденовые стали (Вr = 1 Т, Нс = 60 А/см); сплав алнико (Al, Ni, CO) и др.
Для магнитно-мягких материалов характерны большая магнитная проницаемость и малая коэрцитивная сила (узкая петля магнитного гистерезиса).
К магнитно-мягким материалам относятся электротехническая сталь (малоуглеродистая с присадкой кремния от 1,7 до 4%), чистое электролитическое железо, электротехнический чугун, пермаллой (80% Ni и 20% Fe) и др.
Магнитно-мягкие материалы применяются для устройства магнитных цепей электрических машин, аппаратов, электромагнитов и т. п. Свойства материалов обеспечивают в этих устройствах создание сильных магнитных полей при относительно небольших величинах намагничивающих сил IN и относительно малые потери энергии при перемагничивании.
Задача 8.27.
Решить задачу 8.21, если сердечник выполнен из электротехнической стали, характеристика намагничивания которой приведена на рис. 8.30.
Решение. Магнитную проницаемость стали можно принять постоянной условно в предположении, что в тех пределах изменения магнитной индукции, какие имеют место при переключении обмоток, характеристика намагничивания стали близка к прямой. Если характеристику намагничивания нельзя хотя бы приближенно считать прямолинейной, то формула (8.27) в этом случае непригодна. Взаимную индуктивность обмоток можно определить по формуле (8.25), предполагая без тока сначала одну, а затем другую обмотки.
В этом случае
Для определения индуктивности катушки нельзя воспользоваться и формулой (8.28), так как неизвестна магнитная проницаемость стали.
При разомкнутой второй обмотке найдем индуктивность L1 и взаимоиндуктивность М1.2.
Намагничивающая сила обмотки
Напряженность поля
Магнитную индукцию находят по кривой намагничивания электротехнической стали в следующем порядке (см. рис. 8.30 и 8.31). На оси абсцисс определяют точку 1, отстоящую от начала координат на расстоянии 0-1, выражающем в принятом масштабе найденную величину напряженности поля. Из этой точки проводят прямую, параллельную оси ординат, до пересечения с кривой намагничивания в точке 2. Эту точку проектируют на ось ординат, где и читают ответ — величину магнитной индукции (отрезок 0-3).
Для H1 = 20 А/см
Магнитный поток
Собственное потокосцепление первой обмотки
Индуктивность первой обмотки
Найдем взаимное потокосцепление, считая поток рассеяния
Взаимная индуктивность
Расчет электрических полей
В рабочем состоянии электрических устройств и установок между токоведущими частями имеется разность потенциалов, т. е. существует электрическое поле.
Кроме основного (разрешенного) канала тока имеется бесчисленное множество потенциальных каналов, которые закрыты электрической изоляцией. Таким образом, электрическая изоляция находится под действием электрического поля и должна быть рассчитана на то, чтобы надежно выполнять свои функции. Для расчета необходимо определить характеристики электрического поля.
Эти и другие вопросы, относящиеся к электрическому полю, рассматриваются в данной главе.
Применение закона кулона для расчета электрического поля
Расчет электрических полей на основе закона Кулона применяется в тех случаях, когда электрические заряды тел можно рассматривать сосредоточенными в весьма малом объеме, т. е. полагать заряженные тела точечными.
Электрическое поле уединенного заряженного тела
Из закона Кулона следует, что напряженность элегического поля уединенного точечного заряженного тела
где Q — величина заряда тела; Q0 — заряд пробного тела; r — расстояние от заряженного тела до точки, в которой определяется напряженность поля.
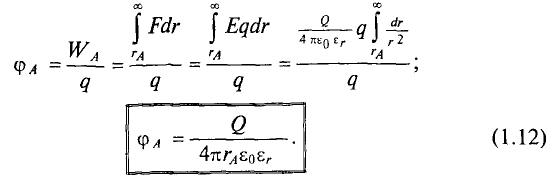
Электрическое поле уединенного точечного заряженного тела неравномерно. Найдем потенциал поля в некоторой точке 1 (см. рис. 7.3), используя выражение (1.3), с помощью которого выразим работу в поле на пути от некоторой точки 1 до бесконечности:
где r1 — расстояние от заряженного тела до точки 1.
Положение точки 1 выбрано произвольно, поэтому полученное выражение можно записать для любой точки
Напряжение между точками 1 и 2
Между напряженностью электрического поля и потенциалом в некоторой точке имеется определенная связь, которую выразим в общем виде.
Из выражения (1.3) следует:
Знак минус в этих выражениях указывает на то, что энергия убывает, если перемещение происходит в направлении напряженности поля.
Отсюда
Еn — величина проекции вектора Е на направление dl.
Электрическое поле группы заряженных тел
При рассмотрении электрического поля в вакууме (а также в воздухе) установили, что напряженность поля линейно зависит от заряда тела [в выражении (7.1) Q = const]. Поэтому при определении напряженности результирующего поля от действия нескольких заряженных тел можно пользоваться принципом наложения полей.
В каждой точке пространства, окружающего заряженные тела, электрическое поле одного тела накладывается на поле другого.
Для определения общей напряженности нужно найти величину и направление вектора напряженности каждого из составляющих полей, а затем сложить векторы:
Принцип наложения действителен и при определении потенциала в некоторой точке результирующего поля. Но потенциалы складываются алгебраически, так как они скалярные величины:
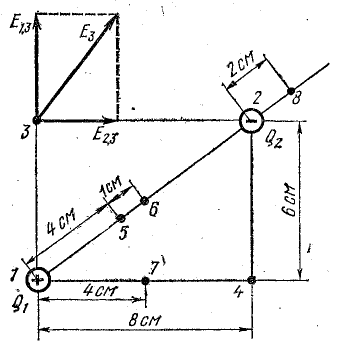
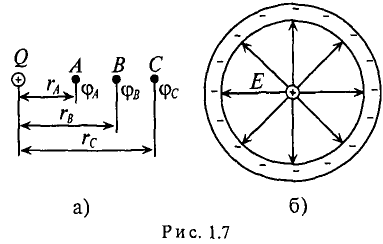
Задача 7.1. Два точечных тела, заряды которых Q1 = 3,2 • 10-11 Кл и Q2 = -4,267 • 10-11 Кл, расположены в воздухе в противоположных вершинах воображаемого прямоугольника со сторонами 6 и 8 см (рис. 7.1). Определить напряженность и потенциал в двух других вершинах и в точках 5, 6, 7, 8.
Рис. 7.1. К задаче 7.1
Решение. Определим в заданных точках напряженность электрического поля каждого заряженного тела в отдельности по формуле (7.1), обозначая напряженность буквой Е с индексами. Первая цифра индекса указывает, с каким заряженным телом связано поле, вторая — точку, где определяется напряженность этого поля.
В точке 3
По формуле (7.2),
Согласно принципу наложения, общую напряженность поля найдем геометрическим (векторным) сложением составляющих.
По условию задачи векторы Е1.3 и Е2.3 направлены под углом 90° друг к другу. Поэтому напряженность результирующего поля можно подсчитать как гипотенузу прямоугольного треугольника, катетами которого являются эти векторы:
В общем случае определение напряженности результирующего поля можно выполнить графически, по правилам векторного сложения или по теореме косинусов.
В точке 5
По условию задачи векторы Е1.5 и Е2.5 направлены по прямой 1-2 в одну сторону. Поэтому величину напряженности результирующего поля можно найти как сумму численных значений Е1.5 и Е2.5:
Е5 = Е1.5 + Е2.5 = 180 + 106,7 = 286,7 В/м;
V5 = V1.5 + V2.5 = 13,6 В.
Напряженность и потенциал результирующего поля в точках 4, 6, 7, 8 определите самостоятельно.
Теорема Гаусса и ее применение
В практике чаще встречаются случаи, когда заряд тела распределен по его поверхности с некоторой плотностью. В таких случаях задачи решаются более просто на основе теоремы Гаусса.
Поток вектора напряженности электрического поля
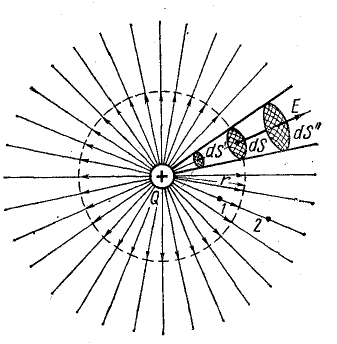
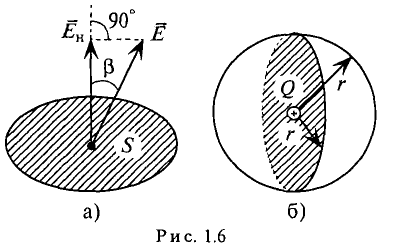
Рассматривая электрическое поле, изображенное на рис. 7.3, выделим элемент поверхности площадью dS. Он представляет собой маленькую часть сферы радиусом r, в центре которой помещено точечное тело с положительным зарядом Q.
Рис. 7.3. К определению потока вектора напряженности электрического поля
В силу геометрической симметрии поля вектор напряженности Е по величине одинаков во всех точках поверхности и направлен перпендикулярно ей. Произведение ЕdS выражает величину элементарного потока dN вектора напряженности электрического поля через элемент поверхности dS, если линии напряженности перпендикулярны пронизываемой ими поверхности:
Определим полный поток N вектора напряженности электрического поля, для чего сложим элементарные потоки по всей поверхности сферы:
Вынося постоянную величину Е за знак суммы и учитывая, что вектор Е всюду перпендикулярен поверхности сферы, получаем
где 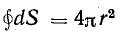
Подставляя напряженность поля в формулу (7.1), получим
Теорема Гаусса
Приведенные рассуждения справедливы и при отрицательном заряде с той лишь разницей, что поток вектора напряженности в этом случае отрицательный.
Из формулы (7.8) следует, что поток N не зависит от радиуса сферической поверхности.
Потоку вектора напряженности электрического поля можно придать некоторую наглядность с помощью линий напряженности.
Вследствие симметрии электрического поля в рассматриваемом случае линии напряженности пронизывают всю поверхность сферы и их плотность (число линий на единицу площади) одинакова. Предположим, что эта плотность выбрана численно равной напряженности поля. Тогда общее число линий, пронизывающих поверхность сферы, будет численно равно полному потоку вектора напряженности поля N.
Число линий напряженности, а следовательно, и поток вектора напряженности остаются одинаковыми для сферы любого радиуса. Это справедливо и для элементов dS‘ и dS» сферических поверхностей, через которые проходят одни и те же линии напряженности (рис. 7.3), образующие конус с вершиной в центре сферы.
Элементарный поток вектора напряженности заключен внутри указанного конуса и пронизывающие элемент поверхности dS линии напряженности образуют элементарную трубку поля. Сложив потоки всех трубок по всему объему шара, получим полный поток вектора напряженности электрического поля точечного заряженного тела.
Можно доказать, что формула (7.8) справедлива не только для сферы, окружающей точечное заряженное тело, но и для любой замкнутой поверхности.
В общем случае направление вектора напряженности Е может быть не перпендикулярно элементу поверхности dS около выбранной точки А (рис. 7.4). Угол между направлением вектора Е и внешней нормалью n к поверхности в точке А обозначим а (внешняя нормаль — это линия, перпендикулярная поверхности в выбранной точке, направленная от этой поверхности с внешней стороны). Для определения потока через элемент поверхности нужно взять проекцию вектора Е на направление внешней нормали
где
Тогда
Рис. 7.4. К определению потока вектора напряженности электрического поля
Рис. 7.5. К определению напряженности электрического поля заряженной плоскости
Суммирование элементарных потоков по всей замкнутой поверхности дает полный поток
Если внутри замкнутой поверхности находится любое число тел с разноименными зарядами, в формулы (7.8) и (7.9) следует ввести алгебраическую сумму всех зарядов:
Алгебраическая сумма зарядов берется в данном случае потому, что линии напряженности при положительных и отрицательных зарядах направлены противоположно.
Формула (7.10) является математическим выражением теоремы Гаусса, которая формулируется так: поток вектора напряженности электрического поля сквозь замкнутую поверхность в вакууме равен отношению электрического заряда, заключенного внутри этой поверхности к электрической постоянной.
Поле заряженной плоскости
Бесконечная плоскость (рис. 7.5) имеет заряд, распределенный с плотностью а. Выделим вокруг части этой плоскости замкнутую поверхность, которая образована двумя плоскими поверхностями S, параллельными заряженной плоскости, и цилиндрической боковой поверхностью, перпендикулярной ей. Вследствие симметрии все точки поверхности S имеют одинаковую напряженность поля.
Кроме того, вектор напряженности направлен перпендикулярно заряженной плоскости, т. е. перпендикулярно поверхности S и параллельно цилиндрической боковой поверхности. В этом случае поток вектора напряженности через цилиндрическую поверхность равен нулю и, следовательно, общий поток равен потоку через поверхности S.
Заряд, заключенный внутри выделенной поверхности, составляет σS.
Согласно теореме Гаусса,
Отсюда
Рис. 7.6. К определению напряженности и потенциала электрического поля между двумя заряженными плоскостями
Электрическое поле двух параллельных бесконечных плоскостей, несущих разноименные заряды одинаковой плотности (рис. 7.6), определяется наложением полей положительной и отрицательной пластин.
Как видно из формулы (7.11), напряженность поля бесконечной плоскости не связана с расстоянием от нее. Поэтому вне пластин (точка А) поля положительной и отрицательной пластин взаимно скомпенсированы, т. е. результирующая напряженность поля равна нулю (Е = 0).
Между пластинами (точка В) поля их складываются, поэтому
Таким образом, между двумя бесконечными плоскостями, заряженными противоположно с одинаковой плотностью заряда, напряженность поля одинакова во всех точках по величине и направлению, т. е. электрическое поле равномерно.
Поле заряженного шара
Наметим в пространстве, окружающем заряженный шар, произвольную точку 1, отстоящую от центра шара на расстоянии r (рис. 7.7) Выделим сферическую поверхность, концентричную с поверхностью заряженного шара, так, чтобы точка 1 лежала на этой поверхности. Вследствие симметрии все точки выделенной поверхности имеют одинаковую напряженность. В данном случае вектор напряженности Е направлен радиально в каждой точке, т. е. перпендикулярно выбранной сферической поверхности.
Поток вектора напряженности поля через выделенную сферическую поверхность
Заряд шара
где σ — поверхностная плотность заряда; R — радиус шара.
Согласно теореме Гаусса [см. формулу (7.8)],
Отсюда для напряженности поля получим выражение
Напряженность поля заряженного шара имеет такое же выражение, какое получено из закона Кулона для точечного заряженного тела. Следовательно, заряд шара можно считать сосредоточенным в центре и рассматривать заряженный шар как точечное заряженное тело. При r = R
На рис. 7.7 показаны графики зависимости напряженности и потенциала поля уединенного заряженного шара от расстояния r.
Поле заряженного прямого провода
Проведем через некоторую точку 1 пространства цилиндрическую поверхность, ось которой совпадает с осью провода круглого сечения (рис. 7.8).
Вследствие симметрии во всех точках выделенной поверхности линии напряженности перпендикулярны ей, а напряженность поля одинакова:
Рис. 7.7. К определению напряженности и потенциала электрического поля заряженного шара
Рис. 7.8. К определению напряженности электрического поля прямого заряженного провода
Поток вектора напряженности
где 2πrl — боковая поверхность цилиндра.
Поток через основания цилиндра равен нулю, так как линии напряженности не пронизывают их.
Согласно теореме Гаусса,
где Q = τl; τ — линейная плотность заряда на проводе.
Задача 7.3.
Построить графики напряженности электрического поля заряженного шара (поверхностная плотность заряда σ = 2 • 10-8 Кл/м2, радиус шара R = 5 см) и заряженного прямого провода (линейная плотность заряда τ = 4 • 10-8 Кл/м).
Решение. Для построения графиков нужно задаться несколькими значениями расстояния r от центра шара или оси провода до точек, в которых предполагается определить напряженность поля. По формуле (7.13) определяют напряженность электрического поля заряженного шара E1, по формуле (7.14) — заряженного провода E2.
При r = 10 см
Определите напряженность электрического поля в обоих случаях в точках, положение которых определяется расстоянием r = 5, 20, 50, 100 см и ∞; постройте графики Е(r) в прямоугольной системе координат.
Электрическое поле в однородном диэлектрике
По сравнению с проводниками количество свободных заряженных частиц в единице объема диэлектрика очень мало. Поэтому при наличии электрического поля направленным движением свободных заряженных частиц можно пренебречь и считать, что в диэлектрике преобладают электростатические явления.
При этом электрическое поле воздействует на вещество диэлектрика, которое определенным образом изменяет электрическое поле.
Поляризация диэлектрика
Различают диэлектрики с полярными и неполярными молекулами. Полярные молекулы в электрическом отношении можно уподобить электрическому диполю (рис. 7.9, а). Электрическим диполем называют совокупность двух точечных заряженных тел, обладающих равными по величине и противоположными по знаку зарядами, расстояние между которыми очень мало по сравнению с расстоянием от них до точек, в которых рассматривается поле диполя.
Рис. 7.9. Диэлектрик в электрическом поле
Электрической характеристикой диполя является его электрический момент р, численное значение которого равно произведению величины заряда точечных тел на расстояние между ними:

Вектор электрического момента направлен от отрицательного заряда к положительному.
Полярные молекулы в диэлектрике расположены так, что электрические моменты их направлены беспорядочно. Поэтому тела, в состав которых входят полярные молекулы, в целом нейтральны, хотя каждая полярная молекула создает свое электрическое поле.
Рассмотрим диэлектрик, помещенный в равномерное электрическое поле с напряженностью Е между двумя заряженными металлическими пластинами (рис. 7.9).
Во внешнем электрическом поле полярная молекула (диполь) испытывает действие пары сил, которая поворачивает ее таким образом, что электрический момент диполя оказывается направленным так же, как и напряженность поля (рис. 7.9, б).
В неполярных молекулах диэлектрика под действием внешнего электрического поля происходит смещение заряженных частиц вдоль его направления, в результате чего они приобретают свойство диполей. Это явление называется поляризацией диэлектрика.
Поляризованность диэлектрика
Степень поляризации диэлектрика оценивают вектором поляризованности P. Для однородного по всем направлениям диэлектрика величина вектора поляризованности представляет геометрическую сумму электрических моментов р молекул, заключенных в единице объема:
Поляризованность тем больше, чем сильнее электрическое поле. Зависит она и от свойства диэлектрика. Поэтому поляризованность можно выразить произведением
где 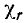
В результате поляризации диэлектрика диполи стремятся располагаться вдоль линий напряженности электрического поля. При этом внутри диэлектрика в любом объеме, не меньшем объема молекулы, сохраняется равенство общих зарядов того и другого знака, так что диэлектрик остается нейтральным. По поверхностям диэлектрика, прилегающим к металлическим пластинам, распределены частицы, имеющие заряд одного знака: отрицательный — на границе с положительной пластиной и положительный— на границе с отрицательной пластиной (рис. 7.9, в).
На обеих поверхностях заряд распределен равномерно с одинаковой плотностью σ. Таким образом, на границе между металлической пластиной и диэлектриком распределены два вида заряженных частиц: свободные частицы металлической пластины с общим зарядом Q0 и связанные частицы диэлектрика с общим зарядом Qп противоположного знака.
Электрическое поле в диэлектрике соответствует общему заряду частиц Q = Q0 — Qп; оно физически существует в пространстве между молекулами диэлектрика. Это поле можно также представить как результат наложения двух полей — внешнего (напряженность Е0) и внутреннего (напряженность Еп).
В данном случае внешним полем называется поле свободных заряженных частиц металлических пластин при отсутствии диэлектрика, а внутренним — поле связанных заряженных частиц диэлектрика, существующее независимо от внешнего поля. Независимое существование внутреннего поля диэлектрика до некоторой степени условно, так как оно возникает только при наличии внешнего поля и в большинстве случаев исчезает при его отсутствии.
Однако имеются такие диэлектрики, которые, будучи поляризованными внешним электрическим полем, сохраняют остаточную поляризацию (сегнетоэлектрики и электреты).
Электрическое смещение
На основании теоремы Гаусса [см. формулу (7.8)] для равномерного поля свободных заряженных частиц
а для поля в диэлектрике
Найдем величину вектора поляризованности Р (рис. 7.9, в). Электрический момент элементарного поверхностного заряда имеет значение σdSl, где l — расстояние между пластинами или толщина диэлектрика; σSl — момент всего объема диэлектрика.
Таким образом числитель выражения (7.16) в данном случае имеет величину σSl, а знаменатель — Sl.
Тогда поляризованность
Величина поляризованности равна плотности заряда на поверхности диэлектрика.
Вместе с тем заряд связанных частиц на поверхности диэлектрика равен общему заряду частиц, которые смещаются в диэлектрике через любую плоскость, параллельную обкладкам.
Согласно выражению (7.19),
Общий заряд связанных частиц с учетом выражения (7.20)
Тогда
или
Из этого выражения следует, что электрическое поле в диэлектрике можно рассматривать только в связи с зарядом Q0 свободных заряженных частиц и не учитывать явление поляризации, если в качестве характеристики поля принять другую векторную величину D, называемую электрическим смещением:
С введением этого понятия формула (7.21) упрощается:
Электрическое смещение как характеристика электрического поля не зависит от свойств среды, а определяется только зарядом свободных частиц, что значительно облегчает расчеты электрических полей.
В выражение (7.22) подставим численное значение вектора поляризованности согласно (7.17):
В этой формуле величина ε0Е характеризует только электрическое поле в вакууме, обозначается D0 и называется электрическим смещением в вакууме:
Слагаемым 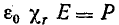
Диэлектрическая проницаемость
Сравнивая выражения (7.18) и (7.19), нетрудно установить, что при внесении диэлектрика в пространство между металлическими пластинами электрическое поле становится слабее того поля, которое создается при отсутствии диэлектрика и прочих одинаковых условиях, т. е. Е < Е0.
Это обстоятельство формально можно учесть, введя в выражения, определяющие напряженность поля, вместо электрической постоянной ε0 величину εa > ε0, считая заряд по-прежнему равным заряду Q0 свободных частиц.
Величина εa, называемая диэлектрической проницаемостью веществ, наряду с диэлектрической восприимчивостью 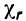
Из выражения (7.23) электрическое смещение можно выразить формулой
Величина 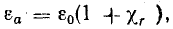
Диэлектрическая проницаемость имеет такую же размерность, что и электрическая постоянная.
Рис. 7.10. Вольт-кулоновые характеристики конденсаторов
Обычно электрические свойства веществ оценивают отношением их диэлектрической проницаемости εa к электрической постоянной ε0:
Диэлектрическая восприимчивость 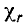
Величина εr называется относительной диэлектрической проницаемостью и показывает, во сколько раз электрическое поле в диэлектрике слабее, чем в пустоте, при прочих равных условиях.
Емкость конденсаторов, изготовленных с применением таких диэлектриков, не зависит от величины напряжения между его обкладками. Такие конденсаторы называются, линейными, так как зависимость их заряда от напряжения — Q(U) — прямолинейная (рис. 7. 10, а). Диэлектрическая проницаемость сегнетоэлектриков сильно зависит от напряженности электрического поля, что видно из рис. 7.10, б, на котором эта зависимость показана вместе с графиком D (Е). Конденсатор с сегнетоэлектриком имеет нелинейную вольт-кулоновую характеристику Q(U). Такие конденсаторы применяются в устройствах автоматики.
Электрическая емкость
Связь уединенного проводника, имеющего электрический заряд Q, с собственным электрическим полем характеризуется величиной заряда. В этом поле поверхность проводника является поверхностью равного потенциала V; такой же потенциал имеют все точки в объеме проводника, поэтому можно говорить о потенциале проводника.
При увеличений или уменьшении заряда совершается работа и энергетическая характеристика (потенциала) проводника соответственно увеличивается или уменьшается.
Однако при равном изменении зарядов двух проводников, каждый из которых уединен, изменения их потенциалов могут быть неравными. На зависимость между потенциалом и зарядом уединенного проводника влияют форма и размеры его поверхности, а также среда, в которую проводник помещен. Для выражения этого влияния введено понятие электрической емкости уединенного проводника С.
Общее выражение емкости
Электрическая емкость проводника есть величина, характеризующая способность проводника накапливать электрический заряд, численно равная отношению заряда проводника к его потенциалу:
Связь потенциала и заряда проводника в данном случае выражена в предположении, что все другие проводники бесконечно удалены, а потенциал бесконечно удаленной точки равен нулю.
В вакууме это отношение для данного проводника остается неизменным независимо от величины заряда. Во многих диэлектриках, используемых в практике, емкость проводника тоже постоянна в широких пределах изменения заряда.
Единица емкости
[С] = кулон/вольт = фарад (Ф).
Фарад — очень крупная единица емкости, поэтому в практических расчетах часто выражают емкость в долях фарада — микрофарадах (мкФ) и пикофарадах (пФ): 1Ф = 106 мкФ = 1012 пФ.
В системе заряженных проводников на заряд и потенциал каждого проводника влияют форма, расположение и величина зарядов других проводников. В этом случае применяется понятие о емкости системы проводников.
Наибольшее значение для практики имеют системы из двух проводников, получающих равные по величине, но противоположные по знаку заряды. Устройства из двух изолированных друг от друга проводников, которые получают равные по величине, но противоположные по знаку заряды, называются конденсаторами.
Проводники конденсатора, имея равные по величине, но противоположные по знаку заряды (см. рис. 1.6, а), имеют разные потенциалы V1 и V2. Следовательно, между проводниками имеется напряжение U = V1 — V2.
Величина, характеризующая связь заряда конденсатора с напряжением между его обкладками, численно равная отношению заряда к напряжению, называется емкостью конденсатора:
Емкость конденсатора зависит от формы и размеров обкладок, расстояния и свойств среды между обкладками.
Проводимость диэлектриков, используемых для заполнения пространства между обкладками конденсатора, ничтожно мала. Поэтому конденсаторы могут служить для накопления и сохранения электрического поля и его энергии.
Емкость плоского конденсатора
Конденсатор называется плоским, если его обкладками являются две плоскопараллельные металлические пластины (см.рис. 1.6, а).
Обычно расстояние между пластинами мало по сравнению с их линейными размерами, поэтому электрическое поле плоского конденсатора можно считать равномерным.
Для определения емкости воспользуемся формулой (7.12), в которой электрическую постоянную ε0 заменим диэлектрической проницаемостью εa диэлектрика. С учетом формулы (1.5) получим
Умножим обе части равенства на S — площадь одной пластины:
Емкость плоского конденсатора
Емкость цилиндрического конденсатора
Обкладками цилиндрического конденсатора служат две цилиндрические поверхности, оси которых совпадают (рис. 7.11). Электрическое поле неравномерное, но имеет радиальную симметрию.
Рис. 7.11. К определению емкости цилиндрического конденсатора
Полагая и в этом случае расстояние между обкладками малым по сравнению с длиной конденсатора, т. е. пренебрегая искажением поля у его краев, для определения емкости используем выводы [формулу (7.14)]. Обозначим радиусы обкладок: внутренней — r1, внешней — r2; потенциалы— V1 и V2. Потенциал внутренней обкладки V1 можно найти, если к потенциалу V2 прибавить работу по перемещению заряженных частиц между обкладками конденсатора, отнесенную к единице заряда.
Напряженность электрического поля на пути между обкладками не постоянна, поэтому работу определим как сумму работ на элементарных участках пути dr, столь малых, что в пределах таких участков напряженность поля можно считать постоянной:
Напряжение между обкладками
Емкость цилиндрического конденсатора
Емкость двухпроводной линии
Определим емкость двухпроводной линии, у которой радиус проводов r0, расстояние между осями проводов а, длина проводов l, напряжение между проводами U, а заряд этой системы проводов Q (рис. 7.12).
При а >> r0 будем полагать, что заряд каждого провода распределен равномерно по его поверхности. Это значит, что взаимное влияние проводов на распределение зарядов по поверхности не учитывается.
Для определения разности потенциалов между проводами воспользуемся формулой (7.14). В некоторой точке А, находящейся между проводами в плоскости, проведенной через их оси, напряженность поля:
первого провода
второго провода
Рис. 7.12. К определению емкости двухпроводной линии
Заряды проводов имеют противоположные знаки, поэтому между проводами векторы E1 и E2 направлены в одну сторону. Общая напряженность поля в точке А
Напряженность поля зависит от расстояния r, поэтому напряжение между проводами
Учитывая, что а >> r0, напряжение между проводами
Емкость двухпроводной линии
Задача 7.8.
Определить емкость и заряд плоского воздушного конденсатора, у которого площадь обкладки S = 100 см2, расстояние между обкладками l = 5 мм, напряжение между обкладками U = 100 В.
Решение.
Задача 7.9.
Определить емкость цилиндрического воздушного конденсатора, имеющего радиусы обкладок r1 = 40 мм; r2 = 50 мм и длину l = 0,5 м.
Решение.
Электрическая прочность диэлектрика
Диэлектрик, разделяющий проводники с разными электрическими потенциалами (электроизоляция), находится в электрическом поле и несет электрическую нагрузку, величина которой ограничена электрической прочностью диэлектрика.
В электрических устройствах электрическую изоляцию часто выполняют из нескольких диэлектриков с различной диэлектрической проницаемостью. Например, обмотки силового трансформатора, изолированные хлопчатобумажной изоляцией, погружают в трансформаторное масло, которое также является изолятором и одновременно охлаждающей средой. Между обмотками устанавливаются барьеры из электротехнического картона.
Таким образом, электрическая изоляция, имеющая различные конструктивные формы, должна быть не только сконструирована, но и рассчитана на электрическую прочность.
Пробивная напряженность
Напряженность электрического поля в диэлектрике зависит, как уже известно, от напряжения между проводниками (электродами), расстояния между ними, формы и размеров электродов, свойств диэлектрика.
При увеличении напряженности электрического поля, т. е. увеличении электрической нагрузки изоляции, наступает в конце концов разрушение диэлектрика (пробой).
Величина напряженности электрического поля, при которой начинается пробой диэлектрика и изоляционные свойства его нарушаются, называют пробивной напряженностью или электрической прочностью диэлектрика.
Отношение электрической прочности к действительной величине напряженности поля называют запасом прочности:
Изменение электрического поля на границе двух диэлектриков
Рассмотрим плоский конденсатор, между обкладками которого имеется два слоя диэлектриков с диэлектрическими проницаемостями εr1 и εr2 (рис. 7.13).
Величина и направление вектора напряженности электрического поля на границе раздела диэлектриков изменяются тем больше, чем больше отличаются их диэлектрические проницаемости.
Плоскость раздела диэлектриков параллельна плоскости обкладок. В этом случае линии напряженности поля перпендикулярны плоскости раздела, т. е. в обоих диэлектриках их направления совпадают.
На основании теоремы Гаусса напишем выражения для электрического смещения в диэлектриках:
Как видно, при направлении поля, перпендикулярном плоскости раздела диэлектриков, электрическое смещение в обоих диэлектриках одинаково: численно оно равно поверхностной плотности заряда обкладок конденсатора:
Нетрудно убедиться в том, что напряженность поля в обоих диэлектриках не будет одинакова:
или
Рис. 7.13. Конденсатор с двумя слоями разнородных диэлектриков
Напряженность поля больше в диэлектрике с меньшей диэлектрической проницаемостью.
Скачкообразное изменение напряженности поля на границе раздела двух диэлектриков, имеющих разные диэлектрические проницаемости, физически объясняется тем, что вследствие разной поляризованности диэлектриков на границе образуется избыточный связанный заряд плотностью 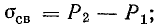
Наличие заряда на границе раздела диэлектриков дает основание считать конденсатор с двумя или несколькими слоями составленным из двух или нескольких конденсаторов.
Устройство изоляции из нескольких слоев различных диэлектриков в неравномерном электрическом поле позволяет в определенной мере выравнять напряженность электрического поля и тем создать более благоприятные условия для работы изоляции и сократить ее размеры.
Задача 7.12.
Между обкладками плоского воздушного конденсатора, имеющими площадь S = 1800 см2 и напряжение U0 = 1,2 кВ, расстояние l составляет 0,5 см. Определить напряженность электрического поля и заряд конденсатора. Как изменятся эти величины, если конденсатор отключить от источника напряжения, а пространство между обкладками заполнить парафином (εr = 2)?
Решение. Напряженность электрического поля плоского конденсатора определяется отношением напряжения к расстоянию между обкладками [см. формулу (1.5)]:
Для определения заряда найдем емкость конденсатора по формуле (7.29):
заряд
После отключения конденсатора от источника напряжения заряд Q сохраняется неизменным и в том случае, если воздух как диэлектрик между пластинами заменить парафином. При этом предполагается, что утечки заряда нет.
Емкость конденсатора с парафином будет уже другой, так как в формулу (7.29) вместо ε0 должна быть подставлена величина εa = ε0 [см. формулу (7.26)]:
При этом же заряде Q0 и увеличении емкости напряжение между обкладками уменьшится:
Напряженность поля также уменьшится:
Вывод. При замене диэлектрика заряд конденсатора, отключенного от источника напряжения, сохраняется неизменным; напряжение между обкладками и напряженность поля изменяются обратно пропорционально относительной диэлектрической проницаемости.
Задача 7.13.
Решить задачу 7.12 при условии, что конденсатор остается подключенным к источнику напряжения.
Решение. Если конденсатор после замены диэлектрика остается подключенным к источнику напряжения, то напряженность поля при любом диэлектрике остается неизменной (геометрические размеры конденсатора также не изменились):
Изменение емкости конденсатора (в данном случае увеличение в два раза) приведет к увеличению заряда в два раза:
Рис. 7.14. К задаче 7.16
Задача 7.16.
Плоский воздушный конденсатор находится под напряжением 20 кВ. Расстояние между обкладками равно 2 см, площадь обкладок 200 см2. Определить емкость, запас электрической прочности конденсатора, если электрическая прочность воздуха 30 кВ/см.
Определить емкость конденсатора, распределение напряжения между слоями и запас электрической прочности, если, не отключая конденсатора от источника заряда, в воздушный промежуток между обкладками параллельно им внести лист стекла толщиной 0,5 см (рис. 7.14) с относительной диэлектрической проницаемостью εr1 = 7. Электрическая прочность стекла больше, чем воздуха.
Решение. Напряженность электрического поля воздушного конденсатора [см. формулу (1.5)]:
Запас прочности
После внесения в воздушный промежуток стекла найдем распределение напряжения между слоями, имея в виду, что общее напряжение конденсатора равно сумме напряжений слоев:
где l1 и l2 — толщина слоев.
Согласно формулам (7.33) и (7.25),
Отсюда
Запас электрической прочности конденсатора определяется по менее электрически прочному диэлектрику, в данном случае воздуху:
Таким образом, при внесении в воздушный промежуток стекла запас электрической прочности конденсатора уменьшился, несмотря на то что электрическая прочность стекла сама по себе больше, чем воздуха.
Емкость воздушного конденсатора
Емкость конденсатора после внесения стекла определим из выражения, полученного раньше для напряжения на конденсаторе, умножив и разделив правую его часть на S:
Соединения конденсаторов
Система заряженных проводников может содержать не два, а больше проводников. Каждая пара проводников, полностью изолированных друг от друга, характеризуется электрической емкостью.
Практический интерес обычно представляет вопрос о распределении заряда и потенциалов в системе проводников, когда она заряжена от источника постоянного напряжения. Во многих случаях системы заряженных проводников по отношению к источнику можно рассматривать как последовательное, параллельное или смешанное соединение конденсаторов.
Последовательное соединение
На рис. 7.15 изображены три конденсатора, соединенные последовательно. К зажимам источника постоянного напряжения (точки 1, 2, 3, 4) присоединены две крайние обкладки последовательной цепочки конденсаторов, другие обкладки с источником непосредственно не соединяются и заряжаются вследствие электростатической индукции. Поэтому заряд всех конденсаторов и каждого в отдельности один и тот же:
Для упрощения расчетов можно группу конденсаторов заменить одним с эквивалентной емкостью.
Рис. 7.15. Последовательное соединение конденсаторов
Рис. 7.16. Параллельное соединение конденсаторов
Напряжение на эквивалентном конденсаторе равно общему напряжению группы последовательно соединенных конденсаторов:
Учитывая (7.28) и (7.36), получим:
Если в последовательную цепь соединяются n конденсаторов одинаковой емкости Сn, то эквивалентная емкость
Параллельное соединение
При параллельном соединении все конденсаторы соединены одной обкладкой в общей точке 1, а другой обкладкой — в общей точке 2 (рис. 7.16). К этим точкам подводится напряжение источника. В таком случае группу конденсаторов тоже можно заменить одним с эквивалентной емкостью С.
Все конденсаторы имеют между обкладками одно и то же напряжение U, а заряды получаются разными:
Каждый конденсатор получает заряд независимо от другого, поэтому общий заряд равен сумме зарядов конденсаторов:
Подставляя сюда выражения зарядов (7.39) и сокращая на U, получим
Эквивалентная емкость равна сумме емкостей. При параллельном соединении n конденсаторов одинаковой емкости Сn эквивалентная емкость
Задача 7.18. Определить заряд и напряжение каждого конденсатора в схеме рис. 7.17, а, если емкости их С1 = 8 мкФ, С2 = 5 мкФ, С3 = 3 мкФ, а общее напряжение U = 100 В.
Решение. Такого типа задачу нужно решать, начав с определения эквивалентной емкости. Конденсаторы С2 и Сз соединены параллельно относительно точек 1, 2 схемы. Заменим эти два конденсатора одним с эквивалентной емкостью С2.3 (рис. 7.17, б). Согласно формуле (7.40),
В новой, упрощенной схеме между точками 1, 2 вместо двух конденсаторов включен один С2.3. Емкость его равна емкости двух конденсаторов С2 и С3. При такой замене распределение напряжений в схеме не изменилось, не изменился и общий заряд в системе. По отношению к точкам 1 и 3 конденсаторы С2.3 и С1 соединены последовательно.
Заменим эти два конденсатора одним с эквивалентной емкостью С, которая является общей емкостью между точками 1 и 3 в схеме рис. 7.17, а. После замены получим схему рис. 7.17, в, где к зажимам источника напряжения (точки 1, 3) подключен один конденсатор.
Рис. 7.17. к задаче 7.18
Согласно формуле (7.37),
Общий заряд системы конденсаторов в схеме рис. 7.17, а
Общий заряд системы равен заряду конденсаторов С1 и С2.3:
На основании этого определяют напряжения:
Напряжение U2 является общим для конденсаторов С2 и С3. Заряды этих конденсаторов:
Проверка:
Задача 7.19.
Определить емкость каждого конденсатора в цепи рис. 7.17, а, если известно, что общий заряд ее Q = 1 Кл при напряжении U = 200 В, а заряд третьего конденсатора Q3 = 0,4 Кл при напряжении U2 = 40 В.
Решение. Эквивалентная емкость всей цепи
Емкость третьего конденсатора
Заряд, напряжение и емкость второго конденсатора:
Заряд, напряжение и емкость первого конденсатора:
Проверка определения емкостей для схемы рис. 7.17:
Электрическое поле
Каждый химический элемент (вещество) состоит из совокупности мельчайших материальных частиц — атомов.
В состав атомов любого вещества входят элементарные частицы, часть которых обладает электрическим зарядом. Атом представляет собой систему, состоящую из ядра, вокруг которого вращаются электроны.
В ядре атома сосредоточены протоны, несущие в себе положительный заряд. Электроны имеют отрицательный электрический заряд. В электрически нейтральном атоме заряд электронов равен по абсолютной величине заряду протонов.
Электроны вращаются вокруг ядра по строго определенным орбитам (слоям). В каждом слое количество электронов не должно превышать определенного числа (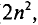
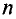
Порядковый номер химического элемента в Периодической таблице Менделеева численно равен положительному заряду ядра этого элемента, следовательно, и числу вращающихся вокруг него электронов. На рис. 1.1 схематически показана структура атомов Водорода (а), кислорода (б) и алюминия (в) с порядковыми номерами 1, 8 и 13.
Атомы, у которых внешние электронные слои целиком заполнены, имеют устойчивую электронную оболочку. Такой атом прочно держит все электроны и не нуждается в получении добавочного их количества.
Атом кислорода, например, имеющий шесть электронов, размешенных во внешнем слое, обладает возможностью притянуть к себе два недостающих электрона для заполнения внешнего электронного слоя. Это достигается путем соединения с атомами таких элементов, у которых внешние электроны слабо связаны со своим ядром. Например, электронами внешнего (третьего) слоя атома алюминия, которые слабо удерживаются и легко могут быть вырваны из атома.
Если нарушается равенство числа электронов и протонов, то из электрически нейтрального атом становится заряженным. Заряженный атом называется ионом.
Если в силу каких-либо причин атом потеряет один или несколько электронов, то в нем нарушится равенство зарядов и такой атом становится положительным ионом, поскольку в нем преобладает положительный заряд протонов ядра. Если атом приобретает один или несколько электронов, то он становится отрицательным ионом, так как в нем преобладает отрицательный заряд.
Вещество (твердое тело, жидкость, газ) считается электрически нейтральным, если количество положительных и отрицательных зарядов в нем одинаково. Если же в нем преобладают положительные или отрицательные заряды, то оно считается соответственно положительно или отрицательно заряженным.
В Единой системе конструкторской документации (ЕСКД), которая используется в данном учебнике, электрический заряд (количество электричества) обозначается буквой Q или q, а единицей заряда (в системе СИ) является 1 кулон, то есть [Q] = Кл (кулон). Электрон и протон имеют равный по величине, но противоположный по знаку заряд 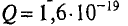
Электрический заряд или заряженное тело создают электрическое поле.
Электрическое поле — это пространство вокруг заряженного тела или заряда, в котором обнаруживается действие сил на пробный заряд, помещенный в это пространство.
Электрическое поле, создаваемое неподвижными зарядами, называется электростатическим.
Напряженность электрического поля
Обнаружить электрическое поле можно пробным зарядом, если поместить его в это поле. Пробным называется положительный заряд, внесение которого в исследуемое поле не приводит к его изменению. То есть пробный заряд не влияет ни на силу, ни на энергию, ни на конфигурацию поля.
Если в точку А электрического поля (рис. 1.2), созданного зарядом Q, расположенную на расстоянии r от него, внести пробный заряд q, то на него будет действовать сила 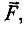
Величина силы 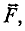
где 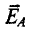
Из (1.1) видно, что
То есть напряженность каждой точки электрического поля характеризуется силой, с которой поле действует на единицу заряда, помещенного в эту точку. Таким образом, напряженность является силовой характеристикой каждой точки электрического поля.
Измеряется напряженность электрического поля в вольтах на метр
Напряженность электрического поля — величина векторная.
Направление вектора напряженности в любой точке электрического поля совпадает с направлением силы, действующей на положительный пробный заряд, помещенный в эту точку поля (см. рис. 1.2).
Поскольку в дальнейшем будут учитываться только значения силы и напряженности, будем обозначать их Fu £ соответственно.
Напряженность является параметром каждой точки электрического поля и не зависит от величины пробного заряда q. Изменение величины q приводит к пропорциональному изменению силы F(l.l), а отношение 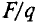
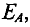
Для наглядности электрическое поле изображают электрическими линиями, которые иногда называют линиями напряженности электрического поля, или силовыми линиями. Электрические линии направлены от положительного заряда к отрицательному. Линия проводится так, чтобы вектор напряженности поля в данной точке являлся касательной к ней (рис. 1.3в).
Электрическое поле называется однородным, если напряженность его во всех точках одинакова по величине и направлению. Однородное электрическое поле изображается параллельными линиями, расположенными на одинаковом расстоянии друг от друга.
Однородное поле, например, существует между пластинами плоского конденсатора (рис. 1.3г).
Напряженность поля точечных зарядов
Точечным считается заряд, размерами которого можно пренебречь по сравнению с расстоянием, на котором рассматривается его действие.
Сила взаимодействия 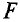
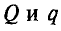
где 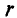
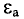
Из (1.3) следует, что напряженность электрического поля заряда Q в точке А (рис. 1.2) равна
Таким образом, напряженность поля 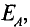
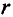
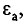
Единицей измерения абсолютной диэлектрической проницаемости среды является фарад на метр
так как
Различные среды имеют разные значения абсолютной диэлектрической проницаемости. Абсолютная диэлектрическая проницаемость вакуума
называется электрической постоянной.
Абсолютную диэлектрическую проницаемость любой среды 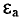
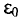
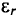
Диэлектрическая проницаемость 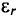
Из (1.6) следует
Таким образом, напряженность электрического поля, созданного зарядом Q на расстоянии 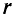
Напряженность электрического поля, созданного несколькими зарядами в какой-либо точке А этого поля, определяется геометрической суммой напряженностей, созданных в этой точке каждым точечным зарядом: 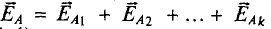
Пример 1.1
Расстояние между точечными зарядами 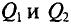
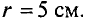
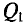
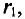
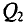
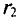
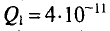
Решение
Напряженность, созданная зарядом 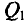
Напряженность, созданная зарядом 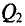
Направление векторов напряженности 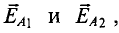
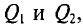
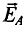
Между векторами напряженности в данном примере угол равен 90° 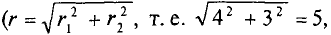
Теорема Гаусса
Произведение напряженности электрического поля Е и площадки S, перпендикулярной к ней, в однородном электрическом поле называют потоком вектора напряженности поля N сквозь эту площадку (рис. 1.6а)
где 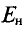
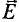
Как следует из рис. 1.6а,
Единица измерения потока вектора напряженности
Для неоднородного электрического поля площадку Sразбивают на элементарные бесконечно малые площадки 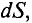
Тогда элементарный поток
Для определения потока вектора напряженности сквозь всю площадку S элементарные потоки 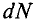
Если, например, точечный заряд Q расположен в центре сферической поверхности радиусом r (рис. 1.66), то напряженность во всех точках этой поверхности, как следует из (1.8), равна
Векторы напряженности перпендикулярны этой поверхности, т.е. 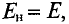
где 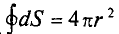
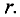
То есть поток вектора напряженности N не зависит ни от формы поверхности, ни от места расположения зарядов внутри нее.
Таким образом, поток вектора напряженности электрического поля сквозь замкнутую поверхность определяется отношением суммы зарядов, расположенных внутри этой поверхности, к абсолютной диэлектрической проницаемости среды
Формула (1.11) является математическим выражением теоремы Гаусса, которая применяется для расчета электрического поля.
Пример 1.2
Определить поток вектора напряженности электрического поля сквозь сферическую поверхность радиусом r = 3 см (рис. 1.66), заполненную маслом 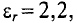
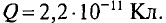
Решение
Поток вектора напряженности сквозь сферическую поверхность
Тогда напряженность на поверхности сферы
где
Напряженность на поверхности сферы можно определить также по формуле (1.8)
То есть результат получился таким же.
Потенциал и напряжение в электрическом поле
Для энергетической характеристики каждой точки электрического поля вводится понятие «потенциал». Обозначается потенциал буквой
Потенциал в каждой точке электрического поля характеризуется энергией W, которая затрачивается (или может быть затрачена) полем на перемещение единицы положительного заряда q из данной точки за пределы поля, если поле создано положительным зарядом, или из-за пределов поля в данную точку, если поле создано отрицательным зарядом (рис. 1.7а).
Из приведенного выше определения следует, что потенциал в точке А равен 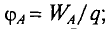
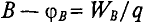
Измеряется потенциал в вольтах
Величина потенциала в каждой точке электрического поля определяется выражением
Потенциал — скалярная величина. Если электрическое поле создано несколькими зарядами, то потенциал в каждой точке поля определяется алгебраической суммой потенциалов, созданных в этой точке каждым зарядом.
Так как (рис. 1.7а) 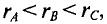

Если в точку А (рис. 1.7а) электрического поля поместить положительный пробный заряд q, то под действием сил поля он будет перемещаться из точки А в точку В, а затем в точку С, т. е. в направлении поля. Таким образом, положительный пробный заряд перемещается из точки с большим потенциалом в точку с меньшим потенциалом. Между двумя точками с равными потенциалами заряд перемещаться не будет. Следовательно, для перемещения заряда между двумя точками электрического поля должна быть разность потенциалов в этих точках. . Разность потенциалов двух точек электрического поля характеризует напряжение 
Напряжение между двумя точками электрического поля характеризуется энергией, затраченной на перемещение единицы положительного заряда между этими точками, т. е.
Измеряется напряжение в вольтах (В). Между напряжением и напряженностью в однородном электрическом поле (рис. 1.8) существует зависимость
откуда следует
Из (1.13) видно, что напряженность однородного электрического поля определяется отношением напряжения между двумя точками поля к расстоянию между этими точками.
В общем случае для неоднородного электрического поля значение напряженности определяется отношением
где 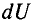
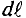
Единица напряженности электрического поля определяется из выражения (1.13)
Потенциалы в точках электрического поля могут иметь различные значения. Однако в электрическом поле можно выделить ряд точек с одинаковым потенциалом. Поверхность, проходящая через эти точки, называется равнопотенциальной, или эквипотенциальной.
Равнопотенциальная поверхность любой конфигурации перпендикулярна к линиям Рис 19 электрического поля. Обкладки цилиндрического конденсатора (рис. 1.76) и плоского конденсатора (рис. 1.9) имеют одинаковый потенциал по всей площади каждой обкладки и являются равнопотенциальными поверхностями.
Пример 1.3
Для условия примера 1.1 определить потенциал 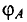
Решение
Следовательно, алгебраическая сумма потенциалов равна
Пример 1.4
Точечный заряд 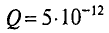
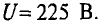
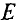
Решение
Напряженность однородного электрического поля между пластинами конденсатора
Напряженности, созданные зарядом Q в точках А и В,
Напряженности, созданные в точках А и В однородным электрическим полем конденсатора и зарядом Q, определяются геометрической суммой векторов напряженностей
В точке В векторы напряженностей 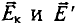
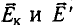
Электропроводность и проводники
Способность вещества проводить электрический ток называется электропроводностью.
По электропроводности все вещества делятся на проводники, диэлектрики и полупроводники.
Проводники обладают высокой электропроводностью. Различают проводники первого и второго рода.
К проводникам первого рода относятся все металлы, некоторые сплавы и уголь. В этих проводниках связь между электронами и ядром атома слаба, в результате чего электроны легко покидают пределы атома и становятся свободными. Направленное перемещение свободных электронов и обуславливает электропроводность проводников первого рода. Таким образом, проводники первого рода обладают электронной проводимостью.
К проводникам второго рода относятся электролиты, в которых происходит процесс электролитической диссоциации, разделение молекул на положительные и отрицательные ионы (ионизация). Направленное перемещение ионов обуславливает электропроводность проводников второго рода, т. е. в проводниках второго рода v имеет место ионная проводимость.
В проводниках отсутствует электростатическое поле (рис. 1.106).
Если проводник поместить в электростатическое поле, то пол действием сил этого поля происходит перемещение зарядов в проводнике: положительных — в направлении внешнего поля, отрицательных — в противоположном направлении (рис. 1.10а). Такое разделение зарядов в проводнике под действием внешнего поля называется электростатической индукцией.
Разделенные внутри проводника заряды создают свое электрическое поле, направленное от положительных зарядов к отрицательным, т. е. против внешнего поля (рис. 1.10а).
Очевидно, разделение зарядов в проводнике прекратится тогда, когда напряженность поля разделенных зарядов 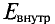
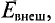
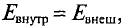
Таким образом, результирующее поле внутри проводника станет равным нулю (рис. 1.106). На этом принципе работает электростатический экран, защищающий часть пространства от внешних электрических полей (рис. 1.11). Для того чтобы внешние электрические поля не влияли на точность электроизмерения, измерительный прибор помещают внутрь замкнутой проводящей оболочки (экрана), в которой электрическое поле отсутствует (рис. 1.11).
Электропроводность и диэлектрики
Электропроводность диэлектриков практически равна нулю в силу весьма сильной связи между электронами и ядром атомов диэлектрика.
Если диэлектрик поместить в электростатическое поле, то в нем произойдет поляризация атомов, т. е. смещение разноименных зарядов в самом атоме, но не разделение их (рис. 1.12а). Поляризованный атом (молекула) может рассматриваться как электрический диполь (рис. 1.126), в котором «центры тяжести» положительных и отрицательных зарядов смешаются. Диполь — это система двух разноименных зарядов, расположенных на малом расстоянии друг от друга в замкнутом пространстве атома или молекулы.
Электрический диполь — это атом диэлектрика, в котором орбита электрона вытягивается в направлении, противоположном направлению внешнего поля 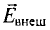
Поляризованные атомы создают свое электрическое поле, напряженность которого направлена против внешнего поля. В результате поляризации результирующее поле внутри диэлектрика ослабляется.
Интенсивность поляризации диэлектрика зависит от его диэлектрической проницаемости (Приложение 2). Чем больше диэлектрическая проницаемость, тем интенсивней поляризация в диэлектрике и тем слабее электрическое поле в нем:
Этим еще раз подтверждается справедливость формулы (1.8)
Таким образом, напряженность электрического поля обратно пропорциональна абсолютной диэлектрической проницаемости среды 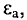
Если диэлектрик поместить в сильное электрическое поле, напряженность которого можно увеличивать, то при каком-то значении напряженности произойдет пробой диэлектрика, при этом электроны отрываются от атома, т. е. происходит ионизация диэлектрика. Таким образом, диэлектрик становится проводником.
Напряженность внешнего поля, при которой происходит пробой диэлектрика, называется пробивной напряженностью диэлектрика.
А напряжение, при котором происходит пробой диэлектрика, называют напряжением пробоя, или электрической прочностью диэлектрика.
где 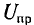
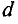
Напряженность электрического поля, которая допускается в диэлектрике при использовании его в электрических установках, называется допустимой напряженностью. Допустимая напряженность должна быть в несколько раз меньше электрической прочности. Электрическая прочность некоторых диэлектриков приведена в Приложении 2.
Электропроводность и полупроводники
К полупроводникам относятся материалы, которые по своим электрическим свойствам занимают промежуточное положение между проводниками и диэлектриками.
Широкое применение в полупроводниковой технике получили такие материалы, как германий, кремний, селен, арсенид галлия и др.
Электропроводность и концентрация носителей зарядов в полупроводниках зависит от температуры, освещенности, примесей, степени сжатия и т. д.
Электрическая проводимость полупроводника зависит от рода примесей, имеющихся в основном материале полупроводника, и от технологии изготовления его составных частей.
Различают две основные разновидности электрической проводимости полупроводников — электронную и «дырочную».
Природа электрического тока в полупроводниках с электронной проводимостью та же, что и в проводниках первого рода. Однако так как свободных электронов в единице объема полупроводника во много раз меньше, чем в единице объема металлического проводника, то ток в полупроводнике будет во много раз меньше, чем в металлическом проводнике. В технике электронная проводимость называется проводимостью 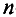
Полупроводник обладает «дырочной» проводимостью, если атомы его примеси стремятся захватить электроны атомов основного вещества полупроводника, не отдавая своих внешних электронов.
Если атом примеси «отберет» электрон у атома основного вещества, то в последнем образуется свободное место — «дырка» (рис. 1.13).
Атом полупроводника, потерявший электрон, называют «дыркой». Если «дырка» заполняется электроном, перешедшим из соседнего атома, то она «ликвидируется» и атом становится электронейтральным, а «дырка» смешается на место его атома, потерявшего электрон. Таким образом, если на полупроводник, обладающий «дырочной» проводимостью, действует электрическое поле, то «дырки» будут перемещаться в направлении поля.
Перемещение «дырок» в направлении электрического поля аналогично перемещению положительных электрических зарядов в поле, т. е. электрическому току в полупроводнике.
«Дырочная проводимость» в технике называется 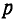
Нельзя строго разграничивать полупроводники по проводимости, так как наряду с «дырочной» проводимостью полупроводник обладает и электронной проводимостью.
Рассмотрим природу полупроводниковой проводимости на примере вентиля, представляющего собой контактное соединение двух проводников, один из которых обладает электронной проводимостью 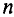
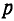
Вследствие большой концентрации электронов в полупроводнике типа п по сравнению с полупроводником 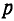
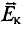
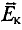
Эта напряженность 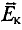
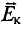
Если к полупроводникам, образующим 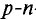
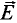
При прямом включении источника 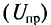
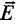
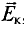
Если напряженность 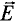
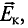
При обратном включении источника 
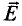
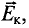
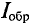
Таким образом, контактное соединение двух полупроводников с разными проводимостями 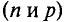
Односторонняя проводимость, малые габариты и другие свойства полупроводников используются в разнообразных приборах и устройствах (выпрямители, усилители и пр.). Полупроводники являются основным «строительным» материалом современных диодов, транзисторов, фоторезисторов, микропроцессоров и другой электронной техники.
- Расчет неразветвленной однородной магнитной цепи
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
- Дуальные цепи
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
Содержание
- Способы расчёта
- Через силу тока
- Соленоид конечной длины
- Катушка с тороидальным сердечником
- Длинный проводник
- Одновитковой контур и катушка
- Что такое индуктивность
- ЭДС индукции
- Применение катушек в технике
- Соленоид
- ÐагниÑное поле
- «Катушка ниток»
- Основные формулы для вычисления вектора МИ
- Закон Био-Савара-Лапласа
- Принцип суперпозиции
- Теорема о циркуляции
- Магнитный поток
- ÐÐ¸Ð´Ñ ÐºÐ°ÑÑÑек
- Основные уравнения
- В магнитостатике
- В общем случае
- Вариометр
- ÐÑÑоÑиÑ
- Общие сведения
- Свойства магнетизма
- Линии магнитной индукции
- Материал сердечника
- Современные магнитные материалы
- Как найти активную, реактивную и полную мощность
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
- µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
- l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Одновитковой контур и катушка
Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
L=Ф/I.
Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
L=L1∙N2.
Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.
Что такое индуктивность
Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):
L = Ф/ I.
С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.
Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
Применение катушек в технике
Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:
- сглаживание пульсаций и помех, накопление энергии;
- создание магнитных полей в различных устройствах;
- фильтры цепей обратной связи;
- создание колебательных контуров;
- трансформаторы (устройство из двух катушек, связанных индуктивно);
- силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
- ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
- применение катушек в качестве электромагнитов различных исполнительных механизмов;
- обмотки электромагнитных реле;
- индукционные печи;
- установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.
Соленоид
Соленоид отличается от обычной катушки по двум признакам:
- Длина обмотки превышает диаметр в несколько раз;
- Толщина обмотки меньше диаметра катушки также в несколько раз.
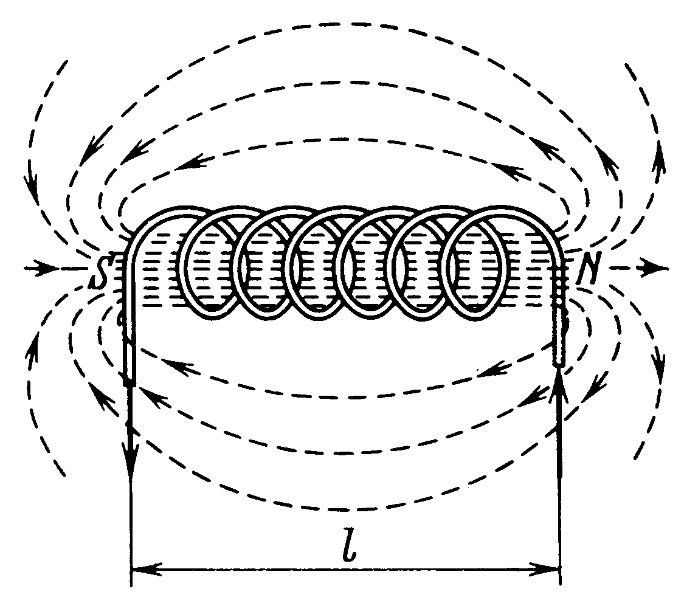
Параметры соленоида можно узнать из такого выражения:
L=µ0N2S/l,
где:
- µ0 – магнитная постоянная;
- N – количество витков;
- S – площадь поперечного сечения обмотки;
- l – длина обмотки.
Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника
Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.
ÐагниÑное поле
ÐÑо ÑловоÑоÑеÑание знакомо нам Ñо ÑколÑной ÑкамÑи. Ðо многие Ñже забÑли о Ñом, ÑÑо оно ознаÑаеÑ. ХоÑÑ ÐºÐ°Ð¶Ð´Ñй из Ð½Ð°Ñ Ð¿Ð¾Ð¼Ð½Ð¸Ñ, ÑÑо магниÑное поле ÑпоÑобно воздейÑÑвоваÑÑ Ð½Ð° пÑедмеÑÑ, пÑиÑÑÐ³Ð¸Ð²Ð°Ñ Ð¸Ð»Ð¸ оÑÑÐ°Ð»ÐºÐ¸Ð²Ð°Ñ Ð¸Ñ. Ðо, помимо ÑÑого, Ñ Ð½ÐµÐ³Ð¾ еÑÑÑ Ð¸ дÑÑгие оÑобенноÑÑи: напÑимеÑ, магниÑное поле Ð¼Ð¾Ð¶ÐµÑ Ð²Ð¾Ð·Ð´ÐµÐ¹ÑÑвоваÑÑ Ð½Ð° ÑлекÑÑиÑеÑки заÑÑженнÑе обÑекÑÑ, а ÑÑо знаÑиÑ, ÑÑо ÑлекÑÑиÑеÑÑво и магнеÑизм ÑеÑно ÑвÑÐ·Ð°Ð½Ñ Ð¼ÐµÐ¶Ð´Ñ Ñобой, и одно Ñвление Ð¼Ð¾Ð¶ÐµÑ Ð¿Ð»Ð°Ð²Ð½Ð¾ пеÑеÑекаÑÑ Ð² дÑÑгое. УÑÑнÑе понÑли ÑÑо доÑÑаÑоÑно давно и поÑÑÐ¾Ð¼Ñ ÑÑали назÑваÑÑ Ð²Ñе ÑÑи пÑоÑеÑÑÑ Ð²Ð¼ÐµÑÑе одним Ñловом — «ÑлекÑÑомагниÑнÑе Ñвлениѻ. Ðа Ñамом деле ÑлекÑÑомагнеÑизм — доволÑно инÑеÑеÑÐ½Ð°Ñ Ð¸ еÑÑ Ð½Ðµ до конÑа изÑÑÐµÐ½Ð½Ð°Ñ Ð¾Ð±Ð»Ð°ÑÑÑ Ñизики. Ðна оÑÐµÐ½Ñ Ð¾Ð±ÑиÑна, и Ñе знаниÑ, ÑÑо Ð¼Ñ Ð¼Ð¾Ð¶ÐµÐ¼ здеÑÑ Ð¸Ð·Ð»Ð¾Ð¶Ð¸ÑÑ Ð²Ð°Ð¼, — ÑÑо оÑÐµÐ½Ñ Ð¼Ð°Ð»Ð°Ñ ÑаÑÑÑ Ñого, ÑÑо извеÑÑно ÑеловеÑеÑÑÐ²Ñ Ð¾ магнеÑизме ÑегоднÑ.
Ð ÑейÑÐ°Ñ Ð¿ÐµÑейдÑм непоÑÑедÑÑвенно к пÑедмеÑÑ Ð½Ð°Ñей ÑÑаÑÑи. СледÑÑÑий Ñаздел бÑÐ´ÐµÑ Ð¿Ð¾ÑвÑÑÑн ÑаÑÑмоÑÑÐµÐ½Ð¸Ñ Ð½ÐµÐ¿Ð¾ÑÑедÑÑвенно ÑÑÑÑойÑÑва каÑÑÑки индÑкÑивноÑÑи.
«Катушка ниток»
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от «витков в квадрате».
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB
dB = µ0 *I*dl*sin α /4*π*r2,
где
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме
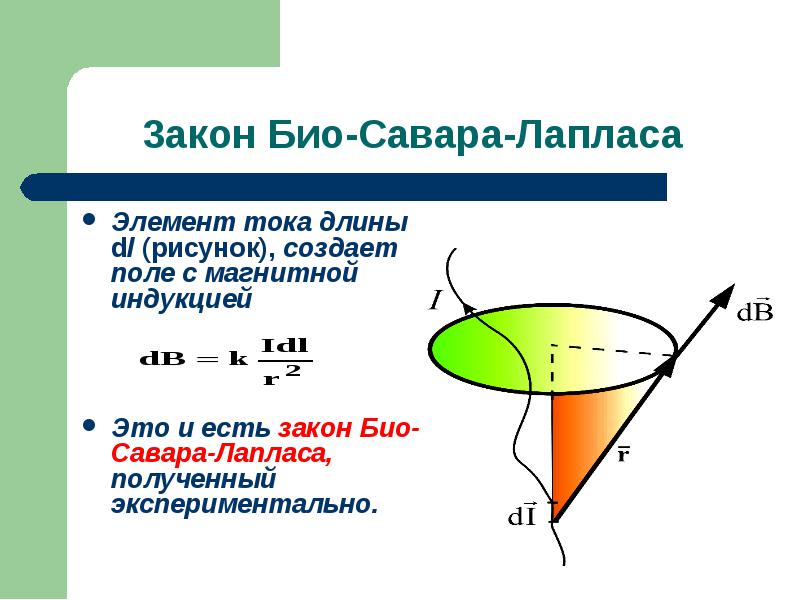
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→

Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.

где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
108 Мкс = 1 Вб.
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
φ = |B*S| = B*S*cosα,
где
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900)

Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
ÐÐ¸Ð´Ñ ÐºÐ°ÑÑÑек
Ðо ÑÑнкÑионалÑноÑÑи ÑазлиÑаÑÑ ÐºÐ¾Ð½ÑÑÑнÑе каÑÑÑки, наÑодÑÑие пÑименение в ÑадиоÑизике, каÑÑÑки ÑвÑзи, иÑполÑзÑемÑе в ÑÑанÑÑоÑмаÑоÑаÑ, и ваÑиомеÑÑÑ, Ñо еÑÑÑ ÐºÐ°ÑÑÑки, показаÑели коÑоÑÑÑ Ð¼Ð¾Ð¶Ð½Ð¾ ваÑÑиÑоваÑÑ Ð¸Ð·Ð¼ÐµÐ½ÐµÐ½Ð¸ÐµÐ¼ взаимного ÑаÑÐ¿Ð¾Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ ÐºÐ°ÑÑÑек.
Также ÑÑÑеÑÑвÑÐµÑ Ñакой вид каÑÑÑек, как дÑоÑÑели. ÐнÑÑÑи ÑÑого клаÑÑа Ñакже еÑÑÑ Ð´ÐµÐ»ÐµÐ½Ð¸Ðµ на обÑÑнÑе и ÑдвоеннÑе. Ðни имеÑÑ Ð²ÑÑокое ÑопÑоÑивление пеÑÐµÐ¼ÐµÐ½Ð½Ð¾Ð¼Ñ ÑÐ¾ÐºÑ Ð¸ оÑÐµÐ½Ñ Ð½Ð¸Ð·ÐºÐ¾Ðµ — поÑÑоÑнномÑ, благодаÑÑ ÑÐµÐ¼Ñ Ð¼Ð¾Ð³ÑÑ ÑлÑжиÑÑ ÑоÑоÑим ÑилÑÑÑом, пÑопÑÑкаÑÑим поÑÑоÑннÑй Ñок и задеÑживаÑÑим пеÑеменнÑй. СдвоеннÑе дÑоÑÑели оÑлиÑаÑÑÑÑ Ð±Ð¾Ð»ÑÑей ÑÑÑекÑивноÑÑÑÑ Ð¿Ñи болÑÑÐ¸Ñ ÑÐ¾ÐºÐ°Ñ Ð¸ ÑаÑÑоÑÐ°Ñ Ð¿Ð¾ ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ Ñ Ð¾Ð±ÑÑнÑми.
Основные уравнения
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике
В магнитостатическом пределе наиболее важными являются:
-
Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:
- B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{displaystyle {vec {B}}left({vec {r}}right)={mu _{0} over 4pi }int limits _{L_{1}}{frac {Ileft({vec {r}}_{1}right){vec {dL_{1}}}times left({vec {r}}-{vec {r}}_{1}right)}{left|{vec {r}}-{vec {r}}_{1}right|^{3}}},}
- B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{displaystyle {vec {B}}left({vec {r}}right)={mu _{0} over 4pi }int {frac {{vec {j}}left({vec {r}}_{1}right)dV_{1}times left({vec {r}}-{vec {r}}_{1}right)}{left|{vec {r}}-{vec {r}}_{1}right|^{3}}},}
-
Теорема Ампера о циркуляции магнитного поля:
- ∮∂SB→⋅dl→=μIS≡μ∫Sj→⋅dS→,{displaystyle oint limits _{partial S}{vec {B}}cdot {vec {dl}}=mu _{0}I_{S}equiv mu _{0}int limits _{S}{vec {j}}cdot {vec {dS}},}
- rotB→≡∇→×B→=μj→.{displaystyle mathrm {rot} ,{vec {B}}equiv {vec {nabla }}times {vec {B}}=mu _{0}{vec {j}}.}
В общем случае
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{displaystyle {vec {B}}}:
Три из четырех уравнений Максвелла (основных уравнений электродинамики)
-
- divE→=ρε, rotE→=−∂B→∂t{displaystyle mathrm {div} ,{vec {E}}={frac {rho }{varepsilon _{0}}}, mathrm {rot} ,{vec {E}}=-{frac {partial {vec {B}}}{partial t}}}
- divB→=, rotB→=μj→+1c2∂E→∂t{displaystyle mathrm {div} ,{vec {B}}=0, ,mathrm {rot} ,{vec {B}}=mu _{0}{vec {j}}+{frac {1}{c^{2}}}{frac {partial {vec {E}}}{partial t}}}
- а именно:
Закон отсутствия монополя:
-
- divB→=,{displaystyle mathrm {div} ,{vec {B}}=0,}
Закон электромагнитной индукции Фарадея:
-
- rotE→=−∂B→∂t,{displaystyle mathrm {rot} ,{vec {E}}=-{frac {partial {vec {B}}}{partial t}},}
Закон Ампера — Максвелла:
-
- rotB→=μj→+1c2∂E→∂t.{displaystyle mathrm {rot} ,{vec {B}}=mu _{0}{vec {j}}+{frac {1}{c^{2}}}{frac {partial {vec {E}}}{partial t}}.}
Формула силы Лоренца:
-
- F→=qE→+qv→×B→,{displaystyle {vec {F}}=q{vec {E}}+qleft,}
-
- Следствия из неё, такие как
Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
-
- dF→=Idl→×B→,{displaystyle d{vec {F}}=left,}
- dF→=j→dV×B→,{displaystyle d{vec {F}}=left,}
выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
-
- M→=m→×B→,{displaystyle {vec {M}}={vec {m}}times {vec {B}},}
выражение для потенциальной энергии магнитного диполя в магнитном поле:
-
- U=−m→⋅B→,{displaystyle U=-{vec {m}}cdot {vec {B}},}
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
-
- F→=Kqmr→r3.{displaystyle {vec {F}}=K{frac {q_{m}{vec {r}}}{r^{3}}}.}
(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
Выражение для плотности энергии магнитного поля
-
- w=B22μ{displaystyle w={frac {B^{2}}{2mu _{0}}}}
Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
Вариометр
Что такое катушка, показано выше на простых примерах. На практике для обозначения однотипных групп применяют специфическую терминологию. Вариометром, например, называют деталь с переменной индуктивностью. В типовой конструкции применяют две катушки, установленные одна внутри другой. Необходимый результат получают регулировкой взаимного положения функциональных компонентов. Для перемещения применяют ручной привод или автоматизированный механизм с внешней схемой управления.
К сведению. Не следует путать определения. Мультипликаторная катушка, например, – это приспособление для рыбной ловли. Такое устройство будет обладать индуктивностью при наматывании лески из проводящего материала. Однако в радиотехнических схемах подобные устройства не используют.

Особенности других конструкций:
- Дроссель обеспечивает высокое сопротивление цепи переменному току, поэтому такой пассивный индуктивный элемент часто применяют для создания фильтров. При подключении к сети питания 220В/ 50 Гц используют железные сердечники. При повышении частоты – ферритовые аналоги.
- Контурные катушки магнитные устанавливают в комбинации с конденсаторами для создания схем с определенной полосой пропускания.
- Электрическим реактором называют крупные конструкции, которые применяют в силовых сетях.
- Сдвоенные катушки применяют для разделения цепей по постоянной составляющей.

Выше отмечены типовые области применения элементов с индуктивными характеристиками. Они пригодны для создания фильтров, ограничения тока и разделения цепи прохождения постоянных и переменных составляющих сигнала. Магнитное поле катушки с током распространяется в пространстве. Чтобы предотвратить паразитное воздействие, отдельные компоненты размещают на достаточном расстоянии.
ÐÑÑоÑиÑ
ÐагнеÑизм наÑÐ¸Ð½Ð°ÐµÑ ÑÐ²Ð¾Ñ Ð¸ÑÑоÑÐ¸Ñ ÐµÑÑ Ñ ÐÑевнего ÐиÑÐ°Ñ Ð¸ ÐÑевней ÐÑеÑии. ÐÑкÑÑÑÑй в ÐиÑае магниÑнÑй железнÑк иÑполÑзовалÑÑ Ñогда в каÑеÑÑве ÑÑÑелки компаÑа, ÑказÑваÑÑей на ÑевеÑ. ÐÑÑÑ ÑпоминаниÑ, ÑÑо киÑайÑкий импеÑаÑÐ¾Ñ Ð¸ÑполÑзовал его во вÑÐµÐ¼Ñ Ð±Ð¸ÑвÑ.
Ðднако вплоÑÑ Ð´Ð¾ 1820 года магнеÑизм ÑаÑÑмаÑÑивалÑÑ Ð»Ð¸ÑÑ ÐºÐ°Ðº Ñвление. ÐÑÑ ÐµÐ³Ð¾ пÑакÑиÑеÑкое пÑименение бÑло заклÑÑено в Ñказании ÑÑÑелки компаÑа на ÑевеÑ. Ðднако в 1820 Ð³Ð¾Ð´Ñ ÐÑÑÑед пÑовÑл Ñвой опÑÑ Ñ Ð¼Ð°Ð³Ð½Ð¸Ñной ÑÑÑелкой, показÑваÑÑий влиÑние ÑлекÑÑиÑеÑкого Ð¿Ð¾Ð»Ñ Ð½Ð° магниÑ. ÐÑÐ¾Ñ Ð¾Ð¿ÑÑ Ð¿Ð¾ÑлÑжил ÑолÑком Ð´Ð»Ñ Ð½ÐµÐºÐ¾ÑоÑÑÑ ÑÑÑнÑÑ, взÑвÑиÑÑÑ Ð·Ð° ÑÑо вÑеÑÑÑз, ÑÑÐ¾Ð±Ñ ÑазÑабоÑаÑÑ ÑеоÑÐ¸Ñ Ð¼Ð°Ð³Ð½Ð¸Ñного полÑ.
СпÑÑÑÑ Ð²Ñего 11 леÑ, в 1831 годÑ, ФаÑадей оÑкÑÑл закон ÑлекÑÑомагниÑной индÑкÑии и ввÑл в обиÑод Ñизиков понÑÑие «Ð¼Ð°Ð³Ð½Ð¸Ñное поле». Ðменно ÑÑÐ¾Ñ Ð·Ð°ÐºÐ¾Ð½ поÑлÑжил оÑновой Ð´Ð»Ñ ÑÐ¾Ð·Ð´Ð°Ð½Ð¸Ñ ÐºÐ°ÑÑÑек индÑкÑивноÑÑи, о коÑоÑÑÑ ÑÐµÐ³Ð¾Ð´Ð½Ñ Ð¸ пойдÑÑ ÑеÑÑ.
РпÑежде Ñем пÑиÑÑÑпиÑÑ Ðº ÑаÑÑмоÑÑÐµÐ½Ð¸Ñ Ñамого ÑÑÑÑойÑÑва ÑÑÐ¸Ñ ÐºÐ°ÑÑÑек, оÑвежим в голове понÑÑие магниÑного полÑ.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Свойства магнетизма
Магнитное поле, как и любое другое физическое явление на Земле, имеет свои характеристики:
- Источник возникновения – движущиеся электрические заряды.
- Индукция магнитного поля – основная силовая его характеристика, которая существует в каждой отдельной его точке и является направленной.
- Его влияние ограничивается магнитами, движущимися зарядами и проводниками тока.
- Оно разделяется учеными на два типа: постоянное и переменное.
- Человек без специальных приборов не может почувствовать воздействие магнетизма.
- Это электродинамическое явление, ведь источник его происхождения – движущиеся частицы электрического тока. И только такие же частицы могут быть подвержены влиянию магнитного поля.
- Траектория движения заряженных частиц может быть лишь перпендикулярной.
Линии магнитной индукции
Сама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой.
Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках.
Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей.
Материал сердечника
Как и в предыдущем примере, для вычисления индукции катушки с сердечником в представленные выше формулы добавляют множитель относительной магнитной проницаемости «m
L = m0 * m * N2 * (S/l) = m0 * m * n2 * V.
С помощью этого коэффициента учитывают ферромагнитные свойства определенного материала.
Если для примера взять бесконечный (очень длинный) прямой провод с круглым сечением, то он будет обладать определенной индуктивностью:
L = (m0/2π) * l *(mc * ln(l/r) +1/4m,
где:
- mc – магнитная проницаемость (относительная) среды;
- r – радиус, который намного меньше длины (l) проводника.
Однако простые зависимости действуют только до определенной частоты. С определенного уровня волны малой длины начинают распространяться в поверхностной части проводников (скин-эффект). Дополнительно приходится учитывать влияние вихревых составляющих, экранирующих излучение и меняющих силовые параметры поля.
Современные магнитные материалы
Катушка будет работать в точном соответствии с расчетом, если правильно подобраны все функциональные компоненты конструкции. Как показано выше, существенное значение имеют параметры сердечника. Ниже отмечены важные особенности соответствующих материалов:
- Сталь с низким содержанием примесей стоит недорого. Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери.
- В специальные сорта (трансформаторную сталь) добавляют кремний. Для уменьшения вредного влияния поверхностных эффектов сердечник собирают из пластин. Однако и такие решения не следует использовать при частоте более 1 кГц.
- Сплавы из железа с никелем отличаются увеличенной магнитной проницаемостью. Рабочий диапазон – до 80-120 кГц.
- Порошковые материалы создают со слоем диэлектрика на поверхностях отдельных микроскопических гранул. Они хорошо приспособлены для работы с высокочастотными сигналами, однако не обладают большой магнитной проницаемостью.
- Ферриты – это материалы, созданные на основе керамических компонентов. Они отличаются хорошими техническими характеристиками, малыми потерями. Следует учитывать значительную зависимость от температуры, а также ухудшение рабочих параметров при длительной эксплуатации.

Как найти активную, реактивную и полную мощность
Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.
В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.
При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.
Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.
Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).
Что такое активная и реактивная электроэнергия, мощность
Как найти реактивную мощность
Активное и реактивное сопротивление
Компенсация реактивной мощности в электрических сетях
Активное и индуктивное сопротивление кабелей – таблица
Онлайн калькулятор расчета тока по мощности
Допустим имеется катушка индуктивности, известны: её длинна l, её число витков w и сила тока протекающего в витках катушки I. Пусть I=1А, w=3, l=0.01м.
Рисунок 1 — Катушка индуктивности
Направление магнитной индукции совпадает с направлением магнитного потока. Посмотреть как определить направление магнитного потока, правилом правой руки, можно в статье «обозначение индуктивно связанных катушек».
Чтобы рассчитать индукцию можно воспользоваться формулой (1):
Где
магнитные проницаемости, H — напряженность магнитного поля которую можно найти из формулы (2):
Из формулы (2) найдем напряженность:
Преобразуем формулу (1) с учётом формулы (3) и рассчитаем магнитную индукцию для приведенного примера:
Для расчета магнитной индукции можно воспользоваться программой:
Программа расчёта магнитной индукции.
Если программа не работает скопируйте её HTML-код в блокнот и сохраните в формате html.





















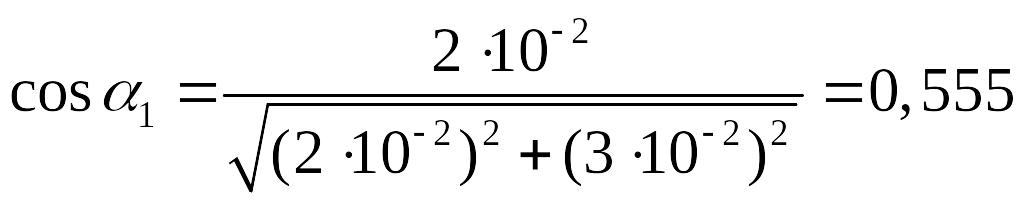
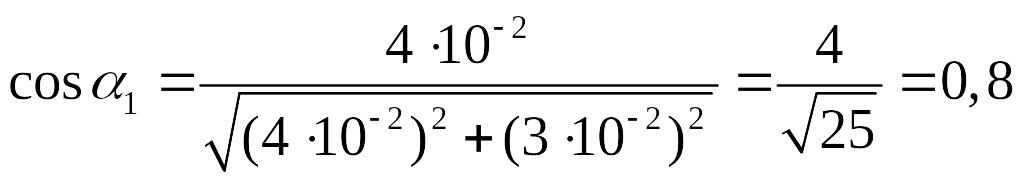
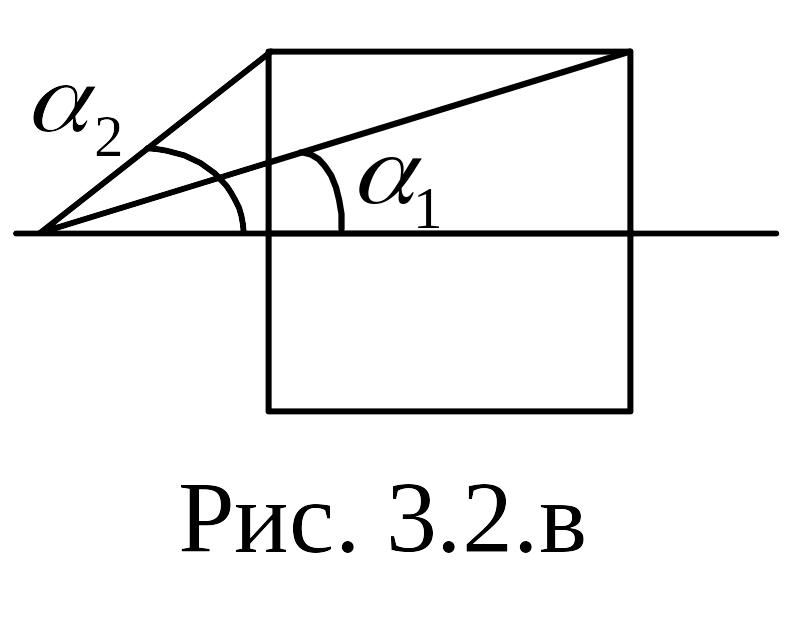
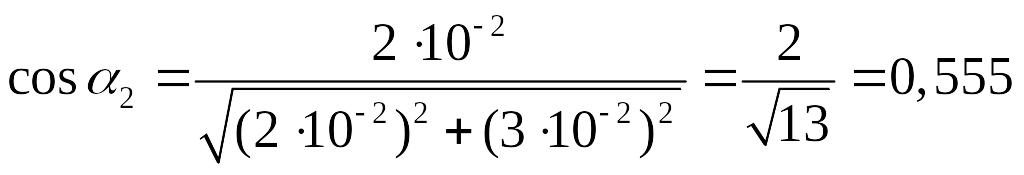
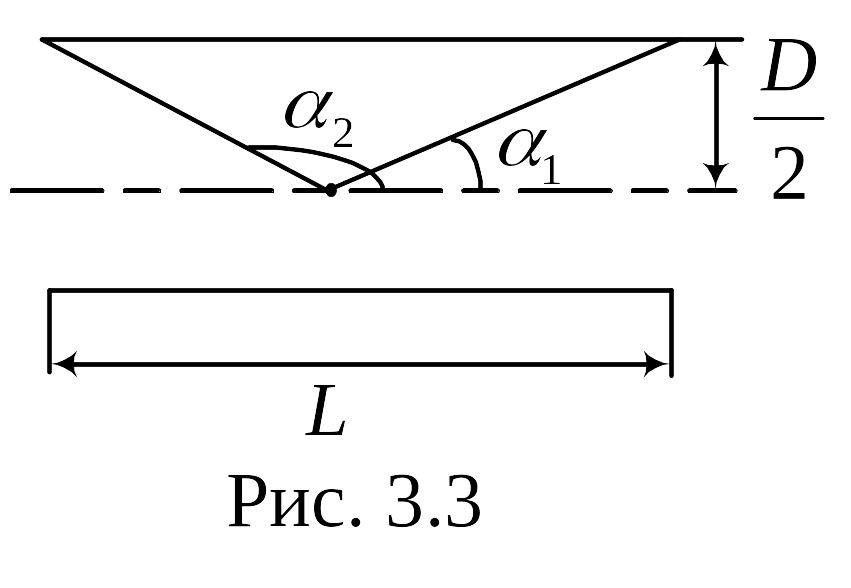
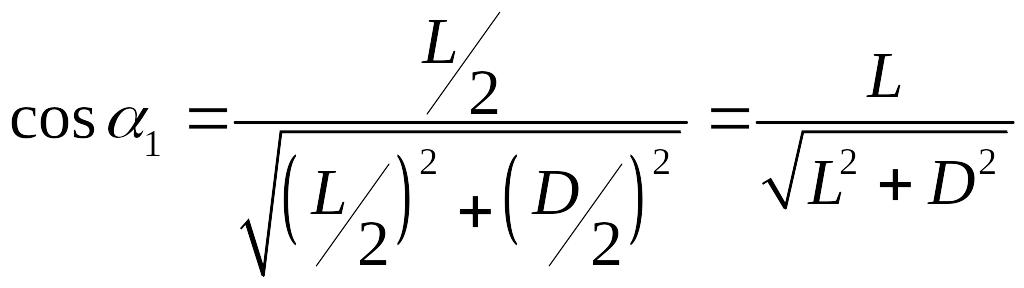


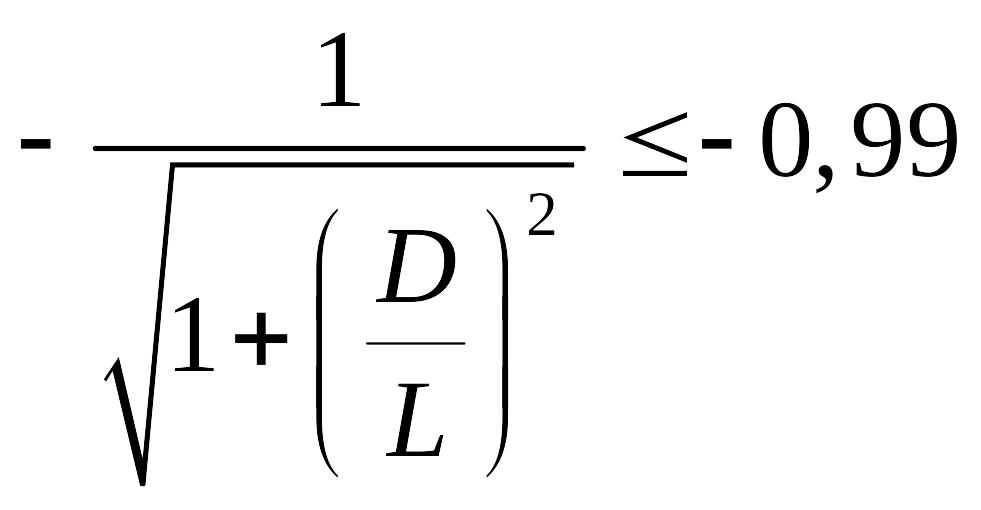
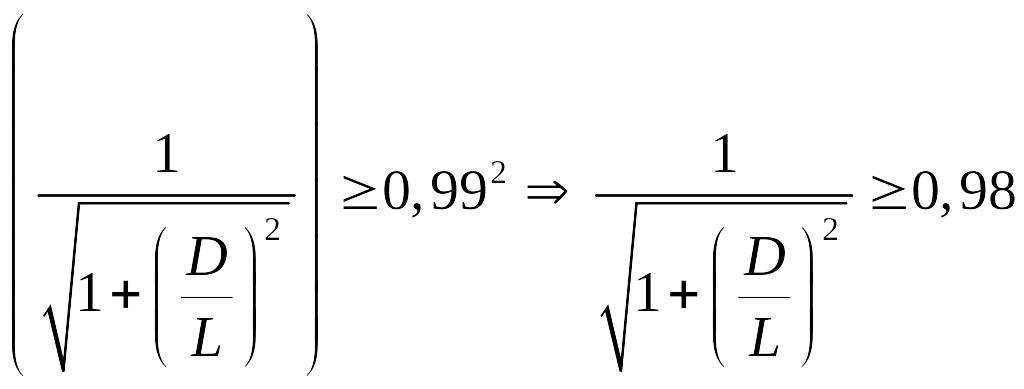
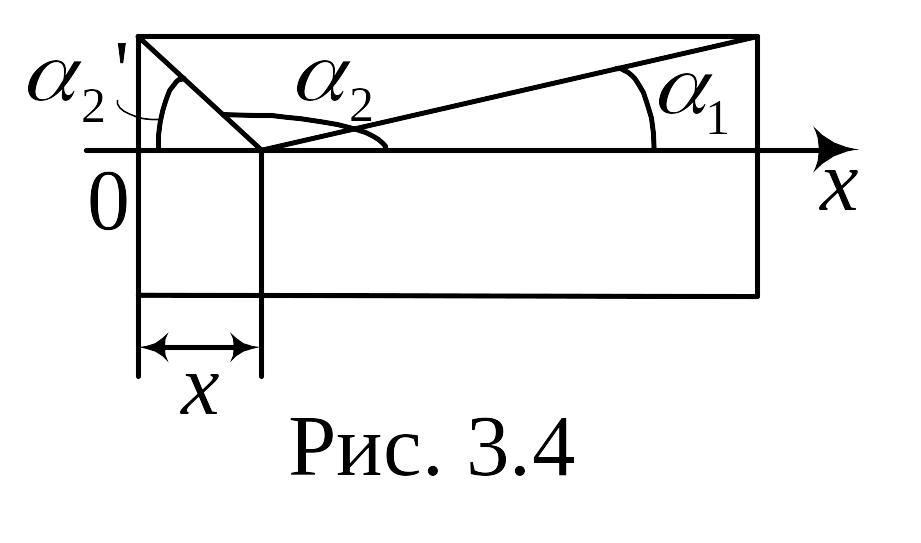
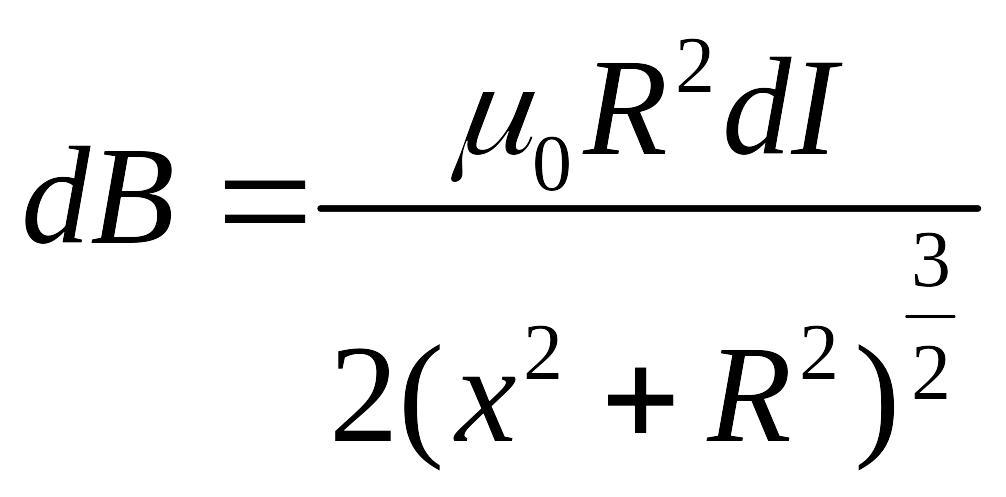
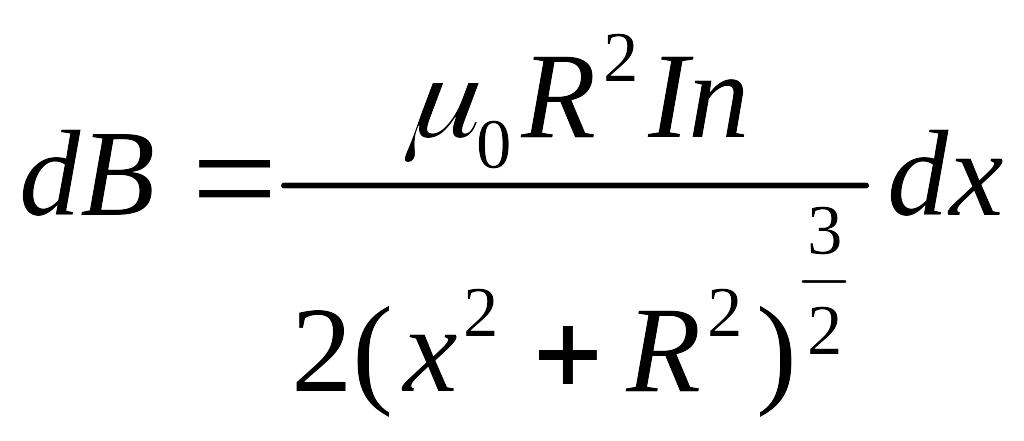
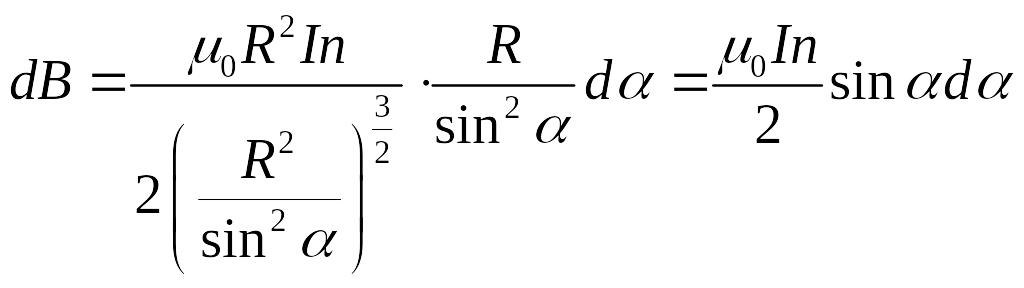
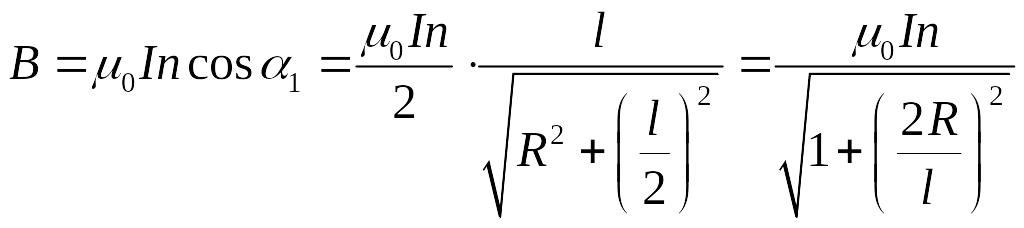

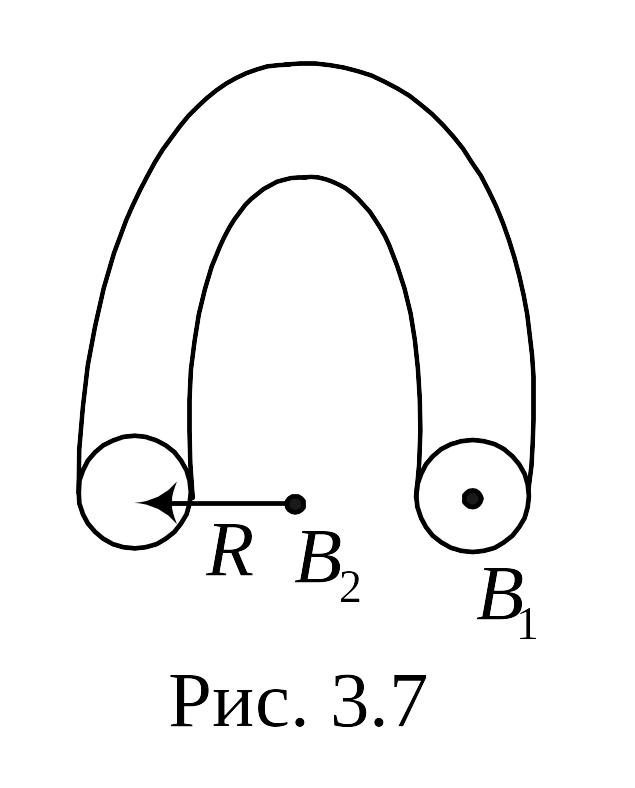

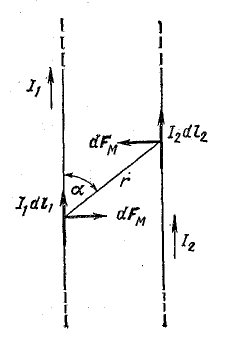
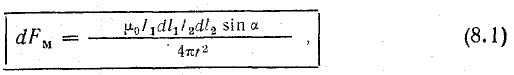
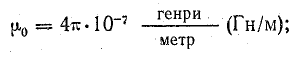

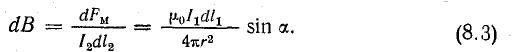
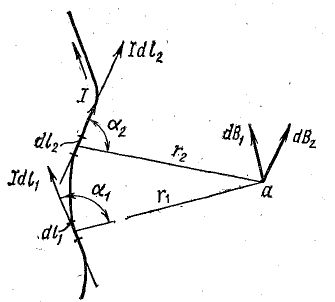
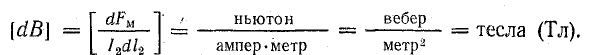
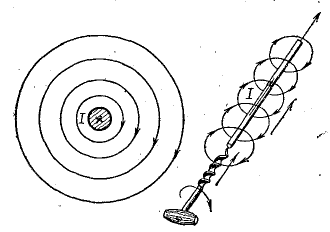
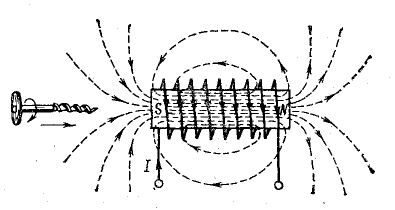
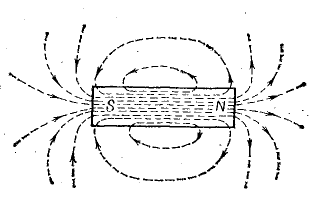
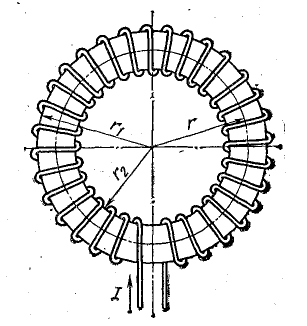

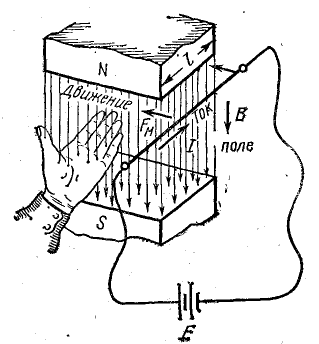
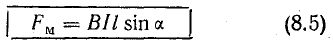
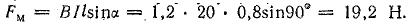
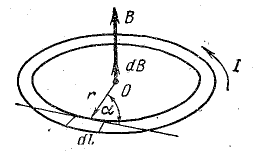
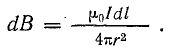
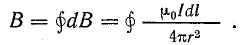
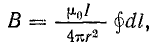
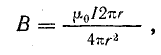
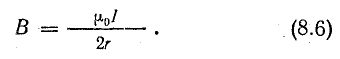
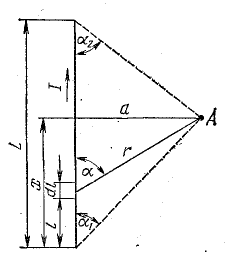
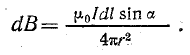
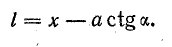
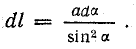
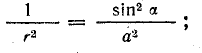
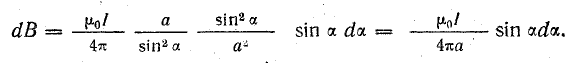
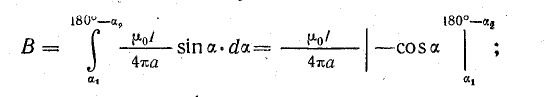
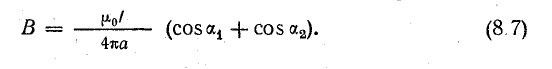
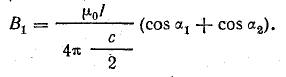
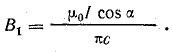
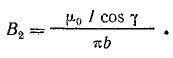
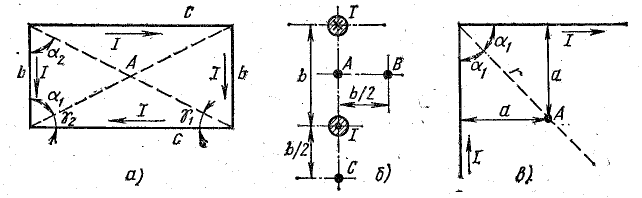
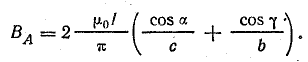

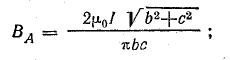
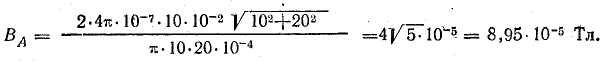

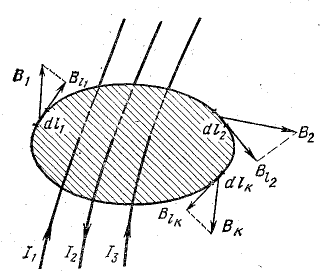
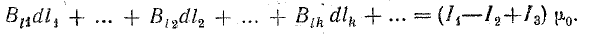
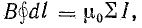

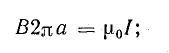
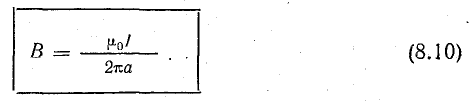
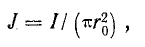
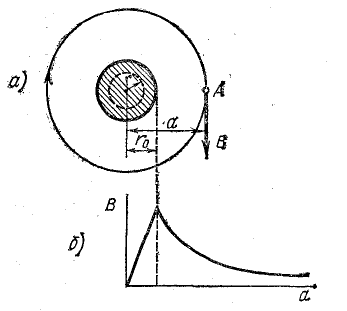
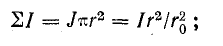
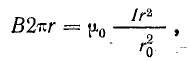
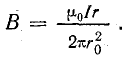
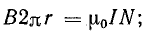

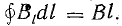
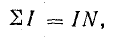
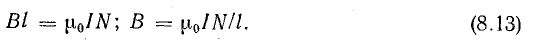
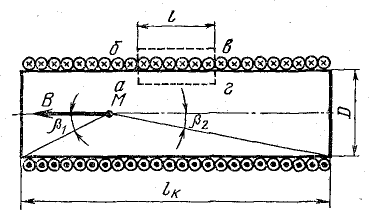
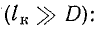
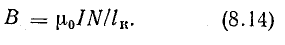
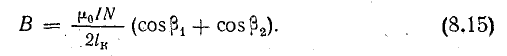

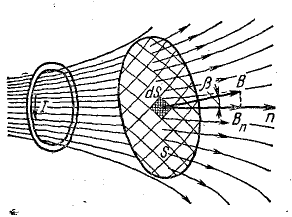
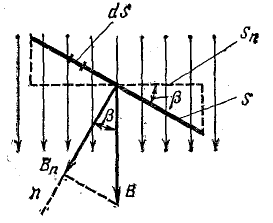
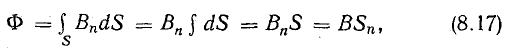

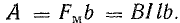
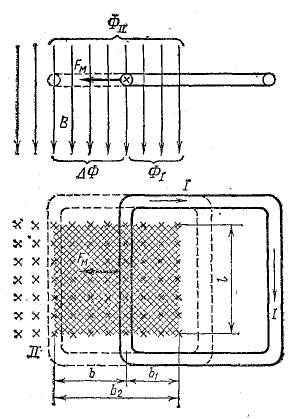
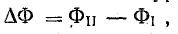
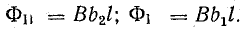
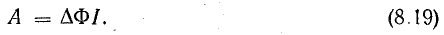


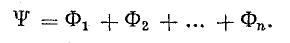
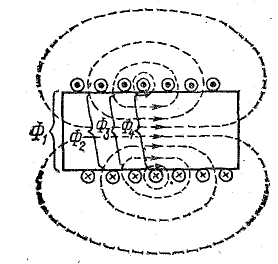
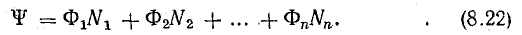
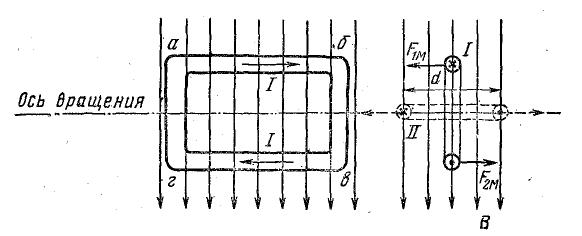
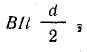
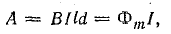
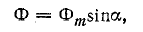
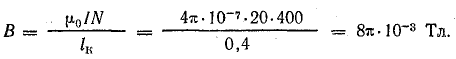
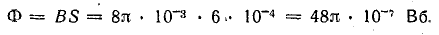

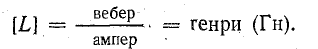
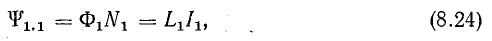
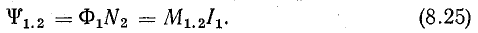
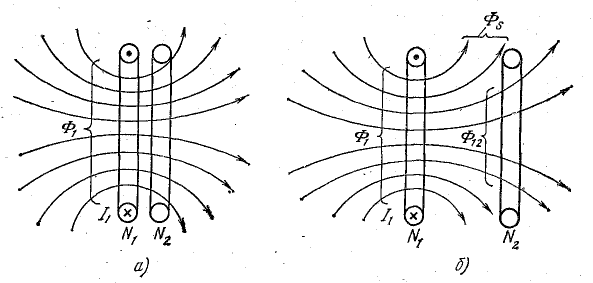
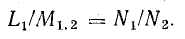
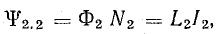
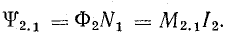
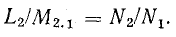
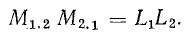
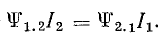
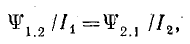
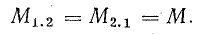


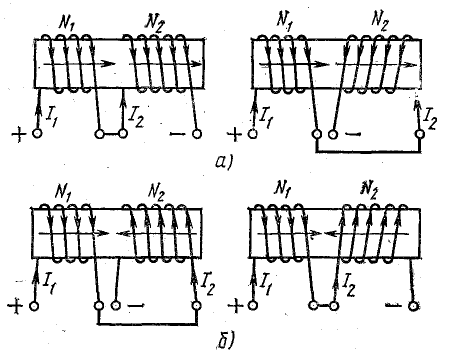
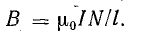
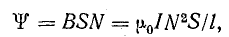

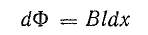
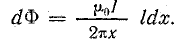
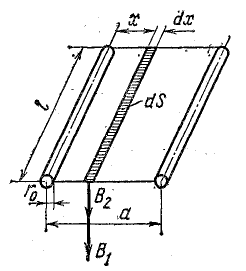
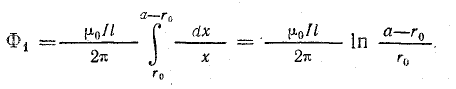
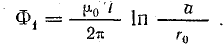
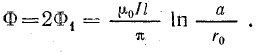
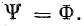
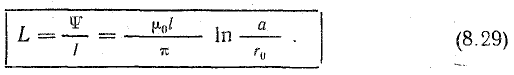
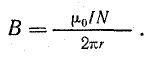
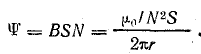

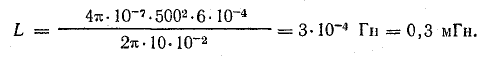

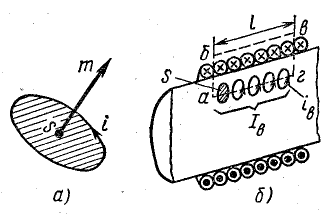


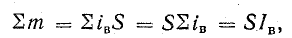
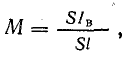
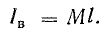
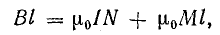


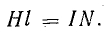
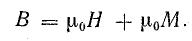

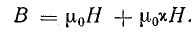

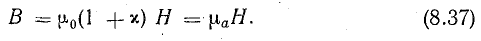


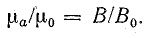

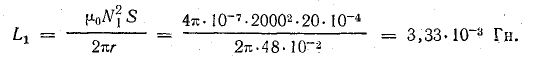
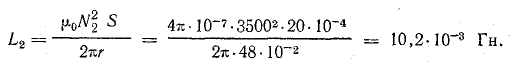
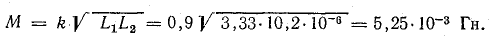
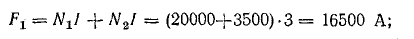
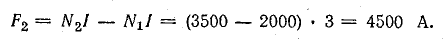
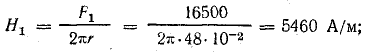
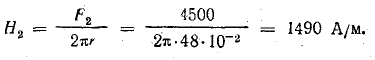
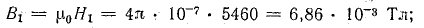
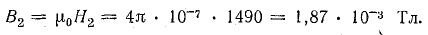
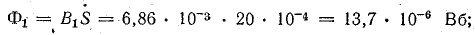
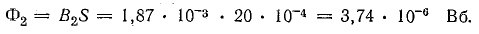
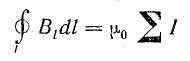


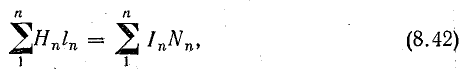
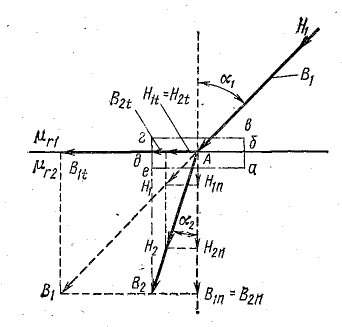
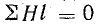
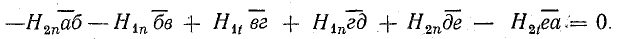

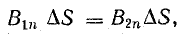

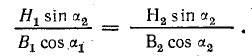
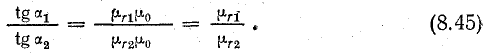

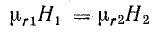
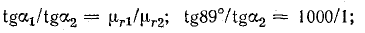
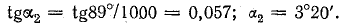
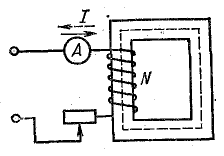
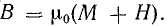
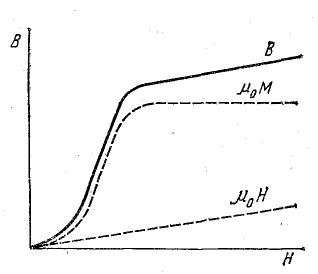
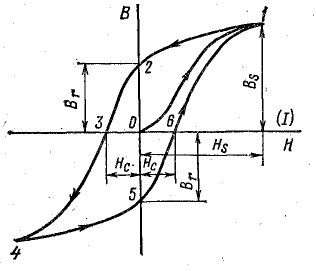
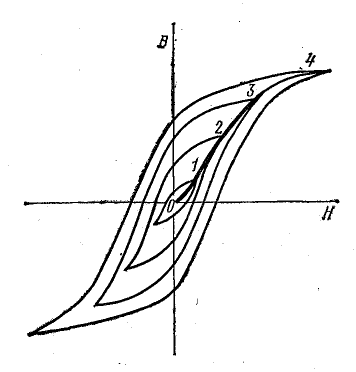
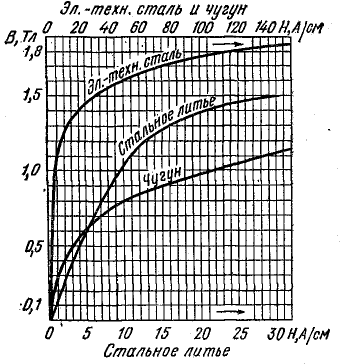
 и магнитная проницаемость μr — не постоянные величины, а зависят от намагниченности М.
и магнитная проницаемость μr — не постоянные величины, а зависят от намагниченности М.