Магнитное поле соленоида
Соленоидом
называется совокупность N
одинаковых витков изолированного
проводящего провода, равномерно
намотанных на общий каркас или сердечник.
По виткам проходит одинаковый ток.
Магнитные поля, созданные каждым витком
в отдельности, складываются по принципу
суперпозиции. Индукция магнитного поля
внутри соленоида велика, а вне его —
мала. Для бесконечно длинного соленоида
индукция магнитного поля вне соленоида
стремится к нулю. Если длина соленоида
во много раз больше диаметра его витков,
то соленоид можно практически считать
бесконечно
длинным.
Магнитное
поле такого соленоида целиком сосредоточено
внутри него и является однородным
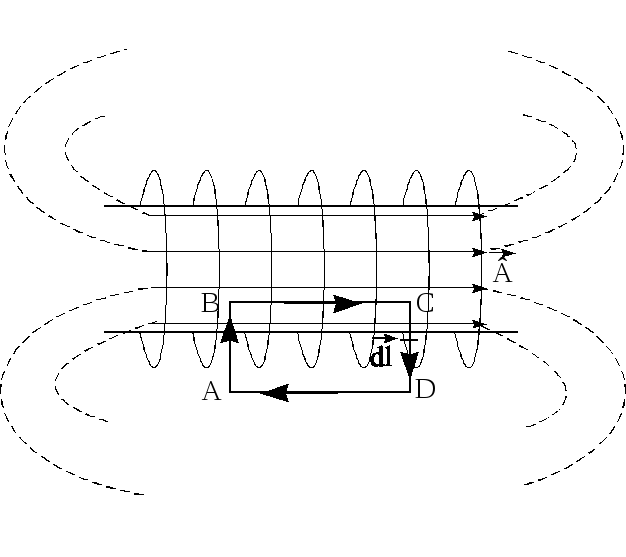
(рис.6).
Величину
индукции магнитного поля внутри
бесконечно длинного соленоида можно
определить, используя теорему
о циркуляции вектора
:циркуляция
вектора
по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых контуром, умноженной на
магнитную постоянную μо:
,
(20)
где
μ0 =
4π 10-7
Гн/м.
Рис.6.
Магнитное поле соленоида
Для
определения величины магнитной индукции
В внутри соленоида выберем замкнутый
контур ABCD
прямоугольной формы, где
— элемент длины контура, задающий
направление обхода (рис.6). При этом длиныAB
и CD
будем считать бесконечно малыми.
Тогда
циркуляция вектора
по замкнутому контуруABCD,
охватывающему N
витков, равна:
(21)
На
участках AB
и CD
произведение
,
так как вектораи
взаимно перпендикулярны. Поэтому
.
(22)
На
участке DA
вне соленоида интеграл,
так как магнитное поле вне контура
равно нулю.
Тогда формула (21)
примет вид:
,
(23)
где
l
– длина участка BC.
Сумма токов, охватываемых контуром,
равна
,
(24)
где
Ic
– сила
тока соленоида; N – число
витков, охватываемых контуром ABCD.
Подставив (23) и
(24) в (20), получим:
. (25)
Из
(25) получим выражение для индукции
магнитного поля бесконечно длинного
соленоида:
.
(26)
Так
как число витков на единицу длину
соленоида n
равно:
(27)
то
окончательно получим:
.
(28)
Если внутрь
соленоида помещен сердечник, то формула
(28) для В примет вид:
.
(29),
где
— магнитная проницаемость материала
сердечника.
Таким
образом, индукция
В магнитного поля соленоида определяется
током соленоида Ic,
числом витком n
на единицу длины соленоида и магнитной
проницаемостью материала сердечника.
Цилиндрический магнетрон
Магнетроном
называется двухэлектродная электронная
лампа (диод), содержащая накаливаемый
катод и холодный анод и помещенная во
внешнее магнитное поле.
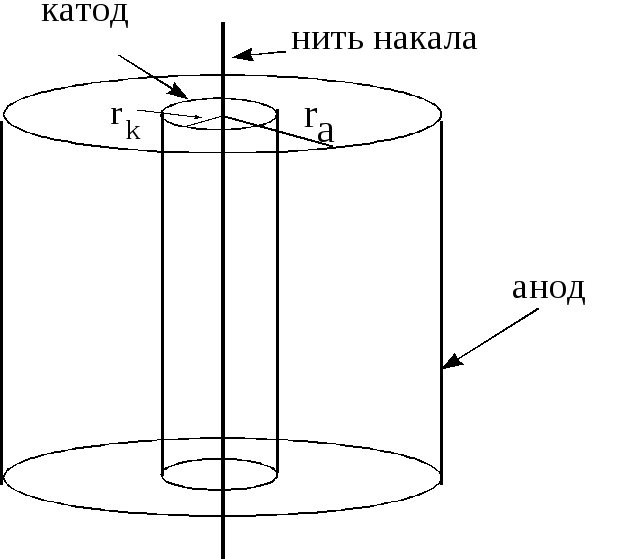
Анод
диода имеет форму цилиндра радиусом
.
Катод представляет собой полый цилиндр
радиусом,
вдоль оси которого расположена нить
накала, как правило, изготавливаемая
из вольфрама (рис.7).
Раскалённый
катод в результате явления термоэлектронной
эмиссии испускает термоэлектроны,
которые образуют вокруг катода электронное
облако. При подаче анодного напряжения
(рис.8),
электроны начинают перемещаться от
катода к аноду вдоль радиусов, что
приводит к возникновению анодного тока.
Анодный ток регистрируется миллиамперметром.
Рис.7.
Схема диода
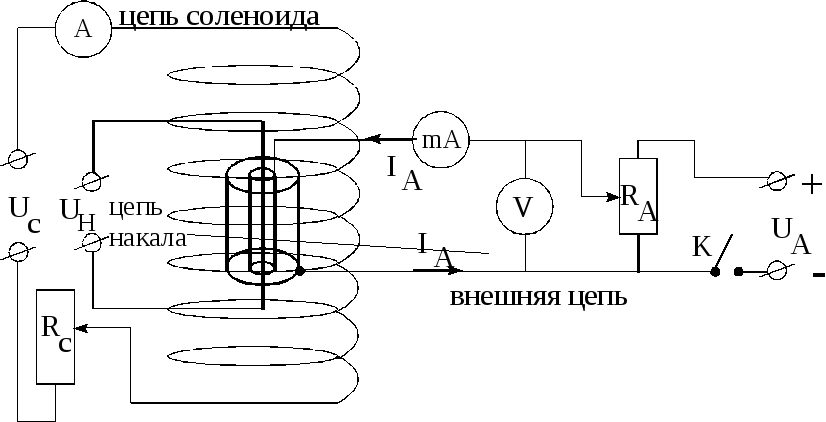
Электрическая схема цепи
Величина
анодного напряжения регулируется
потенциометром RA.
Чем больше анодное напряжение, тем
большее количество электронов за единицу
времени достигает анода, следовательно,
тем больше анодный ток.
Напряжённость
электрического поля Е между катодом и
анодом такая же, как и в цилиндрическом
конденсаторе:
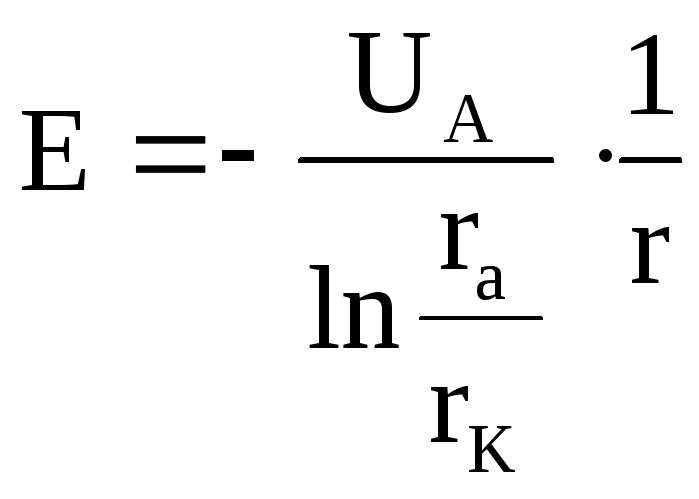
(30)
где
r
– расстояние от оси катода до данной
точки пространства между катодом и
анодом.
Из
формулы (30) следует, что напряжённость
поля Е обратно пропорциональна расстоянию
r
до оси катода. Следовательно, напряженность
поля максимальна у катода.
Так как
rк <<ra,
(31)
то
значение логарифма ln
стремится к большой величине. Тогда с
увеличением расстояния r
напряженность электрического поля
между катодом и анодом снижается до
нуля. Поэтому, можно считать, что электроны
приобретают скорость под действием
поля только вблизи катода, и дальнейшее
их движение к аноду происходит с
постоянной по величине скоростью.
Внешнее
магнитное поле, в которое помещён диод,
создаётся соленоидом (рис.8). Длина
соленоида l
много больше диаметра его витков, поэтому
поле внутри соленоида можно считать
однородным. Ток в цепи соленоида
изменяется с помощью потенциометра RC
(рис.8) и регистрируется амперметром.
Характер
движения электронов в зависимости от
величины поля соленоида показан на
рис.9. Если ток в цепи соленоида отсутствует,
то индукция магнитного поля В = 0.
Тогда электроны движутся от катода к
аноду практически по радиусам.
Увеличение
тока в цепи соленоида приводит к
возрастанию величины В. При этом,
траектории движения электронов начинают
искривляться, однако все электроны
достигают анода. В анодной цепи будет
течь ток такой же, как и в отсутствии
магнитного поля.
Рис.9.
Зависимость анодного тока IA
от величины тока соленоида Ic
в идеальном (1) и реальном (2) случаях, а
также характер движения электронов в
зависимости от величины поля соленоида.
При
некотором значении тока в соленоиде
радиус окружности, по которой движется
электрон, становится равным половине
расстояния между катодом и анодом:
..
(32)
Электроны
в этом случае касаются анода и уходят
к катоду (рис.9). Такой режим работы диода
называется критическим.
При этом по соленоиду течёт критический
ток Iкр,
которому соответствует критическое
значение индукции магнитного поля В =
Вкр.
При
В = Вкр
анодный ток в идеальном случае должен
скачком уменьшиться до нуля. При В > Вкр
электроны не попадают на анод (рис.9), и
анодный ток также будет равен нулю
(рис.9, кривая 1).
Однако
на практике, вследствие некоторого
разброса скоростей электронов и нарушения
соосности катода и соленоида, анодный
ток уменьшается не скачком, а плавно
(рис.9, кривая 2). При этом значение силы
тока соленоида, соответствующее точке
перегиба на кривой 2, считается критическим
Iкр.
Критическому значению тока соленоида
соответствует анодный ток, равный:
,
(33)
где
– максимальное значение анодного тока
при В = 0.
Зависимость
анодного тока IA
от величины индукции магнитного поля
В (или от тока в соленоиде) при постоянном
анодном напряжении и постоянном накале
называется сбросовой
характеристикой магнетрона.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вывод формул индукции поля соленоида, созданного переменным током
Акопов Вачакан Ваграмович /AkopovVachakanVagramovich – учитель физики МОУ СОШ №6, Ставропольский край Курский район,
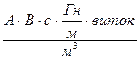 =
= 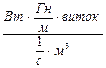 , (9)
Тогда заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:
В2 =
, (9)
Тогда заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:
В2 = | Дано: | СИ: | Решение: |
| N = 2000 витков d= 2,8 см В = 0,72 мТл n = 50 Гц | = 2,8× 10-2 м =0,72× 10-3 Тл |
Индукция поля соленоида определяется формулой:
В = |
| U – ? | ||
|
Подставляя исходные данные в выражение (3), получим: |
||
| Ответ: U = 0,278 В. |
| Дано: | СИ: | Решение: |
| U = 0,2 В d= 2,8 см В = 0,52 мТл n = 50 Гц | = 2,8× 10-2 м =0,52× 10-3 Тл |
Индукция поля соленоида выражается формулой:
В = |
| N – ? | ||
Подставляя исходные данные в выражение (3), получим: 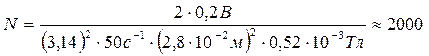 витков витков
|
||
| Ответ: N = 2000 витков. |
| Дано: | СИ: | Решение: |
|
B = 0,72 мТл
n = 50 Гц
µо=1,256×10-6 |
=0,72× 10-3 Тл |
Индукция поля соленоида определяется по формуле (10):
В = 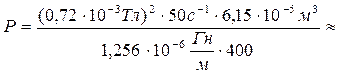
|
| P – ? | ||
| »3,2 мкВт. Ответ: Р » 3,2 мкВт. | ||
Есть вопрос? Задайте его Вашему персональному менеджеру. Служба поддержки призвана помочь пользователям в решении любых проблем, связанных с вопросами публикации своих работ и другими аспектами работы издательства «Проблемы науки».
Решение.
Если соленоид бесконечно длинный, то индукция магнитного поля на оси соленоида определяется по формуле:
[ B = {mu _0}cdot mu cdot I cdot n, ] где μ0=4π∙10-7 Гн/м – магнитная постоянная; μ-магнитная проницаемость среды, внутри соленоида; I— сила тока в соленоиде; n – плотность намотки соленоида (число витков на единицу длины).
Так как в условии задачи не сказано, какая среда внутри соленоида, то будем считать, что он находится в вакууме (μ=1).
[ n = frac{2N}{l}, ] где N – число витков, 2N, т.к. катушка двухслойная; l – длина соленоида.
Так как витки плотно прилегают друг к другу, то Связь между N и l имеет вид: [ l = N cdot d, ] где d – диаметр провода.
[ B = {mu _0}cdot I cdot n = frac{{{mu _0} cdot{I}cdot{N}}}{l} = frac{{{mu _0}cdot{I}cdot{2N}}}{{{N}cdot{d}}} = frac{{{2 mu _0}cdot{I}}}{d}. ]
Ответ: В = 6,28 мТл.
51. Магнитное поле тороида и соленоида
Тороидом называется последовательность
круговых токов, центры которых расположены на окружности (рис.58).
Рис.58
Из симметрии тороида очевидно, что во
всех точках окружности, центр которой совпадает с центром тороида, индукция
магнитного поля имеет одинаковое значение. Магнитное напряжение вдоль
окружности равно. Эта окружность охватывает все витки
тороида. Если полное число витков обозначить как N, а силу тока в витках как I, то окружность охватывает полный ток NI, поэтому , откуда

Заметим, что поле внутри тороида не вполне
однородно. Индукция поля больше с внутренней стороны тороида 

Относительная разность индукций поля равна 
Соленоидом называется последовательность
круговых токов, центры которых расположены на прямой. Мы рассмотрим бесконечно
длинный соленоид, удовлетворяющий условию l>>d, где l и d – длина и диаметр соленоида соответственно.
Индукцию магнитного поля в соленоиде можно получить из формулы для тороида,
если радиус тороида увеличить неограниченно. Тогда тороид становится
соленоидом и 
становится однородным. Индукция магнитного поля в соленоиде найдем из формулы
для тороида, замечая, что 
соленоида.
,
(12)
Индукция магнитного поля в соленоиде
пропорционально числу ампер-витков на метр ((А-в)/м).