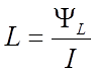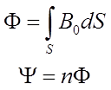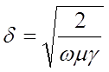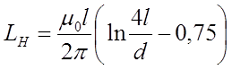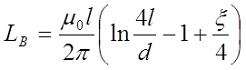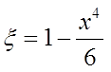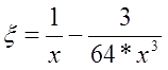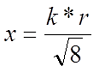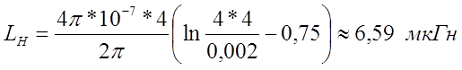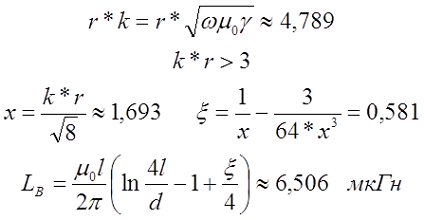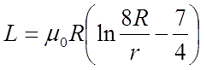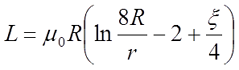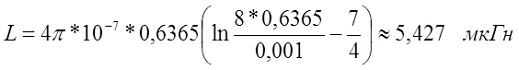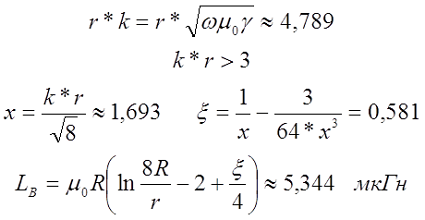Как найти индуктивность кольца

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­_L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B₀ (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­_L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*10⁷ См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

На частоте 50 кГц

Online калькулятор индуктивности прямолинейного проводника

Индуктивность кругового кольца круглого сечения

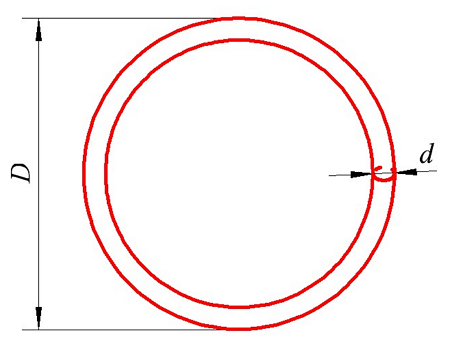
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*10⁷ См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

Online калькулятор индуктивности кольца кругового сечения

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Главная >> Применение >> Типовые примеры >>

Индуктивность кольца с током

индуктивность витка с током, круговой виток с током индуктивность

Тип задачи

Осесимметричная задача магнитостатики

Геометрия

Индуктивность кольца с током
Расчет индуктивности одиночного витка и сравнение с аналитическим решением

n
R
r

I
B

Дано

Ток в кольце I = 50 A,

средний радиус витка R =40 мм.

диаметр провода 2r = 10 мм.

Задача:

Найти индуктивность L кольца с током.

Решение

Величина индуктивности кругового витка с током можно определить по формуле:

L = μ₀ R · ( ln(8R/r) — 1.75 )

Результаты:

r, мм	R/r	L, мкГн	Погрешность
ELCUT	Теория
5	8	0.1213	0.1211	0.17%
10	4	0.0875	0.0862	1.5%
16	2.5	0.0657	0.0622	5.6%
20	2	0.0560	0.0514	8.9%

Исходя из полученных результатов расчета, можно сделать вывод: при больших значениях среднего радиуса витка R по отношению к радиусу его сечения r, результаты расчета индуктивности по аналитическим зависимостям и численными методами сопоставимы, однако с уменьшением вышеуказанного параметра растет и погрешность расчета с помощью приведенной аналитической зависимости.

• Видео: Индуктивность кольца с током
  

• Смотреть на YouTube.
• Скачать файлы задачи

1. Методики расчета индуктивности катушек

Основным
элементом катушек индуктивности является
токовод. Величина индуктивности
определяется конструкцией токовода и
его размерами.

Полная
индуктивность медного провода круглого
сечения длиной l_ПРи диаметромd₀равна

(3.1)

Из
(3.1) следует, что индуктивность провода
уменьшается с ростом его диаметра. Это
свойство широко используют в УКВ
аппаратуре для уменьшения индуктивности
соединительных проводов за счет
увеличения их диаметра.

Если
одиночный проводник согнуть, например,
в кольцо, то его индуктивность уменьшится
из-за встречного направления токов в
соседних частях кольца. Однако, для
круглого кольца индуктивность будет
наибольшей по сравнению с индуктивностью
витка любой другой конфигурации,
поскольку круглый виток охватывает
наибольшую площадь, обеспечивая
наибольшее потокосцепление.

Индуктивность
круглого плоского витка диаметром Dиз провода круглого сечения длинойl_ПРи диаметромd_ПРравна

(3.2)

При
сворачивании проводника в несколько
витков wодинакового
диаметра образуется катушка, индуктивность
которой можно определить как суммарную
индуктивность всех витков с учетом
взаимоиндукцииMмежду
ними:

(3.3)

Индексы при Муказывают на взаимную индуктивность
между первым и вторым, вторым и третьим,
первым и третьим витками и т.д. Если
известен коэффициент связи, который
определяется равенством

,
(3.4)

то индуктивность
катушки с произвольным числом витков
определяется из

. (3.5)

Коэффициент связи
между витками, расположенными на
расстоянии τ, в однослойной катушке
определяется выражением

(3.6)

Для сплошной намотки
τ=d₀.

Индуктивность
многослойной катушки незначительно
зависит от диаметра провода, так как
определяется в основном взаимоиндукцией
между витками.

Из-за трудности
определения коэффициента связи выражение
(3.5) обычно применяют для расчета катушек
индуктивности с небольшим числом витков
(обычно не более шести).

Для катушек с однородным
замкнутым магнитопроводом (с тороидальным
сердечником) выражение для определения
индуктивности принимает вид

, (3.7)

где μ– начальная магнитная
проницаемость сердечника (μ=1 для
диэлектрического каркаса или воздуха);

μ₀=4π·10^-7Гн/м – магнитная постоянная;

w– число витков обмотки;

S
— площадь поперечного сечения катушки;

— длина намотки катушки;

Таким
образом, увеличение индуктивности
катушки может быть достигнуто за счет
увеличения числа витков, магнитной
проницаемости сердечника, площади
поперечного сечения магнитопровода, а
также уменьшения длины намотки.

В
высокочастотных катушках замкнутый
магнитопровод как правило отсутствует,
поэтому индуктивность катушки будет
меньше, рассчитанной по (3.7). Для учета
рассеивания магнитного потока на краях
катушки вводится поправочный коэффициент
k, который зависит от
отношения диаметра катушки к длине
намотки

(3.8)

Для
практических расчетов однослойных
цилиндрических катушек, намотанных
виток к витку (рис.3.2 а),используют
выражение

, (3.9)

где
— коэффициент формы катушки, учитывающий
краевые эффекты;

μ– начальная магнитная
проницаемость сердечника (μ=1 для
катушек без магнитного сердечника);

μ₀=4π·10^-7Гн/м –
магнитная постоянная;

w– число витков обмотки;

— площадь поперечного сечения круглой
катушки;

D– диаметр катушки;

— длина намотки.

Для
практических расчетов однослойных
цилиндрических катушек без сердечника,
намотанных с принудительным шагом τ(рис.3.2 б),индуктивность
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL

, (3.10)

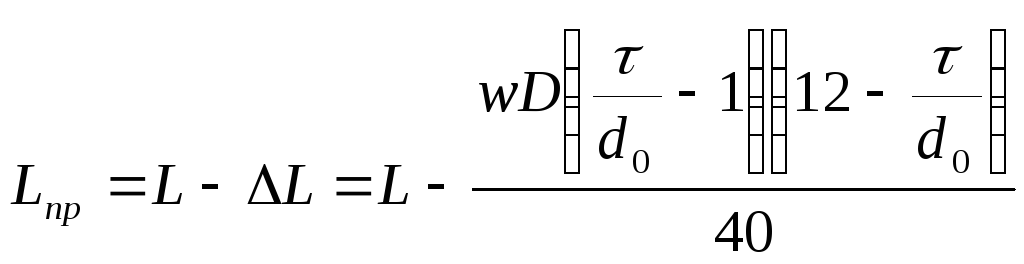
где τ– шаг намотки;

L–
индуктивность катушки, определенная
по (3.9) приμ=1.

Для
практических расчетов индуктивности
тороидальной однослойной катушки,
намотанной сплошным слоем на круглом
магнитном сердечнике прямоугольного
сечения (рис.3.2 в), используют
выражение

, (3.11)

где
— площадь поперечного сечения сердечника
тороида;

— средняя длина сердечника тороида;

D– внешний диаметр сердечника тороида;

d– внутренний диаметр сердечника тороида;

h– высота сердечника тороида.

Для практических
расчетов многослойных катушек без
сердечника(рис.3.2 г) используют
выражение

, (3.12)

гдеD_CP
– средний диаметр катушки;

t— толщина катушки;

l— длина катушки.

Для
практических расчетов многослойных
секционированных катушек без сердечника
(рис.3.2 д) используют выражение

, (3.13)

где L_C
– индуктивность одной секции катушки;

n– число секций;

k_CB– коэффициент связи между смежными
секциями, зависящий от отношения(рис.3.3);

b
– расстояние между секциями.

Для
практических расчетов плоских круглых
спиральных катушек (рис.3.2 е) используют
выражение

, (3.14)

где D_BH,D_H –внутренний и наружный диаметры
катушки, соответственно.

Для
практических расчетов плоских
квадратных спиральных катушек (рис.3.2
ж) используют выражение

, (3.15)

где А_BH,А_H
–внутренняя и наружная стороны
катушки, соответственно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  10.02.20165.15 Mб192.doc

• #
• #
• #
• #
• #
• #

1
 ^3.00

Найдите индуктивность проволочного кольца, у которого все геометрические размеры в 2 раза больше.

Прежде всего заметим, что индуктивность кольца пропорциональна его радиусу. В самом деле, величина магнитной индукции в каждой точке пространства уменьшается обратно пропорционально радиусу кольца, а площадь увеличивается пропорционально квадрату радиуса. При заданной величине тока в кольце магнитный поток через плоскость кольца, таким образом, прямо пропорционален радиусу. Поэтому индуктивность кольца радиуса $frac{R}{2}$ равна $frac{L}{2}$ , а кольца радиуса 2$R$ — $2L$.

Ответ:

$$2L$$

2
 ^9.00

Какой станет индуктивность кольца $L_2$ радиуса $R$ при помещении его внутрь сверхпроводящего кольца со вдвое большими геометрическими размерами? Плоскости и центры колец во втором случае также совпадают.

Магнитный поток через внутреннюю область нашего кольца (область А) в виде концентрического круга радиуса $frac{R}{2}$ составляет некоторую часть $alpha $ от полного потока через плоскость кольца

[Phi_A=alpha LI]

Тогда магнитный поток через область с внутренним радиусом $frac{R}{2}$ и внешним радиусом $R$ (область В) внутри нашего кольца

[Phi_B=(1-alpha )LI ]

Введем также обозначение для потока $Phi_{textrm{С}}$ через область С с внутренним радиусом $R$ и внешним радиусом $2R$, охватывающую снаружи наше кольцо

[Phi_C=beta LI]

В первом случае (сверхпроводящее колечко внутри) магнитный поток через область А, ограниченную сверхпроводящим контуром равен нулю

$$Phi_{A1}=alpha LI-frac{L}{2}I_1=0$$

Здесь $I_1$ — ток, возникающий в сверхпроводящем колечке. Полный поток через плоскость кольца радиуса $R$ при этом

$$Phi_1=L_1I=left(1-alpha right)LI+beta frac{L}{2}I_1$$

Во втором случае наше кольцо с током $I$ охвачено сверхпроводящим кольцом радиуса $2R$ с индуктивностью $2L$. Во внешнем кольце возникает такой ток $I_2$, при котором полный поток магнитного поля через его плоскость равнялся нулю

$$LI-beta LI-2LI_2=0$$

Полный поток через плоскость кольца радиуса $R$ при этом

$$Phi_2=L_2I=LI-alpha cdot 2LI_2$$

Из предыдущих уравнений получаем

[L_1I=left(1-alpha right)LI+alpha beta LI=left(1-alpha +alpha beta right)LI,]

И далее

[L_2I=LI-alpha cdot left(1-beta right)LI=left(1-alpha +alpha beta right)LI]

Таким образом, $L_2=L_1$.

Ответ:

$$L_2=L_1$$

Как рассчитать количество витков для катушки или дросселя на ферритовом кольце, онлайн калькулятор и формула расчета индуктивности.

Маркировку магнитной проницаемости и материала, из которого изготовлен кольцевой сердечник, наносят в виде цифр и букв, примеры:

2000НН, 1500НН.

Цифры указывают на магнитную проницаемость, а буквы в конце обозначают тип материала, из которого изготовлено кольцо.

Размеры тороидального кольца их феррита обозначают в виде чисел, пример:

20 Х 10 Х 6

Расшифровка маркировки:

• 20 — внешний диаметр кольца в миллиметрах, D1;
• 10 — внутренний диаметр кольца в миллиметрах, D2;
• 6 — высота кольца в миллиметрах, h.

Рис. 1. Ферритовые кольца, размеры кольцевого ферромагнитного сердечника.

Формула для расчета

Чтобы рассчитать индуктивность дросселя или катушки индуктивности на тороидальном ферритовом сердечнике можно использовать формулу:

L = m * m0 * N2 * (h*(D - d)/2) / (π*(D + d)/2)

Где:

• L — индуктивность катушки (Гн);
• m — магнитная проницаемость;
• m0 — магнитная постоянная, 4π*10^-7 Гн/м =1,256637*10^-6 Гн/м;
• N — число витков провода, намотанного на ферритовом кольце;
• D — внешний диаметр кольца (м);
• d — внутренний диаметр кольца (м);
• h — высота (м);
• π - постоянная Пи, 3,141592653589.

Если принять что:

• S = h(D — d)/2 — это сечение сердечника (м²);
• l = Pi(D + d)/2 — это длина намотки катушки (м);

то формула будет выглядеть так:

L = m * m0 * N2 * S / l

Расчет количества витков провода для катушки с требуемой индуктивностью L:

N = SQRT(L / m * m0 * S / l)

SQRT — функция «корень квадратный из числа».

Калькулятор 

Чтобы упростить расчет витков для изготовления дросселя или катушки индуктивности на тороидальном магнитном сердечнике можете воспользоваться нашим онлайн-калькулятором.

При вводе индуктивности помните что: 1 мГн (mH) = 1000 мкГн (µH).

Примеры результатов расчета:

Размеры кольца	Магнитная проницаемость	Индуктивность	Количество витков провода
25х11.5х11 мм	2000	100 мкГн, 0.1 мГн	5,5 витков
16х9.6х6.3 мм	2000	200 мкГн, 0.2 мГн	12.6 витков
18х10х6 мм	2000	50 мкГн, 0.05 мГн	6 витков
10х5х4 мм	1000	5500 мкГн, 5.5 мГн	102 витка

Литература:

• Википедия — Магнитная проницаемость.
• Д. Алексеев. alexeevd.narod.ru.