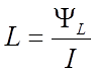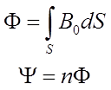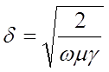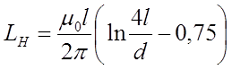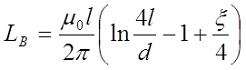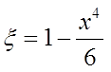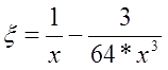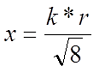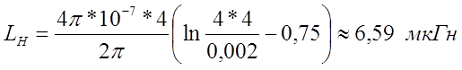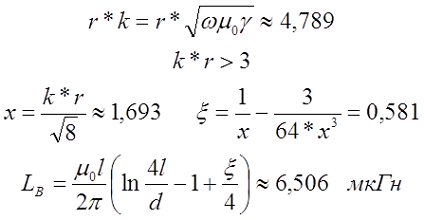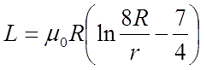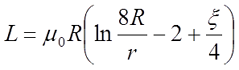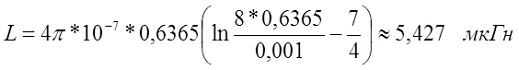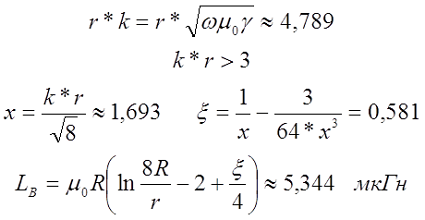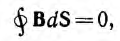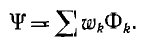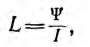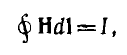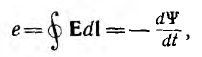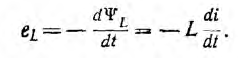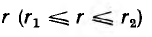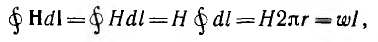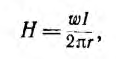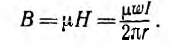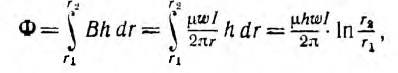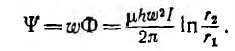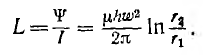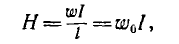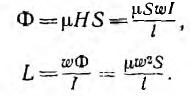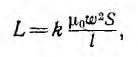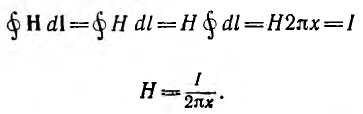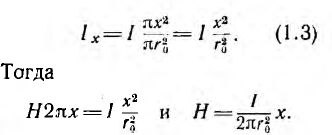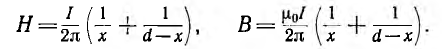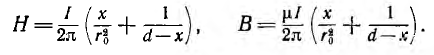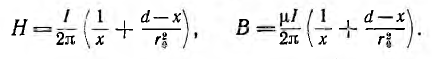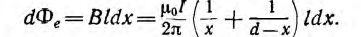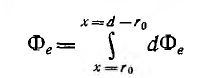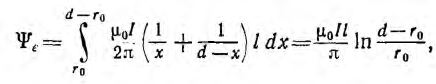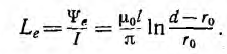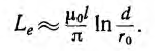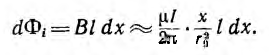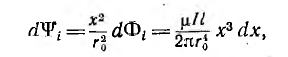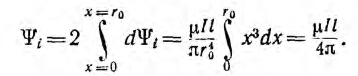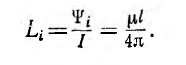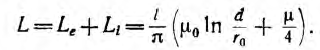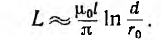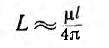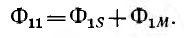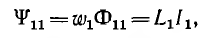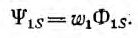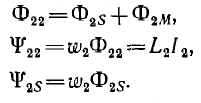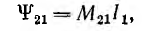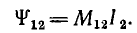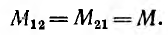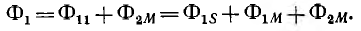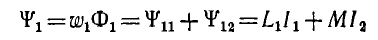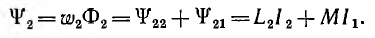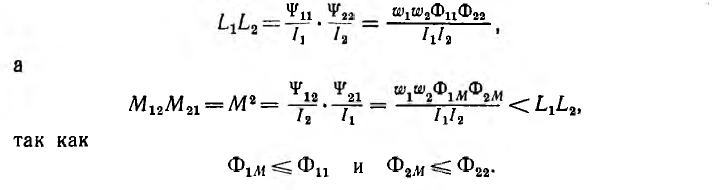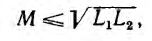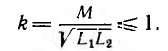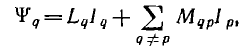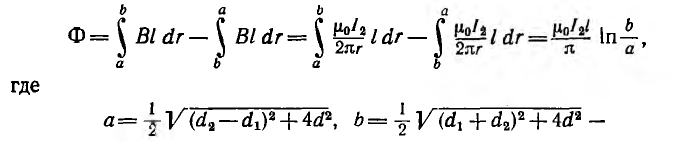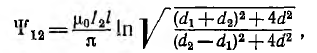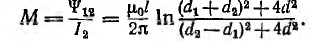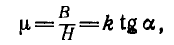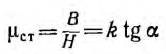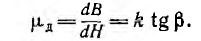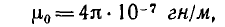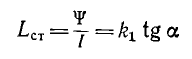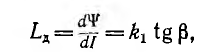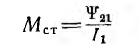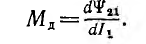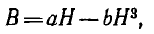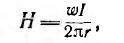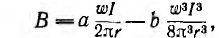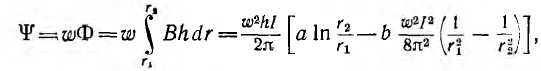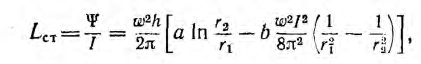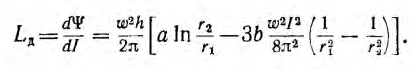Как найти индуктивность нагрузки

Содержание

• — Что такое индуктивные нагрузки?
• — Какой пример индуктивной нагрузки?
• — Что такое индуктивная нагрузка и резистивная нагрузка?
• — Как найти индуктивную нагрузку?
• — Светодиодные лампы имеют индуктивную или резистивную нагрузку?
• — Как определить, является ли нагрузка индуктивной или емкостной?
• — Вентилятор — это емкостная нагрузка?
• — Какую нагрузку имеют обогреватели?
• — В чем разница между резистивными индуктивными и емкостными нагрузками?
• — Насос представляет собой индуктивную нагрузку?
• — Какой пример емкостной нагрузки?
• — Что такое формула кажущейся мощности?
• — Что такое кажущаяся мощность?

Высокоиндуктивные нагрузки, которые используют магнитные поля, такие как двигатели постоянного тока, создают скачок напряжения (называемый «обратным напряжением») при размыкании реле, отключая питание электрической цепи. Этот всплеск обратного напряжения создается за счет сжатия магнитного поля катушки якоря.

Что такое индуктивные нагрузки?

Реактивная / индуктивная нагрузка — индуктивная нагрузка преобразует ток в магнитное поле. Индуктивное реактивное сопротивление сопротивляется изменению тока, в результате чего ток в цепи отстает от напряжения. Примеры устройств, создающих реактивную / индуктивную нагрузку, включают двигатели, трансформаторы и дроссели.

Какой пример индуктивной нагрузки?

Любые устройства или оборудование, в которых есть катушки, по своей природе являются индуктивными. Примеры индуктивной нагрузки: двигатели, соленоиды, катушки контакторов, компрессоры, динамики, реле, трансформаторы, индукторы, генераторы, так далее.

Что такое индуктивная нагрузка и резистивная нагрузка?

В резистивных нагрузках, таких как электрические лампочки, волны напряжения и тока совпадают, либо они находятся в фазе. Как можно догадаться из названия, резистивные нагрузки сопротивляются только току и являются самым простым типом нагрузки. В индуктивных нагрузках, таких как электродвигатель, волна напряжения опережает текущую волну.

Как найти индуктивную нагрузку?

В индукторах напряжение ведет ток на 90 градусов. Формула для расчета индуктивного сопротивления катушки: индуктивное реактивное сопротивление, или X_L, является произведением удвоенной p (pi), или 6,28, частоты переменного тока в герцах и индуктивности катушки, в генри. Икс_L =2^п x f x L.

Светодиодные лампы имеют индуктивную или резистивную нагрузку?

Светодиоды — это полупроводники, которые резистивный и немного емкостной на стыке. Они излучают свет, когда к ним прикладывается прямое напряжение постоянного тока. Драйвер, создающий напряжение постоянного тока, не является линейной нагрузкой. По сути, драйверы представляют собой электронные импульсные источники питания постоянного тока.

Как определить, является ли нагрузка индуктивной или емкостной?

Если присутствуют и катушки индуктивности, и конденсаторы, просто найдите эквивалентное сопротивление сети нагрузки. Если мнимая часть эквивалентного импеданса положительна, то нагрузка индуктивна, если отрицательный, значит емкостной, а если он равен нулю, то резистивный.

Вентилятор — это емкостная нагрузка?

Лампочки, тостеры, электрические водонагреватели и т. Д. Являются резистивными нагрузками. … Все электрические нагрузки, которые имеют катушку с проволокой для создания магнитного поля, называются индуктивными нагрузками. Примеры индуктивные нагрузки вентиляторы, пылесосы и многие другие моторизованные устройства.

Какую нагрузку имеют обогреватели?

Резистивная нагрузка

Двумя распространенными примерами резистивных нагрузок являются лампы накаливания и электрические нагреватели. Резистивные нагрузки потребляют электроэнергию таким образом, что волна тока остается в фазе с волной напряжения. Это означает, что коэффициент мощности для резистивной нагрузки равен единице.

В чем разница между резистивными индуктивными и емкостными нагрузками?

По сравнению с резистивными нагрузками, пики тока индуктивной нагрузки после напряжения. Следовательно, индуктивные катушки производят отстающие коэффициенты мощности. … В емкостных элементах нагрузки используются конденсаторы, накапливающие электрический заряд. Они сопротивляются изменениям напряжения, в результате чего ток достигает пика перед напряжением во время каждого электрического цикла.

Насос представляет собой индуктивную нагрузку?

Индуктивные нагрузки: Сопротивляйтесь изменениям тока и поэтому, когда вы измеряете ток, он отстает (отстает) от напряжения. Электромагнитные поля являются ключом к индуктивным нагрузкам, и поэтому все двигатели (вентиляторы, насосы и т. Д.), Соленоиды и реле являются индуктивными по своей природе.

Какой пример емкостной нагрузки?

Конденсаторы, переменные или фиксированные батареи конденсаторов, пусковые конденсаторы двигателей, генераторы и синхронные двигатели являются примерами емкостных нагрузок. По своей природе активные и емкостные нагрузки различаются. Система будет иметь реальную мощность только при равном количестве обеих нагрузок.

Что такое формула кажущейся мощности?

Полная мощность: S = V x I (кВА) Активная мощность: P = V x Ia (кВт) Реактивная мощность: Q = V x Ir (квар)

Что такое кажущаяся мощность?

Кажущаяся мощность Общая протекающая мощность

Когда электроэнергия в системе переменного тока поступает на нагрузку (компьютер, двигатель, освещение, охлаждение и т. д.) вся мощность необязательно поглощается и используется для выполнения полезной работы — часть энергии может отражаться обратно в источник энергии (энергокомпания).

Интересные материалы:

Как я могу использовать камеру Sony в качестве веб-камеры?
Как я могу использовать мою камеру в качестве светового датчика?
Как я могу найти потерянную камеру Sony?
Как я могу посмотреть записи, снятые с камеры видеонаблюдения?
Как я могу проверить запись с моей камеры?
Как я могу сбросить пароль моей IP-камеры Hikvision?
Как я могу сделать свой старый мобильный телефон камерой видеонаблюдения?
Как я могу стабилизировать камеру без подвеса?
Как я могу улучшить качество передней камеры?
Как я могу увеличить динамический диапазон моей камеры?

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­_L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B₀ (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­_L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*10⁷ См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

На частоте 50 кГц

Online калькулятор индуктивности прямолинейного проводника

Индуктивность кругового кольца круглого сечения

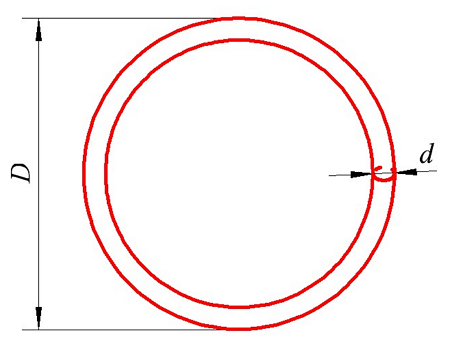
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*10⁷ См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

Online калькулятор индуктивности кольца кругового сечения

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Содержание:

Индуктивность и ее расчет:

Основным соотношением для магнитного поля является принцип непрерывности магнитного потока:

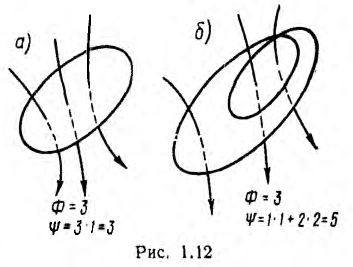
На рис. 1.12, а и б проиллюстрировано различие между потоком и
потокосцеплением, причем число линий в условном масштабе равно
величине потока.

Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб).
Индуктивность уединенного контура, равная отношению потокосцепления к току:

пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн).
Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:

устанавливающему связь между напряженностью магнитного поля 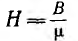и полным током I — алгебраической суммой токов, сцепляющихся с путем интегрирования. При этом положительное направление тока I связано с направлением dI обхода правилом правого винта.
Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м.
Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:

где Е — вектор напряженности наведенного в контуре электрического поля.
Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем.
Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.

Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром.
При изменении тока в контуре изменяется потокосцепление ψ_L созданное этим током, и в контуре наводится э. д. с. самоиндукции

Индуктивность тороида и соленоида

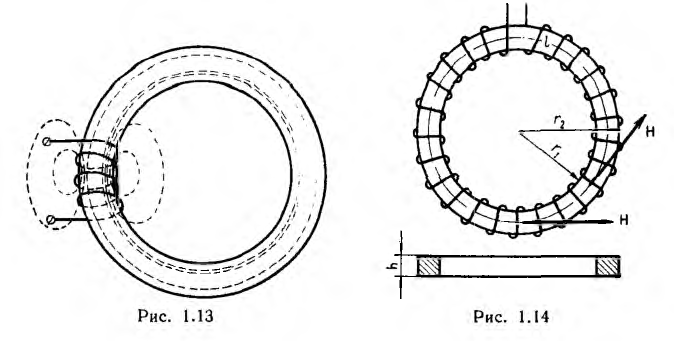
Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ₀, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.

Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.

Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г₁ и г₂, магнитная проницаемость материала µ.

По закону полного тока для окружности с радиусом

откуда

т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции

Поток в сердечнике тороида

а потокосцепление

Отсюда индуктивность тороида

Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность

где w₀ — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,

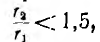
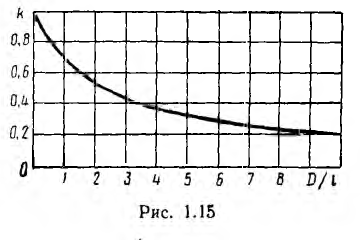
Обычно в реальных тороидах отношение что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ₀

где k < 1 — коэффициент, учитывающий, что в таком соленоиде не весь поток пронизывает все витки.

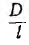
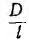
Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При = 0,1 коэффициент k — 0,96, поэтому при < 0 ,1 приближенно принимают k = 1.

Индуктивность двухпроводной линии

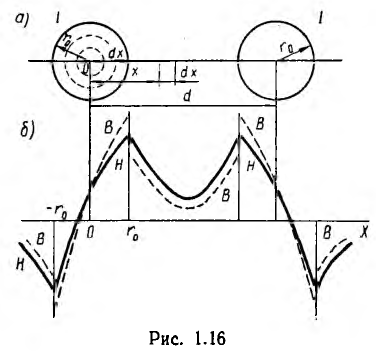
Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г₀, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ₀. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.

Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса 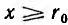дает:

При интегрировании по окружности, лежащей внутри отдельного провода 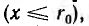охватывается лишь часть L_Х всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению

В воздухе между проводами на линии, соединяющей центры их сечений 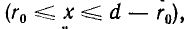направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:

Эти же формулы справедливы и для 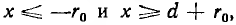т. е. снаружи линии, но здесь они дают разность полей.

Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:

Внутри правого провода 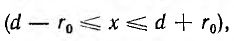соответственно,

На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ₀. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.

На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,

Весь поток между проводами — внешний поток

одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому

а соответствующая ему внешняя индуктивность

Для большинства линий расстояние d между проводами значительно превышает радиус r₀ проводов. В этом случае

Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r₀ поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода

Так как поток dФ_i охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление

Весь поток между проводами — внешний поток

Соответственно, внутренняя индуктивность

Суммарная индуктивность линии

При медных или алюминиевых проводах (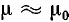) в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда

Для стальных проводов (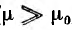) основной частью потока является
внутренний поток и индуктивность

практически не будет зависеть от расстояния между проводами.

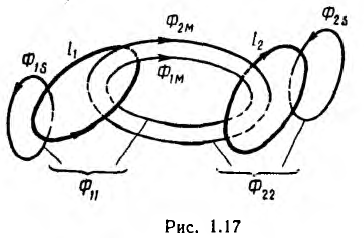
Взаимоиндуктивность и ее расчет

Для двух контуров, имеющих w₁ и w₂ витков с токами I₁ и I₂ (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф_1l—может быть разложен на поток рассеяния Ф_1s, пронизывающий только этот контур, и поток взаимоиндукции Ф_1m, пронизывающий также и второй контур:

Потокосцепление, соответствующее потоку Ф₁₁ (при условии, что этот поток пронизывает все витки первого контура, равно

а потокосцепление рассеяния

Аналогично для второго контура

Потокосцепление второго контура, определяемое током первого,

а потокосцепление первого контура, определяемое током второго,

Можно показать, что

Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн).
Суммарный поток, пронизывающий первый контур,

Суммарное потокосцепление первого контура

и соответственно для второго контура

В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф_1м и Ф_2м (см. рис. 1.17).
Из изложенного видно, что

Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству

а используемый в технических расчетах коэффициент связи двух контуров

Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:

где L_q — индуктивность q-то контура, М_qp = М_рq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается
в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.

Взаимоиндуктивность двух параллельных двухпроводных линий

Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г₀ внутренним потоком в проводах по сравнению с внешним можно пренебречь.
Магнитный поток, пронизывающий первую линию и созданный током I₂ второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности.
Тогда магнитный поток, пронизывающий первую линию,

расстояния от провода линии 1 до проводов линии 2 .

Магнитный поток Ф одновременно является потокосцеплением 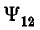первой линии, так как сцепляется с ней один раз; поэтому

а взаимоиндуктивность

Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление 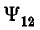будет равно нулю.

Линейные и нелинейные катушки индуктивности

У линейных материалов магнитная проницаемость µ, не зависит от напряженности поля и характеристика 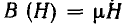для них изображается прямой линией (рис. 1.18, а). Магнитная проницаемость пропорциональна тангенсу угла а наклона этой прямой:

где k — масштабный коэффициент.

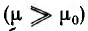
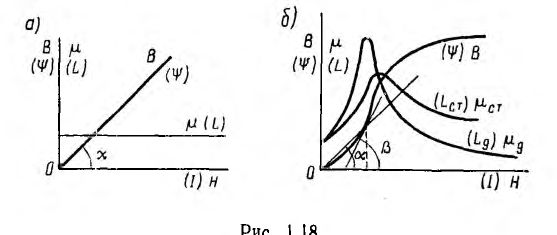
К нелинейным материалам относятся ферромагнетик и — железо, никель, кобальт и гадолиний. Важное значение в электротехнике имеют первые три элемента, главным образом в виде сплавов. У нелинейных материалов магнитная проницаемость очень велика и зависит от напряженности поля.

Подобно нелинейным диэлектрикам по кривой первоначальногo намагничивания В (Н) (рис. 1.18, б) могут быть определены статическая магнитная проницаемость

и дифференциальная, а при быстрых изменениях поля — динамическая магнитная проницаемость

На рис. 1.18, б эти проницаемости представлены в функции напряженности поля. Максимальные значения магнитной проницаемости в очень чистом железе и в некоторых сплавах, например в пермаллое (сплав железа и-никеля с различными присадками), в сотни тысяч раз превышают магнитную постоянную равную

магнитной проницаемости вакуума.

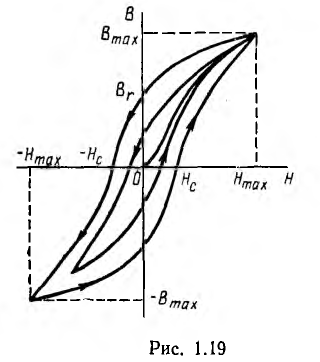
В переменных магнитных полях в ферромагнетиках имеет место явление магнитного гистерезиса (рис. 1.19), заключающееся в несовпадении кривой В (Н) при возрастании напряженности поля с кривой при убывании поля.

Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания и практически совпадает с кривой первоначального намагничивания, Ферромагнитные свойства зависят от температуры и проявляются лишь в определенном ее интервале.

Для тороида и веберамперные характеристики ψ (I) в соответствующем масштабе совпадают с кривыми В (H); поэтому прямая и кривые на рис. 1.18 а и б соответствуют также веберамперным характеристикам при величинах, указанных в скобках.

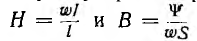
Для нелинейных тороидов вводятся понятия статической индуктивности

и дифференциальной, а также динамической индуктивности

являющихся функциями тока (см. рис. 1.18, б); для линейных тороидов эти индуктивности совпадают.

Аналогично индуктивностям в нелинейных системах контуров вводятся статическая взаимоиндуктивность

и дифференциальная, взаимоиндуктивность, а также динамическая

Индуктивность нелинейного тороида

Расчет нелинейного тороида может быть произведен, если задана зависимость В (H) или µ(H). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой В(H) аппроксимирующую функцию.

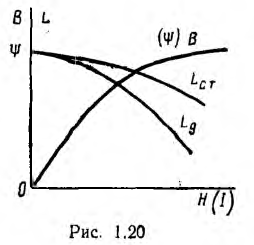
Пусть аппроксимирующая функция для характеристики В (H) (рис. 1.20)
материала сердечника тороида будет

где а и b — постоянные.

Так как для тороида с ферромагнитным однородным cердечником напряженность поля по-прежнему определяется формулой 

то индукция будет равна

а потокосцепление

откуда статическая индуктивность

а дифференциальная индуктивность

Кривые зависимости этих индуктивностей от тока представлены
на рис. 1.20.

Была ли эта статья полезной?