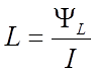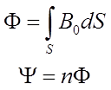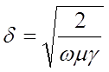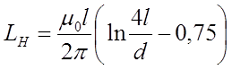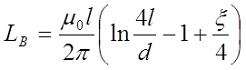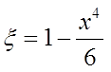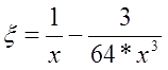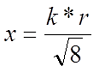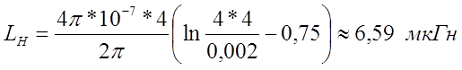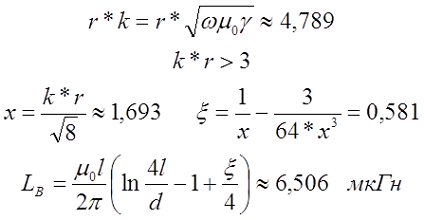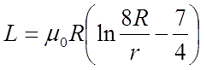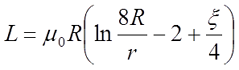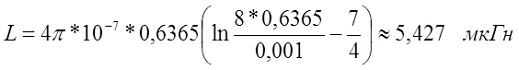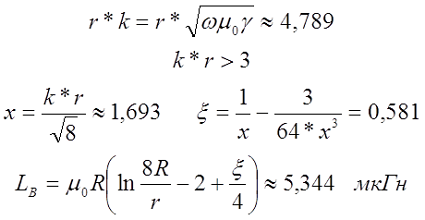Как найти индуктивность одного витка

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­_L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B₀ (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­_L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*10⁷ См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

На частоте 50 кГц

Online калькулятор индуктивности прямолинейного проводника

Индуктивность кругового кольца круглого сечения

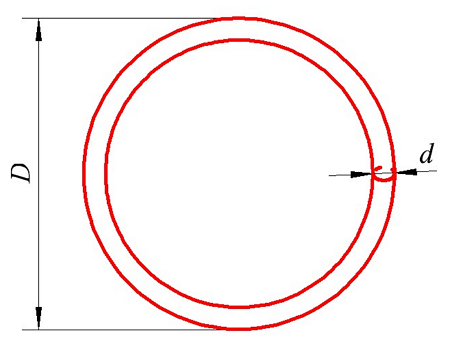
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*10⁷ См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

Online калькулятор индуктивности кольца кругового сечения

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Информация о материале

Опубликовано: 28 августа 2013

Обновлено: 22 декабря 2022

Просмотров: 9796

На рисунке выше показана однослойная катушка индуктивности: D_c — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и d_i — диаметр провода с изоляцией

Для расчета индуктивности L_S применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:

Здесь

D — диаметр оправки или каркаса катушки в см,

l — длина катушки в см,

N — число витков и

L — индуктивность в мкГн.

Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):

Здесь L_S — индуктивность плоской спирали, описанная выше, и

где k_s — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; k_m — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; D_c — диаметр катушки в см, измеренный между центрами проводов и N — число витков.

Величина коэффициента Роса k_m определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:

Коэффициент Роса k_s, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:

Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют несколько факторов.

• Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.



• Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.



• Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.



• Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Если индуктивность большая, то сопротивление обмотки (R_w на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

1. Методики расчета индуктивности катушек

Основным
элементом катушек индуктивности является
токовод. Величина индуктивности
определяется конструкцией токовода и
его размерами.

Полная
индуктивность медного провода круглого
сечения длиной l_ПРи диаметромd₀равна

(3.1)

Из
(3.1) следует, что индуктивность провода
уменьшается с ростом его диаметра. Это
свойство широко используют в УКВ
аппаратуре для уменьшения индуктивности
соединительных проводов за счет
увеличения их диаметра.

Если
одиночный проводник согнуть, например,
в кольцо, то его индуктивность уменьшится
из-за встречного направления токов в
соседних частях кольца. Однако, для
круглого кольца индуктивность будет
наибольшей по сравнению с индуктивностью
витка любой другой конфигурации,
поскольку круглый виток охватывает
наибольшую площадь, обеспечивая
наибольшее потокосцепление.

Индуктивность
круглого плоского витка диаметром Dиз провода круглого сечения длинойl_ПРи диаметромd_ПРравна

(3.2)

При
сворачивании проводника в несколько
витков wодинакового
диаметра образуется катушка, индуктивность
которой можно определить как суммарную
индуктивность всех витков с учетом
взаимоиндукцииMмежду
ними:

(3.3)

Индексы при Муказывают на взаимную индуктивность
между первым и вторым, вторым и третьим,
первым и третьим витками и т.д. Если
известен коэффициент связи, который
определяется равенством

,
(3.4)

то индуктивность
катушки с произвольным числом витков
определяется из

. (3.5)

Коэффициент связи
между витками, расположенными на
расстоянии τ, в однослойной катушке
определяется выражением

(3.6)

Для сплошной намотки
τ=d₀.

Индуктивность
многослойной катушки незначительно
зависит от диаметра провода, так как
определяется в основном взаимоиндукцией
между витками.

Из-за трудности
определения коэффициента связи выражение
(3.5) обычно применяют для расчета катушек
индуктивности с небольшим числом витков
(обычно не более шести).

Для катушек с однородным
замкнутым магнитопроводом (с тороидальным
сердечником) выражение для определения
индуктивности принимает вид

, (3.7)

где μ– начальная магнитная
проницаемость сердечника (μ=1 для
диэлектрического каркаса или воздуха);

μ₀=4π·10^-7Гн/м – магнитная постоянная;

w– число витков обмотки;

S
— площадь поперечного сечения катушки;

— длина намотки катушки;

Таким
образом, увеличение индуктивности
катушки может быть достигнуто за счет
увеличения числа витков, магнитной
проницаемости сердечника, площади
поперечного сечения магнитопровода, а
также уменьшения длины намотки.

В
высокочастотных катушках замкнутый
магнитопровод как правило отсутствует,
поэтому индуктивность катушки будет
меньше, рассчитанной по (3.7). Для учета
рассеивания магнитного потока на краях
катушки вводится поправочный коэффициент
k, который зависит от
отношения диаметра катушки к длине
намотки

(3.8)

Для
практических расчетов однослойных
цилиндрических катушек, намотанных
виток к витку (рис.3.2 а),используют
выражение

, (3.9)

где
— коэффициент формы катушки, учитывающий
краевые эффекты;

μ– начальная магнитная
проницаемость сердечника (μ=1 для
катушек без магнитного сердечника);

μ₀=4π·10^-7Гн/м –
магнитная постоянная;

w– число витков обмотки;

— площадь поперечного сечения круглой
катушки;

D– диаметр катушки;

— длина намотки.

Для
практических расчетов однослойных
цилиндрических катушек без сердечника,
намотанных с принудительным шагом τ(рис.3.2 б),индуктивность
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL

, (3.10)

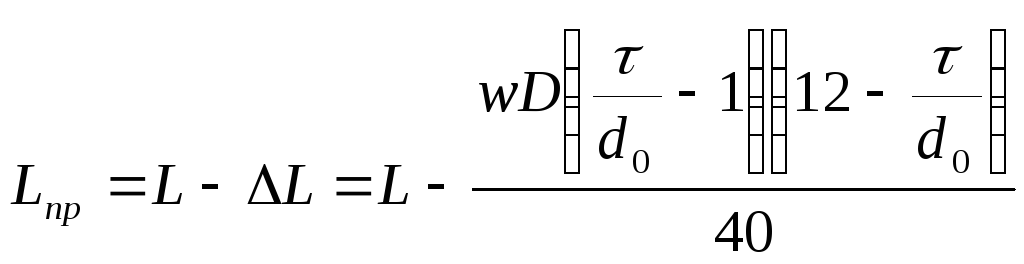
где τ– шаг намотки;

L–
индуктивность катушки, определенная
по (3.9) приμ=1.

Для
практических расчетов индуктивности
тороидальной однослойной катушки,
намотанной сплошным слоем на круглом
магнитном сердечнике прямоугольного
сечения (рис.3.2 в), используют
выражение

, (3.11)

где
— площадь поперечного сечения сердечника
тороида;

— средняя длина сердечника тороида;

D– внешний диаметр сердечника тороида;

d– внутренний диаметр сердечника тороида;

h– высота сердечника тороида.

Для практических
расчетов многослойных катушек без
сердечника(рис.3.2 г) используют
выражение

, (3.12)

гдеD_CP
– средний диаметр катушки;

t— толщина катушки;

l— длина катушки.

Для
практических расчетов многослойных
секционированных катушек без сердечника
(рис.3.2 д) используют выражение

, (3.13)

где L_C
– индуктивность одной секции катушки;

n– число секций;

k_CB– коэффициент связи между смежными
секциями, зависящий от отношения(рис.3.3);

b
– расстояние между секциями.

Для
практических расчетов плоских круглых
спиральных катушек (рис.3.2 е) используют
выражение

, (3.14)

где D_BH,D_H –внутренний и наружный диаметры
катушки, соответственно.

Для
практических расчетов плоских
квадратных спиральных катушек (рис.3.2
ж) используют выражение

, (3.15)

где А_BH,А_H
–внутренняя и наружная стороны
катушки, соответственно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  10.02.20165.15 Mб192.doc

• #
• #
• #
• #
• #
• #