Колебательный контур LC
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.
Основные свойства индуктивности
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией 
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.
Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t1,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = 
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4),
накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U
(в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний 
Частота свободных колебаний контура ƒ = 1 / T
Частота свободных колебаний является частотой резонанса контура,
на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт частоты:
Частота резонанса колебательного контура LC.
ƒ = 1/(2π√(LC))
Расчёт ёмкости:
Ёмкость для колебательного контура LC
C = 1/(4𲃲L)
Расчёт индуктивности:
Индуктивность для колебательного контура LC
L = 1/(4𲃲C)
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Замечания и предложения принимаются и приветствуются!
Когда-то задался целью найти простой способ измерения индуктивности катушек. И тут вдруг вспомнил университетский курс ТОЭ (теоретические основы электротехники), а именно: резонанс в параллельном колебательном контуре, характерный всплеском напряжения. Взяв этот фактор за основу и вспомнив формулу Томсона — зависимость трех составляющих: индуктивности (L), емкости (C) и частоты (f), сваял простенькую схему.
Суть метода состоит в подборе резонансной частоты для собранного колебательного контура с известной (проверенной) емкостью конденсатора. Резонансная частота засекается любым мультиметром по пику напряжения на контуре. А зная частоту и емкость можно вычислить индуктивность.
В качестве генератора частоты использовал звуковую карточку (ЗК) ПК и скачанную с интернета одну из многочисленных программ – генераторов.
Для примера проведу парочку наглядных измерений.
Опыт №1. Беру известные конденсатор 1,5uF и дроссель ДМ-0,6-50 мкГн. Собираю контур, подключаю блок к ЗК и мультиметру, запускаю генератор и прогоняю частоту в обратном порядке – начиная с 20 кГц в сторону уменьшения. Напряжение сразу начало возрастать и застыло на максимуме в пределах 18,85-18,65 кГц, откуда выбрал среднее значение – 18,75 кГц.
Далее можно проводить расчеты вручную, можно ввести формулу в Excell, можно написать программку, а можно и воспользоваться многочисленными онлайн калькуляторами, что я и сделал, используя первый попавшийся сайт: http://coil32.ru/calc/jslcc.html
Ввожу емкость, частоту и без малого получаю указанную на дросселе индуктивность.
Опыт №2. Беру неизвестный дроссель на ферритовом сердечнике типа «гантелька» и конденсатор 1uF. Собираю схему, прогоняю частоту, вычисляю по предыдущей методе ее среднее значение — 10,45 кГц и снова загоняю данные в калькулятор, который выдал значение 232 мкГн.


Меряю индуктивность недавно приобретенным тестером LCR-T4 и получаю результат (с учетом разрядности) 240 мкГн.
Как видите, метод немного неудобный, заставляет подстраивать контур под ограниченные пределы частоты, но имеет право на жизнь. Насколько точно он меряет – вопрос философский, поскольку все в этом мире относительно. Лично меня в схемотехнике он не подводил и долгое время устраивал простотой и минимальными требованиями к ресурсной базе и измерительной аппаратуре.
Следует также отметить, что данным методом можно измерять и емкость конденсаторов, используя катушки известной индуктивности.
О расчете собственного резонанса однослойной катушки индуктивности

Ведь катушки в подавляющем большинстве практических применений работают на частотах намного ниже частоты собственного резонанса и задачей конструктора является, по сути, обеспечение этого условия. При этом большинство инженеров с этой целью пытались уменьшить эту самую «межвитковую» паразитную емкость. В случае же, если катушка работает на частотах близких к собственному резонансу, как например в спиральных резонаторах или катушках Теслы, RLC-модель дает неверные результаты, но для таких случаев были разработаны альтернативные алгоритмы расчета и все остались довольны не особо задумываясь о причинах таких не стыковок.
В нашу цифровую эпоху появились программы, которые дали возможность моделировать поведение любых высокочастотных устройств с высокой степени точности — так называемые электромагнитные симуляторы. Это мощные пакеты типа CST Studio, ANSYS HFSS и многие другие. Давайте проведем исследование однослойной спиральной катушки в программе HFSS. В первой модели мы поместим катушку над идеальной проводящей поверхностью и запитаем от точечного источника с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Расчет будем вести в режиме HFSS Design, использующий метод конечных элементов. Отметим, что популярный ANSYS Maxwell 3D для подобного расчета непригоден.

В учебниках по электродинамике [1] можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися вдоль провода спирали. Такие волноводы применяются как замедляющие структуры в спиральных антеннах и лампах бегущей волны. Длина одного витка и шаг намотки у них сравним с длиной волны. В частности, у спиральной антенны длина витка L равна длине волны, а шаг намотки p равен четверти длины волны.
 |
[1] |
где:
- vax — скорость волны вдоль оси спирали;
- с — скорость света;
Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку влияние витков друг на друга минимально и ЭМ-волна распространяется вдоль провода такой спирали, так же как и у вибратора. Отметим, что фазовая скорость ЭМ волны относительно провода спирали в таком волноводе близка к скорости света.
В нашей же катушке, и длина отдельного витка, и даже длина всей намотки, и тем более шаг намотки намного меньше длины волны. В этом случае, кроме основной моды в таком спиральном волноводе существуют высшие моды колебаний, распространяющиеся непосредственно вдоль ее оси. Другими словами, ЭМ волна распространяется не только вдоль длины провода, но часть ее «перепрыгивает от витка к витку». Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:
 |
[2] |
где:
- λ0 — длина волны рабочей частоты в свободном пространстве;
- D, p — диаметр и шаг намотки;
- c — скорость света;
Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — тот же спиральный волновод с медленными волнами, но работающий в другом режиме колебаний. Во избежании различных спекуляций отметим то обстоятельство, что благодаря наличию высших мод, волна «добирается» до другого конца катушки быстрее чем непосредственно вдоль провода. Поэтому фазовая скорость волны относительно провода выше скорости света, причем в разы. Это не противоречит теории относительности. Достаточно упомянуть, что в полых волноводах фазовая скорость волны тоже выше скорости света. Для понимания этого кажущегося парадокса следует различать фазовую и групповую скорости электромагнитной волны. Для чего отсылаю к учебникам…
Катушка с одним заземленным концом резонирует на частотах nλ0/4, где n – целое число, λ0 — длина волны рабочей частоты и fsrf = vax/λ0. Поэтому увеличение частоты собственного резонанса сводится к увеличению значения vax. Из-за наличия высших мод ЭМ-волны, частота первого резонанса катушки всегда выше частоты, рассчитанной исходя из длины провода. По этой же причине высшие по частоте резонансы не кратны первому и друг другу. При изменении шага намотки vax имеет максимум при шаге спирали примерно равном радиусу намотки (радиус a = D / 2). Однако катушки с большим шагом намотки (p ≈ a) не представляют практического интереса, поскольку имеют малую индуктивность. При увеличении шага намотки частота собственного резонанса катушки растет (при p < a), но рост этот идет за счет снижения величины индуктивности. При фиксированной индуктивности, если увеличивать шаг намотки, нам приходится добавлять витки и выигрыша мы практически не получаем.
У коротких катушек на каркасах большого диаметра последующие резонансы отстоят от первого далеко выше по частоте, что можно видеть по результатам HFSS моделирования:

Особо хотелось бы отметить следующий момент. На низких частотах, где, как мы выяснили, RLC модель справедлива, можно считать, что как индуктивность так и собственная емкость катушки не зависят от частоты, а определяются только геометрией намотки. Это общеизвестный факт, который зафиксирован например в формуле Нагаока. Однако реально параметры спиральной длинной линии зависят от частоты. Не только vax, но и погонная емкость и погонная индуктивность и, как следствие — величины собственной индуктивности и собственной емкости катушки в целом. Только на низких частотах эта зависимость пренебрежимо мала, а вот уже на частотах близких к первому резонансу значения индуктивности и собственной емкости катушки начинают заметно «плыть» по частоте. В итоге, мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не пригодны для расчета частоты собственного резонанса катушки как LC резонанса по формуле Томсона. Расчет даст неверный результат! Неверный, Карл! Таким образом, мы приходим к выводу, что расчеты, основанные на понятии о LC-резонансе в катушке, полностью теряют смысл, что еще раз доказывает несостоятельность RLC-модели катушки не только для объяснения физических явлений при собственном резонансе, но и для расчетов в этой частотной области. Поэтому приходится прибегать к более сложному численному методу из работы [5], включающему в себя функции Бесселя и прочий суровый матан, что и делает Coil64.
Как видно из HFSS-моделей, у катушки как первый резонанс так и все последующие связаны исключительно с волновыми явлениями в катушке. Возможны практические случаи, когда катушка работает в диапазоне частот, в который попадает не только ее первый резонанс, но и более высокие. Очень хорошо такой случай описан в статье И.Гончаренко об анодном дросселе коротковолнового передатчика [2]. На этом примере хорошо видно, что для правильного понимания механизма резонансных явлений в катушке необходимо пользоваться теорией длинных линий.
Кроме фазовой скорости волны в катушке на частоту собственного резонанса оказывает влияние так называемый торцевой эффект, подобный хорошо известному аналогичному понятию из теории антенн, от которого зависит коэффициент укорочения вибратора. Этот эффект проявляется от того, что ЭМ-поле вокруг катушки занимает пространство большее, чем сама катушка. Наличие торцевого эффекта понижает резонансную частоту и этот эффект более выражен у коротких катушек с большим диаметром, что еще раз подтверждает родственную связь резонансных явлений в катушке и в вибраторе. Учитывая фазовую скорость вдоль оси катушки и явление торцевого эффекта мы можем оценочно определить частоту собственного резонанса катушки по следующей весьма приближенной формуле от G3RBJ:
 |
[3] |
где:
- fsrf — частота собственного резонанса [МГц]
- ĺw — длина провода катушки с учетом торцевого эффекта [м]
- lw — реальная длина провода катушки [м]
- D, p, l — диаметр, шаг и длина намотки, соответственно [м]
- 0,25 — коэффициент, определяющий четвертьволновый резонанс (для полуволнового — 0,5)
Если конструктору необходимо создать катушку, имеющую минимальные габариты и максимальную частоту собственного резонанса при заданной индуктивности, то наиболее оптимальна будет намотка с расстоянием между витками, равном диаметру провода, при отношении l/D ≈ 1..1,5. Хотелось бы обратить внимание конструкторов, что здесь идет речь о вычислении собственной резонансной частоты «голой катушки в вакууме», т.е. одной проволочной спирали без учета влияния каркаса, сердечника, экрана, изоляции провода и т.п. Все эти, трудно поддаваемые учету факторы, приводят к уменьшению этой частоты. Причем влияние оказывает все — любой проводник, печатная плата, корпус конструкции. В наших HFSS-моделях влияющие факторы — это выводы спирали и, особенно, сплошная земля в 1-ой и 3-ей моделях. Даже если вы соберетесь измерить частоту собственного резонанса экспериментально, это будет непростой задачей, так как щупы измерительного оборудования также оказывают влияние, даже если катушка где то висит в воздухе!
Необходимо отметить, что строгого аналитического решения уравнений Максвелла для цилиндрической проволочной спирали не существует, поэтому в теории спиральный волновод представляют в виде эквивалентной модели из тонкостенного сплошного цилиндра с анизотропной проводимостью. Однако численные методы решения уравнений Максвелла (чем в принципе и занимается HFSS) приводят нас к вполне однозначным результатам. В итоге, следует иметь ввиду, что вышеприведенная простая аналитическая формула [3] является весьма приблизительной и не может быть применима к любой катушке с произвольной геометрией намотки. Поэтому в Coil64 расчет частоты собственного резонанса основан не на аналитическом, а на численном методе из работы [5], который проверен практическими измерениями. При этом не учитывается влияние экрана, каркаса и других факторов. Расчет имеет точность около 10% при 0,04 < l/D < 40. Для некоторых катушек, например для очень длинных соленоидов с большим числом витков, этот метод может давать неверный результат. На практике же следует придерживаться следующего простого условия: если длина провода, которым намотана катушка, меньше четверти длины волны на наивысшей рабочей частоте, то катушка будет работать ниже своего первого резонанса.
P.S: В заключении хотелось бы добавить несколько слов о концепции «Двух независимых резонансов в катушке — волновом и LC-резонансе». Эта концепция зиждется на четырех ложных в своей основе предпосылках и поэтому в корне неверна:
- Во первых, автор моделирует катушку как двухпроводную несимметричную длинную линию. Чтобы приблизить модель к реальности предполагается, что «земля» как можно дальше удалена от «горячего» провода линии DL. На самом деле катушка это однопроводная линия и по своему поведению больше похожа на антенный вибратор, чем на классическую длинную линию. Это в корне меняет подход к моделированию такого объекта. Как известно, телеграфные уравнения являются аналитическим решением уравнений Максвелла для двухпроводной длинной линии. Но как мы отметили выше, для однопроводной спиральной линии такого решения не существует. Однако программа HFSS может решать дифференциальные уравнения Максвелла «в лоб» численными методами с помощью итераций. Поэтому она и была выбрана в качестве исследовательского инструмента в этой статье.
С другой стороны, если рассуждения автора распространить на любую подходящую двухпроводную длинную линию, то два независимых резонанса возможны не только в спиральной катушке. Почему тогда только катушка удостоилась такой чести? Да просто потому, что Тесла… - Во вторых, «внешний» относительно катушки конденсатор С1 в авторской модели — это собственная емкость катушки. Поскольку в модели она является сосредоточенным элементом, то предполагается, что это статическая емкость. Между чем и чем? Где обкладки этой емкости? Судя по схеме, между концами катушки. В двухпроводной линии, при распространении волны моды ТЕМ, мы всегда можем определить такую статическую емкость и даже указать что является ее обкладками. Например в коаксиальном кабеле. Однако отметим, что при этом она всегда является суммарной погонной емкостью такой линии. В случае однопроводной линии определить подобным образом некую статическую емкость невозможно. Как мы отметили в статье о собственной емкости однослойной катушки, предполагается, что это суммарная емкость между соседними витками. Но и этот подход неверен. Почему тогда между витками, а не частями витков? В любом случае нам так или иначе придется прийти к модели с распределенными параметрами в которой эта емкость будет «размазана» по всей длине катушки. В таком случае такая «размазанная» собственная емкость приведенная к концам катушки — это, по сути, та же самая суммарная (интегральная) погонная емкость длинной линии. Тогда введение в модель внешней С1 теряет всякий смысл. Здесь уж как говорится «или/или».
Автор утверждает, что изменение C1 никак не сказывается на «волновом процессе». По всей видимости — это главный аргумент наличия второго резонанса. С равным успехом можно утверждать, что подключение параллельно колебательному контуру второго колебательного контура приведет к тому, что в схеме появятся два резонанса. На самом деле добавление емкости С1 просто сдвинет резонансную частоту системы вниз, а на «старой» частоте у системы уже будет емкостный входной импеданс. А при резонансе, как известно, реактивность должна быть равна нулю. «Волновой процесс» — это не какое то особое свойство длинной линии как цепи с распределенными параметрами. Ведь эти параметры — это те же LCR элементы. Просто рассчитать такую цепь с помощью законов Ома и Кирхгофа мы не можем по причине бесконечного числа таких элементов. Поэтому приходится пускать в дело интегральное и дифференциальное исчисление. Но сами законы по прежнему работают. И согласно ним мы параллельно нашей «размазанной» собственной емкости катушки подключили дополнительную емкость. Вот и все.
- Погонная емкость и погонная индуктивность обычной «прямой» длинной линии с малыми потерями зависят только от ее геометрических размеров. В спиральной линии, как мы отметили выше, они зависят также от частоты. Это вторая причина по которой расчет частоты собственного резонанса на основе сосредоточенной собственной емкости по формуле Томсона не имеет смысла. Необходимо использовать только модель с распределенными параметрами.
По всей видимости автор, получив разные результаты по формуле Томсона и по формуле [3], вместо того чтобы усомниться в корректности расчетов, пришел к выводу, что существуют два разных резонанса. На самом деле никаких «двух независимых резонансов» в реальности не существует, что подтверждают и расчеты в HFSS и точные измерения. Повторюсь еще раз — все дело в разных моделях одной реальной катушки и разных уровнях математических абстракций в зависимости от конкретных условий расчета. Одно из двух. Либо мы моделируем реальную катушку как схему из сосредоточенных элементов, либо как схему с распределенными параметрами. И та и другая — это по сути RLC модели разной степени сложности. Смешивать все это в одну кучу и подгонять под выдуманную теорию нельзя.
Ссылки по теме:
- Техническая электродинамика, Семенов Н.А., Изд. «Связь» Москва, 1973, стр.318-323.
- Моделирование анодного дросселя как распределенной структуры — И.Гончаренко (DL2KQ) 2007-2012
- Паразитные резонансы в катушке П-контура — И.Гончаренко (DL2KQ)
- Высокочастотные катушки, спиральные резонаторы и увеличение напряжения из-за когерентных пространственных мод 2001г. (Оригинал статьи здесь)
- THE SELF-RESONANCE AND SELF-CAPACITANCE OF SOLENOID COILS — applicable theory, models and calculation methods. By David W Knight (G3YNH)
- The self-resonance and self-capacitance of solenoid coils by David W Knight — основная статья с массой полезных ссылок по теме, в том числе на экспериментальные исследования с наглядными фото (G3YNH)
- SELF-RESONANCE IN COILS and the self-capacitance myth. By Alane Payne (G3RBJ)
- О собственной емкости катушки.
- Измерение частоты собственного резонанса катушки индуктивности — А. Алексеев (R2AUK)
- Как создать модель и рассчитать параметры однослойной катушки индуктивности в электромагнитном симуляторе ANSYS HFSS;
Федеральное
агентство по образованию
Государственное
образовательное учреждение
высшего
профессионального образования
САМАРСКИЙ
ГОСУДАРСТВЕННЫЙ
АЭРОКОСМИЧЕСКИЙ
УНИВЕРСИТЕТ
имени академика
С.П. Королёва ( СГАУ )
Факультет инженеров
воздушного транспорта
Кафедра электронных
систем и устройств
Расчет катушки индуктивности колебательного контура и обоснование выбора материалов.
Выполнил
студентка: Воробьёва А.Ю.
Группа
№ 3203
Вариант
№ 33
Проверил
преподаватель:
Макарычев
Ю.И.
Самара
2011
Содержание
|
1 Задание для |
3 |
|
2 Расчет |
3 |
|
2.1 |
3 |
|
2.2 Выбор материала |
4 |
|
2.3 Выбор размеров |
4 |
|
2.4 Расчет |
5 |
|
2.5 Определение |
6 |
|
2.6 Определение |
7 |
|
2.7 Учет влияния |
9 |
|
2.8 Расчет |
10 |
|
2.9 Расчет |
11 |
|
3 Расчет ТКИ и |
12 |
|
4 Выбор конденсатора |
13 |
|
5 Итог |
15 |
|
Список используемой |
16 |
1 Задание.
Рассчитать индуктивность колебательного
контура на резонансной частоте
.При
условии, что емкость конденсатора
.
Тип и материалы сердечников,
,
и другие необходимые данные для расчета
приведены
Материал экрана: алюминий.
Тип и материал сердечника: СЦР-1,Р-20.
Выбрать материал и размеры каркаса, тип
намотки. Определить число витков и
оптимальный диаметр провода. Вычислить
собственную емкость, добротность,
температурный коэффициент индуктивности
и температурный коэффициент частоты.
Рисунок 1.Колебательный контур.
где Ск – емкость контура;
Lк – индуктивность
контура.
2 Расчет
2.1 Нахождение индуктивности контура.
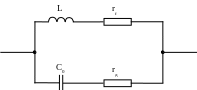
Рисунок 2. Схема замещения катушки
идеальными элементами.
где L – идеальная
индуктивность катушки;
С0 – собственная емкость
катушки;
rf
– сопротивление обмотки катушки;
rд – сопротивление
диэлектрика каркаса за счет поляризации.
Определим индуктивность исходя из
формулы
определим L.
,
2.2 Выбор материала каркаса.
Каркас катушки в значительной степени
определяет ее стоимость и
электрические параметры.
Каркас должен быть
удобным для намотки и крепления в
приборе,
обеспечивать устройство (распайку)
выводов обмотки и надежную фиксацию
положения построечного элемента.
Материал каркаса должен
допускать применение прогрессивных
технологических методов
изготовления, быть дешевым, механически
прочным, вносить малые потери,
обладать необходимой теплостойкостью,
малой влагостойкостью
и небольшим коэффициентом линейного
расширения и, в
ряде случаев, малым значением температурного
коэффициента диэлектрической
проницаемости.
В достаточной степени
этим требованиям отвечают каркасы из
полистирола, фенопластов, пресс-материалов
типов АГ-4С, ДСВ-2Р-2М и им подобных. На
пониженных частотах может оказаться
целесообразным
применение более дешевых каркасов из
бакелизированных
трубок.
Для каркасов катушек
с высокой стабильностью применяют
радиокерамику
типа В, радиофарфор, ультрафарфор и
высокочастотный
стеатитит.
Исходя из заданных параметров наиболее
подходящим материалом является
высокочастотный стеатитит.
2.3 Выбор размеров каркаса.
Прежде чем
приступить к дальнейшим вычислениям,
для удобства, приведем чертеж катушки:

Рисунок 3. Чертеж катушки индуктивности.
где lc
– длина сердечника;
lк – длина намотки;
Dc –
диаметр сердечника;
Dк – диаметр катушки;
d – диаметр провода без
изоляции.
По сводным таблицам для СЦР — 1 можно
найти Dc=0,6см,
lc=0,9см.
Для цилиндрических сердечников Dk=0,9см
и предварительно возьмем lк=0,9см.
2.4 Расчет индуктивности катушки с учетом
сердечника.
где
—
необходимая величина расчетной
индуктивности;
—
действующая магнитная проницаемость
сердечника.
где
—
начальная магнитная проницаемость
материала сердечника;
— коэффициент использования магнитных
свойств;
-поправочный
коэффициент.
определяем по графику
=f(lk/
Dc),
определяем по графику
=f(lc/
Dc)
(lk/
Dc)=0,9/0,6=1,5;
=0,28.
(lc/
Dc)=0,9/0,6=1,5;
=0,9.
определяем по таблице, исходя из того,
что задана марка магнитного материала
Р-20.
=10.
Таким образом
2.5 Определение числа витков и типа
намотки.
Применяемые виды
намотки можно разделить на однослойные
и многослойные.
При однослойной
намотке витки
располагаются на цилиндрической
поверхности каркаса в один слой. При
плотном расположении
витков, разделяемых лишь изоляцией
провода, получается
сплошная однослойная намотка при
расположении витков на некотором
расстоянии друг от друга — намотка с
шагом.
Однослойные катушки
с шагом отличаются высокой добротностью
(150 -400) и
стабильностью; они в основном применяются
в контурах KB
и УКВ.
Для повышения
точности намотки провода применяются
нарезные каркасы,
т. е. каркасы, на поверхности которых
сделана неглубокая (0,2 — 0,3d)
спиральная канавка. Однако погружение
провода в диэлектрик
каркаса несколько понижает добротность
и стабильность катушки.
Для высокостабильных
катушек применяются специальные способы
изготовления намоток — тугая, горячая
и осажденная или нанесенная
намотки.
Катушки без каркаса
могут быть практически выполнены при
числе витков
не более трех. Они отличаются несколько
более высокой добротностью,
но, имеют малую механическую жесткость
и пониженную
стабильность.
Для катушек
индуктивностью выше 15—20
мкГн применяют
сплошную
однослойную намотку. Целесообразность
перехода на сплошную намотку определяется
диаметром катушки: чем больше диаметр
катушки, тем большая индуктивность
может быть получена при
применении намотки с шагом.
Катушки со сплошной
намоткой также отличаются высокой
добротностью (150—250) и стабильностью и
широко используются в контурах
для коротких, промежуточных и средних
волн, если требуется
индуктивность не выше 200—500 мкГн.
Для изготовления
катушек с индуктивностью выше 200—500
мкГн применяют
многослойные намотки.
Целесообразность
перехода на многослойную намотку
определяется
диаметром катушки. Чем больше диаметр
катушки, тем при
большей индуктивности следует переходить
на многослойную
намотку.
Многослойные намотки
могут быть разделены на простые и
сложные.
Широкое применение
имеют сложные многослойные намотки,
например
универсальные.
Катушки, предназначенные
для работы в диапазоне частот до 500 кГц,
имеют многослойную обмотку. Применяют
рядовую многослойную
или универсальную намотки, а также
намотку «внавал».
Катушки для частот выше 1—2 МГц имеют
однослойную намотку.
Для намотки катушек
применяют провода в эмалевой изоляции
марок ПЭЛ, ПЭ,
ПЭВ, комбинированной изоляции марок
ПШО, ПШД, ПЭЛШО,
ПЭШД, а также литцендрат ЛЭШО И ЛЭШД.
Для многослойных
катушек с универсальной намоткой
применяют обычно
провода с волокнистой изоляцией, так
как волокнистая
изоляция обеспечивает большее сцепление
витков.
Для катушек с шагом
применяется неизолированный провод
МГМ, покрытый
слоем серебра.
В данной работе целесообразно применить
однослойную намотку из ПЭЛ.
Для определения числа витков однослойной
катушки воспользуемся формулой:

Значение L0 определяем
по графику, L0=f(lk/
Dк)
(lk/
Dк)=1; L0
=7
Откуда
2.6 Определение оптимального диаметра
провода.
Между сопротивлением провода катушки
и его диаметром существует сложная
зависимость, так как при этом изменяется
проявление поверхностного эффекта и
эффекта близости.
Рассмотрим вопрос о влиянии диаметра
провода на сопротивление катушки. В
случае прямолинейного провода увеличение
диаметра вызывает увеличение его
периметра, а, следовательно, уменьшение
сопротивления току высокой частоты.
Зависимость сопротивления отрезка
прямолинейного провода от диаметра при
некоторой частоте выражается кривой L
на рис. 4 (кривая I представляет
собой зависимость сопротивления току
высокой частоты от диаметра). При
свертывании провода в спираль возникает
эффект близости, который проявляется
тем сильнее, чем больше диаметр провода.
Увеличение сопротивления за счет эффекта
близости примерно пропорционально
диаметру провода и изображается прямой
II. Сложив величины,
характеризуемые кривыми I
и II, получим изменение
полного активного сопротивления провода
катушки в зависимости от его диаметра;
эта зависимость выражается кривой III.
Ход кривой III показывает,
что при вполне определенном диаметре
провода сопротивление катушки имеет
минимальное значение. Можно показать,
что при этом сопротивление провода
катушки (с учетом поверхностного эффекта)
равно увеличению сопротивления за счет
эффекта близости.

Рис. 4
Оптимальный диаметр провода катушки
рассчитывают при помощи вспомогательного
коэффициента:
где
— вспомогательный параметр;
-поправочный
коэффициент.
Dк – диаметр катушки;
N –число витков намотки;
где f 0 – резонансная
частота.
к=f(l/D)
к=4
,т.к.
,
то
;
0,065см,
в целях экономии меди возьмем dопт
= 0,69мм
Используя эмалевую изоляцию провода
типа ПЭЛ принимаем диаметр провода
равным 0,35
Проведем проверку подобранного диаметра
провода:
,
следовательно, выбор параметров каркаса
сделан правильно.
2.7 Учет влияния экрана.
Для устранения
паразитных связей, обусловленных внешним
электромагнитным
полем катушки, и для устранения влияния
внешних полей
катушка экранируется, то есть располагается
внутри замкнутого,
металлического заземленного экрана.
Экранирующее действие
характеризуется отношением напряженности
внешнего поля катушки при наличии экрана
к напряженности
поля при его отсутствии. Для экрана
среднего качества,
выполненного, например, в виде алюминиевого
стакана, это отношение равно приблизительно
0,01 — 0,05, что бывает достаточно для
большинства практических случаев. Для
усиления экранирующего действия
применяются двойные и даже тройные
экраны.
Под влиянием экрана
изменяются основные электрические
параметры
катушки; уменьшается ее индуктивность,
а также увеличиваются
сопротивление и собственная емкость.
Добротность экранированной катушки
оказывается ниже добротности той же
катушки при отсутствии экрана. Изменение
параметров катушки зависит
от соотношения между ее размерами и
размерами экрана.
Для того чтобы индуктивность и добротность
падали не более чем на 10%:, рекомендуются
следующие соотношения м.д. диаметрами
экрана и катушки:[3]
;
где
— диаметр экрана.
Выберем диаметр экрана равным 2,3см,
высоту равную 1,8см;
При помещении катушки в экран ее
индуктивность и добротность уменьшаются.
Индуктивность экранированной катушки
составляет:
где
—
индуктивность неэкранированной катушки;
к – коэффициент связи м.д. экраном и
катушкой.
Для однослойных катушек:
где
— коэффициент зависящий от отношения
длины катушки к ее диаметру.
;
Определяем индуктивность экранированной
катушки:
Т.к
и высота между катушкой и экраном равна
высоте катушки, то потери вносимые
экраном в К.И. можно определить по
формуле:[3]
Где латуни
2.8 Расчет собственной емкости катушки.
В катушке, между
отдельными витками и между витками и
ближайшими
металлическими телами—экранами, шасси
прибора и т. п.,
всегда существует разность потенциалов,
которая создает электрическое
поле. Влияние этого поля подобно влиянию
некоторой емкости, включенной параллельно
катушке; эту емкость называют собственной
(или распределенной) емкостью катушки.
Ее величина зависит
от размеров катушки, конструкции обмотки,
близости расположения
витков со значительной разностью
потенциалов, удаленности
их от экранов, диэлектрической
проницаемости изоляции провода
и каркаса, а также ряда других конструктивных
факторов. Чем
больше диаметр катушки, чем ближе друг
к другу расположены витки со значительной
разностью потенциалов, чем выше
диэлектрическая проницаемость
изоляции провода и материала каркаса,
тем больше
собственная емкость катушки индуктивности.
Наименьшей собственной
емкостью (1—2 пФ) обладают однослойные
катушки, намотанные с шагом. Многослойные
катушки обладают
большей емкостью,- величина которой
зависит от способа намотки.
Например, емкость катушек с простой
универсальной намоткой составляет 5 —
10 пФ, с перекрестной универсальной
намоткой 15 — 30
пФ.
Расчет собственной
емкости однослойных катушек удобнее
производить по
эмпирической формуле:
где
определяется
по графикам.
Тогда
.
2.9 Расчет добротности.
Добротность контура зависит не только
от его параметров, но также и от параметров
внешней цепи — внутреннего сопротивления
источника и сопротивления нагрузки.
Добротность контура определяют по
формуле:
Сопротивление току высокой частоты.
Для катушек, работающих на частотах
выше 10МГц, сопротивление
вычисляется
по формуле:
где d – диаметр провода
без изоляции;
N – число витков катушки;
D – диаметр катушки;
Ом
Потери вносимые сердечником.
Потери вносимые сердечником могут быть
найдены по следующей формуле:
Предположим, что катушка находится в
радиоприемнике, тогда Н=0, и тогда
Ом.
Потери в диэлектрике.
Диэлектрические
потери возникают в поле собственной
емкости катушки
через диэлектрик Сол
и зависят от величины этой емкости,
качества tgδ
материала
каркаса и частоты. Потери в диэлектрике
обусловлены тем, что между соседними
витками катушки существует емкость,
имеющая две составляющих — емкость
через воздух Сов
и емкость
через диэлектрик Сол.

рис.5
Сопротивление, вносимое диэлектрическими
потерями, можно представить включенным
параллельно собственной емкости катушки.
Величина этого сопротивления равна:[3]
.
Пересчитывая это сопротивление на
последовательное, получаем:
Откуда
,
поэтому добротность контура равна:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:
где
L — индуктивность, Гн
С — емкость, Ф
Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R — это суммарное сопротивление потерь катушки и конденсатора
L — собственно сама индуктивность катушки
С — собственно сама емкость конденсатора
Принцип работы последовательного колебательного контура
Генератор частоты и последовательный колебательный контур
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор (Ген)у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН .
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты генератора на сопротивление колебательного контура
В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
3 Килогерца
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
74 Килогерца
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс последовательного колебательного контура
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность последовательного колебательного контура
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Видео на тему «Как работает колебательный контур. Резонанс»:
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.



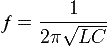
 Автор утверждает, что изменение C1 никак не сказывается на «волновом процессе». По всей видимости — это главный аргумент наличия второго резонанса. С равным успехом можно утверждать, что подключение параллельно колебательному контуру второго колебательного контура приведет к тому, что в схеме появятся два резонанса. На самом деле добавление емкости С1 просто сдвинет резонансную частоту системы вниз, а на «старой» частоте у системы уже будет емкостный входной импеданс. А при резонансе, как известно, реактивность должна быть равна нулю. «Волновой процесс» — это не какое то особое свойство длинной линии как цепи с распределенными параметрами. Ведь эти параметры — это те же LCR элементы. Просто рассчитать такую цепь с помощью законов Ома и Кирхгофа мы не можем по причине бесконечного числа таких элементов. Поэтому приходится пускать в дело интегральное и дифференциальное исчисление. Но сами законы по прежнему работают. И согласно ним мы параллельно нашей «размазанной» собственной емкости катушки подключили дополнительную емкость. Вот и все.
Автор утверждает, что изменение C1 никак не сказывается на «волновом процессе». По всей видимости — это главный аргумент наличия второго резонанса. С равным успехом можно утверждать, что подключение параллельно колебательному контуру второго колебательного контура приведет к тому, что в схеме появятся два резонанса. На самом деле добавление емкости С1 просто сдвинет резонансную частоту системы вниз, а на «старой» частоте у системы уже будет емкостный входной импеданс. А при резонансе, как известно, реактивность должна быть равна нулю. «Волновой процесс» — это не какое то особое свойство длинной линии как цепи с распределенными параметрами. Ведь эти параметры — это те же LCR элементы. Просто рассчитать такую цепь с помощью законов Ома и Кирхгофа мы не можем по причине бесконечного числа таких элементов. Поэтому приходится пускать в дело интегральное и дифференциальное исчисление. Но сами законы по прежнему работают. И согласно ним мы параллельно нашей «размазанной» собственной емкости катушки подключили дополнительную емкость. Вот и все.

























