Время на прочтение
9 мин
Количество просмотров 12K
Давно хотел сделать учебные материалы по теме Теория Информации + Machine Learning. Нашёл старые черновики и решил довести их до ума здесь, на хабре.
Теория Информации и Machine Learning мне видятся как интересная пара областей, глубокая связь которых часто неизвестна ML инженерам, и синергия которых раскрыта ещё не в полной мере.
Когда я говорю коллегам, что LogLoss на тесте и Mutual Information между прогнозом и прогнозируемой величиной связаны напрямую, и по несложной формуле можно из одного получить второе, они часто искренне удивляются. В википедии со страницы LogLoss есть ссылка на Mutual Information, но не более того.
Теория Информация может стать (а, точнее, стала) источником понимания как и почему работают разные методы ML, в частности нейронные сети, а также может дать идеи улучшения градиентных методов оптимизации.
Начнём с базовых понятий Энтропии, Информации в сообщении, Взаимной Информации (Mutual Information), пропускной способности канала. Далее будут материалы про схожесть задач максимизации Mutual Information и минимизации Loss-а в регрессионных задачах. Затем будет часть про Information Geometry: метрику Фишера, геодезические, градиентные методы, и их связь с гауссовскими процессами (движение по градиенту методом SGD — это движение по геодезической с шумом).
Также нужно затронуть AIC, Information Bottleneck, поговорить про то, как устроен поток информации в нейронных сетях – Mutual Information между слоями (Information Theory of Deep Learning, Naftali Tishby) и многое другое. Не факт, что получится всё перечисленное охватить, но попробую начать.
1. Базовые определения
Есть три более менее разных способа прийти к формуле энтропии распределения
Давайте их опишем. Начнём с базовых определений.
Опр. 1.1: Неопределенность — это логарифм по основанию 2 от числа равновероятных вариантов: . Измеряется в битах. Например, неопределенность неизвестного битового слова длины k равна k.
Логарифм
Логарифм числа по основанию 2 – это то, сколько раз нужно делить число на 2, чтобы получить число меньше либо равно 1. Например,
Для не степеней двойки эта функция гладко продолжается. Например,
Важное свойство логарифма:
Поробуйте вывести его из нестрогого определения выше для случая, когда и
степени двойки.
Битовые слова
Битовые слова длины – это последовательности нулей и единиц длины
. Каждый знак в битовом слове называется битом. Например, вот битовые слова длины 5:
00000, 00001, 00010, 00011, 00100, 00101, … , 11100, 11101, 111110, 11111
Их 32 штуки. , то есть неопределённость слова длины 5 равна 5.
Именно столько неизвестных бит в неизвестном битовом слове длины 5.
Таким образом, каждый знак в битовом слове называется битом, но ещё бит – это единица измерения неопределённости. И из этого примера понятно почему.
Для краткости везде далее обозначается просто как
.
Опр. 1.2: Информация в сообщении — это разница неопределенностей до получения сообщения и после
Тоже измеряется в битах.
Например, Ваня загадал число от 1 до 100. Нам сообщили, что оно меньше либо равно 50. Неопределённость до сообщения равна , а после —
. То есть в этом сообщении 1 бит информации. Умело задавая бинарные вопросы (вопросы, на которые ответ ДА или НЕТ), можно извлекать ровно 1 бит информации.
Некоторые вопросы неэффективны, например, вопрос «верно ли, что число меньше либо равно 25?» уменьшит неопределенность на бита с вероятностью 0.25, а с вероятностью 0.75 только на
бит, то есть в среднем на
бит. Если вы своим вопросом разбиваете множество вариантов в пропорции
, то среднее количество бит информации в ответе равно
.
Это выражение будем обозначать через или
. Здесь мы как программисты перегрузим функцию H так, чтобы она работала для двух случаев — когда на вход поступает пара чисел, сумма которых равна 1, и когда одно число из отрезка [0, 1].
Опр. 1.3:
График H(x)

Видно, что задавая бинарные вопросы, в можно извлекать максимум 1 бит информации в среднем (максимальное значение функции . Ещё раз: да, можно сразу задавать вопросы типа «Число равно 57?» и если повезёт, получать log(100) бит информации. Но если не повезёт, вы получите лишь log(100/99) бит информации. Среднее число бит информации для такого сорта вопросов равно
что заметно меньше 1.
В этом примере 100 вариантов, а значит начальная неопределенность равна — это то, сколько всего в среднем бинарных вопросов нужно задать Ване, чтобы выведать ответ. Правда число получается нецелое и нужно округлять вверх.
Если мы будем задавать не бинарные вопросы, а вопросы, которые подразумевают в качестве ответа натуральное число от 1 до M, то мы сможем в одном ответе получать более, чем один бит информации. Если мы задаём такой вопрос, для которого все M ответов равновероятны, то в среднем мы будем получать бит. Если же вероятность ответа i равна p(i), то среднее число бит в ответе будет равно:
Опр. 1.4: Энтропия дискретного распределения задаётся формулой (1) выше.
Здесь мы перегрузили функцию H для случая, когда на вход поступает дискретное распределение.
ИТАК: Первый простой способ прийти к формуле энтропии — это посчитать среднее число бит информации в ответе на вопрос с разновероятными ответами.
Давайте пойдём дальше. Пусть Ваня не загадывает число, а сэмплирует его из распределения . Сколько бинарных вопросов нужно задать Ване, чтобы узнать выпавшее число? Интуитивно понятно, что нужно разбить множество вариантов на два подмножества уже равных не по количеству элементов, а по суммарному значению вероятности, и спросить Ваню, в каком из двух находится выпавшее число. Получить ответ и продолжить в том же духе с новым уменьшенным множеством вариантов — снова разбить его на два с примерно равным весом, спросить в каком из двух находится выпавшее число и так далее. Идея хорошая, но не совсем рабочая. Оказывается, правильнее поступать с конца и начать строить дерево разбиений снизу, а именно, найти два самых мало вероятных варианта и объединить их в один новый вариант, тем самым уменьшив число вариантов на 1. Потом снова найти два самых маловероятных и снова объединить их в один новый, и так далее, построив конечном итоге бинарное дерево. В листьях этого дерева находятся числа. Внутренние вершины помечены множеством чисел из поддерева, корнем которого они являются. Корень дерева помечен множеством всех чисел. Это дерево и даёт алгоритм того, как нужно задавать вопросы Ване. Нужно двигаться с корня дерева и спрашивать Ваню, куда по этому дереву идти — влево или вправо (в каком из двух множеств вершин детей находится выпавшее число). Это дерево даёт не только рецепт самого быстрого в среднем метода угадывания числа, но ещё и алгоритм Хаффмана сжатия данных.
Задача 1.1: Изучите код Хаффмана. Докажите, что текст с исходной длиной символов N имеет в сжатом виде длину, ограниченную снизу величиной бит и при удачных обстоятельствах её достигает.
ИТАК: Формула возникает при решении задачи о минимальном среднем числе бинарных вопросов, которые нужно задать, чтобы выведать выпавшее значение случайной величины с распределением
Это второй способ прийти к формуле (1).
Есть ещё один, третий, простой способ прийти к формуле энтропии, но нужно знать формулу Стирлинга.
Задача 1.2: Есть неизвестное битовое слово длины k (последовательность единиц и ноликов, всего k символов). Нам сообщили, что в нём 35% единичек. Чему равно при больших k?
Ответ
Примерно , где
Задача 1.3: У Вани есть неизвестное слово длины в алфавите длины M. Он сообщил доли всех букв в слове —
.
Чему равно при больших
?
Ответ
ИТАК: Задача 1.3 и есть третий способ прийти к формуле (1).
Опр. 1.5: Информация в сообщении по некоторую случайную величину — это разница энтропий:
Значения случайной дискретной величины можно рассматривать как буквы, каждая следующая буква слова — это просто очередное измерение случайной величины. Вот и получается, что информация в сообщении про некоторую случайную величину — это количество бит информации про измерения этой случайной величины нормированное на число измерений.
Задача 1.4: Чему равна энтропия дискретного распределения ?Сколько информации содержится в сообщении
где
имеет распределение
?
Ответ:
Этот результат требует принятия. Как же так? – Нам сообщили ненулевую на первый взгляд информацию, отсекли самый вероятный вариант из возможных. Но неопределённость на множестве оставшихся вариантах осталась прежней, поэтому формула даёт ответ 0.
Задача 1.5: Приведите пример конечного распределения и сообщения, которое не уменьшает, а увеличивает неопределённость.
Ответ:
, а сообщение message = «это не первый элемент». Тогда
Древняя мудрость «во многих знаниях многие печали» в этом контексте получает ещё одну интересную интерпретацию: современный мир, наука и человеческая жизнь таковы, что новые «сообщения» о истории и об устройстве мира только увеличивают неопределённость.
Дискретные распределения на счётном множестве значений, которые затухают по экспоненциальному закону (геометрические прогрессии), обладают свойством неизменности неопределённости при получении информации, что среди первых элементов нет правильного ответа. Менее, чем экспоненциальные затухания (например, ), только растят неопределённость при откидывании первых элементов.
Задача 1.6: Напишите формулу для энтропии распределения Пуассона
,
.
Найдите простое приближение для больших .
Ответ
Задача 1.7: Дано распределение вещественной случайной величины. Пусть
— это сколько бинарных вопросов в среднем нужно задать, чтобы узнать какое-то выпавшее значение случайной величины с точностью до
. Найдите приближённое выражение
для малых значений
.
Ответ:
Нужно разбить ось x на корзинки длиной посчитать вероятности
каждой корзинки и посчитать
Если значение
достаточно мало, то ответ можно приблизить интегралом:
(см. определение энтропии непрерывного распределения ниже).
Опр. 1.6: Энтропия непрерывного распределения равна
Здесь мы ещё раз перегрузили значение символа H для случая, когда аргумент есть функция плотности вероятности (PDF).
Задача 1.8: Даны два распределения и
двух вещественных случайных величин. К чему стремится разница
при
?
Ответ:
Задача 1.9: Чему равна энтропия нормального распределения ?
Ответ:
Задача 1.10: Напишите формулу для энтропии экспоненциального распределения .
Задача 1.11: Случайная величина является смесью двух случайных величин, то есть её распределение
есть взвешенная сумма распределений:
Пусть множество значений, которые принимает , не пересекается с множеством значений
, другими словами, пусть носители этих двух случайных величин не пересекаются. Найдите выражение для энтропии
через энтропии
и
.
Ответ
Последнее равенство тут возможно только благодаря тому, что носители и
двух распределений по условию задачи не пересекаются. Дальше мы это выражение преобразуем в
В этой задаче хотелось показать, что даже в простом случае непересекающихся носителей энтропии не просто складываются с соответствующими весами, а появляется добавка . Если веса равны 1/2, то эта добавка равна 1.
Интерпретация формулы такая: результат измерения с вероятностью находится в
и с вероятностью
– в
и соответственно нам достанется неопределённость
значений на множестве
или неопределённость
на множестве
. Но чтобы выяснить, в каком из них находится измерение мы потратим в среднем
вопросов.
Из этого в частности следует, что смесь с коэффициентами 1/2 двух нормальных величин с одинаковой дисперсией, но сильно разными средними, имеет энтропию на 1 больше, чем энтропия одного нормального распределения. Носители нормальных случайных величин равны всей прямой, а значит пересекаются, но в случае сильно разных средних можно этим пренебречь.
Задача 1.12: Случайная величина равновероятно равна 0 или 1. Случайная величина
зависит от
: если
, то
сэмплируется из
, а если
, то
сэмплируется из
. Сколько бит информацию про случайную величину
содержится в сообщении
(как функция от
)?
Ответ
Есть такой численный ответ:
Понятно, что график начинается с 0 и стремится к 1:
-
при
два гаусса одинаковые и сообщение про то, какой из них был выбран ничего не даёт;
-
при
имеем смесь (mixture) двух гауссовских распределений с сильно разнесёнными центрами; сообщение про значение
говорит, в каком из двух «гауссовских колпаков» находится ответ, и число вариантов уменьшается примерно в два раза, а неопределённость уменьшается на 1; «примерность» связана с тем, что «колпаки» перекрываются, но размер перекрытия быстро уменьшается с ростом
.
-
в окрестности
рост квадратичный, примерно
.
-
а приближение к 1 происходит примерно по закону
Задача 1.13: Случайная величина устроена так: сначала сэмплируется число
из экспоненциального распределения со средним
, а потом сэмплируется случайное число
из распределения Пуассона, с параметром
. Мы получили сообщение, что одно измерение дало
. Сколько бит информации мы получили про случайную величину
? Дайте численный ответ. Сколько бит информации даст последовательность измерений 10, 9, 11, 8, 10?
Ответ
.
.
Задача 1.14: Случайная величина устроена так: сначала один раз сэмплируется число
из бета-распределения с параметрами
, а потом сэмплируется случайное число из биномиального распределения с параметрами
. Мы получили сообщение, что одно измерение
дало 10 (то есть 10 из 100 бросаний монетки выпали орлом). Сколько бит информации мы получили про скрытую случайную величину
? Дайте численный ответ. Сколько бит информации даст последовательность измерений 10, 9, 11, 8, 10?
Задача 1.15: Случайные величины сэмплированы из бета-распределения с параметрами
. Сами
нам неизвестны, но нам дали 10 измерений
из 10 биномиальных распределений с параметрами
и это наше знание про
. Сколько бит информации мы получим в среднем про случайную биномиальную величину с параметрами
и когда нам назовут значение
? А если
известны абсолютно точно (случай
)? А если 10 заменить на
?
Эту задачу можно сформулировать на языке ML так: у нас есть категориальная фичадля прогноза булевой величины (‘кликнет пользователь на баннер или нет’). Насколько хорош будет наш прогноз, если в обучающих данных нам известны лишь исторические данные про количество кликов и некликов по этим 10 категориям?
Задача 1.16. Случайная величина имеет распределение
. Величина
нам неизвестна, но мы знаем, что она была сэмплирована из распределения
. Сколько информации про
мы в среднем получим от первого измерения величины
? Как будет расти количество полученной информации с числом измерений?
Ответ
Продолжение:
-
Часть 2 – Mutual Information. В ней рассказывается про Взаимную Информацию – концепцию, которая открывает двери в помехоустойчивое кодирование, алгоритмы сжатия, а также даёт новый взгляд на задачи Машинного Обучения.
-
Часть 3 – ML & Mutual Information. Основы ML в контексте теории информации.
Энтропи́я (информационная) — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.
Так, возьмём, например, последовательность символов, составляющих какое-либо предложение на русском языке. Каждый символ появляется с разной частотой, следовательно, неопределённость появления для некоторых символов больше, чем для других. Если же учесть, что некоторые сочетания символов встречаются очень редко, то неопределённость ещё более уменьшается (в этом случае говорят об энтропии n-ого порядка, см. Условная энтропия).
Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу. Ср. тж. Термодинамическая энтропия
Формальные определения
Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:
Эта величина также называется средней энтропией сообщения. Величина 
Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.
Шеннон вывел это определение энтропии из следующих предположений:
- мера должна быть непрерывной; т. е. изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение энтропии;
- в случае, когда все варианты (буквы в приведенном примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать полную энтропию;
- должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых энтропия конечного результата должна будет являтся суммой энтропий промежуточных результатов.
Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме:
где K — константа (и в действительности нужна только для выбора единиц измерения).
Шеннон определил, что измерение энтропии (H = − p1 log2 p1 − … − pn log2 pn), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надежной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидания «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т.д. См. Цепи Маркова.
В общем случае b-арная энтропия (где b равно 2,3,… ) источника 
Определение энтропии Шеннона очень связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.
Условная энтропия
Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а следовательно и энтропия) очевидно меньше. Для учёта таких фактов используется условная энтропия.
Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (т.е. вероятности двухбуквенных сочетаний):
где 



Так, для русского алфавита без буквы «ё» 
Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются т.н. канальные матрицы. Так, для описания потерь со стороны источника (т.е. известен посланный сигнал), рассматривают условную вероятность 



|

|
… | 
|
… | 
|
|
|---|---|---|---|---|---|---|

|

|

|
… | 
|
… | 
|

|

|

|
… | 
|
… | 
|
| … | … | … | … | … | … | … |

|

|

|
… | 
|
… | 
|
| … | … | … | … | … | … | … |

|

|

|
… | 
|
… | 
|
Очевидно, вероятности, расположенные по диагонали описывают вероятность правильного приёма, а сумма всех элементов столбца даст вероятность появления соответствующего символа на стороне приёмника — 

Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:





Взаимная энтропия
Взаимная энтропия, или энтропия объединения, предназначена для рассчёта энтропии взаимосвязанных систем (энтропии совместного появления статистически зависимых сообщений) и обозначается 


Взаимосязь переданных и полученных сигналов описывается вероятностями совместных событий 

|

|
… | 
|
… | 
|

|

|
… | 
|
… | 
|
| … | … | … | … | … | … |

|

|
… | 
|
… | 
|
| … | … | … | … | … | … |

|

|
… | 
|
… | 
|
Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером 






Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:
Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:
Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем
Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.
Свойства
Важно помнить, что энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию 

- Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
- Количество энтропии не всегда выражается целым числом бит.
Альтернативное определение
Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет пунктам 1)—3):
1) H(p1, …, pn) определена и непрерывна для всех p1, …, pn, где pi 
2) Для целых положительных n, должно выполняться следующее неравенство:
3) Для целых положительных bi, где b1 + … + bn = n, должно выполняться равенство:
Эффективность
Исходный алфавит, встречающийся на практике, имеет вероятностное распределение, которое далеко от оптимального. Если исходный алфавит имел n символов, тогда он может может быть сравнён с «оптимизированным алфавитом», вероятностное распределение которого однородно. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах.
Из этого следует, что эффективность исходного алфавита с n символами может быть определена просто как равная его n-арной энтропии.
Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля-Зива или арифметического кодирования.
История
В 1948 году, исследуя проблему рациональной передачи информации через зашумленный коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных шифров.
Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.
Литература
- ↑ Д.С. Лебедев, В.А. Гармаш. О возможности увеличения скорости передачи телеграфных сообщений. — М.:Электросвязь, 1958, №1. с.68-69
- 2.Цымбал В.П. Теория информации и кодирование. — К.:Выща Школа, 1977. — 288 с.
См. также
- Энтропийное кодирование
- Цепь Маркова
- Для понимания информационной энтропии можно прибегнуть к примеру из области термодинамической энтропии получившему широко известное название Демона Максвелла.
Внешние ссылки
- http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html
- С.М. Коротаев. Энтропия и информация — Универсальные естественнонаучные понятия
Эта статья содержит материал из статьи Информационная энтропия русской Википедии.
Содержание
Для понимания материалов настоящего раздела рекомендуется ознакомиться с разделом ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
.
Статус документа: черновик.
Теория информации по Шеннону
Энтропия
Пусть случайное событие заключается в осуществлении одного из несовместимых состояний $ S_{1},dots,S_n $, вероятности появления которых даются таблицей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1.
$$
Эти вероятности известны, но это — все, что нам известно относительно того какое состояние осуществится. Можно ли найти «меру» насколько велик выбор из такого набора состояний и сколь неопределено для нас событие?
Если наше событие (опыт) состоит в определении цвета первой встретившейся нам вороны, то мы можем почти с полной уверенностью рассчитывать, что
этот цвет будет черным. Несколько менее определено событие (опыт), состоящее в выяснении того, окажется ли первый встреченный нами человек левшой или нет — здесь тоже предсказать результаты опыта можно, почти не колеблясь, но опасения в относительно правильности этого предсказания будут более обоснованны, чем в предыдущем случае. Значительно труднее предсказать заранее пол первого встретившегося нам на улице человека. Но и этот опыт имеет относительно небольшую степень неопределенности по сравнению, например с попыткой определить победителя в чемпионате страны по футболу с участием двадцати совершенно незнакомых нам команд.
Для практики важно уметь численно оценивать степень неопределенности самых разнообразных случайных событий (опытов), чтобы иметь возможность сравнивать их с этой стороны. Искомая численная характеристика должна быть функцией числа $ n_{} $ возможных состояний. Некоторые свойства этой функции $ f(n) $ определяются соображениями здравого смысла. При $ n_{}=1 $ событие вообще не является случайным, т.е. следует положить $ f(1)=0 $. При возрастании числа $ n_{} $ возможных состояний эта функция должна возрастать поскольку увеличение количества возможных исходов опыта увеличивает неопределенность в предсказании его результатов.
Идем далее: рассмотрим два независимых события $ A_{} $ и $ B_{} $. Пусть событие $ A_{} $ имеет $ k_{} $ равновероятных исходов, а событие $ B_{} $ имеет $ ell_{} $ равновероятных исходов. Рассмотрим событие, состоящее в произведении (совместном осуществлении) событий $ A_{} $ и $ B_{} $, обозначим это событие $ AB_{} $. Например, если событие $ A_{} $ заключается в появлении масти карты — бубновой
♦
, червовой
♥
, трефовой
♣
или пиковой
♠
—
при выборе ее из колоды в $ 36_{} $ карт, а событие $ B_{} $
заключается в появлении достоинства карты — шестерки,семерки, восьмерки, девятки, десятки, валета, дамы, короля или туза — при выборе ее из той же колоды, то событие $ AB_{} $ заключается в появлении конкретной карты колоды. Очевидно, что неопределенность события $ AB_{} $ больше неопределенности события $ A_{} $, так как к неопределенности $ A_{} $ добавляется неопределенность события $ B_{} $. Естественно потребовать, чтобы мера неопределенности события $ AB_{} $ была равна сумме неопределенностей, характеризующих события $ A_{} $ и $ B_{} $. Это требование обеспечивается следующим следующим свойством функции $ f_{} $:
$$
f(kell)=f(k)+f(ell) ,
$$
имеющего тот смысл, что число $ kell $ как раз и дает число возможных исходов события $ AB_{} $.
Последнее равенство наталкивает на мысль принять за меру неопределенности опыта, имеющего $ n_{} $ равновероятных исходов, число $ log n $. Можно доказать, что логарифмическая функция является единственной непрерывной функцией аргумента $ nin mathbb R $, удовлетворяющей такому функциональному уравнению. При этом выбор основания системы логарифмов несуществен, так как, в силу известной формулы $ log_b n = log_b a cdot log_a n $, переход от одной системы логарифмов к другой сводится лишь к умножению функции $ f(n)=log n $ на постоянный множитель $ log_b a $, т.е. равносилен простому изменению единицы измерения степени неопределенности. Единственным ограничением является естественное требование, чтобы основание было большим $ 1 $: число $ log_b n $ должно быть положительным
Как правило, в дальнейшем будем пользоваться логарифмом по основанию $ 2_{} $; такой выбор в одном из последующих пунктов будет подкреплен некоторыми дополнительными «бонусами». В ближайших же пунктах будем просто писать $ log $ без указания основания.
Таблица вероятностей события, имеющего $ n_{} $ равновероятных состояний, имеет вид
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
1/n & 1/n & dots & 1/n
end{array}
$$
Так как общая неопределенность события по нашему условию равна $ log n $, то можно считать, что каждое в отдельности состояние вносит неопределенность равную $ frac{1}{n} log n = — frac{1}{n} log frac{1}{n} $. Но тогда естественно считать, что в событие, таблица вероятностей состояний которого имеет вид
$$
begin{array}{l|l|l}
S_1 & S_2 & S_3 \
hline
1/2 & 1/3 & 1/6
end{array}
$$
состояние $ S_1 $ вносит неопределенность, равную $ left( — frac{1}{2} log frac{1}{2} right) $, состояние $ S_2 $ — неопределенность, равную $ left( — frac{1}{3} log frac{1}{3} right) $, а состояние $ S_3 $ — неопределенность, равную
$ left( — frac{1}{6} log frac{1}{6} right) $, так что суммарная неопределенность события равна
$$
— frac{1}{2} log frac{1}{2} — frac{1}{3} log frac{1}{3} — frac{1}{6} log frac{1}{6} .
$$
Аналогично этому можно положить, что для события $ A_{} $ с таблицей вероятностей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1
$$
мера его неопределенности равна
$$
-sum_{j=1}^n P_j log P_j = — P_1 log P_1 — P_2 log P_2 — dots — P_n log P_n = log frac{1}{P_1^{P_1} P_2^{P_2}times
dots times P_n^{P_n}} .
$$
Это число будем называть энтропией события $ A_{} $ и обозначать либо $ H(A) $ либо $ H(P_1,P_2,dots,P_n) $. Величина энтропии зависит от выбранного основания логарифмической функции; в случае основания $ 2_{} $ единицу измерения энтропии называют «бит», в случае основания $ 10_{} $ — «дит», в случае основания $ e=2.718281828459045dots $ — «нат».
В случае, когда $ P_j=0 $ при каком-то значении $ j_{} $, полагают $ P_j log P_j=0 $ (на основании известного из мат.анализа факта $ displaystyle lim_{xto +0} x log x = 0 $).
Можно проверить, что функция $ H(P_1,P_2,dots,P_n) $ симметрична относительно своих переменных; этот факт имеет тот
смысл, что мера неопределенности события не зависит от способа нумерации его возможных состояний. Кроме того эта функция
обладает следующими свойствами.
1.
$ H_{} $ непрерывна по каждой своей переменной;
2.
Если все вероятности одинаковы: $ P_1=1/n,P_2=1/n,dots,P_n=1/n $, то $ H_{} $ монотонно возрастающая функцией по $ n_{} $:
$$H bigg(underbrace{frac{1}{n},dots,frac{1}{n}}_n bigg)<Hbigg(underbrace{frac{1}{n+1},frac{1}{n+1},dots,frac{1}{n+1}}_{n+1}bigg) $$
(при равновероятности состояний, неопределенность события тем больше, чем больше количество этих состояний).
3.
При распадении какого-то события на два последовательных, величина $ H_{} $ должна вычисляться как взвешенная сумма составляющих значений $ H_{} $. Иллюстрирую на примере, который беру у Шеннона, но при этом излагаю в русском фольклорном стиле.
П
Пример. Предположим, что найденная Иваном-царевичем лягушка в течение минуты либо
-
превращается в бабу-Ягу с вероятностью $ 1/3 $;
-
превращается в красавицу Василису Премудрую с вероятностью $ 1/6 $;
-
остается лягушкой, и вероятность этого события равна $ 1/2 $.
Мера неопределенности этого события $ H(1/3,1/6,1/2) $. Теперь посчитаем меру неопределенности по-другому, объединив сначала первые два состояния в одно. Лягушка в течение минуты
-
превращается в женщину с вероятностью $ 1/2 $;
-
остается лягушкой с вероятностью $ 1/2 $.
Кроме того известно, что если лягушка точно превратилась в женщину, то ( условная ) вероятность того, что она стала бабой-Ягой равна $ 2/3 $, и, следовательно, вероятность появления Василисы Премудрой оказывается равной $ 1/3 $. В результате получаем два значения для функции $ H_{} $, именно $ H(1/2,1/2 ) $ и $ H(2/3 , 1/3 ) $.
Как должны быть связаны эти новые величины со старой — с $ H(1/3,1/6,1/2) $? Конечный результат у обоих событий одинаков, во втором случае мы просто искусственно «вставили» одно промежуточное событие. Так вот, имеет место равенство:
$$H(1/3,1/6,1/2)=H(1/2,1/2 )+frac{1}{2} H(2/3 , 1/3 ) , $$
здесь весовой множитель $ 1/2 $ в составе второго слагаемого возникает из-за того, что ситуация второго события происходит только в половине случаев.
♦
Формализуем: утверждается, что функция $ H_{} $ удовлетворяет условию
$$
H(P_1,P_2,P_3,dots,P_n)=H(P_1+P_2,P_3,dots,P_n)+(P_1+P_2)Hleft(frac{P_1}{P_1+P_2}, frac{P_2}{P_1+P_2} right) ;
$$
а уж из последнего можно вывести и еще более общее:
$$
H(P_1,dots,P_n)=H(P_1+dots+P_m,P_{m+1},dots,P_n)+
$$
$$
+(P_1+dots+P_m)Hleft(frac{P_1}{P_1+dots+P_m}, frac{P_2}{P_1+dots+P_m},dots,
frac{P_m}{P_1+dots+P_m} right)
$$
при $ forall min {2,dots,n-1} $.
Перечисленные свойства
1
—
3
оказываются настолько «жесткими», что будучи формально наложенными на произвольную функцию $ H_{} $, задают ее, фактически,
однозначно:
Т
Теорема [Шеннон]. Единственной функцией, удовлетворяющей условиям
1
—
3
,
является функция
$$ H=- K sum_{j=1}^n P_j log P_j . $$
Здесь $ K_{} $ — положительная константа, а логарифм берется по произвольному основанию большему $ 1_{} $.
Можно сказать, что свойства
1
—
3
являются определяющими свойствами энтропии — по аналогии с определяющими свойствами определителя как функции столбцов (или строк) матрицы.
После приведения этой формулировки, Шеннон пишет:
Эта теорема, равно как и необходимые для ее доказательства условия, не являются необходимыми для собственно излагаемой теории. Она приведена, главным образом, для придания правдоподобия1) некоторым последующим определениям. Действительное же обоснование этих определений, однако, остается за их применениями.
Образно говоря, следующее определение энтропии как меры неопределенности само в себе имеет некоторую меру неопределенности
И
Происхождение слова «энтропия»
☞
ЗДЕСЬ.
В дальнейшем, если не оговаривается особо, будем считать энтропию при логарифмической функции, взятой по основанию $ 2_{} $, и этот индекс при написании будем часто опускать.
П
Пример. Графики энтропии для $ n_{}=2 $

и для $ n_{}=3 $:

Формула для энтропии была получена в XIX веке Больцманом в его работах по статистической физике. Больцман показал, что если в газе, состоящем из большого числа молекул, вероятности состояний отдельных молекул равны $ P_1,dots,P_n $, то энтропия системы определяется соотношением
$$ H=- c sum_{j=1}^n P_j ln P_j , $$
где $ c_{} $ — некоторая константа. Можно считать, что энтропия системы является мерой неопределенности состояния молекул, составляющих эту систему. Эта интерпретация позволяет понять, почему Шеннон использовал ту же формулу в теории информации. Информация — это убыль неопределенности. До осуществления случайного события мы пребываем в полной неопределенности относительно того, какое из своих состояний оно может принять. После осуществления события, неопределенность устраняется. В одном из следующих пунктов мы покажем, что величина энтропии $ H_{} $ может быть интерпретирована как количество информации, содержащейся в событии.
Свойства энтропии
Проанализируем теперь формулу для энтропии.
Т
Теорема 1. $ H=0 $ тогда и только тогда, когда одна из вероятностей равна $ 1_{} $ при всех остальных, равных нулю (мера недостоверности наверняка осуществимого события равна $ 0_{} $).
Т
Теорема 2. При фиксированном $ n_{} $ максимум функции $ H_{} $ достигается при всех вероятностях одинаковых:
$$ max_{P_1+dots+P_n=1} H(P_1,dots,P_n)=Hleft(frac{1}{n},dots,frac{1}{n} right) = log n $$
(при равновероятности состояний предсказание об осуществимости какого-то конкретного из них максимально недостоверно).
Т
Теорема 3. Пусть случайные события $ A_{} $ и $ B_{} $ независимы. Тогда энтропия произведения (совместного осуществления) событий $ A cdot B $ равна сумме энтропий перемножаемых событий:
$$ H ( A cdot B) = H(A) + H(B) . $$
Доказательство. Пусть случайное событие $ A_{} $ может находиться в состояниях $ S_1,dots,S_n $ с вероятностями, заданными таблицей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1,
$$
а случайная величина $ B_{} $ может находиться в состояниях $ U_1,dots,U_m $ с вероятностями, заданными таблицей
$$
begin{array}{l|l|l|l}
U_1 & U_2 & dots & U_m \
hline
Q_1 & Q_2 & dots & Q_m
end{array} quad mbox{ при } quad Q_1+Q_2+dots+Q_m=1.
$$
Тогда случайная величина $ Acdot B $ может находиться в состояниях
$$ { S_jU_k mid quad jin {1,dots,n}, kin {1,dots,m } } ; $$
здесь $ S_jU_k $ означает такое состояние «сложного» события, которое заключается в одновременном выполнении двух условий: событие $ A_{} $ находится в состоянии $ S_j $, a событие $ B_{} $ — в состоянии $ U_k $. Поскольку, по предположению, события $ A_{} $ и $ B_{} $ независимы, то вероятность такого состояния равна $ P_jQ_k $.
Тогда
$$ H(Acdot B)= sum_{j=1}^n sum_{k=1}^{m} P_jQ_k log frac{1}{P_jQ_k}=
sum_{j=1}^n sum_{k=1}^{m} P_jQ_k left( log frac{1}{P_j} + log frac{1}{Q_k}right)=
$$
$$
= underbrace{left( sum_{k=1}^{m} Q_k right)}_{=1} sum_{j=1}^n P_j log frac{1}{P_j} +
underbrace{left( sum_{j=1}^{n} P_j right)}_{=1}
sum_{k=1}^{m} Q_klog frac{1}{Q_k}= H(A) + H(B) .
$$
♦
=>
Для любых случайных событий $ A_{} $ и $ B_{} $ энтропия их произведения (совместного появления) $ A cdot B $ не превосходит суммы энтропий перемножаемых событий:
$$ H ( A cdot B) le H(A) + H(B) . $$
Условная энтропия
Предположим теперь, что события $ A_{} $ и $ B_{} $ не являются независимыми. Выясним, чему равна энтропия произведения этих событий.
Общая формула для энтропии дает
$$
H(AB)=-sum_{j=1}^n sum_{k=1}^{m} P(S_jU_k) log P(S_jU_k) .
$$
В общем случае уже нельзя заменить вероятность $ P(S_jU_k) $ на произведение соответствующих вероятностей; в соответствии с теоремой из пункта
☞
УСЛОВНЫЕ ВЕРОЯТНОСТИ имеет место равенство
$$ P(S_jU_k)=P(S_j)P_{S_j}(U_k)=P_j P_{S_j}(U_k) , $$
где $ P_{S_j}(U_k) $ означает условную вероятность состояния $ U_k $ при условии нахождения события $ A_{} $ в состоянии $ S_j $. Каждое слагаемое под знаком суммы в выражении для энтропии представляется тогда в виде
$$
P(S_jU_k) log P(S_jU_k)=P_j P_{S_j}(U_k) left( log P_j + log P_{S_j}(U_k) right) .
$$
Тогда
$$
H(AB)=-sum_{j=1}^n P_j log P_j left( sum_{k=1}^{m} P_{S_j}(U_k) right)- sum_{j=1}^n P_j left( sum_{k=1}^m P_{S_j}(U_k) log P_{S_j}(U_k) right) .
$$
Сумма
$$
sum_{k=1}^{m} P_{S_j}(U_k)=P_{S_j}(U_1+U_2+dots+U_k)=1 ,
$$
поскольку событие $ U_1+U_2+dots+U_k $ — достоверное (какое-то из состояний $ U_1,U_2,dots,U_k $ событие $ B_{} $ принимает). Поэтому первое слагаемое в правой части формулы для $ H(AB) $ равно просто $ H(A_{}) $. Во втором слагаемом сумма
$$
— sum_{k=1}^m P_{S_j}(U_k) log P_{S_j}(U_k)
$$
представляет собой энтропию события $ B_{} $ при условии, что событие $ A_{} $ оказалось в состоянии $ S_{j} $. Эта энтропия называется условной энтропией события $ B_{} $ при условии нахождения события $ A_{} $ в состоянии $ S_{j} $ (или частной условной энтропией) и обозначается $ H_{S_j}(B) $ или $ H(B mid S_j) $. Тогда сумму
$$
sum_{j=1}^n P_j H_{S_j}(B)
$$
естественно считать средней условной энтропией события $ B_{} $ при условии выполнения события $ A_{} $; эту величину называют условной энтропией $ B_{} $ при условии выполнения $ A_{} $ и обозначается $ H_A(B) $ или $ H(B mid A) $.
Перепишем теперь все эти определения с использованием матричного формализма. Если обозначить
$$ P_{jk}=P_{S_j}(U_k) , $$
т.е. условную вероятность состояния $ U_k $ при условии $ S_{j} $, то из этих вероятностей можно составить матрицу
$$ mathfrak P=left[ P_{jk} right]_{j=1,dots,n atop k=1,dots,m} $$
по следующей схеме
$$
begin{array}{c}
\
S_1 \
dots \
S_n
end{array}
begin{array}{c}
begin{array}{llll}
U_1 & U_2 & dots & U_m
end{array} \
left( begin{array}{llll}
P_{11} & P_{12} & dots & P_{1m} \
dots &&& dots \
P_{n1} & P_{n2} & dots & P_{nm}
end{array} right) .
end{array}
$$
В одном из следующих ПУНКТОВ эта матрица получит специальное название и обозначение, а пока подчеркну только, что элементы этой матрицы неотрицательны и сумма их в каждой строке равна $ 1_{} $.
Введем в рассмотрение новую матрицу:
$$
tilde{mathfrak P}
=
left( begin{array}{llll}
P_{11} log P_{11} & P_{12} log P_{12} & dots & P_{1m} log P_{1m} \
dots &&& dots \
P_{n1} log P_{n1} & P_{n2} log P_{n2} & dots & P_{nm} log P_{nm}
end{array} right) .
$$
Тогда условная энтропия $ H_{S_j}(B) $ равна сумме элементов $ j_{} $-й строки этой матрицы. С использованием операции умножения матриц условные энтропии можно собрать в один столбец:
$$
left( begin{array}{c}
H_{S_1}(B) \
vdots \
H_{S_n}(B)
end{array}
right)= -tilde{mathfrak P}
left( begin{array}{c}
1 \
vdots \
1
end{array}
right) .
$$
Тогда условная энтропия $ B_{} $ при условии выполнения $ A_{} $ вычисляется по формуле
$$ H_A(B) = sum_{j=1}^n P_j H_{S_j}(B) = — (P_1,dots,P_n) tilde{mathfrak P}
left( begin{array}{c}
1 \
vdots \
1
end{array}
right) .
$$
Т
Теорема 4. Для энтропии произведения случайных событий $ A_{} $ и $ B_{} $ имеет место правило сложения энтропий:
$$ H(AB)=H(A)+ H_A(B) . $$
Проиллюстрируем результат теоремы на примере, который подробно будем разбирать во всех последующих пунктах. Источник приведенных в нем данных
☞
ЗДЕСЬ.
П
Пример. Пусть случайный процесс заключается в ежесекундном появлении на экране монитора одной буквы русского алфавита
в соответствии с приведенными ниже вероятностями
| и | м | о | т | пробел | |
|---|---|---|---|---|---|
| $ P_{} $ | 0.219 | 0.104 | 0.295 | 0.148 | 0.234 |
Таким образом, случайным событием $ A_{} $ является появление какой-то из указанных букв и
$$ H(A) = — sum_{j=1}^5 P_j log_2 P_j approx 2.237 quad mbox{ бит .} $$
Теперь предположим, что каждое следующее событие $ B_{} $ — появление на экране буквы — зависит от результата предыдущего по времени (но только от одного предыдущего). Условные вероятности, полученные в результате натурных экспериментов, соберем в матрицу
$$
mathfrak P= left[ P_{jk} right]_{j,k=1}^5=
left(
begin{array}{ccccc}
0.170 & 0.130 & 0.144 & 0.065 & 0.491 \
0.259 & 0.029 & 0.231 & 0.111 & 0.370 \
0.204 & 0.116 & 0.268 & 0.206 & 0.206 \
0.161 & 0.077 & 0.523 & 0.052 & 0.187 \
0.304 & 0.113 & 0.356 & 0.227 & 0
end{array} right)
.
$$
Так, значение $ P_{3,2}=0.116 $ означает, что если в данный момент времени на экране появилась буква о, то в следующий момент времени буква м появится примерно в $ 116 $ случаях из $ 1000 $. Выражение для матрицы $ tilde{mathfrak P} $ приведено в одном из последующих
☞
ПУНКТОВ. С ее помощью вычисляем условную энтропию события $ B_{} $ при условии события $ A_{} $:
$$ H_A(B)=
— (P_1,P_2,P_3,P_4,P_5) tilde{mathfrak P}
left( begin{array}{c}
1 \
1 \
1 \
1 \
1
end{array}
right) approx 2.036 quad mbox{ бит .}
$$
Теперь вычислим энтропию произведения событий $ A_{} $ и $ B_{} $, то есть события, заключающемся в последовательном появлении двух букв. Для этого нам потребуются вероятности появления каждой пары букв, приведенные ☞ ВСЁ ТАМ ЖЕ.
| ии | им | ио | ит | и_ | ми | мм | мо | мт | м_ | ои | ом | оо | от | о_ | ти | тм | то | тт | т_ | _и | _м | _o | _т | _ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $ hat P $ | 0.037 | 0.028 | 0.031 | 0.014 | 0.108 | 0.027 | 0.003 | 0.024 | 0.011 | 0.038 | 0.060 | 0.034 | 0.079 | 0.061 | 0.061 | 0.024 | 0.011 | 0.077 | 0.008 | 0.028 | 0.071 | 0.027 | 0.084 | 0.053 | 0.000 |
Имеем:
$$H(AB)=- sum_{j=1}^{25} hat P_j log_2 hat P_j approx 4.268 quad mbox{ бит .} $$
Проверка: $ H(A)+H_A(B)approx 4.273 $ бит.
♦
§
Пока мы только лишь формально осваиваем введенный математический аппарат, оставляя обсуждение лежащего под ним здравого смысла до следующих пунктов.
Т
Теорема 5. Для условной энтропии выполняются неравенства
$$ 0 le H_A(B) le H(B) . $$
Это утверждение хорошо согласуется со смыслом энтропии как меры неопределенности: предварительное осуществление события $ A_{} $ может лишь уменьшить степень неопределенности события $ B_{} $, но никак не может ее увеличить. Здесь необходимо отметить, что частная условная энтропия $ H_{S_j}(B) $ может быть и больше $ H(B) $, но усреднение всего набора частных энтропий по вероятностям всё-таки
приводит к ограничению типа $ le $.
Поскольку события $ AB_{} $ и $ BA_{} $ одинаковы, то
$$ H(AB)=H(A)+ H_A(B) =H(B)+H_B(A) . $$
Из последнего равенства можно определить и условную энтропию события $ A_{} $ при условии осуществления события $ B_{} $:
$$ H_B(A)=H(A)-H(B)+H_A(B) . $$
П
Пример. Пусть события $ A_{} $ и $ B_{} $ заключаются в извлечении одного шара из ящика, содержащего $ m_{} $ черных и
$ n-m $ белых шаров. Чему равны энтропии $ H(A), H(B), H_A(B), H_B(A) $?
Понятие об информации
Рассмотрим величину $ H(B) $, характеризующую степень неопределенности события $ B_{} $. Равенство этой величины нулю означает, что
состояние события $ B_{} $ заранее известно; большее или меньшее значение числа $ H(B) $ отвечает большей или меньшей неопределенности события. Какое-либо состояние события $ A_{} $, предшествующее событию $ B_{} $, может ограничить количество возможных состояний для события $ B_{} $ и тем самым уменьшить степень его неопределенности. Для того чтобы состояние события $ A_{} $ могло сказаться на последующем событии $ B_{} $, необходимо, чтобы это состояние не было известно заранее; поэтому $ A_{} $ можно рассматривать как вспомогательное событие, также имеющее несколько допустимых состояний. Тот факт, что осуществление $ A_{} $ уменьшает степень неопределенности $ B_{} $, находит свое отражение в том, что условная энтропия $ H_A(B) $ события $ B_{} $ при условии выполнения события
$ A_{} $ оказывается не больше первоначальной энтропии $ H(B) $ того же события. При этом, если событие $ B_{} $ не зависит от $ A_{} $,
то $ H_A(B)=H(B) $; если же состояние события $ A_{} $ полностью предопределяет событие $ B_{} $, то $ H_A(B)=0 $. Таким образом, разность
$$ I(A,B)=H(B)-H_A(B) $$
указывает, насколько осуществление события $ A_{} $ уменьшает неопределенность $ B_{} $, т.е. сколько нового мы узнаем о событии $ B_{} $, осуществив событие $ A_{} $. Эту разность называют количеством информации относительно события $ B_{} $, содержащимся в событии $ A_{} $.
Введенное таким образом определение можно «развернуть», определив энтропию $ H(B) $ события как информацию о событии $ B_{} $, содержащуюся в самом этом событии (поскольку осуществление события $ B_{} $ полностью определяет его исход и, следовательно, $ H_B(B)=0 $), или как наибольшую информацию относительно $ B_{} $, какую только можно иметь. Иными словами, энтропия $ H(B) $ события $ B_{} $ равна той информации, которую мы получаем при осуществлении этого события, т.е. средней информации, содержащейся в состояниях $ U_1,dots, U_m $ события $ B_{} $. Чем больше неопределенность какого-то события, тем бóльшую информацию дает определение его состояния.
Следует также иметь в виду, что информация относительно события $ B_{} $, содержащаяся в событии $ A_{} $, по определению представляет собой среднее значение (математическое ожидание) случайной величины $ { H(B)-H_{S_j}(B) }_{j=1}^n $, связанной с отдельными состояниями $ { S_{j} }_{j=1}^n $ события $ A_{} $; поэтому ее можно назвать средней информацией относительно $ B_{} $, содержащейся в $ A_{} $. Часто может случиться, что при определении состояния какого-либо события $ B_{} $ мы можем по-разному выбирать вспомогательные состояния (опыты, измерения, наблюдения) события $ A_{} $; так, например, при нахождении самого тяжелого груза из заданного набора грузов мы можем в разном порядке сравнивать отдельные грузы.
Информационная избыточность
Задача. Имея сообщение, записанное символами некоторого алфавита $ {S_1,dots,S_n} $, закодировать его наиболее выгодным способом.
Здесь кодирование понимается как процесс перехода от исходного алфавита к некоторому новому $ {U_1,dots,U_m} $, в котором каждому символу $ S_{j} $ однозначно сопоставляется последовательность символов $ (U_{j_1},dots, U_{j_k}) $.
Будем считать кодирование тем более выгодным, чем меньше элементарных сигналов приходится затратить на передачу данного сообщения.
Если считать, что коммуникация каждого из символов нового алфавита «стоит» одинакового количества ресурсов (энергии, времени), то наиболее выгодный код позволит сэкономить эти ресурсы.
П
Пример. Пусть $ n=10, m=2 $, т.е., к примеру, исходный алфавит, состоящий из цифр $ 0,1,dots, 9 $, мы кодируем двоичным кодом. Кодовая таблица
$$
begin{array}{c|c|c|c|c|c|c|c|c|c}
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \
hline
0000 & 0001 & 0010 & 0011 & 0100 & 0101 & 0110 & 0111 & 1000 & 1001
end{array}
$$
фактически соответствует переводу десятичных чисел в двоичную систему счисления. С одним только различием: каждый блок кода состоит из $ 4 $-х цифр, разрядов2) , т.е. код является равномерным. Требование равномерности понятно: оно позволяет получателю закодированного сообщения однозначно выделить блоки, соответствующие закодированным символам. Заметим, что вопрос о количестве этих разрядов равносилен задаче о том сколько вопросов, имеющих ответы «да» или «нет» надо задать, чтобы отгадать задуманное целое число среди $ 0,1,dots, 9 $.
Рассмотрим теперь вопрос о выгодности (т.е. экономности) построенного кода. Каждая цифра числового сообщения, записанного в привычной десятичной системе счисления, может принимать одно из десяти значений, т.е. может содержать информацию, равную, самое большее, $ log_2 10 approx 3.32 $ бит. Следовательно, сообщение, состоящее из $ N_{} $ десятичных цифр, может содержать, самое большее, $ N log_2 10 approx 3.32 N $ бит. Каждый разряд закодированного сообщения может принимать одно из двух значений, т.е. может содержать информацию, равную, самое большее $ log_2 2=1 $ биту. Но при использовании рассмотренного нами двоичного кода мы затрачиваем на передачу одного символа алфавита $ 4_{} $ разряда, а на передачу сообщения из $ N_{} $ символов алфавита — $ 4, N $ разрядов. Однако с помощью $ 4, N $ двоичных разрядов можно было бы передать информацию, равную $ 4, N $ бит. Разность $ 4,N-3.32, N=0.68, N $ отражает величину неэкономичности нашего кода. Нетрудно также объяснить, почему предложенный код не будет наиболее экономичным: в нем значения $ 0_{} $ и $ 1_{} $ не являются равновероятными: если в кодируемом сообщении все цифры $ 0,1,dots, 9 $ равновероятны, то в закодированном сообщении $ 0_{} $ будет встречаться в $ 25/15=5/3 $ раз чаще, чем $ 1_{} $. Между тем для того, чтобы последовательность из определенного количества символов $ 0_{} $ и $ 1_{} $ содержала наибольшую информацию, требуется, чтобы все цифры этой последовательности принимали оба значения с одинаковой вероятностью (и были взаимно независимы).
Легко понять, как можно построить более выгодный двоичный код. Разобьем наше сообщение на последовательные пары цифр и будем переводить в двоичную систему счисления не отдельно каждую цифру, к каждое двузначное десятичное число разбиения. Число двоичных разрядов кодовых блоков, требуемое для записи всех двузначных чисел $ 00,01,dots,99 $ равно $ 7_{} $:
$$
begin{array}{c|c|c|c}
0 & 1 & dots & 99 \
hline
0000000 & 0000001 & dots & 1100011
end{array}
$$
При такой схеме кодирования на два символа исходного алфавита тратится $ 7_{} $ бит, а не $ 8_{} $ — как в первой схеме, т.е. для передачи числа из $ N_{} $ десятичных цифр надо передать $ 7, (N+1)/2 approx 3.5 N $ двоичных цифр.
Еще выгоднее было бы разбить передаваемое число на триплеты — блоки из трех цифр. В этом случае «стоимость» кодирования понижается до $ approx 3.33 N $ бит. Выгода от перехода к разбиению сообщения на еще более крупные блоки практически оказывается уже совсем небольшой.
При переходе от триплетов к квадруплетам (блокам из четырех цифр) экономность кодирования даже уменьшается: на передачу последних требуются $ 14 $-тиразрядные двоичные блоки. Тем не менее, применяя разбиение кодируемого $ N_{} $-значного числа на еще более крупные блоки, мы можем еще более «сжать» получаемый двоичный, подойдя максимально близко к значению $ N log_2 10 $.
♦
Эта последняя граница может быть получена и из других соображений — без использования понятия информации. Количество всевозможных
$ N_{} $-буквенных слов, составленных из букв алфавита $ { S_1,dots,S_n } $, равно $ n^N $, количество всевозможных $ k_{} $-разрядных двоичных блоков равно $ 2^k $. Для однозначности кодирования необходимо, чтобы $ 2^k ge n^N $.
Способ кодирования $ k_{} $-разрядными двоичными блоками фактически заключается в том, что мы разбиваем множество всевозможных $ k_{} $-значных чисел на две равные части и числам из одной части сопоставляем первую разрядную цифру равную $ 0_{} $, а числам из второй части — равную $ 1_{} $. Далее, каждая из половинок множества снова разбивается на две равные части, каждой из которых приписывается $ 0_{} $ или $ 1_{} $.
Т
Теорема [Хартли]. Если в заданном множестве $ mathbb S $, состоящем из $ mathfrak N $ элементов:
$$ operatorname{Card}(mathbb S) = mathfrak N $$
выделен какой-то элемент $ U_{} $, о котором заранее известно, лишь что $ U in mathbb S $, то, для того, чтобы найти $ U_{} $ необходимо получить информацию, равную $ log_2 mathfrak N $ бит.
На первый взгляд кажется, что если число букв в исходном алфавите равно $ n_{} $, а в кодирующем алфавите равно $ m_{} $, то число $ log_m n $ характеризует наиболее экономичный код. Однако это утверждение ошибочно. Разумеется, верно, что текст из $ N_{} $ букв $ n_{} $-буквенного алфавита может содержать информацию, самое большее равную $ N log_2 n $ бит, но в действительности такой текст, если только он является осмысленным, никогда такой информации не содержит. Это ясно из свойств энтропии: каждая буква текста может содержать наибольшую информацию $ log_2 n $ бит лишь в том случае, когда все буквы алфавита будут встречаться одинаково часто. Известно, однако, что частоты встречаемости букв o или е во много раз больше частот встречаемости букв ф или щ.
Частота встречаемости букв в обычном (неспециальном) тексте (без учета пробелов) [2]:
| a | б | в | г | д | е,ё | ж | з | и | й | к | л | м | н | о | п | р |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.075 | 0.017 | 0.046 | 0.016 | 0.030 | 0.087 | 0.009 | 0.018 | 0.075 | 0.012 | 0.034 | 0.042 | 0.031 | 0.065 | 0.110 | 0.028 | 0.048 |
| с | т | у | ф | х | ц | ч | ш | щ | ъ,ь | ы | э | ю | я | |||
| 0.055 | 0.065 | 0.025 | 0.002 | 0.011 | 0.005 | 0.015 | 0.007 | 0.004 | 0.017 | 0.019 | 0.003 | 0.007 | 0.022 |
Энтропия достигает своего максимума, если все символы алфавита $ {S_1,dots,S_n} $ независимы и генерируются источником с одинаковой вероятностью. Можно сказать, что в равновероятном алфавите все символы несут максимальную информационную нагрузку. Если же алфавит неравновероятен, то некоторые его символы будут иметь меньшую информационную нагрузку, чем другие. Так, если считать, что в русском алфавите $ 31_{} $ буква (отождествляем е и ё, а также ь и ъ) и все они равновероятны, то
$$ H_0= — sum_{j=1}^{31} 1/31 log_2 (1/31) = log_2 31 approx 4.954 mbox{ бит } . $$
Если учитывать частоты букв в соответствии с приведенной таблицей, то получим:
$$ H_1= — sum_{j=1}^{31} P_j log_2 (P_j) approx 4.460 mbox{ бит } , $$
т.е. средняя информация, приходящаяся на одну букву русского текста, заметно понижается.
Аналогичные результаты справедливы и для других языков.
Если латинский алфавит содержит $ 26_{} $ букв и, следовательно, $ H_0 = log_2 26 approx 4.700 $ бит,
то значения $ H_{1} $ для основных европейских языков приведены в таблице
| английский | французский | немецкий | |
|---|---|---|---|
| $ H_{1} $ | 4.126 | 3.986 | 4.096 |
Однако, даже с учетом частот появления букв в тексте языков, мы все равно получим значение средней удельной информации на единицу текста,
превосходящую фактическое значение этой величины. В самом деле, для русского алфавита, например, информация в $ 4.460 $ бит на одну букву получилась бы, если бы каждая буква текста определялась с помощью извлечения карточки из ящика с перемешанными $ 1000 $ карточками, среди которых на $ 110 $ карточках написана буква о, на $ 87 $ карточках — буква е, и т.д., на $ 2_{} $ карточках — буква ф. Энтропия каждого такого события (извлечения карточки) $ A_1 $ примерно равна $ 4.460 $ бит; если $ [A_1,A_2,dots,A_N] $ обозначают $ N_{} $ последовательных событий3), то
$$ H([A_1, A_2, dots , A_N])= sum_{ell=1}^N H(A_{ell}) approx N cdot 4.460 mbox{ бит } . $$
Однако, появление каждой буквы текста на «естественном» языке не является независимым событием: вероятности появления каждой буквы зависят от предыдущих букв. Так, например, в русском языке после появления гласной буквы, существенно увеличивается вероятность появления согласной; если последняя появившаяся буква ч, то следующей уже никак не может быть ы, ю, или я, а весьма вероятно появление одной из букв
и, е или т. Аналогичные закономерности имеются и во всех других языках. Поэтому, если $ [A_1,A_2] $ — сложное событие, состоящее в последовательном появлении двух, то информация, содержащаяся в этом событии, равна
$$ H([A_1,A_2])=H(A_1)+H_{A_1}(A_2) le H(A_1)+H(A_2) . $$
Среднюю информацию на одну букву следует вычислять как условную энтропию:
$$
H_2=H_{A_1}(A_2)=-sum_{j,ell=1}^n P([S_j,S_{ell}]) log_2 P_{jell} ,
$$
где $ n_{} $ — число букв алфавита, $ P_{jell}= P_{S_j}(S_{ell}) $
— условная вероятность появления буквы $ S_{ell} $, если известно, что непосредственно перед ней стоит буква $ S_{j} $,
а $ P([S_j,S_{ell}]) $ — вероятность появления двухбуквенного сочетания (диграммы) $ [S_j,S_{ell}] $.
Как правило, $ P([S_j,S_{ell}]) ne P([S_{ell},S_j]) $; сочетание ый встречается значительно чаще йы4).
Можно переписать последнюю формулу в матричном виде с использованием условных вероятностей.
По правилу умножения вероятностей:
$$
P([S_j,S_{ell}])=P(S_j)P_{S_j}(S_{ell})=P_j P_{jell} .
$$
Составим из условных вероятностей матрицу:
$$
mathfrak P =left[ P_{jk} right]_{j,k=1}^n
$$
— она называется матрицей условных (или переходных) **вероятностей. На ее основе построим матрицу
$$
tilde{mathfrak P}= left[P_{jk} log P_{jk} right]_{j,k=1}^n
left( begin{array}{llll}
P_{11} log P_{11} & P_{12} log P_{12} & dots & P_{1n} log P_{1n} \
dots &&& dots \
P_{n1} log P_{n1} & P_{n2} log P_{n2} & dots & P_{nn} log P_{nn}
end{array} right) ;
$$
В нашем случае — в отличие от общего случая пункта
☞
УСЛОВНАЯ ЭНТРОПИЯ — матрицы $ mathfrak P $ и $ tilde{mathfrak P} $ будут квадратными. В полном соответствии с пунктом
☞
УСЛОВНАЯ ЭНТРОПИЯ можем записать:
$$
H_2=
— (P_1,dots,P_n) tilde{mathfrak P}
left( begin{array}{c}
1 \
vdots \
1
end{array}
right) .
$$
П
Пример. Обратимся к примеру сокращенного русского языка из букв $ S_1= $и, $ S_2= $м, $ S_3= $о, $ S_4= $т и $ S_5= $пробел, рассмотренному
☞
ЗДЕСЬ. Сделаем сначала «привязку» к только что введенным обозначениям:
$$ P_1=0.219, P_2=0.104, P_3= 0.295, P_4=0.148, P_5=0.234 . $$
Матрица условных вероятностей:
$$
mathfrak P=left[P_{jk}right]_{j,k=1}^5 =
left(
begin{array}{ccccc}
0.170 & 0.130 & 0.144 & 0.065 & 0.491 \
0.259 & 0.029 & 0.231 & 0.111 & 0.370 \
0.204 & 0.116 & 0.268 & 0.206 & 0.206 \
0.161 & 0.077 & 0.523 & 0.052 & 0.187 \
0.304 & 0.113 & 0.356 & 0.227 & 0
end{array} right)
$$
Вычисляем матрицу
$$
tilde{mathfrak P}=left[P_{jk} log_2 P_{jk} right]_{j,k=1}^5 =
left(
begin{array}{ccccc}
-0.435 & -0.383 & -0.403 & -0.256 & -0.504 \
-0.505 & -0.148 & -0.488 & -0.352 & -0.530 \
-0.467 & -0.360 & -0.509 & -0.470 & -0.470 \
-0.424 & -0.285 & -0.489 & -0.222 & -0.452 \
-0.522 & -0.355 & -0.530 & -0.486 & 0
end{array} right) .
$$
Величины энтропий (в битах):
$$ H_0=log_2 5 approx 2.322, H_1=-sum_{j=1}^5 P_j log_2 P_j approx 2.237,
$$
$$
H_2 =
— (P_1,P_2,P_3,P_4,P_5) tilde{mathfrak P}
left( begin{array}{c}
1 \
1 \
1 \
1 \
1
end{array}
right) approx 2.036 . $$
♦
Продолжаем дальнейшее продвижение в намеченном направлении. Если учесть информацию о двух предыдущих буквах текста, то для средней информации на одну букву получается формула:
$$
H_3=H_{A_1A_2}(A_3)=- sum_{j,ell,r=1}^n P([S_j,S_{ell},S_r]) log_2 P_{[S_j,S_{ell}]}(S_r) ,
$$
где $ P([S_j,S_{ell},S_r]) $ — вероятность трехбуквенного сочетания (триграммы) $ [S_j,S_{ell},S_r] $, а
$ P_{[S_j,S_{ell}]}(S_r) $ — условная вероятность появления буквы $ S_r $ после появления биграммы $ [S_j,S_{ell}] $.
Нетрудно понять как строятся величины $ H_M $ при $ M> 3 $. Также понятно, что с возрастанием $ M_{} $ величины $ H_M $ будут убывать, приближаясь к некоторому предельному значению $ H_{infty} $, которое и можно считать теоретическим значением средней удельной информации при передаче длинного текста.
Значения $ H_{M} $ (в битах) для русского5) и английского языков6):
| $ M $ | $ 0_{} $ | $ 1_{} $ | $ 2_{} $ | $ 3_{} $ |
|---|---|---|---|---|
| русский | 5.000 | 4.348 | 3.521 | 3.006 |
| английский | 4.754 | 4.029 | 3.319 | 3.099 |
Учтя также и статистические данные о частотах появления различных слов в английском языке, Шеннон сумел приблизительно оценить и значения величин $ H_5 $ и $ H_8 $:
$$ H_{5} approx 2.1, H_{8} approx 1.9 . $$
П
Пример [обезьяна за клавиатурой]. Известна теорема о бесконечных обезьянах: абстрактная обезьяна, ударяя случайным образом по клавишам печатной машинки7) в течение неограниченно долгого времени, рано или поздно напечатает любой наперёд заданный текст (например «Войны и мира»). В указанной ссылке приводятся оценки времени наступления этого события. Следующие примеры 
Картинка в тему
☞
ЗДЕСЬ
Приближения нулевого порядка (символы независимы и равновероятны):
ФЮНАЩРЪФЬНШЦЖЫКАПМЪНИФПЩМНЖЮЧГПМ ЮЮВСТШЖЕЩЭЮКЯПЛЧНЦШФОМЕЦЕЭДФБКТТР МЮЕТ
Приближение первого порядка (символы независимы, но с частотами, свойственными русскому языку):
ИВЯЫДТАОАДПИ САНЫАЦУЯСДУДЯЪЛЛЯ Л ПРЕЬЕ БАЕОВД ХНЕ АОЛЕТЛС И
Приближение второго порядка (частотность диграмм такая же как в русском языке):
ОТЕ ДОСТОРО ННЕДИЯРИТРКИЯ ПРНОПРОСЕБЫ НРЕТ ОСКАЛАСИВИ ОМ Р ВШЕРГУ П
Приближение третьего порядка (частотности триграмм такие же как в русском языке):
С ВОЗДРУНИТЕЛЫБКОТОРОЧЕНЯЛ МЕСЛОСТОЧЕМ МИ ДО
Вместо того, чтобы продолжить процесс приближения с помощью тетраграмм, пентаграмм и т.д., легче и лучше сразу перейти к словарным единицам. Приближение первого порядка на уровне слов9): cлова выбираются независимо, но с соответствующими им частотами.
СВОБОДНОЙ ДУШЕ ПРОТЯНУЛ КАК ГОВОРИТ ВСПОМНИТЬ МИЛОСТЬ КОМНАТАМ РАССКАЗА ЖЕНЩИНЫ МНЕ ТУДА ПОНЮХАВШЕГО КОНЦУ ИСКУСНО КАЖДОМУ РЯСАХ К ДРУГ ПЕРЕРЕЗАЛО ВИДНО ВСЕМ НАЧИНАЕТЕ НАД ДВУХ ЭТО СВЕТА ХОДУНОМ ЗЕЛЕНАЯ МУХА ЗВУК ОН БЫ ШЕЮ УТЕР БЕЗДАРНЫХ
Приближение второго порядка на уровне слов. Переходные вероятности от слова к слову соответствуют русскому языку,
но «более дальние» зависимости не учитываются:
ОБЩЕСТВО ИМЕЛО ВЫРАЖЕНИЕ МГНОВЕННОГО ОРУДИЯ К ДОСТИЖЕНИЮ ДОЛЖНОСТЕЙ ОДИН В РАСЧЕТЫ НА БЕЗНРАВСТВЕННОСТИ В ПОЭЗИИ РЕЗВИТЬСЯ ВСЕ ГРЫЗЕТ СВОИ БРАЗДЫ ПРАВЛЕНИЯ НАЧАЛА ЕГО ПОШЛОЙ
С каждым проделанным шагом сходство с обычным текстом заметно возрастает. До текста «Войны и мира» осталось совсем немного…
♦
Уменьшение информационной нагрузки на один символ алфавита вследствие неравновероятности, а также взаимозависимости появления, символов называют избыточностью языка10). Информационная избыточность рассчитывается по формуле
$$ R_{}= frac{H_0-H_{infty}}{H_0}=1-frac{H_{infty}}{log n} . $$
Величина $ H_0-H_{infty} $ называется недогруженностью алфавита, а отношение $ H_{infty}/H_0 = H_{infty}/log n $ — коэффициентом его оптимальности. Равенство избыточности величине $ 1/L_{} $ огрубленно эквивалентно утверждению о том, что каждая $ L_{} $-я буква алфавита является «лишней», однозначно восстанавливаемой по $ (L-1) $-й предыдущей. Избыточность наиболее распространенных европейских языков близка к $ 1/2 $, т.е., огрубляя, можно утверждать, что в тексте на одном из этих языков можно исключить до 50 % букв с тем, чтобы затем восстановить содержание текста по его оставшейся части.
Как определить величину $ H_M $ и оценить $ H_{infty} $ ? Для малых значений $ M_{} $ еще можно произвести частотный анализ, но вот уже для определения $ H_9 $ требуется знание вероятностей $ 32^9 approx 3.5 cdot 10^{13} $
всех девятибуквенных комбинаций. Шеннон предложил для оценки $ H_M $ использовать экспертное оценивание
☞
ЗДЕСЬ.
Явление избыточности влечет за собой как отрицательные, так и положительные последствия. Отрицательные последствия вызваны тем, что наличие «лишних» символов увеличивает затраты ресурсов при коммуникации. Положительный аспект избыточности заключается в повышении помехоустойчивости процесса коммуникации. Наличие высокой избыточности естественных языков позволяет понимать речь при значительных дефектах произношения, смене диалектов, а тексты — при лингвистических ошибках, сокращении слов и плохом почерке. См. также по этому поводу феномены Глокой куздры и Пушистых браздов.
Код Шеннона — Фано
Для понимания материалов настоящего пункта крайне желательно ознакомиться с материалами пункта
☞
ПРЕФИКСНЫЕ КОДЫ.
Для решения задачи наиболее экономичного кодирования приходится расширять алфавит. Поясню эту фразу. Если считать, что «исходный» алфавит состоит из символов $ S_1,dots,S_{n} $, то рассуждения из начала предыдущего пункта показывают, что уже переход к алфавиту, состоящему из набора биграмм $ {[S_j,S_{ell}]}_{j,ell=1}^n $ с последующим кодированием двоичным кодом может существенно снизить «стоимость» кодирования текста. А соображения предыдущего пункта позволят еще больше сэкономить — но, правда, при наличии дополнительной информации о новом алфавите — информации о частоте встречаемости каждой из биграмм в кодируемом тексте. Требование равномерности кода (одинакового количества разрядов в кодовых словах) снимается и в кодовую таблицу допускаются кодовые наборы с варьируемым количеством разрядов. Основным принципом кодирования становится:
чаще встречаемость — короче кодовая последовательность.
Реализация последнего принципа возможна различными способами. Исторически первым является кодирование по методу Шеннона-Фано. Чтобы не вводить новых обозначений, будем считать что алфавит состоит из «букв» $ S_1,dots,S_{n} $, при этом каждая «буква» может быть произвольным символом или набором символов, например: $ S_1 = $
в
, $ S_2 $=
о
с
, $ S_3 = 210 $ Д, $ S_4 = $
शब्द
, $ S_5=sqrt[3]{int_{3}^{-5} sin x^{2y} d, x} $,… лишь бы только алфавит был «полон» («покрывал» весь текст) и не «переполнен» (включенные в него символы реально в тексте присутствовали). И главное требование: частоты встречаемости «букв» в тексте должны быть нам известны. Для кодирования этих «букв» бинарным кодом ранжируем «буквы» по частоте встречаемости и разбиваем алфавит
$ {S_1,S_2,dots,S_n } $ на два подмножества, по возможности, равной вероятности. «Буквам» из одного подмножества ставим в соответствие $ 0_{} $, из второго — $ 1_{} $. Это — первые разряды соответствующих кодовых последовательностей. Далее процесс повторяется для каждого из подмножеств — производится деление их на подмножества по возможности равной вероятности с последующим присвоением им номера $ 0_{} $ или $ 1_{} $. Процесс заканчивается когда в каждом из образовавшихся подмножеств не останется ровно по одной «букве». В результате каждая из них получает свой индивидуальный бинарный «номер» — то есть, кодировку.
П
Пример. Рассмотрим пример с кодированием $ 10_{} $ букв русского алфавита с частотами, полученными на основании искусственного текста, созданного ☞ ЗДЕСЬ.
| е | и | а | в | д | к | з | б | г | ж | всего | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| количество | 236 | 231 | 195 | 111 | 94 | 94 | 46 | 42 | 40 | 30 | 1119 |
| вероятность | 0.211 | 0.206 | 0.174 | 0.099 | 0.084 | 0.084 | 0.041 | 0.038 | 0.036 | 0.027 |
Множество этих букв разобьем на два подмножества, (примерно) одинаковые по вероятности. Например, суммарная вероятность букв е,
и, д равна $ 0.51 $. Так что два образуемых подмножества: $ { mbox{ е, } mbox{ и, } mbox{ д } } $ и
$ { mbox{ а, } mbox{ б, } mbox{ г, } mbox{ в, } mbox{ ж, } mbox{ к, } mbox{ з } } $. Каждое из этих подмножеств снова разобьем на два подмножества (примерно) одинаковые по вероятности. Первое подмножество делится плохо, но что поделать — делим как получится! Продолжаем процесс деления пока не дойдем в таких разбиениях до отдельных букв. Последовательность построения схемы разбиения приведена на рисунке.

Оформляем эту схему в виде дерева и, идя от корня к листьям, нумеруем ветви после каждого узла (точки ветвления): верхней даем номер $ 0_{} $, а нижней — номер $ 1_{} $.

Результатом оказывается кодовая таблица
| е | и | д | а | б | г | в | ж | к | з |
|---|---|---|---|---|---|---|---|---|---|
| 00 | 010 | 011 | 100 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Стоимость кодирования текста по такой таблице равна
$$ 236cdot 2+231cdot 3+94 cdot 3+195 cdot 3+42 cdot 4+40 cdot 4+111 cdot 4+30 cdot 4+94 cdot 4+46 cdot 4=3423 mbox{ бит, } $$
то есть, в среднем, $ 3.11_{} $ бит на букву. Это неплохое достижение, но оно всё-таки хуже полученного использованием кода Хаффмана, также основанного на частотном анализе букв алфавита.
♦
Сходство кода Шеннона-Фано с кодом Хаффмана проявляется и в алгоритмах построения обоих кодов, только направление построения кодового дерева меняется на противоположное: от корня к листьям. Так же как и код Хаффмана, код Шеннона-Фано относится к префиксным кодам: ни одно его кодовое слово не совпадает с начальным отрезком какого-то другого кодового слова. И при всех при этих сходствах, код Шеннона-Фано менее экономичен, чем код Хаффмана и поэтому практически не используется.
Алгоритм построения кода Шеннона-Фано основан на решении задачи из раздела computer science, известной как partition problem: для заданного конечного набора $ mathbb S $ чисел11) требуется найти такое разбиение его на два набора $ mathbb S_1 $ и $ mathbb S_2 $, чтобы разность между суммами чисел составляющих наборов была минимальной. Проблема известна как $ NP $-сложная.
А теперь перейдем к фундаментальному результату теории кодирования, связав код Шеннона-Фано с понятием энтропии.
Т
Теорема [Шеннон]. Сообщение из большого количества $ N_{} $ букв алфавита $ {S_1,dots,S_n} $, частоты встречаемости которых в сообщении заданы таблицей:
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1,
$$
всегда можно закодировать бинарным кодом таким образом, чтобы количество двоичных разрядов в кодовой последовательности было сколь угодно близким к величине
$$Hcdot N quad mbox{ где } quad H=-sum_{j=1}^n P_j log_2 P_j ; $$
но никогда не меньшим ее.
Доказательство (совершенно нестрогое: очень сильная «выжимка» из рассуждений, приведенных в [2]; которые, в свою очередь, тоже не абсолютно строги). Пусть источник сообщений случайным образом генерирует символы из алфавита $ {S_1,dots,S_n} $. Пусть передаваемое сообщение состоит из достаточно большого числа $ N_{} $ символов. Рассмотрим подмножество $ mathbb S $ всевозможных сообщений длины $ N_{} $, в которых количества вхождений символов $ { S_j }_{j=1}^n $ примерно соответствуют указанным вероятностям. Именно, если $ N_j $ — количество вхождений символа $ S_j $, то $ N_j/N approx P_j $. Тогда вероятность вхождения в сообщение всех символов $ S_{j} $ в количестве $ N_{j} $ при $ jin {1,dots,n} $, в соответствии с теоремой об умножении вероятностей, равна
$$ P_1^{N_1} P_2^{N_2}times dots times P_n^{N_n} approx P_1^{N, P_1} P_2^{N,P_2}times dots times P_n^{N,P_n}=underbrace{left(P_1^{P_1}P_2^{P_2} times dots times P_n^{P_n} right)^N}_{=Q} . $$
Строго говоря, здесь надо сослаться на закон больших чисел, но пока не буду с этим заморачиваться.
Будем для простоты считать, что это — вероятность любого сообщения из подмножества $ mathbb S_{} $, т.е. количество элементов во множестве $ mathbb S_{} $ примерно совпадает с $ 1/Q $:
$$ mathfrak N = operatorname{Card} (mathbb S) approx 1/Q . $$
Сколько стоит найти один-единственный элемент этого множества: как найти во множестве $ mathbb S $ какое-то конкретное сообщение — не просто состоящее из нужных букв в требуемом количестве — но, например, определяющее осмысленный текст? В соответствии с теоремой Хартли, это число
$$ approx log_2 mathfrak N approx — N cdot left(P_1 log_2 P_1+P_2 log_2 P_2+dots+ P_n log_2 P_n right) mbox{ бит.} $$
♦
Теперь обсудим полученный результат. Итак, «на входе» имеем документ — самый произвольный, содержащий возможно осмысленный, но не обязательно нам понятный текст (он записан на неизвестном языке, содержит специфические символы из неизвестной нам научной отрасли и т.п.). Наша цель — закодировать его бинарным кодом, с тем, чтобы иметь возможность передать по каналу связи. Первое, что мы делаем — строим алфавит. Слово «алфавит» понимается в том смысле, что упомянут в начале пункта. Пытаемся, по-возможности, определять часто повторяющиеся блоки — их будем включать в состав алфавита целиком, как отдельные «буквы». Стоп.
Стоп!
— Что же получается: для каждого документа — делать свой отдельный алфавит?! — Вообще говоря, да12). Другое дело, что если этот документ не единствен, а предполагается коммуникация целой серии документов, и эти документы написаны на одном языке, и в них содержится разве лишь строго ограниченное количество специальных символов,… — и вот при всех при этих обстоятельствах имеет смысл предварительным анализом составить алфавит общий для всех документов. После того как алфавит создан, вычисляем частоты вхождений составляющих его букв в исходный документ. Кодируем по методу Шеннона-Фано. Кодовую таблицу храним в надежном файле и передаем адресату (на бумажном (электронном) носителе при личной встрече, курьером, по электронной почте и т.п.). И что у нас имеется для оценки стоимости кодирования нашего документа? — Оценка снизу для количества бит на букву: $ H_{} $. Что такое $ H_{} $? — Энтропия случайного события, состоящего в появлении в тексте букв алфавита при известных их вероятностях (т.е. как если бы случайный источник генерировал буквы алфавита независимо друг от друга, но с частотами, примерно соответствующими их вероятностям). Хорошо подобрали алфавит, каждый документ — достаточно длинный, этих документов много — тогда, в среднем, результаты нашего кодирования не должны слишком уж сильно превосходить этой величины. Сколько это: «слишком сильно»? — Решает заказчик. Если ему хочется улучшить результат — придется увеличивать алфавит. Но тогда решение одной проблемы приведет к появлению другой…
П
Пример. Обратимся к рассмотренному
☞
ЗДЕСЬ примеру сокращенного русского языка
| и | м | о | т | пробел | |
|---|---|---|---|---|---|
| $ P_{} $ | 0.219 | 0.104 | 0.295 | 0.148 | 0.234 |
Для алфавита, состоящего из этих букв, с указанными в таблице вероятностями
величина энтропии $ H approx 2.237 $. Следовательно, кодирование приведенного ЗДЕСЬ текста из $ 1050 $ букв по теореме Шеннона оценивается в $ 2349 $ двоичных разряда. Код Шеннона-Фано для этого алфавита имеет вид
| и | м | о | т | пробел |
|---|---|---|---|---|
| 11 | 010 | 10 | 011 | 00 |
и точная стоимость кодирования — $ 2364 $ разряда.
Если же перейти к алфавиту, составленному из биграмм
| ии | им | ио | ит | и_ | ми | мм | мо | мт | м_ | ои | ом | оо | от | о_ | ти | тм | то | тт | т_ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $ hat P $ | 0.037 | 0.028 | 0.031 | 0.014 | 0.108 | 0.027 | 0.003 | 0.024 | 0.011 | 0.038 | 0.060 | 0.034 | 0.079 | 0.061 | 0.061 | 0.024 | 0.011 | 0.077 | 0.008 | 0.028 |
| _и | _м | _o | _т | __ | ||||||||||||||||
| $ hat P $ | 0.071 | 0.027 | 0.084 | 0.053 | 0.000 |
то код Хаффмана этого алфавита (уже из $ 25_{} $ «букв») имеет вид
| ии | им | ио | ит | и_ | ми | мм | мо | мт | м_ | ои | ом | оо | от | о_ | ти | тм | то | тт | т_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11000 | 10001 | 10100 | 010001 | 000 | 01101 | 0010100 | 00100 | 010000 | 11001 | 0101 | 10101 | 1110 | 0111 | 1001 | 01001 | 001011 | 1101 | 0010101 | 10000 |
| _и | _м | _o | _т | ||||||||||||||||
| 1011 | 01100 | 1111 | 0011 |
и стоимость кодирования текста, разбитого на $ 525 $ биграмм по схеме
Ои
|
то
|
ми
|
и_
|
о_
|
им
|
и_
|
оо
|
ои
|
тм
|
и_
|
о_
|
о_
|
о_
|
оо
|
ии
|
им
|
то
|
ми
|
им
|
от
|
ои
|
м_
|
…
будет равна $ 2193 $ бит. Величина энтропии $ H approx 2.036 $ бит и теорема Шеннона дает оценку в $ 2138 $ двоичных разрядов.
♦
Пропускная способность канала связи
Рассуждения предыдущего пункта относились к случаю, когда процесс коммуникации происходит без искажений. Обратимся теперь от теории к реальности: помехи всегда будут.
Предполагаем, что по каналу связи передается последовательность бит (т.е. $ 0_{} $ или $ 1_{} $), задающая символы (или буквы некоторого алфавита) $ S_{1},dots, S_n $. Предполагается, что символ $ S_j $ представлен набором из $ t_{j} $ двоичных сигналов. На передачу по каналу связи каждого информационного двоичного сигнала тратится некоторая единица времени. Исходя из этого будем говорить о сигнале $ S_j $
как имеющем длительность $ t_{j} $.
П
Пример. Шеннон рассматривает пример из телеграфии, где имеется всего $ 4_{} $ «символа алфавита»:
-
точка, создаваемая замыканием линии на $ 1_{} $ единицу времени и последующим размыканием на $ 1_{} $ единицу времени;
-
тире, создаваемая замыканием на $ 3_{} $ единицы времени и последующим размыканием на $ 1_{} $ единицу;
-
пробел между буквами13), создаваемый размыканием линии на $ 3_{} $ единицы времени;
-
пробел между словами, создаваемый размыканием линии на $ 6_{} $ единиц времени.
Если заменить слова «замыкание линии» на $ 1_{} $, а «размыкание линии» — на $ 0_{} $, то получим двоичную кодировку алфавита
$ mathfrak C ( $
точка
$ )=10 $,
$ mathfrak C ( $
тире
$ )=1110 $,
$ mathfrak C ( $
пробел между буквами
$ )=000 $,
$ mathfrak C ( $
пробел между словами
$ )=000000 $.
Таким образом, используя в качестве вспомогательного алфавита для передачи латинских букв азбуку Морзе, получаем кодировку сообщения:
SOS
=
••• − − − •••
$ = 101010000111011101110000101010000000 $
Дополнительно вводятся ограничения на допустимые к передаче последовательности — например, запрет двух пробелов подряд между словами.
♦
Пропускная способность канала связи без помех задается формулой
$$ C=lim_{Tto infty} frac{log_2 N(T)}{T} . $$
Здесь $ N(T) $ — число сигналов длительности $ T_{} $. Очевидно, что $ N(T)le 2^T $.
Пусть все символы алфавита $ S_1,dots,S_n $ допустимы и имеют длительности $ t_1,dots,t_n $.
Если $ N(t) $ число сигналов длительности $ t_{} $, то справедлива следующая формула:
$$ N(t)=N(t-t_1)+N(t-t_2)+dots+N(t-t_n) . $$
Последняя формула представляет тот очевидный факт, что концом любого сигнала длительности $ t_{} $ должен быть один из символов множества $ {S_{j}}_{j=1}^n $ (или набор этих символов).
Эта формула определяет линейное разностное уравнение порядка
$$ tau= max_{jin {1,dots,n}} t_j . $$
Его общее решение может быть явно выражено через корни уравнения
$$ 1= lambda^{-t_1}+lambda^{-t_2}+dots+lambda^{-t_n} . $$
Это уравнение — домножением на $ lambda^{tau} $ — может быть преобразовано в характеристический полином разностного уравнения.
Предположив, для простоты рассуждений, что все корни этого полинома $ lambda_1,dots,lambda_{tau} $ различны, получим общее решение разностного уравнения в виде
$$ N(t)=C_1lambda_1^t+C_2lambda_2^t+dots+C_{tau}lambda_{tau}^t $$
при величинах $ C_1,C_2,dots,C_{tau} $, не зависящих от $ t_{} $.
Тогда если через $ lambda_{ast} $ обозначить максимальный по модулю корень полинома:
$$ | lambda_{ast} | =max_{jin{1,dots,tau}} | lambda_j | , $$
то
$$ lim_{Tto infty} frac{log_2 N(T)}{T} = lim_{Tto infty} frac{log_2 C_{ast} lambda_{ast}^T }{T} = log_2 lambda_{ast} . $$
Тут надо бы проверить несколько предположений, например, что максимальный по
модулю корень характеристического полинома единствен — тогда, хотя бы, он обязательно будет веществен. Пока могу с определенностью утверждать, что при $ nge 2 $ у этого полинома все корни по модулю не превосходят $ 2_{} $ (см. ☞ теорему Маклорена ),что существует единственный положительный вещественный корень (см. ☞ правило знаков Декарта ), и что этот корень лежит в интервале $ ]1,2[ $. Еще одно преположение, нуждающееся в обосновании: коэффициент $ C_{ast} $ не должен равняться нулю,… Но поскольку сам Шеннон не заморачивался такими мелочами, то и я пока не буду.
П
Пример. Для рассмотренного выше «телеграфного» примера имеем разностное уравнение в виде
$$ N(t)=N(t-2)+N(t-4)+N(t-5)+N(t-7)+N(t-8)+N(t-10) . $$
Это уравнение имеет порядок $ 10_{} $, его характеристический полином
$$ lambda^{10}=lambda^{8}+lambda^{6}+lambda^{5}+lambda^{3}+lambda^{2}+1 $$
имеет максимальный по модулю корень $ lambda_{ast} approx 1.453 $. Таким образом,
пропускная способность канала равна $ approx 0.539 $.
♦
Пусть символы алфавита имеют вероятности появления в любом месте сообщения, заданные таблицей
$$
begin{array}{l|l|l|l}
S_1 & S_2 & dots & S_n \
hline
P_1 & P_2 & dots & P_n
end{array} quad mbox{ при } quad P_1+P_2+dots+P_n=1.
$$
Тогда при отсутствии помех сообщение по линии связи может быть передано со скоростью сколь угодно близкой к
$$ v=C/H quad mbox{ букв } / mbox{ единица времени } , $$
где $ C_{} $ — пропускная способность линии связи, а $ H=-sum_{j=1}^n P_j log_2 P_i $ — энтропия одной буквы передаваемого сообщения; однако скорость передачи, превосходящая $ v_{} $ никогда не может быть достигнута.
При наличии помех в линии связи дело будет обстоять иначе. В этом случае только наличие избыточности в передаваемой последовательности сигналов может помочь нам точно восстановить переданное сообщение по принятым данным. Ясно, что использование кода, приводящего к наименьшей избыточности закодированного сообщения здесь уже нецелесообразно и скорость передачи сообщения должна быть уменьшена. Насколько уменьшена?
Для ответа на этот вопрос придется предварительно описать линию связи с помехами. Пусть линия связи использует $ m_{} $ различных элементраных сигналов $ A_1,A_2,dots,A_m $, но из-за наличия помех переданный сигнал $ A_j $ может оказаться по выходе из канала каким-то другим сигналом $ A_k $; пусть известна вероятность этого события $ hat P_{jk}^{} $. Из этих вероятностей можно составить квадратную матрицу
$$
hat{mathfrak P} =
left( begin{array}{llll}
hat P_{11} & hat P_{12} & dots & hat P_{1m} \
hat P_{21} & hat P_{22} & dots & hat P_{2m} \
dots & & & dots \
hat P_{m1} & hat P_{m2} & dots & hat P_{mm}
end{array}
right)
$$
Предположим, для простоты, что по линии связи передается два элементарных сигнала — $ A_1=0 $ и $ A_{2}=1 $ (и на выходе канала связи других сигналов быть не может). Предположим, что вероятность безошибочного приема любого из передаваемых сигналов равна $ 1-p_{} $, а вероятность ошибки равна $ p_{} $. Можно составить матрицу переходных вероятностей:
$$
begin{array}{l}
\
A_1 \
A_2
end{array}
begin{array}{l}
begin{array}{llll}
& & A_{1} & A_{2}
end{array} \
left(begin{array}{cc}
1-p & p \
p & 1-p
end{array}
right)
end{array}
$$
Пусть $ P(A_{j}) $ — вероятность того, что передаваемым сигналом является $ A_{j} $, имеем: $ P(A_1)+P(A_2)=1 $.
Опыт $ B_{} $, заключающийся в выяснении того, какой сигнал передается, будет иметь энтропию
$$ H(B)=-P(A_{1}) log P(A_1) — P(A_2) log P(A_{2}) . $$
Опыт $ A_{} $, заключающийся в выяснении того, какой именно сигнал при этом будет принят на выходе, является опытом
с двумя исходами, зависящими от опыта $ B_{} $. Условные энтропии
$$ H_{A_1}(B)=-(1-p) log (1-p)-p log p,quad H_{A_2}(B)=-p log p — (1-p) log (1-p) $$
оказываются одинаковыми и
$$ H_{A}(B)=P(A_1) H_{A_1}(B) + P(A_2) H_{A_2}(B)=-(1-p) log (1-p)-p log p_{} $$
независимо от величин вероятностей $ P(A_{1}), P(A_{2}) $.

Статья не закончена!
Источники
[1]. Шеннон К. Математическая теория связи. (Shannon C.E. A Mathematical Theory of Communication. Bell System Technical Journal. — 1948. — Т. 27. — С. 379-423, 623–656.)
[2]. Яглом А.М., Яглом И.М. Вероятность и информация. М. Наука. 1973.
.
«Информация есть форма жизни», — писал американский поэт и эссеист Джон Перри Барлоу. Действительно, мы постоянно сталкиваемся со словом «информация» — ее получают, передают и сохраняют. Узнать прогноз погоды или результат футбольного матча, содержание фильма или книги, поговорить по телефону — всегда ясно, с каким видом информации мы имеем дело. Но что такое сама информация, а главное — как ее можно измерить, никто обычно не задумывается. А между тем, информация и способы ее передачи — важная вещь, которая во многом определяет нашу жизнь, неотъемлемой частью которой стали информационные технологии. Научный редактор издания «Лаба.Медиа» Владимир Губайловский объясняет, что такое информация, как ее измерять, и почему самое сложное — это передача информации без искажений.
Читайте «Хайтек» в
Пространство случайных событий
В 1946 году американский ученый-статистик Джон Тьюки предложил название БИТ (BIT, BInary digiT — «двоичное число» — «Хайтек») — одно из главных понятий XX века. Тьюки избрал бит для обозначения одного двоичного разряда, способного принимать значение 0 или 1. Клод Шеннон в своей программной статье «Математическая теория связи» предложил измерять в битах количество информации. Но это не единственное понятие, введенное и исследованное Шенноном в его статье.
Представим себе пространство случайных событий, которое состоит из бросания одной фальшивой монеты, на обеих сторонах которой орел. Когда выпадает орел? Ясно, что всегда. Это мы знаем заранее, поскольку так устроено наше пространство. Выпадение орла — достоверное событие, то есть его вероятность равна 1. Много ли информации мы сообщим, если скажем о выпавшем орле? Нет. Количество информации в таком сообщении мы будем считать равным 0.
Теперь давайте бросать правильную монету: с одной стороны у нее орел, а с другой решка, как и положено. Выпадение орла или решки будут двумя разными событиями, из которых состоит наше пространство случайных событий. Если мы сообщим об исходе одного бросания, то это действительно будет новая информация. При выпадении орла мы сообщим 0, а при решке 1. Для того, чтобы сообщить эту информацию, нам достаточно 1 бита.
Что изменилось? В нашем пространстве событий появилась неопределенность. Нам есть, что о нем рассказать тому, кто сам монету не бросает и исхода бросания не видит. Но чтобы правильно понять наше сообщение, он должен точно знать, чем мы занимаемся, что означают 0 и 1. Наши пространства событий должны совпадать, и процесс декодирования — однозначно восстанавливать результат бросания. Если пространство событий у передающего и принимающего не совпадает или нет возможности однозначного декодирования сообщения, информация останется только шумом в канале связи.
Если независимо и одновременно бросать две монеты, то разных равновероятных результатов будет уже четыре: орел-орел, орел-решка, решка-орел и решка-решка. Чтобы передать информацию, нам понадобится уже 2 бита, и наши сообщения будут такими: 00, 01, 10 и 11. Информации стало в два раза больше. Это произошло, потому что выросла неопределенность. Если мы попытаемся угадать исход такого парного бросания, то имеем в два раза больше шансов ошибиться.
Чем больше неопределенность пространства событий, тем больше информации содержит сообщение о его состоянии.
Немного усложним наше пространство событий. Пока все события, которые случались, были равновероятными. Но в реальных пространствах далеко не все события имеют равную вероятность. Скажем, вероятность того, что увиденная нами ворона будет черной, близка к 1. Вероятность того, что первый встреченный на улице прохожий окажется мужчиной, — примерно 0,5. Но встретить на улице Москвы крокодила почти невероятно. Интуитивно мы понимаем, что сообщение о встрече с крокодилом имеет гораздо большую информационную ценность, чем о черной вороне. Чем ниже вероятность события, тем больше информации в сообщении о таком событии.
Пусть пространство событий не такое экзотическое. Мы просто стоим у окна и смотрим на проезжающие машины. Мимо проезжают автомобили четырех цветов, о которых нам необходимо сообщить. Для этого мы закодируем цвета: черный — 00, белый — 01, красный — 10, синий — 11. Чтобы сообщить о том, какой именно автомобиль проехал, нам достаточно передать 2 бита информации.
Но довольно долго наблюдая за автомобилями, замечаем, что цвет автомобилей распределен неравномерно: черных — 50% (каждый второй), белых — 25% (каждый четвертый), красных и синих — по 12,5% (каждый восьмой). Тогда можно оптимизировать передаваемую информацию.
Больше всего черных автомобилей, поэтому обозначим черный — 0 — самый короткий код, а код всех остальных пусть начинается на 1. Из оставшихся половина белые — 10, а оставшиеся цвета начинаются на 11. В заключение обозначим красный — 110, а синий — 111.
Теперь, передавая информацию о цвете автомобилей, мы можем закодировать ее плотнее.
Энтропия по Шеннону
Пусть наше пространство событий состоит из n разных событий. При бросании монеты с двумя орлами такое событие ровно одно, при бросании одной правильной монеты — 2, при бросании двух монет или наблюдении за автомобилями — 4. Каждому событию соответствует вероятность его наступления. При бросании монеты с двумя орлами событие (выпадение орла) одно и его вероятность p1 = 1. При бросании правильной монеты событий два, они равновероятны и вероятность каждого — 0,5: p1 = 0,5, p2 = 0,5. При бросании двух правильных монет событий четыре, все они равновероятны и вероятность каждого — 0,25: p1 = 0,25, p2 = 0,25, p3 = 0,25, p4 = 0,25. При наблюдении за автомобилями событий четыре, и они имеют разные вероятности: черный — 0,5, белый — 0,25, красный — 0,125, синий — 0,125: p1 = 0,5, p2 = 0,25, p3 = 0,125, p4 = 0,125.
Это не случайное совпадение. Шеннон так подобрал энтропию (меру неопределенности в пространстве событий), чтобы выполнялись три условия:
- 1Энтропия достоверного события, вероятность которого 1, равна 0.
- Энтропия двух независимых событий равна сумме энтропий этих событий.
- Энтропия максимальна, если все события равновероятны.
Все эти требования вполне соответствуют нашим представлениям о неопределенности пространства событий. Если событие одно (первый пример) — никакой неопределенности нет. Если события независимы — неопределенность суммы равна сумме неопределенностей — они просто складываются (пример с бросанием двух монет). И, наконец, если все события равновероятны, то степень неопределенности системы максимальна. Как в случае с бросанием двух монет, все четыре события равновероятны и энтропия равна 2, она больше, чем в случае с автомобилями, когда событий тоже четыре, но они имеют разную вероятность — в этом случае энтропия 1,75.
Клод Элвуд Шеннон — американский инженер, криптоаналитик и математик. Считается «отцом информационного века». Основатель теории информации, нашедшей применение в современных высокотехнологических системах связи. Предоставил фундаментальные понятия, идеи и их математические формулировки, которые в настоящее время формируют основу для современных коммуникационных технологий.
В 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы информации. Он также продемонстрировал, что введенная им энтропия эквивалентна мере неопределенности информации в передаваемом сообщении. Статьи Шеннона «Математическая теория связи» и «Теория связи в секретных системах» считаются основополагающими для теории информации и криптографии.
Во время Второй мировой войны Шеннон в Bell Laboratories занимался разработкой криптографических систем, позже это помогло ему открыть методы кодирования с коррекцией ошибок.
Шеннон внес ключевой вклад в теорию вероятностных схем, теорию игр, теорию автоматов и теорию систем управления — области наук, входящие в понятие «кибернетика».
Кодирование
И бросаемые монеты, и проезжающие автомобили не похожи на цифры 0 и 1. Чтобы сообщить о событиях, происходящих в пространствах, нужно придумать способ описать эти события. Это описание называется кодированием.
Кодировать сообщения можно бесконечным числом разных способов. Но Шеннон показал, что самый короткий код не может быть меньше в битах, чем энтропия.
Именно поэтому энтропия сообщения и есть мера информации в сообщении. Поскольку во всех рассмотренных случаях количество бит при кодировании равно энтропии, — значит кодирование прошло оптимально. Короче закодировать сообщения о событиях в наших пространствах уже нельзя.
При оптимальном кодировании нельзя потерять или исказить в сообщении ни одного передаваемого бита. Если хоть один бит потеряется, то исказится информация. А ведь все реальные каналы связи не дают 100-процентной уверенности, что все биты сообщения дойдут до получателя неискаженными.
Для устранения этой проблемы необходимо сделать код не оптимальным, а избыточным. Например, передавать вместе с сообщением его контрольную сумму — специальным образом вычисленное значение, получаемое при преобразовании кода сообщения, и которое можно проверить, пересчитав при получении сообщения. Если переданная контрольная сумма совпадет с вычисленной, вероятность того, что передача прошла без ошибок, будет довольно высока. А если контрольная сумма не совпадет, то необходимо запросить повторную передачу. Примерно так работает сегодня большинство каналов связи, например, при передаче пакетов информации по интернету.
Сообщения на естественном языке
Рассмотрим пространство событий, которое состоит из сообщений на естественном языке. Это частный случай, но один из самых важных. Событиями здесь будут передаваемые символы (буквы фиксированного алфавита). Эти символы встречаются в языке с разной вероятностью.
Самым частотным символом (то есть таким, который чаще всего встречается во всех текстах, написанных на русском языке) является пробел: из тысячи символов в среднем пробел встречается 175 раз. Вторым по частоте является символ «о» — 90, далее следуют другие гласные: «е» (или «ё» — мы их различать не будем) — 72, «а» — 62, «и» — 62, и только дальше встречается первый согласный «т» — 53. А самый редкий «ф» — этот символ встречается всего два раза на тысячу знаков.
Будем использовать 31-буквенный алфавит русского языка (в нем не отличаются «е» и «ё», а также «ъ» и «ь»). Если бы все буквы встречались в языке с одинаковой вероятностью, то энтропия на символ была бы Н = 5 бит, но если мы учтем реальные частоты символов, то энтропия окажется меньше: Н = 4,35 бит. (Это почти в два раза меньше, чем при традиционном кодировании, когда символ передается как байт — 8 бит).
Но энтропия символа в языке еще ниже. Вероятность появления следующего символа не полностью предопределена средней частотой символа во всех текстах. То, какой символ последует, зависит от символов уже переданных. Например, в современном русском языке после символа «ъ» не может следовать символ согласного звука. После двух подряд гласных «е» третий гласный «е» следует крайне редко, разве только в слове «длинношеее». То есть следующий символ в некоторой степени предопределен. Если мы учтем такую предопределенность следующего символа, неопределенность (то есть информация) следующего символа будет еще меньше, чем 4,35. По некоторым оценкам, следующий символ в русском языке предопределен структурой языка более чем на 50%, то есть при оптимальном кодировании всю информацию можно передать, вычеркнув половину букв из сообщения.
Другое дело, что не всякую букву можно безболезненно вычеркнуть. Высокочастотную «о» (и вообще гласные), например, вычеркнуть легко, а вот редкие «ф» или «э» — довольно проблематично.
Естественный язык, на котором мы общаемся друг с другом, высоко избыточен, а потому надежен, если мы что-то недослышали — нестрашно, информация все равно будет передана.
Но пока Шеннон не ввел меру информации, мы не могли понять и того, что язык избыточен, и до какой степени мы может сжимать сообщения (и почему текстовые файлы так хорошо сжимаются архиватором).
Избыточность естественного языка
В статье «О том, как мы ворпсиманием теcкт» (название звучит именно так!) был взят фрагмент романа Ивана Тургенева «Дворянское гнездо» и подвергнут некоторому преобразованию: из фрагмента было вычеркнуто 34% букв, но не случайных. Были оставлены первые и последние буквы в словах, вычеркивались только гласные, причем не все. Целью было не просто получить возможность восстановить всю информацию по преобразованному тексту, но и добиться того, чтобы человек, читающий этот текст, не испытывал особых трудностей из-за пропусков букв.
Почему сравнительно легко читать этот испорченный текст? В нем действительно содержится необходимая информация для восстановления целых слов. Носитель русского языка располагает определенным набором событий (слов и целых предложений), которые он использует при распознавании. Кроме того, в распоряжении носителя еще и стандартные языковые конструкции, которые помогают ему восстанавливать информацию. Например, «Она бла блее чвствтльна» — с высокой вероятностью можно прочесть как «Она была более чувствительна». Но взятая отдельно фраза «Она бла блее», скорее, будет восстановлена как «Она была белее». Поскольку мы в повседневном общении имеем дело с каналами, в которых есть шум и помехи, то довольно хорошо умеем восстанавливать информацию, но только ту, которую мы уже знаем заранее. Например, фраза «Чрты ее не бли лшны приятнсти, хтя нмнго рспхли и спллсь» хорошо читается за исключением последнего слова «спллсь» — «сплылись». Этого слова нет в современном лексиконе. При быстром чтении слово «спллсь» читается скорее как «слиплись», при медленном — просто ставит в тупик.
Оцифровка сигнала
Звук, или акустические колебания — это синусоида. Это видно, например, на экране звукового редактора. Чтобы точно передать звук, понадобится бесконечное количество значений — вся синусоида. Это возможно при аналоговом соединении. Он поет — вы слушаете, контакт не прерывается, пока длится песня.
При цифровой связи по каналу мы можем передать только конечное количество значений. Значит ли это, что звук нельзя передать точно? Оказывается, нет.
Разные звуки — это по-разному модулированная синусоида. Мы передаем только дискретные значения (частоты и амплитуды), а саму синусоиду передавать не надо — ее может породить принимающий прибор. Он порождает синусоиду, и на нее накладывается модуляция, созданная по значениям, переданным по каналу связи. Существуют точные принципы, какие именно дискретные значения надо передавать, чтобы звук на входе в канал связи совпадал со звуком на выходе, где эти значения накладываются на некоторую стандартную синусоиду (об этом как раз теорема Котельникова).
Теорема Котельникова (в англоязычной литературе — теорема Найквиста — Шеннона, теорема отсчетов) — фундаментальное утверждение в области цифровой обработки сигналов, связывающее непрерывные и дискретные сигналы и гласящее, что «любую функцию F(t), состоящую из частот от 0 до f1, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через 1/(2*f1) секунд.
Помехоустойчивое кодирование. Коды Хэмминга
Если по ненадежному каналу передать закодированный текст Ивана Тургенева, пусть и с некоторым количеством ошибок, то получится вполне осмысленный текст. Но вот если нам нужно передать все с точностью до бита, задача окажется нерешенной: мы не знаем, какие биты ошибочны, потому что ошибка случайна. Даже контрольная сумма не всегда спасает.
Именно поэтому сегодня при передаче данных по сетям стремятся не столько к оптимальному кодированию, при котором в канал можно затолкать максимальное количество информации, сколько к такому кодированию (заведомо избыточному) при котором можно восстановить ошибки — так, примерно, как мы при чтении восстанавливали слова во фрагменте Ивана Тургенева.
Существуют специальные помехоустойчивые коды, которые позволяют восстанавливать информацию после сбоя. Один из них — код Хэмминга. Допустим, весь наш язык состоит из трех слов: 111000, 001110, 100011. Эти слова знают и источник сообщения, и приемник. И мы знаем, что в канале связи случаются ошибки, но при передаче одного слова искажается не более одного бита информации.
Предположим, мы сначала передаем слово 111000. В результате не более чем одной ошибки (ошибки мы выделили) оно может превратиться в одно из слов:
1) 111000, 011000, 101000, 110000, 111100, 111010, 111001.
При передаче слова 001110 может получиться любое из слов:
2) 001110, 101110, 011110, 000110, 001010, 001100, 001111.
Наконец, для 100011 у нас может получиться на приеме:
3) 100011, 000011, 110011, 101011, 100111, 100001, 100010.
Заметим, что все три списка попарно не пересекаются. Иными словами, если на другом конце канала связи появляется любое слово из списка 1, получатель точно знает, что ему передавали именно слово 111000, а если появляется любое слово из списка 2 — слово 001110, а из списка 3 — слово 100011. В этом случае говорят, что наш код исправил одну ошибку.
Исправление произошло за счет двух факторов. Во-первых, получатель знает весь «словарь», то есть пространство событий получателя сообщения совпадает с пространством того, кто сообщение передал. Когда код передавался всего с одной ошибкой, выходило слово, которого в словаре не было.
Во-вторых, слова в словаре были подобраны особенным образом. Даже при возникновении ошибки получатель не мог перепутать одно слово с другим. Например, если словарь состоит из слов «дочка», «точка», «кочка», и при передаче получалось «вочка», то получатель, зная, что такого слова не бывает, исправить ошибку не смог бы — любое из трех слов может оказаться правильным. Если же в словарь входят «точка», «галка», «ветка» и нам известно, что допускается не больше одной ошибки, то «вочка» это заведомо «точка», а не «галка». В кодах, исправляющих ошибки, слова выбираются именно так, чтобы они были «узнаваемы» даже после ошибки. Разница лишь в том, что в кодовом «алфавите» всего две буквы — ноль и единица.
Избыточность такого кодирования очень велика, а количество слов, которые мы можем таким образом передать, сравнительно невелико. Нам ведь надо исключать из словаря любое слово, которое может при ошибке совпасть с целым списком, соответствующим передаваемым словам (например, в словаре не может быть слов «дочка» и «точка»). Но точная передача сообщения настолько важна, что на исследование помехоустойчивых кодов тратятся большие силы.
Сенсация
Понятия энтропии (или неопределенности и непредсказуемости) сообщения и избыточности (или предопределенности и предсказуемости) очень естественно соответствуют нашим интуитивным представлениям о мере информации. Чем более непредсказуемо сообщение (тем больше его энтропия, потому что меньше вероятность), — тем больше информации оно несет. Сенсация (например, встреча с крокодилом на Тверской) — редкое событие, его предсказуемость очень мала, и потому велика информационная стоимость. Часто информацией называют новости — сообщения о только что произошедших событиях, о которых мы еще ничего не знаем. Но если о случившемся нам расскажут второй и третий раз примерно теми же словами, избыточность сообщения будет велика, его непредсказуемость упадет до нуля, и мы просто не станем слушать, отмахиваясь от говорящего со словами «Знаю, знаю». Поэтому СМИ так стараются быть первыми. Вот это соответствие интуитивному чувству новизны, которое рождает действительно неожиданное известие, и сыграло главную роль в том, что статья Шеннона, совершенно не рассчитанная на массового читателя, стала сенсацией, которую подхватила пресса, которую приняли как универсальный ключ к познанию природы ученые самых разных специальностей — от лингвистов и литературоведов до биологов.
Но понятие информации по Шеннону — строгая математическая теория, и ее применение за пределами теории связи очень ненадежно. Зато в самой теории связи она играет центральную роль.
Семантическая информация
Шеннон, введя понятие энтропии как меры информации, получил возможность работать с информацией — в первую очередь, ее измерять и оценивать такие характеристики, как пропускная способность каналов или оптимальность кодирования. Но главным допущением, которое позволило Шеннону успешно оперировать с информацией, было предположение, что порождение информации — это случайный процесс, который можно успешно описать в терминах теории вероятности. Если процесс неслучайный, то есть он подчиняется закономерностям (к тому же не всегда ясным, как это происходит в естественном языке), то к нему рассуждения Шеннона неприменимы. Все, что говорит Шеннон, никак не связано с осмысленностью информации.
Пока мы говорим о символах (или буквах алфавита), мы вполне можем рассуждать в терминах случайных событий, но как только мы перейдем к словам языка, ситуация резко изменится. Речь — это процесс, особым образом организованный, и здесь структура сообщения не менее важна, чем символы, которыми она передается.
Еще недавно казалось, что мы ничего не можем сделать, чтобы хоть как-то приблизиться к измерению осмысленности текста, но в последние годы ситуация начала меняться. И связано это прежде всего с применением искусственных нейронных сетей к задачам машинного перевода, автоматического реферирования текстов, извлечению информации из текстов, генерированию отчетов на естественном языке. Во всех этих задачах происходит преобразование, кодирование и декодирование осмысленной информации, заключенной в естественном языке. И постепенно складывается представление об информационных потерях при таких преобразованиях, а значит — о мере осмысленной информации. Но на сегодняшний день той четкости и точности, которую имеет шенноновская теория информации, в этих трудных задачах еще нет.
In information theory, the entropy of a random variable is the average level of «information», «surprise», or «uncertainty» inherent to the variable’s possible outcomes. Given a discrete random variable 

![{displaystyle p:{mathcal {X}}to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f219961c04ea0285eff7416f743c7684e0da25fa)
where 

Two bits of entropy: In the case of two fair coin tosses, the information entropy in bits is the base-2 logarithm of the number of possible outcomes; with two coins there are four possible outcomes, and two bits of entropy. Generally, information entropy is the average amount of information conveyed by an event, when considering all possible outcomes.
The concept of information entropy was introduced by Claude Shannon in his 1948 paper «A Mathematical Theory of Communication»,[2][3] and is also referred to as Shannon entropy. Shannon’s theory defines a data communication system composed of three elements: a source of data, a communication channel, and a receiver. The «fundamental problem of communication» – as expressed by Shannon – is for the receiver to be able to identify what data was generated by the source, based on the signal it receives through the channel.[2][3] Shannon considered various ways to encode, compress, and transmit messages from a data source, and proved in his famous source coding theorem that the entropy represents an absolute mathematical limit on how well data from the source can be losslessly compressed onto a perfectly noiseless channel. Shannon strengthened this result considerably for noisy channels in his noisy-channel coding theorem.
Entropy in information theory is directly analogous to the entropy in statistical thermodynamics. The analogy results when the values of the random variable designate energies of microstates, so Gibbs formula for the entropy is formally identical to Shannon’s formula. Entropy has relevance to other areas of mathematics such as combinatorics and machine learning. The definition can be derived from a set of axioms establishing that entropy should be a measure of how informative the average outcome of a variable is. For a continuous random variable, differential entropy is analogous to entropy.
Introduction[edit]
The core idea of information theory is that the «informational value» of a communicated message depends on the degree to which the content of the message is surprising. If a highly likely event occurs, the message carries very little information. On the other hand, if a highly unlikely event occurs, the message is much more informative. For instance, the knowledge that some particular number will not be the winning number of a lottery provides very little information, because any particular chosen number will almost certainly not win. However, knowledge that a particular number will win a lottery has high informational value because it communicates the outcome of a very low probability event.
The information content, also called the surprisal or self-information, of an event 



where 

Hence, we can define the information, or surprisal, of an event 
or equivalently,
Entropy measures the expected (i.e., average) amount of information conveyed by identifying the outcome of a random trial.[5]: 67 This implies that casting a die has higher entropy than tossing a coin because each outcome of a die toss has smaller probability (about 

Consider a coin with probability p of landing on heads and probability 1 − p of landing on tails. The maximum surprise is when p = 1/2, for which one outcome is not expected over the other. In this case a coin flip has an entropy of one bit. (Similarly, one trit with equiprobable values contains 
Information theory is useful to calculate the smallest amount of information required to convey a message, as in data compression. For example, consider the transmission of sequences comprising the 4 characters ‘A’, ‘B’, ‘C’, and ‘D’ over a binary channel. If all 4 letters are equally likely (25%), one can’t do better than using two bits to encode each letter. ‘A’ might code as ’00’, ‘B’ as ’01’, ‘C’ as ’10’, and ‘D’ as ’11’. However, if the probabilities of each letter are unequal, say ‘A’ occurs with 70% probability, ‘B’ with 26%, and ‘C’ and ‘D’ with 2% each, one could assign variable length codes. In this case, ‘A’ would be coded as ‘0’, ‘B’ as ’10’, ‘C’ as ‘110’, and D as ‘111’. With this representation, 70% of the time only one bit needs to be sent, 26% of the time two bits, and only 4% of the time 3 bits. On average, fewer than 2 bits are required since the entropy is lower (owing to the high prevalence of ‘A’ followed by ‘B’ – together 96% of characters). The calculation of the sum of probability-weighted log probabilities measures and captures this effect. English text, treated as a string of characters, has fairly low entropy, i.e., is fairly predictable. We can be fairly certain that, for example, ‘e’ will be far more common than ‘z’, that the combination ‘qu’ will be much more common than any other combination with a ‘q’ in it, and that the combination ‘th’ will be more common than ‘z’, ‘q’, or ‘qu’. After the first few letters one can often guess the rest of the word. English text has between 0.6 and 1.3 bits of entropy per character of the message.[6]: 234
Definition[edit]
Named after Boltzmann’s Η-theorem, Shannon defined the entropy Η (Greek capital letter eta) of a discrete random variable 

![{displaystyle p:{mathcal {X}}to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f219961c04ea0285eff7416f743c7684e0da25fa)
![{displaystyle p(x):=mathbb {P} [X=x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa0ae7ad3abfcf67512937135163355464fa594)
Here 

The entropy can explicitly be written as:
where b is the base of the logarithm used. Common values of b are 2, Euler’s number e, and 10, and the corresponding units of entropy are the bits for b = 2, nats for b = e, and bans for b = 10.[9]
In the case of 

One may also define the conditional entropy of two variables 



where ![{displaystyle p_{X,Y}(x,y):=mathbb {P} [X=x,Y=y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78582c96838c79f6c42f9e40afd3a01d4cbfaf6a)
![{displaystyle p_{Y}(y)=mathbb {P} [Y=y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92fdcaec99cdc3e8031abfeffc84addb07477e2c)


Measure theory[edit]
Entropy can be formally defined in the language of measure theory as follows:[11] Let 


The expected surprisal of 
A 





Let 


Finally, the entropy of the probability space is 


Ellerman definition[edit]
David Ellerman wanted to explain why conditional entropy and other functions had properties similar to functions in probability theory. He claims that previous definitions based on measure theory only worked with powers of 2.[12]
Ellerman created a «logic of partitions» that is the dual of subsets of a universal set. Information is quantified as «dits» (distinctions), a measure on partitions. «Dits» can be converted into Shannon’s bits, to get the formulas for conditional entropy, etc..
Example[edit]
Entropy Η(X) (i.e. the expected surprisal) of a coin flip, measured in bits, graphed versus the bias of the coin Pr(X = 1), where X = 1 represents a result of heads.[10]: 14–15
Here, the entropy is at most 1 bit, and to communicate the outcome of a coin flip (2 possible values) will require an average of at most 1 bit (exactly 1 bit for a fair coin). The result of a fair die (6 possible values) would have entropy log26 bits.
Consider tossing a coin with known, not necessarily fair, probabilities of coming up heads or tails; this can be modelled as a Bernoulli process.
The entropy of the unknown result of the next toss of the coin is maximized if the coin is fair (that is, if heads and tails both have equal probability 1/2). This is the situation of maximum uncertainty as it is most difficult to predict the outcome of the next toss; the result of each toss of the coin delivers one full bit of information. This is because
However, if we know the coin is not fair, but comes up heads or tails with probabilities p and q, where p ≠ q, then there is less uncertainty. Every time it is tossed, one side is more likely to come up than the other. The reduced uncertainty is quantified in a lower entropy: on average each toss of the coin delivers less than one full bit of information. For example, if p = 0.7, then
Uniform probability yields maximum uncertainty and therefore maximum entropy. Entropy, then, can only decrease from the value associated with uniform probability. The extreme case is that of a double-headed coin that never comes up tails, or a double-tailed coin that never results in a head. Then there is no uncertainty. The entropy is zero: each toss of the coin delivers no new information as the outcome of each coin toss is always certain.[10]: 14–15
Entropy can be normalized by dividing it by information length. This ratio is called metric entropy and is a measure of the randomness of the information.
Characterization[edit]
To understand the meaning of −Σ pi log(pi), first define an information function I in terms of an event i with probability pi. The amount of information acquired due to the observation of event i follows from Shannon’s solution of the fundamental properties of information:[13]
- I(p) is monotonically decreasing in p: an increase in the probability of an event decreases the information from an observed event, and vice versa.
- I(1) = 0: events that always occur do not communicate information.
- I(p1·p2) = I(p1) + I(p2): the information learned from independent events is the sum of the information learned from each event.
Given two independent events, if the first event can yield one of n equiprobable outcomes and another has one of m equiprobable outcomes then there are mn equiprobable outcomes of the joint event. This means that if log2(n) bits are needed to encode the first value and log2(m) to encode the second, one needs log2(mn) = log2(m) + log2(n) to encode both.
Shannon discovered that a suitable choice of 
In fact, the only possible values of 




-
Proof Let be the information function which one assumes to be twice continuously differentiable, one has:
This differential equation leads to the solution
for some
. Property 2 gives
. Property 1 and 2 give that
for all
, so that
.
The different units of information (bits for the binary logarithm log2, nats for the natural logarithm ln, bans for the decimal logarithm log10 and so on) are constant multiples of each other. For instance, in case of a fair coin toss, heads provides log2(2) = 1 bit of information, which is approximately 0.693 nats or 0.301 decimal digits. Because of additivity, n tosses provide n bits of information, which is approximately 0.693n nats or 0.301n decimal digits.
The meaning of the events observed (the meaning of messages) does not matter in the definition of entropy. Entropy only takes into account the probability of observing a specific event, so the information it encapsulates is information about the underlying probability distribution, not the meaning of the events themselves.
Alternative characterization[edit]
Another characterization of entropy uses the following properties. We denote pi = Pr(X = xi) and Ηn(p1, …, pn) = Η(X).
- Continuity: H should be continuous, so that changing the values of the probabilities by a very small amount should only change the entropy by a small amount.
- Symmetry: H should be unchanged if the outcomes xi are re-ordered. That is,
for any permutation
of
.
- Maximum:
should be maximal if all the outcomes are equally likely i.e.
.
- Increasing number of outcomes: for equiprobable events, the entropy should increase with the number of outcomes i.e.
- Additivity: given an ensemble of n uniformly distributed elements that are divided into k boxes (sub-systems) with b1, …, bk elements each, the entropy of the whole ensemble should be equal to the sum of the entropy of the system of boxes and the individual entropies of the boxes, each weighted with the probability of being in that particular box.
The rule of additivity has the following consequences: for positive integers bi where b1 + … + bk = n,
Choosing k = n, b1 = … = bn = 1 this implies that the entropy of a certain outcome is zero: Η1(1) = 0. This implies that the efficiency of a source alphabet with n symbols can be defined simply as being equal to its n-ary entropy. See also Redundancy (information theory).
Alternative characterization via additivity and subadditivity[edit]
Another succinct axiomatic characterization of Shannon entropy was given by Aczél, Forte and Ng,[15] via the following properties:
- Subadditivity:
for jointly distributed random variables
.
- Additivity:
when the random variables
are independent.
- Expansibility:
, i.e., adding an outcome with probability zero does not change the entropy.
- Symmetry:
is invariant under permutation of
.
- Small for small probabilities:
.
It was shown that any function 

It is worth noting that if we drop the «small for small probabilities» property, then 
Further properties[edit]
The Shannon entropy satisfies the following properties, for some of which it is useful to interpret entropy as the expected amount of information learned (or uncertainty eliminated) by revealing the value of a random variable X:
- Adding or removing an event with probability zero does not contribute to the entropy:
-
.
- It can be confirmed using the Jensen inequality and then Sedrakyan’s inequality that
-
.[10]: 29
- This maximal entropy of logb(n) is effectively attained by a source alphabet having a uniform probability distribution: uncertainty is maximal when all possible events are equiprobable.
- The entropy or the amount of information revealed by evaluating (X,Y) (that is, evaluating X and Y simultaneously) is equal to the information revealed by conducting two consecutive experiments: first evaluating the value of Y, then revealing the value of X given that you know the value of Y. This may be written as:[10]: 16
-
- so
, the entropy of a variable can only decrease when the latter is passed through a function.
- If X and Y are two independent random variables, then knowing the value of Y doesn’t influence our knowledge of the value of X (since the two don’t influence each other by independence):
- More generally, for any random variables X and Y, we have
-
.[10]: 29
-
- for all probability mass functions
and
.[10]: 32
- Accordingly, the negative entropy (negentropy) function is convex, and its convex conjugate is LogSumExp.
Aspects[edit]
Relationship to thermodynamic entropy[edit]
The inspiration for adopting the word entropy in information theory came from the close resemblance between Shannon’s formula and very similar known formulae from statistical mechanics.
In statistical thermodynamics the most general formula for the thermodynamic entropy S of a thermodynamic system is the Gibbs entropy,
where kB is the Boltzmann constant, and pi is the probability of a microstate. The Gibbs entropy was defined by J. Willard Gibbs in 1878 after earlier work by Boltzmann (1872).[16]
The Gibbs entropy translates over almost unchanged into the world of quantum physics to give the von Neumann entropy, introduced by John von Neumann in 1927,
where ρ is the density matrix of the quantum mechanical system and Tr is the trace.[17]
At an everyday practical level, the links between information entropy and thermodynamic entropy are not evident. Physicists and chemists are apt to be more interested in changes in entropy as a system spontaneously evolves away from its initial conditions, in accordance with the second law of thermodynamics, rather than an unchanging probability distribution. As the minuteness of the Boltzmann constant kB indicates, the changes in S / kB for even tiny amounts of substances in chemical and physical processes represent amounts of entropy that are extremely large compared to anything in data compression or signal processing. In classical thermodynamics, entropy is defined in terms of macroscopic measurements and makes no reference to any probability distribution, which is central to the definition of information entropy.
The connection between thermodynamics and what is now known as information theory was first made by Ludwig Boltzmann and expressed by his famous equation:
where 
In the view of Jaynes (1957),[19] thermodynamic entropy, as explained by statistical mechanics, should be seen as an application of Shannon’s information theory: the thermodynamic entropy is interpreted as being proportional to the amount of further Shannon information needed to define the detailed microscopic state of the system, that remains uncommunicated by a description solely in terms of the macroscopic variables of classical thermodynamics, with the constant of proportionality being just the Boltzmann constant. Adding heat to a system increases its thermodynamic entropy because it increases the number of possible microscopic states of the system that are consistent with the measurable values of its macroscopic variables, making any complete state description longer. (See article: maximum entropy thermodynamics). Maxwell’s demon can (hypothetically) reduce the thermodynamic entropy of a system by using information about the states of individual molecules; but, as Landauer (from 1961) and co-workers[20] have shown, to function the demon himself must increase thermodynamic entropy in the process, by at least the amount of Shannon information he proposes to first acquire and store; and so the total thermodynamic entropy does not decrease (which resolves the paradox). Landauer’s principle imposes a lower bound on the amount of heat a computer must generate to process a given amount of information, though modern computers are far less efficient.
Data compression[edit]
Shannon’s definition of entropy, when applied to an information source, can determine the minimum channel capacity required to reliably transmit the source as encoded binary digits. Shannon’s entropy measures the information contained in a message as opposed to the portion of the message that is determined (or predictable). Examples of the latter include redundancy in language structure or statistical properties relating to the occurrence frequencies of letter or word pairs, triplets etc. The minimum channel capacity can be realized in theory by using the typical set or in practice using Huffman, Lempel–Ziv or arithmetic coding. (See also Kolmogorov complexity.) In practice, compression algorithms deliberately include some judicious redundancy in the form of checksums to protect against errors. The entropy rate of a data source is the average number of bits per symbol needed to encode it. Shannon’s experiments with human predictors show an information rate between 0.6 and 1.3 bits per character in English;[21] the PPM compression algorithm can achieve a compression ratio of 1.5 bits per character in English text.
If a compression scheme is lossless – one in which you can always recover the entire original message by decompression – then a compressed message has the same quantity of information as the original but communicated in fewer characters. It has more information (higher entropy) per character. A compressed message has less redundancy. Shannon’s source coding theorem states a lossless compression scheme cannot compress messages, on average, to have more than one bit of information per bit of message, but that any value less than one bit of information per bit of message can be attained by employing a suitable coding scheme. The entropy of a message per bit multiplied by the length of that message is a measure of how much total information the message contains. Shannon’s theorem also implies that no lossless compression scheme can shorten all messages. If some messages come out shorter, at least one must come out longer due to the pigeonhole principle. In practical use, this is generally not a problem, because one is usually only interested in compressing certain types of messages, such as a document in English, as opposed to gibberish text, or digital photographs rather than noise, and it is unimportant if a compression algorithm makes some unlikely or uninteresting sequences larger.
A 2011 study in Science estimates the world’s technological capacity to store and communicate optimally compressed information normalized on the most effective compression algorithms available in the year 2007, therefore estimating the entropy of the technologically available sources.[22]: 60–65
| Type of Information | 1986 | 2007 |
|---|---|---|
| Storage | 2.6 | 295 |
| Broadcast | 432 | 1900 |
| Telecommunications | 0.281 | 65 |
The authors estimate humankind technological capacity to store information (fully entropically compressed) in 1986 and again in 2007. They break the information into three categories—to store information on a medium, to receive information through one-way broadcast networks, or to exchange information through two-way telecommunication networks.[22]
Entropy as a measure of diversity[edit]
Entropy is one of several ways to measure biodiversity, and is applied in the form of the Shannon index.[23] A diversity index is a quantitative statistical measure of how many different types exist in a dataset, such as species in a community, accounting for ecological richness, evenness, and dominance. Specifically, Shannon entropy is the logarithm of 1D, the true diversity index with parameter equal to 1. The Shannon index is related to the proportional abundances of types.
Limitations of entropy[edit]
There are a number of entropy-related concepts that mathematically quantify information content in some way:
- the self-information of an individual message or symbol taken from a given probability distribution,
- the entropy of a given probability distribution of messages or symbols, and
- the entropy rate of a stochastic process.
(The «rate of self-information» can also be defined for a particular sequence of messages or symbols generated by a given stochastic process: this will always be equal to the entropy rate in the case of a stationary process.) Other quantities of information are also used to compare or relate different sources of information.
It is important not to confuse the above concepts. Often it is only clear from context which one is meant. For example, when someone says that the «entropy» of the English language is about 1 bit per character, they are actually modeling the English language as a stochastic process and talking about its entropy rate. Shannon himself used the term in this way.
If very large blocks are used, the estimate of per-character entropy rate may become artificially low because the probability distribution of the sequence is not known exactly; it is only an estimate. If one considers the text of every book ever published as a sequence, with each symbol being the text of a complete book, and if there are N published books, and each book is only published once, the estimate of the probability of each book is 1/N, and the entropy (in bits) is −log2(1/N) = log2(N). As a practical code, this corresponds to assigning each book a unique identifier and using it in place of the text of the book whenever one wants to refer to the book. This is enormously useful for talking about books, but it is not so useful for characterizing the information content of an individual book, or of language in general: it is not possible to reconstruct the book from its identifier without knowing the probability distribution, that is, the complete text of all the books. The key idea is that the complexity of the probabilistic model must be considered. Kolmogorov complexity is a theoretical generalization of this idea that allows the consideration of the information content of a sequence independent of any particular probability model; it considers the shortest program for a universal computer that outputs the sequence. A code that achieves the entropy rate of a sequence for a given model, plus the codebook (i.e. the probabilistic model), is one such program, but it may not be the shortest.
The Fibonacci sequence is 1, 1, 2, 3, 5, 8, 13, …. treating the sequence as a message and each number as a symbol, there are almost as many symbols as there are characters in the message, giving an entropy of approximately log2(n). The first 128 symbols of the Fibonacci sequence has an entropy of approximately 7 bits/symbol, but the sequence can be expressed using a formula [F(n) = F(n−1) + F(n−2) for n = 3, 4, 5, …, F(1) =1, F(2) = 1] and this formula has a much lower entropy and applies to any length of the Fibonacci sequence.
Limitations of entropy in cryptography[edit]
In cryptanalysis, entropy is often roughly used as a measure of the unpredictability of a cryptographic key, though its real uncertainty is unmeasurable. For example, a 128-bit key that is uniformly and randomly generated has 128 bits of entropy. It also takes (on average) 
Other problems may arise from non-uniform distributions used in cryptography. For example, a 1,000,000-digit binary one-time pad using exclusive or. If the pad has 1,000,000 bits of entropy, it is perfect. If the pad has 999,999 bits of entropy, evenly distributed (each individual bit of the pad having 0.999999 bits of entropy) it may provide good security. But if the pad has 999,999 bits of entropy, where the first bit is fixed and the remaining 999,999 bits are perfectly random, the first bit of the ciphertext will not be encrypted at all.
Data as a Markov process[edit]
A common way to define entropy for text is based on the Markov model of text. For an order-0 source (each character is selected independent of the last characters), the binary entropy is:
where pi is the probability of i. For a first-order Markov source (one in which the probability of selecting a character is dependent only on the immediately preceding character), the entropy rate is:
[citation needed]
where i is a state (certain preceding characters) and 
For a second order Markov source, the entropy rate is
Efficiency (normalized entropy)[edit]
A source alphabet with non-uniform distribution will have less entropy than if those symbols had uniform distribution (i.e. the «optimized alphabet»). This deficiency in entropy can be expressed as a ratio called efficiency[This quote needs a citation]:
Applying the basic properties of the logarithm, this quantity can also be expressed as:
Efficiency has utility in quantifying the effective use of a communication channel. This formulation is also referred to as the normalized entropy, as the entropy is divided by the maximum entropy 
Entropy for continuous random variables[edit]
Differential entropy[edit]
The Shannon entropy is restricted to random variables taking discrete values. The corresponding formula for a continuous random variable with probability density function f(x) with finite or infinite support 
This is the differential entropy (or continuous entropy). A precursor of the continuous entropy h[f] is the expression for the functional Η in the H-theorem of Boltzmann.
Although the analogy between both functions is suggestive, the following question must be set: is the differential entropy a valid extension of the Shannon discrete entropy? Differential entropy lacks a number of properties that the Shannon discrete entropy has – it can even be negative – and corrections have been suggested, notably limiting density of discrete points.
To answer this question, a connection must be established between the two functions:
In order to obtain a generally finite measure as the bin size goes to zero. In the discrete case, the bin size is the (implicit) width of each of the n (finite or infinite) bins whose probabilities are denoted by pn. As the continuous domain is generalized, the width must be made explicit.
To do this, start with a continuous function f discretized into bins of size 
By the mean-value theorem there exists a value xi in each bin such that
the integral of the function f can be approximated (in the Riemannian sense) by
where this limit and «bin size goes to zero» are equivalent.
We will denote
and expanding the logarithm, we have
As Δ → 0, we have
Note; log(Δ) → −∞ as Δ → 0, requires a special definition of the differential or continuous entropy:
which is, as said before, referred to as the differential entropy. This means that the differential entropy is not a limit of the Shannon entropy for n → ∞. Rather, it differs from the limit of the Shannon entropy by an infinite offset (see also the article on information dimension).
Limiting density of discrete points[edit]
It turns out as a result that, unlike the Shannon entropy, the differential entropy is not in general a good measure of uncertainty or information. For example, the differential entropy can be negative; also it is not invariant under continuous co-ordinate transformations. This problem may be illustrated by a change of units when x is a dimensioned variable. f(x) will then have the units of 1/x. The argument of the logarithm must be dimensionless, otherwise it is improper, so that the differential entropy as given above will be improper. If Δ is some «standard» value of x (i.e. «bin size») and therefore has the same units, then a modified differential entropy may be written in proper form as:
and the result will be the same for any choice of units for x. In fact, the limit of discrete entropy as 

Relative entropy[edit]
Another useful measure of entropy that works equally well in the discrete and the continuous case is the relative entropy of a distribution. It is defined as the Kullback–Leibler divergence from the distribution to a reference measure m as follows. Assume that a probability distribution p is absolutely continuous with respect to a measure m, i.e. is of the form p(dx) = f(x)m(dx) for some non-negative m-integrable function f with m-integral 1, then the relative entropy can be defined as
In this form the relative entropy generalizes (up to change in sign) both the discrete entropy, where the measure m is the counting measure, and the differential entropy, where the measure m is the Lebesgue measure. If the measure m is itself a probability distribution, the relative entropy is non-negative, and zero if p = m as measures. It is defined for any measure space, hence coordinate independent and invariant under co-ordinate reparameterizations if one properly takes into account the transformation of the measure m. The relative entropy, and (implicitly) entropy and differential entropy, do depend on the «reference» measure m.
Use in combinatorics[edit]
Entropy has become a useful quantity in combinatorics.
Loomis–Whitney inequality[edit]
A simple example of this is an alternative proof of the Loomis–Whitney inequality: for every subset A ⊆ Zd, we have
where Pi is the orthogonal projection in the ith coordinate:
The proof follows as a simple corollary of Shearer’s inequality: if X1, …, Xd are random variables and S1, …, Sn are subsets of {1, …, d} such that every integer between 1 and d lies in exactly r of these subsets, then
where 
We sketch how Loomis–Whitney follows from this: Indeed, let X be a uniformly distributed random variable with values in A and so that each point in A occurs with equal probability. Then (by the further properties of entropy mentioned above) Η(X) = log|A|, where |A| denotes the cardinality of A. Let Si = {1, 2, …, i−1, i+1, …, d}. The range of 
![mathrm {H} [(X_{j})_{jin S_{i}}]leq log |P_{i}(A)|](https://wikimedia.org/api/rest_v1/media/math/render/svg/e775922b5cf13b31bbf4fec16e82d4f492378cba)
Approximation to binomial coefficient[edit]
For integers 0 < k < n let q = k/n. Then
where
[27]: 43
-
Proof (sketch) Note that is one term of the expression
Rearranging gives the upper bound. For the lower bound one first shows, using some algebra, that it is the largest term in the summation. But then,
since there are n + 1 terms in the summation. Rearranging gives the lower bound.
A nice interpretation of this is that the number of binary strings of length n with exactly k many 1’s is approximately 
Use in machine learning[edit]
Machine learning techniques arise largely from statistics and also information theory. In general, entropy is a measure of uncertainty and the objective of machine learning is to minimize uncertainty.
Decision tree learning algorithms use relative entropy to determine the decision rules that govern the data at each node.[29] The Information gain in decision trees 




Bayesian inference models often apply the Principle of maximum entropy to obtain Prior probability distributions.[30] The idea is that the distribution that best represents the current state of knowledge of a system is the one with the largest entropy, and is therefore suitable to be the prior.
Classification in machine learning performed by logistic regression or artificial neural networks often employs a standard loss function, called cross entropy loss, that minimizes the average cross entropy between ground truth and predicted distributions.[31] In general, cross entropy is a measure of the differences between two datasets similar to the KL divergence (also known as relative entropy).
See also[edit]
- Approximate entropy (ApEn)
- Entropy (thermodynamics)
- Cross entropy – is a measure of the average number of bits needed to identify an event from a set of possibilities between two probability distributions
- Entropy (arrow of time)
- Entropy encoding – a coding scheme that assigns codes to symbols so as to match code lengths with the probabilities of the symbols.
- Entropy estimation
- Entropy power inequality
- Fisher information
- Graph entropy
- Hamming distance
- History of entropy
- History of information theory
- Information fluctuation complexity
- Information geometry
- Kolmogorov–Sinai entropy in dynamical systems
- Levenshtein distance
- Mutual information
- Perplexity
- Qualitative variation – other measures of statistical dispersion for nominal distributions
- Quantum relative entropy – a measure of distinguishability between two quantum states.
- Rényi entropy – a generalization of Shannon entropy; it is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system.
- Randomness
- Sample entropy (SampEn)
- Shannon index
- Theil index
- Typoglycemia
References[edit]
- ^ Pathria, R. K.; Beale, Paul (2011). Statistical Mechanics (Third ed.). Academic Press. p. 51. ISBN 978-0123821881.
- ^ a b Shannon, Claude E. (July 1948). «A Mathematical Theory of Communication». Bell System Technical Journal. 27 (3): 379–423. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:10338.dmlcz/101429. (PDF, archived from here)
- ^ a b Shannon, Claude E. (October 1948). «A Mathematical Theory of Communication». Bell System Technical Journal. 27 (4): 623–656. doi:10.1002/j.1538-7305.1948.tb00917.x. hdl:11858/00-001M-0000-002C-4317-B. (PDF, archived from here)
- ^ «Entropy (for data science) Clearly Explained!!!». YouTube.
- ^ MacKay, David J.C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge University Press. ISBN 0-521-64298-1.
- ^ Schneier, B: Applied Cryptography, Second edition, John Wiley and Sons.
- ^ Borda, Monica (2011). Fundamentals in Information Theory and Coding. Springer. ISBN 978-3-642-20346-6.
- ^ Han, Te Sun; Kobayashi, Kingo (2002). Mathematics of Information and Coding. American Mathematical Society. ISBN 978-0-8218-4256-0.
- ^ Schneider, T.D, Information theory primer with an appendix on logarithms, National Cancer Institute, 14 April 2007.
- ^ a b c d e f g h i j k Thomas M. Cover; Joy A. Thomas (1991). Elements of Information Theory. Hoboken, New Jersey: Wiley. ISBN 978-0-471-24195-9.
- ^ Entropy at the nLab
- ^ Ellerman, David (October 2017). «Logical Information Theory: New Logical Foundations for Information Theory» (PDF). Logic Journal of the IGPL. 25 (5): 806–835. doi:10.1093/jigpal/jzx022. Retrieved 2 November 2022.
- ^ Carter, Tom (March 2014). An introduction to information theory and entropy (PDF). Santa Fe. Retrieved 4 August 2017.
- ^ Chakrabarti, C. G., and Indranil Chakrabarty. «Shannon entropy: axiomatic characterization and application.» International Journal of Mathematics and Mathematical Sciences 2005.17 (2005): 2847-2854 url
- ^ a b c Aczél, J.; Forte, B.; Ng, C. T. (1974). «Why the Shannon and Hartley entropies are ‘natural’«. Advances in Applied Probability. 6 (1): 131-146. doi:10.2307/1426210. JSTOR 1426210. S2CID 204177762.
- ^ Compare: Boltzmann, Ludwig (1896, 1898). Vorlesungen über Gastheorie : 2 Volumes – Leipzig 1895/98 UB: O 5262-6. English version: Lectures on gas theory. Translated by Stephen G. Brush (1964) Berkeley: University of California Press; (1995) New York: Dover ISBN 0-486-68455-5
- ^ Życzkowski, Karol (2006). Geometry of Quantum States: An Introduction to Quantum Entanglement. Cambridge University Press. p. 301.
- ^ Sharp, Kim; Matschinsky, Franz (2015). «Translation of Ludwig Boltzmann’s Paper «On the Relationship between the Second Fundamental Theorem of the Mechanical Theory of Heat and Probability Calculations Regarding the Conditions for Thermal Equilibrium»«. Entropy. 17: 1971–2009. doi:10.3390/e17041971.
- ^ Jaynes, E. T. (15 May 1957). «Information Theory and Statistical Mechanics». Physical Review. 106 (4): 620–630. Bibcode:1957PhRv..106..620J. doi:10.1103/PhysRev.106.620.
- ^ Landauer, R. (July 1961). «Irreversibility and Heat Generation in the Computing Process». IBM Journal of Research and Development. 5 (3): 183–191. doi:10.1147/rd.53.0183. ISSN 0018-8646.
- ^ Mark Nelson (24 August 2006). «The Hutter Prize». Retrieved 27 November 2008.
- ^ a b «The World’s Technological Capacity to Store, Communicate, and Compute Information», Martin Hilbert and Priscila López (2011), Science, 332(6025); free access to the article through here: martinhilbert.net/WorldInfoCapacity.html
- ^ Spellerberg, Ian F.; Fedor, Peter J. (2003). «A tribute to Claude Shannon (1916–2001) and a plea for more rigorous use of species richness, species diversity and the ‘Shannon–Wiener’ Index». Global Ecology and Biogeography. 12 (3): 177–179. doi:10.1046/j.1466-822X.2003.00015.x. ISSN 1466-8238.
- ^ Massey, James (1994). «Guessing and Entropy» (PDF). Proc. IEEE International Symposium on Information Theory. Retrieved 31 December 2013.
- ^ Malone, David; Sullivan, Wayne (2005). «Guesswork is not a Substitute for Entropy» (PDF). Proceedings of the Information Technology & Telecommunications Conference. Retrieved 31 December 2013.
- ^ Pliam, John (1999). «Selected Areas in Cryptography». International Workshop on Selected Areas in Cryptography. Lecture Notes in Computer Science. Vol. 1758. pp. 62–77. doi:10.1007/3-540-46513-8_5. ISBN 978-3-540-67185-5.
- ^ Aoki, New Approaches to Macroeconomic Modeling.
- ^ Probability and Computing, M. Mitzenmacher and E. Upfal, Cambridge University Press
- ^ Batra, Mridula; Agrawal, Rashmi (2018). Panigrahi, Bijaya Ketan; Hoda, M. N.; Sharma, Vinod; Goel, Shivendra (eds.). «Comparative Analysis of Decision Tree Algorithms». Nature Inspired Computing. Advances in Intelligent Systems and Computing. Singapore: Springer. 652: 31–36. doi:10.1007/978-981-10-6747-1_4. ISBN 978-981-10-6747-1.
- ^ Jaynes, Edwin T. (September 1968). «Prior Probabilities». IEEE Transactions on Systems Science and Cybernetics. 4 (3): 227–241. doi:10.1109/TSSC.1968.300117. ISSN 2168-2887.
- ^ Rubinstein, Reuven Y.; Kroese, Dirk P. (9 March 2013). The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation and Machine Learning. Springer Science & Business Media. ISBN 978-1-4757-4321-0.
This article incorporates material from Shannon’s entropy on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
Further reading[edit]
Textbooks on information theory[edit]
- Cover, T.M., Thomas, J.A. (2006), Elements of Information Theory — 2nd Ed., Wiley-Interscience, ISBN 978-0-471-24195-9
- MacKay, D.J.C. (2003), Information Theory, Inference and Learning Algorithms , Cambridge University Press, ISBN 978-0-521-64298-9
- Arndt, C. (2004), Information Measures: Information and its Description in Science and Engineering, Springer, ISBN 978-3-540-40855-0
- Gray, R. M. (2011), Entropy and Information Theory, Springer.
- Martin, Nathaniel F.G.; England, James W. (2011). Mathematical Theory of Entropy. Cambridge University Press. ISBN 978-0-521-17738-2.
- Shannon, C.E., Weaver, W. (1949) The Mathematical Theory of Communication, Univ of Illinois Press. ISBN 0-252-72548-4
- Stone, J. V. (2014), Chapter 1 of Information Theory: A Tutorial Introduction, University of Sheffield, England. ISBN 978-0956372857.
External links[edit]
- «Entropy», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- «Entropy» at Rosetta Code—repository of implementations of Shannon entropy in different programming languages.
- Entropy an interdisciplinary journal on all aspects of the entropy concept. Open access.

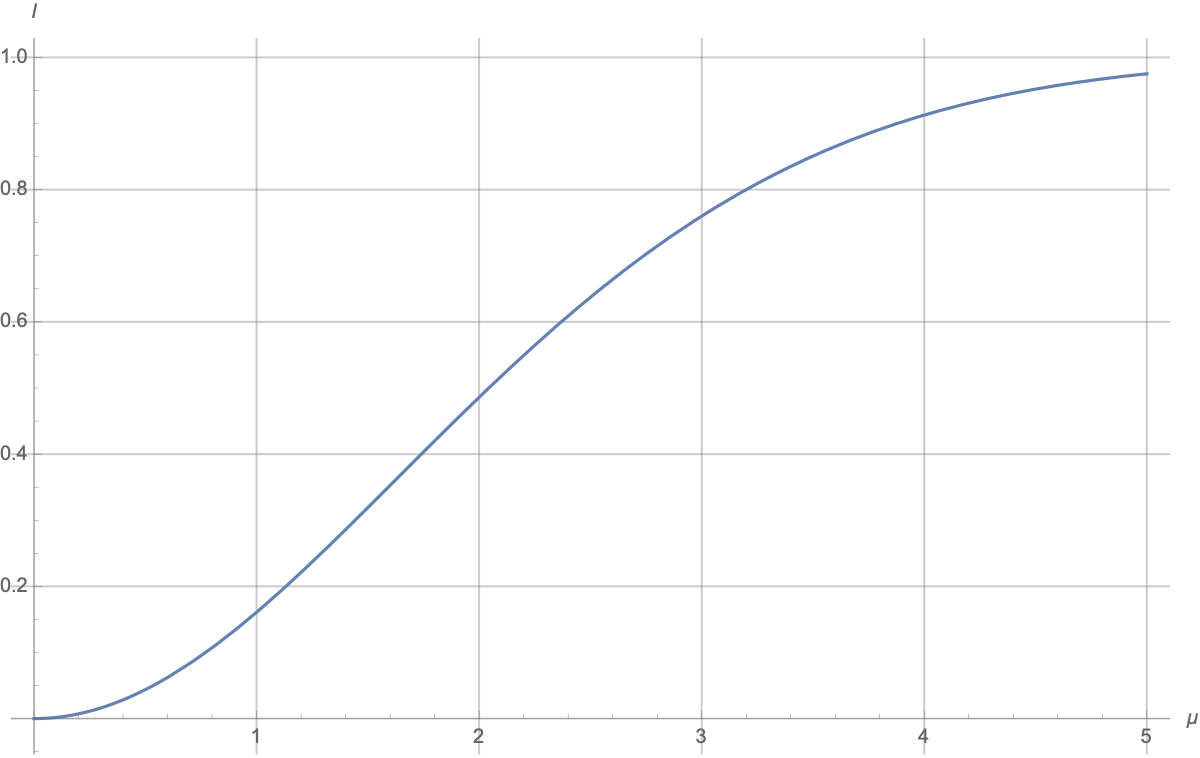

















![{displaystyle mathrm {H} (X):=-sum _{xin {mathcal {X}}}p(x)log p(x)=mathbb {E} [-log p(X)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a9e707eb6c54290db4ee6be05582944e34e30c8)




![{displaystyle mathrm {H} (X)=mathbb {E} [operatorname {I} (X)]=mathbb {E} [-log p(X)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ff47e0ff30877da3b4c93b311fe1cc4b4194a86)

















![{displaystyle pin [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)













![{displaystyle mathrm {H} (X)=mathbb {E} [-log _{b}p(X)]leq -log _{b}left(mathbb {E} [p(X)]right)leq log _{b}n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3adc8a7d3442cf093e15df11d4cb64a3fbd650bd)
















![{displaystyle mathrm {H} (X)=mathbb {E} [-log f(X)]=-int _{mathbb {X} }f(x)log f(x),mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e222b735b621457042c194ed573f7455ffd8393)





![h[f]=lim _{Delta to 0}left(mathrm {H} ^{Delta }+log Delta right)=-int _{-infty }^{infty }f(x)log f(x),dx,](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d522982a9afc1539b88695a28b7aa3ffd2fa2d8)




![mathrm {H} [(X_{1},ldots ,X_{d})]leq {frac {1}{r}}sum _{i=1}^{n}mathrm {H} [(X_{j})_{jin S_{i}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6d219e5f3250e54a77586cd05731ff2ee0db7ee)




