Интегрирование дробно-рациональных выражений
Выражение
вида
называется дробно-рациональной
функцией
или рациональной
дробью,
— многочлен степени m,
— многочлен степени n.
Рациональная дробь называется правильной,
если m
< n,
неправильной
– если
.
Если под интегралом находится неправильная
рациональная дробь, то нужно выделить
целую часть и найти остаток от деления.
Например,
если требуется найти интеграл от дроби
,
которая является неправильной (степень
многочлена в числителе больше степени
многочлена в знаменателе), то нужно
осуществить деление «уголком».
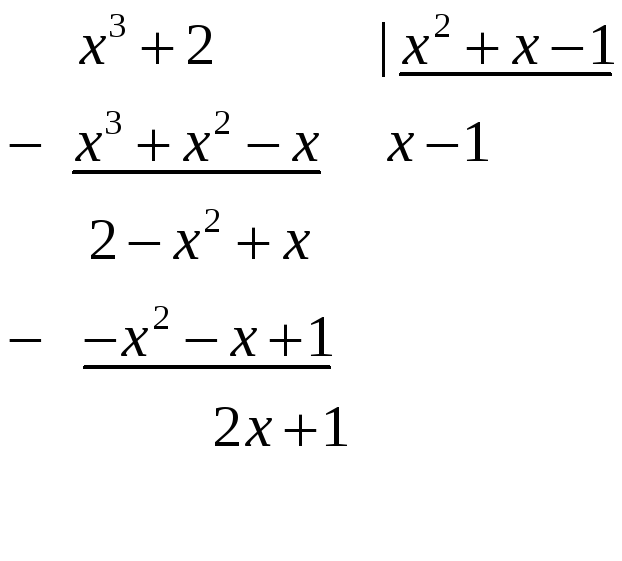
— целая часть,
— остаток от деления.
Дробь
раскладывается следующим образом:
.
В
дальнейшем находят интеграл от целой
и дробной части. Для нахождения интеграла
правильной дроби используется метод
неопределённых коэффициентов.
Метод неопределённых коэффициентов
Рассмотрим
правильную дробь
.
Всякий многочлен
имеет точно n
действительных или комплексно-сопряжённых
корней с учётом их кратности, и при этом
многочлен
может быть представлен в виде сомножителей,
содержащих корни этого многочлена.
Например,
,
где
— действительный корень кратности 1,
— действительный корень кратности 5,
многочлен
имеет два комплексно-сопряжённых корня,
— содержит 2 комплексно-сопряжённых
корня кратности 3.
Всякая правильная
рациональная дробь может быть представлена
в виде суммы четырёх типов простейших
дробей.
1.
2.
,
k
– кратность корня
.
3.
4.
— k
– кратность пары комплексно-сопряжённых
корней.
а)
Если в знаменателе
корень
— корень кратности 1, то ему соответствует
одна простейшая дробь 1-го типа.
б)
Если корень
имеет кратность k,
то ему соответствует сумма дробей 1-го
и 2-го типа до степени k
включительно, т.е.
.
Например,
для дроби
.
в)
Если многочлену
соответствует пара простых
комплексно-сопряжённых корней, то в
разложении
ему соответствует одна дробь 3-го типа.
г)
Если многочлену
соответствуют комплексные корни
кратности k,
то в разложении для
ему соответствует сумма дробей 3-го и
4-го типа до степени k
включительно, т.е.
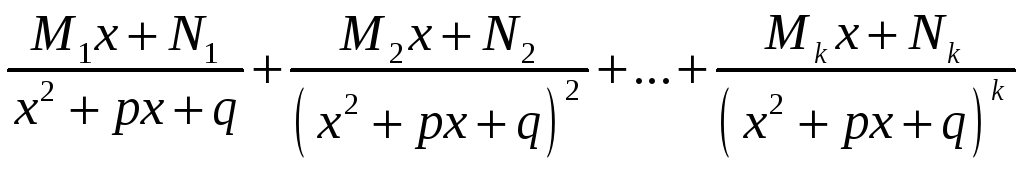
Например, для дроби
Неизвестные
коэффициенты
необходимо определить так, чтобы левая
и правая части равенства (*) были равны
друг другу при любом х.
Определение этих коэффициентов проводится
методом неопределённых коэффициентов.
Правая часть (*)
приводится к общему знаменателю,
знаменатели отбрасываются и приравниваются
числители левой и правой частей (*).
Далее возможны
два пути:
1)
В правой части (*) группируются слагаемые
с одинаковой степенью х,
затем приравниваются коэффициенты при
одинаковых степенях х
в правой и левой части, из полученной
системы линейных алгебраических
уравнений находятся неизвестные
коэффициенты.
2)
В соответствии неизвестных коэффициентов
выбираются значения х
(лучше брать корни) и подставляются в
числители левой и правой части (*); также
получается система уравнений для
нахождения неизвестных коэффициентов.
Часто используются
комбинированно оба способа.
Таким образом,
интегрирование рациональных дробей
сводится к интегрированию четырёх типов
простейших дробей.
Интегрирование
дробей 1-го, 2-го и 3-го типов:
1.
2.
3.
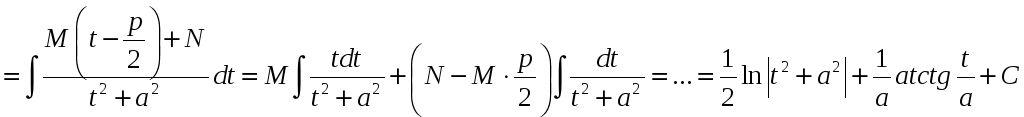
Пример
1.
Решение.
Запишем
рациональную дробь без интеграла:
.
Она является правильной (степень
числителя меньше степени знаменателя).
В знаменателе находится квадратный
трёхчлен, корни которого равны
:
Значит, дробь можно
разложить на сумму двух дробей 1-го типа:
.
Приводим дроби к
общему знаменателю и записываем только
числители:
.
Подставляем
по очереди корни знаменателя вместо х
и решаем
уравнение относительно неопределённых
коэффициентов:
Подставляем
найденные коэффициенты
в разложение первоначального интеграла
и находим интеграл:
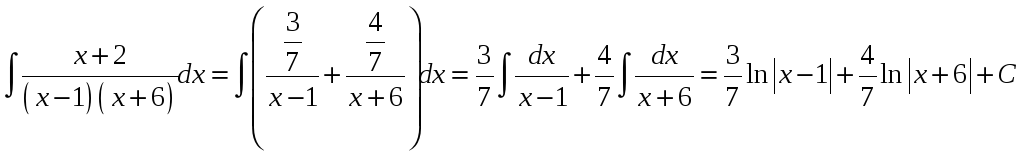
Пример
2.
Решение.
Дробь правильная. Знаменатель имеет
один действительный корень
и два комплексных
,
следовательно, дробь будет раскладываться
на сумму дробей 1-го и 3-го типа:
.
(*)
Подставляем
корень
в полученное равенство (*):
Для
того чтобы найти коэффициенты M
и N,
раскроем скобки в равенстве (*):
.
Вынесем
в правой части этого равенства
и
за скобки:
Таким
образом, коэффициенты в правой части
равенства сгруппированы по степеням
х.
Приравниваем
коэффициенты при соответствующих
степенях х
в левой и правой части равенства:
Коэффициент
А был
найден ранее, подставляем его значение
в систему и находим коэффициенты M
и N:
Подставляем
найденные коэффициенты A,
M,
N
в разложение первоначального интеграла
и находим интеграл:
Пример
3.
Решение.
Дробь неправильная, т.к. степень числителя
(4) больше степени знаменателя (3). Выделим
целую часть с помощью деления уголком:
Запишем отдельно
правильную дробь и её разложение на 3
дроби 1-го типа:
Пример
4.
Решение.
Дробь правильная. Знаменатель имеет
один действительный корень
кратности 1 и 1 действительный корень
кратности 3 (т.к. выражение (х
– 3) имеет степень 3), следовательно,
дробь будет раскладываться на сумму
дробей 1-го и 2-го типа:
.
Коэффициенты
А и
были найдены ранее, подставляем их
значения в систему и находим коэффициенты
и
:
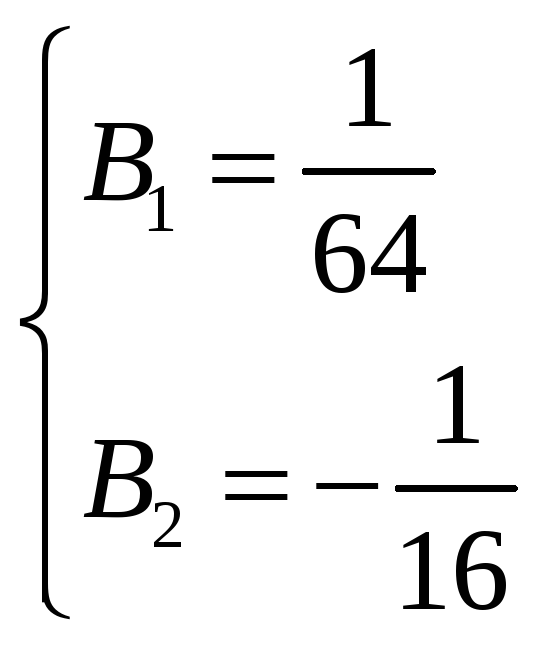
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
И снова здравствуйте, друзья!
Как я и обещал, с этого урока мы начнём бороздить бескрайние просторы поэтического мира интегралов и приступим к решению самых разнообразных (порой, очень красивых) примеров. 
Чтобы грамотно ориентироваться во всём интегральном многообразии и не заблудиться, нам потребуется всего четыре вещи:
1) Таблица интегралов. Все подробности о ней — в предыдущем материале. Как именно с ней работать — в этом.
2) Свойства линейности неопределённого интеграла (интеграл суммы/разности и произведения на константу).
3) Таблица производных и правила дифференцирования.
Да-да, не удивляйтесь! Без умения считать производные, в интегрировании ловить совершенно нечего. Согласитесь, бессмысленно, например, учиться делению, не умея умножать. 
4) Методы интегрирования.
Их очень и очень много. Для конкретного класса функций — свой. Но среди всего их богатого разнообразия выделяется три базовых:
– метод подведения функции под знак дифференциала,
– метод замены переменной,
– метод интегрирования по частям.
О каждом из них — в отдельных уроках.
А теперь, наконец, приступим к решению долгожданных примеров. Чтобы не скакать из раздела в раздел, я продублирую ещё разок весь джентльменский набор, который пригодится для нашей дальнейшей работы. Пусть весь инструментарий будет под рукой.)
Прежде всего, это таблица интегралов:
Кроме того, нам понадобятся базовые свойства неопределённого интеграла (свойства линейности):
Что ж, необходимая снаряга подготовлена. Пора в путь! 
Прямое применение таблицы
В данном параграфе будут рассматриваться самые простые и безобидные примеры. Алгоритм здесь прост до ужаса:
1) Смотрим в таблицу и ищем нужную формулу (формулы);
2) Применяем свойства линейности (где требуется);
3) Осуществляем превращение по табличным формулам и прибавляем в конце константу С (не забываем!);
4) Записываем ответ.
Итак, поехали.)
Пример 1
Такой функции в нашей таблице нет. Зато есть интеграл от степенной функции в общем виде (вторая группа). В нашем случае n = 5. Вот и подставляем пятёрку вместо n и аккуратно считаем результат:
Готово. 
Разумеется, этот пример совсем примитивный. Чисто для знакомства.) Зато умение интегрировать степени позволяет легко считать интегралы от любых многочленов и прочих степенных конструкций.
Пример 2
Под интегралом сумма. Ну и ладно. У нас на этот случай есть свойства линейности. 
Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла! Конечно, после этого приходится её постоянно таскать за собой. А что делать…
Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить.)
Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к монстрам типа:
Многочлены — самые халявные функции в интегралах.) А уж в диффурах, в физике, в сопромате и прочих серьёзных дисциплинах интегрировать многочлены придётся постоянно. Привыкайте.)
Следующий примерчик будет чуть покруче.
Пример 3
Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:
Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.
Замечание: в этом уроке множитель dx в процессе интегрирования пока никак не участвует, и мы на него пока что мысленно «забиваем». 
А пока наш взор обращён на подынтегральную функцию
Не очень похоже на степенную функцию, но это она. 
А икс в степени минус две трети — это уже табличная функция! Вторая группа, n=-2/3. А константа 1/2 нам не помеха. Выносим её наружу, за знак интеграла, и прямо по формуле считаем:
В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:
Заменяем дроби степенями с отрицательными показателями;
Заменяем корни степенями с дробными показателями.
А вот в окончательном ответе переход от степеней обратно к дробям и корням — дело вкуса. Лично я перехожу обратно — так эстетичнее, что ли.
И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт — что в числитель, а что знаменатель.
Что? Надоели уже скучные степенные функции? Ну ладно! Берём быка за рога!
Пример 4
Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго.) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:
Первый интеграл — обычная степенная функция, (2-я группа, n = -1): 1/x = x-1.
Традиционная наша формула для первообразной степенной функции
здесь не работает, но зато у нас для n = -1 есть достойная альтернатива — формула с натуральным логарифмом. Вот эта:
Тогда, согласно этой формуле, первая дробь проинтегрируется так:
А вторая дробь — тоже табличная функция! Узнали? Да! Это седьмая формула с «высоким» логарифмом:
Константа «а» в этой формуле равна двойке: a=2.
Важное замечание: Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно.) Строго говоря, константу надо писать после каждого отдельного интегрирования — хоть промежуточного, хоть окончательного: так уж неопределённый интеграл требует…)
Например, после первого интегрирования я должен был бы написать:
После второго интегрирования:
Но вся фишка в том, что сумма/разность произвольных констант — это тоже некоторая константа! В нашем случае для окончательного ответа нам надо из первого интеграла вычесть второй. Тогда у нас получится разность двух промежуточных констант:
С1-С2
И мы имеем полное право эту самую разность констант заменить одной константой! И просто переобозначить её привычной нам буквой «С». Вот так:
С1-С2 = С
Вот и приписываем эту самую константу С к окончательному результату и получаем ответ:
Да-да, дроби они такие! Многоэтажные логарифмы при их интегрировании — самое обычное дело. Тоже привыкаем.)
Запоминаем:
При промежуточном интегрировании нескольких слагаемых константу С после каждого из них можно не писать. Достаточно включить её в окончательный ответ всего примера. В самом конце.
Следующий пример тоже с дробью. Для разминки.)
Пример 5
В таблице, понятное дело, такой функции нет. Но зато есть похожая функция:
Это самая последняя, восьмая формула. С арктангенсом. 
Вот эта:
И нам сам бог велел подстроить наш интеграл под эту формулу! Но есть одна проблемка: в табличной формуле перед х2 никакого коэффициента нету, а у нас — девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби.)
А новая дробь — уже нужная нам табличная функция под номером 8! Здесь а2=4/9. Или а=2/3.
Всё. Выносим 1/9 за знак интеграла и пользуемся восьмой формулой:
Вот такой ответ. Этот пример, с коэффициентом перед х2, я специально так подобрал. Чтобы ясно было, что делать в таких случаях. 
Например:
Здесь а2 = 5, поэтому само «а» будет «корень из пяти». В общем, вы поняли.)
А теперь немного видоизменим нашу функцию: напишем знаменатель под корнем.) Вот такой интеграл теперь будем брать:
Пример 6
В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования, да.) Опять лезем в таблицу и ищем подходящую. Корни у нас есть в формулах 5-й и 6-й групп. Но в шестой группе под корнями только разность. А у нас — сумма. Значит, работаем по пятой формуле, с «длинным» логарифмом:
Число А у нас — пятёрка. Подставляем в формулу и получаем:
И все дела. Это ответ. Да-да, так просто!)
Если закрадываются сомнения, то всегда можно (и нужно) проверить результат обратным дифференцированием. Проверим? А то вдруг, лажа какая-нибудь?
Дифференцируем (на модуль внимания не обращаем и воспринимаем его как обычные скобки):
Всё честно. 
Кстати, если в подынтегральной функции под корнем поменять знак с плюса на минус, то формула для интегрирования останется той же самой. Не случайно в таблице под корнем стоит плюс/минус. 
Например:
Важно! В случае минуса, на первом месте под корнем должно стоять именно х2, а на втором — число. Если же под корнем всё наоборот, то и соответствующая табличная формула будет уже другая!
Пример 7
Под корнем снова минус, но х2 с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формулка.) Формула номер шесть, с ней мы ещё не работали:
А вот теперь — аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A. Здесь же пятёрка будет выступать уже в роли числа а2!
Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:
И теперь пример решается в одно действие. 
Вот так вот! Всего лишь поменялись местами слагаемые под корнем, а результат интегрирования изменился существенно! Логарифм и арксинус… Так что, пожалуйста, не путайте эти две формулы! Хотя подынтегральные функции и очень похожи…
Бонус:
В табличных формулах 7-8 перед логарифмом и арктангенсом присутствуют коэффициенты 1/(2а) и 1/а соответственно. И в тревожной боевой обстановке при записи этих формул даже закалённые учёбой ботаны частенько путаются, где просто 1/а, а где 1/(2а). Вот вам простой приёмчик для запоминания.
В формуле №7
в знаменателе подынтегральной функции стоит разность квадратов х2 — а2. Которая, согласно боянной школьной формуле, раскладывается как (х-а)(х+а). На два множителя. Ключевое слово — два. И эти две скобки при интегрировании идут в логарифм: с минусом вверх, с плюсом — вниз.) И коэффициент перед логарифмом тоже 1/(2а).
А вот в формуле №8
в знаменателе дроби стоит сумма квадратов. Но сумма квадратов x2+a2 неразложима на более простые множители. Поэтому, как ни крути, в знаменателе так и останется один множитель. И коэффициент перед арктангенсом тоже будет 1/а.
А теперь для разнообразия проинтегрируем что-нибудь из тригонометрии.)
Пример 8
Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же радостно ответ пишет и… приехали. 
Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!
Да, (sin x)’ = cos x и (cos x)’ = —sin x.
Но!
Поскольку производные народ обычно худо-бедно помнит, то, чтобы не путаться в знаках, приём для запоминания интегралов тут очень простой:
Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.
Например, мы ещё со школы знаем, что производная синуса равна косинусу:
(sin x)’ = cos x.
Тогда для интеграла от того же синуса будет справедливо:
И всё.) С косинусом то же самое.
Исправляем теперь наш пример:
Предварительные элементарные преобразования подынтегральной функции
До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)
Конечно, мы делали кое-какие простенькие преобразования — множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)
А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной. 
Применение формул тригонометрии
Продолжим развлекаться с тригонометрией.
Пример 9
Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:
Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:
Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!
Смотрите:
А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать — применять формулу производной сложной функции:
И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.
А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование — более творческий процесс, нежели дифференцирование. Искусство, я бы даже сказал. 
Пример 10
Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно откопать весьма и весьма полезную формулу косинуса двойного угла:
Вот и применяем эту формулу к нашей подынтегральной функции. В роли «альфа» у нас х/2.
Получаем:
Эффект потрясающий, правда?
Эти два примера наглядно показывают, что предварительное преобразование функции перед интегрированием вполне допускается и порой колоссально облегчает жизнь! И в интегрировании эта процедура (преобразование подынтегральной функции) на порядок более оправдана, чем при дифференцировании. В дальнейшем всё увидите.)
Разберём ещё парочку типовых преобразований.
Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.
Обычные банальные школьные преобразования. Но порой только они и спасают, да.)
Пример 11
Если бы мы считали производную, то никаких проблем: формула производной произведения и — вперёд. Но стандартной формулы для интеграла от произведения не существует. И единственный выход здесь — раскрыть все скобки, чтобы под интегралом получился многочлен. А уж многочлен мы как-нибудь проинтегрируем.) Но скобки раскрывать тоже будем с умом: формулы сокращённого умножения — штука мощная!
(x2 — 1)2(x2 + 1)2 = ((x2 — 1)(x2 + 1))2 = ((x2)2 — 12)2 = (x4 — 1)2 = x8 — 2x4 + 1
А теперь считаем:
И все дела.)
Пример 12
Опять же, стандартной формулы для интеграла от дроби не существует. Однако в знаменателе подынтегральной дроби стоит одинокий икс. Это в корне меняет ситуацию.) Поделим почленно числитель на знаменатель, сведя нашу жуткую дробь к безобидной сумме табличных степенных функций:
Особо комментировать процедуру интегрирования степеней не буду: не маленькие уже.)
Интегрируем сумму степенных функций. По табличке.)
Вот и все дела.) Кстати, если бы в знаменателе сидел не икс, а, скажем, х+1, вот так:
то этот фокус с почленным делением уже так просто не прошёл бы. Именно из-за наличия корня в числителе и единицы в знаменателе. Пришлось бы замену вводить и избавляться от корня. Но такие интегралы гораздо сложнее. О них — в других уроках.
Видите! Стоит только чуть-чуть видоизменить функцию — тут же меняется и подход к её интегрированию. Порой кардинально!) Нету чёткой стандартной схемы. К каждой функции — свой подход. Иногда даже уникальный.)
В некоторых случаях преобразования в дробях ещё более хитрые.
Пример 13
А здесь как можно свести интеграл к набору табличных? Здесь можно ловко извернуться добавлением и вычитанием выражения x2 в числителе дроби с последующим почленным делением. Очень искусный приём в интегралах! Смотрите мастер-класс! 
И теперь, если заменить исходную дробь на разность двух дробей, то наш интеграл распадается на два табличных — уже знакомую нам степенную функцию и арктангенс (формула 8):
Ну, что тут можно сказать? Вау!
Этот трюк с добавлением/вычитанием слагаемых в числителе — очень популярен в интегрировании рациональных дробей. Очень! Рекомендую взять на заметку.
Пример 14
Здесь тоже рулит эта же технология. Только добавлять/вычитать надо единичку, чтобы из числителя выделить выражение, стоящее в знаменателе:
Вообще говоря, рациональные дроби (с многочленами в числителе и знаменателе) — отдельная очень обширная тема. Дело всё в том, что рациональные дроби — один из очень немногих классов функций, для которых универсальный способ интегрирования существует. Метод разложения на простейшие дроби вкупе с методом неопределённых коэффициентов. Но способ этот очень трудоёмкий и обычно применяется как тяжёлая артиллерия. Ему будет посвящён не один урок. А пока что тренируемся и набиваем руку на простых функциях.
Подытожим сегодняшний урок.
Сегодня мы подробно рассмотрели, как именно пользоваться таблицей, со всеми нюансами, разобрали множество примеров (и не самых тривиальных) и познакомились с простейшими приёмами сведения интегралов к табличным. И так мы теперь будем поступать всегда. Какая бы страшная функция ни стояла под интегралом, с помощью самых разнообразных преобразований мы будем добиваться того, чтобы, рано или поздно, наш интеграл, так или иначе, свёлся к набору табличных.
Несколько практических советов.
1) Если под интегралом дробь, в числителе которой сумма степеней (корней), а в знаменателе — одинокая степень икса, то используем почленное деление числителя на знаменатель. Заменяем корни степенями с дробными показателями и работаем по формулам 1-2.
2) В тригонометрических конструкциях в первую очередь пробуем базовые формулы тригонометрии — двойного/тройного угла, основные тригонометрические тождества:
Может очень крупно повезти. А может и нет…
3) Где нужно (особенно в многочленах и дробях), применяем формулы сокращённого умножения:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
(a-b)(a+b) = a2-b2
и так далее…
4) При интегрировании дробей с многочленами пробуем искусственно выделить в числителе выражение(я), стоящее(щие) в знаменателе. Очень часто дробь упрощается и интеграл сводится к комбинации табличных.
Ну что, друзья? Я вижу, интегралы вам начинают нравиться. 
Что? Не знаете, как интегрировать арксинус/арккосинус? Да! Мы этого ещё не проходили.) Но здесь их напрямую интегрировать и не нужно. И да поможет вам школьный курс!)
Ответы (в беспорядке):
Для лучших результатов настоятельно рекомендую приобрести сборник задач по матану Г.Н. Бермана. Классная штука!
А у меня на сегодня всё. Успехов!
Интеграл от дроби, все формулы и примеры
Нужно запомнить, что интеграл от дроби не равен интегралу числителя, деленному на интеграл знаменателя:
Для интегрирования подобных выражений существует несколько методов, которые зависят от вида подынтегральной функции.
Первый метод вычисления интеграла от дроби
Подынтегральная функция является отношением двух многочленов и представляет собою неправильную дробь (степень числителя больше или равна степени знаменателя). Тогда нужно выделить целую часть, для этого в числителе либо нужно выделить выражение, стоящее в знаменателе, либо поделить числитель на знаменатель в столбик.
Замечание. Если степень многочлена, стоящего в числителе, большее степени многочлена, стоящего в знаменателе, то рациональнее для выделения целой части делить числитель на знаменатель в столбик.
Второй метод
Для дробей типа
применяется метод замены переменной или заданный интеграл сводится к табличным.
Третий метод вычисления интеграла от дроби
Интегралы вида
находятся с помощью выделения полного квадрата в знаменателе, что позволит свести их к табличным интегралам.
Четвертый метод
Для интегралов вида
применяется следующий подход. В числителе выделяется производная знаменателя, далее дробь почленно делится: получаем сумму двух интегралов, в числителе одного из них стоит производная знаменателя, а второго – константа. Первый из интегралов находится методом замены, метод нахождения второго описан выше.
| Понравился сайт? Расскажи друзьям! | |
ru.solverbook.com
Интегрирование дробей
Рациональной дробью называется дробь P(x)/Q(x), числитель P(x) и знаменатель Q(x) которой – многочлены. Рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе.
У любой неправильной дроби можно выделить её целую часть. Для этого следует по правилу деления многочленов разделить числитель на знаменатель. Поэтому любую неправильную дробь можно представить в виде суммы её целой части и некоторой правильной дроби.
Например, неправильную дробь
можно представить в виде
Таким образом, если необходимо проинтегрировать неправильную дробь, то, представив её в виде суммы многочлена и правильной дроби, с помощью метода разложения сведём решение к интегрированию правильной дроби.
Подготовиться к интегрированию дробей самостоятельно, а затем посмотреть ответ.
Пример 0. Представить в виде суммы многочлена и правильной дроби следующие
дроби:
1) ;
2) .
Посмотреть ответ.
Ограничимся интегрированием лишь правильных рациональных дробей, знаменателями которых являются многочлены первой и второй степени. В общем виде интегралы от таких дробей записываются следующим образом:
(1)
(2)
Пример 1. Найти
интеграл дроби
Подынтегральная функция является неправильной рациональной дробью. Используя приведённое выше её представление в виде суммы многочлена и правильной дроби, а также формулу (3), последовательно получим
Любой интеграл вида (2) сводится к нахождению одного или двух следующих интегралов:
(4)
Поэтому рассмотрим эти интегралы. Первый из них находится по формуле (3) при a = 1.
А теперь формулы для вычисления остальных приведённых интегралов.
(5)
(6)
(7)
(8)
(9)
Формулы (5)-(9) можно условно считать табличными интегралами. С их помощью можно найти любой интеграл вида (2). Предварительно такой интеграл приводят к интегралам группы (4).
Для этого в знаменателе подынтегральной функции выделяют полный квадрат (это делается при помощи формул
сокращённого умножения
и ) и представляют его в одном из следующих видов:
или
где m > 0 и n > 0.
В первых двух случаях замена переменной
в третьем непосредственное применение метода разложения приведёт к одному или двум интегралам группы (4).
Пример 2. Найти интеграл дроби
Решение. Результат применения формулы (5) при a = 8:
Пример 3. Найти интеграл дроби
Решение. Выделим в знаменателе подынтегральной функции полный квадрат:
а затем произведём замену переменной t = x + 3
(тогда dt = dx
). В результате этого:
,
то есть получили табличный интеграл. Применяем формулу 5):
,
откуда, возвращаясь к старой переменной, окончательно получим
.
Пример 4. Найти интеграл дроби
Решение. Выделяя в знаменателе подынтегральной функции полный квадрат, получаем
Произведём теперь замену переменной t = x – 3
(или x = t + 3; тогда dx = dt). Поэтому
Результат применения формул (8) и (5) при a = 1:
Возвращаясь к “старой” переменной, окончательно получим
.
Пример 5. Найти интеграл дроби
Решение. Знаменатель представляет собой полный квадрат разности:
.
Поэтому
.
Применяя далее формулы (7) и (6), найдём
Пример 6. Найти интеграл дроби
.
Решение. Выделим в знаменателе подынтегральной функции полный квадрат:
Произведём замену переменной t = x – 4
(или x = t + 4; тогда dx = dt):
Результат применения форумул (8) и (9):
.
Возвращаясь к “старой” переменной, окончательно получим
.
Начало темы “Интеграл”
Продолжение темы “Интеграл”
function-x.ru
Интегрирование рациональных функций
Рациональная функция – это дробь вида ,
числитель и знаменатель которой – многочлены или произведения многочленов.
Из урока “Интегрирование некоторых
рациональных дробей и иррациональностей” известно, что рациональные дроби
бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в
знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в
знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её
целой части и некоторой правильной дроби.
На этом уроке будем учиться интегрировать такие рациональные функции, которые
представлены в виде правильных дробей
. Для этого существует метод неопределённых коэффициентов, основанный
на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
Приведённый ниже алгоритм интегирования рациональных функций будет пошагово
проиллюстрирован в примерах.
Алгоритм интегрирования рациональных функций
- Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные,
кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить
дробь на простые дроби, в числителях которых – неопределённые коэффициенты, число которых равно степени
знаменателя. - Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется
решить систему уравнений, сводящуюся к системе линейных уравнений. - Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов
полученных простых дробей, к которым применяются табличные интегралы.
Переходим к первому шагу алгоритма
Многочлен в знаменателе имеет действительные корни.
То есть, в знаменателе имеет место цепочка сомножителей вида
, в которой
каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых
коэффициентов будет следующим:
Пример 1. Шаг 1. Дан интеграл от рациональной функции
.
От нас требуется разложить подынтегральное выражение – правильную дробь
на простые дроби.
Решение. Дискриминант уравнения
положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение
исходной дроби на сумму простых дробей:
.
Пример 2. Шаг 1.Дан интеграл от рациональной функции
.
Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала
можно вынести за скобки x. Получаем следующую дробь:
.
Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:
Получаем разложение знаменателя на множители в подынтегральном выражении:
.
Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело
со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби
подынтегрального выражения будет следующим:
.
Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название – метод неопределённых коэффициентов.
Многочлен в знаменателе имеет кратные действительные корни.
Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида
,
то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
Пример 3. Шаг 1. Дан интеграл от рациональной функции
.
Решение. Представляем разность квадратов
в виде произведения суммы и разности .
Тогда подынтегральное выражение запишется в виде
,
все уравнения с многочленами которого имеют действительные корни. Это случай кратных
действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее
разложение исходной дроби на простые дроби:
Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой
и записывать простую дробь с каждой из этих степеней в знаменатель.
Пример 4. Шаг 1. Дан интеграл от рациональной функции
.
Решение. Уравнения с многочленами в знаменателе имеют действительные корни,
а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее
разложение исходной дроби на простые дроби:
.
Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения
, присутствующего в
цепочке сомножителей в знаменателе, меньше нуля.
В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в
числителе нужно записывать линейное выражение с переменной x (это выражение – последнее в следующей записи):
Пример 5. Шаг 1. Дан интеграл от рациональной функции
.
Решение. Уравнение в скобках имеет комплексные корни,
а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее
разложение исходной дроби на простые дроби:
.
Пример 6. Шаг 1. Дан интеграл от рациональной функции
.
Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего
произведения сомножителей:
.
Решение. Уравнение с последним сомножителем имеет комплексные корни,
а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее
разложение исходной дроби на простые дроби:
Многочлен в знаменателе имеет кратные комплексные корни:
дискриминант квадратного уравнения
, присутствующего в
цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше.
В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
То есть в сумме простых дробей число простых дробей с линейным выражением
в числителе должно быть равно степени сомножителя, имеющего комплексные корни.
Пример 7. Шаг 1. Дан интеграл от рациональной функции
.
Решение. Квадратный трёхчлен имеет
комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
.
Пример 8. Шаг 1. Дан интеграл от рациональной функции
.
Решение. Квадратный трёхчлен в знаменателе имеет
комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
.
На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными
коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю.
После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет
в данной отдельной дроби, но которые есть в других полученных дробях.
Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем
составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся
неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются
методом подстановки и методом сложения.
Пример 1. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Умножаем неопределённые коэффициенты на многочлены, которых нет
в данной отдельной дроби, но которые есть в других полученных дробях:
.
Раскрываем скобки и приравниваем полученое к полученному выражению числитель
исходной подынтегральной дроби:
.
В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и
составляем из них систему уравнений:
.
Сокращаем все иксы и получаем эквивалентную систему уравнений:
.
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 2. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю
выражения, полученного после приведения суммы дробей к общему знаменателю:
Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:
Решаем полученную систему:
Итак, , отсюда
получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 3. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю
выражения, полученного после приведения суммы дробей к общему знаменателю:
Как и в предыдущих примерах составляем систему уравнений:
Сокращаем иксы и получаем эквивалентную систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 4. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби
на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров.
Поэтому лишь для контроля приведём получившуюся систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
Пример 5. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель
этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 6. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
Производим с этой суммой те же действия, что и в предыдущих примерах.
В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 7. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
После известных действий с полученной суммой должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 8. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Внесём некоторые изменения в уже доведённые до автоматизма действия для получения
системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних
вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения
к числителю исходной дроби, получаем:
Можно заметить, что если принять за значение икса единицу, то второе и третье
слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем,
что .
Далее по уже отработанной схеме получаем систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Полученные простые дроби и интегировать проще. К исходной сумме дробей применяется
правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы.
Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу.
Пример 1. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный
интеграл, приводящий к натуральному логарифму:
Последнее действие с натуральным логарифмом – приведение к единому выражению под
логарифмом – может требоваться при выполнении работ,
но требуется не всегда.
Пример 2. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
Вновь применяем табличный интеграл, приводящий к натуральному логарифму:
Пример 3. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби,
на случай, если требуется преобразование к единому логарифму, делаем и это:
Пример 4. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
В результате интегрирования получаем сумму натуральных логарифмов и одной дроби,
на случай, если требуется преобразование к единому логарифму, делаем и это:
Пример 5. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
Интегрируем и получаем сумму натурального логарифма и арктангенса:
Пример 6. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
Опять получаем сумму натурального логарифма и арктангенса:
Пример 7. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
Интегрируя, получаем натуральные логарифмы и дробь:
Приведение к единому логарифму попробуйте выполнить самостоятельно.
Пример 8. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
.
Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби:
Начало темы “Интеграл”
Продолжение темы “Интеграл”
function-x.ru
Примеры интегрирования рациональных функций (дробей)
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .
Пример 1
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3) меньше степени многочлена числителя (4). Поэтому, вначале необходимо выделить целую часть дроби.
1. Выделим целую часть дроби. Делим x4 на x 3 – 6x 2 + 11x – 6:
Отсюда
.
2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим на x – 1:
Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
3. Разложим дробь на простейшие.
.
Итак, мы нашли:
.
Интегрируем.
Ответ
.
Пример 2
Вычислить интеграл:
.
Решение
Здесь в числителе дроби – многочлен нулевой степени (1 = x 0). В знаменателе – многочлен третьей степени. Поскольку 0 < 3, то дробь правильная. Разложим ее на простейшие дроби.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x). То есть целый корень может быть одним из чисел:
1, 3, –1, –3.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим x 3 + 2x – 3 на x – 1:
Итак,
.
Решаем квадратное уравнение:
x 2 + x + 3 = 0.
Находим дискриминант: D = 1 2 – 4·3 = –11. Поскольку D < 0, то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x – 1)(x 2 + x + 3):
(2.1) .
Подставим x = 1. Тогда x – 1 = 0,
.
Подставим в (2.1) x = 0:
1 = 3A – C;
.
Приравняем в (2.1) коэффициенты при x 2:
;
0 = A + B;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
;
;
.
Вычисляем I2.
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0. Поэтому знак модуля можно опустить.
Поставляем в (2.2):
.
Ответ
.
Пример 3
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли один корень x = –1. Делим на x – (–1) = x + 1:
Итак,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли еще один корень x = –1. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2(x 2 + 2):
(3.1) .
Подставим x = –1. Тогда x + 1 = 0,
.
Продифференцируем (3.1):
;
.
Подставим x = –1 и учтем, что x + 1 = 0:
;
; .
Подставим в (3.1) x = 0:
0 = 2A + 2B + D;
.
Приравняем в (3.1) коэффициенты при x 3:
;
1 = B + C;
.
Итак, мы нашли разложение на простейшие дроби:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: 10-05-2015
1cov-edu.ru
Правила интегрирования | Математика
Основные правила интегрирования и таблица интегралов на начальном этапе изучения темы — полезные подсказки, которые удобно всегда иметь перед собой.
Основные правила интегрирования
Постоянный множитель выносится за знак интеграла.
Интеграл от суммы равен сумме интегралов от слагаемых.
В частности,
где k и b — числа.
Таблица неопределенных интегралов
adminНеопределенный интеграл
www.matematika.uznateshe.ru
Интегрирование дифференциального бинома
Применяемые подстановки
Рассмотрим интеграл:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Подынтегральное выражение называется дифференциальным биномом. Интеграл от него сводится к интегралам от рациональных функций в трех случаях.
1) Если p – целое, то выполняется подстановка x = t N, где N – общий знаменатель дробей m и n.
2) Если – целое, то подстановка a x n + b = t M, где M – знаменатель числа p.
3) Если – целое, подстановка a + b x – n = t M, где M – знаменатель числа p.
Если ни одно из трех чисел не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.
Формулы приведения (понижения или повышения показателей степеней)
В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям показателей степеней m и p. Это можно сделать с помощью формул приведения:
;
.
Доказательство формул приведения
Доказательство первой формулы
Докажем первую формулу:
Выполняем преобразования.
Интегрируем по частям, умножив на na(p+1).
u = xm–n+1, v = (axn + b) p+1, du = (xm–n+1)′ dx = (m–n+1) xm–n dx.
Преобразуем оставшийся интеграл.
Подставляем.
Отсюда
Или
.
Доказательство второй формулы
Докажем вторую формулу:
.
Выполняем преобразования.
Интегрируем по частям, умножив на m + 1.
u = (axn + b)p, v = xm+1,
Преобразуем оставшийся интеграл.
Подставляем.
Отсюда
.
Пример
Вычислить интеграл.
Решение
Преобразуем.
Это интеграл от дифференциального бинома
со значениями m = 1/3, p = 1/3, n = 2, a = – 1, b = 1.
Поскольку
– целое, то интеграл сводится к интегралу от рациональной функции третьей подстановкой:
– 1 + x – 2 = t3.
Возьмем дифференциал от обеих частей этого равенства.
Подставляем
Разложим дробь на простейшие.
Выделим в числителе второй дроби производную знаменателя и преобразуем знаменатель.
(t2 – t + 1)′ = 2t – 1
Подставляем
Интегрируем
Окончательно имеем
Ответ
где .
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: 05-12-2014
1cov-edu.ru
Интеграл от дроби
Нужно запомнить, что интеграл от дроби не равен интегралу числителя, деленному на интеграл знаменателя:
Для интегрирования подобных выражений существует несколько методов, которые зависят от вида подынтегральной функции.
Первый метод вычисления интеграла от дроби
Подынтегральная функция является отношением двух многочленов и представляет собою неправильную дробь (степень числителя больше или равна степени знаменателя). Тогда нужно выделить целую часть, для этого в числителе либо нужно выделить выражение, стоящее в знаменателе, либо поделить числитель на знаменатель в столбик.
Замечание. Если степень многочлена, стоящего в числителе, большее степени многочлена, стоящего в знаменателе, то рациональнее для выделения целой части делить числитель на знаменатель в столбик.
Второй метод
Для дробей типа
применяется метод замены переменной или заданный интеграл сводится к табличным.
Третий метод вычисления интеграла от дроби
Интегралы вида
находятся с помощью выделения полного квадрата в знаменателе, что позволит свести их к табличным интегралам.
Четвертый метод
Для интегралов вида
применяется следующий подход. В числителе выделяется производная знаменателя, далее дробь почленно делится: получаем сумму двух интегралов, в числителе одного из них стоит производная знаменателя, а второго – константа. Первый из интегралов находится методом замены, метод нахождения второго описан выше.
| Понравился сайт? Расскажи друзьям! | |
Содержание этой главы предполагает, что читатель знаком с основными результатами теории рациональных функций и знаком с методам разложения рациональной функции на простые дроби. Более подробно об этом можно прочитать в Дополнении.
Интегрирование многочленов[править]
Многочленом, или полиномом, от одной переменной 
(6.1)
где 

Вычисление интеграла от многочлена 
(6.2)
-
Пример 6.1. Найти интеграл
(6.3)
Решение. Используя свойства линейности интеграла, получим:
(6.4)
Пример 6.2. Найти интеграл
(6.5)
Решение. Раскроем скобки в подынтегральном выражении:
(6.6)
Теперь беря интегралы от каждого слагаемого, получим:
(6.7)
Пример 6.3. Найти интеграл
(6.8)
Решение. Здесь можно было поступить также, как и в примере 6.2, но проще сделать замену 



(6.9)
Разобьём на два интеграла и проинтегрируем каждое слагаемое:
(6.10)
Возвращаясь к переменной 
(6.11)
Интегрирование рациональных функций[править]
Вводные замечания[править]
Рациональной функцией от переменной 
(6.12)
где предполагается, что 




Из теории рациональных функций известно, что если 


(6.13)
Далее, известно, что любой полином с комплексными коэффициентами на множестве комплексных чисел может быть представлен в виде произведения неприводимых многочленов:
(6.14)
где 





Поэтому в случае, если 

(6.15)
-
-
где 
В данном учебнике нас больше интересуют многочлены с действительными коэффициентами и действительными корнями. На множестве 
(6.16)
где 


Если рассматривать разложение дроби на простейшие на 
(6.17)
-
-
-
где все коэффициенты 
Рассмотрим пример на разложение дроби.
Пример 6.4 Разложить на простые дроби:
(6.18)
Решение. Как мы видим, степень числителя превосходит степень знаменателя, значит у дроби можно выделить целую часть, а затем получившуюся правильную дробь можно разложить на простые дроби. Но мы воспользуемся методом неопределённых коэффициентов и сразу получим интересующее нас разложение. Решая уравнение четвёртой степени методом подбора (можно воспользоваться методом Феррари), найдём корни знаменателя и разложим многочлен на неприводимые множители:
(6.19)
следовательно дробь (6.18) согласно (6.13) и (6.17) можно представить в виде:
(6.20)
Приводя к общему знаменателю и приравнивая коэффициенты при равных степенях, получим следующую систему относительно неизвестных коэффициентов 
(6.21)
Решая систему линейных уравнений, найдём:
(6.22)
Подставим найденные коэффициенты в формулу (6.20):
(6.23)
Пример 6.5 Разложить на простые дроби:
(6.24)
Решение. Случай, когда 



Найдём корни уравнения 
![{displaystyle x={sqrt[{n}]{-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f33933243642c11fc04200275d0c4b83c47799f5)
(6.25)
где 

На множестве действительных чисел у многочлена с действительными коэффициентами помимо комплексного корня 


(6.26)
(доказательство этого факта см. в Дополнении).
Если воспользоваться основным тригонометрическим тождеством, получим, что
(6.27)
Известно, что у многочлена нечётной степени с действительными коэффициентами имеется по крайней мере один действительный корень (в данном случае 
(6.28)
Значит выражение (6.24) имеет следующее разложение на простые дроби:
(6.29)
где
Теперь останется только методом неопределённых коэффициентов найти 


Например, для 
(6.30)
После необходимых преобразований и решения системы относительно неизвестных коэффициентов будем иметь следующее разложение:
(6.31)
Для 
(6.32)
или после соответствующих манипуляций:
(6.33)
Иногда при взятии интеграла от рациональной функции, нет нужды разбивать её на простейшие дроби, это, например, происходит, если числитель является производной знаменателя (или основания степенного выражения, стоящего в знаменателе) или если возможно сокращение числителя или знаменателя дроби.
Пример 6.6 Найти интеграл
(6.34)
Решение. Замечая, что числитель представляет собой производную основания степенного выражения, стоящего в знаменателе (только производная умножена на 
(6.35)
-
Пример 6.7 Найти интеграл
(6.36)
Решение. Можно заметить, что числитель представляет собой куб разности:
(6.37)
Сократим дробь:
(6.38)
Теперь вычислить интеграл не составит труда:
(6.39)
Интегрирование простых дробей[править]
Как мы видели из предыдущего пункта, интегрирование рациональной функции сводится к интегрированию суммы простых дробей вида:
и
(6.40)
а в случае неправильной дроби ещё и к интегрированию многочлена (см. пункт «Интегрирование многочленов» этой главы).
Возьмём интеграл от дроби первого типа:
(6.41)
Исследуем интегралы от дробей второго типа. Сначала рассмотрим следующий интеграл:
(6.42)
где 

Постоянную 
(6.43)
где 
Выделим в квадратном трёхчлена полный квадрат:
(6.44)
Исследуем выражение в зависимости от знака 


(6.45)
или возвращаясь к 
(6.46)
Допустим теперь, что 

(6.47)
-
Если же 
(6.48)
Подведём итог:
(6.49)
Хочется отметить, что в случае 
Пример 6.8. Решить интеграл
(6.50)
Решение. Выделим в знаменателе полный квадрат:
(6.51)
Теперь можно взять интеграл:
(6.52)
Рассмотрим теперь интеграл вида:
(6.53)
где 
Как и в случае интеграла (6.42) выделим в знаменателе полный квадрат:
(6.53)
-
Будем считать, что 


(6.54)
В примере 5.9 нами уже была получена рекуррентная формула для нахождения интеграла в зависимости от 
(6.55)
В первом слагаемом после сокращения на 

(6.56)
-
Здесь мы снова пришли к интересующему нас интегралу, но в меньшей степени. Подставим найденные выражения в (6.55):
(6.57)
Приведём подобные:
(6.58)
Вернёмся снова к переменной 

(6.59)
-
Проведя упрощения, окончательно получим:
(6.60)
Сейчас приступим непосредственно к рассмотрению интегралов вида:
(6.61)
где знаменатель не приводим на 
Как и прежде дополним квадратный трёхчлен в знаменателе до полного квадрата:
(6.62)
Сделаем подстановку 


(6.63)
Разобьём сумму на два интеграла:
(6.64)
Вычислим первый интеграл:
(6.65)
Второй интеграл табличный:
(6.66)
Подставляя два последних выражения в (6.64) и возвращаясь к переменной 


(6.67)
Рассмотрим интеграл вида:
(6.68)
где 
Дополняя до полного квадрата и применяя подстановку 
(6.69)
Для первого интеграла получаем:
(6.70)
Ко второму интегралу можно применить формулу приведения (6.58):
(6.71)
После соответствующих подстановок и преобразований окончательно получим следующую формулу:
(6.72)
Пример 6.9. Решить интеграл
(6.73)
Решение. Выделим в знаменателе полный квадрат:
(6.74)
Применим подстановку 
(6.75)
Вычислим интеграл в первом слагаемом:
(6.76)
Для нахождения интеграла во втором слагаемом преобразуем его:
(6.77)
-
Первый интеграл в сумме является табличным:
(6.78)
Ко второму слагаемому применим интегрирование по частям:
(6.79)
-
Подставим найденные интегралы в (6.75):
(6.80)
-
Вернёмся к исходной переменной:
(6.81)
-
Как мы видели, при интегрировании дробей 
Итак, преобразуем интеграл (6.68):
(6.82)
-
Интегралом первого слагаемого в зависимости от показателя 


Пример 6.10. Решить интеграл
(6.83)
Решение. Преобразуем интеграл к виду (6.82):
(6.84)
Теперь найти интеграл от первого слагаемого не составит труда:
(6.85)
Во втором слагаемом выделим полный квадрат:
(6.86)
-
В итоге имеем следующий ответ:
(6.87)
Метод Остроградского[править]
Как мы видели из предыдущих пунктов, результатом интегрирования любой рациональной функции может быть другая рациональная функция, логарифм или арктангенс, то есть может представлять собой линейную комбинацию алгебраической и трансцендентной функций. При этом из рассмотрения методов интегрирования простых дробей можно сделать вывод, что одни трансцендентные функции (логарифм и арктангенс) появляются только в том случае, когда знаменатель дроби имеет только простые нули, в противном случае, при наличие кратных нулей появляется ещё и алгебраическая часть.
Так как по теореме Абеля — Руффини уравнение со степенью, выше четвёртой, не разрешимо в радикалах, то разложение знаменателя на неприводимые множители сопряжено со значительными трудностями. Если все коэффициенты многочлена, стоящего в знаменатели дроби, целые[1], то существуют алгоритмы нахождения корней методом перебора делителей старшего и свободного члена. Этот процесс трудоёмкий, особенно если делителей очень много. Позднее появился так называемый полиномиальный LLL-алгоритм (алгоритм Ленстры — Ленстры — Ловаса).
Из-за вычислительных трудностей хотелось бы иметь некий метод, позволяющий сразу получить разбиение исходной дроби на алгебраическую часть и трансцендентную без нахождения нулей знаменателя. Таким метод стал метод, предложенный М. В. Остроградским. В 1844 году он доказал следующую теорему.
Теорема 6.1. Если 



(6.88)
где 


и
— многочлены с неопределёнными коэффициентами (
).
Доказательство теоремы 6.1
Как уже известно, любой многочлен на 
(6.89)
где 


(
) — неприводимый на множестве действительных чисел квадратный трёхчлен. Он представляет собой произведение двух комплексно сопряжённых корней многочлена
кратности
(
);
В разложении 


(6.90)
а каждой паре комплексно сопряжённых корней (соответственно, неприводимому квадратному трёхчлену) — слагаемые:
(6.91)
где все 
При интегрировании от первых слагаемых в (6.90) и (6.91) согласно (6.41) (случай 

Объединим рациональные части интегралов от (6.90) и (6.91), в результате получим правильную рациональную дробь 

(6.92)
является многочленом степени 

Как уже сказано выше, трансцендентную часть интеграла от дроби 
и
,(6.93)
где 
Приведя эту сумму к общему знаменателю, получим правильную рациональную дробь 

(6.94)
где 
Из (6.92) и (6.94) следует, что
(6.95)
Таким образом мы доказали верность формулы (6.88).
Теперь покажем, что для нахождения 







Итак, мы установили, что имеет место тождество (6.88). Многочлен 






(6.96)
Применим формулу производной от частного:
(6.97)
Разобьём дробь в правой части:
(6.98)
Домножим обе части равенства (6.98) на многочлен 
(6.99)
Так как в первом слагаемом отношение 




(6.100)
Продифференцируем теперь равенство (6.95):
(6.101)
Выразим из (6.101) 
(6.102)
Снова разобьём на две дроби:
(6.103)
Дробь 



Обобщая исследование правой части (6.99), можно записать следующее выражение:
(6.104)
где
(6.105)
многочлен степени 
Теперь, воспользовавшись методом неопределённых коэффициентов, можно получить выражения для 


Рассмотрим пример на применение метода Остроградского.
Пример 6.11. Найти интеграл:
(6.106)
Решение. Для нахождения этого интеграла воспользуемся методом Остроградского. Здесь мы имеем 

(6.107)
Теперь найдём НОД 











(6.108)
является кубическим многочленом. Значит в трансцендентную часть входят логарифмы и арктангенс.
Поделив 

(6.109)
Таким образом, мы имеем всё, что нужно для определения коэффициентов у 


Итак, согласно (6.88) мы имеем[4]:
(6.110)
В свою очереди интеграл от трансцендентной части можно разбить на простые дроби с неизвестными коэффициентами:
(6.111)
Продифференцируем равенство (6.111):
(6.112)
-
-
Теперь умножим на 
(6.112)
Решая это систему линейных уравнений, найдём:
(6.113)
Подставляя эти значения в (6.111), будем иметь:
(6.114)
-
Теперь можно взять интегралы в правой части известными методами:
(6.115)
-
Окончательно получим[5]:
(6.116)
-
Метод Эрмита[править]
Приведём теперь описание ещё одного метода выделения алгебраической части интеграла от правильной рациональной дроби. Этот метод был предложен Ш. Эрмитом (1822—1901).
Пусть 



Вновь рассмотрим представление вещественного многочлена в виде произведения линейных полиномов:
(6.117)
где 
Если перегруппировать в представлении (6.117) сомножители, то это выражение можно переписать так:
(6.118)
где 



Значит дробь 
(6.119)
где многочлены 


Докажем это.
Доказательство формулы (6.119)
Многочлены 

(6.120)
где 


Теперь поделим на 
(6.121)
-
Многочлен 







Применяя те же рассуждения к 

Из разложения (6.119) следует, что нам нужно научиться выделять рациональную часть у интегралов вида:
(6.122)
где степень 





Применим снова соотношение Безу к 

[7](6.123)
и подставим его в (6.122):
(6.124)
Проинтегрируем по частям для второе слагаемое, положив 
![{displaystyle dv={frac {V'(x)}{[V(x)]^{k}}},dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2a917aa86f18c143a8ab942dc0b1564277823b1)

![{displaystyle v=int {frac {V'(x)}{[V(x)]^{k}}},dx={frac {d[V(x)]}{[V(x)]^{k}}}=-{frac {1}{(k-1)[V(x)]^{k-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db9cf69ffa8878b88885e7b5bad18d7bb68ea391)
(6.125)
Объединяя первое и третье слагаемое в один интеграл, получим:
(6.126)
где 
Если 
![{displaystyle int {frac {T(x)}{[V(x)]^{k-1}}},dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/617028174064065e98c301f80e2323663a45aeeb)
(6.127)
где 



Рассмотрим теперь пример.
Пример 6.12. Найти интеграл:
(6.128)
Решение. В соответствии с методом Эрмита представим знаменатель дроби в виде:
(6.129)
где 
Значит, подынтегральное выражение можно разбить на две дроби:
(6.130)
Методом неопределённых коэффициентов найдём:
(6.131)
Итак, исходный интеграл можно представить в виде суммы двух:
(6.132)
-
Первое слагаемое легко интегрируется:
(6.133)
Для второго интеграла будем использовать метод Эрмита. Найдём производную многочлена 
(6.134)
Подберём два таких многочлена, чтобы выполнялось соотношение Безу (6.123):
(6.135)
Так как степень многочлена, стоящего справа выше стоящего слева, то для определения неизвестных коэффициентов мы получаем переопределённую систему линейных уравнений, чтобы это исправить разделим многочлен 


(6.136)
Рассмотрим теперь новое соотношение:
(6.137)
где 
Таким образом, мы пришли к линейной системе, где количество неизвестных равно количеству уравнений, относительно этих неизвестных.
Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях, получим следующую систему линейных уравнений:
(6.138)
Решением системы будут следующие коэффициенты:
(6.139)
Теперь нужно вернуться к выражению (6.135). Для этого сделаем замену 
(6.140)
Итак, по методу Эрмита второй интеграл в правой части выражения (6.132) можно разбить на два интеграла следующим образом:
(6.141)
-
Разбивая интеграл в первом слагаемом на части получим:
(6.142)
Беря интегралы, получаем:
(6.143)
Ко второму слагаемому в (6.141) применим интегрирование по частям:
(6.144)
-
Второе слагаемое можно разбить на простые дроби:
(6.145)
Вычислим интегралы:
(6.146)
Чтобы получить окончательный ответ, сложим результаты интегрирования отдельных слагаемых тем, самым получая:
(6.147)
-
Приведя подобные, получим окончательный ответ:
(6.148)
-
Интегрирование рациональных дробей специального вида[править]
Рациональные дроби специального вида можно интегрировать, применяя методы, основанные на специфичности данного интеграла. Рассмотри некоторые из них.
Интегрирование дробей вида:
(6.149)
где 
(6.150)
где 


Очень часто при интегрировании таких выражений появляются члены вида 

Пример 6.12. Найти интеграл
(6.151)
Решение. Произведя почленное деление под знаком интеграла, получим:
(6.152)
-
Интегралы вида:
(6.153)
где 

сводятся к предыдущему случаю с использованием подстановки 

(6.154)
Этим интеграл преобразуется к интегралу (6.149).
Пример 6.13. Найти интеграл
(6.155)
Решение. Сделаем замену 


(6.156)
-
Вернувшись обратно к переменной 
(6.157)
Пример 6.14. Найти интеграл
(6.158)
Решение. Применим интегрирование по частям:
(6.159)
-
Подынтегральное выражение второго слагаемого разобьём на простые дроби. Так как 
(6.160)
Методом неопределённых коэффициентов устанавливаем, что
(6.161)
Таким образом, интеграл (6.158) можно представить как:
(6.162)
После взятия интегралов ответом будет служить следующее выражение:
(6.163)
Интегралы
(6.164)
где 

интегрируются следующим образом: сделаем подстановку 
![{displaystyle x={sqrt[{n}]{z}},;dx={frac {dz}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca31532d4ebfaa0b0f6db06cc4b2e18bd33c1af7)
(6.165)
Если сделать подстановку 

(6.166)
Пример 6.15. Найти интеграл
(6.167)
Решение. Вынесем в числителе 
(6.168)
Сделаем подстановку 
(6.169)
Сделаем ещё одну подстановку: 
(6.170)
Раскрывая скобки в числителе и приводя подобные, получим:
(6.171)
Почленно поделим:
(6.172)
Вернёмся сначала к переменной 
(6.173)
Окончательно получим:
(6.174)
где 
Исследуем интеграл вида:
(6.175)
где 
Если 
(6.176)
который берётся заведением под дифференциал.
Случай, когда 

(6.177)
Вычислим следующий интеграл:
(6.178)
Сделаем подстановку 
(6.179)
Интеграл (6.178) примет вид:
(6.180)
Если 
Описанным выше способом можно брать интегралы вида
(6.181)
где 
В этом случае квадратный трёхчлен обладает двумя различными вещественными корнями 



(6.182)
Формула, в принципе действительна и при 

Остановимся на интегралах вида
(6.183)
более подробно.
Вводя подстановку ![{displaystyle x=z{sqrt[{n}]{frac {b}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/631b861e4e2b3376f7233898aa03cc9c444397a3)
(6.184)
Рассмотрим несколько случаев значений показателей 

В знаменателе стоит знак «плюс».
Случай 1. 



(6.185)
где 
Следовательно, разложение имеет следующий вид:
(6.186)
где 
Так как все корни (6.185) простые, то для нахождения коэффициентов 

(6.187)
где все 

Конкретно для нашего случая:
(6.188)
По формуле Муавра имеем:
(6.189)
Раскрывая скобки в аргументах тригонометрических функций и вычисляя их, получим:
(6.190)
Аналогично для 
(6.191)
Таким образом,
(6.192)
-
После несложных преобразований будем иметь следующее выражение:
(6.193)
В этом интеграле 


(6.194)
-
Случай 2. 

(6.195)
Выполняя аналогичные преобразования, для коэффициентов 

(6.196)
Значит интеграл от дроби 
(6.197)
-
-
-
-
-
Теперь, если воспользоваться формулой (6.67), окончательно получим:
(6.198)
-
Как мы видим, формула (6.198) пригодна для 
Случай 3. 


(6.199)
Разложение подынтегральной функции на простые дроби в этом случае будет:
(6.200)
где 
Найдём коэффициенты:
(6.201)
Подставляя коэффициенты в (6.200) и интегрируя получившиеся дроби, получаем для нечётного 
(6.202)
-
Случай 4. 

(6.203)
-
Формулу (6.203) можно обобщить для 
Теперь рассмотрим выражения (6.184), когда в знаменателе стоит знак «минус».
Случай 5. 


(6.204)
Разложение дроби 
(6.205)
где 
(6.206)
-
Случай 6. 




(6.207)
-
Фактически во всех этих случаях можно считать, что 

(6.208)
Рассмотрим теперь интегралы вида:
(6.209)
где 
Уже известная подстановка ![{displaystyle x=z{sqrt[{n}]{frac {b}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/631b861e4e2b3376f7233898aa03cc9c444397a3)
(6.210)
Если 
(6.211)
Чтобы его вычислить, преобразуем его следующим образом:
(6.212)
Оба интеграла нам известны: первый — табличный, а второй мы можем найти по формуле (6.208):
(6.213)
Если 
(6.214)
Интеграл в первом слагаемом равен:
(6.215)
Значит
(6.216)
Если 


Приступим теперь исследованию интегралов более общего вида, чем (6.183):
(6.217)
где 


Интеграл (6.217) является частным случаем, так называемого, биномиального дифференциала (см. соответствующую главу). Этот интеграл обычно берётся интегрированием по частям, выбирая функции 


Если в выражении (6.217) 
(6.218)
Если 




(6.219)
Повторяя эту процедуру для интеграла в правой части, в конечном итоге мы придём к интегралу вида:
(6.220)
который в зависимости от знака показателя 

Если 
(6.221)
где 








В первом случае мы можем применить следующее преобразование:
(6.222)
во втором:
(6.223)
Так как, по условию, мы подбирали 







Пример 6.16. Найти интеграл:
(6.224)
Решение. Здесь мы имеем интеграл (6.217) при 
(6.225)
Для интеграла в правой части имеем 



(6.226)
Сократим в первом интеграле на 

(6.227)
Второй интеграл берётся заведением под дифференциал:
(6.228)
Объединяя найденные интегралы, получим ответ:
(6.229)
Примечания[править]
- ↑ Коэффициенты могут быть и рациональными, суть от этого не меняется, так как всегда можно домножить многочлен на некую постоянную величину, чтобы сделать его коэффициенты целочисленными.
- ↑ Не нарушая общности, можно считать, что коэффициент при старшей степени равен 1, потому что на него всегда можно поделить и учесть уже при интегрировании.
- ↑ Такая степень получается из того, что
имеет степень
; отношение
— степень
. Производная
также имеет степень
.
- ↑ Постоянный множитель
мы сделали частью неопределённых коэффициентов.
- ↑ Можно ещё объединить все логарифмы в один.
- ↑ По теореме о корнях производной многочлена производная
должна содержать те же корни, что и
, но меньшей кратности, а так как все корни
просты, то
и
вообще не будут содержать общих корней.
- ↑ Многочлены
и
имеют степень на единицу меньше, чем
и
соответственно, если степень многочлена
не превосходит суммарной степени
и
; в противном случае, эти степени могут быть равны или быть больше.

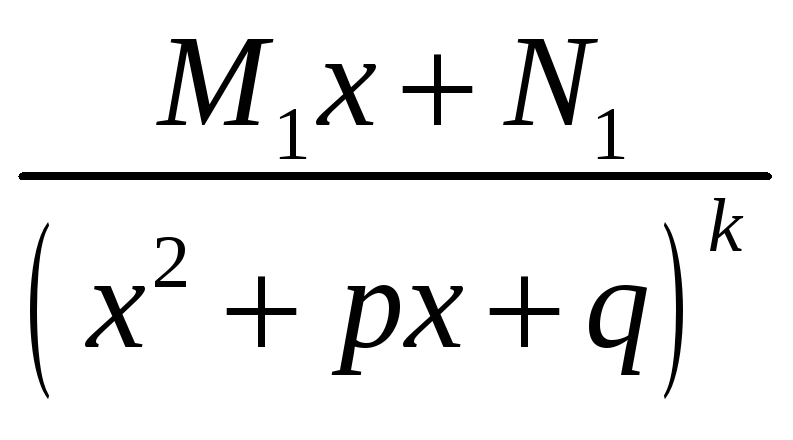
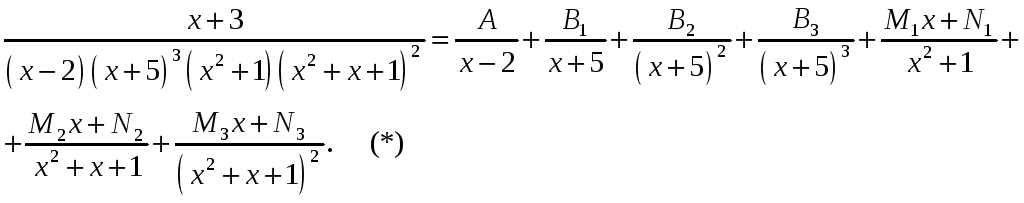
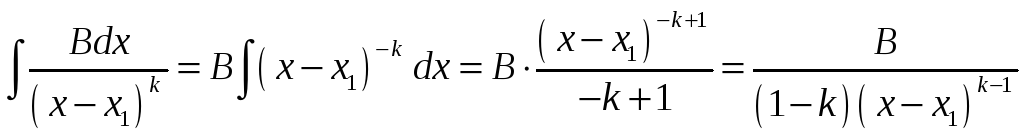
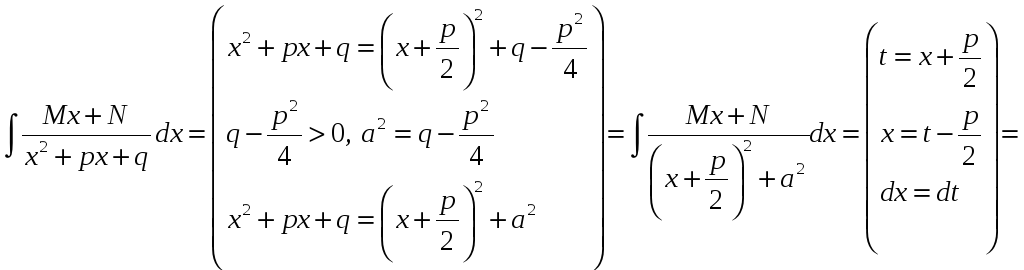
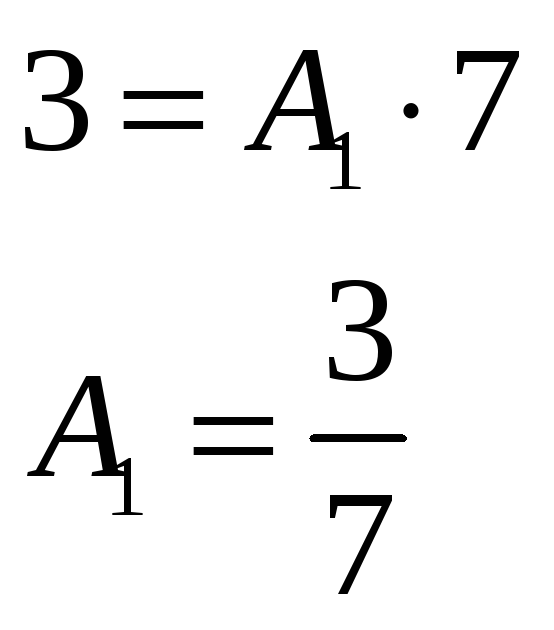
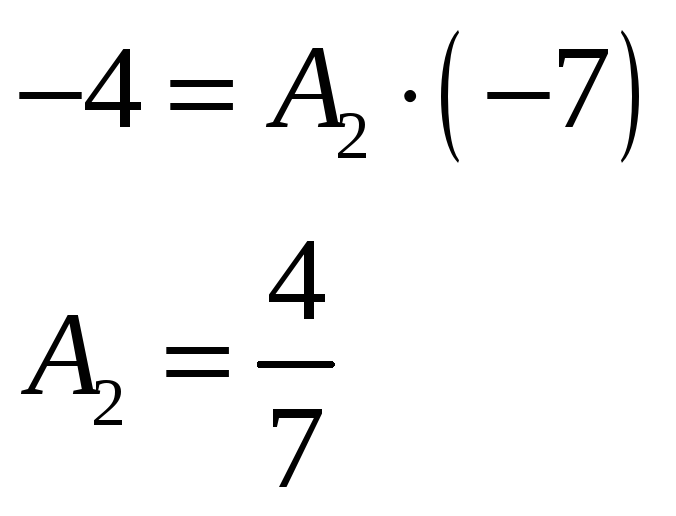
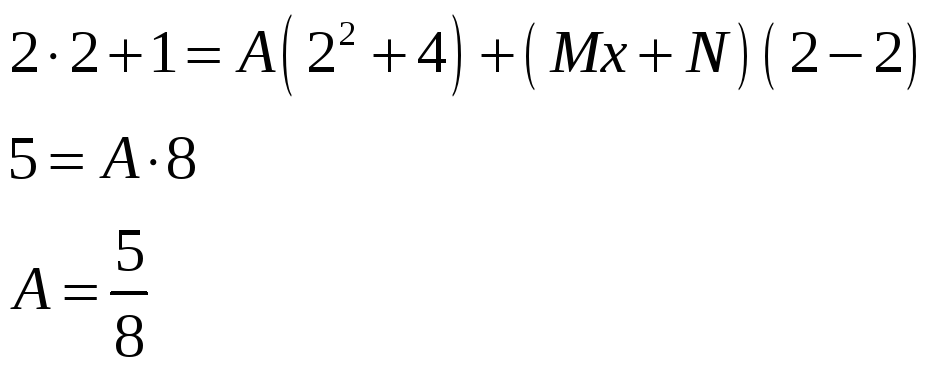
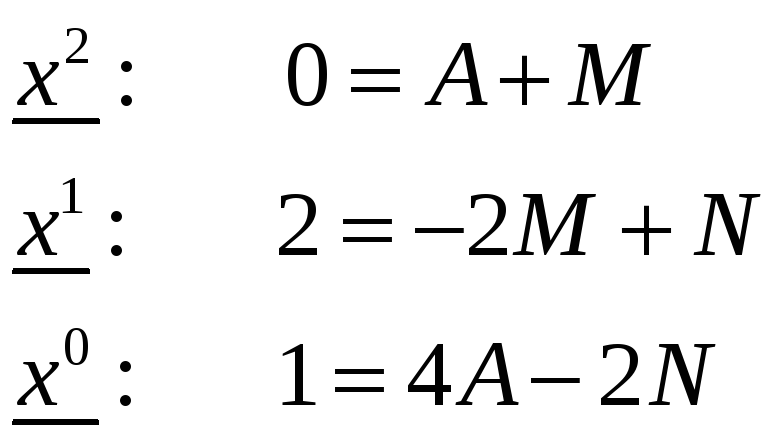
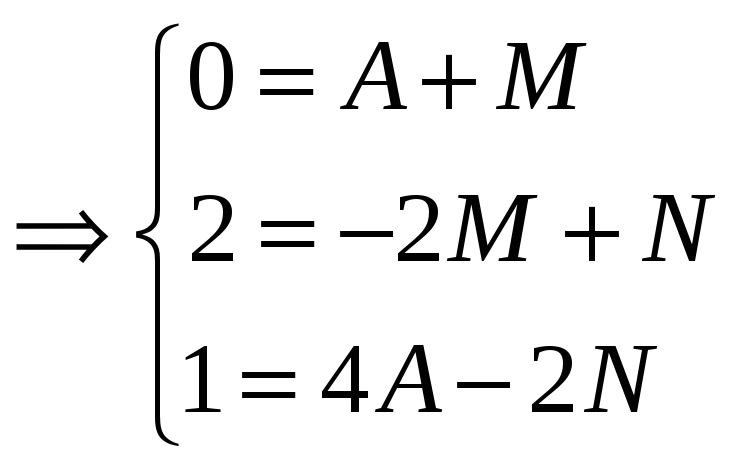
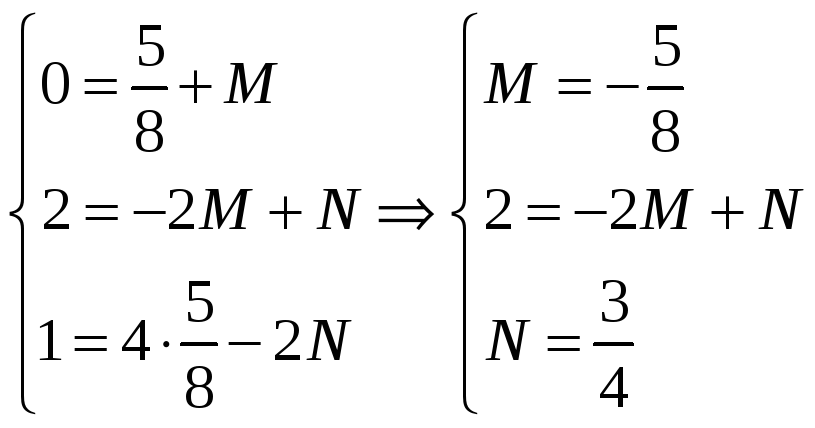
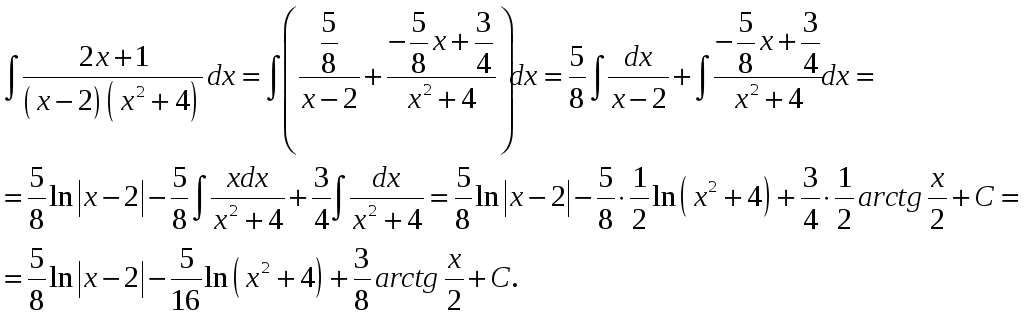
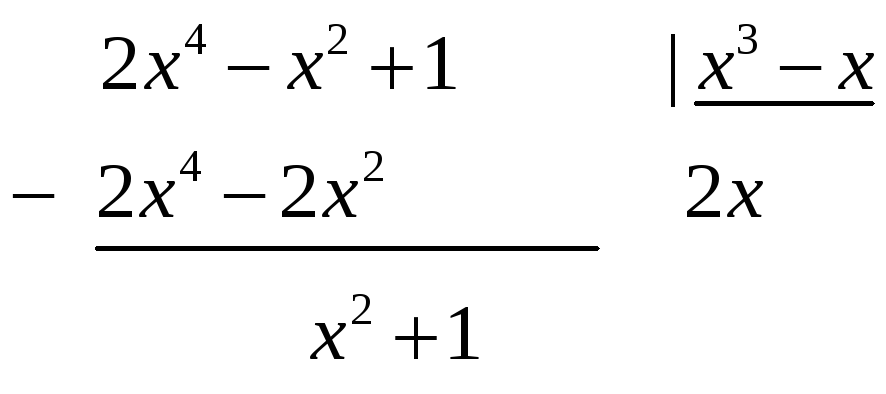
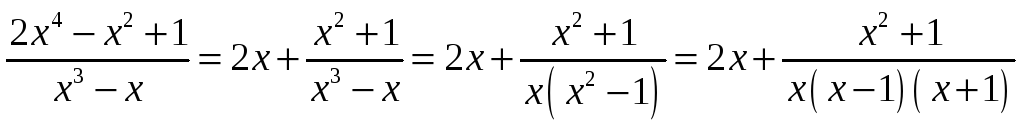
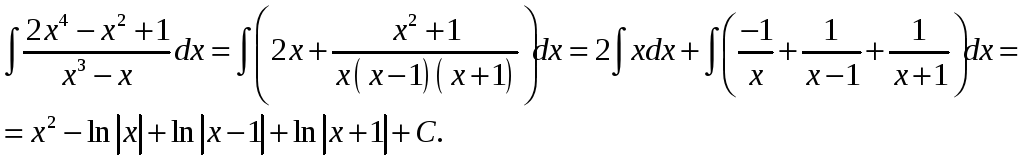
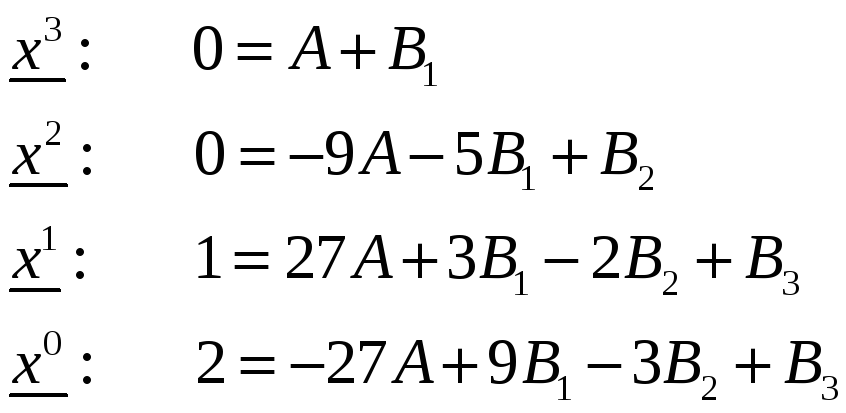
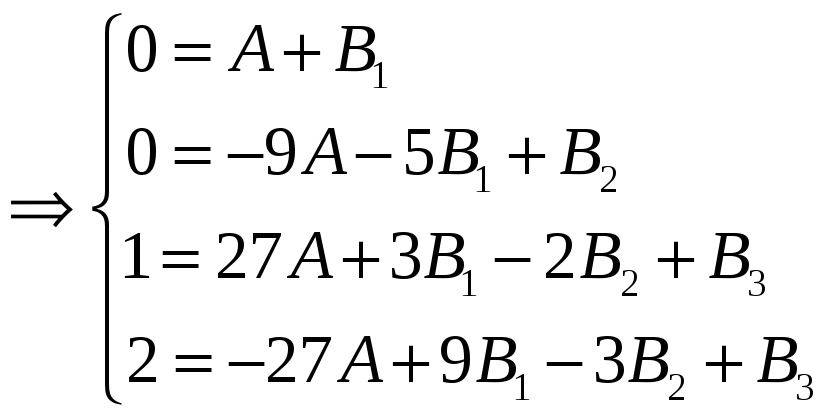
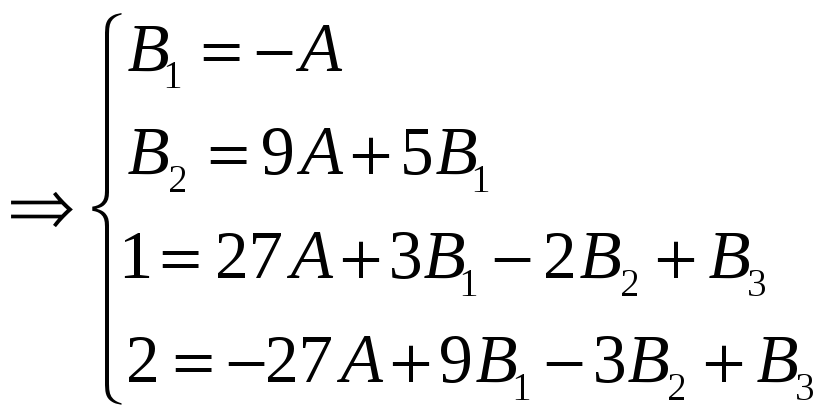
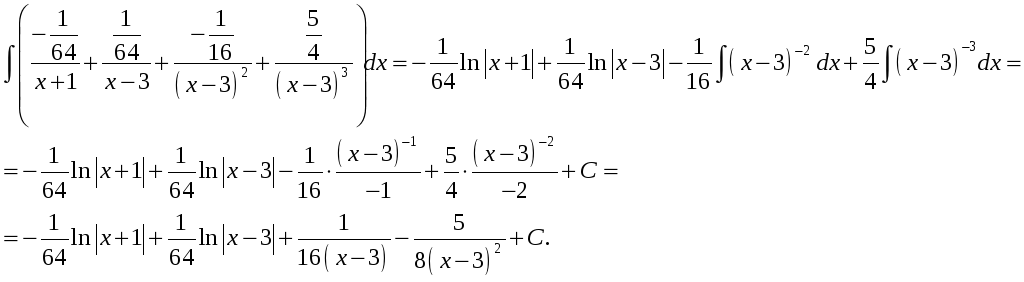

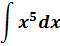
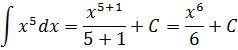
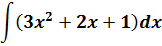
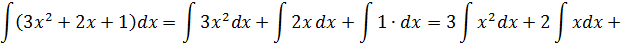
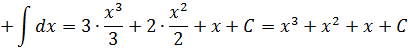
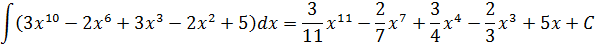
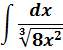
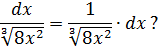
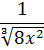
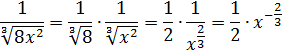
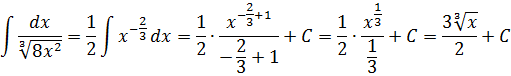
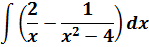
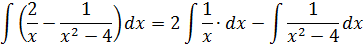
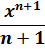
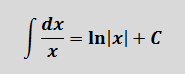
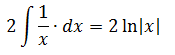
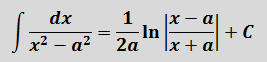
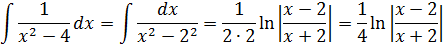
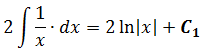
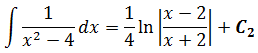
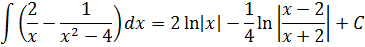
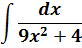
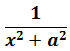
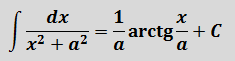
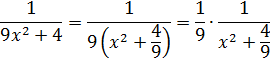
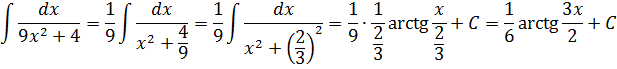
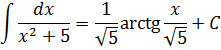
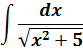
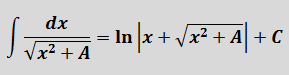
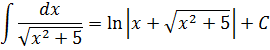
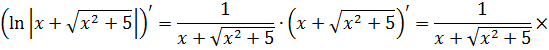
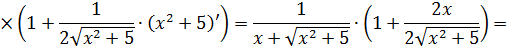
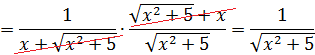
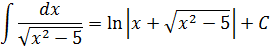
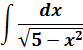
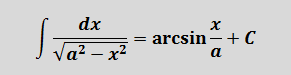
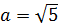
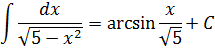
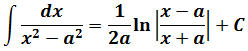
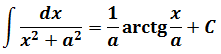
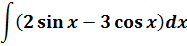
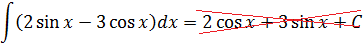
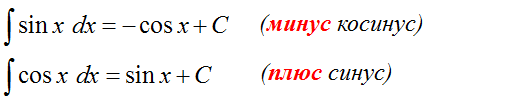
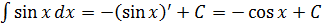
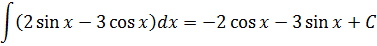
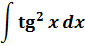
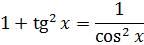
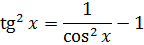
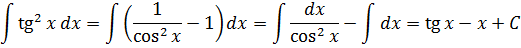
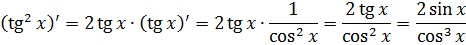
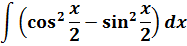
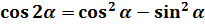
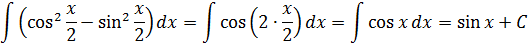
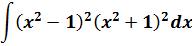
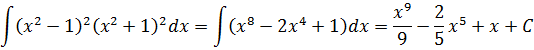
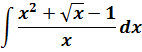
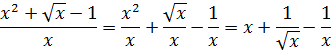
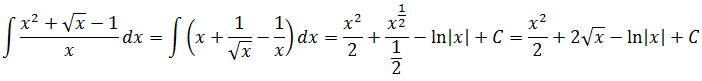
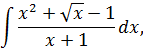
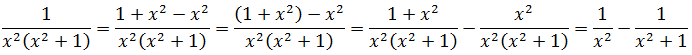
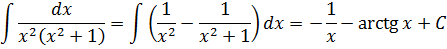
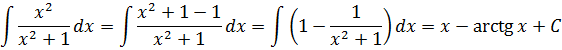
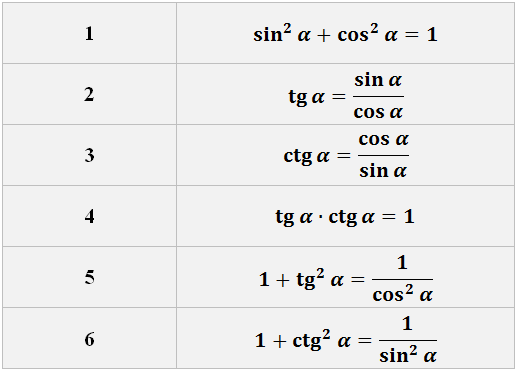
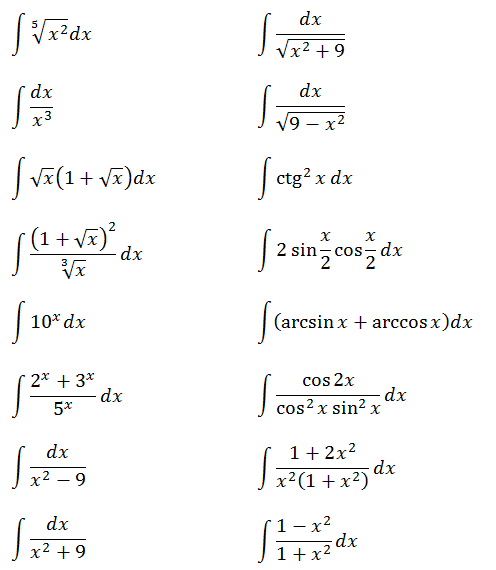
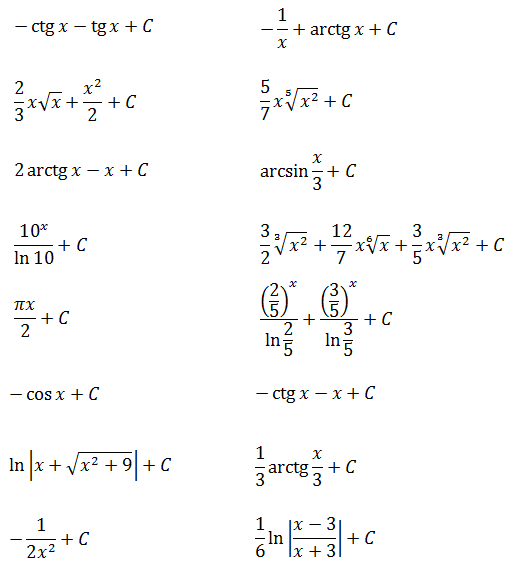

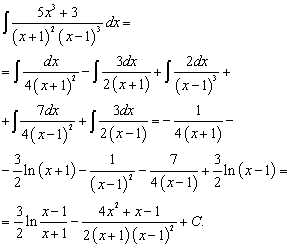
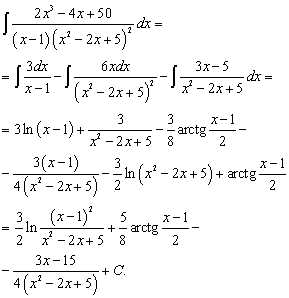
![Rendered by QuickLaTeX.com [ int{frac{fleft( x right)}{gleft( x right)}dx}ne frac{int{fleft( x right)dx}}{int{gleft( x right)dx}} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-60788e9aa223830e26ed4f14f1d23c22_l3.png)



































































![{displaystyle int {frac {t^{2},dt}{(t^{2}+s^{2})^{n}}}left[{begin{array}{ll}u=t&du=dt\dv={dfrac {t,dt}{(t^{2}+s^{2})^{n}}}&displaystyle {v=int {frac {t,dt}{(t^{2}+s^{2})^{n}}}={dfrac {1}{2}}int {frac {d(t^{2}+s^{2})}{(t^{2}+s^{2})^{n}}}=}\&displaystyle {=-{frac {1}{2}}{frac {1}{n-1}}{frac {1}{(t^{2}+s^{2})^{n-1}}}}end{array}}right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5f3e330e07c8830cedb58e5c0f848e077a3d1e)

























![{displaystyle -{frac {2}{3}}int {frac {t^{2},dt}{left(t^{2}+{dfrac {3}{4}}right)^{2}}}left[{begin{array}{ll}u=t&du=dt\displaystyle {dv=-{frac {2}{3}}{frac {t,dt}{left(t^{2}+{dfrac {3}{4}}right)^{2}}}}&displaystyle {v=-{frac {2}{3}}int {frac {t,dt}{left(t^{2}+{dfrac {3}{4}}right)^{2}}}=-{frac {1}{3}}int {frac {dleft(t^{2}+{dfrac {3}{4}}right)}{left(t^{2}+{dfrac {3}{4}}right)^{2}}}=}\&={dfrac {1}{3}}{dfrac {1}{t^{2}+{dfrac {3}{4}}}}end{array}}right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fddbabb47f0db82fbc755e115ae4830133dbd0b1)





























































![{displaystyle int {frac {U(x)}{[V(x)]^{k}}},dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b97ec6d697cd478d26d007a1402247190132113)

![{displaystyle int {frac {U(x)}{[V(x)]^{k}}},dx=int {frac {M(x)V(x)+N(x)V'(x)}{[V(x)]^{k}}},dx=int {frac {M(x)}{[V(x)]^{k-1}}},dx+int {frac {N(x)V'(x)}{[V(x)]^{k}}},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e66d1359234ab5b18173c4f2ad31475fcd31639)
![{displaystyle int {frac {M(x)}{[V(x)]^{k-1}}},dx+int {frac {N(x)V'(x)}{[V(x)]^{k}}},dx=int {frac {M(x)}{[V(x)]^{k-1}}},dx-{frac {N(x)}{(k-1)[V(x)]^{k-1}}}+{frac {1}{k-1}}int {frac {N'(x)}{[V(x)]^{k-1}}},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50128d4a87e2f9fffb88eb1308279ef333310f2)
![{displaystyle int {frac {U(x)}{[V(x)]^{k}}},dx=-{frac {N(x)}{(k-1)[V(x)]^{k-1}}}+int {frac {T(x)}{[V(x)]^{k-1}}},dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10360afa9df0db620683cd1dccf95b0ef883002f)
![{displaystyle int {frac {U(x)}{[V(x)]^{k}}},dx=R(x)+int {frac {varphi (x)}{V(x)}},dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2e81d93e4ec2cef3e79070c6ca8cd89ed76894d)


![{displaystyle {frac {x^{5}+35x^{4}-234x^{3}+566x^{2}-511x+63}{(x-2)(x+1)^{2}(x^{2}-2x+5)^{2}}}={frac {A}{x-2}}+{frac {B_{5}x^{5}+B_{4}x^{4}+B_{3}x^{3}+B_{2}x^{2}+B_{1}x+B_{0}}{[(x+1)(x^{2}-2x+5)]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4e791357fd5419198060a7e3da294a844796ba9)


![{displaystyle {frac {1}{9}}int {frac {dx}{x-2}}-{frac {1}{9}}int {frac {x^{5}-9x^{4}-326x^{3}+1,458x^{2}-2,179x+271}{[(x+1)(x^{2}-2x+5)]^{2}}},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c380cede270329bc185277c8b642b6a9b889f731)










![{displaystyle -{frac {1}{9}}int {frac {x^{5}-9x^{4}-326x^{3}+1,458x^{2}-2,179x+271}{[(x+1)(x^{2}-2x+5)]^{2}}},dx=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24aee314b96ab07f4638bc3374b7807991ac2969)
![{displaystyle =-{frac {1}{9}}int {frac {x^{2}-98x-214}{(x+1)(x^{2}-2x+5)}},dx-{frac {1}{9}}int {frac {(30x^{2}-51x+447)(3x^{2}-2x+3)}{[(x+1)(x^{2}-2x+5)]^{2}}},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ef6fd8b87bbce4b8483eb3e5fa48e1619552cf4)


![{displaystyle -{frac {1}{9}}int {frac {(30x^{2}-51x+447)(3x^{2}-2x+3)}{[(x+1)(x^{2}-2x+5)]^{2}}},dx=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c7307ed62fc1fcbaf8e7a82c9d7e12cc05166ff)








![{displaystyle int {frac {x^{3}-7{sqrt {x}}+10{sqrt[{3}]{x^{2}}}}{x^{5}}},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f50692924a48f6d4ae48d170fd7bc04dbb5da552)
![{displaystyle int {frac {x^{3}-7{sqrt {x}}+10{sqrt[{3}]{x^{2}}}}{x^{5}}},dx=int {frac {x^{3}-7x^{frac {1}{2}}+10x^{frac {2}{3}}}{x^{5}}},dx=int x^{-2},dx-7int x^{-{frac {9}{2}}},dx+10int x^{-{frac {13}{3}}},dx=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12b96a3c32dafdbd7bdf417b5bb3ab1edb30a3d3)
![{displaystyle =-{frac {1}{x}}+7cdot {frac {2}{7}}x^{-{frac {7}{2}}}-10cdot {frac {3}{10}}x^{-{frac {10}{3}}}+C=-{frac {1}{x}}+{frac {2}{sqrt {x^{7}}}}-{frac {3}{sqrt[{3}]{x^{10}}}}+C.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee94d9de55b7e5eb3ba37e86163a49e2173e981f)







![{displaystyle int {frac {x^{4},dx}{(x^{3}+1)^{2}}}left[{begin{array}{ll}u=x^{2}&du=2x,dx\dv={dfrac {x^{2},dx}{(x^{3}+1)^{2}}}&displaystyle {v=int {dfrac {x^{2},dx}{(x^{3}+1)^{2}}}={frac {1}{3}}int {frac {d(x^{3}+1)}{(x^{3}+1)^{2}}}}=\&=-{dfrac {1}{3}}{dfrac {1}{x^{3}+1}}end{array}}right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb5cdee22b8263f5aab59911998dddd08607af7e)


















![{displaystyle {frac {1}{a^{n+1}}}int {frac {[cz+ad-cb]^{n}}{z^{m}}},dz.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/199e7dee494eb9e23d9c3300330e9034a971c801)






![{displaystyle {sqrt[{n}]{frac {b^{m-n+1}}{a^{m+1}}}}int {frac {z^{m},dz}{1pm z^{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b0f083d59c04e64478a73bac33f157462f88cf8)

![{displaystyle {frac {1}{1+x^{n}}}=sum _{k=0}^{frac {n-2}{2}}left[{frac {A_{k}}{x-left(cos {dfrac {2k+1}{n}}pi +isin {dfrac {2k+1}{n}}pi right)}}+{frac {B_{k}}{x-left(cos {dfrac {2k+1}{n}}pi -isin {dfrac {2k+1}{n}}pi right)}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/310dd3af8b1917b7b61368ec45cdcb703d9d8425)






![{displaystyle +{frac {1}{cos {dfrac {2k+1}{n}}pi +isin {dfrac {2k+1}{n}}pi }}cdot {frac {1}{x-left(cos {dfrac {2k+1}{n}}pi -isin {dfrac {2k+1}{n}}pi right)}}{Bigg ]},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471efc2e90948f45f0e4c025ada0f42d11c81204)









![{displaystyle times {frac {1}{x-left(cos {dfrac {2k+1}{n}}pi -isin {dfrac {2k+1}{n}}pi right)}}{Bigg ]},dx=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d081f5f959a2ccdfcb3c6be08436ece4f1860c33)

![{displaystyle -{frac {2sin {dfrac {(2k+1)(m+1)}{n}}pi sin {dfrac {2k+1}{n}}pi }{x^{2}-2xcos {dfrac {2k+1}{n}}pi +1}}{Bigg ]},dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d2a1c8358dca6e649825016d8793f8fe70ab68f)



![{displaystyle {frac {1}{1+x^{n}}}={frac {C}{x+1}}+sum _{k=0}^{frac {n-3}{2}}left[{frac {A_{k}}{x-left(cos {dfrac {2k+1}{n}}pi +isin {dfrac {2k+1}{n}}pi right)}}+{frac {B_{k}}{x-left(cos {dfrac {2k+1}{n}}pi -isin {dfrac {2k+1}{n}}pi right)}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d4390995b8836f25af821f059a5a9a15e7dc6c)







![{displaystyle {frac {x^{m}}{1-x^{n}}}={frac {C_{1}}{1+x}}+{frac {C_{2}}{1-x}}+sum _{k=1}^{frac {n-2}{2}}left[{frac {A_{k}}{x-left(cos {dfrac {2k}{n}}pi +isin {dfrac {2k}{n}}pi right)}}+{frac {B_{k}}{x-left(cos {dfrac {2k}{n}}pi -isin {dfrac {2k}{n}}pi right)}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/766b06e155383c8b5b5af59976c2d5c9aa13e55c)




![{displaystyle int {frac {x^{n-1},dx}{1pm x^{n}}}=pm {frac {1}{n}}int {frac {d(1pm x^{n})}{1pm x^{n}}}=pm {frac {1}{n}}ln |1pm x^{n}|+C=pm ln {sqrt[{n}]{|1pm x^{n}|}}+C.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1480e188502bd95b7ca66bc204ceb7dd9700476)

![{displaystyle {sqrt[{n}]{frac {b^{m-n+1}}{a^{m+1}}}}int {frac {dz}{z^{m}(1pm z^{n})}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90fa553bf2f1e11cf82a2b08b3addc00d62a0666)


![{displaystyle int {frac {dx}{x(1pm x^{n})}}=ln |x|-ln {sqrt[{n}]{|1pm x^{n}|}}+C=ln {frac {|x|}{{sqrt[{n}]{|1pm x^{n}}}|}}+C.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5f76026f18ce5ea54679ea1fb8881cbdc4e10bf)



























