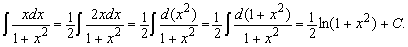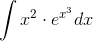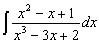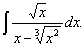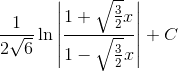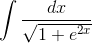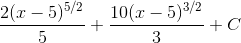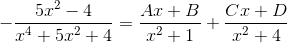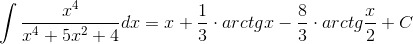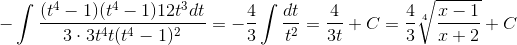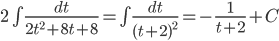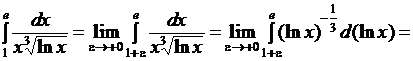Как найти интеграл функции онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое интеграл в математике

Интеграл — одно из важнейших понятий математического анализа, возникающее при решении задач нахождения площади под кривой, пройденного расстояния при неравномерном движении, массы неоднородного тела и т. П., А также задачи восстановления функция от своей производной (неопределенный интеграл).

Упрощенный интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых членов. В зависимости от пространства, на котором задается подынтегральное выражение, интеграл может быть — двойным, тройным, криволинейным, поверхностным и так далее.

Зачем может потребоваться вычисление интеграла

Ученые пытаются выразить все физические явления в виде математической формулы. Как только у нас есть формула, с ее помощью уже можно что угодно считать. А интеграл — один из основных инструментов для работы с функциями.

Например, если у нас есть формула круга, мы можем использовать интеграл для вычисления его площади. Если у нас есть формула шара, то мы можем вычислить его объем. Благодаря интеграции они находят энергию, работу, давление, массу, электрический заряд и многие другие величины.

Источник

Неопределенный интеграл онлайн

В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!

Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?

Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!

Вводная к интегралам

В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.

Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.

В этом заключается один из физических смыслов интеграла.

Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.

Решение интегралов

Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.

Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.

Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.

Калькулятор решения интегралов

Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.

И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.

Источник

Вычисление интегралов

Множество всех первообразных функции f(x) (дифференциала f(x)dx) называется неопределенным интегралом от этой функции и обозначается ∫f(x)dx.

Решение онлайн
Видеоинструкция
Также решают

С помощью данного онлайн-калькулятора можно вычислять любые интегралы. Например, найти интеграл x³sin(x²). Запишем как x^3*sin(x^2) и нажимаем кнопку Получить решение.

Если интеграл определенный, например, 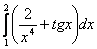, то записываем 2/x^4+tan(x), в качестве пределов интегрирования указываем 1, 2.

Примечание: число «пи» (π) записывается как pi; знак «бесконечность» (∞) ≡ infinity

Примеры правильной записи некоторых выражений

Таблица интегралов

Приемы нахождения неопределенных интегралов

Способы нахождения неопределенных интегралов:

Подведение под знак дифференциала:
Интегрирование по частям: ∫xe^xdx
Простейшие преобразования подынтегрального выражения (пример):
Интегрирование рациональных дробей:
Интегрирование простейших иррациональностей:
Интегрирование выражений, содержащих тригонометрические функции: ∫cos⁴(x)sin³(x)dx

Пример 1. Вычислить ∫(3x+15)¹⁷dx.

Решение.

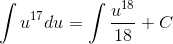
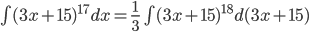
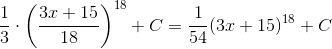
Возводить двучлен в 17-ю степень нецелесообразно. Исходя из табличного интеграла , получаем

= .

Пример 2. Вычислить .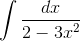

Решение.

Аналогично предыдущему,

=

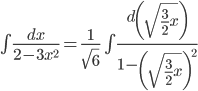
Пример 3. .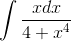

Решение. Поскольку

, то .

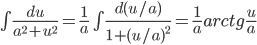
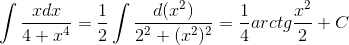
Пример 4. Вычислить

Решение. Так как

, то .

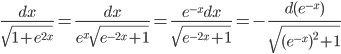
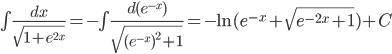
Пример 5. Вычислить .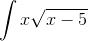

Решение.

Применим подстановку 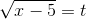. Отсюда x-5=t², x=t²+5, dx=2tdt.

Подставив в интеграл, получим

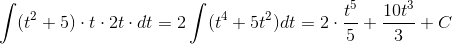
Пример 6. Вычислить ∫x²e^xdx.

Решение.

Положим u=x², dv=e^xdx; тогда du=2xdx, v=e^x. Применим формулу интегрирования по частям:

∫x²e^xdx=x²e^x-2∫xe^x.

Мы добились понижения степени x на единицу. Чтобы найти ∫xe^x, применим еще раз интегрирование по частям. Полагаем u=x, dv=e^xdx; тогда du=dx, v=e^x и

∫xe^x=x²e^x-2xe^x+2e^x+C.

Пример 7. Вычислить .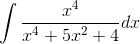

Решение. Выделяя целую часть, получим: .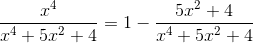

Учитывая, что x⁴+5x²+4=(x²+1)(x²+4), для второго слагаемого получаем разложение

Приводя к общему знаменателю, получим равенство числителей:

-5x²–4=(Ax+B)(x²+4)+(Cx+D)(x²+1).

Приравнивая коэффициенты при одинаковых степенях x, получаем

x³: 0=A+C

x₂: -5=B+D

x: 0=4A+C

x⁰: -4=4B+D

Отсюда находим A=C=0, B=¹/₃, D=-¹⁶/₃.

Подставляя найденные коэффициенты в разложение и интегрируя его, получаем:

Пример 8. Вычислить .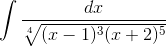

Решение. Так как

,

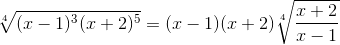
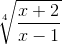
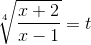
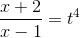
то подынтегральное выражение есть рациональная функция от x и ; поэтому введем подстановку:

; ,

откуда

; ; ;.

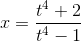
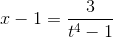
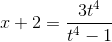
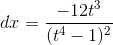
Следовательно,

Пример 9. Вычислить .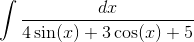

Решение.

Подынтегральная функция рационально зависит от sinx(x) и cos(x); применим подстановку tg^x/₂=t, тогда

, , и

=

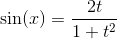
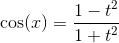
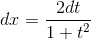
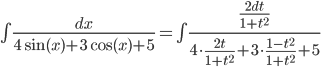
Возвращаясь к старой переменной, получим

= .

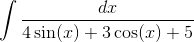
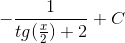
Пример 10. Вычислить .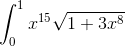

Решение.

Произведем замену 1+3x⁸ = z². Тогда , ;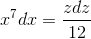

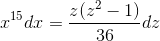
таким образом,

.

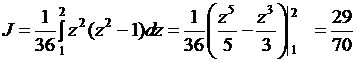
Следует обратить внимание, что при замене переменной в определенном интеграле пределы интегрирования в общем случае изменяются.

Пример 11.Вычислить несобственный интеграл 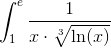или доказать его расходимость.

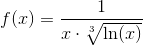
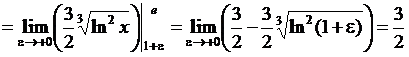
Решение. Подынтегральная функция не ограничена в окрестности точки x=1. На любом же отрезке [1+ε;e] она интегрируема, так как является непрерывной функцией. Поэтому

Пример 12. Вычислить несобственный интеграл 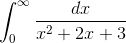или доказать его расходимость.

Решение.

Подынтегральная функция непрерывна и интегрируема на R. По определению

= =

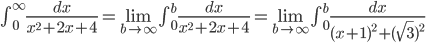
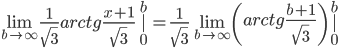
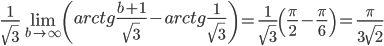
Интеграл сходится.

Пример 13. Найти площадь фигуры, ограниченной параболой y=x² и прямой x+y=2.

Решение.

Найдем абсциссы точек пересечения параболы y=x² и прямой y=2-x. Решая уравнение x²=2-x, находим x₁=-2, x₂=1. Так как фигура ограничена сверху прямой, а снизу параболой, по известной формуле находим

.

Источник

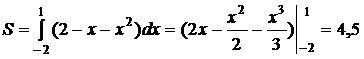
bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

int e^xcos(x)dx
int cos^3(x)sin (x)dx
int frac{2x+1}{(x+5)^3}
int_{0}^{pi}sin(x)dx
int_{a}^{b} x^2dx
int_{0}^{2pi}cos^2(theta)dtheta
неполные:дроби:int_{0}^{1} frac{32}{x^{2}-64}dx
подстановка:intfrac{e^{x}}{e^{x}+e^{-x}}dx,:u=e^{x}
Показать больше

Описание

Поэтапное интегрирование функций

integral-calculator

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Integral Calculator, advanced trigonometric functions, Part II

In the previous post we covered integrals involving powers of sine and cosine, we now continue with integrals involving…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Step-by-Step Examples

Calculus

Integral Calculator

Step 1:

Enter the function you want to integrate into the editor.

The Integral Calculator solves an indefinite integral of a function. You can also get a better visual and understanding of the function and area under the curve using our graphing tool.

Integration by parts formula: ?udv=uv-?vdu

Step 2:

Click the blue arrow to submit. Choose «Evaluate the Integral» from the topic selector and click to see the result!

Источник