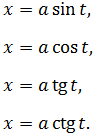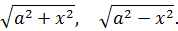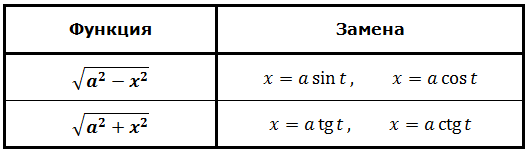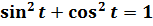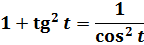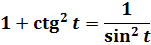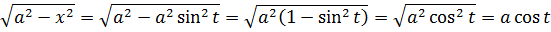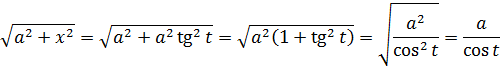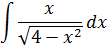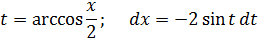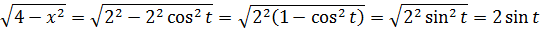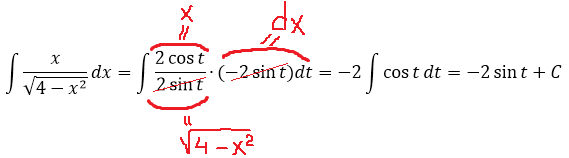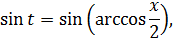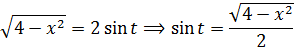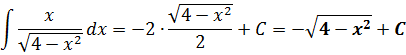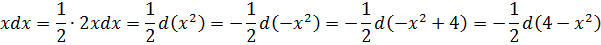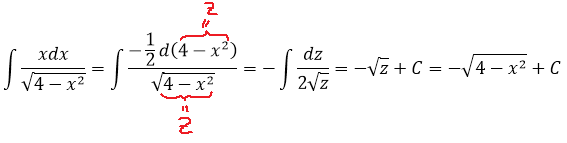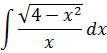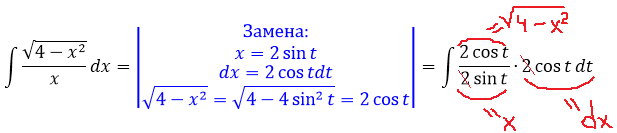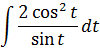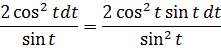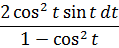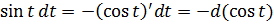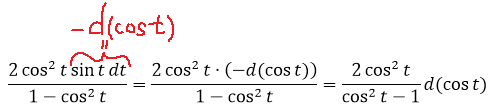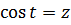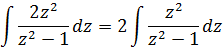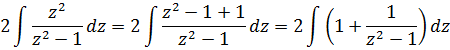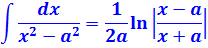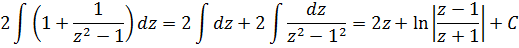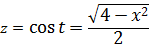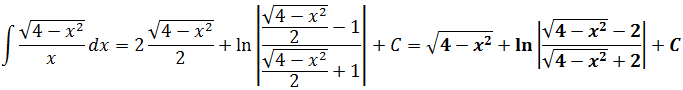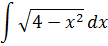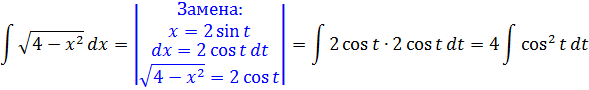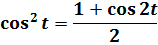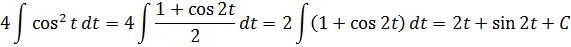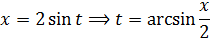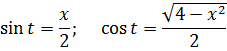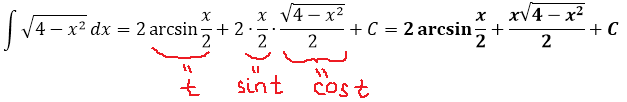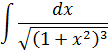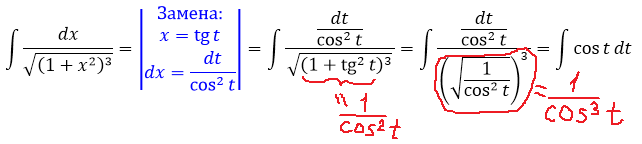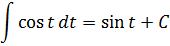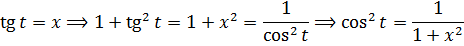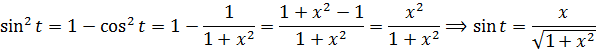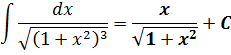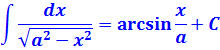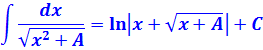При решении задач на нахождение интегралов от тригонометрических функций часто требуется найти неопределенный интеграл от косинуса во второй степени, в этом случае удобно воспользоваться формулой понижения степени
Рассмотрим следующий неопределенные интегралы от косинуса в квадрате:
где 
— произвольная вещественная постоянная.
Значит, неопределенный интеграл от косинуса в квадрате:
Здесь при нахождении неопределенного интеграла от косинуса во второй степени были использованы:
В приведенном видео-занятии по теме «Неопределенный интеграл: интегрировании некоторых тригонометрических функций» демонстрируется подробное решение этой задачи, а также задачи нахождения неопределенного интеграла от синуса в квадрате.
Заказать задачи по любым предметам можно здесь от 10 минут
Интеграл косинуса
Интеграл косинуса по таблице интегрирования основных элементарных функций равен:
$$ int cos x dx = sin x + C $$
Словами это запомнить легче и звучит так: интеграл косинуса равен сумме синуса и константы. Выполним разбор частных примеров.
| Пример 1 |
|
Найти интеграл от косинуса 2х: $$ int cos 2x dx $$ |
| Решение |
|
2х под косинусом называется двойным углом. Из-за того, что аргумент косинуса равен $ 2x $, то нельзя сразу применить формулу. Нужно чтобы $ 2x $ находилось и под знаком дифференциала. Выполним подведение $ 2x $ под дифференциал: $$ frac{1}{2}int cos 2x d(2x) = frac{1}{2}sin 2x + C $$ Перед интегралом появилась дробь $ frac{1}{2} $, так как $ d(2x) = 2 dx $ и нам необходимо уничтожить лишнюю двойку. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int cos 2x dx = sin 2x + C $$ |
| Пример 2 |
| Найти интеграл от произведения синуса и косинуса: $$ int sin x cos x dx $$ |
| Решение |
|
Данный интеграл можно взять двумя методами: подведением $ sin x $ под знак дифференциала $ cos x dx = d(sin x) $ или заменой $ t = sin x, dt = cos x dx $ Проще будет решить внесением под дифференциал. Получаем: $$ int sin x cos x dx = int sin x d(sin x) = frac{sin^2 x}{2} + C $$ |
| Ответ |
| $$ int sin x cos x dx = frac{sin^2 x}{2} + C $$ |
| Пример 3 |
| Вычислить интеграл косинуса от 0 до пи: $$ int_0^pi cos x dx $$ |
| Решение |
|
Выражение стоящее под знаком интеграла полностью готово к непосредственному интегрированию. Но стоит заметить, что интеграл определенный, а это значит нужно воспользоваться дополнительно формулой Ньютона-Лейбница: $ int_a^b f(x) dx = F(b) — F(a) $, где $ F(x) $ — это первообразная функции. $$ int_0^pi cos x dx = sin x bigg |_0^pi = sinpi — sin 0 = -1 — 0 = -1 $$ |
| Ответ |
| $$ int_0^pi cos x dx = -1 $$ |
| Пример 4 |
| Найти интеграл от косинуса в квадрате: $$ int cos^2 x dx $$ |
| Решение |
|
Непосредственно взять интеграл не получится, так как косинус в квадрате не является табличной функцией, поэтому воспользуемся еще одной формулой понижения степени: $$ cos^2 x = frac{1+ cos 2x}{2} $$ Подставляем правую часть формулы в интеграл: $$ int cos^2 x dx = int frac{1+cos 2x}{2} dx = frac{1}{2} int (1+cos 2x) dx = $$ $$ = frac{1}{2}int 1dx + frac{1}{2} int cos 2x dx = frac{1}{2}x + frac{1}{4}sin 2x + C $$ |
| Ответ |
| $$ int cos^2 x dx = frac{1}{2}x + frac{1}{4}sin 2x + C $$ |
Интеграл от косинуса
Интеграл от косинуса равен синусу такого же аргумента плюс константа интегрирования
(
int cos x d x=sin x+C
)
Примеры решения задач
ПРИМЕР 1
Найти интеграл (
int(cos x+4 x) d x
)
Интеграл суммы равен сумме интегралов:
(
int(cos x+4 x) d x=int cos x d x+int 4 x d x=sin x+4 cdot frac{x^{2}}{2}+C=sin x+2 x^{2}+C
)
(
int(cos x+4 x) d x=sin x+2 x^{2}+C
)
ПРИМЕР 2
Решить (
int cos ^{2} x d x
)
Чтобы найти интеграл от косинуса в квадрате используем формулу понижения степени:
(
cos ^{2} alpha=frac{1+cos 2 alpha}{2}
)
будем иметь:
(
int cos ^{2} x d x=int frac{1+cos 2 x}{2} d x=frac{1}{2} int d x+frac{1}{2} int cos 2 x d xleft|begin{array}{c}{2 x=t} \ {2 d x=d t} \ {d x=frac{d t}{2}}end{array}right|=
)
(
=frac{x}{2}+frac{1}{2} int cos t cdot frac{d t}{2}=frac{x}{2}+frac{1}{4} int cos t d t=frac{x}{2}+frac{1}{4} sin t+C=frac{x}{2}+frac{sin 2 x}{4}+C
)
(
int cos ^{2} x d x=frac{x}{2}+frac{sin 2 x}{4}+C
)
2
интеграл от 0 до пи/6 от cos в квадрате х/3 по dх — Учеба и наука
Лучший ответ по мнению автора |
|
|||||||||||||
Другие ответы
|
||||||||
03.17
|
|
|
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.
75 . Найдите АС.
Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81%
Дано: геометрическая прогрессия (bn) задана условиями: b1=-2 , bn+1=3bn. Найдите b6. Объясните пожалуйста, как это решить?
Решено
дана арифмитическая прогрессия (аn)в которой a9=-22,2,a23=-41,8 найдите разность прогрессии
Вычислите длину дуги окружности с радиусом 4см,если ее градусная мера равна 120 градусов.Чему равна площадь соответствующего данной дуге
Пользуйтесь нашим приложением
2(x)) поначалу может показаться сложным, поскольку похоже, что мы пытаемся интегрировать комбинацию тригонометрической и степенной функций. Вскоре мы поймем, что ни один из наших предыдущих подходов к интегральному исчислению не делает эту задачу простой и понятной для выполнения.
Однако мы можем воспользоваться некоторыми тригонометрическими свойствами, чтобы разработать метод решения этих проблем.
Результаты учебной программы NESA
После изучения этой темы учащиеся должны овладеть следующими результатами: 92 пхдх)
Предполагаемые знания
Учащиеся должны быть знакомы с тригонометрическими тождествами, такими как составные формулы и формулы двойного угла для основных тригонометрических соотношений. Студенты также должны быть знакомы с интегральным исчислением и уметь интегрировать различные функции, такие как степенные, тригонометрические и экспоненциальные функции.
Этот контент можно найти в наших предыдущих руководствах по математике, если учащиеся хотят закрепить свое понимание. 92(x)= frac{1+cos(2x)}{2})
Из нашего предыдущего исследования интегрирования тригонометрических функций мы можем вспомнить, что мы можем интегрировать тригонометрические функции линейной степени, т.
е. тригонометрические функции, которые имеют степень 1, независимо от угла внутри. Мы можем учесть внутренний угол, просто применив правило обратной цепочки и разделив его обратно. Например, если мы рассмотрим следующий интеграл:
(int cos(ax) dx)
Этот интеграл является одним из наших фундаментальных результатов для интегрирования тригонометрических функций, которые, как мы знаем, должны быть просто (frac{1}{a}sin(ax) + C). 92 (х) dx = int frac {1-cos (2x)} {2} dx )
Теперь нам становится намного проще интегрировать, так как мы можем просто разделить дробь:
begin{align*}
& int left( frac{1}{2} – frac{1} {2}cos(2x) right) dx\
&= frac{1}{2} int dx – frac{1}{2} int cos(2x) dx\
& = frac{1}{2} x – frac{1}{2}⋅frac{1}{2}sin(2x)+C\
&= frac{1}{2}x- frac{1}{4}sin(2x)+C\
end{align*}
Это дает нам результат интеграла, который мы искали: 9{ гидроразрыва {3π} {2}} )
Подставив эти границы, мы найдем объем этой фигуры.
V &= left( frac{3}{2} ( frac{3π}{2} ) +sin left( 2 (frac{3π}{ 2}) right) + 2sin left( 4 ( frac{3π}{2} ) right) right) – left( frac{3}{2} ( frac{π}{2} ) +sin left( 2 (frac{π}{2} ) right) + 2sin left( 4 (frac{π}{2}) right) right)\
V &= left( frac{9π}{4} +sin(3π)+2sin(6π) right) – left( frac{3π}{4} +sin(π) + 2sin(π) right)\ 93)
Все еще боретесь с квадратом синуса и косинуса?
На онлайн-курсах Matrix+ наши эксперты HSC проведут вас по всем понятиям Math Ext 1, таким как интегрирование синуса и косинуса в квадрате, с помощью четких и структурированных видеоуроков. Мы также предоставляем вам обширные ресурсы, которые отправляются по почте прямо к вашему порогу! Узнайте больше прямо сейчас.
Продвигайтесь вперед с Matrix+ Online
Опытные преподаватели, подробная обратная связь и индивидуальная помощь.
Учитесь в своем собственном темпе, где бы вы ни находились.
© Matrix Education и www.matrix.edu.au, 2022. Несанкционированное использование и/или копирование этого материала без письменного разрешения автора и/или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указаны с соответствующим и конкретным указанием на исходный контент.
интегрирование — вычисление интеграла с квадратным косинусом
спросил
5 лет, 6 месяцев назад
Изменено
5 лет, 6 месяцев назад
Просмотрено
70 раз
$begingroup$
Как вычислить этот интеграл? Я уже пробовал менять переменную внутри косинуса, считать по частям и применять тригонометрические соотношения, но это не дает мне нужного результата.
No related posts.
Итак, друзья, продолжаем знакомиться с типовыми заменами при вычислении неопределённых интегралов. В прошлый раз мы познакомились с наиболее часто употребляемой степенной заменой, усвоили, как и где именно она применяется, порешали несложные примеры с корнями. Суть степенной замены заключалась в том, что старая переменная интегрирования икс заменялась степенной функцией от новой переменной t. И после такой замены у нас пропадали все корни.
В этом уроке речь пойдёт о так называемой тригонометрической замене. Суть её тоже очень простая и заключается в следующем: старая переменная икс заменяется на некоторую… тригонометрическую функцию от t. Да-да! Всего возможно четыре варианта:
Параметр а — некоторая положительная константа. Зачем она там нужна, станет ясно чуть ниже. На примерах.)
А теперь будем разбираться, где именно применяется такая замена и что она нам даёт. Заодно и элементарную тригонометрию повторим. 
Тригонометрическая замена, так же, как и степенная, применяется при интегрировании некоторых функций с корнями. Только, в отличие от степенной замены, для тригонометрической есть два важных условия её применения:
1) Подынтегральная функция содержит квадратный (и только квадратный!) корень;
2) Под корнем стоит квадратичная конструкция вида a2±x2.
Иными словами, в сегодняшнем уроке речь пойдёт о вычислении интегралов, содержащих вот такие корни:
Для плюса и для минуса используется своя замена. Вот вам небольшая сводная табличка:
Выбирать можно любую из предложенных подстановок: для минуса хоть синус, хоть косинус, а для плюса — либо тангенс, либо котангенс. Что больше нравится.
Суть тригонометрической замены полностью аналогична — убрать корень. То есть, добиться того, чтобы под корнем получился точный квадрат и корень извлекался начисто. И, тем самым, исчез из примера.)
Как же это происходит? Для полного понимания нам понадобится три до боли знакомых школьных тождества:
А теперь возьмём какой-нибудь из корней (пусть первый корень, с минусом в подкоренном выражении) и подставим в него нашу замену (допустим, с синусом a·sin t). Что у нас получится:
Для корня с плюсом проделаем всё то же самое, но на примере подстановки с тангенсом:
Вот и вся суть. Был корень — и нету корня! Возможно, кто-то хмыкнет скептически: какая, мол, разница, корень под интегралом или тригонометрия?! Хрен редьки не слаще… А в чём-то тригонометрия даже и похуже корней будет!
Что ж, настало время удивить скептиков. На примерах.) Итак, начнём!
Пример 1
Подынтегральная функция содержит корень вида
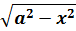
Число а у нас — двойка: 4 = 22. Раз под корнем минус, то используем замену либо с синусом, либо с косинусом. Давайте, с косинусом возьмём. Для разнообразия.)
Итак, замена: x = 2cos t
Сразу же можно выразить само t, а также dx:
А теперь, используя нашу замену, упрощаем сам корень, который нам так мешает:
Вот и отлично. Корня больше нет. Теперь посмотрим, что же у нас получится под интегралом после такой замены:
И как вам? Был интеграл от ужасного корня, а после замены стал табличный (!) интеграл. От косинуса, правда, ну и что в этом страшного?
Осталось лишь вернуться обратно к переменной икс и записать ответ. Только я не буду сейчас тупо в лоб считать что-то типа
а сразу найду синус t из равенства, где мы упрощали наш корень:
Всё. Подставляем это выражение в наш результат вместо sin t и окончательно получаем:
И все дела.) Да-да, вот такой вот простенький ответ у этого примера.) Можете даже в уме его продифференцировать и получить подынтегральную функцию.
Особо глазастые студенты при первом взгляде на пример, возможно, узрели вот такую взаимосвязь:
Что ж, респект глазастым! Да, действительно, если внести подкоренное выражение 4-х2 под дифференциал, то пример элементарно сведётся к табличной степенной функции:
Можно так интегрировать? А почему — нет? Математика не запрещает. Но нам ведь размяться с тригонометрической заменой нужно! Вот и изучаем на несложном примере.
А теперь пример посложнее. Поменяем местами в нашей подынтегральной функции числитель и знаменатель. То есть, просто перевернём подынтегральную функцию. Вот такой пример будем решать:
Пример 2
Давайте, в этот раз используем замену с синусом. Сразу пишем:
И теперь, после подстановки, наш новый интеграл стал выглядеть вот так:
Что делать дальше? Главное — не бояться! И смекалки немного.
Вообще говоря, на такого рода функции есть свой приём интегрирования (тоже замена, кстати), но мы пока сделаем вид, что про неё не знаем. И попробуем выкрутиться с помощью элементарных преобразований, которые мы с вами уже знаем. )
Что здесь можно сделать? Ну, напрашивается подведение под дифференциал, ибо в дроби сидят синус и косинус — родственнички по производной.) Для этого надо попробовать преобразовать подынтегральное выражение так, чтобы везде осталась одна функция — либо синус, либо косинус. Здесь можно всё свести к косинусу. Смотрите, как это делается! По пунктам:
1. Умножаем числитель и знаменатель дроби (вместе с dt!) на sin t. Что именно это даст — узнаем дальше.
2. Заменяем в знаменателе sin2t на 1-cos2t. Согласно основному тригонометрическому тождеству, ага.
3. Замечаем, что
и подводим косинус под знак дифференциала (про минус тоже не забываем, да).
Вот так. Теперь всё подынтегральное выражение у нас сведено к косинусу. Я согласен, что ещё надо было додуматься домножить всё на sin t, чтобы выйти на такую комбинацию. Но тут уже только богатый опыт рулит. Такое чутьё приходит только с практикой. Так что — решайте примеры! Чем больше, тем лучше.)
Итак, теперь смело заменяем косинус новой буквой. Тэ у нас уже использовано, пусть зэт будет:
Выражаем наш интеграл теперь уже через переменную z:
А теперь в дело вступает наш старый добрый излюбленный приёмчик — отнять/прибавить единичку. Продолжаем:
Единичка, я надеюсь, ни у кого проблем в интегрировании не вызывает? А что же касается дроби 1/(z2-1), то это не что иное, как табличный интеграл! Открывайте нашу таблицу и ищите похожую формулу. Это седьмая формула, с «высоким» логарифмом:
В роли «а» у нас выступает единичка. Возвращаемся к нашим баранам:
Что ж, заготовка для ответа получена. Теперь поэтапно возвращаемся обратно к иксу:
Итого, окончательно:
Вот такой вот интересный пример. И довольно красивый ответ.)
Маньяки могут его продифференцировать. Я продифференцировал. Всё гуд.)
Продолжаем развлекаться. Теперь вообще уберём знаменатель и решим вот такой примерчик:
Пример 3
Под интегралом теперь стоит просто чистый корень, безо всего. И тут тоже на помощь придёт тригонометрическая замена.) Давайте, снова будем всё выражать через синус, ибо он удобнее: минус лишний не всплывает, который легко потерять. Действуем:
Как теперь быть с косинусом в квадрате? Если в прошлом примере нам пришлось домножать всё на синус, то тут всё гораздо проще. Призываем на помощь школьную тригонометрию! На сей раз — формулы понижения степени. А чуть конкретнее — вот эту:
И после такого преобразования наш интеграл легко превращается в сумму табличных (ну, или почти табличных :)):
Надеюсь, особо не нужно комментировать, как именно при интегрировании получился синус двух t? Кто не понял — читаем урок «Подведение функции под знак дифференциала». Там всё популярно изложено.
Всё. «Рыба» для ответа готова. Осталось правильно перейти к иксу да подставить вместо t в выражения 2t и sin 2t.
Прежде всего, выясним из нашей замены, что же такое это самое t:
Теперь раскроем синус двойного угла: sin2t = 2sin t·cos t
Зачем так сделано? А затем, что теперь и синус и косинус легко выражаются через x (смотрим синюю табличку с нашей заменой)! Вот так:
И теперь наш окончательный ответ полностью готов:
Ну как? Да, я согласен, не самые простые примеры. Так и мы с вами уже всё-таки на приличном уровне, правда?
Что-то мы всё с синусами да косинусами возимся, а тангенс/котангенс как-то обделили вниманием. Давайте и такой примерчик рассмотрим! На десерт.) Он совсем несложный: хватит с вас жести на сегодня! Просто чтобы суть замены уловить.)
Пример 4
Не пугаемся внешнего вида примера! Внешность иногда бывает обманчива, да.)
Сразу замечаем под корнем сумму 1+х2. Раз сумма, то, стало быть, подходящая замена для ликвидации корня — с тангенсом (или котангенсом). Опять же, по причине нежелания возиться с лишним минусом, я выберу тангенс (а = 1, x = tg t):
И снова перед нами безобидный табличный интеграл! Интегрируем косинус и — готово дело:
Всё. Выражаем теперь нашу первообразную через икс. Как? По формулам тригонометрии, вестимо! У нас есть тангенс, а нас интересует синус.
Так. Квадрат косинуса готов. Осталось лишь из основного тригонометрического тождества вытащить квадрат синуса, извлечь корень и — цель достигнута!
Вот и наш ответ. Довольно простенький на сей раз:
Подытожим наш урок. Давайте разберёмся, зачем в самом начале урока я высказал два обязательных требования, чтобы сам корень был только квадратным (а не кубическим или какой-то более высокой степени), а также чтобы под корнем находилась конструкция вида x2±a2. Догадались, почему?
Да потому, что в любой другой ситуации (кубический корень или же под корнем многочлен более высокой степени) у нас просто-напросто не исчезнет иррациональность, и данная замена нам уже никак не поможет свести интеграл к красивому виду. И, если вам, вдруг, попался такой пример, то, скорее всего, преобразования более хитрые.
Разумеется, подобные интегралы не ограничиваются этими четырьмя примерами. И для интегралов, содержащих квадратичные иррациональности, есть и более суровые подстановки — Эйлера и Абеля. Но такие подстановки — уже высший пилотаж в интегрировании. Их мы будем изучать ближе к концу раздела. Зато тщательный разбор этих четырёх примеров даст вам возможность уверенно брать хотя бы некоторые интегралы подобного типа. Так что тригонометрическая замена — штука весьма полезная. Мы с ней дружить будем. А для дружбы, конечно же, необходимо хорошо знать школьную тригонометрию — основные тождества (их шесть), двойные углы, формулы понижения степени и т.д.
Что ж, на сегодня хватит. А в качестве тренировочного упражнения в этот раз я дам небольшое творческое задание. Чтобы скучно не было.)
Есть в нашей замечательной табличке интегралов парочка довольно страшных формул. Вот эти:
И теперь, в качестве задания, я предлагаю вам доказать эти формулы! С помощью тригонометрической замены, да.) Чтобы вы прочувствовали, откуда что в математике берётся. И берётся явно не с потолка.)
С первой формулой проблем возникнуть не должно: там всё очевидно. А вот со второй («длинным логарифмом») я немного подскажу. В формуле число А для определённости предполагается положительным. Раз оно положительное, то можно совершенно спокойно заменить это самое А на a2. И дальше работать уже с заменой через тангенс.) Материала этого (и прошлых) уроков вполне достаточно, чтобы одолеть это задание. Будет вам там парочка сюрпризов! Выручат свойства логарифмов и первообразных (это подсказка! :)).
Удачи!