Содержание:
- Формула
- Примеры вычисления интеграла котангенса
Формула
$$int operatorname{ctg} x d x=ln |sin x|+C$$
Интеграл от котангенса равен логарифму натуральному от синуса плюс константа интегрирования.
Примеры вычисления интеграла котангенса
Пример
Задание. Найти неопределенный интеграл $int frac{operatorname{ctg} x d x}{2}$
Решение. Константу вынесем за знак интеграла, и полученный интеграл найдем по формуле:
$$int frac{operatorname{ctg} x d x}{2}=frac{1}{2} int operatorname{ctg} x d x=frac{1}{2} ln |sin x|+C$$
Ответ. $int frac{operatorname{ctg} x d x}{2}=frac{1}{2} ln |sin x|+C$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти интеграл $intleft(operatorname{ctg} x-2^{x}right) d x$
Решение. Интеграл от разности
функций равен разности интегралов, расписываем заданный интеграл:
$$intleft(operatorname{ctg} x-2^{x}right) d x=int operatorname{ctg} x d x-int 2^{x} d x=ln |sin x|-frac{2^{x}}{ln 2}+C$$
Ответ. $intleft(operatorname{ctg} x-2^{x}right) d x=ln |sin x|-frac{2^{x}}{ln 2}+C$
Читать дальше: интеграл натурального логарифма.
Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: «Как вычислить интеграл от тангенса и котангенса?«.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
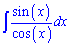
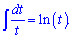
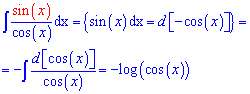
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
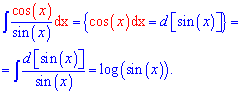
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Примеры интегрирования тангенса и котангенса
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
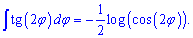
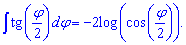
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
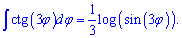
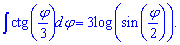
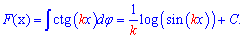
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории «Интегрирование функции» в левом меню сайта.
Интегрирование сложных тригонометрических функций
Прилагательное
«сложный» для большинства примеров
вновь носит во многом условный характер.
Начнем с тангенсов и котангенсов в
высоких степенях. С точки зрения
используемых методов решения тангенс
и котангенс – почти одно и тоже, поэтому
я больше буду говорить о тангенсе,
подразумевая, что продемонстрированный
прием решения интеграла справедлив и
для котангенса тоже.
На
уроке Интегралы
от тригонометрических функций мы
разобрали интеграл от тангенса в
квадрате. На уроке Как
вычислить площадь фигуры? в
примере 10 фигурировал тангенс в кубе.
В том примере для нахождения интеграла
от тангенса в кубе мы применяли
тригонометрическую формулу
.
Интеграл от тангенса в четвертой, пятой
степени (редко в более высоких степенях)
решается с помощью этой же формулы!
Пример
15
Найти
неопределенный интеграл
Идея
решения подобных интегралов состоит в
том, чтобы с помощью формулы
«развалить»
исходный интеграл на несколько более
простых интегралов:
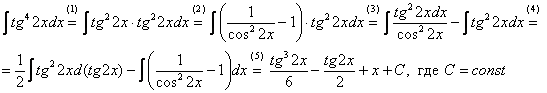
(1)
Готовим подынтегральную функцию к
применению формулы.
(2) Для одного из
множителей используем формулу
(3)
Раскрываем скобки и сразу же используем
свойство линейности неопределенного
интеграла.
(4) В первом интеграле
используем метод
подведения функции под знак дифференциала.
Во втором интеграле еще раз используем
формулу
,
в данном случае
.
(5)
Берём все три интеграла и получаем
ответ.
Пример
16
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Для котангенса существует аналогичная
формула:
.
Полное решение и ответ в конце урока.
Если
возникли затруднения или недопонимание,
следует вернуться к уроку Интегралы
от тригонометрических функций.
На
вышеупомянутом уроке мы
рассматривали универсальную
тригонометрическую подстановку для
решения определенного вида интегралов
от тригонометрических функций. Недостаток
универсальной тригонометрической
подстановки заключается в том, что при
её применении часто возникают громоздкие
интегралы с трудными вычислениями. И в
ряде случаев универсальной тригонометрической
подстановки можно избежать!
Рассмотрим
еще один канонический пример, интеграл
от единицы, деленной на синус:
Пример
17
Найти
неопределенный интеграл
Здесь
можно использовать универсальную
тригонометрическую подстановку и
получить ответ, но существует более
рациональный путь. Я приведу полное
решение с комментами к каждому шагу:

(1)
Используем тригонометрическую формулу
синуса двойного угла
.
(2)
Проводим искусственное преобразование:
В знаменателе делим и умножаем на
.
(3)
По известной формуле в знаменателе
превращаем дробь в тангенс.
(4) Подводим
функцию под знак дифференциала.
(5)
Берём интеграл.
Пара
простых примеров для самостоятельного
решения:
Пример
18
Найти
неопределенный интеграл
Указание:
Самым первым действием следует
использовать формулу приведения
и
аккуратно провести аналогичные
предыдущему примеру действия.
Пример
19
Найти
неопределенный интеграл
Ну,
это совсем простой пример.
Полные
решения и ответы в конце урока.
Думаю,
теперь ни у кого не возникнет проблем
с интегралами:
и
т.п.
В
чём состоит идея метода? Идея состоит
в том, чтобы с помощью преобразований,
тригонометрических формул организовать
в подынтегральной функции только
тангенсы и производную тангенса
.
То есть, речь идет о замене:
.
В Примерах 17-19 мы фактически и применяли
данную замену, но интегралы были настолько
просты, что дело обошлось эквивалентным
действием – подведением функции под
знак дифференциала.
Примечание:
аналогичные рассуждения, как я уже
оговаривался, можно провести и для
котангенса.
Существует
и формальная предпосылка для применения
вышеуказанной замены:
Сумма
степеней косинуса и синуса – целое
отрицательное число.
Для
интеграла
–
целое отрицательное число.
Для
интеграла
–
целое отрицательное число.
Для
интеграла
–
целое отрицательное число.
Рассмотрим
пару более содержательных примеров на
это правило:
Пример
20
Найти
неопределенный интеграл
Сумма
степеней синуса и косинуса
:
2 – 6 = –4 – целое отрицательное число,
значит, интеграл можно свести к тангенсам
и его производной:

(1)
Преобразуем знаменатель.
(2) По
известной формуле получаем
.
(3)
Преобразуем знаменатель.
(4) Используем
формулу
.
(5)
Подводим функцию под знак дифференциала.
(6)
Проводим замену
.
Более опытные студенты замену могут и
не проводить, но все-таки лучше заменить
тангенс одной буквой – меньше риск
запутаться.
Далее
берётся простой интеграл и проводится
обратная замена.
Пример
21
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Держитесь,
начинаются чемпионские раунды =)
Зачастую
в подынтегральной функции находится
«солянка»:
Пример
22
Найти
неопределенный интеграл
В
этом интеграле изначально присутствует
тангенс, что сразу наталкивает на уже
знакомую мысль:

Искусственное
преобразование в самом начале и остальные
шаги оставлю без комментариев, поскольку
обо всем уже говорилось выше.
Пара
творческих примеров для самостоятельного
решения:
Пример
23
Найти
неопределенный интеграл
Пример
24
Найти
неопределенный интеграл
Да,
в них, конечно, можно понизить степени
синуса, косинуса, использовать
универсальную тригонометрическую
подстановку, но решение будет гораздо
эффективнее и короче, если его провести
через тангенсы. Полное решение и ответы
в конце урока
У
многих читателей могло сложиться
впечатления, что я немного подустал.
Отнюдь. За окном февральский ветер –
самая атмосфера для лекций. Естественно,
данная страничка создана не за один
день, я успел несколько раз побриться,
регулярно кушаю и так далее. К тому же,
загружать студентов – удовольствие
бесконечное =). …Шутка! На самом деле
моя миссия – разгружать посетителей
сайта. Вагонами.
Переходим
к заключительному пункту познавательного
путешествия в мир сложных интегралов:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интегралы тригонометрических функций
Интеграл от синуса равен минус косинусу плюс константа интегрирования
(
int sin x d x=-cos x+C
)
Интеграл от косинуса равен синусу плюс константа интегрирования
(
int cos x d x=sin x+C
)
Интеграл от тангенса равен минус логарифму натуральному косинуса плюс константа интегрирования
(
int operatorname{tg} x d x=-ln |cos x|+C
)
Интеграл от котангенса равен логарифму натуральному синуса плюс константа интегрирования
(
int operatorname{ctg} x d x=ln |sin x|+C
)
Примеры решения задач
ПРИМЕР 1
Найти интеграл (
int(2 sin x+x) d x
)
Согласно свойствам интеграла, интеграл суммы равен сумме интегралов и постоянный множитель можно выносить за знак интеграла. Тогда заданный интеграл перепишется в виде:
(
int(2 sin x+x) d x=2 int sin x d x+int x d x
)
Интеграл от первого слагаемого
(
int sin x d x=-cos x+C
)
а от второго, как от степенной функции,
(
int x^{n} d x=frac{x^{n+1}}{n+1}+C
)
При (
mathrm{n}=1
) будем иметь:
(
int x d x=frac{x^{2}}{2}+C
)
Итак, искомый интеграл
(
int(2 sin x+x) d x=2 cdot(-cos x)+frac{x^{2}}{2}+C=-2 cos x+frac{x^{2}}{2}+C
)
(
int(2 sin x+x) d x=-2 cos x+frac{x^{2}}{2}+C
)
ПРИМЕР 2
Доказать, что (
int operatorname{ctg} x d x=ln sin x+C
)
Выведем записанную формулу. Для этого преобразуем подынтегральное выражение и применим метод подстановки для нахождения неопределенного интеграла:
(
int operatorname{ctg} x d x=int frac{cos x}{sin x} d x | operatorname{cin} x=t
)
Таблица первообразных
Таблица
первообразных («интегралов»).
Таблица интегралов. Табличные
неопределенные интегралы. (Простейшие
интегралы и интегралы с параметром).
Формулы интегрирования по частям.
Формула Ньютона-Лейбница.
|
Таблица |
|
|
Интеграл |
Интеграл |
|
Интеграл, |
|
|
Интеграл |
Интеграл |
|
Интеграл |
Интеграл |
|
Интеграл, |
Интеграл |
|
Интеграл |
|
|
Интеграл |
Интеграл, |
|
Интеграл |
|
|
|
|
|
Интеграл |
Интеграл |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
|
Интеграл, |
Интеграл, |
Формулы
интегрирования по частям. Правила
интегрирования.
|
Формулы |
|
|
Интегрирование |
|
|
Интегрирование |
|
|
Формула неопределенные |
|
|
Формула определенные |
|
|
Формула определенные |
Где |
Таблица
производных. Табличные производные.
Производная произведения. Производная
частного. Производная сложной функции.
Если
x — независимая переменная, то:
|
Таблица |
|
|
Производная |
Производная |
|
Производная |
Производная |
|
Производная |
Производная |
|
|
Производная |
|
Производная |
|
|
Производная |
Производная |
|
Производная |
Производная |
|
Производная |
|
|
Производная |
Производная |
|
|
Производная |
|
Производная |
Производная |
|
|
|
|
Производная |
Производная |
|
Производная |
Производная |
|
Производная
Производная |
Производная
Производная |
|
Производная |
Производная |
|
Производная |
Производная |
|
Правила |
|
|
Производная |
|
|
Производная |
|
|
Производная |
|
|
Производная |
|
|
Производная |
Свойства
логарифмов. Основные формулы логарифмов.
Десятичные (lg) и натуральные логарифмы
(ln).
|
Основное |
|
|
Покажем |
|
|
Любая |
Натуральный
логарифм ln (логарифм по основанию е =
2,718281828459045… )
ln(e)=1; ln(1)=0
|
При |
логарифм |
|
|
Например, |
||
Ряд
Тейлора. Разложение функции в ряд
Тейлора.
Оказывается,
большинство практически
встречающихся
математических функций могут быть с
любой точностью представлены в
окрестностях некоторой точки в виде
степенных рядов, содержащих степени
переменной в порядке возрастания.
Например, в окрестности точки х=1:
При
использовании рядов, называемых рядами
Тейлора,
смешанные функции, содержащие, скажем,
алгебраические, тригонометрические и
экспоненциальные функции, могут быть
выражены в виде чисто алгебраических
функций. С помощью рядов зачастую можно
быстро осуществить дифференцирование
и интегрирование.
Ряд
Тейлора в окрестности точки a имеет
виды:
1),
где f(x) — функция, имеющая при х=а производные
всех порядков. Rn
— остаточный член в ряде Тейлора
определяется выражением
2)
k-тый
коэффициент (при хk)
ряда определяется формулой
3)
Частным
случаем ряда Тейлора является ряд
Маклорена (=Макларена) (разложение
происходит вокруг точки а=0)
при
a=0
члены
ряда определяются по формуле
Условия
применения рядов Тейлора.
1.
Для того, чтобы функция f(x) могла быть
разложена в ряд Тейлора на интервале
(-R;R) необходимо и достаточно, чтобы
остаточный член в формуле Тейлора
(Маклорена (=Макларена)) для данной
функции стремился к нулю при k→∞ на
указанном интервале (-R;R).
2.
Необходимо чтобы существовали производные
для данной функции в точке, в окрестности
которой мы собираемся строить ряд
Тейлора.
Свойства
рядов Тейлора.
-
Если
f есть аналитическая функция, то ее ряд
Тейлора в любой точке а области
определения f сходится к f в некоторой
окрестности а. -
Существуют
бесконечно дифференцируемые функции,
ряд Тейлора которых сходится, но при
этом отличается от функции в любой
окрестности а. Например:
Ряды
Тейлора применяются при аппроксимации
( приближение — научный метод, состоящий
в замене одних объектов другими, в том
или ином смысле близкими к исходным, но
более простыми) функции многочленами.
В частности, линеаризация ((от linearis
— линейный), один из методов приближённого
представления замкнутых нелинейных
систем, при котором исследование
нелинейной системы заменяется анализом
линейной системы, в некотором смысле
эквивалентной исходной.) уравнений
происходит путём разложения в ряд
Тейлора и отсечения всех членов выше
первого порядка.
Таким
образом, практически любую функцию
можно представить в виде полинома с
заданной точностью.
Примеры
некоторых распространенных разложений
степенных функций в ряды Маклорена
(=Макларена,Тейлора в окрестностях точки
0) и Тейлора в окрестностях точки 1. Первые
члены разложений основных функций в
ряды Тейлора и Макларена.
Примеры
некоторых распространенных разложений
степенных функций в ряды Маклорена(
=Макларена, Тейлора в окрестностях точки
0)
Примеры
некоторых распространенных разложений
в ряды Тейлора в окрестностях точки 1
konspekt — Формулы
Тригонометрия
тригонометрические функции (определение через треугольник). Синус – отношение противолежащего катета к гипотенузе; косинус – отношение прилежащего катета к гипотенузе; тангенс – отношение противолежащего катета к прилежащему; котангенс – отношение прилежащего катета к противолежащему
тригонометрические функции (определение через окружность).
отсчет угла на декартовой системе координат (от нуля в положительном направлении) производится от положительного направления оси абсцисс к положительному направлению оси ординат, т.е. против часовой стрелки. В соответствии с этим производится нумерация координатных четвертей (в отрицательном направлении угол отсчитывается по часовой стрелке от положительного направления оси абсцисс)
градусная система измерения углов: полный оборот по окружности составляет 360°, половина оборота 180°, четверть оборота 90°
радиан – мера центрального угла, опирающегося на дугу, длина которой равна радиусу. Полный оборот по окружности составляет 2Π радиан, половина оборота Π радиан, четверть оборота Π/2 радиан
знаковые диаграммы тригонометрических функций для углов, соответствующих точкам на окружности в каждой координатной четверти: у синуса знак такой же, как и у ординаты точки; у косинуса знак такой же как и у абсциссы точки; у тангенса и котангенса: знак положительный, если знаки абсциссы и ординаты точки одинаковые, и отрицательный, если различные
таблица основных значений тригонометрических функций (первая часть таблицы получается из равнобедренного прямоугольного треугольника и из половины равностороннего треугольника; вторая часть таблицы получается из точек пересечения единичной окружности, с центром в начале координат, с осями системы координат)
формула перевода из радиан в грудусы (для запоминания: градусы стоят вверху, а радианы сокращаются)
формула перевода из градусов в радианы (для запоминания: радианы стоят вверху, а градусы сокращаются)
период синуса и косинуса равен 2Π
период тангенса и котангенса равен Π
формулы периодичности тригонометрических функций (в соответствии с определением периодической функции)
формулы приведения (общий конструктор): 1) если формула конструируется от горизонтального диаметра, то исходная функция не изменяется; 2) если формула конструируется от вертикального диаметра, то исходная функция изменяется на кофункцию; 3) перед полученной функцией ставится знак исходной функции, который определяется из знаковых диаграмм, считая: 0°<Α<90°.
Графики тригонометрических функций
график синуса (с отмеченными ключевыми точками)
график косинуса (с отмеченными ключевыми точками)
график тангенса (с отмеченными ключевыми точками)
график котангенса (с отмеченными ключевыми точками)
ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА:
Основные
Суммы и разности аргументов
Двойного аргумента
Тройного аргумента
Понижения степени
Половинного аргумента
Выражения функций через тангенс половинного угла
Суммы и разности функций
Произведения функций
Обратные тригонометрические тождества
определение обратных тригонометрических функций: 1) арксинус числа А, это угол α, если синус α равен А и α находится в указанном интервале; 2) арккосинус числа А, это угол α, если косинус α равен А и α находится в указанном интервале; 3) арктангенс числа А, это угол α, если тангенс α равен А и α находится в указанном интервале; 4) арккотангенс числа А, это угол α, если котангенс α равен А и α находится в указанном интервале;
тождества для обратных тригонометрических функций, содержащих знак минуса в аргументе
обратные тригонометрические тождества
тригонометрические тождества, содержащие в аргументе обратные тригонометрические функции (обратные функции соответствуют прямым)
тригонометрические тождества, содержащие в аргументе обратные тригонометрические функции (обратные функции не соответствуют прямым)
график арксинуса и график арккосинуса (с отмеченными ключевыми точками)
график арктангенса (с отмеченными ключевыми точками)
график арккотангенса (с отмеченными ключевыми точками)
Тригонометрические уравнения
1) линия тангенса (линия, каждая точка которой соответствует тангенсу угла между отрезком, проведенным в эту точку из начала координат, и положительным направлением оси абсцисс) 2) линия котангенса (линия, каждая точка которой соответствует котангенсу угла между отрезком, проведенным в эту точку из начала координат, и положительным направлением оси абсцисс)
тригонометрическое уравнение для синуса и его решение (при помощи окружности и синусоиды)
тригонометрическое уравнение для косинуса и его решение (при помощи окружности и косинусоиды)
тригонометрическое уравнение для тангенса и его решение (при помощи окружности и тангенсоиды)
тригонометрическое уравнение для котангенса и его решение (при помощи окружности и котангенсоиды)
Частные случаи решения тригонометрических уравнений
частные случаи решения тригонометрических уравнений (получаются графически)
Тригонометрические неравенства
тригонометрическое неравенство для синуса и его решение (при помощи окружности и синусоиды)
тригонометрическое неравенство для косинуса и его решение (при помощи окружности и косинусоиды)
тригонометрическое неравенство для тангенса и его решение (при помощи окружности и тангенсоиды)
тригонометрическое неравенство для котангенса и его решение (при помощи окружности и котангенсоиды)
Методы решения уравнений
однородное тригонометрическое уравнение (решается делением на косинус старшей степени с последующщей заменой тангенса и переходом к полиномиальному уравнению)
метод введения вспомогательного аргумента
Мэтуэй | Популярные задачи
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | ||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | ||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | |
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
92)
9(3x) по отношению к x
92+1
Справка по математике от арифметики до исчисления и далее
5 мая 2022 г.
VI. Видео исчисления
первообразная, постоянная, раскладушка, котангенс, производная, семейство, формула, функции, неопределенный, интеграл, интегрирование, джеймс, mathispower4u, произведение, пифагорейский, суза, подстановка, тригонометика
В этом видеоролике объясняется, как определить неопределенный интеграл или первообразную тригонометрической функции, требующей подстановки по Пифагору.
Оставить комментарий
4 мая 2022 г. 2 мая 2022 г. mathispower4u
VI. Видео исчисления
площадь, исчисление, косеканс, кроватка, котангенс, csc, определенный, график, интеграл, интегрирование, Джеймс, пределы, mathispower4u, sousa, подстановка, тригонометрический, значение
В этом видео показано, как вычислить определенный интеграл с помощью тригонометрической функции.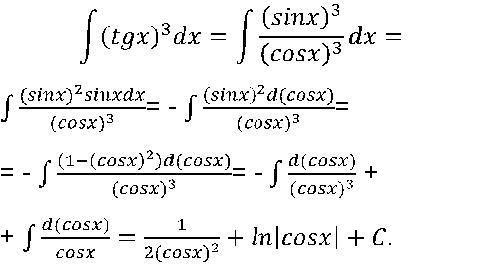
Оставить комментарий
4 апреля 2022 г. mathispower4u
VI. Видео исчисления
исчисление, косеканс, кроватка, котангенс, csc, производные, дифференцирование, формулы, джеймс, mathispower4u, частное, правило, суса, тригонометрия, тригонометрия
В этом видео показано, как применить правило дифференцирования для определения производной функции.
Оставить комментарий
9 сентября 2021 г.
IV. Видео по тригонометрии
круг, cos, кроватка, csc, точный, функция, джеймс, mathispower4u, радианы, сек, грех, соуза, загар, тригонометрический, тригонометрия, единица измерения, значения
В этом видеоролике объясняется, как определить значения тригонометрических функций с помощью единичного круга.
Оставить комментарий
9 сентября 2021 г. mathispower4u
IV. Видео по тригонометрии
cos, кроватка, csc, точно, функция, джеймс, mathispower4u, радианы, ссылка, сек, грех, суза, загар, треугольники, тригонометрия, тригонометрия, значения
В этом видеоролике объясняется, как определять значения тригонометрических функций с помощью эталонных треугольников.
Оставить комментарий
31 октября 2020 г. 31 октября 2020 г. mathispower4u
IV. Видео по тригонометрии
все, углы, круг, кроватка, котангенс, котерминал, уравнение, выражения, джеймс, mathispower4u, радианы, ссылка, решения, суза, тангенс, тангенс, треугольник, тригонометрический, блок
В этом видеоролике объясняется, как найти все решения основного тригонометрического уравнения с помощью опорных треугольников и единичной окружности.
Оставить комментарий
31 октября 2020 г.
IV. Видео по тригонометрии
все, углы, круг, кроватка, котангенс, котерминал, градусы, уравнение, выражения, джеймс, mathispower4u, ссылка, решения, суза, тангенс, тангенс, треугольник, тригонометрический, единица измерения
В этом видеоролике объясняется, как найти все решения основного тригонометрического уравнения с помощью опорных треугольников и единичной окружности.
Оставить комментарий
31 октября 2020 г. 31 октября 2020 г. mathispower4u
IV.
все, углы, круг, кроватка, котангенс, котерминал, уравнение, выражения, джеймс, mathispower4u, радианы, ссылка, решения, суза, тангенс, тангенс, треугольник, тригонометрический, блок
В этом видеоролике объясняется, как найти все решения основного тригонометрического уравнения с помощью опорных треугольников и единичной окружности.
Оставить комментарий
31 октября 2020 г. 31 октября 2020 г. mathispower4u
IV. Видео по тригонометрии
все, углы, круг, кроватка, котангенс, котерминал, градусы, уравнение, выражения, джеймс, mathispower4u, ссылка, решения, суза, тангенс, тангенс, треугольник, тригонометрический, единица измерения

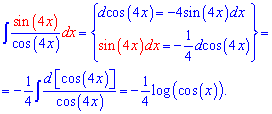
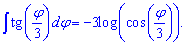
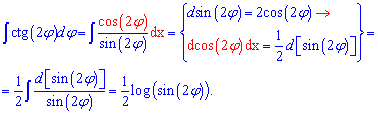
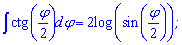
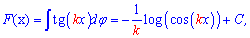

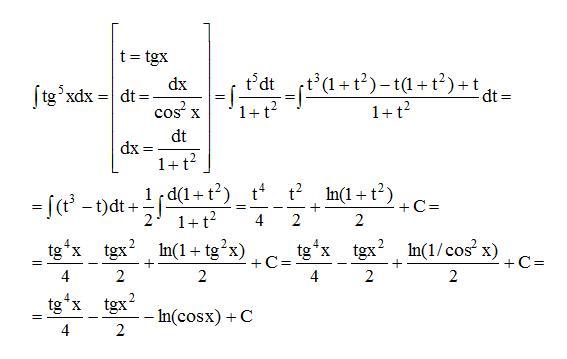

 Производная
Производная Поскольку
Поскольку