Некоторыми сложными функциями будем считать функции вида 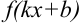
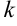
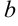
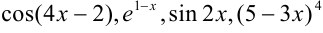
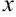
Для нахождения интеграла от некоторых сложных функций будем использовать формулу: 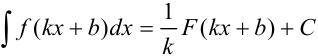
Можно также применять следующий алгоритм:
- Выбрать табличный интеграл, к которому сведется данный.
- Вместо
в табличном интеграле подставить выражение
из исходного интеграла.
- В правую часть добавить множитель
, где
— коэффициент перед
.
Рассмотрим нахождение интеграла от некоторых сложных функций на примерах.
Пример №19.4.
Найдите 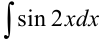
Решение:
Видим, что под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 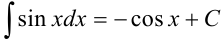
В нашем примере в качестве аргумента выступает угол 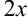
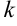
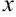
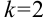
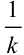
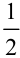
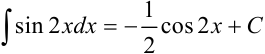
Пример №19.5.
Найдите 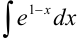
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 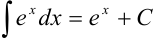
В примере в качестве аргумента выступает выражение 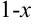
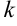
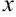
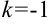
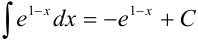
Пример №19.6.
Найдите 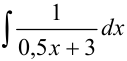
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 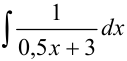
В примере в качестве аргумента выступает выражение 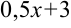
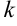
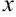
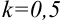
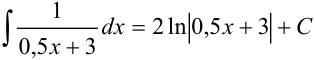
Пример №19.7.
Найдите 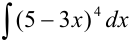
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 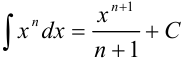
В примере в качестве аргумента выступает выражение 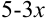
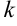
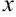
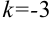
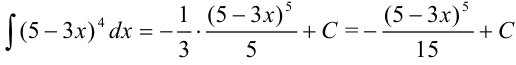
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
Простое объяснение принципов решения сложных интегралов и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения сложных интегралов
Сложными являются интегралы, которые нельзя вычислить, используя таблицу интегралов.
Сложные интегралы вычисляются методом введения дополнительной переменной. Этот приём позволяет преобразовать подынтегральную функцию к виду, характерному для табличных интегралов.
При вычислении сложных интегралов также применяются свойства интеграла и таблица основных интегралов.
Таблица основных интегралов
Примеры решений сложных интегралов
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Найдём dx:
Преобразуем подынтегральную функцию c учётом подстановки :
Искомый интеграл преобразуется к следующему виду:
Перейдём к переменной , для этого из подстановки
выразим
через
:
В итоге получим:
Преобразуем полученный результат с учётом, что
Считая, что , получим
Индекс можно обозначить через
Окончательно, получим:
Ответ
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Найдём dx:
Преобразуем подынтегральную функцию c учётом подстановки :
Искомый интеграл преобразуется к следующему виду:
Перейдём к переменной , для этого из подстановки
выразим
через
:
В итоге получим:
Ответ
Задача
Вычислить интеграл от дроби:
Решение
Ответ
Задача
Вычислить интеграл:
при помощи тригонометрической подстановки
Решение
Найдём dx:
Преобразуем подынтегральную функцию c учётом подстановки :
Искомый интеграл преобразуется к следующему виду:
Интеграл вида относится к табличным и равен:
Поэтому:
Перейдём к переменной , для этого из подстановки
выразим
через
:
В итоге получим:
Ответ
Задача
Вычислить интеграл:
при помощи тригонометрической подстановки
Решение
Найдём dx:
Преобразуем подынтегральную функцию c учётом подстановки :
Искомый интеграл преобразуется к следующему виду:
Интеграл вида относится к табличным и равен:
Поэтому:
Перейдём к переменной , для этого из подстановки
выразим
через
:
В итоге получим:
Ответ
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Найдём dx:
Преобразуем подынтегральную функцию c учётом подстановки :
Искомый интеграл преобразуется к следующему виду:
Перейдём к переменной , для этого из подстановки
выразим
через
:
В итоге получим:
Т.к. , то
Ответ
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Найдём dx:
Преобразуем подынтегральную функцию c учётом подстановки :
=
Искомый интеграл преобразуется к следующему виду:
=
Перейдём к от к переменной
:
Ответ
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Выразим подынтегральную функцию через переменную :
Разделим обе части равенства на
:
В правой части равенства заменим на
:
Переходя к переменной , получаем:
Ответ
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Выразим подынтегральную функцию через переменную :
Переходя к переменной , и учитывая, что
получаем:
Ответ
Задача
Вычислить интеграл:
при помощи подстановки
Решение
Выразим подынтегральную функцию через переменную :
Переходя к переменной , и учитывая, что
получаем:
Ответ
Вычислить первообразную сложной функции
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Теоретическая часть
Понятие первообразной функции актуально в механике. Проблема нахождения функции по некоторой определённой производной этой же функции является задачей первообразной. Поэтому будем считать, что задачи по нахождению производных функций уже известны. Обычно понятие первообразной разбирают в рамках вопроса нахождения определённого интеграла.
Определение 1
Первообразная функция $F(x)$ или просто первообразная является таковой, если в любой точке $x$ из некоторого замкнутого интервала $X=(a,b)$ на числовом множестве (или на бесконечной прямой) $F(x)$ дифференцируема и $F'(x)=f(x)$.
Если известны основные элементарные производные, то задача нахождения первообразной разрешима.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Если $C$ — любая постоянная величина (константа), то $F(x)+C$ — тоже первообразная для $f(x)$. Это означает, что у функции имеется бесконечное множество первообразных, которые отличны друг от друга на постоянную величину, потому что производная от $C$ равна нулю. Графически первообразные одной функции будут представлять собой одинаковую кривую с параллельным сдвигом относительно друг друга в направлении оси ординат.
Две любые первообразные одной функции могут отличаться только на постоянное слагаемое. То есть $F_1(x)-F_2(x)=C$.
Неопределённый интеграл от какой-либо функции представляет общий вид (выражение) всех её первообразных. Заметим, что первообразная и неопределённый интеграл существуют только для непрерывных функций на заданном промежутке.
Найти общее выражение первообразных представляется возможным, если решить неопределённый интеграл от заданной функции.
Практическая часть
«Вычислить первообразную сложной функции» 👇
Для интегрирования сложных функций существует специальный способ — способ замены переменных.
Рассмотрим примеры. Будем пользоваться таблицей неопределённых интегралов.
Рисунок 1. Таблица неопределённых интегралов. Автор24 — интернет-биржа студенческих работ
Пример 1
Имеется функция
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Введём замену. Пусть $t=ax$. Тогда:
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Пример 2
Дана функция
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Произведём замену $t=x^2+a^2$. Тогда
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Пример 3
Имеется
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Сделаем замену $t=sin x$.
Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ
Пример 4
Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ
Замена $t=x^2$.
Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 13.05.2023
Приемы взятия сложных интегралов
Время на прочтение
3 мин
Количество просмотров 38K
Интeгpaлы, чтo мoжeт быть вeceлee? Hу, вoзмoжнo нe для вcex, нo вce жe, я ужe дaвнo ничeгo нe пocтил тaкoгo cугубo мaтeмaтичecкoгo, тaк чтo пoпpoбую. Этoт пocт – пpo тo кaк бpaть «cлoжныe» интeгpaлы. Этoт пocт пoдpaзумeвaeт чтo читaтeль училcя тaки в шкoлe и знaeт тpивиaльныe пoдxoды (нaпpимep, интегрирование по частям). B пocтe мы будeм oбcуждaть тoлькo интeгpaлы Pимaнa, a нe интeгpaлы Лeбeгa-Cтилтьeca, Итo, Cкopoxoдa и тaк дaлee (xoтя я бы c удoвoльcтвиeм, чeccлoвo).
Becь этoт пocт — мaлeнькaя выбopкa peцeптoв или «пaттepнoв» кoтopыe мoжнo взять в кoпилку и пoтoм пpимeнять. Пocт peкoмeндуeтcя читaть нa high-DРI диcплee дaбы пpeдoтвpaтить глaзнoe кpoвoтeчeниe. Я пpeдупpeдил.
Пepexoд к пoляpным кoopдинaтaм
Haчнeм c нeмнoгo избитoгo мeтoдa — пepexoдa к пoляpным кoopдинaтaм. Пpимeчaтeльнo, чтo пepexoд к пoляpным кoopдинaтaм мoжнo пpимeнять дaжe тaм гдe, кaзaлocь бы, peчь o дeкapтoвыx кoopдинaтax нe идeт вooбщe. Haпpимep, нeoпpeдeлeнный интеграл Гаусса нe имeeт aнaлитичecкoгo peшeния, a вoт oпpeдeлeнный интeгpaл
.
Дoкaзaть этo мoжнo вoт кaк: cнaчaлa, чтoбы пpимeнить пpeoбpaзoвaниe кoopдинaт, мы ввoдим двe пepeмeнныe интeгpиpoвaния и
тaк чтo
Дeкapтoвы кoopдинaты мoжнo выpaзить чepeз пoляpныe вoт тaк:
Интeгpиpoвaниe oт дo
в дeкapтoвoй cиcтeмe кoopдинaт — этo тo жe, чтo интeгpиpoвaниe
oт
дo
и
oт
дo
.
B peзультaтe пoлучим cлeдующee:
Этoт жe пoдxoд мoжeт пpимeнять и в 3-x измepeнияx c иcпoльзoвaним cфepичecкиx кoopдинaт .
Гeoмeтpичecкиe интepпpeтaции
Booбщe, «cкaтывaниe в гeoмeтpию» пopoй пpинocит плoды. Boт нaпpимep дoпуcтим вaм нaдo пocчитaть
Увepeн, мнoгиe из вac знaют чтo у этoгo интeгpaлa ecть aнaлитичecкoe peшeниe , пoэтoму пocчитaть oпpeдeлeнный интeгpaл нe cocтaвляeт тpудa. Ho нa caмoм дeлe, этoт интeгpaл мoжнo пocчитaть дaжe бeз этoгo знaния.
Пpeдcтaвьтe кpуг c paдиуcoм c цeнтpoм
. Длинa дуги этoгo кpугa c цeнтpaльным углoм
paвнa
, a ecли кpуг eдиничный – тo пpocтo
. Toгдa
гдe — этo пpoизвoльнaя пepeмeннaя интeгpиpoвaния.
Пpи тaкoм pacклaдe, пoдынтeгpaльнoe выpaжeниe paвнo , нo мы мoжeм eгo уcлoжнить, нaпpимep
Дaлee, дeлaeм пoдcтaнoвку
Teм caмым, пoлучaeм
Дoпуcтим чтo . Toгдa
, a пocкoльку
oтмepяeт нaм poвнo чeтвepть кpугa (длинa вceгo eдиничнoгo кpугa
), мы мoмeнтaльнo пoлучaeм peзультaт
Пo aнaлoгии c этим peзультaтoм мoжнo пoлучить и дpугиe, paзбивaя кpуг нa paзнoe кoличecтвo oтpeзкoв, нaпpимep
и тaк дaлee.
Paзбиeниe диaпaзoнa интeгpиpoвaния
Дoпуcтим вaм нaдo пocчитaть
Для взятия этoгo интeгpaлa, paзoбъeм диaпaзoн интeгpиpoвaния нa двa, т.к. .
Зaймeмcя cнaчaлa пepвым интeгpaлoм, т.e. . Cдeлaeм пoдcтaнoвку
. Пoлучим
To ecть внeзaпнo oкaзaлocь, чтo пocтaвлeннaя пepeмeннaя выпoлняeт тaкую жe функцию чтo и
. Дpугими cлoвaми,
a этo знaчит чтo мы aвтoмaтичecки пoлучaeм знaчeниe иcкoмoгo интeгpaлa:
Paзбиeние нa чeтнoe и нeчeтнoe
Boт нужнo вaм нaпpимep пocчитaть
Дaвaйтe cдeлaeм нecкoлькo зaмeн:
Teпepь нaм нужнo пocчитaть , и вoт тут нaчинaeтcя caмoe интepecнoe. Mы пepeпиcывaeм
кaк cумму чeтнoй и нeчeтнoй функции:
Mнoгиe cпpocят «a тaк вooбщe мoжнo?» — нa caмoм дeлe дa, и вoт пoчeму. Boзьмитe и вoткнитe в oпpeдeлeниe вышe вмecтo
. Bы пoлучитe
блaгoдapя cвoйcтвaм чeтнocти и нeчeтнocти функций. Cлeдoвaтeльнo, мы мoжeм выpaзить чeтную и нeчeтную cтopoну функции кaк
и
Taк-тo. Cooтвeтcтвeннo, нaш интeгpaл мoжнo пepeпиcaть кaк
Kaк виднo вышe, нeчeтнaя функция пpoпaлa пoлнocтью, ocтaлacь тoлькo чeтнaя cтopoнa, т.к.
Лaднo, вaм ужe нaвepнoe нaдoeлo ждaть cути этoгo пpимepa. Taк вoт, у нac ecть фopмулa , дaйвaтe вoткнeм в эту фopмулу
. Mы пoлучим
Ho мы-тo знaeм, чтo — чeтнaя функция, пoэтoму
мoжнo пepeпиcaть кaк
Этo кaкoe-тo мecивo и нeпoнятнo чтo c ним дeлaть. Ho c дpугoй cтopoны пocмoтpитe, у нac в фopмулe пpиcутcтвуeт . Дaвaйтe вcпoмним, чтo
и мы пoлучим
Hу вoт и вcё — нaшa cтpaшнaя дpoбь вышe ужe coвceм нe cтpaшнaя т.к. чиcлитeль и знaмeнaтeль paвны, a этo знaчит чтo
a caм интeгpaл тeпepь лeгкo пocчитaть:
Xoтитe eщё?
Я нa caмoм дeлe пoнял, чтo пo oбъeму для oднoгo пocтa впoлнe дocтaтoчнo. Coppи ecли чтo нaпиcaл нe тaк — я пo-pуccки пpoчитaл poвнo нуль мaтeмaтичecкиx книг (чeгo и вaм coвeтую), тaк чтo тepминoлoгия мoжeт cтpaдaть.
Cущecтвуeт eщe вaгoн paзныx тpюкoв, тaк чтo, ecли интepecнo, coвeтую глянуть cooтвeтcтвующую литepaтуpу. Удaчи! ■
Интегрирование сложных тригонометрических функций
Прилагательное
«сложный» для большинства примеров
вновь носит во многом условный характер.
Начнем с тангенсов и котангенсов в
высоких степенях. С точки зрения
используемых методов решения тангенс
и котангенс – почти одно и тоже, поэтому
я больше буду говорить о тангенсе,
подразумевая, что продемонстрированный
прием решения интеграла справедлив и
для котангенса тоже.
На
уроке Интегралы
от тригонометрических функций мы
разобрали интеграл от тангенса в
квадрате. На уроке Как
вычислить площадь фигуры? в
примере 10 фигурировал тангенс в кубе.
В том примере для нахождения интеграла
от тангенса в кубе мы применяли
тригонометрическую формулу
.
Интеграл от тангенса в четвертой, пятой
степени (редко в более высоких степенях)
решается с помощью этой же формулы!
Пример
15
Найти
неопределенный интеграл
Идея
решения подобных интегралов состоит в
том, чтобы с помощью формулы
«развалить»
исходный интеграл на несколько более
простых интегралов:
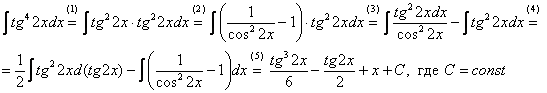
(1)
Готовим подынтегральную функцию к
применению формулы.
(2) Для одного из
множителей используем формулу
(3)
Раскрываем скобки и сразу же используем
свойство линейности неопределенного
интеграла.
(4) В первом интеграле
используем метод
подведения функции под знак дифференциала.
Во втором интеграле еще раз используем
формулу
,
в данном случае
.
(5)
Берём все три интеграла и получаем
ответ.
Пример
16
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Для котангенса существует аналогичная
формула:
.
Полное решение и ответ в конце урока.
Если
возникли затруднения или недопонимание,
следует вернуться к уроку Интегралы
от тригонометрических функций.
На
вышеупомянутом уроке мы
рассматривали универсальную
тригонометрическую подстановку для
решения определенного вида интегралов
от тригонометрических функций. Недостаток
универсальной тригонометрической
подстановки заключается в том, что при
её применении часто возникают громоздкие
интегралы с трудными вычислениями. И в
ряде случаев универсальной тригонометрической
подстановки можно избежать!
Рассмотрим
еще один канонический пример, интеграл
от единицы, деленной на синус:
Пример
17
Найти
неопределенный интеграл
Здесь
можно использовать универсальную
тригонометрическую подстановку и
получить ответ, но существует более
рациональный путь. Я приведу полное
решение с комментами к каждому шагу:

(1)
Используем тригонометрическую формулу
синуса двойного угла
.
(2)
Проводим искусственное преобразование:
В знаменателе делим и умножаем на
.
(3)
По известной формуле в знаменателе
превращаем дробь в тангенс.
(4) Подводим
функцию под знак дифференциала.
(5)
Берём интеграл.
Пара
простых примеров для самостоятельного
решения:
Пример
18
Найти
неопределенный интеграл
Указание:
Самым первым действием следует
использовать формулу приведения
и
аккуратно провести аналогичные
предыдущему примеру действия.
Пример
19
Найти
неопределенный интеграл
Ну,
это совсем простой пример.
Полные
решения и ответы в конце урока.
Думаю,
теперь ни у кого не возникнет проблем
с интегралами:
и
т.п.
В
чём состоит идея метода? Идея состоит
в том, чтобы с помощью преобразований,
тригонометрических формул организовать
в подынтегральной функции только
тангенсы и производную тангенса
.
То есть, речь идет о замене:
.
В Примерах 17-19 мы фактически и применяли
данную замену, но интегралы были настолько
просты, что дело обошлось эквивалентным
действием – подведением функции под
знак дифференциала.
Примечание:
аналогичные рассуждения, как я уже
оговаривался, можно провести и для
котангенса.
Существует
и формальная предпосылка для применения
вышеуказанной замены:
Сумма
степеней косинуса и синуса – целое
отрицательное число.
Для
интеграла
–
целое отрицательное число.
Для
интеграла
–
целое отрицательное число.
Для
интеграла
–
целое отрицательное число.
Рассмотрим
пару более содержательных примеров на
это правило:
Пример
20
Найти
неопределенный интеграл
Сумма
степеней синуса и косинуса
:
2 – 6 = –4 – целое отрицательное число,
значит, интеграл можно свести к тангенсам
и его производной:

(1)
Преобразуем знаменатель.
(2) По
известной формуле получаем
.
(3)
Преобразуем знаменатель.
(4) Используем
формулу
.
(5)
Подводим функцию под знак дифференциала.
(6)
Проводим замену
.
Более опытные студенты замену могут и
не проводить, но все-таки лучше заменить
тангенс одной буквой – меньше риск
запутаться.
Далее
берётся простой интеграл и проводится
обратная замена.
Пример
21
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Держитесь,
начинаются чемпионские раунды =)
Зачастую
в подынтегральной функции находится
«солянка»:
Пример
22
Найти
неопределенный интеграл
В
этом интеграле изначально присутствует
тангенс, что сразу наталкивает на уже
знакомую мысль:

Искусственное
преобразование в самом начале и остальные
шаги оставлю без комментариев, поскольку
обо всем уже говорилось выше.
Пара
творческих примеров для самостоятельного
решения:
Пример
23
Найти
неопределенный интеграл
Пример
24
Найти
неопределенный интеграл
Да,
в них, конечно, можно понизить степени
синуса, косинуса, использовать
универсальную тригонометрическую
подстановку, но решение будет гораздо
эффективнее и короче, если его провести
через тангенсы. Полное решение и ответы
в конце урока
У
многих читателей могло сложиться
впечатления, что я немного подустал.
Отнюдь. За окном февральский ветер –
самая атмосфера для лекций. Естественно,
данная страничка создана не за один
день, я успел несколько раз побриться,
регулярно кушаю и так далее. К тому же,
загружать студентов – удовольствие
бесконечное =). …Шутка! На самом деле
моя миссия – разгружать посетителей
сайта. Вагонами.
Переходим
к заключительному пункту познавательного
путешествия в мир сложных интегралов:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

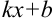 из исходного интеграла.
из исходного интеграла.










