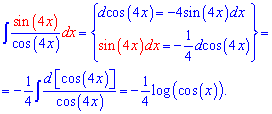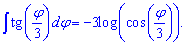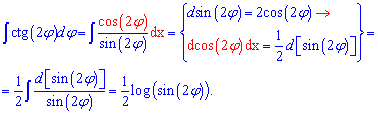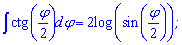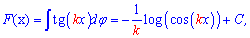Содержание:
- Формула
- Примеры вычисления интеграла тангенса
Формула
$$int operatorname{tg} x d x=-ln |cos x|+C$$
Интеграл от тангенса равен минус
логарифму натуральному от косинуса плюс константа интегрирования.
Примеры вычисления интеграла тангенса
Пример
Задание. Найти неопределенный интеграл $int 2 operatorname{tg} x d x$
Решение. Согласно
свойствам интеграла, константу можно выносить за знак интеграла, тогда
$$int 2 operatorname{tg} x d x=2 int operatorname{tg} x d x=2(-ln |cos x|)+C=-2 ln |cos x|+C$$
Ответ. $int 2 operatorname{tg} x d x=-2 ln |cos x|+C$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти интеграл $int(x-operatorname{tg} x) d x$
Решение. Интеграл от разности равен
разности интегралов, тогда
$$int(x-operatorname{tg} x) d x=int x d x-int operatorname{tg} x d x$$
Первый интеграл берем как интеграл от степенной функции, а второй как от тангенса. В итоге будем иметь:
$$int(x-operatorname{tg} x) d x=frac{x^{1+1}}{1+1}-(-ln |cos x|)+C=$$
$$=frac{x^{2}}{2}+ln |cos x|+C$$
Ответ. $int(x-operatorname{tg} x) d x=frac{x^{2}}{2}+ln |cos x|+C$
Читать дальше: интеграл котангенса.
Интеграл тангенса
Интеграл тангенса равен минус натуральному логарифму косинуса того же аргумента плюс константа интегрирования
(
int operatorname{tg} x d x=-ln |cos x|+C
)
Примеры решения задач
ПРИМЕР 1
Доказать формулу (
int operatorname{tg} x d x=-ln |cos x|+C
)
Указанный интеграл находится методом замены переменной:
(
int operatorname{tg} x d x=int frac{sin x d x}{cos x}|-sin x d x=-d t|=int frac{-d t}{t}=-ln |t|+C=-ln |cos x|+C
)
ПРИМЕР 2
Найти интеграл (
int operatorname{tg} 2 x d x
)
Данный интеграл сведем к указанной выше формуле заменой переменной:
(
int operatorname{tg} 2 x d x |left|begin{array}{c}{2 x=t} \ {2 d x=d t} \ {d x=frac{d t}{2}}end{array}right|=int operatorname{tg} t cdot frac{d t}{2}=frac{1}{2} int operatorname{tg} t d t=frac{1}{2}(-ln |cos t|)+C=-frac{ln |cos 2 x|}{2}+C
)
(
int operatorname{tg} 2 x d x=-frac{ln |cos 2 x|}{2}+C
)
Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: «Как вычислить интеграл от тангенса и котангенса?«.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
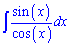
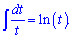
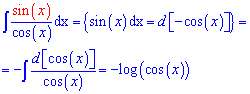
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
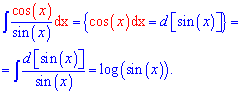
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Примеры интегрирования тангенса и котангенса
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
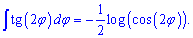
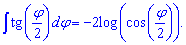
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
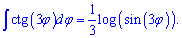
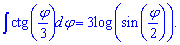
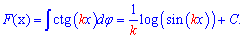
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории «Интегрирование функции» в левом меню сайта.
Интеграл тангенса и котангенса
Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: «Как вычислить интеграл от тангенса и котангенса?«.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
Сейчас Вам понятно. Далее нужно внести синус под дифференциал, чтобы свести интеграции в логарифма
В результате получимТаким образом вывели простую и нужную на практике формулу — интеграл от тангенса равен логарифму косинуса со знаком минус.
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
Интеграл от котангенса равный логарифму от синуса.
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории «Интегрирование функции» в левом меню сайта.
- Назад
- Вперёд
5.1.3.Интегралы от тригонометрических функций. Примеры решений
На данном уроке
мы рассмотрим интегралы от тригонометрических
функций, то есть начинкой интегралов у
нас будут синусы, косинусы, тангенсы
и котангенсы в различных комбинациях.
Все примеры будут разобраны подробно,
доступно и понятно даже для чайника.
Для
успешного изучения интегралов от
тригонометрических функций Вы должны
хорошо ориентироваться в простейших
интегралах, а также владеть некоторыми
приемами интегрирования.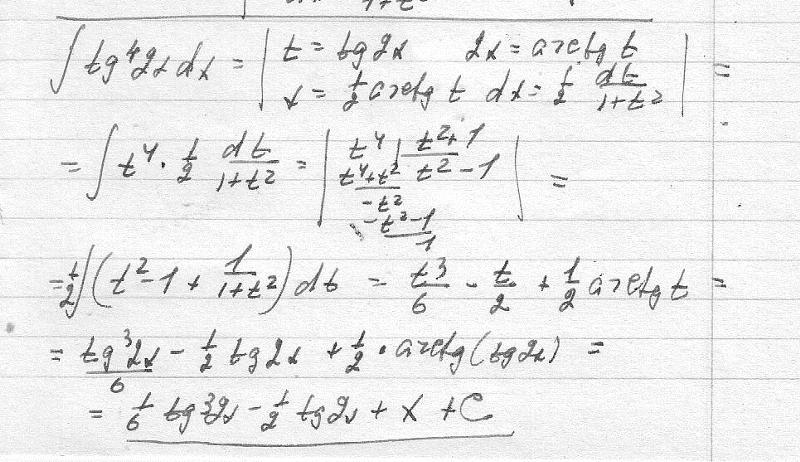
с этими материалами можно на
лекциях Неопределенный
интеграл. Примеры решений и Метод
замены переменной в неопределенном
интеграле.
А
сейчас нам потребуются: Таблица
интегралов, Таблица
производных и Справочник
тригонометрических формул.
Все методические пособия можно найти
на страницеМатематические
формулы и таблицы.
Рекомендую всё распечатать. Особо
заостряю внимание на тригонометрических
формулах,
они
должны быть перед глазами –
без этого эффективность работы заметно
снизится.
Но
сначала о том, каких интегралов в данной
статье нет.
Здесь не найдется интегралов вида
,
–
косинус, синус, умноженный на какой-нибудь
многочлен (реже что-нибудь с тангенсом
или котангенсом). Такие интегралы
интегрируются по частям, и для изучения
метода посетите урок Интегрирование
по частям. Примеры решений.Также
здесь не найдется интегралов с
«арками» – арктангенсом, арксинусом и
др.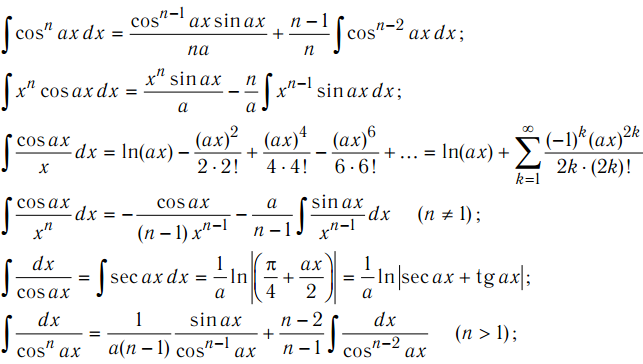
по частям.
При нахождении
интегралов от тригонометрических
функций используется ряд методов:
Использование
тригонометрических формул
Понижение
степени подынтегральной функции
(частный
случай п.1)
Метод
замены переменной
Универсальная
тригонометрическая подстановка (частный
случай п.3)
В рамках урока я
постараюсь подробно разобрать все
перечисленные методы и привести примеры
решения типовых интегралов. Следует
отметить, что данное разделение по
параграфам весьма условно, поскольку
очень часто вышеперечисленные правила
используются одновременно.
Пример 1
Найти
неопределенный интеграл.
Сначала
полное решение, потом комментарии.
Используем
формулу:
(1) Мы
видим, что в подынтегральном выражении
находится произведение двух функций.
К сожалению, в интегральном исчислении
нет удобной формулы для интегрирования
произведения:
,
поэтому приходится прибегать к различным
ухищрениям. В данном случае мы прерываем
решение значком
и
поясняем, что используется тригонометрическая
формула. Данная формула превращает
произведение в сумму.
(2) Используем
свойства линейности неопределенного
интеграла – интеграл от суммы равен
сумме интегралов; константу можно (и
нужно) вынести за знак интеграла.
! Справка:
При работе с тригонометрическими
функциями следует помнить, что:
Косинус
– это четная функция, то есть ,
минус исчезает без всяких последствий.
В рассматриваемом примере:
Синус
– функция нечетная: –
здесь минус, наоборот – не пропадает,
а выносится.
(3) Под
интегралами у нас сложные функции
(косинусы не просто от
,
а от сложного аргумента).
Это простейшие
из сложных функций, интегралы от них
удобнее найти методом подведения под
знак дифференциала. Более подробно с
данным приёмом можно ознакомиться на
уроке
Метод
замены переменной в неопределенном
интеграле
.
(4)
Используем табличную формулу
,
единственное отличие, вместо «икса» у
нас сложное выражение.
Готово.
Пример
2
Найти
неопределенный интеграл.
Это пример для
самостоятельного решения, полное решение
и ответ – в конце урока.
Пример 3
Найти
неопределенный интеграл.
Классика жанра
для тех, кто тонет на зачёте. Как Вы,
наверное, заметили, в таблице интегралов
нет интеграла от тангенса и котангенса,
но, тем не менее, такие интегралы найти
можно.
(1)
Используем тригонометрическую формулу
(2) Подводим функцию
под знак дифференциала.
(3)
Используем табличный интеграл
.
Пример 4
Найти
неопределенный интеграл.
Это пример для
самостоятельного решения, полное решение
и ответ – в конце урока.
Пример 5
Найти
неопределенный интеграл.
Степени у нас будут
потихоньку повышаться =).
Сначала
решение:
(1)
Используем формулу
(2)
Используем основное тригонометрическое
тождество
,
из которого следует, что
.
(3) Почленно делим
числитель на знаменатель.
(4) Используем
свойство линейности неопределенного
интеграла.
(5) Интегрируем с
помощью таблицы.
Пример 6
Найти
неопределенный интеграл.
Это пример для
самостоятельного решения, полное решение
и ответ – в конце урока.
Также
существуют интегралы от тангенсов и
котангенсов, которые находятся в более
высоких степенях.
в кубе рассмотрен на уроке Как
вычислить площадь плоской фигуры? Интегралы
от тангенса (котангенса) в четвертой и
пятой степенях можно раздобыть на
странице Сложные
интегралы.
Интегрирование тангенса x
Стандартный результат интегрирования тангенса x: ln|sec x| + C. Тригонометрическая функция tan x интегрируема, и этот стандартный результат интегрирования tan x запоминается как формула. Давайте узнаем, как решить интеграцию tan x в следующем разделе.
| 1. | Что такое интеграция Tan X? |
| 2. | Как решить интеграцию Tan X? |
| 3. | Определенная интеграция Tan X |
| 4. | График интеграции Tan X |
| 5. | Часто задаваемые вопросы по интеграции Tan X |
Что такое интеграция Tan X?
Интегрирование tan x равно -ln|cos x| + C (или) ln|sec x| + C.
Как решить интеграцию Tan X?
Чтобы найти интегрирование тангенса х по х, мы выражаем тангенс х через синус и косинус так, чтобы он стал интегрируемой функцией. В соответствии с определением тангенса x мы имеем тангенс x = sin x / cos x
∫ tan x =∫ (sin x /cos x) .dx
Это можно переписать как (int dfrac{1} { соз х} ). грех х. dx
Найдем неопределенный интеграл от tan x, используя метод подстановки интегрирования.
∫ f(g(x)) g'(x) dx = ∫ f(u) du = F(u) + C
Пусть u = cos x. Тогда du = — sin x . dx
⇒ dx = — du/ sin x
∫(sin x /cos x). dx = — ∫ du/ u
По стандартной формуле интегрирования мы знаем, что ∫ dx/x = ln x+ C
Таким образом, ∫ (sin x /cos x) .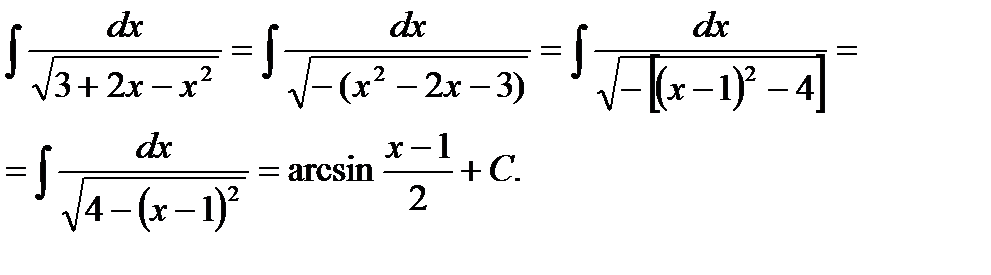
= -ln |(cos x)+C
= ln |(cos x) -1 +C
= ln (sec x) + C
∫ (sin x /cos x) . dx = ln (сек x) + C
∫ tan x = ln (сек x) + C 9{pi/2}_0)
= ln|sec π/2| — ln|сек 0|
=ln(∞)- ln(1)
= ∞
Таким образом, график интеграла от tan x расходится к бесконечности в интервале [0,π/2].
☛ Также проверьте
- Формулы интегрирования
- Производное tan x
Часто задаваемые вопросы по интеграции Tan X
Что такое интеграция Tan X?
Интегрирование тангенса x равно ln|sec x| + C (или) -ln|cos x| + С.
Является ли Tan x интегрируемым?
Да, Tan x интегрируем. Tan x — непрерывная функция в своей области определения. Интегрирование тангенса x равно -ln|cos x| + C.
Как сделать интеграцию Tan X?
Интегрирование тангенса х производится методом интегрирования подстановкой.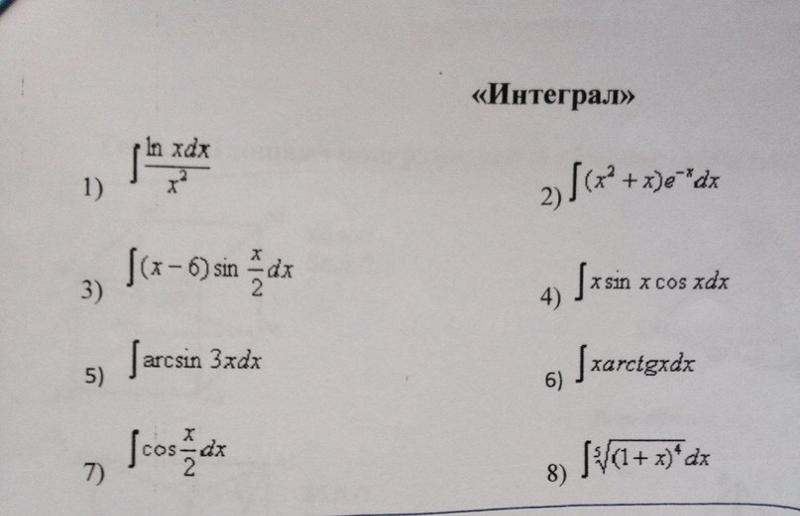
=-∫ du/ u = -ln u + C
= -ln|cos x| + C.
Таким образом, ∫ tan x = = -ln|cos x| + С.
Что такое интеграция 2Tan X?
Интегрирование tan x равно -ln|cos x| + C. Таким образом, (int) 2 tan x = 2 (int) tan x
∫ 2 tan x = -2 ln|cos x| + C.
= — ln|cos 2 x| + C.
Является ли дифференциация и интеграция Tan x одним и тем же?
Нет. дифференцирование и интегрирование тангенса х не одно и то же. Дифференциация тангенса х есть сек 2 х, а интегрирование тангенса х есть ln|сек х| + C.
Какую технику мы используем, чтобы найти интеграцию Tan X?
интегрирование тангенса x производится методом интегрирования u-подстановкой. Запишем tan x в интегрируемой форме sin x / cos x, а затем возьмем u(x) как cos(x).
Методом подстановки мы знаем, что ∫ f(g(x)) g'(x) dx =∫ f(u) du = F(u) + C, где g(x) = f(u) .
Интегральный тангенс(х)
Интегральный тангенс(х)
|
Дом | Учитель | Родители | Глоссарий | О нас |
|||||
|

|
sect |
= |
x |
; |
tgt = |
x2 − |
4 |
||||||||||||||||
|
Так как |
2 |
2 |
. |
|||||||||||||||||||
|
2 |
x2 |
− 4 |
||||||||||||||||||||
|
cost |
= |
; |
sin t |
= |
||||||||||||||||||
|
x |
2 |
|||||||||||||||||||||
|
Следовательно: |
||||||||||||||||||||||
|
I = |
2 |
sin t |
+ |
1 |
ln sect + tgt + C = 2 |
x2 |
− 4 x2 |
+ |
1 |
ln |
x |
+ |
x2 − 4 |
+ C = |
||||||||
|
cos2 t |
2 |
4x |
2 |
2 |
2 |
|||||||||||||||||
|
. |
||||||||||||||||||||||
|
x x2 |
− 4 |
1 |
x + x2 − 4 |
|||||||||||||||||||
|
= |
+ |
ln |
+ C |
|||||||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||
|
Ответ: |
x x2 − 4 |
+ |
1 |
ln |
x + x2 |
− 4 |
+ C . |
|||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||
Интегралы от тригонометрических выражений различного типа во многих ситуациях удается рационализировать либо существенно упростить.
Типы тригонометрических выражений и способы их интегрирования
|
1. Универсальная тригонометрическая подстановка t = tg |
u |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
2dt |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
tg |
= t; x = 2arctg t; dx = |
2t |
1− t 2 |
2dt |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∫ R(sin x, cos x)dx = |
2 |
(1+ t 2 ) |
= |
∫ R( |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1− t 2 |
2t |
;1+ t2 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
cos x |
= |
; sin x = |
1+ t 2 |
1+ t 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1+ t 2 |
1+ t 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 32. Найти интеграл ∫ |
dx |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
sin3 3x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
dx |
tg |
x |
= t; x = 2arctg t; dx = |
2dt |
dt |
1 |
(1+ t 2 ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
1+ t |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∫ |
= |
2t |
= 2∫ |
= |
4 ∫ |
dt |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
sin3 3x |
sin x = |
(1+ t 2 )( |
2t |
)3 |
t3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
+ t2 |
1+ t 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 2 |
1 1 |
2 |
1 |
2 x |
1 |
x |
2 x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= 4 |
∫( |
+ t |
+ t)dt = − |
+ 2 ln |
t |
+ t |
+ C |
= − |
8 ctg |
+ |
2 ln |
tg |
+ tg |
+ C |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
t3 |
8t2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ответ: − |
1 |
ctg |
2 |
x |
+ |
1 |
ln |
tg |
x |
+ tg 2 |
x |
+ C . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8 |
2 |
2 |
dx
Пример 33. Найти интеграл∫ 5 + 2sin x + 3cos x .
Решение
27
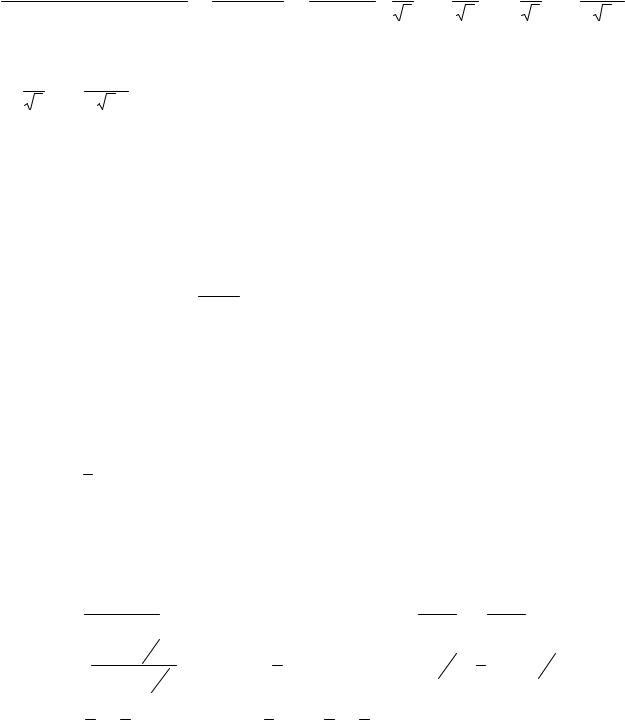
|
dx |
tg |
x |
= t; x |
= 2arctg t; dx |
= |
2dt |
2dt |
||||||||||||||||||||||||||||||||||
|
(1+ t 2 ) |
|||||||||||||||||||||||||||||||||||||||||
|
∫ |
= |
2 |
− t 2 |
= ∫ |
= |
||||||||||||||||||||||||||||||||||||
|
5 + 2sin x + 3cos x |
1 |
2t |
2 |
4t |
3 − 3t 2 |
||||||||||||||||||||||||||||||||||||
|
cos x = |
2 ; sin x = |
(1+ t |
) 5 |
+ |
+ |
||||||||||||||||||||||||||||||||||||
|
1 |
+ t |
1+ t |
2 |
||||||||||||||||||||||||||||||||||||||
|
1+ t |
2 |
1+ t |
2 |
||||||||||||||||||||||||||||||||||||||
|
tg |
x |
+ 1 |
|||||||||||||||||||||||||||||||||||||||
|
2dt |
2dt |
dt |
2 |
t + 1 |
2 |
||||||||||||||||||||||||||||||||||||
|
∫ |
= ∫ |
2 |
|||||||||||||||||||||||||||||||||||||||
|
2 |
5 + 5t 2 |
+ 4t + 3 − 3t 2 = ∫ |
2t 2 + 4t + 8 |
(t + 1)2 + 3 |
= |
3 arctg |
3 |
+ C = |
3 arctg |
3 |
+ C |
||||||||||||||||||||||||||||||
|
(1+ t |
) |
||||||||||||||||||||||||||||||||||||||||
|
1+ t |
2 |
||||||||||||||||||||||||||||||||||||||||
|
tg |
x |
||||||||||||||||||||||||||||||||||||||||
|
2 |
+ 1 |
||||||||||||||||||||||||||||||||||||||||
|
Ответ: |
2 |
||||||||||||||||||||||||||||||||||||||||
|
3 arctg |
3 |
+ C |
2. Применение замены t = tgx .
|
m + n = 2 p; tgx = t; sin2 x = |
t2 |
|||||||||||
|
∫ sinm x cosn x dx = |
1 |
+ t2 |
= ∫ R(t)dt |
|||||||||
|
1 |
||||||||||||
|
cos2 x = |
; x = arctg t; dx = |
dt |
||||||||||
|
1 |
+ t2 |
1 + t2 |
||||||||||
dx
Пример 34. Найти интеграл ∫ cos4 x .
Решение
|
∫ |
dx |
= |
tg x = t; cos |
2 |
x = |
1 |
; dx = |
dt |
= ∫ |
(1+ t 2 )2 dt |
= ∫(1+ t2 )dt |
|
1+ t 2 |
1+ t 2 |
||||||||||
|
cos4 x |
1+ t2 |
||||||||||
|
x = arctg t |
= tg x + 13 tg3 x + C
Ответ: tg x + 13 tg3 x + C .
|
cos6 x |
||||
|
Пример 35. Найти интеграл ∫ sin 4 x dx . |
||||
|
Решение |
||||
|
cos6 x |
(1− sin 2 x)3 |
dx = ∫ |
1− 3sin2 x + 3sin 4 x − sin6 x |
dx |
|
∫ sin 4 x dx = ∫ |
sin 4 x |
sin 4 x |
dx = ∫ sin 4 x |
|
− ∫sin |
2 |
x dx = ∫ |
d(x + π 2) |
+ 3ctg x + 3x − |
1 |
∫(1− cos 2x)dx = tg(x + |
π |
2 |
) + |
1 |
tg |
3 |
(x + π |
2 |
) + |
|||||||||||||
|
cos |
4 |
(x + |
π |
2) |
2 |
3 |
||||||||||||||||||||||
|
1 ctg3 x + |
5 x + |
1 sin 2x + C |
||||||||||||||||||||||||||
|
+ 3ctg x + 3x − |
1 x + |
1 sin 2x + C |
= −ctg x − |
|||||||||||||||||||||||||
|
2 |
4 |
3 |
2 |
4 |
||||||||||||||||||||||||
|
Ответ: − ctg x − |
1 |
ctg3 x + |
5 |
x + |
1 |
sin 2x + C . |
||||||||||||||||||||||
|
3 |
2 |
4 |
||||||||||||||||||||||||||
3. Внесение под знак дифференциала функции в нечетной степени
28

|
∫sin m x cosn x dx = |
sin |
|
∫ (1.5.3) |
|
|
= −∫ (1 − t2 ) p tn dt = |
|
|
, |
т.е. m — нечетное число.
Пример 36. Найти интеграл ∫cos5 x dx .
Решение
∫cos5 x dx = ∫cos4 x d(sin x) = ∫(1− sin 2 x)2 d(sin x) = ∫(1− 2sin x + sin 4 x) d(sin x) =
|
= sin x − |
2 sin3 |
x + |
1 sin5 |
. |
|
x + C |
||||
|
3 |
5 |
Ответ: sin x − 23 sin3 x + 15 sin5 x + C .
Пример 37. Найти интеграл ∫ sindxx .
Решение
|
∫ |
dx |
= ∫ |
sin x dx |
= −∫ |
d(cos x) |
= |
1 |
1 − cos x |
+ С |
||
|
sin2 x |
2 ln |
||||||||||
|
sin x |
1 − cos2 x |
1 + cos x |
Ответ: 12 ln 11 +− coscos xx + С .
|
4). Понижение порядка выражения |
|||||||||||||||||||||||||||||
|
m + n = 2 p; m ≥ 0; n ≥ 0 |
|||||||||||||||||||||||||||||
|
∫sin m x cosn x dx = |
sin 2 x = |
1 |
(1− cos 2x); cos2 x = 1 (1+ cos 2x) |
(1.5.4) |
|||||||||||||||||||||||||
|
2 |
1 |
2 |
|||||||||||||||||||||||||||
|
sin x cos x = |
sin 2x |
||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||
|
Пример 38. Найти интеграл∫sin 2 5x cos4 5x dx . |
|||||||||||||||||||||||||||||
|
Решение |
|||||||||||||||||||||||||||||
|
∫sin 2 5x cos4 5x dx = ∫ |
(sin 5x cos5x) cos2 5x dx = ∫ |
sin 2 10x |
(1+ cos10x) |
dx = |
|||||||||||||||||||||||||
|
1 |
1 |
1 |
4 |
2 |
|||||||||||||||||||||||||
|
∫sin 2 10x dx + |
∫sin 2 |
10x cos10x dx = |
∫(1− cos 20x)dx + |
1 |
∫sin 2 |
10x d(sin10x) = |
|||||||||||||||||||||||
|
8 |
80 |
||||||||||||||||||||||||||||
|
1 |
1 |
8 |
16 |
||||||||||||||||||||||||||
|
= |
x − |
sin 20x + |
1 |
sin3 10x + C |
|||||||||||||||||||||||||
|
16 |
320 |
240 |
|||||||||||||||||||||||||||
|
Ответ: |
1 |
x − |
1 |
sin 20x + |
1 |
sin3 10x + C . |
|||||||||||||||||||||||
|
16 |
320 |
||||||||||||||||||||||||||||
|
240 |
5). Случай четных степеней тригонометрических функций
29
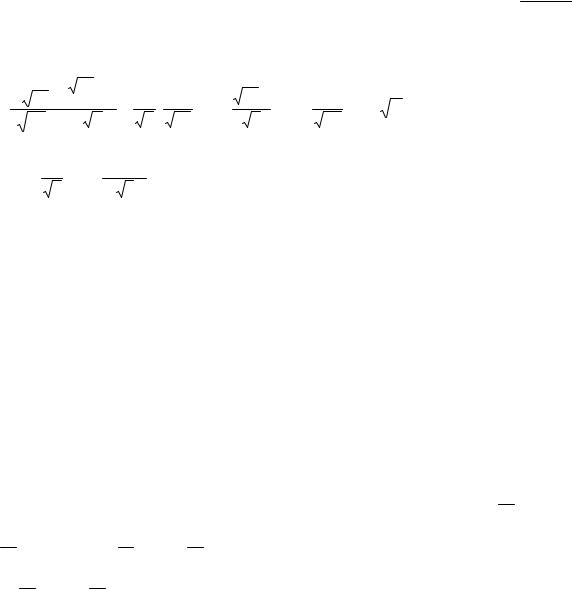
|
tgx = t; x = arctgt |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
∫ R(sin 2 x, cos2 x,sin x cos x)dx = |
dx = |
dt |
; sin 2 x = |
t 2 |
= |
|||||||||||||||||||||||||||||||||||||||||||||
|
(1 |
2 |
) |
1+ t |
2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
+ t |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
cos2 x = |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
1+ t 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
= ∫ R( |
t 2 |
; |
1 |
; |
t |
) |
2dt |
= ∫ R |
** |
(t)dt |
||||||||||||||||||||||||||||||||||||||||
|
1+ t 2 |
1+ t 2 |
1+ t 2 |
1+ t 2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 39. Найти интеграл ∫ |
dx |
. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
2cos2 x + 10sin 2 x |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
dx |
tgx = t; x = arctgt |
t2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
∫ |
= |
dx = |
dt |
; sin |
2 |
x |
= |
= ∫ |
dt |
= |
||||||||||||||||||||||||||||||||||||||||
|
2 cos2 x + 10 sin 2 x |
(1 + t2 ) |
1 + t2 |
(1 + t |
2 |
2 |
+ |
10t2 |
|||||||||||||||||||||||||||||||||||||||||||
|
1 |
) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
+ t |
2 |
1 + t |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
cos |
2 x = |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
+ t2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
d( |
10 t) |
1 |
1 |
10 t |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
= ∫ |
10 |
= |
arctg |
+ C = |
arctg |
2 tgx + C |
||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
( 10 t) |
+ ( 2) |
5 |
20 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 10 |
|
2 |
tg |
x |
+ 1 |
||
|
Ответ: |
2 |
||||
|
3 arctg |
3 |
+ C . |
6. Использование формул для преобразования произведений тригонометрических функций от различных аргументов
|
sin u sin v = − 1 [sin(u − v) + sin(u + v)] |
(1.5.6) |
|||
|
2 |
||||
|
cos u cos v = |
1 |
[cos(u − v) + cos(u + v)] |
(1.5.7) |
|
|
2 |
||||
|
sin u sin v = |
1 |
[cos(u − v) − cos(u + v)] |
(1.5.8) |
|
|
2 |
||||
Пример 40. Найти интеграл ∫cos7x cos x dx .
Решение
∫cos7x cos x dx = 12 ∫[cos(7 −1)x + cos(7 + 1)x]dx = 12 ∫cos6xdx + 12 ∫cos8xdx = 121 ∫cos6xd(6x) + + 161 ∫cos8xd(8x) = 121 sin 6x + 161 sin 8x + C
Ответ: 121 sin 6x + 161 sin 8x + C .
Пример 41. Найти интеграл∫sin 6x sin 4x dx .
30
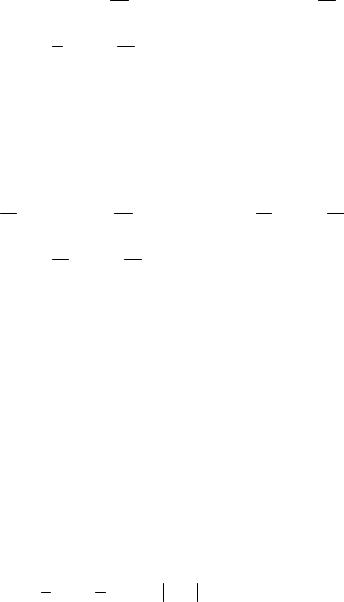
Решение
∫sin 6x sin 4x dx = − 12 ∫[cos(6 − 4)x − cos(6 + 4)x]dx = − 12 ∫cos 2xdx + 12 ∫cos10xdx = − 14 ∫cos 2xd(2x) + 201 ∫cos10xd(10x) = − 14 sin 2x + 201 sin10x + C
Ответ: − 14 sin 2x + 201 sin10x + C .
Пример 42. Найти интеграл∫sin12x cos6x dx .
Решение
∫sin12x cos6x dx = 12 ∫[sin(12 − 6)x + sin(12 + 6)x]dx = 12 ∫sin 6xdx + 12 ∫sin18xdx = = 121 ∫sin 6xd(6x) + 361 ∫sin18xd(18x) = − 121 cos6x − 361 cos18x + C
Ответ: − 121 cos6x − 361 cos18x + C .
|
7). Интегралы вида ∫tg m x |
secn xdx и ∫ctg m x cosecn xdx , (где n — четное число вычисляются |
|
с помощью формул sec2 x = 1 |
+ tg 2 x или cosec2 x = 1+ ctg 2 x |
Пример 43. Найти интеграл∫tg 5 x dx .
Решение
|
∫tg |
5 |
x dx = ∫tg |
2 |
x tg |
3 |
xdx = ∫ |
1 |
−1)tg |
3 |
xdx = ∫tg |
3 |
x |
dx |
− ∫tg |
2 |
x tgx |
dx |
= |
|||||||||||||||
|
( |
|||||||||||||||||||||||||||||||||
|
cos2 x |
cos2 x |
cos2 |
x |
||||||||||||||||||||||||||||||
|
3 |
1 |
4 |
1 |
1 |
4 |
dx |
|||||||||||||||||||||||||||
|
= ∫tg |
xd(tgx) |
−∫tgxd(tgx) = |
4 tg |
x |
− ∫( |
−1)tgxdx = 4 tg |
x − ∫tgx |
+ ∫tgxdx = |
|||||||||||||||||||||||||
|
cos2 x |
cos2 x |
||||||||||||||||||||||||||||||||
|
= 1 tg 4 x − 1 tg 2 x − ln |
cos x |
+ C |
|||||||||||||||||||||||||||||||
|
4 |
2 |
||||||||||||||||||||||||||||||||
Ответ: 14 tg 4 x − 12 tg 2 x − ln cos x + C .
Пример 44. Найти интеграл∫ctg3 x dx .
Решение
|
∫ctg |
3 |
x dx = ∫ctg |
2 |
x ctgxdx = ∫( |
1 |
− 1)ctgxdx = ∫ctgx |
dx |
− ∫ctgxdx = − ∫ctgxd(ctgx) − |
|||||||||||||||||||
|
sin |
2 |
x |
sin |
2 |
x |
||||||||||||||||||||||
|
− ∫ |
cos x |
dx = − |
1 |
ctg 2 x − ∫ |
d(sin x) |
= − |
1 |
ctg 2 x − ln |
sin x |
+ C |
|||||||||||||||||
|
sin x |
2 |
sin x |
2 |
||||||||||||||||||||||||
|
8). Интегралы вида ∫sec2n+1 xdx и ∫cosec2n+1 xdx вычисляются по рекуррентным формулам |
|||||||||||||||||||||||||||
|
как интегралы от нечетной положительной степени секанса и косеканса: |
|||||||||||||||||||||||||||
|
∫sec |
2n+1 |
1 |
sin x |
1 |
)∫sec |
2n−1 |
|||||||||||||||||||||
|
xdx = |
+ (1 |
− |
xdx |
(1.5.10) |
|||||||||||||||||||||||
|
2n |
cos2n |
2n |
31

|
∫cosec |
2n+1 |
1 |
cos x |
1 |
)∫cosec |
2n−1 |
||||
|
xdx = − |
sin 2n |
+ (1− |
xdx |
(1.5.11) |
||||||
|
2n |
2n |
Пример 45. Найти интеграл∫tg 4 x sec6 xdx .
Решение
∫tg 4 x sec6 xdx = ∫tg 4 x(1+ tg 2 x)2 sec2 xdx = ∫tg 4 x(1+ tg 2 x)2 d(tgx) =
=∫tg 4 x(1+ 2tg 2 x + tg 4 x)d(tgx) = ∫tg 4 xd(tgx) + 2∫tg 6 xd(tgx) + ∫tg8 xd(tgx) =
=15 tg 5 x + 72 tg 7 x + 19 tg9 x + C
Ответ: 15 tg5 x + 72 tg7 x + 19 tg9 x + C .
Пример 46. Найти интеграл∫cosec5 xdx .
Решение
|
∫ cos ec |
5 |
xdx = |
используем рекурентную |
= − |
1 |
cos x |
+ |
3 |
∫ cos ec |
3 |
xdx = |
(1.5.11) |
= |
|||
|
формулу(1.5.11) |
||||||||||||||||
|
4 |
sin4 x |
4 |
2n + 1 = 3, n = 1 |
|||||||||||||
|
2n + 1 = 5, n = 2 |
||||||||||||||||
|
1 |
cos x |
3 |
1 |
cos x |
1 |
1 |
cos x |
||||||||||||||||||
|
= − |
+ |
− |
+ |
∫ cos ecxdx |
= − |
||||||||||||||||||||
|
4 |
sin |
4 |
x |
4 |
2 |
sin |
2 |
x |
2 |
4 |
sin |
4 |
x |
||||||||||||
|
Ответ: − |
1 |
cos x |
− |
3 |
cos x |
+ |
3 |
ln |
tg |
x |
+ C |
||||||||||||||
|
4 |
sin4 x |
sin2 x |
8 |
||||||||||||||||||||||
|
8 |
2 |
Пример 47. Найти интеграл∫sec3 xdx .
Решение
|
− |
3 |
cos x |
+ |
3 ln |
tg |
x |
+ C |
||
|
8 |
sin 2 x |
2 |
|||||||
|
8 |
|
∫sec |
3 |
xdx |
= |
используем рекурентную |
= |
1 |
sin x |
+ |
1 |
∫sec xdx = |
1 |
sin x |
+ |
1 |
∫ |
dx |
= |
|||||||||||||||||||||
|
фомулу(1.5.10) |
2 |
2 |
2 |
2 |
||||||||||||||||||||||||||||||||||
|
cos2 x |
cos2 x |
cos x |
||||||||||||||||||||||||||||||||||||
|
2n + 1 = 3, n = 1 |
||||||||||||||||||||||||||||||||||||||
|
= 1 |
sin x |
+ 1 ln |
tg( |
x |
+ π ) |
+ C |
||||||||||||||||||||||||||||||||
|
cos2 x |
||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
4 |
|||||||||||||||||||||||||||||||||||
|
Ответ: |
1 |
sin x |
+ |
1 |
x |
+ π ) |
+ C . |
|||||||||||||||||||||||||||||||
|
ln |
tg( |
|||||||||||||||||||||||||||||||||||||
|
cos2 x |
||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
4 |
32
1.6.Тесты (теория)
1.Дать определение первообразной.
2.Чем отличаются две первообразные для одной и той же функции?
3.Для каких функций существует первообразная на заданном интервале?
4.Что называется неопределенным интегрированием?
5.Что называется неопределенным интегралом?
6.В чем заключается основное отличие операции интегрирования от операции дифференцирования?
7.Каким знаком обозначается интеграл?
8.Какая функция называется подынтегральной функцией?
9.Какие выражения называются подынтегральными выражениями?
10.Перечислите основные свойства неопределенного интеграла?
11.Перечислите основные способы вычисления интегралов
12.Назовите основные способы вычисления интегралов?
13.В чем заключается замена переменной в неопределенном интеграле?
14.Запишите и объясните формулу интегрирования по частям.
15.Приведите пример применения формулы интегрирования по частям.
16.Что называется рациональным выражением?
17.Какая рациональная дробь называется правильной?
18.Каким образом не правильная рациональная дробь переводится в правильную?
19.Какие правильные дроби называются простейшими?
20.Сколько типов простейших дробей вы знаете?
21.Какие числа называются корнями многочлена?
22.Можно ли правильную рациональную дробь представить в виде суммы простейших дробей?
23.При каких условиях правильную рациональную дробь можно разложить на простейшую?
24.Изложите методы интегрирования простейших рациональных дробей 1, 2, 3 типов.
25.Сформулируйте теорему о разложении многочлена на простейшие множители.
26.Изложите правило разложения правильной рациональной дроби на простейшие дроби в случае простейших действительных корней знаменателя. Приведите пример.
27.Изложите правило разложения правильной рациональной дроби на простейшие дроби в случае действительных кратных корней знаменателя. Приведите пример.
28.Изложите правило разложения правильной дроби на простейшие для случая, когда среди корней знаменателя имеются пары простых комплексно-сопряженных корней.
29.Какие выражения называются иррациональными?
30.В чем состоит общая идея метода рационализации при интегрировании иррациональных и трансцендентных функций?
31.Приведите наиболее типичные случаи рационализации интегралов от иррациональных функций.
32.Какого вида интегралы от иррациональных функций сводятся к интегралам от функций, зависящих от тригонометрических функций?
33.В каких случаях интегралы от дифференциальных биномов сводятся к интегралам от рациональных функций?
34.Перечислите типы тригонометрических выражений и способы их интегрирования?
33
35.Приведите интегралы от тригонометрических функций, которые рационализируются с помощью подстановки t = sin kx и t = cos kx .
36.Интегралы какого вида от тригонометрических функций целесообразно рационализировать с помощью подстановки t = tgkx .
37.Интегралы какого вида при помощи универсальной тригонометрической подстановки сводятся к интегралу от рациональной дроби новой переменной?
38.В каких случаях можно упростить подынтегральную функцию с помощью формул понижения четных степеней синуса и косинуса?
39.При вычислении интегралов какого вида используется тригонометрические формулы преобразования произведения в сумму?
40.С помощью каких формул можно понизить степень тангенса или котангенса при интегрировании тригонометрических функций?
41.Приведите прием вычисления интегралов от нечетной положительной степени секанса или косеканса с помощью рекуррентных формул.
42.Интегралы какого вида можно упростить с помощью формул понижения четных степеней секанса и косеканса?
34
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #