Формула Ньютона-Лейбница
Пусть есть непрерывная функция $ f(x) $ на отрезке $ [a,b] $, а первообразная её $ F(x) $. Тогда имеет место равенство, которое есть формула Ньютона-Лейбница:
$$ int _a^b f(x) dx = F(x)bigg |_a^b = F(b) — F(a) $$
В этой формуле $ a $ и $ b $ называются пределами интегрирования. Нижний — $ a $, верхний — $ b $. Функция $ f(x) $ — это подынтегральное выражение. А её первообразная обозначается $ F(x) $, то есть такая функция, что $ F'(x) = f(x) $. А сам интеграл называется определенным, так как есть пределы интегрирования.
Формула Ньютона-Лейбница используется только для определенного интеграла и заключает его связь с неопределенным интегралом.
Сначала находим первообразную $ F(x) $ любыми известными методами решения неопределенных интегралов, а затем находим её разность в точках $ a $ и $ b $.
Стоит обратить внимание на порядок вычитания: из $ F(b) $ вычитается $ F(a) $. Иначе нужно поменять знак полученного ответа на противоположный.
Примеры решений
| Пример 1 |
| Вычислить интеграл по формуле Ньютона-Лейбница: $$ int_1^2 x^3 dx $$ |
| Решение |
|
Первым делом проверяем, что подынтегральная функция $ f(x)=x^3 $ является непрерывной на отрезке $ xin [a;b] $. Если всё нормально, то приступаем ко второму шагу, а именно нахождение первообразной $ F(x) $. Для этого достаточно убрать пределы интегрирования и решить его любым методом. В нашем случае нужно применить метод непосредственного интегрирования. По таблице интегрирования находим, что $ int x^p dx = frac{x^{p+1}}{p+1} $. $$ F(x) = int x^3 dx = frac{x^{3+1}}{3+1} dx = frac{x^4}{4} + C $$ Положим $ C = 0 $ и получаем одну из первообразных: $ F(x) = frac{x^4}{4} $. Теперь зная $ F(x) $ можно использовать формулу Ньютона-Лейбница для вычисления окончательного результата. Подставляем $ a $ и $ b $ в $ F(x) $ поочередно, а затем ищем разность: $$ F(a) = F(1) = frac{1}{4} $$ $$ F(b) = F(2) = frac{16}{4} = 4 $$ $$ F(b) — F(a) = F(2) — F(1) = 4 — frac{1}{4} = frac{15}{4} $$ В результате мы получили, что: $$ int_1^2 x^3 dx = F(2) — F(1) = 4 — frac{1}{4} = frac{15}{4} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int_1^2 x^3 dx = frac{15}{4} $$ |
| Пример 2 |
|
Вычислить определенный интеграл с помощью формулы Ньютона-Лейбница: $$ int_0^pi xsin x dx $$ |
| Решение |
|
Для нахождения этого определенного интеграла воспользуемся методом интегрирования по частям: $$ int_0^pi xsin x dx = begin{vmatrix} u = x & du = dx \ dv = sin x dx & v = -cos x end{vmatrix} = $$ $$ = -xcos x bigg |_0^pi — int_0^pi (-cos x)dx = — (picdot cos pi — 0cdot cos 0) + int_0^pi cos x dx = $$ $$ = -(pi cdot (-1) — 0cdot 1) + int_0^pi cos x dx = pi + int_0^pi cos x dx = $$ Обратите внимание на то, что при вычислении $ uv $ мы использовали формулу Ньютона-Лейбница. Теперь дорешиваем второй интеграл опять же с учетом этой же формулы и записываем ответ: $$ = pi +sin x bigg |_0^pi=pi + (sin pi — sin 0)=pi + (0 — 0)=pi $$ |
| Ответ |
| $$ int_0^pi xsin x dx = pi $$ |
Пусть
функция y
= f(x) непрерывна
на отрезке [a;
b] и F(x) —
одна из первообразных функции на этом
отрезке, тогда справедлива формула
Ньютона-Лейбница: 
Формулу
Ньютона-Лейбница называют основной
формулой интегрального исчисления.
Для
доказательства формулы Ньютона-Лейбница
нам потребуется понятие интеграла с
переменным верхним пределом.
Если
функция y
= f(x) непрерывна
на отрезке [a;
b],
то для аргумента интеграл
вида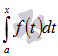
функцией верхнего предела. Обозначим
эту функцию
причем эта функция непрерывная и
справедливо равенство
Действительно,
запишем приращение функции ,
соответствующее приращению аргументаи
воспользуемся пятымсвойством
определенного интегралаи следствием
из десятого свойства: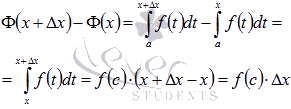
.
Перепишем
это равенство в виде .
Если вспомнитьопределение
производной функциии перейти к
пределу при,
то получим.
То есть,—
это одна из первообразных функцииy
= f(x) на
отрезке [a;
b].
Таким образом, множество всех
первообразных F(x) можно
записать как 
гдеС –
произвольная постоянная.
Вычислим F(a),
используя первое свойство определенного
интеграла: 
следовательно,.
Воспользуемся этим результатом при
вычисленииF(b): 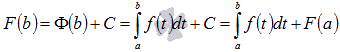
то есть
Это равенство дает доказываемую формулу
Ньютона-Лейбница
Приращение
функции принято обозначать как .
Пользуясь этим обозначением, формула
Ньютона-Лейбница примет вид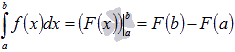
Для
применения формулы Ньютона-Лейбница
нам достаточно знать одну из
первообразныхy=F(x) подынтегральной
функции y=f(x) на
отрезке [a;
b] и
вычислить приращение этой первообразной
на этом отрезке. В статье методы
интегрированияразобраны основные
способы нахождения первообразной.
Приведем несколько примеров вычисления
определенных интегралов по формуле
Ньютона-Лейбница для разъяснения.
Пример.
Вычислить
значение определенного интеграла по
формуле Ньютона-Лейбница.
Решение.
Для
начала отметим, что подынтегральная
функция непрерывна
на отрезке[1;3],
следовательно, интегрируема на нем. (Об
интегрируемых функциях мы говорили в
разделе функции,
для которых существует определенный
интеграл).
Из таблицы
неопределенных интеграловвидно,
что для функциимножество
первообразных для всех действительных
значений аргумента (следовательно, и
для)
записывается как
Возьмем первообразную приC
= 0: .
Теперь
осталось воспользоваться формулой
Ньютона-Лейбница для вычисления
определенного интеграла: 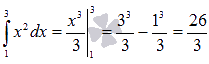
Пример.
По
формуле Ньютона-Лейбница вычислите
определенный интеграл 
Решение.
Подынтегральная
функция непрерывна на отрезке [-1;2],
поэтому, интегрируема на нем.
Найдем
неопределенный интеграл методом
подведения под знак дифференциала:.
Так мы получили множество всех
первообразных функциидля
всех действительныхx,
следовательно, и для .
Возьмем
первообразную при С=0 и
применим формулу Ньютона-Лейбница:
19. Несобственные интегралы первого рода
Определение 4.1
Предположим, что функция задана
на бесконечном промежутке видаи
интегрируема на любом конечном отрезке,
где.
Таким образом, мы можем рассмотреть
функцию
Если
эта функция имеет предел то
числоназываетсязначением
несобственного интеграла первого рода
а
сам интеграл называетсясходящимся (иными
словами, интеграл сходится).
Если
же предела не
существует (например, еслипри
),
то интегралназываетсярасходящимся (то
есть расходится)
и не имеет никакого числового значения.
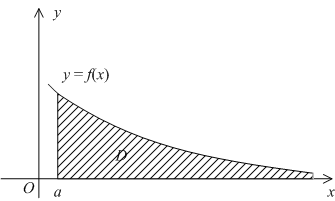
Геометрически,
в случае ,
величина несобственного интегралаозначает,
по определению, площадь бесконечно
длинной области,
лежащей в координатной плоскости между
лучомна
оси,
графикоми
вертикальным отрезком(см. рис.).
Рис.4.1.
Сходящиеся
интегралы соответствуют таким областям ,
площадь которых конечна (хотя сама
областьнеограничена),
а расходящиеся (в случае) —
неограниченным областям с бесконечной
площадью. В случае, когдапри
,
часто пишут формально:
однако
нужно ясно понимать, что эта запись
означает расходимость интеграла и
отсутствие у него числового значения.
Само
определение значения интеграла через
предел интегралов по конечным, но
увеличивающимся отрезкам означает
исчерпание площади путем
учёта все большей её части
вертикальный отрезок, проведённый
при,
отодвигается всё дальше и дальше в
бесконечность; в пределе будет учтена
вся площадь под графиком(см. рис.).
Рис.4.2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
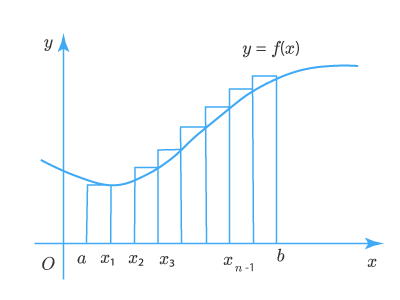
Пусть дан подграфик функции f(x)f(x) на участке [a;b][a; b]:
Разобьем отрезок [а;b][а; b] точками x1x_1, x2x_2, x3x_3, xn−1x_{n-1} на nn равных отрезков: [а;x1][а; x_1], [x1;x2][x_1; x_2], [x2;x3],…[xn−1;b][x_2; x_3], …[ x_{n-1}; b].
Построим на первом из этих отрезков прямоугольник с высотой f(x1)f(x_1), на втором — прямоугольник высоты f(x2)f(x_2)… на n-ном — прямоугольник с высотой f(b)f(b). В результате получим восходящий многоугольник, составленный из n прямоугольников. Пусть основание каждого из построенных прямоугольников равно ΔxΔx тогда площадь всего ступенчатого многоугольника составит:
Sn=Δx⋅f(x1)+Δx⋅f(x2)+…+Δx⋅f(b){{S}_{n}}=Delta xcdot f({{x}_{1}})+Delta xcdot f({{x}_{2}})+…+Delta xcdot f(b)
Суммы такого вида называют интегральными суммами. Полученную интегральную сумму можно считать приближенным значением площади SS подграфика функции f(x)f(x) на [a;b][a; b]. При этом если n→∞n → ∞, то Sn→SS_n→S.
Не только задача о нахождении площади подграфика, но и многие другие важные прикладные задачи приводят к вычислению границ подобных интегральных сумм. Поэтому для этого понятия введено специальное название и обозначение.
Границу интегральной суммы Δx⋅f(x1)+Δx⋅f(x2)+…+Δx⋅f(xn),Delta xcdot f({{x}_{1}})+Delta xcdot f({{x}_{2}})+…+Delta xcdot f({{x}_{n}}), если n→∞n → ∞, называют определенным интегралом функции f(x)f(x) от aa до bb.
Его обозначают символом ∫abf(x)dxintlimits_{a}^{b}{f(x)}dx (читают: (определенный) интеграл от aa до bb эф от икс дэ икс). Здесь числа от aa до bb – пределы (границы) интегрирования, ∫∫ – знак интеграла, f(x)f(x) – подынтегральная функция, xx – переменная интегрирования.
Из всего сказанного следует, что площадь подграфика функции f(x)f(x) на [a;b][a; b] равна ∫abf(x)dxintlimits_{a}^{b}{f(x)}dx.
Главная теорема интегрального исчисления
Если у функции f(x)f(x) на отрезке [a,b][a, b] существует первоначальная F(x)F(x), то
I=∫abf(x)dx=F(b)−F(a)I=intlimits_{a}^{b}{f(x)}dx=F(b)-F(a)Это формула Ньютона-Лейбница, основная формула интегрального исчисления в математическом анализе.
Она дает возможность решать многие важные задачи не вычислением границ интегральных сумм, что достаточно трудно, а с помощью первоначальной.
Свойства определенных интегралов
Рационализировать вычисления интеграла часто помогает знание об их свойствах.
При формулировке определения определенного интеграла мы считали, что a<ba < b. Удобно расширить понятие определенного интеграла, и для случая a>ba > b принять по определению, что
∫abf(x)dx=−∫baf(x)dxintlimits_{a}^{b}{f(x)}dx=-intlimits_{b}^{a}{f(x)}dx
Для случая a=ba = b также по определению будем считать, что
∫aaf(x)dx=0intlimits_{a}^{a}{f(x)}dx=0]
Отметим, что формальное применение формулы Ньютона-Лейбница к вычислению интегралов в данных формулах дает такой же результат. Действительно, если функция F(x)F(x) является первообразной для функции f(x)f(x), то
∫aaf(x)dx=F(x)∣aa=F(a)−F(a)intlimits_{a}^{a}{f(x)}dx=left. F(x) right|_{a}^{a}=F(a)-F(a)
Также
∫abf(x)dx=F(b)−F(a)=−(F(a)−F(b))=−∫baf(x)dxintlimits_{a}^{b}{f(x)}dx=F(b)-F(a)=-(F(a)-F(b))=-intlimits_{b}^{a}{f(x)}dx
С помощью формулы Ньютона-Лейбница легко обосновываются и другие свойства определенных интегралов:
- Если F(x)F(x) является первообразной для функции f(x)f(x), то для функции kf(x)kf(x) первоначальной будет функция kF(х)kF(х). Тогда
∫abkf(x)dx=kF(x)∣ab=kF(b)−kF(a)=k(F(b)−F(a))=k∫abf(x)dxintlimits_{a}^{b}{kf(x)}dx=kleft. F(x) right|_{a}^{b}=kF(b)-kF(a)=k(F(b)-F(a))=kintlimits_{a}^{b}{f(x)}dx
Таким образом,
∫abk⋅f(x)dx=k⋅∫abf(x)dxintlimits_{a}^{b}{kcdot f(x)}dx=kcdot intlimits_{a}^{b}{f(x)}dx
- Если F(x)F(x) является первообразной для функции f(x)f(x), a G(х)G(х) — первоначальной для функции g(x)g(x), то для функции f(x)+g(x)f(x) + g(x) первоначальной будет функция F(x)+G(х)F(x) + G (х).
Tогда
∫ab(f(x)+g(x))dx=(F(x)+G(x))∣ab=(F(b)+G(b))−(F(a)+G(a))=(F(b)−F(a))+(G(b)−G(a))=∫abf(x)dx+∫abg(x)dxintlimits_{a}^{b}{(f(x)}+g(x))dx=(left. F(x)+G(x)) right|_{a}^{b}=(F(b)+G(b))-(F(a)+G(a))=(F(b)-F(a))+(G(b)-G(a))=intlimits_{a}^{b}{f(x)}dx+intlimits_{a}^{b}{g(x)}dx
Таким образом ∫ab(f(x)+g(x))d=∫abf(x)dx+∫abg(x)dxintlimits_{a}^{b}{(f(x)}+g(x))d=intlimits_{a}^{b}{f(x)}dx+intlimits_{a}^{b}{g(x)}dx
- Если F(x)F(x) является первообразной для функции f(х)f(х) и сс на отрезке [a;b][a; b], то
∫ac(f(x))dx+∫cb(f(x))dx=F(x)∣ac+F(x)∣cb=F(c)−F(a)+F(b)−F(c)=F(b)−F(a)=∫ab(f(x))dxintlimits_{a}^{c}{(f(x)})dx+intlimits_{c}^{b}{(f(x)})dx=left. F(x) right|_{a}^{c}+left. F(x) right|_{c}^{b}=F(c)-F(a)+F(b)-F(c)=F(b)-F(a)=intlimits_{a}^{b}{(f(x)})dx
Итак, если функция f(x)f (x) интегрирована на отрезке [a;b][a; b] и с∈[a;b]с ∈ [a; b], то
∫ab(f(x))dx=∫ac(f(x))dx+∫cb(f(x))dxintlimits_{a}^{b}{(f(x)})dx=intlimits_{a}^{c}{(f(x)})dx+intlimits_{c}^{b}{(f(x)})dx
Пример 1
Вычислить ∫0π41cos2xdxintlimits_{0}^{frac{pi }{4}}{frac{1}{{{cos }^{2}}x}}dx.
Поскольку для функции f(x)=1cos2xf(x)=frac{1}{{{cos }^{2}}x} мы знаем первообразную – это F(х)=tgхF(х) = tgх, то заданный интеграл вычисляется непосредственным применением формулы Ньютона-Лейбница I=∫abf(x)dx=F(b)−F(a)I=intlimits_{a}^{b}{f(x)}dx=F(b)-F(a).
Решение
∫0π4dxcos2x=tgx∣0π4=tgπ4−tg0=1−0=1intlimits_{0}^{frac{pi }{4}}{frac{dx}{{{cos }^{2}}x}}=left. tgx right|_{0}^{frac{pi }{4}}=tgfrac{pi }{4}-tg0=1-0=1
Ответ: 1.
Пример 2
Вычислите ∫13(4x−x)dxintlimits_{1}^{3}{left( frac{4}{x}-x right)}dx
Решение
Возможны два пути вычисления заданного интеграла.
-
Сначала найти первообразную для функции, используя правила исчисления первообразных и таблицу первобытных, а затем найти интеграл по формуле Ньютона-Лейбница.
-
Использовать правило (∫ab(f(x)+g(x))d=∫abf(x)dx+∫abg(x)dxintlimits_{a}^{b}{(f(x)}+g(x))d=intlimits_{a}^{b}{f(x)}dx+intlimits_{a}^{b}{g(x)}dx и записать заданный интеграл как алгебраическую сумму двух интегралов, каждый из которых можно непосредственно вычислить, как в примере 1.
1 способ
Для функции f(x)=(4/x−x)f(x) = (4/x — x) одной из первообразных является F(х)=4ln∣х∣−x2/2F(х) = 4ln|х| — x2/2. Тогда
∫13(4x−x)dx=(4ln∣x∣−x22)∣13=(4ln∣3∣−322)−(4ln∣1∣−122)=4ln3−4intlimits_{1}^{3}{left( frac{4}{x}-x right)}dx=left. left( 4ln left| x right|-frac{{{x}^{2}}}{2} right) right|_{1}^{3}=(4ln left| 3 right|-frac{{{3}^{2}}}{2})-(4ln left| 1 right|-frac{{{1}^{2}}}{2})=4ln 3-4
2 способ
∫13(4x−x)dx=∫134xdx−∫13xdx=4ln∣x∣∣13−x22∣13=4(ln∣3∣−ln∣1∣)−(322−122)=4ln3−4intlimits_{1}^{3}{left( frac{4}{x}-x right)}dx=intlimits_{1}^{3}{frac{4}{x}}dx-intlimits_{1}^{3}{x}dx=left. 4ln left| x right| right|_{1}^{3}-left. frac{{{x}^{2}}}{2} right|_{1}^{3}=4(ln left| 3 right|-ln left| 1 right|)-(frac{{{3}^{2}}}{2}-frac{{{1}^{2}}}{2})=4ln 3-4
Ответ: 4ln(3)−4.4ln(3) — 4.