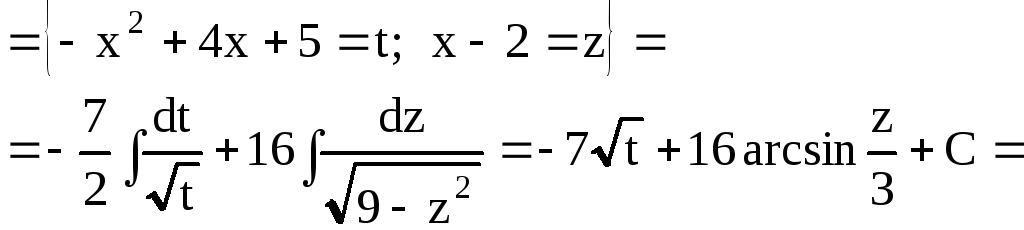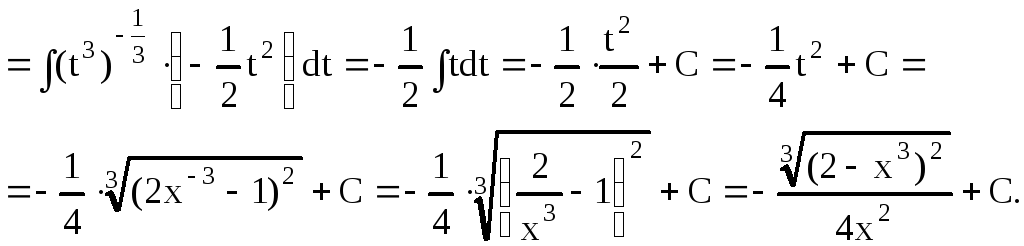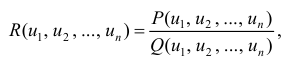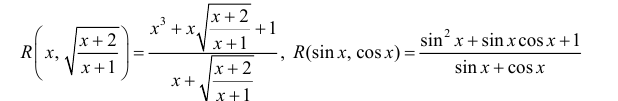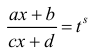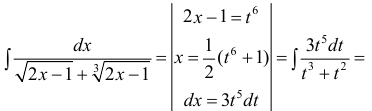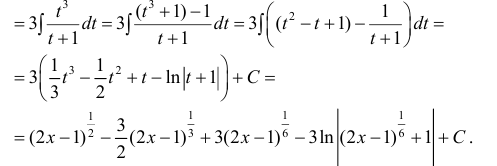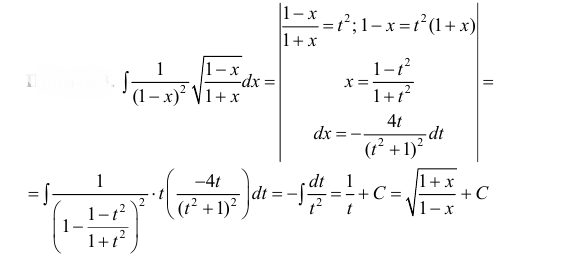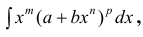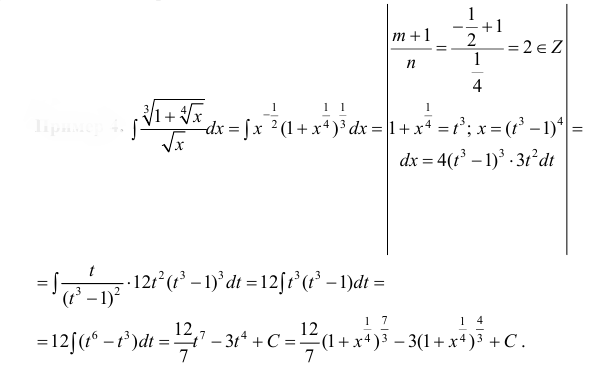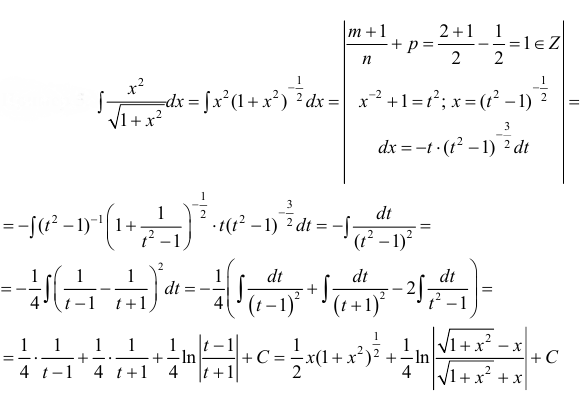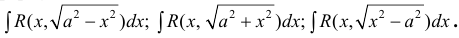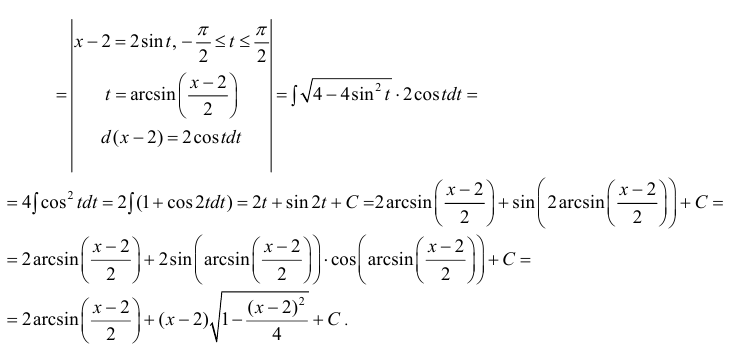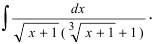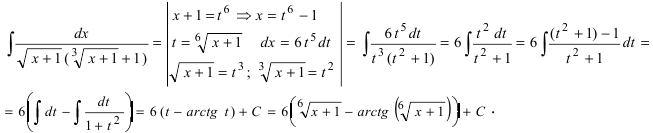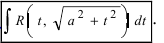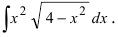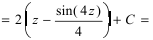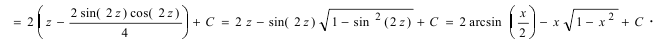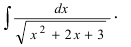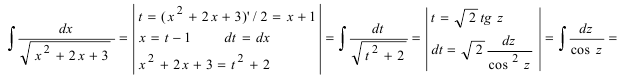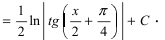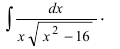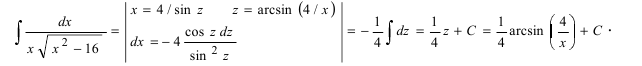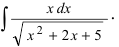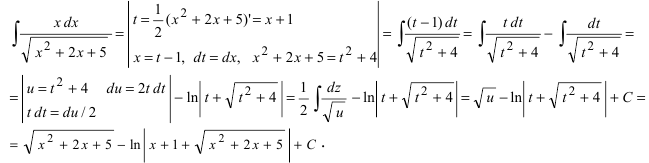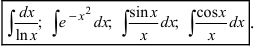Как найти интеграл подкоренного выражения - Исправление недочетов и поиск решений вместе с Examum.ru

Не от всякой
иррациональной функции интеграл
выражается через элементарные функции.
В дальнейшем будем стремиться отыскивать
такие подстановки
которые привели бы подынтегральное
выражение к рациональному виду. Если
при этом функциявыражается через элементарные функции,
то интеграл представится в конечном
виде и в функции от х.

Назовем этот прием
методом
рационализации подынтегрального
выражения.

1)
Интегралы
вида

,

где R
означает рациональную функцию от двух
аргументов,

постоянные.

Полагаем,
.

Интеграл приводится
к виду

здесь

рациональные функции.

Вычислив этот
интеграл по правилам интегрирования
рациональных функций, вернемся к старой
переменной, подставив

К интегралу вида
(1) сводятся более общие интегралы

где показатели r,
s,…

рациональны.

Нужно привести
эти показатели к общему знаменателю m,
чтобы под знаком интеграла получить
рациональную функцию от х и радикала

Пример 22. Найти
интеграл
.

Решение:

где

2)
Интегралы
вида
.

Такие интегралы
сводятся к табличному, если в квадратном
трехчлене выделить полный квадрат.

Пример 23.
Найти
.

Решение.
Преобразуем квадратный трехчлен

Тогда

3) Интегралы вида .

Для отыскания
этого интеграла в числителе необходимо
выделить такую линейную функцию, которая
равнялась бы производной квадратного
трехчлена. Далее разбиваем интеграл на
сумму двух, один из которых табличный,
а второй рассмотрен в предыдущем пункте.

Пример 24.
Найти
.

Решение.
Выделим в числителе производную
подкоренного выражения

Тогда

4) Интегралы вида

Эти интегралы
приводятся к интегралу от рациональной
функции нового переменного с помощью
следующих подстановок Эйлера.

I
–я подстановка Эйлера.
Если
,
то полагаем

Для определенности
рассмотрим случай

.
Тогда

то

рациональная
функция от t,
dx
также выражается рационально через t.

II-я
подстановка Эйлера.
Если
,
то полагаем

Для определенности
считаем, что перед
стоит знак «+». Тогда

При этом dx
и
выражаются рационально черезt,
поэтому
сводится к интегралу рациональной
функции зависящей отt.

Пример 25.
Найти интеграл

Решение.
Применим 2-ю подстановку Эйлера

;

где
.

III-я
подстановка Эйлера.
Квадратный трехчлен
имеет действительные корни
и .
Тогда
сводится к интегралу от рациональной
функции отt
с помощью замены

или

1.5. Интегрирование биномиальных дифференциалов

Биномиальными
называются дифференциалы вида

где m,n,p

рациональные числа, a,b

постоянные величины.

Рассмотрим интеграл

.
(1.5)

1) n

целое число. Данный интеграл сводится
к интегралу от рациональной функции от
t,
если положить
,

наименьшее общее кратное знаменателей
дробей m
и n.

2)

целое число, тогда рационализации
подынтегрального выражения можно
достигнуть, используя замену

,


знаменатель дроби р.

3)

целое.

Замена
,

знаменатель дроби р, позволяет
рационализировать подынтегральную
функцию в исходном интеграле.

Эти случаи
интегрируемости были известны еще
Ньютону. Однако, только в середине
прошлого столетия П.Л.Чебышев установил
факт, что других случаев интегрируемости
в конечном виде для биномиальных
дифференциалов нет. Поэтому подстановки
1-3 называют подстановками
Чебышева.

Пример 26.
Найти интеграл

Решение:

Применим II
подстановку Чебышева, т.к.

целое число

Пример 27.
Найти интеграл
.

Решение.
Подынтегральную функцию можно записать
в виде
Здесьи
целое число. Поэтому имеет место третий
случай интегрируемости дифференциального
бинома. Произведем замену переменной:
,
тогдаилиили.

Преобразуем
исходный интеграл

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
17.12.2018552.96 Кб34KA.doc
#

Источник

Интегрирование иррациональных функций

Формула

Формула на интегрирование иррациональных функций зависит от типа предлагаемого к решению интеграла, в частности от подкоренного выражения:

Линейная функция: $$ sqrt[n]{ax+b}, (a neq 0) $$ Для решения такого интеграла удобно применить подстановку $ t = sqrt[n]{ax+b} $
Квадратный многочлен: $$ sqrt{ax^2+bx+c} $$ В этом случае необходимо дополнить многочлен до полного квадрата, а затем по одной из формул таблицы интегрирования решить полученный интеграл вида $ int frac{dx}{sqrt{alpha^2 pm x^2}} $
Разность квадратов: $$ sqrt{a^2-x^2} $$ Используем подстановку $ x = asin t $, затем по формуле $ 1-sin^2 t = cos^2 t $ продолжаем нахождение интеграла

Примеры решений

Пример 1

Найти интеграл иррациональной функции: $$ int frac{xdx}{sqrt[3]{x+1}} $$

Решение

Выполняем замену: $$ t = sqrt[3]{x+1} $$

Выражаем из замены $ x $: $$ x = t^3-1 $$

Находим $ dx $: $$ dx = 3t^2 dt $$

Подставляем в интеграл полученные данные:

$$ int frac{xdx}{sqrt[3]{x+1}} = int frac{(t^3-1)3t^2}{t} dt = $$

Выполняем разложение подынтегрального выражения на две дроби:

$$ = int 3t^4 dt — int 3t dt = frac{3t^5}{5} — frac{3t^2}{2} + C = $$

Возвращаем замену назад:

$$ = frac{3}{5}(sqrt[3]{x+1})^5 — frac{3}{2}(sqrt[3]{x+1})^2 + C = frac{3}{5}sqrt[3]{(x+1)^5}-frac{3}{2}sqrt[3]{(x+1)^2} + C $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int frac{xdx}{sqrt[3]{x+1}} = frac{3}{5}sqrt[3]{(x+1)^5}-frac{3}{2}sqrt[3]{(x+1)^2} + C $$

Пример 2

Выполнить интегрирование иррациональных функций: $$ int frac{dx}{sqrt{x^2-6x+13}} $$

Решение

Замечаем, что под корнем находится квадратный многочлен. Это значит, что можно выделить под корнем полный квадрат, а затем решить интеграл по таблице интегрирования основных функций.

Выделяем полный квадртат:

$$ x^2-6x+13 = x^2 — 2cdot 3 + 3^2 + 4 = (x — 3)^2 + 4 $$

Подставляем полученное выражение под корень в интеграле:

$$ int frac{dx}{sqrt{x^2-6x+13}} = int frac{dx}{sqrt{(x-3)^2+4}} = $$

$$ = int frac{dx}{sqrt{x^2-6x+13}} = ln | x-3 + sqrt{x^2-6x+13}| + C $$

Ответ

$$ int frac{dx}{sqrt{x^2-6x+13}} = ln | x-3 + sqrt{x^2-6x+13}| + C $$

Пример 3

Решить интеграл с иррациональностью: $$ int sqrt{1-x^2} dx $$

Решение

Интеграл попадает под третий случай, в котором необходимо выполнить подстановку:

$$ x = sin t; dx = cos t; t = arcsin x $$

Записываем решение:

$$ int sqrt{1-x^2} dx = int sqrt{(1-(sin t)^2}) cos t dt = $$

Воспользовавшись тригонометрической формулой $ 1 — sin^2 t = cos^2 t $ получаем:

$$ = int sqrt{cos^2 t} cos t = int cos^2 t dt = $$

С учётом формулы понижения степени косинуса $ cos^2 t = frac{1+cos 2t}{2} $ имеем:

$$ = int frac{1+cos 2t}{2} dt = frac{1}{2} int (1+cos 2t) dt = $$

Воспользуемся свойством разложения интеграла:

$$ frac{1}{2} int dt + frac{1}{2} int cos 2t dt = frac{1}{2} t + frac{1}{4} sin 2t + C = $$

Выполняем обратную подстановку:

$$ = frac{1}{2} arcsin x + frac{1}{4} sin (2arcsin x) + C $$

Ответ

$$ int sqrt{1-x^2} dx = frac{1}{2} arcsin x + frac{1}{4} sin (2arcsin x) + C $$

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Интегрирование иррациональных функций с примерами решения

Содержание:

Интегрирование иррациональных функций.

Определение 1. Функция вида

Пример 1.
— рациональная функция переменных u и v, при этом:

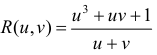
п.1. Интегралы вида:

Пусть s – общий знаменатель дробей 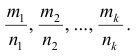Тогда подстановка
делает подинтегральную функцию рациональной.

Пример 2.

Пример 3

п.2. Интегралы вида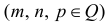— интегралы от дифференциального бинома.
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z — интегралы рассмотрены в п.1.
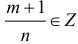
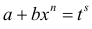
б) , тогда подстановка , где s – знаменатель р приводит интегральную функцию к рациональной.
в) , тогда подстановка , где s – знаменатель р приводит интегральную функцию к рациональной.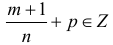
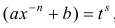
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).

Пример 4.

Пример 5.

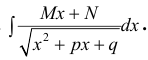
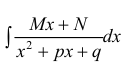
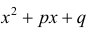
п.3. Интегралы вида Вычисление интегралов проводится аналогично интегралам выделением полного квадрата в трехчлене
(см. § 21, примеры 1, 2).

Пример 6.

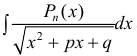
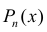
п 4. Интегралы вида , где — многочлен степени n.
Для вычисления интегралов используют равенство:
многочлен степени n−1 . Коэффициенты многочлена а также число λ находятся, если продифференцировать правую и левую часть равенства (2).

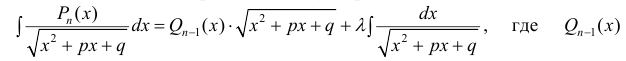
Заказать решение задач по высшей математике

Пример 7.
После взятия производной:

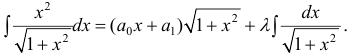
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.

Решив систему (3), получим :

(сравни с примером 5).

п.5. Интегралы вида
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
— для первого интеграла,
— для второго,
— для третьего (см. § 23).

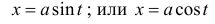
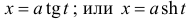
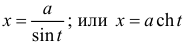
Пример 8.

Пример 9.

Интегрирование некоторых иррациональных функций

1. Интегралы вида .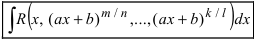

Интегралы такого типа вычисляются по следующей схеме:

В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.

Пример:

Вычислить

Решение:

В данном примере 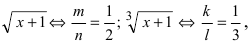следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.

2. Интегралы вида .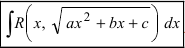

Такие интегралы путем замены 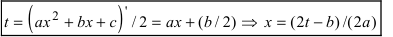приводятся к одному из интегралов вида:

1. 2. 3.

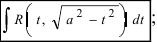
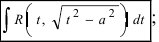
Для вычисления этих интегралов применяют следующие тригонометрические замены

1. 2. 3. — которые позволяют избавиться от квадратного корня.

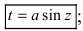
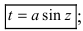
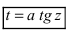
Пример:

Вычислить

Решение:

Данный интеграл соответствует интегралам типа 1., поэтому

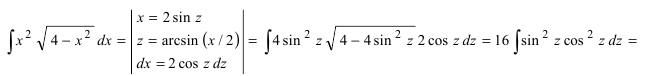
Пример:

Вычислить

Решение:

Воспользуемся указанной выше заменой

(интеграл вычислен в п. 2а)

Пример:

Вычислить

Решение:

Пример:

Вычислить

Решение:

Воспользуемся указанной выше заменой

Понятие о неберущихся интегралах

Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися:

Прямоугольная система координат на плоскости и ее применение
Линии второго порядка
Полярные координаты
Непрерывность функции
Формула Тейлора и ее применение
Интегрирование рациональных дробей
Интегрирование тригонометрических функций
Интегрирование тригонометрических выражений

Источник

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Интегралы от иррациональных функций

Интеграл от корня равен двум таким же корням в кубе, деленным на три, плюс константа интегрирования

$[int{sqrt{x}dx}=frac{2sqrt{{{x}^{3}}}}{3}+C]$

Для интегрирования иррациональной функции, содержащей ${{left( xpm a right)}^{frac{m}{n}}}$ применяется подстановка $xpm a={{t}^{n}} ,$ которая позволяет избавиться от иррациональности.

Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней переменной делается подстановка $x={{t}^{s}} ,$ где – общий знаменатель всех дробных степеней, входящих в данную функцию.

Рациональная функция, содержащая выражение $sqrt[n]{frac{ax+b}{cx+d}}$ , интегрируется с помощью подстановки $frac{ax+b}{cx+d}={{t}^{n}}$ .

Интегрирование иррациональных функций, содержащих $sqrt{{{a}^{2}}pm {{x}^{2}}}, sqrt{{{x}^{2}}-{{a}^{2}}} ,$ производится с помощью тригонометрических и гиперболических подстановок.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник