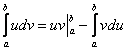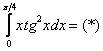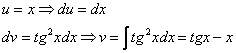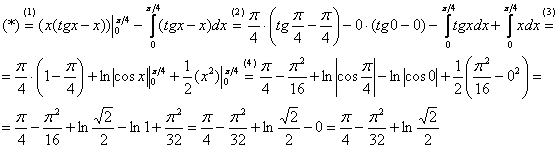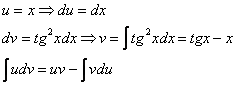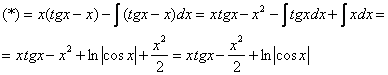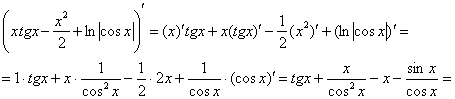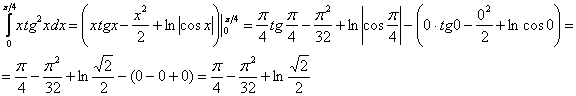Как найти интеграл применяя интегрирование по частям - Исправление недочетов и поиск решений вместе с Examum.ru

Интегрирование по частям

Пусть U(x) и V(x) — дифференцируемые функции. Тогда d(U(x)V(x)) = U(x)dV(x) + V(x)dU(x). Поэтому U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x). Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫d(U(x)V(x))=U(x)V(x)+C, получаем соотношение

называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

Решение онлайн
Видеоинструкция

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.

Также рекомендуется изучить сервис вычисление интегралов онлайн

Примеры

≡ x^2/(x+2)

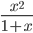
cos²(2x+π) ≡ (cos(2*x+pi))^2

≡ x+(x-1)^(2/3)

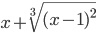
Применение метода интегрирования по частям

В связи с особенностями нахождения определенных величин, формулу интегрирования по частям очень часто используют в следующих задачах:

Математическое ожидание непрерывной случайной величины. Формула для нахождения математического ожидания и дисперсии непрерывной случайной величины включает в себя два сомножителя: функцию полинома от x и плотность распределения f(x).
Разложение в ряд Фурье. При разложении необходимо определять коэффициенты, которые находятся интегрированием от произведения функции f(x) и тригонометрической функции cos(x) или sin(x).

Типовые разложения по частям

Вид интеграла	Разложения на части
`∫P_n(x)cos(ax)dx`, `∫P_n(x)sin(ax)dx`, `∫P_n(x)e^axdx`, где `P_n(x)` — некоторый полином (многочлен) степени `n`	`U(x)=P_n(x)`, `dV(x)=cos(ax)dx`
`∫ln(P(x))dx`	`U=ln(P(x))`; `dV=dx`
`∫arcsin(ax)dx`	`U=arcsin(ax)`; `dV=dx`
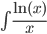	`U=ln(x)`; `dV=dx/x`

При использовании формулы интегрирования по частям нужно удачно выбрать U и dV, чтобы интеграл, полученный в правой части формулы находился легче. Положим в первом примере U=e^x, dV=xdx. Тогда dU=e^xdx, 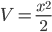и Вряд ли интеграл ∫x²e^xdx можно считать проще исходного.

Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла ∫x²sin(x)dx.

Интегралы ∫e^axcos(bx)dx и ∫e^axsin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.

Пример №1. Вычислить ∫xe^xdx.

Положим U=x, dV=e^xdx. Тогда dU=dx, V=e^x. Поэтому ∫xe^xdx=xe^x-∫e^xdx=xe^x-e^x+C.

Пример №2. Вычислить ∫xcos(x)dx.

Полагаем U=x, dV=cos(x)dx. Тогда dU=dx, V=sin(x) и ∫xcos(x)dx=xsin(x) - ∫sin(x)dx = xsin(x)+cos(x)+C

Пример №3. ∫(3x+4)cos(x)dx

Решение:

Ответ: (3x+4)sin(x)+3cos(x)+C

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Здесь новизны еще меньше. Всё, что справедливо для неопределенного интеграла, в полной мере справедливы и для определенного интеграла. Плюсом идёт то, что в формуле интегрирования по частям добавляются пределы интегрирования:

Формулу Ньютона-Лейбница здесь нужно применить дважды: для произведения и после того, как мы возьмём интеграл . Ну и, конечно, подынтегральные функции должна быть непрерывны на , ибо на «нет» и интеграла нет.

Пример я подобрал не самый простой, но очень и очень познавательный:

Пример 8
Вычислить определенный интеграл

Сразу начинаем решение и сразу прерываем его «звёздочкой». Этот тип интеграла не встречался ранее, он тоже берётся по частям. Используем стандартную схему интегрирования по частям:

Интеграл от квадрата тангенса я разбирал в 1-й части курса, но на чистовике, естественно, всё расписываем подробно, вспоминая заодно насущные тригонометрические формулы:

Далее открываем решение и на первом шаге

(1) расписываем правую часть формулы :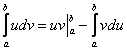

(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойство линейности, разделяя его на два интеграла. Не путаемся в знаках!

(3) Берем два оставшихся интеграла. Интеграл также разобран ранее, однако, не поленюсь:

(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.

Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.

Если честно, я недолюбливаю формулу 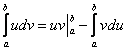и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, который, с моей точки зрения, более рационален:

На первом этапе находим неопределенный интеграл:

Интегрируем по частям:

Первообразная функция найдена. …Кстати, все ли поняли, почему в определённом интеграле не имеет смысла приплюсовывать константу ?

В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования.

На втором этапе проводим проверку (обычно на черновике).

Тоже логично. Ведь если неправильно найден неопределённый интеграл, то… правильно! И это лучше выяснить немедленно, дифференцируем ответ:

– получена исходная подынтегральная функция, значит, первообразная найдена верно.

И третий этап – применение формулы Ньютона-Лейбница:

Здесь тоже есть существенная выгода! – это гораздо меньший риск запутаться в подстановках и вычислениях, т.к. формула Ньютона-Лейбница применяется всего лишь один раз.

Рассмотренный алгоритм решения
можно применить для любого определенного интеграла!

И нужно, если интеграл трудный. Так, если «чайник» решит разобранный интеграл по формуле 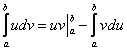(1-м способом), то 99% где-нибудь допустит ошибку.

Уважаемый студент, распечатай и наклей рядом с формулой Ньютона-Лейбница:

1) Сначала находим неопределенный интеграл (первообразную функцию). Если не получилось, повышаем свои навыки интегрирования.

2) Проверяем найденную первообразную дифференцированием. Здесь, кстати, может статься, позабылись производные – и тогда самое время подтянуть свои навыки!

3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания. Царь тут!

И на холодную закуску интеграл для самостоятельного решения.

Пример 9
Вычислить определенный интеграл

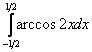
1.7. Геометрический смысл определённого интеграла

1.5. А если подвести функцию под знак дифференциала?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Интегрирование по частям

Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.

Формула для неопределенного интеграла:

$$ int udv = uv — int vdu $$

Формула для определенного интеграла:

$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} — int limits_{a}^{b} vdu $$

Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.

Пример 1

Найти интеграл $ int xe^xdx $

Решение

Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $

Подставляем найденные значения в первую формулу интегрирования и получаем

$$ int xe^x dx = xe^x — int e^x dx = xe^x — e^x + C. $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int xe^x dx = xe^x — e^x + C $$

Пример 2

Найти интеграл $ int xcos x dx $

Решение

В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $.

Подставим функции $ u $ и $ v $ в первую формулу

$$ int x cos x dx = x sin x — int sin x dx = x sin x + cos x + C. $$

Ответ

$$ int x cos x dx = x sin x + cos x + C $$

Пример 3

Вычислить интеграл $ int limits_1 ^e xln x dx $

Решение

В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения

$$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$

Осталось подставить это в формулу

$$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e — int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} — 0 — frac{1}{2} int limits_1 ^e xdx = $$

$$ =frac{e^2}{2} — frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} — frac{1}{2}(frac{e^2}{2} — frac{1}{2}) = frac{e^2}{2} — frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$

Ответ

$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$

Пример 4

Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $

Решение

По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет «на руку». Поэтом поступаем так

$$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$

Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу

$$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 — int limits_0 ^1 frac{3^x dx}{ln 3} = $$

$$ = frac{18}{ln 3} — frac{5}{ln 3} — frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} — frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$

Ответ

$$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$

Источник

Простое объяснение принципов решения интегралов функций с использованием метода интегрирования по частям и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения интегралов функций с использованием метода интегрирования по частям

Для нахождения интегралов функций с использованием метода интегрирования по частям используется формула интегрирования по частям, свойства интеграла, а также таблица интегралов.

Формула интегрирования по частям:

Таблица основных интегралов

Примеры решений интегралов функций с использованием метода интегрирования по частям

Задача

Вычислить интеграл:

$[int xe^{x}dx]$

Решение

Обозначим:

$[u = x, dv = e^{x}dx, du = dx, v = e^{x}]$

Применяя формулу интегрирования по частям

получаем:

$[int xe^{x}dx = xe^{x} - int e^{x}dx = xe^{x} - e^{x} + C = e^{x}(x -1) + C]$

Ответ

$[int xe^{x}dx = e^{x}(x -1) + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

Применяя формулу интегрирования по частям

получаем:

Ответ

Задача

Вычислить интеграл:

Решение

Обозначим:

$[u = ln{x}, dv = dx, du = frac{dx}{x}, v = x]$

Применяя формулу интегрирования по частям

, получаем:

$[int ln{x}dx = xln{x} - int xfrac{dx}{x} = xln{x} - int dx = xln{x} - x + C = x(ln{x} - 1) + C]$

Ответ

Задача

Вычислить интеграл:

Решение

Обозначим:

$[u = arctg{x}, dv = dx, du = frac{dx}{1 + x^{2}}, v = x]$

Применяя формулу интегрирования по частям

получаем:

$[int arctg{x}dx = x arctg{x} - int frac{x}{1 + x^{2}}dx = x arctg{x} - frac{1}{2}ln{(1 + x^{2})} + C]$

Ответ

$[int arctg{x}dx = x arctg{x} - frac{1}{2}ln{(1 + x^{2})} + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

$[u = arcsin{x}, dv = dx, du = frac{dx}{sqrt{1 - x^{2}}}, v = x]$

Применяя формулу интегрирования по частям

получаем:

$[int arcsin{x}dx = xarcsin{x} - int frac{x}{sqrt{1 - x^{2}}}dx = xarcsin{x} + sqrt{1 - x^{2}} + C]$

Ответ

$[int arcsin{x}dx = xarcsin{x} + sqrt{1 - x^{2}} + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

Применяя формулу интегрирования по частям

получаем:

Ответ

Задача

Вычислить интеграл:

$[int x^{3}ln{x}dx]$

Решение

Обозначим:

$[u = ln{x}, dv = x^{3}dx, du = frac{dx}{x}, v = frac{x^{4}}{4}]$

Применяя формулу интегрирования по частям

получаем:

$[int x^{3}ln{x}dx = ln{x}frac{x^{4}}{4} - int frac{x^{4}}{4}frac{dx}{x}]$

$[ln{x}frac{x^{4}}{4} - frac{1}{4}int x^{3}dx = ln{x}frac{x^{4}}{4} - frac{1}{4}frac{x^{4}}{4} + C = frac{x^{4}ln{x}}{4} - frac{x^{4}}{16} + C]$

Ответ

$[int x^{3}ln{x}dx = frac{x^{4}ln{x}}{4} - frac{x^{4}}{16} + C]$

Задача

Вычислить интеграл:

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx]$

Решение

Обозначим:

$[u = arcsin{x}, dv = frac{xdx}{sqrt{1 - x^{2}}}, du = frac{dx}{sqrt{1 - x^{2}}}, v = -sqrt{1 - x^{2}}]$

Применяя формулу интегрирования по частям

получаем:

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx = -sqrt{1 - x^{2}}arcsin{x} - int frac{-sqrt{1 - x^{2}}}{sqrt{1 - x^{2}}}dx]$

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx = -sqrt{1 - x^{2}}arcsin{x} + x + C]$

Ответ

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx = -sqrt{1 - x^{2}}arcsin{x} + x + C]$

Задача

Вычислить интеграл:

$[int frac{ln{x}}{x^{2}}dx]$

Решение

Обозначим:

$[u = ln{x}, dv = frac{dx}{x^{2}}, du = frac{dx}{x}, v = -frac{1}{x}]$

Применяя формулу интегрирования по частям

получаем:

$[int frac{ln{x}}{x^{2}}dx = -frac{ln{x}}{x} - int -frac{dx}{x^{2}} = -frac{ln{x}}{x} - frac{1}{x} + C]$

Ответ

$[int frac{ln{x}}{x^{2}}dx = -frac{ln{x}}{x} - frac{1}{x} + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

Применяя формулу интегрирования по частям

получаем:

Ответ

Источник

Пусть
и— непрерывно дифференцируемые функции.
На основании формулы дифференциала
произведения имеем

Отсюда

Интегрируя,
получим:

или окончательно

(4)

Формула (4) называется формулой
интегрирования по частям.

Выведенная формула показывает, что
интеграл
приводится к интегралу,
который может оказаться более простым,
чем исходный, или даже табличным. Сущность
метода интегрирования по частям вполне
соответствует его названию. Дело в том,
что при вычислении интеграла этим
методом подынтегральное выражениепредставляется в виде произведения
множителейuиdv.
При этом dx обязательно входит в
dv. В результате получается, что заданный
интеграл находится по частям: сначала
находим,
а затем.

Пример 1.

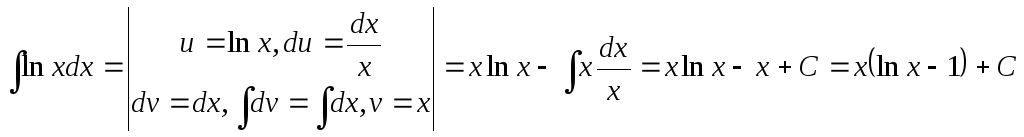
В представленном примере, как и в
дальнейших, вертикальными черточками
отделены вспомогательные записи. Отметим
также, что в качестве vможно взять любую функцию видаx+C,гдеС– постоянная. Мы взялиv=x,
т.е.С=0.

Пример
2.
.

Пример
3.

Пример 4.

Иногда для вычисления
интеграла формулу интегрирования по
частям приходится применять несколько
раз.

Пример
5.

Таким образом, интеграл
вычислен двукратным интегрированием
по частям.

Пример 6.

Если бы выражение
u
и dv
мы выбрали иначе, т.е.
,
то получили бы,
откуда,
и пришли бы к интегралу более сложному,
чем исходный, т.к. степень сомножителя
при тригонометрической функции повысилась
на единицу.

Приведенный пример показывает, что при
вычислении интегралов методом
интегрирования по частям главным
является разумное разбиение подынтегрального
выражения на множители uиdv. Общих установок
по этому вопросу не имеется. Однако, для
некоторых типов интегралов сделать это
возможно.

а) В интегралах вида

где
P(х)
– многочлен относительно x,
а –
некоторое число, полагают u=P(x),
а остальные сомножители за
.

Пример 7.
Найти
.


Положим
,,
тогда,.
Следовательно,



б) В интегралах вида

полагают

а
остальные сомножители – заu.

Пример 8.
Найти
.

Следовательно,

Вычислим отдельно последний интеграл:

Итак,
.

Отметим, что на
практике важно научиться применять
формулу (4), не выписывая по возможности
в стороне выражения для функций u
и v.

Так, решение приведенного примера может
быть представлено в виде:



=.

Возвращение к исходному интегралу

Формула интегрирования
по частям применима и для нахождения
интегралов вида
и,
гдеа
и b
– числа. При
нахождении этих интегралов она применяется
последовательно два раза, причем оба
раза за u
выбирается либо показательная функция,
либо тригонометрическая. После
двукратного интегрирования по частям
получается линейное уравнение относительно
искомого интеграла.