Метод интегрирования по частям.
Продолжаем осваивать базовые приёмы интегрирования. В предыдущих уроках мы рассмотрели три таких приёма — непосредственное интегрирование (то бишь, по таблице), метод подведения функции под знак дифференциала и метод замены переменной. Три ножки для стула. Сидеть уже можно, но… как-то неудобно.)
Сегодняшний наш урок будет началом изучения ещё одной обширной темы интегрального исчисления. Последней, четвёртой ножки для нашего стула.) А именно — метода интегрирования по частям. Великого и могучего. Фраза «интегрируем по частям» вселяет уверенность и так же обнадёживает студентов, как и фраза «решаем через дискриминант» у школьников. 
В чём же заключается столь сильная мощь данного метода и почему именно он так популярен при вычислении львиной доли неопределённых интегралов? А дело вот в чём.
Ключевой момент №1
Как мы уже знаем, в отличие от производных, в матанализе не существует стандартных правил для интегралов от произведения, частного и сложной функции. Но в процессе интегрирования такие операции с функциями встречаются сплошь и рядом. И очень часто именно метод интегрирования по частям позволяет свести вычисление интеграла от навороченной функции к совсем простенькому выражению, проинтегрировать которое не составит труда. Если таблицу знать, конечно.
Ключевой момент №2
Нередко под интегралом могут стоять всякие нехорошие трансцендентные конструкции — логарифмы, арксинусы, арктангенсы и прочие ужасы. Таблица интегралов не катит: нету в ней ни логарифмов, ни арков. И замена не годится тоже.
И в таких случаях тоже надо уметь как-то выкручиваться, да…
Какие же именно интегралы берутся по частям?
Вот типовые схемы подынтегральных функций:
Например, что-то в таком духе:
Что общего во всех таких интегралах? А общее то, что подынтегральная функция представляет собой произведение (а в ряде случаев и частное) «разнородных» функций. Многочлена и логарифма, синуса и экспоненты и так далее… Или же под интегралом тусуются всякие там арксинусы, арктангенсы и прочая жесть.
Под последним шестым пунктом стоит слово «прочие». Это такие функции, которые не относятся к предыдущим пяти типам, но которые также вполне можно проинтегрировать по частям (а иногда и только по частям). Как правило, сочетая в себе и другие способы интегрирования — замену переменной, подведение под дифференциал и т.п. Это всякие сложные экзотические функции, а также некоторые дроби и функции с корнями.
Например:
И тому подобные примеры. Их разберём в соответствующем уроке.
Ну вот. Про таинственный метод упомянули, какие именно интегралы с его помощью вычисляются — тоже. Пора бы уже начать более близкое знакомство. Знакомимся? Поехали!
Формула интегрирования по частям — вывод и смысл.
Итак, прошу любить и жаловать:
Это и есть формула интегрирования по частям собственной персоной.)
Откуда же она берётся и почему так называется? Она берётся из обычного правила дифференцирования произведения.
Все вы (надеюсь) его хорошо помните ещё со школы:
Или почти то же самое, только по-взрослому, через дифференциалы:
Все формулы в матанализе, если слева и справа стоят функции или их производные (или дифференциалы), можно почленно интегрировать. Вот и проинтегрируем левую и правую части нашего правила. Имеем полное право!
Подвешиваем на крючки левую и правую части и получаем:
Осталось сообразить, что значок интеграла всегда «съедает» значок дифференциала (согласно соответствующему свойству). Стало быть, слева останется просто произведение u∙v. А справа приведём первый интеграл к приличному виду и отправим его влево к u·v (со сменой знака, разумеется). Получим:
И, наконец, финальный бросок. Меняем местами левую и правую части и получаем:
Всё! Больше никаких научных хитростей.)
Собственно, формула производной произведения и формула интегрирования по частям — это две взаимно обратных формулы. 
Запоминается формула на удивление легко и просто. Чаще всего, в виде секретного заклинания:
Интеграл у-дэ-вэ равен у на вэ минус интеграл вэ-дэ-у. 
Итак, будем считать, что с происхождением формулы разобрались. Теперь разбираемся с названием — что ещё там за части какие-то. 
Смотрим на формулу ещё разок:
В чём основная суть? Исходное подынтегральное выражение (то, что слева) разбивается на два кусочка. Или две части.) Причём только с помощью умножения! Именно поэтому в общей формуле я отдельно и выделяю знаки умножения.
Первая часть (первый множитель) — это некоторая функция u. Функция как функция. Выражаемая какой-то формулой.
Вторая часть (второй множитель) — это не функция, а дифференциал некоторой другой функции v. То есть, dv.
Что это за таинственные u и v? Об этом дальше подробненько будет. Никаких тайн.)
Что же происходит при применении формулы? С точки зрения математики ничего особенного не происходит:
1. Первый множитель — u — дифференцируется. Было u, а становится du.
2. Второй множитель — dv – наоборот, интегрируется. Было dv, а после интегрирования стало просто v.
Зато с точки зрения наших хотелок происходит оч-чень много полезного! Исходный интеграл:
который, по каким-то причинам, нам не очень нравится, заменяется на другой интеграл
вычисление которого должно оказаться проще исходного.
Вот и всё. Вот и вся ключевая идея применения формулы!
Что брать за u, а что за dv?
Вопрос хороший! Этот момент — стратегически самый важный при применении формулы. Давайте разбираться. В самых общих чертах.) Выпишем ещё раз формулу:
Как видно из формулы, нам надо интегрировать новое выражение v∙du. И оно должно оказаться проще старого подынтегрального выражения u∙dv. Вот такая ключевая идея — упростить исходное подынтегральное выражение!
Поскольку в новом подынтегральном выражении стоит дифференциал du, то за функцию u всегда принимается функция, упрощающаяся при дифференцировании.
И какие же функции упрощаются при дифференцировании? Как правило, это всякие ужасы типа логарифмов или «арков». Почему же они упрощаются при дифференцировании? А потому, что их производные — гораздо более простые функции! Рациональные дроби или, в худшем случае, выражения с корнями (для арксинуса/арккосинуса). Вспоминаем нашу старую добрую таблицу производных:
И так далее. С дробью 1/х всяко проще работать в процессе интегрирования, чем с логарифмом, правда? И с арками та же история.
Точно так же упрощаются при дифференцировании и многочлены, степень которых после каждого дифференцирования понижается на единичку:
В общем, принцип выбора функции u предельно ясен — упрощение после дифференцирования. А что же со вторым множителем dv?
Поскольку множитель dv нам придётся интегрировать, то за dv всегда берётся конструкция, не усложняющаяся при интегрировании!
Например, это вполне может быть экспонента. Или же тригонометрическая функция — синус там или косинус… Или степенная функция или многочлен. Эти функции никак не усложняются при интегрировании! Почему? Вспоминаем теперь уже таблицу интегралов (первообразных): экспонента при интегрировании превращается сама в себя, синус/косинус — друг в друга (с точностью до знака), а любой многочлен степени n — также в многочлен, но степени n+1.
Запоминаем:
За функцию u всегда принимаем выражение, упрощающееся при дифференцировании.
За dv принимаем выражение, не усложняющееся при интегрировании.
Разумеется, сразу увидеть и сообразить в уме, что упростится/усложнится после дифференцирования/интегрирования, не всегда возможно. Всё от конкретного примера и от опыта зависит. Не всегда с первого раза получается. Бывает.)
Но для некоторых типовых схем я всё же приведу небольшую сводную табличку. Пользуйтесь на здоровье! 
Что ж, думаю, хватит грузной теории, давайте перейдём к конкретным примерам — всё станет куда понятнее.) В этом уроке рассмотрим интегралы из группы №1.
Произведение многочлена и показательной/тригонометрической функции.
Это интегралы из первой группы нашей сводной таблички.
Общий рецепт здесь следующий:
Если под интегралом стоит произведение многочлена и показательной/тригонометрической функции, то за функцию u всегда берётся МНОГОЧЛЕН.
А что берётся за dv? А за dv всегда берётся оставшаяся часть подынтегрального выражения вместе с dx! Что уж там осталось, то и берётся, так уж формула интегрирования по частям устроена: всё подынтегральное выражение надо по кусочкам распределить между u и dv.
Вот так:
Ну что, посмотрим на формулу интегрирования по частям в действии?)
Например, пусть надо найти вот такой интересный интеграл:
Пример 1
Казалось бы, всё просто. Под знаком интеграла стоит произведение знакомых табличных функций — икса и ex. Вроде, всё хорошо. Но есть одна проблемка: общей стандартной формулы для интеграла от произведения не существует! По отдельности каждая функция интегрируется без проблем, а вот произведение — уже проблема, да…) Как быть?
Как-как… Надо разделить разные типы функций!
Вот и разбиваем наше подынтегральное выражение на кусочки! Наша задача представить конструкцию
xexdx
в виде произведения функции u и дифференциала другой функции dv.
Определяемся, что выбираем за u и за dv!
Работаем прямо по правилу для группы №1. В роли показательной функции у нас, очевидно, ex. А множитель х служит как раз тем самым многочленом, который целесообразно брать в качестве функции u. Не так очевидно, что это многочлен, но это именно он.) Состоящий всего из одного члена — икса. Бывает.)
А вот к dv мы должны отнести то, что осталось — выражение exdx.
Так и пишем:
Да-да, именно так и выделяем, прямо в тетрадке!
Итак, выбор u и dv сделан. Вот он:
Теперь следующим шагом мы начинаем операцию, которую я условно называю «миграция дифференциала»: функцию u мы будем дифференцировать и превращать в du, а dv — наоборот интегрировать и превращать в v. Таким образом, под дифференциалом вместо функции v окажется функция u. Вспоминаем нашу картинку с пляшущими человечками.)
Поехали!
Дифференцируем функцию u, считаем du:
Интегрируем множитель dv и ищем функцию v:
Внимание! Не прибавляем константу С после отыскания функции v! Ведь в качестве функции v нам нужна только какая-то одна конкретная первообразная! А не всё бесконечное множество, да…) Самая простая такая первообразная — очевидно, с константой С, равной нулю (С=0). Именно поэтому я и пишу
v = ex,
а не
v = ex + C.
А теперь берём формулу интегрирования по частям
и аккуратно подставляем все исходные данные на свои места:
И считаем:
Вот и все дела.)
Ответ:
Как всегда, для пущей уверенности, дифференцируем результат:
Ура! Совпало! 
Что у нас произошло после применения формулы интегрирования по частям? А произошло то, что мешающий нам множитель х исчез из примера, и исходный интеграл от нехорошего произведения
свёлся к табличному (!) интегралу от безобидной экспоненты
Берущемуся в уме. Если таблицу знать.) Здорово, правда?
Именно так и работает формула интегрирования по частям. Разделяет разнотипные функции и превращает ужасный на вид интеграл в белый и пушистый. Вот и вся суть метода интегрирования по частям.)
А что будет, если поступить наоборот — за u принять ex, а за dv — xdx?
Не вопрос, давайте посмотрим:
Тогда, подставляя всё в формулу, получим:
Хм… И что нам с таким интегралом делать?! Даже ещё хуже стало, чем было…
Да! При таком выборе u и dv новый интеграл не упрощается, а, наоборот, усложняется! Экспоненте-то всё равно, что с ней делают — дифференцируют/интегрируют. У неё ко всем воздействиям врождённый иммунитет.) В отличие от многочлена, который при таком раскладе не понижает свою степень, а повышает. Что никак не делает пример проще, да…)
Собственно в этом-то и кроется причина выбора именно многочлена в качестве функции u для интегралов первой группы — понизить его степень.
А для общего развития запоминаем:
Если после применения формулы новый интеграл получился сложнее исходного, то, скорее всего, неудачно сделан выбор u и dv. Не падаем духом и пробуем другую комбинацию.
Эта рекомендация относится не только к этому уроку, на примеры из первой группы, а ко всему интегрированию по частям вообще.
Но самое надёжное — не бездумно расчленять подынтегральное выражение и комбинировать кусочки, задумчиво глядя на пример, а понимать общий смысл формулы и принцип выбора u и dv для конкретного типа интеграла. Уметь заранее просчитывать ситуацию и оценивать последствия того или иного выбора. Такой опыт только с практикой приходит. Прорешаете хотя бы 20-30 примеров — и проблема выбора u и dv отпадёт сама собой.)
Ну вот. Первый пример разобран по косточкам. Разумеется, так подробно расписывать следующие примеры я уже не буду. Это чисто для знакомства сделано. Чтобы общую идею уловить.)
А теперь можно записать и общий алгоритм вычисления неопределённых интегралов по частям.
Алгоритм вычисления неопределённых интегралов по частям.
1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.
2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
3. Дифференцируем функцию u и считаем дифференциал du.
4. Интегрируем дифференциал dv и ищем саму функцию v.
5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.
6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.
Ну что, потренируемся в применении алгоритма?)
Пример 2
И опять под интегралом стоит произведение функций разной природы — икса и косинуса. Значит, разделяем разнородные функции и интегрируем по частям: у нас просто нет других вариантов!
Работаем строго по пунктам.
1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.
Очевидно, это интеграл из первой группы — типа «многочлен на синус/косинус». Переходим к пункту 2.
2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
Наше правило для первой группы гласит, что за функцию u следует принимать многочлен — то есть, просто множитель x.
Ну, а за dv, ясен перец, принимаем то что осталось, т.е. cos x dx.
Вот так:
Итак, выбор сделан. Переходим к пунктам 3 и 4. Тут всё просто, без фокусов:
3. Дифференцируем функцию u и считаем дифференциал du.
4. Интегрируем дифференциал dv и ищем саму функцию v.
5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.
Итак, все исходные данные для применения формулы подготовлены. Подставляем:
6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.
Вперёд!
Ответ:
Готово дело.)
Проверяем ответ дифференцированием:
Всё путём.)
Мы видим, что новый интеграл опять оказался табличным и берущимся в уме! От синуса. Халява! 
Пример 3
Чем-то похоже на предыдущий пример, правда? Только синус ещё затесался, в качестве третьего множителя. Поскольку перед нами снова произведение разнородных функций — икса и тригонометрии, то такой интеграл можно попробовать взять только по частям. Но под интегралом произведение трёх функций, а не двух, как обычно! Что делать?
Что-что… Не бояться, вот что! Ибо из трёх множителей всегда можно сделать два. Нас спасут… скобочки! Вот так:
А дальше опять по алгоритму. Поехали!
1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.
Всё ясно. Это первая группа, т.к. под интегралом произведение многочлена (икса) и тригонометрии (sinx∙cosx).
2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
И здесь вопросов нет. Икс — это u. То, что осталось (т.е. sinx∙cosxdx) — это dv.
Итого имеем следующее:
3. Дифференцируем функцию u и считаем дифференциал du.
4. Интегрируем дифференциал dv и ищем саму функцию v.
А вот здесь начинается самое интересное.) Для поиска v нам надо проинтегрировать выражение sinx∙cosxdx.
Вот так:
Вот тут уже с ходу, в уме, этот интеграл не возьмёшь. В одно действие. Подумать надо.)
Варианта два. Можно внести косинус (или синус) под знак дифференциала и старым добрым способом, но в данном случае гораздо выгоднее искусственно выделить под интегралом синус двойного угла:
А проинтегрировать синус двойного угла уже никакого труда не составляет. В уме интегрируется. Как это делается, смотрим этот урок. Самое главное — не забываем про дополнительные коэффициенты и про знаки.
Всё. Функцию v мы нашли. Идём дальше по алгоритму.
5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.
6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.
И снова мы видим, что новый интеграл, от косинуса двойного угла, много проще старого интеграла от сборной солянки x∙sinx∙cosx. Интегрируем косинус двойного угла, «причёсываем» ответ и добиваем наш злой пример.
Пишу подробно, со всеми знаками и коэффициентами, поскольку именно в них народ и косячит на 99%:
Ответ:
Вот и все дела.) Кому не нравятся двойные углы, те могут перейти обратно к одинарным по соответствующим формулам, но в таком виде ответ выглядит гораздо компактнее.
Что, сомнения нахлынули? Не ленимся, дифференцируем:
Нет, всё честно.)
Всё бы ничего, но… могут случаться и такие сюрпризы, когда по частям приходится интегрировать несколько раз. Разберём ещё один пример.
Пример 4
Надеюсь, общий алгоритм интегрирования по частям уже запомнился? Можно не расписывать подробно в четвёртый раз?)
В этот раз на экспоненту умножается не одинокий икс, а вполне себе полноценный многочлен. Но схема выбора u и dv та же самая.
Действуем в соответствии с алгоритмом:
Отлично. Функции u и v, а также их дифференциалы du и dv найдены. Пора приступать к интегрированию по частям. Снова прямо по формуле вставляем все исходные данные, упрощаем что упрощается и получаем:
А вот и обещанный сюрприз! Что делать с новым интегралом
В таблице такого и близко нет, обычными преобразованиями с подынтегральной функцией тоже ничего не сделаешь… Но! Можно заметить, что под новым интегралом у нас опять произведение многочлена и экспоненты! Поэтому… снова интегрируем по частям (да-да!). Утешает то, что новый многочлен (2х+1) стал уже линейным (а не квадратичным, как был изначально)! Казалось бы, мелочь, но очень существенная: новый интеграл в целом проще старого! Как и должно быть.)
Если мы сейчас отдельно возьмём этот интеграл по частям и упростим до упора, то получим такой результат:
Что, у вас не так получилось? А за знаками следили? А за коэффициентами? Не забываем, что е-2х — сложная функция! Со всеми вытекающими.)
Вот практически и всё. Возвращаемся к исходному примеру, вставляем результат промежуточного интегрирования по частям на своё место и константу не забываем.)
Получим:
В принципе, интеграл мы уже нашли. Если требуются дальнейшие упрощения и наведение марафета, то, раскрыв скобки и приведя подобные, окончательно получим:
Ответ:
Вот такой ответ. Проверочное обратное дифференцирование предлагаю провести самостоятельно.)
Чем поучителен этот пример? Как видите, здесь нам пришлось интегрировать по частям два раза! Почему? Всему виной является вторая степень нашего многочлена x2+x+1. Проблема в том, что после каждого применения формулы (т.е. взятии дифференциала du) степень многочлена понижается лишь на единичку. Как и при любом дифференцировании, да.
Например, если бы под интегралом стоял многочлен 10-й степени (да даже хотя бы простое произведение x10ex), то последовательно интегрировать по частям пришлось бы (о, ужас!) десять раз! Это огорчает. Но зато при каждом новом интегрировании степень многочлена будет становиться всё ниже. Пускай на единичку, но — ниже. Это радует.)
Запоминаем:
Интегрировать по частям требуется столько раз, какова степень многочлена.
Между прочим, в качестве показательной функции совершенно не обязательно должна стоять именно экспонента (ex, е2х и тому подобные конструкции). Запросто может оказаться вообще не «е», а что-то типа 23х и т. п. Не надо пугаться. Принцип интегрирования тот же самый. Отличие состоит лишь в том, что при вычислении функции v будут всплывать дополнительные коэффициенты с логарифмами, которые ни в коем случае нельзя терять.
Например:
И так далее…
Итак, с первой группой интегралов, берущихся по частям, поработали. Переходим ко второй группе — логарифмам, аркам и прочим питомцам нашего зоопарка элементарных функций. В следующей теме.)
Интеграл произведения функций
ОПРЕДЕЛЕНИЕ
Интеграл произведения функций (
int f(x) g(x) d x
) в общем случае не равен произведению интегралов от каждого из факторов:
(
int f(x) g(x) d x neq int f(x) d x cdot int g(x) d x
)
В зависимости от того, какие функции находятся под знаком интеграла, интеграл от произведения в некоторых случаях может быть выражен через элементарные функции, а в некоторых случаях можно оценить определенный интеграл произведения функций. Для этого используются теоремы о среднем значении.
Средние теоремы
Теорема 1. Пусть функции (
f(x)
)и (
g(x)
) интегрируемы на отрезке (
[a ; b]
), с (
m leq f(x) leq M, x in[a ; b]
) и (
g(x) geq 0
) на (
[mathrm{a} ; mathrm{b}]
), затем
(
m(b-a) leq int_{a}^{b} f(x) g(x) d x leq M(b-a)
)
Следствие 1. Пусть функция (
f(x)
) интегрируема на отрезке (
[a ; b]
) и ограничены на этом отрезке: (
m leq f(x) leq M
) . затем
(
m(b-a) leq int_{a}^{b} f(x) g(x) d x leq M(b-a)
)
Теорема 2. Пусть функция (
f(x)
) непрерывна на отрезке (
[mathrm{a} ;mathrm{b}]
), функция (
g(x) geq 0
) интегрируема на этом сегменте. Тогда существует точка (
c in[a ; b]
) такая, что имеет место равенство:
(
int_{a}^{b} f(x) g(x) d x=f(c) cdot int_{a}^{b} g(x) d x
)
Следствие 2. Пусть функция (
f(x)
) непрерывна на отрезке (
[mathrm{a} ; mathrm{b}]
). Тогда существует (
c in[a ; b]
) такое, что
(
int_{a}^{b} f(x) g(x) d x=f(c)(b-a)
)
Примеры решения проблем на тему «Интегральные работы»
ПРИМЕР 1
Задача
Оцените Интеграл
(
int_{0}^{2} frac{5-x}{9-x^{2}} d x
)
Подынтегральная функция (
f(x)=frac{5-x}{9-x^{2}}
) определена на отрезке (
[0 ; 2]
). Используя дифференциальное исчисление, можно показать, что на этом отрезке функция принимает наименьшее значение, равное (
frac{1}{2}
) ; и самый маленький (
-frac{3}{5}
) . Тогда, согласно следствию 1, мы можем написать:
(
frac{1}{2} cdot(2-0) leq int_{0}^{2} frac{5-x}{9-x^{2}} d x leq frac{3}{5} cdot(2-0)
)
или же
(
1 leq int_{0}^{2} frac{5-x}{9-x^{2}} d x leq frac{6}{5}
)
1 leq int_{0}^{2} frac{5-x}{9-x^{2}} d x leq frac{6}{5}
)
ПРИМЕР 2
Оценить Интеграл
(
int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x
)
Интегральная функция (
f(x)=frac{sin x}{x}
) убывает на сегменте интегрирования (
left[frac{pi}{4} ; frac{pi}{2}right]
), поэтому справедлива оценка:
(
fleft(frac{pi}{2}right) leq f(x)=frac{sin x}{x} leq fleft(frac{pi}{4}right) Rightarrow frac{2}{pi} leq f(x)=frac{sin x}{x} leq frac{2 sqrt{2}}{pi}
)
Тогда, согласно следствию 1, имеем:
(
frac{2}{pi} cdotleft(frac{pi}{2}-frac{pi}{4}right) leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{2 sqrt{2}}{pi} cdotleft(frac{pi}{2}-frac{pi}{4}right)
)
или же
(
frac{2}{pi} cdot frac{pi}{4} leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{2 sqrt{2}}{pi} cdot frac{pi}{4} Rightarrow frac{1}{2} leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{sqrt{2}}{2}
)
(
frac{1}{2} leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{sqrt{2}}{2}
)
Интеграл произведения функций, формулы и примеры
ОПРЕДЕЛЕНИЕ
Интеграл произведения функций в общем случае не равен произведению интегралов от каждого из сомножителей:
В зависимости от того, какие функции стоят под знаком интеграла, интеграл от произведения в некоторых случаях можно выразить через элементарные функции, а в некоторых определенный интеграл произведения функций можно оценить. Для этого используются теоремы про среднее.
Теоремы про среднее
ТЕОРЕМА
Теорема 1. Пусть функции и являются интегрируемыми на отрезке причем и на Тогда
Следствие 1. Пусть функция интегрируема на отрезке и является ограниченной на этом отрезке: Тогда
ТЕОРЕМА
Теорема 2. Пусть функция непрерывна на отрезке функция интегрируема на этом отрезке. Тогда существует такая точка что выполняется равенство:
Следствие 2.
Пусть функция непрерывна на отрезке Тогда существует такое, что
Примеры решения задач по теме «Интеграл произведения»
ПРИМЕР 1
| Задание | Оценить интеграл |
| Решение | Подынтегральная функция задана на отрезке С помощью дифференциального исчисления можно показать, что на этом отрезке функция принимает свое наименьшее значение, равное и наименьшее Тогда, согласно следствию 1, можно записать:
или |
| Ответ |
ПРИМЕР 2
| Задание | Оценить интеграл |
| Решение | Подынтегральная функция является убывающей на отрезке интегрирования следовательно, имеет место оценка:
Тогда, согласно следствию 1, имеем: или |
| Ответ |
Читайте также:
Интеграл от натурального логарифма
Интегралы тригонометрических функций
Интеграл разности
Интеграл суммы
Интегралы от иррациональных функций
Интеграл от числа
Метод интегрирования по частям
Формула интегрирования по частям
Формула интегрирования по частям имеет вид:
.
Метод интегрирования по частям состоит в применении этой формулы. При практическом применении стоит отметить, что u и v являются функциями от переменной интегрирования. Пусть переменная интегрирования обозначена как x (символ после знака дифференциала d в конце записи интеграла) . Тогда u и v являются функциями от x: u(x) и v(x).
Тогда
, .
И формула интегрирования по частям принимает вид:
.
То есть подынтегральная функция должна состоять из произведения двух функций:
,
одну из которых обозначаем как u: g(x) = u, а у другой должен вычисляться интеграл (точнее находиться первообразная):
, тогда dv = f(x) dx.
В некоторых случаях f(x) = 1. То есть в интеграле
,
можно положить g(x) = u, x = v.
Резюме
Итак, в данном методе, формулу интегрирования по частям стоит запомнить и применять в двух видах:
;
.
Интегралы, вычисляющиеся интегрированием по частям
Интегралы, содержащие логарифм и обратные тригонометрические (гиперболические) функции
По частям часто интегрируются интегралы, содержащие логарифм и обратные тригонометрические или гиперболические функции.
Вот примеры таких интегралов, которые вычисляются методом интегрирования по частям:
, , , , , , .
Подробное решение этих интегралов >>>
Интегралы, содержащие произведение многочлена и sin x, cos x или e
x
По формуле интегрирования частям находятся интегралы вида:
, , ,
где P(x) – многочлен от x. При интегрировании, многочлен P(x) обозначают через u, а eax dx, cos ax dx или sin ax dx – через dv.
Вот примеры таких интегралов:
, , .
Подробное решение этих интегралов >>>
Примеры вычисления интегралов методом интегрирования по частям
Примеры интегралов, содержащих логарифм и обратные тригонометрические функции
Пример
Вычислить интеграл:
Подробное решение
Здесь подынтегральное выражение содержит логарифм.
u = ln x,
dv = x2 dx.
Тогда
,
.
.
Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений нужно обязательно добавить постоянную C, поскольку неопределенный интеграл – это множество всех первообразных. Также ее можно было добавлять и в промежуточных вычислениях, но это лишь загромождало бы выкладки.
Более короткое решение
Можно представить решение и в более коротком варианте. Для этого не нужно делать подстановки с u и v, а можно сгруппировать сомножители и применить формулу интегрирования по частям во втором виде.
.
Ответ
Другие примеры
Примеры решений подобных интегралов >>>
Примеры интегралов, содержащих произведение многочлена и sin x, cos x или ex
Пример
Вычислить интеграл:
.
Решение
Введем экспоненту под знак дифференциала:
e – x dx = – e – x d(–x) = – d(e – x).
Интегрируем по частям.
.
Также применяем метод интегрирования по частям.
.
.
.
Окончательно имеем:
.
Ответ
.
Другие примеры
Примеры решений подобных интегралов >>>
Автор: Олег Одинцов. Опубликовано: 19-10-2014
для каких функций интеграл произведения равен произведению и : Анализ-I
Dan_Te писал(а):
Цитата:
Причём по моему это действует только для мат ожидания, т.к. сами функции распределения и плотности нужно считать через свёртку.
У независимых случайных величин совместная функция распределения факторизуется на маргинальные компоненты, это свойство эквивалентно независимости. В абсолютно непрерывном также факторизуется совместная плотность. (факторизуемость = возможность разложить на множители)
Да, правильно, я допустила ошибку написав для зависимых! Плотность независимых является продуктом маргинальных плотностей и имеет следующее свойство:
Правда при этом все должны иметь абсолютно непрерывные распределения.
Идея Лебега: я не знаю, насколько это всё будет верно, но идея у меня следующая. Задаём две функции определяя её, например, для всех нечётных целых чисел равной 1 и 0 остальное и определяя её, для всех чётных целых чисел равной 1 и 0 остальное.
Теперь, использую обыкновенное правило перемножение функций, получаю их произведение равным 0. Отсюда, надо полагать, интеграл слева, вне зависимости от выбора будет равен 0. Но и интеграл справа будет также равен 0, т.к. если я определю, к примеру для моей первой функции, то есть как покрытие всех чётных чисел, то соотвественно сразу обнулиться интеграл моей второй функции.
Соответстенно зеркальное отображение (остальные я не рассматриваю, т.к. обнуляются обе функции). Но произведения чего-то с 0 равно 0. Отсюда моя правая часть тождественна равна левой, для функций не равных 0 всюду.
Интегрирование по частям, формулы и примеры решений
Содержание:
Рассмотрим функции $u=u(x)$ и
$v=v(x)$, которые имеют непрерывные
производные.
Согласно свойствам дифференциалов, имеет место следующее равенство:
$d(u v)=u d v+v d u$
Проинтегрировав левую и правую части последнего равенства, получим:
$int d(u v)=int(u d v+v d u) Rightarrow u v=int u d v+int v d u$
Полученное равенство перепишем в виде:
$int u d v=u v-int v d u$
Эта формула называется
формулой интегрирования по частям. С ее помощью интеграл
$int u d v$ можно свести к нахождению интеграла
$int v d u$, который может быть более простым.
Замечание
В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
2)$int P_{n}(x) arcsin x d x$ ;
$int P_{n}(x) arccos x d x$ ;
$int P_{n}(x) ln x d x$
Здесь принимают, что $d v=P_{n}(x) d x$, а в
качестве $u$ оставшиеся сомножители.
Пример
Задание. Найти интеграл
$int ln x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.
$$int ln x d xleft|begin{array}{l}
u=ln x quad d v=d x \
d u=frac{d x}{x} quad v=x
end{array} quadright|=x ln x-int x cdot frac{d x}{x}=$$
$=x ln x-int d x=x ln x-x+C=x(ln x-1)+C$
Ответ. $int ln x d x=x(ln x-1)+C$
Больше примеров решений
Решение интегралов онлайн
Пример
Задание. Найти интеграл
$int arcsin x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.
Больше примеров решений
Решение интегралов онлайн
Читать дальше: простейшие дроби.
Примеры на интегрирование
Примеры на интегрирование функций подобного состава заданий задают студентам 1, 2 курсов. Это в основном задания для математиков, экономистов, статистов, программистов. Данные интегралы задавали на контрольной работе в ЛНУ им. И. Франка, другие ВУЗы Украины также практикует подобные здания на контрольных по интегрированию. Чтобы формулы в задачах и ответах не повторялись условия заданий выписывать не будем. Всем и так известно что в задачах нужно или «Найти интеграл», или «Вычислить интеграл».
Пример 18. Для раскрытия иррациональности в знаменателе дроби необходимо в подобных примерах выполнять такую замену переменных — «икс» в наименьшей степени. В результате придем к интегралу от дробной функции
дальше выполняем деления числителя на знаменатель и упрощение
Таким образом без громоздких расписаний дробей придем к интегралу
Пример 19.
В результате замены получим дробь которая разделяется на два интеграла. Второй интеграл равен разнице логарифмов
Пример 20. Следующие интегралы касаются исключительно тригонометрических функций, а именно их произведения, квадратов, кубов, рациональных функций. Первый из приведенных интегралов нужно свести к синусу. Для этого косинус в 5 степени расписываем на произведение косинуса в 4 степени на косинус, который вносим под дифференциал
Для упрощения вводим замену переменных и приходим к интегрированию полинома
После интегрирования возвращаемся к замене и вместо t везде записываем sin(x).
Пример 21. Для вычисления интеграла нужно снизить степень синуса. Таким образом используем тригонометрические формулы, понижаем степень первой, а дальше находим интеграл по табличным формулам.
Пример 22. Нужно найти интеграл от произведения двойного синуса на тройной косинус. Под дифференциал ничего внести не удастся, поскольку имеем различные переменные. Для упрощения распишем произведение тригонометрических функций через разницу синусов
Пример 23. Данный интеграл без универсальной тригонометрической замены переменных найти не удастся. Поэтому пусть тангенс половины угла равный t, тогда синус превратится по формуле
После раскрытия скобок в знаменателе получим квадратный трехчлен
Для сведения такой дроби к табличному арктангенсу в знаменателе сначала выделяем квадратный трехчлен
Не забываем в конце вернуться к выполненной в начале замены. Это важно при тестах и контрольных.
Пример 24. Здесь можем использовать универсальную тригонометрическую замену, а может пойти другим путем. Вынесем в знаменателе синус в квадрате за скобки и перегруппируем слагаемые в скобках, чтобы по тригонометрическим формулам получить котангенс.
В результате интегрирования получим табличную формулу арктангенса
Пример 25. Необходимо вычислить интеграл от тангенса в квадрате от тройного аргумента. Сначала расписываем тангенс как часть синуса к косинусу. Далее синус в квадрате расписываем через косинус. После деления числителя на знаменатель получим два интеграла которые без труда находим по формулам интегрирования
Как только Вы изучите приведенные схемы и методики сведения интегралов под то или иное правило, научитесь видеть в примерах табличные интегралы и преобразования, которые в несколько шагов позволят Вам найти интеграл — тогда контрольная работа, или «срезы» для Вас не будут препятствием в обучении. Для этого нужно решить с десяток различных интегралов к каждому из приведенных типов. Все остальные после этого будут для Вас подобными, а схема их вычислений очевидной и понятной. Если в обучении встречаются сложные интегралы или сомневаетесь в собственных силах помните — мы всегда готовы оказать помощь.
Готовые решения контрольной по интеграции
Интегралы от произведения функций — Справочник химика 21
Перекрестный ток. Аналитическое решение для этой схемы движения потоков было дано Нуссельтом [49] в виде определенного интеграла произведения функций е и функции Бесселя. Это решение связано со сложным интегрированием для каждого частного случая геометрии поверхности теплообмена. Более общее решение, данное также Нуссельтом, основано на переходе к обобщенным переменным [50]. На фиг. 61,г представлены результаты, полученные путем пересчета первоначального уравнения Нуссельта, в которое были введены параметры [c.105]
После подстановки (2.3.29) и (2.
Выше мы уже показали, что средняя энергия колебания, обладающего частотой V, определяется формулой (П1.61). Тогда средняя энергия колебаний кристалла во всем интервале возможных частот определится как интеграл от произведения функции распре- [c.72]
Покажем, что верхняя граница для дисперсии коэффициентов разложения зависит от скалярного произведения функций О (со) и а((в). Для интеграла в уравнении (VII. 36) можно записать неравенство Буняковского
[c.175]
Нас интересует асимптотическое п оо поведение величины когда разницей между I и п можно пренебречь. Пусть вначале граф (riO) состоит из единственного блока, т. е. не содержит точек сочленения. Выполнив вначале суммирование в формуле (III.121), мы получим интеграл, в знаменателе которого имеется (и— 1) произведений функций, каждая из которых ведет себя при малых q, определяющих поведение интеграла, как а числитель [c.
В квантовомеханическом описании свойств молекул часто приходится вычислять интегралы от произведения функций, и оказывается полезным знать их отношение к преобразованиям симметрии. Почему так Причина состоит в том, что интеграл будет обращаться в нуль, если только подынтегральное выражение, состоящее из произведения двух или более функций, не будет инвариантно ко всем операциям симметрии данной точечной группы. Это означает, что интеграл не равен нулю, только если подынтегральное выражение принадлежит к полностью симметричному неприводимому представлению точечной группы данной молекулы.
[c.221]
Условие, необходимое для того, чтобы интеграл от произведения функций не был равен нулю, было сформулировано в гл. 4, Для колебательных переходов это условие можно записать в виде [c.236]
При обсуждении электронного строения атомов понадобится также важный интеграл от произведения трех сферических функций, который выражают через коэффициенты Клебша — Гордана по формуле [c.
Дельта-функция Дирака равна нулю при всех значениях Г, кроме при котором она стремится к бесконечности. Интеграл этой функции по времени (ее площадь) равен единице, а интеграл произведения дельта-функции на другую функцию равен значению последней в момент времени
[c.280]
Преобразуем выражение (П. 125), заменив интеграл произведения двух функций на произведение среднего значения одной на интеграл другой. Тогда можно представить решение исходного уравнения в виде [c.118]
Условие ортогональности выражено формулой (1.8). Значит, нужно построить интеграл из произведений функции ехр Нкц>) и [ехр (П )] = ехр (—Иц>) и проинтегрировать по ф в пределах от О до 2я. В результате должен получиться нуль. [c.49]
При вычислении энергии взаимодействия электронов, описываемых одноэлектронными функциями, из всех я перестановок, образующих антисимметричную функцию (6.16), остаются лишь транспозиции, и интеграл ко всем переменным от произведения функций, отличающихся перестановкой электронов в состояниях р м д, дает сразу формулу Дирака
[c.
Отметим, что расчет результатов измерения при использовании самопишущих потенциометров довольно трудоемок (необходимо взять интеграл произведения двух переменных функций). [c.161]
Таким образом, второй член разложения равен произведению функции распространения N — 2 свободных частиц на интеграл (11.1.26). Изобразим интеграл (II. 1.26) в виде двух вертикальных линий, соединенных горизонтальной волнистой линией (рис. 2). На этой диаграмме отрезки [c.245]
Интеграл в равенстве (2.19) представляет изменение плотности частиц /-го компонента в контрольном объеме, происходящее в результате их столкновений с частицами /-Г0 компонента и отклонения вследствие этого частиц 1-го компонента внутрь или за пределы этого объема. Произведение функций распределения частиц г-го и /-Г0 компонентов, вычисленное в точке с радиусом-вектором г, дает наиболее вероятное число,таких частиц в контрольном объеме фазового пространства. Таким образом, постановка задачи завершена.
Процедура, с помощью которой можно будет отделить одночастичную функцию распределения от многочастичной, заключается в том, чтобы найти такой параметр малости, который позволит разорвать цепочку уравнений и затем разложить эту функцию распределения в ряд по степеням этого малого параметра, так что низшая степень разложения соответствует расщепленным функциям распределения. Процедура разложения по малому параметру будет неоднократно использована в книге, поэтому она подробно рассмотрена ниже. Здесь же отметим что если увеличивать до бесконечности число частиц, но оставить е п постоянным, то четвертый член в (1.90) исчезает, в то время как пятый член (1.91) остается конечным. На первый взгляд кажется, что это мало даст, так как уравнения зацепляются через пятый член. Отметим, однако, что эта процедура физически означает, что эффекты, вызванные столкновениями индивидуальных частиц, становятся незначительными, в то время как силы взаимодействия между частицами представимы в виде интеграла по функции распределения.
Определенный интеграл — предел суммы однотипно построенных произведений /( ,)Ад ,-, где f( )—значение функции в точке лежащей на отрезке Ах, при всех Ах — 0 (рис. I) а и Ь — нижний и верхний пределы интегрирования.
Важное свойство собственных функций уравнения Шредингера, относящихся к различным собственным значениям, — их взаимная ортогональность интеграл по всему пространству от произведения любой пары собственных функций равен нулю [c.14]
Прежде чем приступать к определению коэффициентов dn(p) в соответствии с указанной схемой, докажем одно важное свойство системы функции sin п=1, 2,. .. Вычислим интеграл от произведения двух таких функций при разных значениях п n — k]in = i. [c.210]
Методы преобразования статистического интеграла основаны на следующем общем его свойстве если функция Гамильтона есть сумма независимых слагаемых, то статистический интеграл можно записать как произведение соответствующего числа независимых сомножителей. Этим свойством функции Z мы неоднократно пользовались. [c.287]
Для количественного расчета величины 8 требуется задать потенциал парного взаимодействия молекул.
Чтобы связать коэффициенты а с- топологией графа, изобразим ее элементарный представитель и зададим произвольным образом ориентацию его ребер (рис. III.13). Поскольку функция А (г) четная, то разность Г — Гр в показателе экспоненты (III.91) можно записать таким образом, чтобы номер i обозначал вершину, из которой выходит а-е ребро орграфа, а р — в которое оно входит. Тогда Ьга оказываются в точности равными элементам матрицы инциденций В орграфа, а аргумент б-функции (III.
Прямое произведение представлений. Очень часто в прикладных задачах встречаются выражения, которые содержат произведения функций, преобразующихся по тем или иным представлениям точечных групп. В частности, в 2 и 3 предшествующей главы уже встречались интегралы вида , в которых как функции и ф, так и оператор дипольного момента могут преобразовываться по различным неприводимым представлениям.
Из приведенного примера видно, что различные орбитали симметрии для одной группы эквивалентных АО или ГАО отличаются тем свойством, что, если взять любую пару из них, то обязательно наДцется хотя бы один такой элемент симметрии, относительно которого одна МОС из пары будет симметричной, а вторая — антисимметричной Такой элемент симметрии делит все пространство задания функций на две симметричные части, в которых произведения функций равны н различаются лишь знаком Поэтому для таких функций интеграл взятый по всему пространству, должен быть равен нулю Будут равны нулю также и интегралы типа [c.269]
Разные свойства синглетного и триплетного состояний количественно определяются значениями обменного интеграла А. Из вида этого интеграла (130,12) непосредственно следует, что его подынтегральное выражение отлично от нуля только в тех точках пространства, где произведение функций Фа(1) Фв(1) и 1 а(2) )в(2) отлично от нуля, т.
Как и следует из общей теории (см. разд. 1.3), атомные орбитали, принадлежащие разным энергетнчески.м уровням, ортогональны. Так, ортогональность 5- н /-функций неносредственно видна из рис. 1.2, поскольку произведение, скажем, 5 принимает положительные значения при г >0 и такие же по моду.лю, но отрицательные значения при 2 произведения функций обращается в нуль. (Ортогональность функций с разными п и одинаковыми /, например 15- и 25-АО. из рисунка, конечно, не видна для ее доказательства надо принять во внимание радиальную зависимость АО.) [c.17]
Таким образом, величина 2у конф представится как сумма всех возможных членов вида . .. dru, которые можно записать для системы из N пронумерованных частиц.
Интеграл (3.45) может быть вычислен графически при условии, что реактор работает при одной температуре. Для этого каждое измеренное значение / умножается на величину 1 — е при одинаковом значении Л Такие произведения затем наносят на график в функции от 1 и находят площадь под кривой, ограниченной = оо или тем значением /, при котором подынтегральное ьыражение является еще существенной величиной.
Покажем, что линейно независимые детерминантные функции, построенные из функций ортонормированной системы Фр , являются орто-нормированными. Рассмотрим интеграл от произведения детерминант-ных функций ZJpj рд, и построенных из спин-орбиталей [c.57]
Здесь принято x— f вынесена за знак интеграла как величина, не зависящая от точки А, а 1гавти 1г как медленно меняющаяся функция. Выражение (1.55) является произведением двух функций, одна из которых зависит только от расстояния, а другая — только от углов наблюдения Qy и 0г, что подтверждает возможность представления поля в виде диаграммы направленности. Ее ампли- [c.80]
Преимущество такой замены заключается в том, что произведение любых двух гауссовских функций с центрами на атомах а и Ь представляет собой новую гауссовскую функцию с центром в некоторой точке с. В связи с этим вычисление четырехцентрового интеграла по гауссовским функциям (СаСь (7,Су) сводится к вычислению двухцентрового 1интеграла, который вычисляется значительно проще.
Преимущество такой замены заключается в том, что произведение любых двух гауссовских функций с центрами на атомах а и Ь представляет собой новую гауссовскую функцию с центром в некоторой точке с. В связи с этим вычисление четырехцентрового интеграла по гауссовским функциям (GaGb GeGf) сводится к вычислению двухцентрового (G lGd) интеграла, который вычисляется значительно проще. Основной недостаток гауссовских функций в том, что они плохо отражают поведение хартри-фоковских АО. Для аппроксимации АО Хартри — Фока с достаточной точностью необходимо брать большее число гауссовских АО, чем слэтеровских. Например, в так называемом базисе STO—3G каждая слэтеров- ская АО аппроксимируется тремя гауссовыми с коэффициентами разложения, подбираемыми по методу наименьших квадратов.
В последнем члене выражения (15) безразлично, подставить ли V или У, так как здесь стоит произведение двух членов волновой функции и электрон 1 частично находится у адра а, а частично у ядра Ь. Однако это безразлично, так как последний интеграл (15) не меняется при замене V на V. Чтобы убедиться в этом, заметим, что от замены обозначений переменных интегрирований величина интеграла не меняется. Если мы поменяем обозначения электронов 1 — 2 и 2 1, то произведение (1) ijJa (2) (1) ь (2) не меняется, а V переходит а V. Подобным же образом заметим, что два первых интеграла равны друг другу. [c.36]
Интегрирования произведения двух функций — CodeRoad
Я немного смущен результатом моего следующего кода:
import scipy. integrate as intg
Phi_0 = lambda x: x**4
Phi_1= lambda x: x**2
f = lambda x: Phi_0*Phi_1
I = intg.quadrature(lambda x: Phi_0(x)*Phi_1(x), -1, 1)
print("I =", I[0], "Tolerance =", I[1])
integrate as intg
Phi_0 = lambda x: x**4
Phi_1= lambda x: x**2
f = lambda x: Phi_0*Phi_1
I = intg.quadrature(lambda x: Phi_0(x)*Phi_1(x), -1, 1)
print("I =", I[0], "Tolerance =", I[1])
Что, конечно же, дает результат.
Но когда я пишу код для интеграции как и любой другой метод снизу он выдает ошибку:
I = intg.quadrature(lambda x: Phi_0*Phi_1, -1, 1)
I = intg.quadrature(f, -1, 1)
I = intg.quadrature(f(x), -1, 1)
Можете ли вы объяснить, почему первый метод работает, но не другие?
python
function
lambda
Поделиться
Источник
gune
19 марта 2020 в 21:18
1 ответ
-
Python3-Sympy: расширьте произведения тригонометрических функций
Я не могу найти способ, чтобы SymPy расширял произведения, подобные cos(a)*cos(b) , в сумму тригонометрических функций суммы углов. from sympy import * init_printing() wrf,wlo,t = symbols(‘omega_RF omega_LO t’) c = cos(wrf*t)*cos(wlo*t) expand_trig(c) Сохраняет продукт в целости.
Поделиться
Mureinik
19 марта 2020 в 21:22
Похожие вопросы:
Как найти самый большой палиндром, сделанный из произведения двух 3-значных чисел в vb.net?
Я пытаюсь решить головоломку и … Постановка задачи такова: найти наибольший палиндром, составленный из произведения двух 3-значных чисел. Я новичок в этом деле, так что, пожалуйста, помогите!
Агрегация декартова произведения двух иерархических деревьев с использованием Java
Нужно сделать агрегацию декартова произведения двух иерархических древовидных структур с помощью Java, пожалуйста, предложите несколько хороших методов или API для этого. Древовидная Структура:…
численное интегрирование матрицы в Matlab
Я должен численно оценить в Matlab Интеграл произведения двух функций A(x,y) и B (x,y). Эти две функции находятся в 2-мерной форме массива.
4 В вольфраме я ввожу int(sin(2*x)/4 -…
sympy log_expand произведение двух неопределенных функций
Я создал две неопределенные функции в Sympy. Когда я беру log произведения двух неопределенных функций и применяю log_expand() , я не получаю сумму логов двух неопределенных функций. Минимальный…
R найдите самый большой палиндром, составленный из произведения двух 3-значных чисел
Палиндромное число читается одинаково в обоих направлениях. Самый большой палиндром, полученный из произведения двух двухзначных чисел, равен 9009 = 91 × 99. Напишите программу, которая находит…
Как создать функцию, которая возвращает функцию произведения списка функций
Я хотел бы создать функцию, которая возвращает функцию произведения списка функций. Список функций должен быть переменной длины, и функции должны иметь разные параметры. E.g.: def f(a, b, **kwargs):…
Найдите самый большой палиндром, сделанный из произведения двух 3-значных чисел C#
Я попытался решить 4-й проект projecteuler с помощью C#, но не получил правильного ответа, я получил 90909.
Может ли кто-нибудь заметить мою ошибку? Проблема заключается в следующем: Палиндромное…
Интеграция по частям
Интеграция по частям — это особый метод интеграции, который часто бывает полезен, когда две функции перемножаются, но также полезен и другими способами.
Скоро вы увидите множество примеров, но сначала давайте посмотрим на правило:
∫u v dx = u∫v dx −∫u ‘(∫v dx) dx
- u — функция u (x)
- v — функция v (x)
- u ‘ — производная функции u (x)
Правило в виде диаграммы:
Давайте сразу рассмотрим пример:
Пример: Что такое ∫x cos (x) dx?
Хорошо, у нас есть x , умноженное на cos (x) , поэтому интегрирование по частям — хороший выбор.
Сначала выберите, какие функции для u и v :
Итак, теперь он в формате ∫ u v dx , мы можем продолжить:
Дифференциация u : u ‘= x’ = 1
Интегрировать v : ∫v dx = ∫cos (x) dx = sin (x) (см.
Правила интеграции)
Теперь мы можем собрать все вместе:
Упростить и решить:
x sin (x) — ∫sin (x) dx
х грех (х) + соз (х) + С
Итак, мы выполнили следующие шаги:
- Выберите u и v
- Дифференцировать u: u ‘
- Интеграция v: ∫v dx
- Поместите u, u ‘и ∫v dx в: u∫v dx −∫u’ (∫v dx) dx
- Упростить и решить
На английском языке мы можем сказать, что ∫u v dx становится:
(интеграл u) минус интеграл (производная u, интеграл v)
Давайте попробуем еще несколько примеров:
Пример: что такое ∫ln (x) / x
2 dx?
Сначала выберите u и v:
Дифференцировать u: ln (x) ‘= 1 x
Интегрировать v: ∫1 / x 2 dx = ∫x -2 dx = −x -1 = −1 x (по правилу мощности)
Теперь сложим:
Упростить:
−ln (x) / x — ∫ − 1 / x 2 dx = −ln (x) / x — 1 / x + C
— лин (x) + 1 x + C
Пример: Что такое ∫ln (x) dx?
Но есть только одна функция! Как выбрать u и v?
Эй! Мы можем просто выбрать v как «1»:
Дифференцировать u: ln (x) ‘= 1 / x
Интегрировать v: ∫1 dx = x
Теперь сложим:
Упростить:
x ln (x) — ∫1 dx = x ln (x) — x + C
Пример: что такое ∫e
x x dx?
Выберите u и v:
Дифференцировать u: (e x ) ‘= e x
Интегрировать v: ∫x dx = x 2 /2
Теперь сложим:
Что ж, это была грандиозная катастрофа! Все стало еще сложнее.
Может быть, мы могли бы выбрать другие u и v?
Пример: ∫e
x x dx (продолжение)
Выберите по-разному u и v:
Дифференцировать u: (x) ‘= 1
Интегрировать v: ∫e x dx = e x
Теперь сложим:
Упростить:
x e x — e x + C
е х (х − 1) + С
Мораль истории: выбирайте u и v внимательно!
Выберите и , который станет проще, если вы его дифференцируете, и v , который не станет более сложным после интеграции.
Полезное эмпирическое правило — Я ПОЗДНУЮ. Выберите и в зависимости от того, что из них будет первым:
И последний (и хитрый) пример:
Пример: ∫e
x sin (x) dx
Выберите u и v:
Дифференцировать u: sin (x) ‘= cos (x)
Интегрировать v: ∫e x dx = e x
Теперь сложим:
∫e x sin (x) dx = sin (x) e x −∫cos (x) e x dx
Выглядит хуже, но будем настаивать! Чтобы найти ∫cos (x) e x dx, мы можем снова использовать интеграцию по частям :
Выберите u и v:
Дифференцировать u: cos (x) ‘= -sin (x)
Интегрировать v: ∫e x dx = e x
Теперь сложим:
∫e x sin (x) dx = sin (x) e x — (cos (x) e x −∫ − sin (x) e x dx)
Упростить:
∫e x sin (x) dx = e x sin (x) — e x cos (x) −∫ e x sin (x) dx
Теперь у нас одинаковый интеграл с обеих сторон (за исключением вычитания одного).
..
… так что переместим правую руку влево и получим:
2∫e x sin (x) dx = e x sin (x) — e x cos (x)
Упростить:
∫e x sin (x) dx = ½ e x (sin (x) — cos (x)) + C
Сноска. Откуда взялась «интеграция по частям»?
Он основан на Правиле продукта для деривативов:
(УФ) ‘= УФ’ + УФ
Объединить обе стороны и переставить:
∫ (uv) ‘dx = ∫uv’ dx + ∫u’v dx
uv = uv ‘dx + u’v dx
∫uv ‘dx = uv — u’v dx
Некоторые люди предпочитают эту последнюю форму, но мне нравится заменять v ‘на w и v на w dx , что упрощает левую часть:
∫uw dx = u∫w dx — ∫u ‘(∫w dx) dx
Calculus II — Интеграция по частям
Показать уведомление для мобильных устройств
Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-1: Интеграция по частям
Давайте начнем с этого раздела с пары интегралов, которые мы уже должны уметь делать для начала.2}}} + c ]
Опять же, это достаточно просто, если вы помните, как делать замены. Кстати, убедитесь, что вы можете делать такие замены быстро и легко. С этого момента мы будем производить подобные замены в своей голове. Если вам придется останавливаться и записывать их при каждой проблеме, вы обнаружите, что на решение этих задач у вас уйдет значительно больше времени.
{6x}} ) сам по себе, мы могли бы сделать интеграл достаточно легко. prime} , dx}} = int {{f ‘, g + f , g’ , dx}} ]
Левая часть достаточно проста для интегрирования (мы знаем, что интегрирование производной просто «отменяет» производную), и мы разделим правую часть интеграла.
[fg = int {{f ‘, g , dx}} + int {{f , g’ , dx}} ]
Обратите внимание, что технически у нас должна была отображаться константа интегрирования слева после выполнения интегрирования. Мы можем отбросить его на этом этапе, поскольку другие константы интеграции будут отображаться в будущем, и они просто поглотят эту.
Наконец, перепишите формулу следующим образом, и мы придем к формуле интегрирования по частям.
[ int {{f , g ‘, dx}} = fg — int {{f’ , g , dx}} ]
Однако это не самая простая формула. Итак, сделаем пару замен.
[ begin {align *} u = f left (x right) hspace {0,5in} v = g left (x right) \ & du = f ‘ left (x right) , dx hspace {0,5 дюйма} dv = g ‘ left (x right) , dx end {align *} ]
Обе из них — стандартные замены Calculus I, к которым, надеюсь, вы уже привыкли.
Не радуйтесь тому факту, что мы используем здесь две замены. Они будут работать так же.
Использование этих замен дает нам формулу, которую большинство людей считают формулой интегрирования по частям.
Интеграция по частям
[ int {{u , dv}} = uv — int {{v , du}} ]
Чтобы использовать эту формулу, нам нужно будет идентифицировать (u ) и (dv ), вычислить (du ) и (v ), а затем использовать формулу. Также обратите внимание, что вычислить (v ) очень просто.Все, что нам нужно сделать, это интегрировать (dv ).
[v = int {{dv}} ]
Одна из самых сложных вещей при использовании этой формулы — это то, что вам нужно правильно идентифицировать как (u ), так и (dv ). Не всегда будет ясно, каков правильный выбор, и иногда мы делаем неправильный выбор. Это не повод для беспокойства. Если мы сделаем неправильный выбор, мы всегда можем вернуться и попробовать другой набор вариантов.
Это приводит к очевидному вопросу: как узнать, правильно ли мы сделали выбор для (u ) и (dv )? Ответ на самом деле довольно прост.{6x}} , dx}} ]
Показать решениеИтак, на некотором уровне проблема здесь в (x ), стоящем перед экспонентой. Если бы этого не было, мы могли бы сделать интеграл. Также обратите внимание, что при выполнении интеграции по частям все, что мы выбираем для (u ), будет дифференцироваться. Таким образом, кажется, что выбор (u = x ) будет хорошим выбором, поскольку при дифференцировании (x ) выпадет.
Теперь, когда мы выбрали (u ), мы знаем, что (dv ) будет всем остальным, что останется.{6x}} + c end {align *} ]
После того, как мы выполнили последний интеграл в задаче, мы добавим константу интегрирования, чтобы получить окончательный ответ.
Также обратите внимание, что, как отмечалось выше, мы знаем, что сделали правильный выбор для (u ) и (dv ), когда получили новый интеграл, который мы фактически вычисляем после применения формулы интегрирования по частям.
Теперь давайте посмотрим на интегрирование по частям для определенных интегралов.b ) в первом члене — это просто стандартное обозначение интегральной оценки, с которым вы должны быть знакомы на этом этапе. Все, что мы делаем, это оцениваем член, в данном случае uv , в (b ), затем вычитаем оценку члена в (a ).
На каком-то уровне нам здесь действительно не нужна формула, потому что мы знаем, что при вычислении определенных интегралов все, что нам нужно сделать, это вычислить неопределенный интеграл, а затем выполнить вычисление. На самом деле, это, вероятно, будет немного проще, поскольку нам не нужно отслеживать таким образом оценку каждого термина.{- 6}} end {align *} ]
Любой из методов вычисления определенных интегралов с интегрированием по частям довольно прост, так что выбор, который вы выберете, в значительной степени зависит от вас.
Поскольку нам нужно уметь вычислять неопределенный интеграл, чтобы вычислить определенный интеграл, а выполнение определенного интеграла сводится к не более чем вычислению неопределенного интеграла в паре точек, мы сконцентрируемся на вычислении неопределенных интегралов в остальной части этого раздел.
Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов.
Давайте взглянем еще на несколько примеров.
Пример 3 Вычислите следующий интеграл.
[ int {{ left ({3t + 5} right) cos left ({ frac {t} {4}} right) , dt}} ]
Показать решениеЕсть два способа продолжить этот пример. Для многих первое, что они пробуют, — это умножить косинус через скобки, разделить интеграл, а затем выполнить интегрирование по частям для первого интеграла.
Хотя это вполне приемлемый способ решения проблемы, это больше работы, чем нам действительно нужно. Вместо того, чтобы разделять интеграл, давайте вместо этого воспользуемся следующими вариантами для (u ) и (dv ).
[ begin {align *} u & = 3t + 5 & hspace {0,5 дюйма} dv & = cos left ({ frac {t} {4}} right) , dt \ du & = 3 , dt & hspace {0,5 дюйма} v & = 4 sin left ({ frac {t} {4}} right) end {align *} ]
Тогда интеграл равен
.
[ begin {align *} int {{ left ({3t + 5} right) cos left ({ frac {t} {4}} right) , dt}} & = 4 left ({3t + 5} right) sin left ({ frac {t} {4}} right) — 12 int {{ sin left ({ frac {t} {4}} right) , dt}} \ & = 4 left ({3t + 5} right) sin left ({ frac {t} {4}} right) + 48 cos left ({ frac {t} {4}} right) + c end {align *} ]Обратите внимание, что мы вытащили все константы из интеграла, когда использовали формулу интегрирования по частям.2}}} {{10}} cos left ({10w} right) + frac {1} {5} int {{w cos left ({10w} right) , dw}} ]
В этом примере, в отличие от предыдущих примеров, новый интеграл также потребует интегрирования по частям. Для этого второго интеграла мы будем использовать следующие варианты.
[ begin {align *} u & = w & hspace {0,5 дюйма} dv & = cos left ({10w} right) , dw \ du & = , dw & hspace {0,5 дюйма } v & = frac {1} {{10}} sin left ({10w} right) end {align *} ]
Итак, интеграл принимает вид
[ begin {align *} int {{{w ^ 2} sin left ({10w} right) , dw}} & = — frac {{{w ^ 2}}} {{10 }} cos left ({10w} right) + frac {1} {5} left ({ frac {w} {{10}} sin left ({10w} right) — frac {1} {{10}} int {{ sin left ({10w} right) , dw}}} right) \ & = — frac {{{w ^ 2}}} {{ 10}} cos left ({10w} right) + frac {1} {5} left ({ frac {w} {{10}} sin left ({10w} right) + frac {1} {{100}} cos left ({10w} right)} right) + c \ & = — frac {{{w ^ 2}}} {{10}} cos left ({10w} right) + frac {w} {{50}} sin left ({10w} right) + frac {1} {{500}} cos left ({10w} вправо) + c end {align *} ]
Будьте осторожны с коэффициентом интеграла для второго применения интегрирования по частям.Поскольку интеграл умножается на ( frac {1} {5} ), нам нужно убедиться, что результаты фактического выполнения интеграла также умножаются на ( frac {1} {5} ). Забывание сделать это — одна из наиболее распространенных ошибок при интеграции по частям.
Как показал этот последний пример, иногда нам потребуется несколько приложений интегрирования по частям, чтобы полностью оценить интеграл. Это то, что произойдет, поэтому не волнуйтесь, когда это произойдет.
В следующем примере нам нужно признать важный момент, касающийся методов интеграции. Некоторые интегралы могут быть получены с использованием нескольких различных методов. Так обстоит дело с интегралом в следующем примере.
Пример 5 Вычислите следующий интеграл
[ int {{х sqrt {x + 1} , dx}} ]- Использование интеграции по частям.
- Используя стандартную замену Calculus I.
Показать все решения Скрыть все решения
a Использование интеграции по частям.Показать решениеСначала обратите внимание, что в этом интеграле нет триггерных функций или экспонент. Хотя довольно много интегралов по частям будет включать триггерные функции и / или экспоненты, не все из них будут слишком зациклены на идее ожидания их появления.
В этом случае мы будем использовать следующие варианты для (u ) и (dv ).
[ begin {align *} u & = x & hspace {0,5 дюйма} dv & = sqrt {x + 1} , dx \ du & = dx & hspace {0.{ frac {5} {2}}} + c end {align *} ]
b Используя стандартную замену Calculus I. Показать решениеТеперь займемся интегралом с заменой. Мы можем использовать следующую замену.
[u = x + 1 hspace {0,5 дюйма} x = u — 1 hspace {0,5 дюйма} du = dx ]
Обратите внимание, что на самом деле мы будем использовать замену дважды: один раз для количества под квадратным корнем и один раз для (x ) перед квадратным корнем. { frac {3} {2}}} + c end {align *} ]
Итак, в этом примере мы использовали два разных метода интеграции и получили два разных ответа.Тогда возникает очевидный вопрос: мы сделали что-то не так?
На самом деле, мы не сделали ничего плохого. Нам необходимо помнить следующий факт из исчисления I.
[{ rm {If}} , , f ‘ left (x right) = g’ left (x right) , , , { rm {then}} , , , е влево (х вправо) = г влево (х вправо) + с ]
Другими словами, если две функции имеют одинаковую производную, то они будут отличаться не более чем на константу. Итак, как это применимо к указанной выше проблеме? Сначала определите следующее:
[f ‘ left (x right) = g’ left (x right) = x sqrt {x + 1} ]
Затем мы можем вычислить (f left (x right) ) и (g left (x right) ) путем интегрирования следующим образом:
[е left (x right) = int {{f ‘ left (x right) , dx}} hspace {0.5in} g left (x right) = int {{g ‘ left (x right) , dx}} ]
Мы будем использовать интегрирование по частям для первого интеграла и замену для второго интеграла. Тогда согласно тому, что (f left (x right) ) и (g left (x right) ) должны отличаться не более чем на константу. Давайте проверим это и посмотрим, так ли это. Мы можем убедиться, что они различаются не более чем на константу, если мы посмотрим на разницу между ними и сделаем небольшие алгебраические манипуляции и упрощения.{ frac {3} {2}}} left (0 right) \ hspace {2.0in} = 0 end {array} ]
Итак, в этом случае оказывается, что две функции — это одна и та же функция, поскольку разница равна нулю. Учтите, что это происходит не всегда. Иногда разница дает ненулевую константу. Пример этого можно найти в разделе «Константа интеграции» в примечаниях к исчислению I.
Итак, что мы узнали? Во-первых, иногда будет несколько методов вычисления интеграла.Во-вторых, мы увидели, что разные методы часто приводят к разным ответам. Наконец, даже несмотря на то, что ответы разные, иногда с большим трудом можно показать, что они отличаются не более чем на константу.
Когда мы сталкиваемся с интегралом, первое, что нам нужно решить, — это то, есть ли более одного способа сделать интеграл. Если существует несколько способов, нам нужно будет определить, какой из них следует использовать. Общее практическое правило, которое я использую в своих классах, заключается в том, что вы должны использовать метод, который вы считаете наиболее простым.Возможно, это не самый простой способ, но это не значит, что это неправильный метод.
Одна из наиболее распространенных ошибок интеграции по частям — это слишком сильная привязанность людей к воспринимаемым шаблонам. Например, во всех предыдущих примерах использовался базовый шаблон, согласно которому (u ) принимался за многочлен, стоящий перед другой функцией, а затем позволял (dv ) быть другой функцией. Это не всегда будет происходить, поэтому нам нужно быть осторожными и не связываться с какими-либо шаблонами, которые, как нам кажется, мы видим.
Давайте взглянем на некоторые интегралы, которые не вписываются в приведенный выше шаблон.
Пример 6 Вычислите следующий интеграл.
[ int {{ ln x , dx}} ]
Показать решениеИтак, в отличие от любого другого интеграла, который мы сделали до этого момента, в интеграле есть только одна функция и нет полинома перед логарифмом.
Первый выбор многих людей здесь — попытаться вписать это в шаблон сверху и сделать следующие выборы для (u ) и (dv ).
[u = 1 hspace {0,5 дюйма} dv = ln x , dx ]
Однако это приводит к реальной проблеме, поскольку это означает, что (v ) должно быть,
[v = int {{ ln x , dx}} ]
Другими словами, нам нужно знать ответ заранее, чтобы решить проблему. Так что этот выбор просто не сработает.
Следовательно, если логарифм не принадлежит (dv ), он должен принадлежать вместо (u ).Итак, давайте использовать следующие варианты вместо
[ begin {align *} u & = ln x & hspace {0,5 дюйма} dv & = , dx \ du & = frac {1} {x} dx & hspace {0,5 дюйма} v & = х конец {выравнивание *} ]
Тогда интеграл равен
.
[ begin {align *} int {{ ln x , dx}} & = x ln x — int {{ frac {1} {x} , x , dx}} \ & = x ln x — int {{dx}} \ & = x ln x — x + c end {align *} ]
Пример 7 Вычислите следующий интеграл.{ frac {5} {2}}} + c end {align *} ]Итак, в двух предыдущих примерах мы видели случаи, которые не совсем вписывались в какой-либо воспринимаемый шаблон, который мы могли бы получить из первых двух примеров. Это всегда то, к чему мы должны обращать внимание при интеграции по частям.
Давайте взглянем на другой пример, который также иллюстрирует другой метод интеграции, который иногда возникает из-за проблем интеграции по частям.
Пример 8 Вычислите следующий интеграл. theta} cos theta , d theta}} ]
Показать решениеХорошо, до сих пор мы всегда выбирали (u ) таким образом, чтобы при дифференцировании эта часть исчезла или, по крайней мере, превратила ее в интеграл в форму, которая упростила бы работу с . В этом случае, какую бы часть мы ни составляли (u ), она никогда не уйдет в процессе дифференцирования.
Не имеет большого значения, какой мы выбираем (u ), поэтому мы выберем следующий путь. theta} sin theta} right) + c ]
Обратите внимание, что после деления на два мы добавляем постоянную интегрирования в этой точке.
Эту идею интегрирования до тех пор, пока вы не получите одинаковый интеграл по обе стороны от знака равенства, а затем простое решение для интеграла, неплохо запомнить. Это не так уж и часто, но когда это происходит, это может быть единственный способ на самом деле выполнить интеграл.
Также обратите внимание, что это на самом деле просто алгебра, по общему признанию, сделанная таким образом, что вы, возможно, не привыкли к этому, но на самом деле это просто алгебра.
На данном этапе вашей математической карьеры каждый может решить,
[x = 3 — x hspace {0,5 дюйма} to hspace {0,5 дюйма} x = frac {3} {2} ]
Мы все еще решаем «уравнение». Единственное отличие состоит в том, что вместо решения для (x ) в мы решаем для интеграла, и вместо хорошей константы «3» в приведенной выше задаче алгебры мы получили функцию «беспорядка».
У нас есть еще один пример. Как мы увидим, некоторые проблемы могут потребовать от нас выполнять интеграцию по частям много раз, и существует короткий метод, который позволит нам быстро и легко выполнять несколько приложений интеграции по частям.{ frac {x} {2}}} , dx}} ]
Показать решениеНачнем с выбора (u ) и (dv ), как всегда. Однако вместо того, чтобы вычислять (du ) и (v ), мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий (u ), пока не дойдем до нуля. В столбце, соответствующем (dv ), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается со знака «+», а затем чередуются знаки, как показано.{ frac {x} {2}}} + c end {align *} ]
У нас есть интеграл. Это намного проще, чем записывать все различные (u ) и (dv ), которые нам пришлось бы делать в противном случае.
Итак, в этом разделе мы увидели, как выполнять интеграцию по частям. На более поздних уроках математики это, вероятно, будет одним из наиболее частых методов интеграции, с которыми вы столкнетесь.
Важно не зацикливаться на шаблонах, которые, как вы думаете, вы видели.В большинстве случаев любой шаблон, который, как вы думаете, вы видели, может (и будет) нарушен в какой-то момент времени. Будь осторожен!
Видео с вопросом: Нахождение интеграла произведения между экспоненциальной функцией и тригонометрической функцией
Стенограмма видео
Положив 𝑢 равным 𝑒 в степени и d𝑣 равным cos d𝑥, вычислите интеграл 𝑒 в степени 𝑥, умноженный на cos по отношению к 𝑥, путем интегрирования по частям.
Нам дается интеграл для вычисления, и мы видим, что наше интегральное выражение является произведением двух функций. Это 𝑒 в степени, умноженной на cos. И мы знаем несколько разных способов вычисления интеграла, который является произведением двух функций. В этом вопросе нас просят использовать интеграцию по частям. Давайте начнем с того, что вспомним, что мы подразумеваем под интеграцией по частям. Это говорит нам, что интеграл от, умноженного на d𝑣 на d𝑥, относительно 𝑥 равен 𝑢, умноженному на 𝑣, за вычетом интеграла от 𝑣, умноженного на d𝑢 на d𝑥 относительно 𝑥.
Другими словами, это дает нам метод интегрирования произведения двух функций 𝑢 и d𝑣 на d𝑥. Фактически, в вопросе мы видим, что нам говорят, чему присвоить наши функции 𝑢 и 𝑣 равными. Нам говорят установить 𝑢 равным 𝑒 в степени. И сказать, что d𝑣 равно cos d𝑥, является дифференциальным обозначением, чтобы сказать, что d𝑣 через d𝑥 равно cos. Итак, мы положим 𝑢 равным 𝑒 в степени 𝑥 и d𝑣 на d𝑥, чтобы равняться cos.
Теперь, чтобы использовать интегрирование по частям, мы видим, что нам нужны выражения для 𝑣 и d𝑢 через d𝑥.Начнем с d𝑢 by d. Это производная экспоненциальной функции 𝑒 в степени по 𝑥. Но мы знаем, что производная экспоненциальной функции по 𝑥 — это просто экспоненциальная функция. Итак, d𝑢 от d𝑥 — это 𝑒 в степени. Теперь давайте найдем выражение для 𝑣. 𝑣 будет первообразной cos of. Один из способов найти это — проинтегрировать cos относительно. Мы знаем, что это даст нам грех 𝑥 плюс постоянную интегрирования. Но нам просто нужно любое первообразное, поэтому мы просто воспользуемся грехом 𝑥.
Теперь мы готовы вычислить интеграл в степени, умноженной на cos по отношению к 𝑥, используя интегрирование по частям. Подставляя в наши выражения для 𝑢, 𝑣, d𝑢 на d𝑥 и d𝑣 на d𝑥 в нашу формулу интегрирования по частям, мы получаем 𝑒 в степени, умноженной на грех минус интеграл греха, умноженный на 𝑒, чтобы степень 𝑥 относительно 𝑥. И теперь мы видим проблему. Мы не знаем, как вычислить интеграл греха, умноженного на 𝑒, до степени по отношению к.У него те же проблемы, что и у нашего исходного интеграла.
Наша интегральная функция является продуктом двух функций. Однако на этот раз мы можем заметить кое-что интересное. Если бы мы еще раз применили этот процесс интегрирования по частям, мы бы интегрировали грех, дав нам отрицательный cos. Итак, в нашей формуле интегрирования по частям, поскольку, когда мы дифференцируем экспоненциальную функцию, мы просто получаем экспоненциальную функцию, мы получим интеграл от отрицательного cos от, умноженного на 𝑒, в степень относительно.Но это именно тот интеграл, который мы пытаемся вычислить. Таким образом, мы можем переставить и найти значение этого интеграла.
Итак, давайте попробуем еще раз применить интеграцию по частям. На этот раз мы воспользуемся этим, чтобы вычислить интеграл от греха, умноженного на 𝑒, до степени по отношению к. Мы положим 𝑢 экспоненциальной функцией 𝑒 в степени и d𝑣 на d𝑥 как грех. Дифференцируя 𝑢 по 𝑥, получаем, что d𝑢 на d𝑥 равно 𝑒 в степени. И, интегрируя грех по отношению к we, мы получаем, что 𝑣 равно отрицательному cos 𝑥.Подставляя в наши выражения для 𝑢, 𝑣, d𝑢 на d𝑥 и d𝑣 на d𝑥 в нашу формулу для интегрирования по частям, мы получаем 𝑒 в степени 𝑥 отрицательных cos of минус интеграл от отрицательного cos, умноженный на 𝑒 в степени относительно.
И мы можем упростить это выражение. Во-первых, мы можем записать в степени, умноженной на отрицательное значение cos, как отрицательное 𝑒 в степени, умноженной на cos. Точно так же мы можем упростить наш интеграл. У нас есть отрицательный множитель внутри нашего подынтегрального выражения.Мы можем вынести это за пределы нашего интеграла, поэтому вместо этого мы просто добавляем интеграл. Затем мы можем просто переписать подынтегральное выражение как в степени, умноженной на cos. Итак, мы показали, что интеграл от греха, умноженного на 𝑒, до степени по отношению к 𝑥, равен отрицательному в степени, умноженной на cos, плюс интеграл от 𝑒 в степени, умноженной на на cos относительно.
Теперь все, что нам нужно сделать, это подставить это выражение для интеграла греха, умноженного на, на степень по отношению к 𝑥 в нашу формулу для нашего исходного интеграла.Подставляя это выражение в, мы получаем в степени, умноженной на грех 𝑥 минус отрицательное 𝑒 в степень, умноженную на cos плюс интеграл в степени, умноженной на cos of по отношению к 𝑥. А теперь можно приступить к упрощению этого выражения. Начнем с того, что разместим отрицательную единицу в скобках. Это дает нам 𝑒 в степени sin 𝑥 плюс 𝑒 в степень cos 𝑥 минус интеграл 𝑒 в степень cos числа 𝑥 по отношению к 𝑥.
И помните, что это равно интегралу от до степени cos от 𝑥 по отношению к.И мы видим, что это выражение появляется с обеих сторон нашего уравнения. Таким образом, мы можем решить эту проблему, добавив интеграл от 𝑒 к степени cos от по отношению к 𝑥 к обеим сторонам этого уравнения. Добавив это к обеим частям нашего уравнения в левой части, мы получим удвоенный интеграл от в степени, умноженный на cos of по отношению к. И в правой части этого уравнения наш третий член сокращен. Это дает нам 𝑒 в 𝑥 степени, умноженной на грех 𝑥 плюс, в, умноженную на cos the.
Теперь разделим обе части уравнения пополам. И помните, поскольку мы вычисляем определенный интеграл, нам понадобится постоянная интегрирования. Назовем это 𝐶. Последнее, что мы сделаем, — изменим это выражение и возьмем общий множитель в степень. И это дает нам половину 𝑒 в степени, умноженную на грех 𝑥, плюс cos плюс наша постоянная интегрирования.
Таким образом, дважды применив интегрирование по частям, мы смогли показать, что интеграл в степени, умноженной на cos of по отношению к 𝑥, равен половине 𝑒 в степени, умноженной на sin плюс cos плюс постоянная интегрирования.x} dx}, ; ;} kern0pt { int {x ln xdx},} ]
, в котором подынтегральное выражение является произведением двух функций, может быть решено с помощью интегрирования по частям.
Этот метод основан на правиле продукта для дифференциации.
Предположим, что (u left (x right) ) и (v left (x right) ) — дифференцируемые функции. Тогда правило продукта с точки зрения дифференциалов дает нам:
[{d left ({uv} right) = udv + vdu.} ]
Переставляя это правило, мы можем написать
[{udv = d left ({uv} right) — vdu.} ]
Интегрирование обеих сторон относительно (x ) дает
[{{ int {{{u} {dv}}}} = uv — { int {vdu}}.} ]
Это формула интегрирования по частям. Цель использования этой формулы — заменить один интеграл (слева) другим (справа), который может быть легче вычислить.
Ключевым моментом при интеграции по частям является правильный выбор (u ) и (dv ).
Аббревиатура ILATE подходит для выбора (u. {- x}}, ldots )
Чем ближе функция к вершине, тем больше вероятность, что ее следует использовать как (u.n} xdx}, ) (n ge 2. )
Пример 1.
Вычислить ( int {x sin left ({3x — 2} right) dx}. )
Решение.
Используем интегрирование по частям: ( int {udv} = uv — int {vdu}. ) Пусть (u = x, ) (dv = sin left ({3x — 2} right ) dx. ) Тогда
[
{v = int { sin left ({3x — 2} right) dx}}
= {- frac {1} {3} cos left ({3x — 2} right) ), ; ;} kern-0.3pt
{du = dx.}
]Следовательно, интеграл равен
[
{ int {x sin left ({3x — 2} right) dx}}
= {{- frac {x} {3} cos left ({3x — 2} right) )}} — {{ int { left ({- frac {1} {3} cos left ({3x — 2} right)} right) dx}}}
= {{- frac {x} {3} cos left ({3x — 2} right)} + { frac {1} {3} int { cos left ({3x — 2} right) dx}}}
= {{- frac {x} {3} cos left ({3x — 2} right)}} + {{ frac {1} {3} cdot frac {1} {3} sin left ({3x — 2} right) + C}}
= {{ frac {1} {9} sin left ({3x — 2} right)} — { frac {x} { 3} cos left ({3x — 2} right)} + {C.2} xdx}} = {- x cot x} + { ln left | { sin x} right | } + {C.} ]Пример 3.
Вычислить интеграл ( int {x cos 2xdx}. )
Решение.
Выбираем
[{u = x, ; ;} kern0pt {dv = cos 2xdx.} ]
Отсюда
[{du = dv, ; ;} kern0pt {v = int { cos 2xdx}} = { frac {1} {2} sin 2x.} ]
Подставляя эти выражения в формулу интегрирования по частям
[ int {udv} = uv — int {vdu}, ]
у нас
[{ int {x cos 2xdx}} = {x cdot frac {1} {2} sin 2x — int { frac {1} {2} sin 2xdx}} = { frac {x} {2} sin 2x — frac {1} {2} int { sin 2xdx}} = { frac {x} {2} sin 2x — frac {1} {2} cdot left ({- frac {1} {2} cos 2x} right) + C} = { frac {x} {2} sin 2x + frac {1} {4} cos 2x + C .} ]
Пример 4.
Интегрируйте ( int { ln xdx}. )
Решение.
Мы должны интегрировать по частям: (u = ln x, ) (dv = dx. 2}}}} normalsize dx}.2}}}}} = {- frac {{ ln x}} {x} — frac {1} {x} + C.} ]
Пример 6.
Вычислить интеграл ( int {{{ log} _2} xdx}. )
Решение.
Чтобы использовать интегрирование по частям, перепишем интеграл следующим образом:
[ int {{{ log} _2} xdx} = int {1 cdot {{ log} _2} xdx} ]
Теперь мы можем применить правило ILATE, то есть
[{u = { log _2} x, ; ;} {dv = 1dx.} ]
Это дает
[{du = frac {{dx}} {{x ln 2}}, ; ;} {v = int {1dx} = x.} ]
Интегрируя по частям, получаем
[{ int {{{ log} _2} xdx}} = {x { log _2} x — int {x cdot frac {{dx}} {{x ln 2}}}} = {x { log _2} x — frac {1} {{ ln 2}} int {dx}} = {x { log _2} x — frac {x} {{ ln 2}} + C.} ]
методов интеграции | Безграничное исчисление
Основные принципы интеграции
Интегрирование — это процесс поиска области, ограниченной функцией; этот процесс использует несколько важных свойств. b ! f (x) , dx [/ latex] неофициально определяется как область области на плоскости [latex] xy [/ latex], ограниченная графиком [latex] f [/ latex], [latex] ] x [/ latex] -ось, а вертикальные линии [latex] x = a [/ latex] и [latex] x = b [/ latex], так что область над [latex] x [/ latex] -осью прибавляет к общей сумме, а то, что ниже оси [latex] x [/ latex], вычитает из общей суммы.Термин интеграл может также относиться к понятию антипроизводной, функции [латекс] F [/ латекс], производной которой является заданная функция [латекс] f [/ латекс].
Определенный интеграл : Определенный интеграл функции может быть представлен в виде области со знаком области, ограниченной ее графиком.
Более строго, если антипроизводная [латекс] F [/ латекс] [латекса] f [/ латекса] известна для непрерывной действительной функции [латекс] f [/ латекс], определенной на закрытом интервале [латекс] ] [a, b] [/ latex], определенный интеграл [latex] f [/ latex] по этому интервалу равен
[латекс] displaystyle { int_a ^ b ! f (x) , dx = F (b) — F (a)} [/ латекс]
Если [latex] F [/ latex] является одним из антипроизводных [latex] f [/ latex], тогда все другие антипроизводные будут иметь форму [latex] F (x) + C [/ latex] для некоторых константа [латекс] C [/ латекс]. a f (x) , dx} [/ latex]
Интеграция путем замены
Обращая цепное правило, мы получаем метод, называемый интегрированием путем подстановки.Учитывая две функции [latex] f (x) [/ latex] и [latex] g (x) [/ latex], мы можем использовать следующую идентичность:
[латекс] Displaystyle { int [е ‘(г (х)) cdot g’ (х)] ; mathrm d x = f (g (x)) + C} [/ латекс]
или в виде «фиктивной переменной» [latex] u = g (x) [/ latex]:
[латекс] displaystyle { int f ‘(u) ; mathrm d u = f (u) + C} [/ латекс]
Если мы собираемся использовать интегрирование подстановкой для вычисления определенного интеграла, мы должны соответственно изменить верхнюю и нижнюю границы интегрирования.
Интеграция по частям
Интеграция по частям — это способ интеграции сложных функций путем разделения их на отдельные части и их индивидуальной интеграции.
Цели обучения
Решите интегралы путем интегрирования по частям
Основные выводы
Ключевые моменты
- Интегрирование по частям — это теорема, которая связывает интеграл от произведения функций с интегралом от их производной и антипроизводной.
- Теорема выражается как [латекс] int u (x) v ‘(x) , dx = u (x) v (x) — int u’ (x) v (x) , dx [/ latex ].
- Интегрирование по частям можно интерпретировать не только математически, но и графически.
Ключевые термины
- интегральный : также иногда называют первообразным; предел сумм, вычисленных в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, после чего все эти продукты суммируются
- производная : мера того, как функция изменяется при изменении ее входных данных
Введение
В исчислении интегрирование по частям — это теорема, которая связывает интеграл от произведения функций с интегралом от их производной и антипроизводной.Он часто используется для нахождения антипроизводной произведения функций в идеально более простую антипроизводную. Правило можно вывести в одну строку, просто интегрировав правило дифференциации продукта.
Теорема интегрирования по частям
Возьмем функции [латекс] u = u (x) [/ latex] и [latex] v = v (x) [/ latex]. Взяв их производные, мы останемся с [латексом] du = u ‘(x) [/ latex] и [latex] dxdv = v ‘(x) dx [/ latex]. Теперь давайте посмотрим на принцип интеграции по частям:
[латекс] displaystyle { int u (x) v ‘(x) , dx = u (x) v (x) — int u’ (x) v (x) dx} [/ латекс]
или, более компактно,
[латекс] displaystyle { int u , dv = uv- int v , du} [/ латекс]
Проба
Предположим, что [latex] u (x) [/ latex] и [latex] v (x) [/ latex] — две непрерывно дифференцируемые функции.{i = 2} [/ латекс]. Предполагая, что кривая гладкая в пределах окрестности, это обобщается до неопределенных интегралов [latex] int xdy + int y dx = xy [/ latex], которые можно преобразовать в форму теоремы: [latex] int xdy = xy — int y dx [/ латекс].
Пример
Чтобы вычислить [латекс] I = int x cos (x) , dx [/ latex], пусть:
[латекс] u = x \ поэтому du = dx [/ latex]
и
[латекс] dv = cos (x) , dx \ поэтому v = int cos (x) , dx = sin x [/ latex]
, затем:
[латекс] begin {align} int x cos (x) , dx & = int u , dv \ & = uv — int v , du \ & = x sin (x) — int sin (x) , dx \ & = x sin (x) + cos (x) + C end {align} [/ latex]
Тригонометрические интегралы
Тригонометрические интегралы — это особый набор функций, используемых для упрощения сложных математических выражений с целью их вычисления.
Цели обучения
Решите основные тригонометрические интегралы
Основные выводы
Ключевые моменты
- Некоторые выражения для тригонометрических интегралов находятся с использованием свойств тригонометрических функций.
- Некоторые выражения были получены с использованием таких методов, как интегрирование по частям.
- Нет гарантии, что тригонометрический интеграл имеет аналитическое выражение.
Ключевые термины
- тригонометрический : относящийся к функциям, используемым в тригонометрии: [latex] sin [/ latex], [latex] cos [/ latex], [latex] tan [/ latex], [latex] csc [ / латекс], [латекс] кроватка [/ латекс], [латекс] сек [/ латекс]
- интегральный : также иногда называют первообразным; предел сумм, вычисленных в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, после чего все эти продукты суммируются
Тригонометрические интегралы
Тригонометрические интегралы — это семейство интегралов, которые включают тригонометрические функции ([latex] sin [/ latex], [latex] cos [/ latex], [latex] tan [/ latex], [latex] csc [ / латекс], [латекс] кроватка [/ латекс], [латекс] сек [/ латекс]).Ниже приводится список интегралов от тригонометрических функций. Некоторые из них были вычислены с использованием свойств тригонометрических функций, в то время как другие использовали такие методы, как интегрирование по частям.
Как правило, если функция [latex] sin (x) [/ latex] является любой тригонометрической функцией, а [latex] cos (x) [/ latex] является ее производной, то
[латекс] displaystyle { int a cos nx ; mathrm {d} x = frac {a} {n} sin nx + C} [/ latex]
Во всех формулах предполагается, что константа [latex] a [/ latex] отлична от нуля, а [latex] C [/ latex] обозначает константу интегрирования.2 x = frac {1} {2} (1 — sin 2x) [/ latex] и [латекс] sin x cos x = frac {1} {2} sin 2x [/ latex].
Тригонометрическая замена
Тригонометрические функции могут быть заменены другими выражениями, чтобы изменить форму подынтегральных выражений и упростить интегрирование.
Цели обучения
Используйте тригонометрическую замену для решения интеграла
Основные выводы
Ключевые моменты
- Если подынтегральное выражение содержит [latex] a ^ 2 — x ^ 2 [/ latex], пусть [latex] x = a sin ( theta) [/ latex].2 [/ latex], пусть [latex] x = a sec ( theta) [/ latex].
Ключевые термины
- тригонометрический : относящийся к функциям, используемым в тригонометрии: [latex] sin [/ latex], [latex] cos [/ latex], [latex] tan [/ latex], [latex] csc [ / латекс], [латекс] кроватка [/ латекс], [латекс] сек [/ латекс]
Тригонометрические функции могут быть заменены другими выражениями, чтобы изменить форму подынтегральных выражений. Можно использовать тригонометрические тождества для упрощения некоторых интегралов, содержащих радикальные выражения (или выражения, содержащие корни [latex] n [/ latex] th).2 ( theta)}} \ & = int frac {d theta} {a} \ & = frac { theta} {a} + C \ & = frac {1} {a} arctan left ( frac {x} {a} right) + C end {align} [/ latex]
Метод неполных дробей
Разложение на частичные дроби обеспечивает подход к интеграции общей рациональной функции.
Цели обучения
Использовать частичное дробное разложение для интегрирования рациональных функций
Основные выводы
Ключевые моменты
- Любая рациональная функция действительной переменной может быть записана как сумма многочлена и конечного числа рациональных дробей, знаменателем которых является степень неприводимого многочлена, а числитель имеет степень ниже, чем степень этого неприводимого многочлена.2 + 1 [/ латекс]
Разложение на частичные дроби обеспечивает подход к интеграции общей рациональной функции. Любую рациональную функцию действительной переменной можно записать как сумму многочлена и конечного числа рациональных дробей, знаменателем которых является степень неприводимого многочлена, а числитель имеет степень ниже, чем степень этого неприводимого многочлена. Вот несколько общих примеров.
Полином 1-й степени в знаменателе
Замена [latex] u = ax + b [/ latex], [latex] du = a , dx [/ latex] уменьшает интеграл [latex] int {1 over ax + b} , dx [/ латекс] к:
[латекс] begin {align} int {1 over u} , {du over a} & = {1 over a} int {du over u} \ & = {1 over a } ln left | u right | + C \ & = {1 over a} ln left | ax + b right | + C end {align} [/ latex]
Повторяющийся многочлен 1-й степени в знаменателе
Та же самая замена уменьшает такие интегралы, как [latex] int {1 over (ax + b) ^ 8} , dx [/ latex], до
[латекс] begin {align} int {1 over u ^ 8} , {du over a} & = {1 over a} int u ^ {- 8} , du \ & = {1 over a} cdot {u ^ {- 7} over (-7)} + C \ & = {-1 over 7au ^ 7} + C \ & = {-1 over 7a ( ax + b) ^ 7} + C end {align} [/ latex]
Неприводимый многочлен 2-й степени в знаменателе
Далее мы рассматриваем такие интегралы, как
[латекс] displaystyle { int {x + 6 over x ^ 2-8x + 25} , dx} [/ latex]
Самый быстрый способ увидеть, что знаменатель, [латекс] x ^ 2 — 8x + 25 [/ latex], несократим, — это заметить, что его дискриминант отрицательный.2-8x + 25) + {10 over 3} arctan left ({x-4 over 3} right) + C} [/ latex]
Интеграция с использованием таблиц и компьютеров
Для интегрирования обычно используются таблицы известных интегралов или компьютерных программ.
Цели обучения
Определить, какие интегралы следует решать с помощью таблиц или компьютеров в силу их сложности
Основные выводы
Ключевые моменты
- В то время как дифференцирование имеет простые правила, по которым производная сложной функции может быть найдена путем дифференцирования ее более простых составляющих функций, интегрирование — нет.
- В книгах с интегральными таблицами можно найти компиляцию списка интегралов и методов интегрального исчисления.
- Существует несколько коммерческих программ, таких как Mathematica или Matlab, которые могут выполнять символьную интеграцию.
Ключевые термины
- интегральный : также иногда называют первообразным; предел сумм, вычисленных в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, после чего все эти продукты суммируются
Интегрирование — основная операция в интегральном исчислении.В то время как дифференцирование имеет простые правила, по которым производная сложной функции может быть найдена путем дифференцирования ее более простых составляющих функций, интегрирование этого не делает, поэтому часто полезны таблицы известных интегралов. Нам также, возможно, придется прибегнуть к компьютерам для выполнения интеграла.
Интеграция с использованием таблиц
Сборник списка интегралов и методов интегрального исчисления был опубликован немецким математиком Мейером Хиршем еще в 1810 году. Более обширные таблицы были составлены в 1858 году голландским математиком Давидом де Биренс де Хааном.Новое издание вышло в 1862 году. Эти таблицы, содержащие в основном интегралы от элементарных функций, использовались до середины 20 века. Затем их заменили гораздо более обширные таблицы Градштейна и Рыжика. Вот несколько примеров интегралов в этих таблицах для логарифмических функций:
[латекс] int ln ax ; dx = x ln ax — x [/ латекс]
[латекс] displaystyle { int ln (ax + b) ; dx = frac {(ax + b) ln (ax + b) — ax} {a}} [/ латекс]
[латекс] int ( ln x) ^ 2 ; dx = x ( ln x) ^ 2 — 2x ln x + 2x [/ латекс]
[латекс] Displaystyle { int ( пер х) ^ п ; dx = x sum ^ {n} _ {k = 0} (- 1) ^ {n-k} frac {n!} {k! } ( ln x) ^ k} [/ латекс]
[латекс] Displaystyle { int frac {dx} { ln x} = ln left | ln x right | + ln x + sum ^ infty_ {k = 2} frac {( ln x) ^ k} {k cdot k! }} [/ latex]
[латекс] Displaystyle { int frac {dx} {( ln x) ^ n} = — frac {x} {(n-1) ( ln x) ^ {n-1}} + frac {1} {n-1} int frac {dx} {( ln x) ^ {n-1}} qquad mbox {(для} n neq 1 mbox {)}} [/ латекс ]
Вы, конечно, видите, что эти интегралы сложно сделать просто «вручную».”
Интеграция с использованием компьютеров
Компьютеры могут использоваться для интеграции двумя основными способами. Во-первых, численные методы с использованием компьютеров могут быть полезны при вычислении определенного интеграла. Есть много методов и алгоритмов. Мы вкратце узнаем о численном интегрировании в другом атоме. Во-вторых, существует несколько коммерческих программ, таких как Mathematica или Matlab, которые могут выполнять символьную интеграцию.
Интеграция : Численное интегрирование заключается в нахождении численных приближений для значения [латекс] S [/ латекс].{b} f (x) , dx = frac {ba} {2N} (f (x_1) + 2f (x_2) + 2f (x_3) + ldots + 2f (x_N) + f (x_ {N + 1) }))[/латекс].
Ключевые термины
- трапеция : (выпуклый) четырехугольник с двумя (несмежными) параллельными сторонами
Численное интегрирование, в некоторых случаях также известное как числовая квадратура, требует значения определенного интеграла.Популярные методы используют одну из формул Ньютона – Котеса (например, правило средней точки или правило Симпсона) или квадратуру Гаусса. Эти методы основаны на стратегии «разделяй и властвуй», согласно которой интеграл на относительно большом множестве разбивается на интегралы на меньших множествах. В более высоких измерениях, где эти методы становятся непомерно дорогими с точки зрения вычислительных затрат, можно использовать другие методы, такие как метод Монте-Карло. Здесь мы изучим очень простой метод аппроксимации, называемый правилом трапеции.{b} f (x) , dx приблизительно (b-a) frac {f (a) + f (b)} {2}} [/ latex]
Правило трапеции имеет тенденцию становиться чрезвычайно точным, когда периодические функции интегрированы по их периодам.
Аппроксимация линейными функциями : Функция [латекс] f (x) [/ latex] (синим цветом) аппроксимируется линейной функцией (красным цветом).
Числовая реализация правила трапеции
Для домена, дискретизированного на [латекс] N [/ латекс] равномерно распределенные панели или [латекс] N + 1 [/ latex] точки сетки [латекс] (1, 2, cdots, N + 1) [/ latex] , где шаг сетки равен [latex] h = frac {(ba)} {N} [/ latex], аппроксимация интеграла принимает следующий вид:
[латекс] begin {align} int_ {a} ^ {b} f (x) , dx & приблизительно frac {h} {2} sum_ {k = 1} ^ {N} left ( f (x_ {k + 1}) + f (x_ {k}) right) {} \ & = frac {ba} {2N} (f (x_1) + 2f (x_2) + cdots + 2f ( x_N) + f (x_ {N + 1})) end {align} [/ latex]
Хотя в методе также может использоваться неоднородная сетка, в этом примере для аппроксимации использовалась равномерная сетка. bf (x) , mathrm {d} x [/ latex].bf (x) , mathrm {d} x [/ latex], в котором берется ограничение в одной или другой (а иногда и в обеих) конечных точках.
Ключевые термины
- интегрант : функция, которая должна быть интегрирована
- определенный интеграл : интеграл функции между верхней и нижней границей
Несоответствующий интеграл — это предел определенного интеграла, когда конечная точка интервала (ов) интегрирования приближается либо к заданному действительному числу, либо к [latex] infty [/ latex] или [latex] — infty [/ latex] или , в некоторых случаях, когда обе конечные точки приближаются к пределам.bf (x) , mathrm {d} x [/ latex]
, в котором устанавливается ограничение на одной или другой конечной точке (а иногда и на обеих).
Несобственный интеграл второго рода : Несобственный интеграл Римана второго рода. Интеграл может не существовать из-за вертикальной асимптоты функции.
Интегралы также являются неправильными, если подынтегральное выражение не определено во внутренней точке области интегрирования или в нескольких таких точках. Часто необходимо использовать несобственные интегралы, чтобы вычислить значение интегралов, которые могут не существовать в обычном смысле (например, интеграл Римана) из-за сингулярности функции или бесконечной конечной точки области интегрирования. .2} , mathrm {d} x \ & = lim_ {b to infty} left (- frac {1} {b} + frac {1} {1} right) \ & = 1 end {align} [/ latex]
Пример 2
Узкое определение интеграла Римана также не распространяется на функцию [latex] frac {1} { sqrt {x}} [/ latex] на интервале [latex] [0, 1] [/ latex]. Проблема здесь в том, что подынтегральное выражение не ограничено в области интегрирования (определение требует, чтобы и область интегрирования, и подынтегральное выражение были ограничены). +} (2 sqrt {1} -2 sqrt {a}) \ & = 2 end {align} [/ latex]
Численное интегрирование
Численное интегрирование представляет собой широкое семейство алгоритмов для вычисления числового значения определенного интеграла.б ! f (x) , dx [/ латекс].
Ключевые термины
- трапециевидный : в форме трапеции или с несколькими гранями, имеющими одну пару параллельных сторон
- первообразное : неопределенный интеграл
Численное интегрирование представляет собой широкое семейство алгоритмов для вычисления числового значения определенного интеграла, и, в более широком смысле, этот термин также иногда используется для описания численного решения дифференциальных уравнений. 2) [/ latex], первообразная которого (функция ошибки, умноженная на константу) не может быть записана в элементарной форме.
Методы одномерных интегралов
Большой класс квадратурных правил может быть получен путем построения интерполирующих функций, которые легко интегрировать.b f (x) , dx приблизительно (b-a) , f left ( frac {a + b} {2} right)} [/ latex]
Правило прямоугольника : Иллюстрация правила прямоугольника.
Интерполирующая функция может быть аффинной функцией (полиномом степени 1), проходящей через точки [latex] (a, f (a)) [/ latex] и [latex] (b, f (b)) [/ латекс]. Это называется правилом трапеции.
Линия трапеции : Иллюстрация линейки трапеции.
Для любого из этих правил мы можем сделать более точное приближение, разбив интервал [latex] [a, b] [/ latex] на некоторое количество [latex] n [/ latex] подинтервалов, вычислив приближение для каждый подынтервал, затем складываются все результаты.{n-1} left (f left (a + k frac {b-a} {n} right) right) + {f (b) over 2} right)} [/ латекс]
, где подынтервалы имеют вид [latex] [kh, (k + 1) h] [/ latex], где [latex] h = frac {(ba)} {n} [/ latex] и [latex] k = 0, 1, 2, cdots, n − 1 [/ latex].
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера на прием файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie. - Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
7. Интеграция по частям
М. Борна
Иногда мы встречаем интеграцию, которая является продуктом двух функций. Мы можем интегрировать такие продукты, используя Integration by Parts .
Если u и v являются функциями x ,
правило продукта для дифференциации, которое мы встретили ранее, дает нам:
`d / (dx) (uv) = u (dv) / (dx) + v (du) / (dx)`
Переставив, имеем:
`u (dv) / (dx) = d / (dx) (uv) -v (du) / (dx)`
Интегрируя все относительно x , получаем
формула для интегрирования по частям:
Эта формула позволяет превратить сложный интеграл в
более простые.Мы должны убедиться, что выбрали u и
дв осторожно.
ПРИМЕЧАНИЕ: Функция u выбрана так
что `(du) / (dx)` на проще , чем
u .
Приоритеты выбора
u
Если у вас есть сочетание функций в выражении, которое нужно интегрировать, используйте следующую команду для выбора `u` по порядку.
1. Пусть `u = ln x`
2.(nx) `
Пример 1
`intx sin 2x dx`
Решение
Нам нужно выбрать «u». В этом вопросе у нас нет ни одной из функций, предложенных в списке «приоритетов» выше.
Можно использовать u = x или u = sin 2x, но обычно работает только один из них. В общем, мы выбираем тот, который позволяет `(du) / (dx)`
иметь более простую форму, чем и .
Итак, для этого примера мы выбираем u = x , и поэтому `dv` будет» остатком «интеграла,
дв = sin 2 x dx .
У нас есть u = x, поэтому du = dx.
Также `dv = sin 2x dx` и интегрирование дает:
`v = intsin 2x dx`
`= (- cos 2x) / 2`
Подставляя эти 4 выражения в формулу интегрирования по частям, мы получаем (используя цветовую кодировку, чтобы было легче увидеть, откуда берутся данные):
`int color {green} { underbrace {u}} color {red} { underbrace {dv}} ` `= color {green} { underbrace {u}} color {blue} { underbrace {v}} — int color {blue} { underbrace {v}} color {magenta} { underbrace {du}} `
`int color {green} { fbox {: x:}} color {red} { fbox {: sin 2x dx:}} = color {green} { fbox {: x:}} color {blue} { fbox {: {- cos2x} / 2:}} — int color {blue} { fbox {: {- cos2x} / 2:} color {magenta} { fbox {: dx:}} `
`= (-xcos2x) / 2 + 1/2 int cos2x dx`
`= (-xcos2x) / 2 + 1/2 (sin2x) / 2 + K`
`= (-xcos2x) / 2 + (sin2x) / 4 + K`
Если вышеизложенное сложно понять (из-за разрывов строк), то здесь он снова в другом формате:
Пример 2
`int x sqrt (x + 1) dx`
Ответ
`intxsqrt (x + 1) dx`
Мы могли бы использовать `u = x` или` u = sqrt (x + 1) `. 2) dx`.2) + К`
На этот раз мы интегрировали обратную тригонометрическую функцию (в отличие от более раннего типа, где мы получили обратные тригонометрические функции в нашем ответе). См. Интеграция: обратные тригонометрические формы.
Альтернативный метод интеграции по частям
Вот альтернативный метод решения проблем, который можно решить с помощью интеграции по частям. Возможно, вам будет легче следовать.
Танзалин Метод
.
Интегрирование по частям
Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.
Формула для неопределенного интеграла:
$$ int udv = uv — int vdu $$
Формула для определенного интеграла:
$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} — int limits_{a}^{b} vdu $$
Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.
| Пример 1 |
| Найти интеграл $ int xe^xdx $ |
| Решение |
|
Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $ Подставляем найденные значения в первую формулу интегрирования и получаем $$ int xe^x dx = xe^x — int e^x dx = xe^x — e^x + C. $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ int xe^x dx = xe^x — e^x + C $$ |
| Пример 2 |
| Найти интеграл $ int xcos x dx $ |
| Решение |
|
В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $. Подставим функции $ u $ и $ v $ в первую формулу $$ int x cos x dx = x sin x — int sin x dx = x sin x + cos x + C. $$ |
| Ответ |
|
$$ int x cos x dx = x sin x + cos x + C $$ |
| Пример 3 |
| Вычислить интеграл $ int limits_1 ^e xln x dx $ |
| Решение |
|
В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения $$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$ Осталось подставить это в формулу $$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e — int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} — 0 — frac{1}{2} int limits_1 ^e xdx = $$ $$ =frac{e^2}{2} — frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} — frac{1}{2}(frac{e^2}{2} — frac{1}{2}) = frac{e^2}{2} — frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$ |
| Ответ |
|
$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$ |
| Пример 4 |
| Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $ |
| Решение |
|
По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет «на руку». Поэтом поступаем так $$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$ Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу $$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 — int limits_0 ^1 frac{3^x dx}{ln 3} = $$ $$ = frac{18}{ln 3} — frac{5}{ln 3} — frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} — frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$ |
| Ответ |
| $$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$ |
Содержание:
- Приведем примеры использования метода интегрирования по частям
- Интегрирование по частям примеры с решением
- Примеры с решением
- Интегрирование по частям в неопределенном интеграле
Пусть 


Равенство (1) позволяет утверждать, что
В справедливости (2) убеждаемся, находя производную от левой и правой частей этого равенства — при этом мы приходим к верному равенству (1). Перепишем (2) так:
или, что то же самое,
В чем смысл формулы (3). К сожалению, не существует правила, выражающего интеграл от произведения двух функций через интегралы от каждого из сомножителей. Однако если для произведения двух функций 
то интеграл 

Так как 

или сводится к известному интегралу. В частности, если 



Формула (3), или (5), называется формулой интегрирования по частям. Из нее вытекает и аналогичное соотношение для определенных интегралов:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Приведем примеры использования метода интегрирования по частям
Пример 1:
Найти
Положим 
По формуле (3) имеем
Пример 2:
Найти
Положим 
Пользуясь формулой (3), получаем
откуда, учитывая результаты первого примера, имеем
Для нахождения 







Возможно вам будут полезны данные страницы:
Интегрирование по частям примеры с решением
Теорема Если функции 

По условию теоремы подынтегральные функции в (1.19) непрерывны. Поэтому в силу утверждения 1.1 они имеют первообразные и существуют входящие в (1.19) неопределенные интегралы. Опуская обозначение аргумента 
Отсюда, используя линейность неопределенного интеграла, получаем
В соответствии со свойством 2° (см. 1.3) имеем
Относя произвольную постоянную 

Использование формулы (1.19) целесообразно в том случае, когда представление подынтегрального выражения в виде
приводящее к задаче определения функции 

В исчислении и, в более общем смысле, в математическом анализе, интегрирование по частям или частичное интегрирование — это процесс, который находит интеграл от произведения функций в терминах интеграла от произведения их производной и антипроизводной.
Примеры с решением
Используя формулу (1.19) интегрирования по частям, вычислим
Пример 3:
Следуя высказанным рекомендациям, в первом неопределенном интеграле обозначим 
Пример 4:
Во втором неопределенном интеграле подведем сомножитель 
Для вычисления полученного интеграла в числителе его подынтегрального выражения добавим и вычтем единицу:
В итоге получим
Пример 5:
Третий неопределенный интеграл вычислим, подведя под знак дифференциала многочлен:
Пример 6:
В четвертом неопределенном интеграле примем
Нетрудно проверить, что выбор сочетания 

По аналогии с последним примером при интегрировании по частям функции 


Если 


или
В некоторых случаях интегрированием по частям (иногда — повторным) можно получить в правой части цепочки равенств выражение, содержащее исходный неопределенный интеграл 

Пример 7:
Интегрированием по частям вычисляем
Используя табличный интеграл 15, приходим к равенству
Отсюда, учитывая, что равенство, в обеих частях которого стоят интегралы, верно с точностью до произвольной постоянной, получаем
Пример 8:
Найдем неопределенные интегралы
В данном случае в качестве 
приходим к интегралу 
Подставляя это выражение в предыдущее, получаем
Интегрирование по частям в неопределенном интеграле
Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.
Пусть 

Взяв неопределенный интеграл от обеих частей этого равенства, получим:
Так как
а
то получаем:
откуда
Поскольку 
Полученная формула называется формулой интегрирования по частям.
При выводе формулы (1) мы предположили, что функции 


Заметим, что одно и то же подынтегральное выражение можно различными способами записать в виде 
и т. д. Поэтому иногда приходится испытывать различные формы такой записи, прежде чем метод приведет к успеху. Обычно стараются подынтегральное выражение разбить на части 



Пример 9:
Вычислим
Решение:
Положим 
Используя формулу (1), получаем:
Замечание. При нахождении 

Пример 10:
Вычислим
Решение:
Положим 
Используя формулу (1), получим:
Чтобы вычислить полученный в правой части равенства (2) интеграл, приходится снова использовать метод интегрирования по частям. Получим (см. пример 1):
Возвращаясь к исходному интегралу и воспользовавшись промежуточным равенством (2), окончательно получаем:
Интегрирование по частям в определенном интеграле. Для определенного интеграла формула интегрирования по частям принимает следующий вид:
В самом деле, если
то по формуле интегрирования по частям для неопределенного интеграла имеем:
Поэтому
и
значит
а это и есть формула (4).
Пример 11:
Вычислим
Решение:
Положим
Воспользовавшись формулой (4), получим:
Лекции:
- Преобразования графиков
- Вычитание матриц: примеры решения
- Сходимость знакочередующихся рядов
- Найти область сходимости ряда: пример решения
- Полное исследование графика функции
- Признак Даламбера: пример решения
- Производящие функции
- Сложение и вычитание пределов
- Логарифмические неравенства
- Ломаная


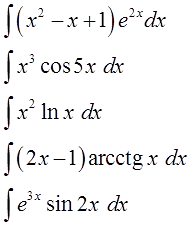
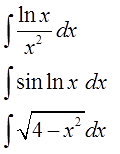
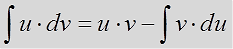
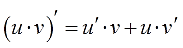
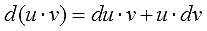
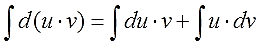
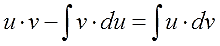
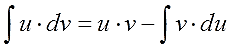
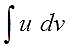
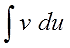
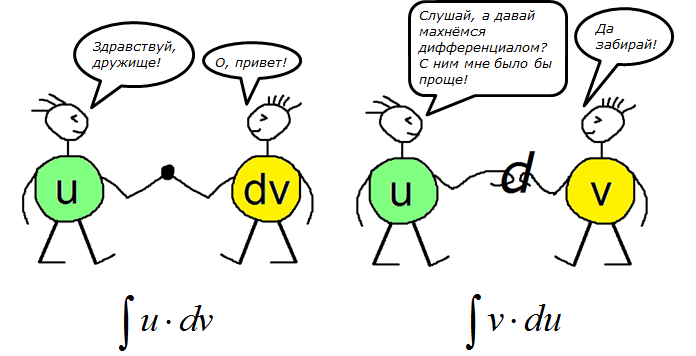
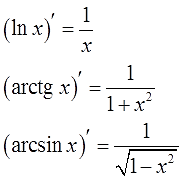
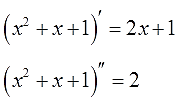
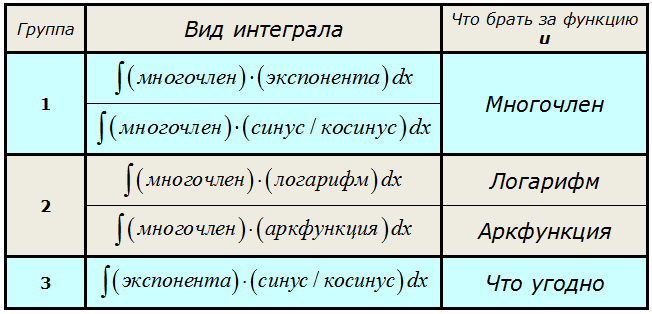
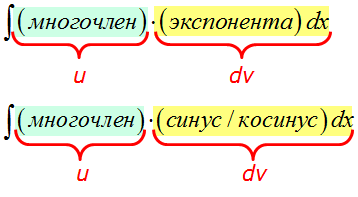
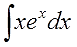
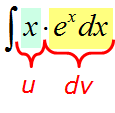
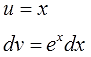
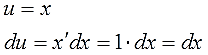
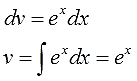
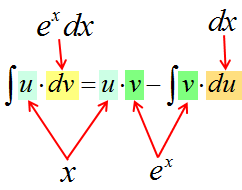
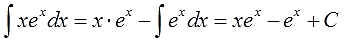
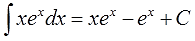
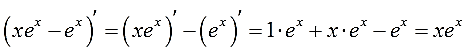
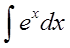
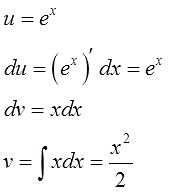
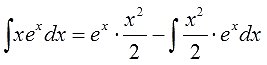
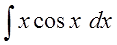
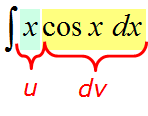
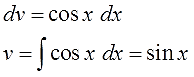
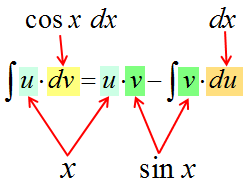
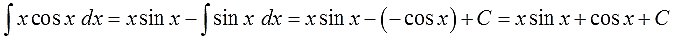

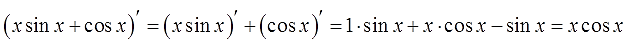
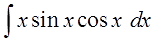
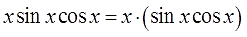
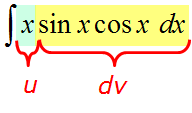
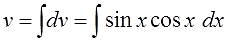
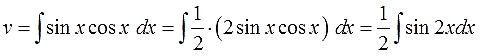
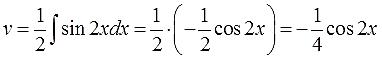
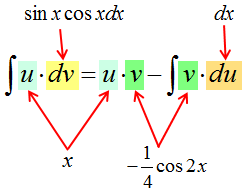
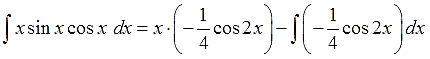
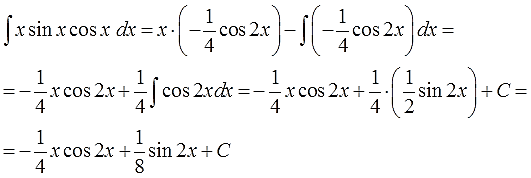
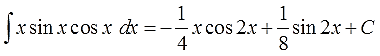
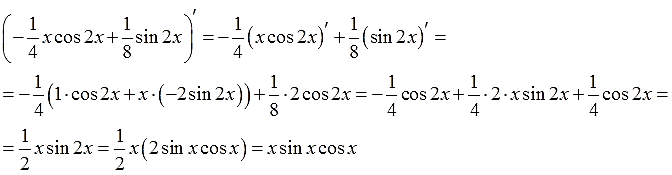
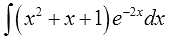
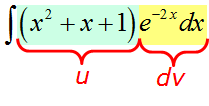
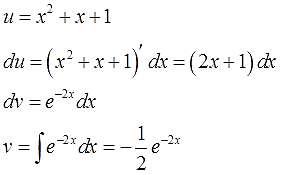
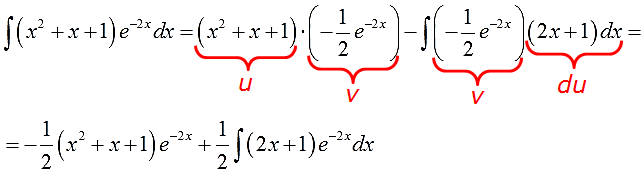
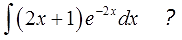
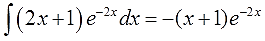
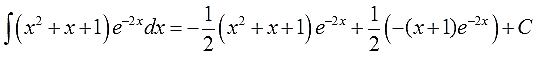
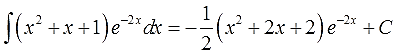
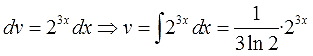



 integrate as intg
Phi_0 = lambda x: x**4
Phi_1= lambda x: x**2
f = lambda x: Phi_0*Phi_1
I = intg.quadrature(lambda x: Phi_0(x)*Phi_1(x), -1, 1)
print("I =", I[0], "Tolerance =", I[1])
integrate as intg
Phi_0 = lambda x: x**4
Phi_1= lambda x: x**2
f = lambda x: Phi_0*Phi_1
I = intg.quadrature(lambda x: Phi_0(x)*Phi_1(x), -1, 1)
print("I =", I[0], "Tolerance =", I[1])

 4 В вольфраме я ввожу int(sin(2*x)/4 -…
4 В вольфраме я ввожу int(sin(2*x)/4 -…
 Может ли кто-нибудь заметить мою ошибку? Проблема заключается в следующем: Палиндромное…
Может ли кто-нибудь заметить мою ошибку? Проблема заключается в следующем: Палиндромное…
 Правила интеграции)
Правила интеграции) 
 ..
..  е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.  {6x}} ) сам по себе, мы могли бы сделать интеграл достаточно легко. prime} , dx}} = int {{f ‘, g + f , g’ , dx}} ]
{6x}} ) сам по себе, мы могли бы сделать интеграл достаточно легко. prime} , dx}} = int {{f ‘, g + f , g’ , dx}} ]
 Не радуйтесь тому факту, что мы используем здесь две замены. Они будут работать так же.
Не радуйтесь тому факту, что мы используем здесь две замены. Они будут работать так же. 

 Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов.
Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов. 






































































