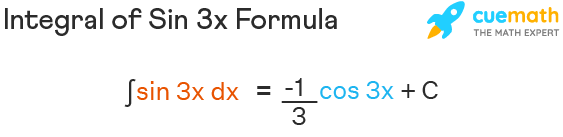Как найти интеграл sin3x

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} — twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{»} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 — pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• x^{2}-x-6=0
  

• -x+3gt 2x+1
  

• линия:(1,:2),:(3,:1)
  

• f(x)=x^3
  

• доказывать:tan^2(x)-sin^2(x)=tan^2(x)sin^2(x)
  

• frac{d}{dx}(frac{3x+9}{2-x})
  

• (sin^2(theta))’
  

• sin(120)
  

• lim _{xto 0}(xln (x))
  

• int e^xcos (x)dx
  

• int_{0}^{pi}sin(x)dx
  

• sum_{n=0}^{infty}frac{3}{2^n}
  

• Показать больше

Описание

Поэтапное решение задач по алгебре, тригонометрии и исчислению

step_by_step

int sin(3x)dx

ru

Блог-сообщения, имеющие отношение к Symbolab

My Notebook, the Symbolab way

Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back…

Read More

Введите Задачу

Сохранить в блокнот!

Войти

Integral of sin 3x is given by (-1/3) cos 3x + C. The integral of sin 3x is called the anti-derivative of sin 3x as integration is the reverse process differentiation. Sin 3x is an important trigonometric formula that is used to solve various problems in trigonometry. The integral of sin 3x can be calculated using the substitution method and using the sin 3x formula.

In this article, we will calculate the integral of sin 3x, prove it using the substitution method and sin 3x formula and determine the definite integral of sin 3x using different limits.

1.	What is Integral of Sin 3x?
2.	Integral of Sin 3x Formula
3.	Integral of Sin 3x Using Substitution Method
4.	Integral of Sin 3x Using Sin 3x Formula
5.	Definite Integral of Sin 3x
6.	FAQs on Integral of Sin 3x

What is Integral of Sin 3x?

The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-1/a) cos ax + C. Mathematically, the integral of sin 3x is written as ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration, dx denotes that the integration of sin 3x is with respect to x, ∫ is the symbol for integration. The integral of sin 3x can also be evaluated using the substitution method and sin 3x formula.

Integral of Sin 3x Formula

Sin 3x formula is given by sin 3x = 3 sin x — 4 sin³x and the formula for the integral of sin 3x is given by, ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration.

Integral of Sin 3x Using Substitution Method

Now, we know that the integral of sin 3x is (-1/3) cos 3x + C, where C is the constant of integration. Let us prove this using the substitution method. We will use the following formulas of integration and differentiation:

• ∫sin x dx = -cos x + C
• d(ax)/dx = a

Assume 3x = u, then differentiating 3x = u with respect to x, we have 3dx = du ⇒ dx = (1/3)du. Using the above formulas, we have

∫sin 3x dx = ∫sin u (du/3)

⇒ ∫sin 3x dx = (1/3) ∫sin u du

⇒ ∫sin 3x dx = (1/3) (-cos u + C) [Because ∫sin x dx = -cos x + C]

⇒ ∫sin 3x dx = (-1/3) cos u + C/3

⇒ ∫sin 3x dx = (-1/3) cos 3x + K, where K = C/3

Hence, we have derived the integral of sin 3x using the substitution method.

Integral of Sin 3x Using Sin 3x Formula

We know that the sin 3x formula is sin 3x = 3 sin x — 4 sin³x. Next, we will prove that the integration of sin 3x is given by (-1/3) cos 3x + C using the sin 3x formula. Before proving the integral of sin 3x, we will derive the integral of sin cube x, that is, sin³x. We will use the following formulas to prove the integral of sin³x:

• cos²x + sin²x = 1 ⇒ sin²x = 1 — cos²x
• ∫sin x dx = -cos x dx

∫sin³x dx = ∫sin x. sin²x dx

= ∫sin x.(1 — cos²x) dx

= ∫sin x dx — ∫sin x. cos²x dx — (1)

= I₁ — I₂ , where I₁ = ∫sin x dx and I₂ = ∫sin x. cos²x dx

Now, I₁ = ∫sin x dx = -cos x + C₁, where C₁ is the constant of integration —- (2)

For I₂ = ∫sin x. cos²x dx, assume cos x = u ⇒ -sin x dx = du ⇒ sin x dx = -du

I₂ = ∫sin x. cos²x dx

= ∫u² (-du)

= — ∫u² du

= — u³/3 + C₂, where C₂ is the constant of integration

= (-1/3) cos³x + C₂ —- (3)

Subsitute the values from (2) and (3) in (1),

∫sin³x dx = (-cos x + C₁) — ((-1/3) cos³x + C₂)

= -cos x + (1/3) cos³x + C₁ — C₂

= -cos x + (1/3) cos³x + C, where C = C₁ — C₂

⇒ ∫sin³x dx = -cos x + (1/3) cos³x + C — (4)

Now that we have derived the integral of sin³x, we will use this formula along with some other formulas to derive the integral of sin 3x:

• ∫sin x dx = -cos x dx
• ∫sin³x dx = -cos x + (1/3) cos³x + C
• sin 3x = 3 sin x — 4 sin³x
• cos 3x = 4cos³x — 3 cos x

Using the above formulas, we have

∫sin 3x dx = ∫(3 sin x — 4 sin³x) dx

= 3 ∫sin x dx — 4 ∫sin³x dx

= 3(-cos x) — 4(-cos x + (1/3) cos³x) + C, where C is the constant of integration

= -3 cos x + 4 cos x — (4/3)cos³x + C

= cos x — (4/3)cos³x + C

= (1/3)(3cos x — 4cos³x + 3C)

= (1/3)(-cos 3x + 3C) [Because cos 3x = 4cos³x — 3 cos x]

= (-1/3) cos 3x + C

Hence, we have derived the integration of sin 3x using the sin 3x formula.

Definite Integral of Sin 3x

We have proved that the integral of sin 3x is (-1/3) cos 3x + C. Now, we will determine the values of the definite integral of sin 3x with different limits. First, we will take the limits from 0 to π/3.

Definite Integral of Sin 3x From 0 to π/3

(begin{align}int_{0}^{frac{pi}{3}}sin 3x dx &= left [ -frac{1}{3}cos 3x+C right ]_0^frac{pi}{3}\&=left ( -frac{1}{3}cos 3frac{pi}{3}+C right )-left ( -frac{1}{3}cos 3(0)+Cright )\&=-frac{1}{3}cos pi+C + frac{1}{3}cos 0-C\&= -frac{1}{3}(-1)+frac{1}{3}(1)\&=frac{2}{3}end{align})

Hence the value of the definite integral of sin 3x with limits from 0 to π/3 is equal to 2/3.

Definite Integral of Sin 3x From 0 to Pi

(begin{align}int_{0}^{pi}sin 3x dx &= left [ -frac{1}{3}cos 3x+C right ]_0^pi\&=left ( -frac{1}{3}cos 3pi+C right )-left ( -frac{1}{3}cos 3(0)+Cright )\&=-frac{1}{3}cos 3pi+C + frac{1}{3}cos 0-C\&= -frac{1}{3}(-1)+frac{1}{3}(1)\&=frac{2}{3}end{align})

Hence the value of the definite integral of sin 3x with limits from 0 to π is equal to 2/3.

Definite Integral of Sin 3x From 0 to Pi/2

(begin{align}int_{0}^{frac{pi}{2}}sin 3x dx &= left [ -frac{1}{3}cos 3x+C right ]_0^frac{pi}{2}\&=left ( -frac{1}{3}cos 3frac{pi}{2}+C right )-left ( -frac{1}{3}cos 3(0)+Cright )\&=-frac{1}{3}cos frac{3pi}{2}+C + frac{1}{3}cos 0-C\&= -frac{1}{3}(0)+frac{1}{3}(1)\&=frac{1}{3}end{align})

Hence the value of the definite integration of sin 3x with limits from 0 to π/2 is equal to 1/3.

Important Notes on Integral of Sin 3x

• The easiest way to determine the integral of sin 3x is using the formula ∫sin (ax) dx = (-1/a) cos ax + C.
• The integral of sin 3x is (-1/3) cos 3x + C and the integral of sin cube x is ∫sin³x dx -cos x + (1/3) cos³x + C.

Related Topics

• Integral of Tan 2x
• Cos 3x
• Sin 3x

FAQs on Integral of Sin 3x

What is Integral of Sin 3x in Trigonometry?

In trigonometry, the integral of sin 3x is written as ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration.

How to Find the Integral of Sin 3x?

The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-1/a) cos ax + C. It can also be calculated using the substitution method and sin 3x formula.

What is the Definite Integral of Sin 3x from 0 to pi?

The value of the definite integral of sin 3x with limits from 0 to π is equal to 2/3.

What is the Integration of Sin³x?

The integral of sin cube x is given by ∫sin³x dx = -cos x + (1/3) cos³x + C.

What is the Integral of Sin 2x?

The integral of sin 2x dx is written as ∫ sin 2x dx = -(cos 2x)/2 + C, where C is the integration constant.

To integrate sin^3x, also written as ∫sin³x
dx, sin cubed x, sin^3(x), and (sin x)^3, we start by using standard trig identities to
simplify the integral.

If we take one of the factors out, then we can express the integration in a
different form, yet it means the same thing.

We then recall this Pythagorean trig identity.

We rearrange it for sin²x.

We substitute the rearranged trig identity for sin²x
in our integration problem to give a new expression that means the same thing.

Let u = cosx.

Then du/dx = -sinx

We rearrange it to give an expression for du.

As you can see, our expression for du is almost the same as that in our
integration problem, except du has a negative sign. We can solve this issue with
a mathematical trick as shown below.

If we were to multiply -1 with -1 then the result is +1 and we have not
changed anything. That is exactly what we are doing here. We place a -1 outside
the integral and another inside the integral. As you can see, we now have -sinx
dx, and therefore we can do a straight swap with du.

We can now rewrite the whole integration in terms of u, by replacing cosx
with u.

The -1 that was behind the integral can be multiplied out, thereby reversing
the signs on the LHS. This is the same as the expression on the RHS where we
integrate each term separately w.r.t. du.

Hence our integration solution is in terms of u is as shown above, and C is
the final integration constant.

We replace u with cosx to give the final solution.

Рассмотрим решение задачи по нахождению неопределенного интеграла от синуса в кубе, т.е.

Прежде всего заметим, что синус в третьей степени   и  а значит,

Далее воспользуемся тем, что и

где — произвольная вещественная постоянная.

Здесь при нахождении неопределенного интеграла от «синуса в кубе» также было использовано свойство линейности неопределенного интеграла:

и то, что

 

Таким образом

 

где — произвольная вещественная постоянная.

В следующем видео продемонстрировано нахождение неопределенного интеграла от синуса в третьей степени. Пояснения и комментарии помогут разобраться с ходом решения задачи и сформировать навык нахождения подобных интегралов.

Калькулятор интегралов

Некорректное выражение: ‘sin3’

 

Калькулятор интегралов, примеры

Больше примеров неопределенных интегралов Математические настройки для вашего сайта Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어 Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

© 2023
numberempire.com
Все права защищены