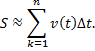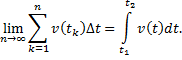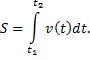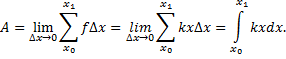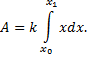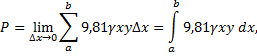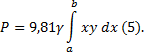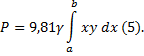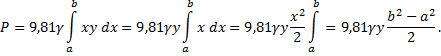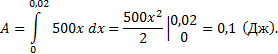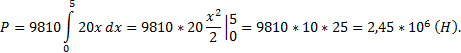Как найти интеграл в физике - Исправление недочетов и поиск решений вместе с Examum.ru

п.1. От ускорения к скорости и координате

Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac{at^2}{2}+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac{at^2}{2}+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).

п.2. Физические величины как интегралы других величин

Если (v(t)) — скорость некоторого физического процесса, уравнение этого процесса можно найти интегрированием: $$ f(t)=int v(t)dt $$ Такие величины часто встречаются в различных разделах физики и техники.

Исходная величина (скорость)

Уравнение процесса (интеграл по времени)

Ускорение (a(t))

Скорость (v(t)=int a(t)dt)

Скорость (v(t))

Координата (x(t)=int v(t)dt)

Угловое ускорение (beta(t))

Угловая скорость (omega(t)=int beta(t) dt)

Угловая скорость (omega(t))

Угол поворота (varphi(t)=intomega(t)dt)

Скорость расходования горючего (u(t))

Масса горючего ракеты (m(t)=int u(t)dt)

Сила тока (I(t))

Заряд (q(t)=int I(t)dt)

Мощность (N(t))

Работа (A(t)=int N(t)dt)

ЭДС индукции (varepsilon(t))

Магнитный поток (Ф(t)=-intvarepsilon(t)dt)

Скорость радиоактивного распада (I(t))

Число атомов радиоактивного вещества (N(t)=int I(t)dt)

Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_{x_1}^{x_2}F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.

В современной физике интеграл по времени берётся также и от самого уравнение движения. Полученная скалярная величина называется действием и носит фундаментальный характер. В простейшем случае: $$ S_0=int overrightarrow{p}cdot overrightarrow{v}dt $$ где (overrightarrow{p}cdot overrightarrow{v}) — скалярное произведение векторов импульса и скорости.

п.3. Примеры

Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin{gather*} s(t)=int_{t_1}^{t_2}v(t)dt\ s=int_{0}^{6}(3t+2t^2)dt=left(frac{3t^2}{2}+frac{2t^3}{3}right)|_{0}^{6}=frac{3cdot 36}{2}+frac{2cdot 36cdot 6}{3}-0=\ =3cdot 18+4cdot 36=54+144=198 text{(м)} end{gather*}
б) (v(t)=2(t+2)^{5/2}, t_1=0, t_2=7) begin{gather*} s=int_{0}^{7}2(t+2)^{5/2}dt =2cdotfrac{(t+2)^{frac52+1}}{frac72}|_{0}^{7}=frac47cdot 9^{frac72}-0=frac47cdot 3^7approx 1250 text{(м)} end{gather*}

Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^{-t}+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin{gather*} Q(t)=int_{t_1}^{t_2}I(t)dt end{gather*} По условию: begin{gather*} Q=int_{2}^{6}(e^{-t}+2t)dt=(-e^{-t}+t^2)|_{2}^{6}=-e^{-6}+6^2+e^{-2}-2^2=frac{1}{e^2}-frac{1}{e^6}+32=\ =frac{e^4-1}{e^6}+32approx 32,1 text{(Кл)} end{gather*}

Пример 3*. Найдите путь, который пройдет тело от начала движения до возвращения в исходную точку, если его скорость (v(t)=18t-9t^2) (время в секундах, скорость в м/с). Движение тела прямолинейное.

Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin{array}{l} t=0\ t=2 end{array} right. $$ (t=0) – начало движения, (t=2) — разворот.

Уравнение движения: $$ x(t)=int(18t-9t^2)dt=9t^2-3t^3+C $$ В начальный момент времени (x_0=0Rightarrow C=0) $$ x(t)=9t^2-3t^3 $$ В точке C(2;12) кривая (x(t)) имеет максимум.
Тело двигалось в течение 2 с в одну сторону и прошло 12 м, а затем за 1 с вернулось обратно.

Общий путь: 12+12 = 24 м.

Ответ: 24 м

Пример 4*. Найдите работу, которую необходимо совершить, чтобы выкачать воду из полусферического котла радиуса R м.

Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) — по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin{gather*} A=int_{0}^{R}dA=int_{0}^{R}pirho gH(R^2-H^2)dH=pirho gint_{0}^{R}(HR^2-H^3)dH=\ =pirho gleft(frac{H^2}{2}R^2-frac{H^4}{4}right)|_{0}^{R}=pirho gleft(frac{R^4}{2}-frac{R^4}{4}-0right)=fracpi 4=rho gR^4 end{gather*} Ответ: (A=fracpi 4=rho gR^4)

Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с², радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с² (R_E=6371) км.

Ускорение свободного падения на поверхности планеты: (g_0=Gfrac{M}{R^2})
Ускорение свободного падения при подъеме на высоту x: begin{gather*} g(x)=Gfrac{M}{(R+x)^2} end{gather*} Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin{gather*} A=int_{0}^{h}mg(x)dx=mint_{0}^{h}Gfrac{M}{(R+x)^2}dx=GmMint_{0}^{h}frac{dx}{(R+x^2)}=\ =GmMcdotleft(-frac{1}{R+x}right)|_{0}^{h}=GmMcdotleft(-frac{1}{R+h}+frac1Rright)=GmMleft(frac1R-frac{1}{R+g}right)=\ =GmMfrac{R+h-R}{R(R+h)}=GmMfrac{h}{R(R+h)} end{gather*} Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=frac{GM}{R^2}frac{mhR^2}{R(R+h)}=mg_0frac{hR}{R+h} $$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac{R^2}{2R}=frac{mg_0R}{2} $$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac{A_E(R_E)}{A_M(R_M)}=frac{mg_ER_E}{mg_MR_M}=frac{g_ER_E}{g_MR_M}, frac{A_E(R_E)}{A_M(R_M)}=frac{9,81cdot 6371}{1,62cdot 1737}approx 22,2 $$ На Земле работа в 22,2 раза больше.

Ответ: (A=GmMfrac{h}{R(R+h)}; frac{A_E(R_E)}{A_M(R_M)}approx 22,2)

Источник

Видеоурок: Применение интегралов в физике и математике

Лекция: Примеры применения интеграла в физике и геометрии

Процесс нахождение первообразной называется интегрированием.

Как и производная, интегралы используются и в физике, и в геометрии, а также в других областях знаний.

Сегодня же мы рассмотрим, каким образом используется интегрирование в физике и геометрии.

Итак, начнем сначала. Мы помним, что скорость – это первая производная перемещения. Но так как мы знаем, что интегрирование и нахождение производной – это два взаимообратных процесса, то мы можем предполагать, что, если для нахождения скорости, нужно было найти производную от перемещения, то для нахождения перемещения по скорости, необходимо произвести интегрирование заданной функции.

Отсюда можно сделать вывод, что перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:

Пример: Итак, предположим, что некоторое тело двигается со скоростью, заданной функцией:

V(t) = t² +1.

По условию задачи мы должны определить путь, который пройдет тело за промежуток времени [0;1].

Итак, найдем определенный интеграл данной функции:

Это означает, что за данный промежуток времени, тело прошло 1,3(3) м.

Точно так же можно найти скорость по заданной функции ускорения.

Еще одной физической величиной, которая находится с помощью интегрирования, является работа.

Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:

Пример: Предположим, что к некоторому телу для его передвижения прикладывают силу, которая изменяется по закону F(x) = x +3. Необходимо найти работу, которую при этом совершает сила для перемещения тела с 1 м до 2 м.

Для нахождения работы следует найти определенный интеграл заданной функции по известным пределам интегрирования:

Это значит, что для передвижения тела потребовалось совершить работу, равную 4,5 Дж энергии.

Кроме рассматриваемых задач, интегрирование в физике используется для нахождения работы по мощности, массы по плотности, заряда по силе тока, количества теплоты по известной теплоемкости, а также многое другое.

Что же касается геометрии, то геометрическим смыслом интегрирования считается нахождение площади фигуры под графиком.

Итак, чтобы найти площадь фигуры, которая ограничена с двух сторон пределами интегрирования и с одной стороны графиком функции, то необходимо найти интеграл данной функции:

Пример: Вычислим площадь фигуры, ограниченной графиком функции у = 4х – х² на пределах рассмотрения х = 0, х = 4.

Итак, найдем интеграл данной функции в заданных пределах и построим полученный график:

Источник

4.3.2 Примеры применения интеграла в физике и геометрии

Видеоурок: Применение интегралов в физике и математике

Лекция: Примеры применения интеграла в физике и геометрии

Процесс нахождение первообразной называется интегрированием.

Как и производная, интегралы используются и в физике, и в геометрии, а также в других областях знаний.

Сегодня же мы рассмотрим, каким образом используется интегрирование в физике и геометрии.

Пример: Итак, предположим, что некоторое тело двигается со скоростью, заданной функцией:

По условию задачи мы должны определить путь, который пройдет тело за промежуток времени [0;1].

Итак, найдем определенный интеграл данной функции:

Это означает, что за данный промежуток времени, тело прошло 1,3(3) м.

Точно так же можно найти скорость по заданной функции ускорения.

Еще одной физической величиной, которая находится с помощью интегрирования, является работа.

Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:

Это значит, что для передвижения тела потребовалось совершить работу, равную 4,5 Дж энергии.

Пример: Вычислим площадь фигуры, ограниченной графиком функции у = 4х – х 2 на пределах рассмотрения х = 0, х = 4.

Итак, найдем интеграл данной функции в заданных пределах и построим полученный график:

Решение задач физики и техники с применением интеграла

п.1. От ускорения к скорости и координате

Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac<2>+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac<2>+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).

п.2. Физические величины как интегралы других величин

Скорость (v(t)=int a(t)dt)

Координата (x(t)=int v(t)dt)

Угловое ускорение (beta(t))

Угловая скорость (omega(t)=int beta(t) dt)

Угловая скорость (omega(t))

Угол поворота (varphi(t)=intomega(t)dt)

Скорость расходования горючего (u(t))

Масса горючего ракеты (m(t)=int u(t)dt)

Заряд (q(t)=int I(t)dt)

Работа (A(t)=int N(t)dt)

ЭДС индукции (varepsilon(t))

Магнитный поток (Ф(t)=-intvarepsilon(t)dt)

Скорость радиоактивного распада (I(t))

Число атомов радиоактивного вещества (N(t)=int I(t)dt)

Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_^F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.

cdot overrightarrowdt $$ где (overrightarrow

cdot overrightarrow) — скалярное произведение векторов импульса и скорости.

п.3. Примеры

Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin s(t)=int_^v(t)dt\ s=int_<0>^<6>(3t+2t^2)dt=left(frac<3t^2><2>+frac<2t^3><3>right)|_<0>^<6>=frac<3cdot 36><2>+frac<2cdot 36cdot 6><3>-0=\ =3cdot 18+4cdot 36=54+144=198 text <(м)>end
б) (v(t)=2(t+2)^<5/2>, t_1=0, t_2=7) begin s=int_<0>^<7>2(t+2)^<5/2>dt =2cdotfrac<(t+2)^<frac52+1>><frac72>|_<0>^<7>=frac47cdot 9^<frac72>-0=frac47cdot 3^7approx 1250 text <(м)>end

Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^<-t>+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin Q(t)=int_^I(t)dt end По условию: begin Q=int_<2>^<6>(e^<-t>+2t)dt=(-e^<-t>+t^2)|_<2>^<6>=-e^<-6>+6^2+e^<-2>-2^2=frac<1>-frac<1>+32=\ =frac+32approx 32,1 text <(Кл)>end

Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin t=0\ t=2 end right. $$ (t=0) – начало движения, (t=2) — разворот.

Общий путь: 12+12 = 24 м.

Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) — по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin A=int_<0>^dA=int_<0>^pirho gH(R^2-H^2)dH=pirho gint_<0>^(HR^2-H^3)dH=\ =pirho gleft(frac<2>R^2-frac<4>right)|_<0>^=pirho gleft(frac<2>-frac<4>-0right)=fracpi 4=rho gR^4 end Ответ: (A=fracpi 4=rho gR^4)

Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с 2 , радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с 2 (R_E=6371) км.

Ускорение свободного падения на поверхности планеты: (g_0=Gfrac)
Ускорение свободного падения при подъеме на высоту x: begin g(x)=Gfrac <(R+x)^2>end Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin A=int_<0>^mg(x)dx=mint_<0>^Gfrac<(R+x)^2>dx=GmMint_<0>^frac<(R+x^2)>=\ =GmMcdotleft(-frac<1>right)|_<0>^=GmMcdotleft(-frac<1>+frac1Rright)=GmMleft(frac1R-frac<1>right)=\ =GmMfrac=GmMfrac end Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=fracfrac=mg_0frac

$$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac<2R>=frac <2>$$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac=frac=frac, frac=frac<9,81cdot 6371><1,62cdot 1737>approx 22,2 $$ На Земле работа в 22,2 раза больше.

Другие приложения интегралов в физике

При решении физических задач изучаемый процесс разбивают на элементарные части, в пределах каждой из которых изменением соответствующих величин можно пренебречь. Теперь задача решается по формулам для постоянных величин, после чего окончательный ответ находится с помощью интегрирования.

а) Найдем работу силы при переходе материальной точки из в , если материальная точка движется по прямой линии под действием силы , направленной вдоль этой прямой, причем величина силы зависит от координаты этой точки: .

Известно, что в случае, если сила постоянна, работа равна , где — изменение координаты точки. Поэтому разобьем отрезок на элементарные части, в пределах каждой из которых считаем силу постоянной. Тогда работа силы на участке равна . Общая работа выражается интегралом

Пример 10. Найдем работу, выполняемую при переносе материальной точки, имеющей массу , из в , если притягивающая ее по закону Ньютона точка имеет массу и находится в начале координат (рис. 66).

Решение. По закону Ньютона сила тяготения равна , где — гравитационная постоянная, а — расстояние между точками. По формуле (2) получаем:

б) Найдем работу, выполненную двигателем за промежуток времени , если мощность двигателя в момент времени равна .

За элементарный промежуток времени двигатель, имеющий мощность , выполняет работу . Поэтому вся работа двигателя равна

Пример 11. Найдем работу переменного тока, изменяющегося по формуле за промежуток времени , если сопротивление цепи равно .

Решение. Как известно из физики, в случае постоянного тока мощность выражается формулой . Поэтому по формуле (3) имеем:

Заметим, что средняя мощность переменного тока равна .

в) Вычислить количество электричества, протекающее через цепь за промежуток времени , если ток изменяется по формуле .

За элементарный промежуток времени протекает количество электричества . Значит, общее количество электричества равно

В заключение рассмотрим еще один физический пример.

Пример 12. Найдем давление воды на плотину, если вода доходит до ее верхнего края и если известно, что плотина имеет вид трапеции с высотой , верхним основанием и нижним основанием .

Решение. Рассмотрим элементарный слой, находящийся на глубине и имеющий высоту (рис. 67). Легко доказать, что длина этого слоя равна . Поэтому его площадь равна

Все давление воды на плотину выражается интегралом

источники:

http://reshator.com/sprav/algebra/10-11-klass/reshenie-zadach-fiziki-i-tekhniki-s-primeneniem-integrala/

http://mathhelpplanet.com/static.php?p=prilozheniya-integralov-v-fizike

Источник

Цель урока:

обобщить и закрепить ключевые задачи по теме;
научиться работать с теоретическими вопросами
темы;
научиться применять интеграл к решению
физических задач.

План урока:

1. Схема решения задач на приложения
определенного интеграла
2. Нахождение пути, пройденного телом при
прямолинейном движении
3. Вычисление работы силы, произведенной при
прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение
или сжатие пружины
5. Определение силы давления жидкости на
вертикально расположенную пластинку

Тип урока: интегрированный.

Воспитательная работа: расширение
кругозора и познавательной деятельности
учащихся, развитие логического мышления и умения
применять свои знания.

Техническое обеспечение:
интерактивная доска. Компьютер и диск.

Приложение: «Рапсодия
природы».

ХОД УРОКА

I. Организационный момент

II. Постановка цели урока

– Урок хотелось бы провести под девизом
Готфрида Вильгельма Лейбница – немецкого философа,
логика,
математика,
физика:
«Общее искусство знаков представляет чудесное
пособие, так как оно разгружает воображение…
Следует заботиться о том, чтобы обозначения были
удобны для открытий. Обозначения коротко
выражают и отображают сущность вещей. Тогда
поразительным образом сокращается работа
мысли».

III. Повторим основные понятия и
ответим на вопросы:

– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с
применением интеграла?

IV. Объяснение нового материала
(рассмотрение теории):

1. Схема решения задач на приложения
определенного интеграла

С помощью определенного интеграла можно решать
различные задачи физики, механики и т. д., которые
трудно или невозможно решить методами
элементарной математики.

Так, понятие определенного интеграла
применяется при решении задач на вычисление
работы переменной силы, давления жидкости на
вертикальную поверхность, пути, пройденного
телом, имеющим переменную скорость, и ряд других.

Несмотря на разнообразие этих задач, они
объединяются одной и той же схемой рассуждений
при их решении. Искомая величина (путь, работа,
давление и т. д.) соответствует некоторому
промежутку изменения переменной величины,
которая является переменной интегрирования. Эту
переменную величину обозначают через Х, а
промежуток ее изменения – через [а, b].

Отрезок [a, b] разбивают на n равных частей, в
каждой из которых можно пренебречь изменением
переменной величины. Этого можно добиться при
увеличении числа разбиений отрезка. На каждой
такой части задачу решают по формулам для
постоянных величин.

Далее составляют сумму (интегральную сумму),
выражающую приближенное значение искомой
величины. Переходя к пределу при , находят искомую величину
I в виде интеграла

I = , где f(x)
– данная по условиям задачи функция (сила,
скорость и т. д.).

2. Нахождение пути, пройденного телом при
прямолинейном движении

Как известно, путь, пройденный телом при
равномерном движении за время t, вычисляется по
формуле S = vt.

Если тело движется неравномерно в одном
направлении и скорость его меняется в
зависимости от времени t, т. е. v = f(t), то для
нахождения пути, пройденного телом за время от до , разделим этот
промежуток времени на n равных частей Δt. В каждой
из таких частей скорость можно считать
постоянной и равной значению скорости в конце
этого промежутка. Тогда пройденный телом путь
будет приблизительно равен сумме , т.е.

Если функция v(t) непрерывна, то

Итак,

3. Вычисление работы силы, произведенной
при прямолинейном движении тела

Пусть тело под действием силы F движется по
прямой s, а направление силы совпадает с
направлением движения. Необходимо найти работу,
произведенную силой F при перемещении тела из
положения a в положение b.

Если сила F постоянна, то работа находится по
формуле
(произведение силы на длину пути).

Пусть на тело, движущееся по прямой Ох,
действует сила F, которая изменяется в
зависимости от пройденного пути, т. е. . Для того чтобы найти
работу, совершаемую силой F на отрезке пути от а
до b, разделим этот отрезок на n равных частей
. Предположим,
что на каждой части сила сохраняет постоянное значение

Составим интегральную сумму, которая
приближенно равна значению произведенной
работы:

т.е. работа, совершенная этой силой на участке
от а до b, приближенно мала сумме:

Итак, работа переменной силы вычисляется по
формуле: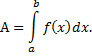

4. Вычисление работы, затраченной на
растяжение или сжатие пружины

Согласно закону Гука, сила F, необходимая для
растяжения или сжатия пружины, пропорциональна
величине растяжения или сжатия.

Пусть х – величина растяжения или сжатия
пружины. Тогда ,
где k – коэффициент пропорциональности,
зависящий от свойства пружины.

Работа на участке выразится формулой , а вся затраченная работа или . Если то погрешность величины
работы стремится к нулю.

Для нахождения истинной величины работы
следует перейти к пределу

Итак,

5. Определение силы давления жидкости на
вертикально расположенную пластинку

Из физики известно, что сила Р давления
жидкости на горизонтально расположенную
площадку S, глубина погружения которой равна h,
определяется по формуле:

, где – плотность жидкости.

Выведем формулу для вычисления силы давления
жидкости на вертикально расположенную пластинку
произвольной формы, если ее верхний край
погружен на глубину a, а нижний – на глубину b.

Так как различные части вертикальной пластинки
находятся на разной глубине, то сила давления
жидкости на них неодинаковa. Для вывода формулы
нужно разделить пластинку на горизонтальных
полос одинаковой высоты . Каждую полосу приближенно
можно считать прямоугольником (рис.199).

По закону Паскаля сила давления жидкости на
такую полосу равна силе движения жидкости на
горизонтально расположенную пластинку той же
площади, погруженной на ту же глубину.

Тогда согласно формуле (4) сила давления на
полосу, находящуюся на расстоянии х от
поверхности, составит , где
– площадь полосы.

Составим интегральную сумму и найдем ее предел,
равный силе давления жидкости на всю пластинку:

т.е.

Если верхний край пластинки совпадает с
поверхностью жидкости, то а=0 и формула (5) примет
вид

Ширина каждой полосы зависит от формы
пластинки и является функцией глубины х
погружения данной полосы.

Для пластинки постоянной ширины формула (5)
упрощается, т.к. эту постоянную можно вынести за
знак интеграла:

V. Разбор задач по теме

1) Скорость движения материальной точки
задается формулой = (4 м/с.
Найти путь, пройденный точкой за первые 4с от
начала движения.

Решение:

2) Скорость движения изменяется по закону м/с . Найти длину
пути, пройденного телом за 3-ю секунду его
движения.

Решение:

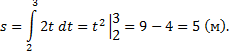
3) Скорость движения тела задана уравнением м/с. Определить
путь, пройденный телом от начала движения до
остановки.

Решение:

Скорость движение тела равна нулю в момент
начала его движения и остановки. Найдем момент
остановки тела, для чего приравняем скорость
нулю и решим уравнение относительно t; получим

Следовательно,

4) Тело брошено вертикально вверх со скоростью,
которая изменяется по закону м/с. Найти наибольшую высоту
подъема.

Решение:

Найдем время, в течении которого тело
поднималось вверх: 29,4–9,8t=0 (в момент наибольшего
подъема скорость равна нулю); t = 3 с. Поэтому

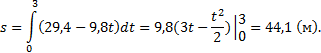
5) Какую работу совершает сила в 10Н при
растяжении пружины на 2 см?

Решение:

По закону Гука сила F, растягивающая пружину,
пропорциональна растяжению пружины , т.е. F = kx.
Используя условие, находим (Н/м), т.е. F = 500x. Получаем

6) Сила в 60Н растягивает пружину на 2 см.
Первоначальная длина пружины равна 14 см. Какую
работу нужно совершить, чтобы растянуть ее до 20
см?

Решение:

Имеем (H/м) и,
следовательно, F=3000x. Так как пружину требуется
растянуть на 0,06 (м), то

7) Определить силу давления воды на стенку
шлюза, длина которого 20 м, а высота 5 м (считая шлюз
доверху заполненным водой).

Здесь y = f(x) = 20, a = 0, b = 5 м, кг/.

Находим

В воду опущена прямоугольная пластинка,
расположенная вертикально. Ее горизонтальная
сторона равна 1 м, вертикальная 2 м. Верхняя
сторона находится на глубине 0,5 м. Определить
силу давления воды на пластинку.

Решение:

Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), = 1000 кг/. Следовательно,

9) Скорость прямолинейного движения точки
задана уравнением . Найти уравнение движения точки.

Решение:

Известно, что скорость прямолинейного движения
тела равна производной пути s по времени t, т.е. , откуда ds = v dt.
Тогда имеем

Это искомое уравнение.

10) Скорость тела задана уравнением . Найти уравнение
движения, если за время тело прошло путь .

Решение:

Имеем ds = v dt = (6+ 1) dt; тогда

Подставив в найденное уравнение начальные
условия s = 60 м, t = 3 c, получим

откуда С = 3.

Искомое уравнение примет вид

11) Тело движется со скоростью м/с. Найти закон движения s(t),
если в начальный момент тело находилось на
расстоянии 5 см от начала отсчета.

Решение:

Так как ds = v dt = (, то

Из условия следует, что если t = 0, то s = 5 см = 0,05 м.
подставив эти данные в полученное уравнение,
имеем откуда
0,05 = С.

Тогда искомое уравнение примет вид

12) Вычислить силу давления воды на плотину,
имеющую форму трапеции, у которой верхнее
основание, совпадающее с поверхностью воды,
имеет длину 10 м, нижнее основание 20 м, а высота 3 м.

Решение:

13) Цилиндрический стакан наполнен ртутью.
Вычислить силу давления ртути на боковую
поверхность стакана, если его высота 0,1 м, а
радиус основания 0,04 м. Плотность ртути равна 13600
кг/.

Решение:

Вычислим площадь круглой полоски

Элементарная сила давления составляет

Следовательно

VI. Самостоятельное решение задач на доске,
коллективный разбор решений задач:

Скорость движения тела задана уравнением . Найти уравнение
движения, если в начальный момент времени
Найти уравнение движения точки, если к моменту
начала отсчета она прошла путь , а его скорость задана
уравнением
Скорость движения тела пропорциональна
квадрату времени. Найти уравнение движения тела,
если известно, что за 3 с оно прошло 18 м.
Тело движется прямолинейно со скоростью м/с. Найти путь,
пройденный телом за 5 с от начала движения.
Скорость движения тела изменяется по закону м/с. Найти путь,
пройденный телом за 4 с от начала движения.
Найти путь пройденный телом за 10-ю секунду, зная,
что что скорость его прямолинейного движения
выражается формулой м/с.
Найти путь, пройденный точкой от начала
движения до ее остановки, если скорость ее
прямолинейного движения изменяется по закону м/с.
Какую работу совершает сила в 8 Н при растяжении
пружины на 6 см?
Сила в 40 Н растягивает пружину на 0,04 м. Какую
работу надо совершить, чтобы растянуть пружину
на 0,02 м?
Вычислить силу давления воды на вертикальную
прямоугольную пластинку, основание которой 30 м, а
высота 10 м, причем верхний конец пластинки
совпадает с уровнем воды.
Вычислить силу давления воды на одну из стенок
аквариума, имеющего длину 30 см и высоту 20 см.

VII. Минутка релаксации

Запуск приложения «Минутка
релаксации»

VIII. Подведение итогов урока:

– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее
сложными? Почему?

Список литературы:

Журнал «Потенциал»
«Алгебра и начала анализа» 11 класс С.М.
Никольский, М.К. Потапов и др.
«Алгебра и математический анализ» Н.Я. Виленкин
и др.
«Учебник по математическому анализу» Град О.Г.,
Змеев О.А.
«Высшая математика: Учебник для вузов». В 3
томах. Бугров Я.С. Никольский С.М.
«Математический анализ». Е.Б. Боронина

Источник

Подготовка к олимпиаде. Метод дифференцирования и интегрирования

Опубликовано пн, 08/05/2019 — 16:17 пользователем fizportal.ru

Метод дифференцирования и интегрирования.

Развитие метода дифференцирования и интегрирования связано с именами Ньютона и Лейбница. В основе его лежат два принципа: 1) принцип возможности представления закона в дифференциальной форме и 2) принцип суперпозиции.

Суть метода состоит в том, что если физический закон выражается в виде

$Z = xy$ (1),

где $x, y, z$ – некоторые физические величины, причем $x = x(varphi)$, то для нахождения $z$ на интервале $[y_1; y_2]$ выражение (1) неприменимо из-за изменения $x$. Тогда интервал $[y_1; y_2]$ разбивают на конечное число малых промежутков $dy(Delta y)$, в пределах каждого из которых можно пренебречь изменением $x(y)$.

Тогда

$dZ = x(Y)dY$ или $Z = intlimits_{y1}^{y2}x(Y)dY$.

Несколько слов о производной и интеграле в физике. Решая задачу о скорости произвольного движения, Ньютон пришел к понятию производной:

$v = x^/ = limlimits_{Delta t to 0}frac{Delta x}{Delta t}$.

То есть производная характеризует быстроту изменения параметров любого физического явления. Лейбниц ввел для производной такое обозначение:

$dot{a} = frac{dx}{dt}$.

Таким образом, $frac{dx}{dt}$ означает отношение конечных соответственных значений малых приращений $dx$ и $dt$.

Известную формулу Ньютона – Лейбница

$intlimits_a^b{f(x)dx} = F(a) — F(b)$,

где $f(x) = frac{dF}{dt}$, в физике следует понимать как сумму большого числа слагаемых $sum{f(x_i)Delta x_i}$.

На первом этапе метода ДИ следует разделить тело на материальные точки либо траекторию или время на такие промежутки, на которых процесс можно считать равномерным. Затем по принципу суперпозиции произвести суммирование (интегрирование). Иными словами, на первом этапе мы находим вклад одного участка в искомую величину, затем производим суммирование по всем участкам.

Рассмотрим конкретные задачи.

Задача 1. Найти силу гравитационного взаимодействия между расположенными на одной прямой материальной точкой массой $m$ и однородным стержнем длиной $l$ и массой $M$. Расстояние от точки до ближайшего конца стержня равно $C$ (рис. ).

Решение

Выделим на расстоянии $x$ от точки элемент стержня длиной $dx$ и массой $frac{M}{l}cdot dx$. Сила его взаимодействия с точкой

$dF = Gfrac{mM}{lx^2}dx$.

Поэтому

$F = intlimits_C^{C+l}Gfrac{mM}{lx^2}dx = Gfrac{mM}{C + l}cdot C$.

Задача 2. Однородный стержень длиной $L$ и массой $M$ вращается с постоянной угловой скоростью $omega$ вокруг оси проходящей через один из его концов. Найти кинетическую энергию стержня.

Решение

Вклад элемента $dx$ стержня в кинетическую энергию всего стержня

$dE = frac{1}{2}frac{M}{L}dx(omega x)^2$,

где $frac{M}{L}dx$ – масса этого элемента, а $x$ – расстояние до оси. Тогда $omega x$ – его скорость.

Осталось проинтегрировать полученное выражение от $0$ до $L$.

$E = intlimits_0^L{frac{1}{2}frac{M}{L}dxomega^2 x^2} = frac{1}{6}ML^2omega^2$.

Задача 3. Найти кинетическую энергию однородного диска радиуса $R$ и массы $M$, вращающегося с постоянной угловой скоростью $omega$ вокруг оси, проходящей через центр диска перпендикулярно его плоскости.

Решение

Разобьем диск на кольца шириной $dx$, каждое из которых отстоит от оси вращения на $x in [0; R]$. Масса каждого кольца, вращающегося с линейной скоростью $omega x$:

$dm = frac{pi M}{pi R^2}[(x + dx)^2 – x^2] approx 2frac{M}{R^2}xdx$.

Величиной $(dx)^2$ в сравнении с $2xdx$ можно пренебречь.

$dE = frac{1}{2} cdot 2frac{Momega^2}{R^2} cdot x^3dx$.

Откуда

$E = intlimits_0^R{frac{Momega^2}{R^2} cdot x^3dx} = frac{1}{4}Momega^2 R^2$.

Метод ДИ успешно применяется для вывода формул.

Задача 4. В поле заряда $Q$ на расстоянии $r_1$ от него находится заряд $q$. Какую работу необходимо совершить, чтобы изменить расстояние между зарядами до $r_2$? (рис.)

Решение

Разобьем отрезок 1 – 2 на такие $dr$, в пределах каждого из которых силу взаимодействия между зарядами можно считать постоянной. Тогда

$dA = kfrac{qQ}{r^2}dr$,

откуда

$A = intlimits_{r1}^{r2}{kfrac{qQ}{r^2}dr} = q(kfrac{Q}{r_2} – kfrac{Q}{r_1})$.

Сравнивая с $A = q(varphi_2 — varphi_1)$, получаем формулу для потенциала поля точечного заряда

$varphi = kfrac{Q}{r}$.

Задача 5. Найти количество теплоты, выделяемое переменным током, значение которого изменяется по закону $i = Isin(omega t + varphi)$ в течение одного периода в проводнике с сопротивлением $R$.

Решение

За время $dt$ в проводнике выделяется

$dQ = i^2Rdt$.

Поэтому

$Q = intlimits_0^T{RI^2sin^2(omega t + varphi)dt}$,

$Q = intlimits_0^{frac{2pi}{omega}}{frac{RI^2}{omega}sin^2(omega t + varphi)dt} = frac{pi}{omega}RI^2$.

Задача 6. Закон Био-Савара-Лапласа устанавливает вклад, вносимый в индукцию магнитного поля элементом $dl$ проводника, по которому течет ток $I$:

$dB = frac{mu_0}{4pi}frac{Idl sinalpha}{r^2}$,

$r$ – расстояние до точки, в которой изменяется модуль вектора магнитной индукции $B$, а $alpha$ – угол между направлением тока и радиус-вектором этой точки. Найти модуль вектора индукции магнитного поля прямого бесконечного тока на кратчайшем расстоянии от проводника (рис.).

Решение

Из рисунка найдем $r = frac{b}{sinalpha}$,

$dl = frac{rdalpha}{sinalpha} = frac{bdalpha}{sin^2alpha}$.

Переменная интегрирования – $alpha$ – лежит в пределах от $0$ до $pi$. Значит,

$B = intlimits_0^pi {frac{mu_0}{4pi}frac{Ibdalpha sinalpha}{frac{b^2}{sin^2alpha}sin^2alpha}} = frac{mu_0 I}{2pi b}$.

Если проводник имеет конечную длину (рис.),

то

$B = frac{mu_0 I}{4pi b}(cosalpha_1 – cosalpha_2)$.

Задача 7. Найти модуль вектора магнитной индукции магнитного поля кругового тока в центре витка радиуса $R$.

Решение

Легко видеть, что для любого элемента

$dl sinalpha = dl$.

Поэтому

$B = intlimits_0^{2pi r}{frac{mu_0}{4pi}frac{I}{R^2}dl} = frac{mu_0 I}{2R}$.

Задача 8. Найдите работу, чтобы изменить заряд конденсатора емкостью $C$ от значения $q_1$ до $q_2$.

Решение

Работа переноса заряда $Delta q$ с одной обкладки на другую при потенциале $U$ на конденсаторе записывается в виде

$Delta A = UDelta q = frac{1}{C}qDelta q$.

Найдем полную работу при изменении значений заряда от $q_1$ до $q_2$:

$A = intlimits_{q1}^{q2}{frac{1}{C}qdq} = frac{1}{C}frac{q^2}{2}|_{q1}^{q2} = frac{1}{2C}(q_2^2 – q_1^2)$.

Из механики известна формула работы, затраченной на деформацию пружины жесткостью $k$ от $x_1$ до $x_2$:

$A = frac{k}{2}(x_2^2 – x_1^2)$.

Заменяя $x_1$ на $q_1, x_2$ на $q_2$, получим значение работы при изменении заряда конденсатора:

$A = frac{1}{2C}(q_2^2 – q_1^2)$.

Задача 9. Пусть тело движется прямолинейно со скоростью $v = 5t$ м/с. Найдите закон движения тела, если за первые три секунды оно прошло 20 м.

Решение

Надо найти функцию $S(t)$, если известна ее производная по времени $v = S(t)$ и значение производной при $t = 3$ c, т. е. $S(3) = 20$ м.

Имеем:

$S(t) = int{5t cdot dt} = frac{5}{2}t^2 + C, C = const$.

При начальных значениях $t = 3$ c и $S = 20$ м получим:

$20 = frac{5}{2} cdot 9 + C$, тогда $C = -frac{5}{2}$.

Функция

$S = frac{5}{2}t^2 -frac{5}{2}$

есть искомый закон движения тела.

Задача 10. Найдите путь, пройденный точкой, движущейся прямолинейно, за отрезок времени от $t_1 = 1$ c до $t_2 = 4$ c, если скорость точки $v(t) = 2t^2 + 3t$. Чему равно ускорение точки в момент $t = 2$ c?

Решение

Так как $v(t) = S^/ (t)$, то

$S(t) = int{(2t^2 + 3t)dt} = frac{2}{3}t^3 + frac{3}{2}t^2 + C$.

Полагая $C = 0$, $S(1) = frac{13}{6}, S(t) = frac{200}{3}$, искомый путь составит:

$S(4) – S(1) = 65,5$ м.

Теперь найдем ускорение точки:

$a(t) = v^/ (t) = 4t + 3$.

Откуда

$a(2) = 11$ м/с².

Составим таблицу, в которой можно указать использование определенного интеграла при решении физических задач:

1) если в каждой точке оси $Ox$ приложена сила $F = F(x)$, то всю работу на отрезке $[a, b]$ можно записать в виде интеграла:

$A = intlimits_a^b{F(x)dx}$.

2) если точка $x in [a, b]$, движется вдоль оси $Ox$ и известна скорость этой точки как функция времени $x = v(t)$, то путь, пройденный точкой $x$ за время $t$, $t in [t_1, t_2]$, вычисляется по формуле

$S = intlimits_{t1}^{t2}{v(t)dt}$.

3) если рассмотреть однородный стержень длиной $l$ и линейной плотностью $rho$, то его масса есть интеграл от его линейной плотности:

$m = intlimits_0^l{rho (x)dx}$.

4) если известна величина заряда $q$, который переносится за время $t in [a, b]$ через сечение проводника, то можно найти его значение:

$q = intlimits_a^b{I(t)dt}$,

где $I(t)$ – изменение силы тока в зависимости от времени $t$;

5) если известен закон поглощения теплоты, т. е. теплоемкость тела $C = c(t)$, то можно найти количество теплоты в виде интеграла:

$Q = intlimits_{t1}^{t2}{c(t)dt}$,

где $t in [t_1, t_2]$.

Задача 11. Найдите силу давления воды на квадратную пластину стороной $a$, помещенную в жидкость так, что плоскость пластины перпендикулярна поверхности жидкости, а одна из сторон пластины расположена на поверхности.

Решение

Используя случай 1) из таблицы, находим

$F = intlimits_a^b{arho xdx} = arho frac{x^2}{2}|_0^a = frac{rho a^3}{2}$,

где $rho$ – плотность жидкости.

Задача 12. Вычислите работу силы $F$ при сжатии пружины на 0,05 м, если пружина сжимается на 0,02 м под действием силы в 180 Н.

Решение

По закону Гука $F = kx$, где $x$ – величина сжатия или растяжения пружины, $k$ – постоянная. При $x$ = 0,2 м сила $F$ = 180 Н. Имеем:

$k = frac{F}{x} = frac{180}{0,02} = 9000$ Н/м.

Значит, $F(x) = kx = 9000x$.

Работа силы $F(x)$ равна:

$A = intlimits_0^{0,05}{9000xdx} = 9000frac{x^2}{2}|_0^{0,05} = 11,25$ Дж.

Сделаем замечания к таблице, на которые надо обратить внимание при решении физических задач.

Замечание 1. Скорость истекания жидкости $v$ через круглую дырку в цилиндрическом баке зависит от высоты столба жидкости x и вычисляется по формуле Бернулли $v = sigma sqrt{2gx}$, где $g = 9,8$ м/с²; $sigma$ – коэффициент, который зависит от свойств жидкости. Для воды он равен 0,6. По мере уменьшения столба жидкости $x$ в баке скорость истекания уменьшается (а не постоянная!).

Замечание 2. Работа газа при расширении, т. е. изменение объема от $V_1$ до $V_2$, равна:

$A = intlimits_{V1}^{V2}{pdV}$,

где $p$ – давление газа.

Если $p = const$, то $A = p(V_2 – V_1)$.

Замечание 3. Сила давления $F$ жидкости на пластинку, которая находится в горизонтальном положении на глубине $h$, вычисляется по закону Паскаля:

$F = rho ghS$, где $g = 9,8$ м/с²,

$S$ – площадь пластинки; $rho$ – плотность жидкости.

Пусть пластинка погружена вертикально в жидкость и ограничена линиями

$y = f(x), x = a, x = b, y = 0$

Сила давления жидкости на пластинку

$F = gintlimits_a^b{rho xf(x)dx}$.

Задача 13. Тело движется прямолинейно со скоростью $v(t) = 2t^2 – t + 1$ (м/с). Найдите путь, пройденный за первые 5 с.

Решение

Согласно формуле,

$S = intlimits_{t1}^{t2}{v(t)dt}$,

для данной задачи находим:

$S(t) = intlimits_0^5{(2t^2 – t + 1)dt = (frac{2}{3}t^3 — frac{t^2}{2} + t_0|_0^5)} = frac{250}{3}$ (м).

Задача 14. Уравнение движения по прямой имеет вид $X = A + Bt + Ct^2$, где $A = 2,0$ м, $B = 2,0$ м/с, $С = –0,5$ м/с². Найти момент времени $t$, в который скорость точки $v = 0$. Чему равна координата $X$и ускорение $a$ в этот момент? Построить графики зависимости от времени координаты, пути, скорости и ускорения.

Решение

По условию задачи мы имеем уравнение движения вида

$X = A + Bt + Ct^2$. (1)

Мы знаем, что быстрота изменения координаты со временем дает нам скорость, тогда

$v = frac{dx}{dt} = B + 2Ct$. (2)

Найдем момент времени, когда скорость точки равна нулю:

$B + 2Ct = 0$, и $t = -frac{B}{2C}$.

Для определения координаты, воспользуемся уравнением (1), подставив в него найденное время:

$X = A + B(-frac{B}{2C}) + C(-frac{B}{2C})^2 = A — frac{B^2}{2C} + frac{B^2}{4C} = A — frac{B^2}{4C}$.

Ускорение найдем как производную скорости по времени

$a = frac{dv}{dt} = 2C$. (3)

Анализируя последнее уравнение, приходим к выводу, что ускорение не зависит от времени и постоянно.

Проведем вычисления:

$t = -frac{2,0}{2(-0,5)} = 2$ c,

$X = 2,0 — frac{2,0^2}{4(-0,5)} = 4$ м,

$a = 2(-0,5) = -1,0$ м/с².

Проверим соответствие единиц измерения:

$[t] = frac{frac{м}{c}}{frac{м}{c^2}} = c$,

$[X] = м — frac{frac{м^2}{c^2}}{frac{м}{c^2}} = м$,

$[a] = frac{м}{c^2}$.

Теперь перейдем к построению графиков. Для этого подставим численные значения в уравнения (1), (2), (3) численные значения и получим зависимости от времени:

$X = 2 + 2t – 0,5t^2, v = 2 – t, a = -1$.

Графиком координаты будет парабола: при $t = 0$ координата будет $x_0 = 2$ м, решая квадратное уравнение при $x = 0$, найдем 2 корня уравнения $t_1 = -0,828$ c и $t_2 = 4,828$ c, при $t = 2,828$ c имеем вершину параболы $x = 3,66$ м. Ветки параболы направлены вниз, так как ускорение отрицательно. Смотри рисунок 1.

Для графика скорости достаточно взять две точки (линейная зависимость скорости от времени):

$t = 0, v = 2$ м/с; $t = 2$ c, $v = 0$.

Смотри график на рисунке 2.

График ускорения будет прямая параллельная оси времени проходящая через точку с $a = -1$ м/с². Смотри рисунок 3.

Из уравнения координаты получим уравнение пути

$S = X – 2 = 2t – 0,5t^2$.

При построении графика пути необходимо помнить, что путь величина положительная. Рассмотрим два этапа: до остановки и после остановки. При $t = 2$ c скорость тела $v = 0$ и $S = 2$ м. После остановки тело меняет свое направление движения на противоположное и движется с прежним ускорением. Смотри рисунок 4.

Ответ: $t = 2$ c, $x = 4$ м, $a = -1$ м/с², графики смотри рисунки

Задачи для самостоятельной работы.

Задача 15. Какую работу необходимо совершить, чтобы перетянуть брусок массой $m$ и длиной $l$ через шероховатую полосу шириной $L$? Коэффициент трения $mu$.

Задача 16. Найти модуль вектора индукции магнитного поля в точке $O$ (рис.).

Ответ

$B = frac{mu_0 I(pi + 1)}{2pi R}$

Задача 17. Зависимость пройденного пути $S$ от времени $t$ дается уравнением $S = A + Bt + Dt^3$, где $C = 0,14$ м/с² и $D = 0,01$ м/с³. Через какое время $t$ тело будет иметь ускорение $a = 1$ м/с²? Найти среднее ускорение $a_{cp}$ тела за этот промежуток времени.

Ответ

$t = 12$ c; $a_{cp} = 0,64$ м/с²

Задача 18. Шар радиусом $R = 6$ см удерживается внешней силой под водой так, что его верхняя точка касается поверхности воды. Какую работу $A$ произведет выталкивающая сила, если отпустить шар и предоставить ему свободно плавать? Плотность материала 500 кг/м³.

Задача 19. Имеется кольцо радиусом $R$R. Радиус проволоки $r$, плотность материала $rho$. Найти силу, с которой это кольцо притягивает материальную точку массой $m$, находящую на оси кольца на расстоянии $L$ от его центра.

Ответ

$F = frac{2pi^2 Gmrho r^2RL}{(R^2 + L^2)^{3/2}}$

Источник