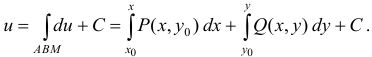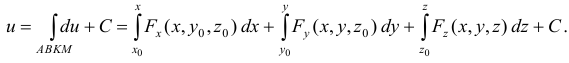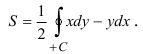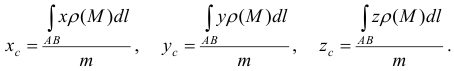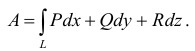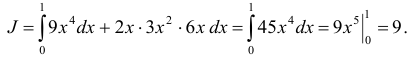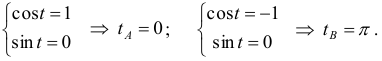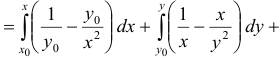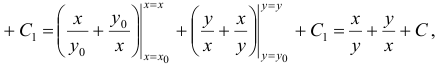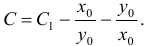В настоящей статье научимся вычислять криволинейный интеграл от полного дифференциала.
Схема решения:
- сначала нужно убедиться, что подынтегральная функция является полным дифференциалом
- дальше найти интеграл между заданными точками.
Формула Ньютона-Лейбница для криволинейного интеграла от полного дифференциала
Криволинейный интеграл имеет одно полезное для вычислений свойство, он не зависит от формы кривой, по которой интегрируем.
Поэтому вместо интегрировать по прямой между двумя точками строят ломаную параллельно осям координат и интегрируют по ней.
За счет этого один из дифференциалов в интеграле превращается в нуль, таким образом упрощаются вычисления.
Детальнее алгоритм проверки подынтегрального выражения на полный дифференциал и вычисление криволинейных интегралов приведены в следующих 6 примерах.
Пример 1 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл int[(x+y)dx+(x-y)dy]
Решение: Подынтегральные функции являются первобытными для полного дифференциала
(x+y)dx+(x-y)dy.
Выпишем P=P(x, y)=x+y, Q=Q(x, y)=x-y.
но найдем частичные производные первого порядка функций P(x, y) и Q(x, y):
Сравнением убеждаемся, что частичные производные равны
поэтому подынтегральное выражение (x+y)dx+(x-y)dy является полным дифференциалом.
Криволинейный интеграл от точки (0,1) к точке (2,3) будем вычислять вдоль прямых y=1 и x=2.
Так верно выполнять, поскольку на каждом интервале один из дифференциалов равен нулю, следовательно, интеграл упрощается.
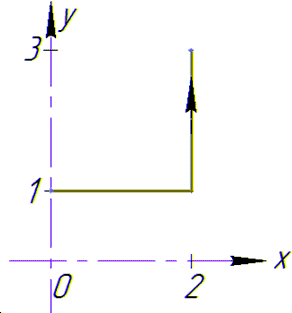
Вычислим заданный криволинейный интеграл:
Пример 2 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
Решение: Имеем подынтегральное выражение:
xdy+ydx.
Выпишем значение при дифференциалах
P=P(x, y)=y, Q=Q(x, y)=x.
Найдем частичные производные первого порядка функций P, Q:
Сравнением значений убеждаемся, что подынтегральное выражение является полным дифференциалом.
Заданный криволинейный интеграл от точки (- 1,2) к точке (2,3) будем вычислять вдоль прямых y=2 и x=2.
На графике направление и контур интегрирования имеют вид
Выпишем как буду изменяться координаты и дифференциалы на каждом интервале
Найдем криволинейный интеграл через сумму двух:
Пример 3 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
где f(u) непрерывная функция.
Решение: Выписываем подынтегральное выражение:
f(x+y)(dx+dy)=f(x+y)dx+f(x+y)dy.
Отсюда P=P(x, y)=f(x+y), Q=Q(x, y)=f(x+y).
Поскольку P, Q симметрично содержат переменные, то их частичные производные
равны, а это значит что подынтегральное выражение является полным дифференциалом.
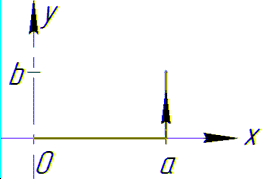
Криволинейный интеграл от точки (0,0) к точке (a, b) будем вычислять вдоль прямых y=0 и x=a.
Выпишем пределы интеграла и дифференциалы
Криволинейный интеграл упрощаем с помощью замены переменных:
здесь f(u) заданная непрерывная функция.
Пример 4 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
Пример 5 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
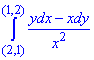
вдоль путей, которые не пересекают ось Oy.
Решение: Имеем подынтегральное выражение:
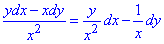
Отсюда P=P(x, y)=y/x2, Q=Q(x, y)=-1/x.
Вычислим частичные производные функций P(x, y), Q(x, y):
они равны между собой, поэтому подынтегральное выражение является полным дифференциалом.
Криволинейный интеграл от точки (2,1) к точке (1,2) будем вычислять вдоль прямых x=2 и y=2.
Запишем диапазон изменения пределов интеграла и дифференциалы
Вычислим заданный криволинейный интеграл:
Пример 6 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
вдоль кривых, что не проходят через начала координат.
Решение: Подынтегральное выражение разобьем на сумму двух:
Выписываем производные при дифференциалах
Найдем частичные производные первого порядка функций P, Q:
Сравнением значений делаем вывод что имеем полный дифференциал под интегралом.
Заданный криволинейный интеграл от точки (1,0) к точке (6,8) будем вычислять вдоль прямых y=0 и x=6, то есть на двух интервалах
В декартовой плоскости контур интегрирования имеет вид
Криволинейный интеграл равен 9
Приведенных примеров на вычисление криволинейного интеграла от полного дифференциала вполне достаточно, чтобы выучить алгоритм проверки подынтегральной функции на полный дифференциал.
Разбивать участок между точками на промежутки параллельные осям тоже не трудно.
Интегрировать Вы должны уметь хорошо прежде чем браться за подобные примеры.
Если имеете трудности в интегрировании обращайтесь к нам за помощью, думаю, договоримся!
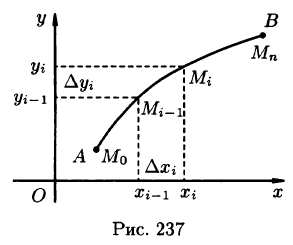
Обобщением определенного интеграла на случай, когда область интегрирования есть некоторая кривая, является так называемый криволинейный интеграл.
Криволинейный интеграл I рода
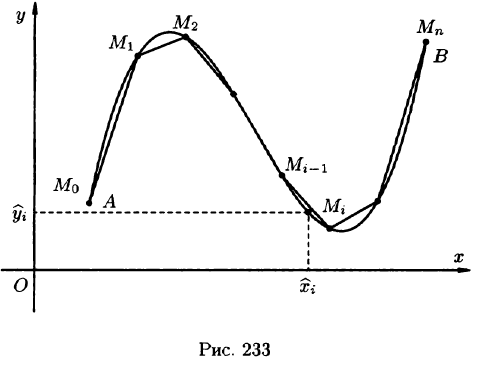
Пусть на плоскости Оху задана непрерывная кривая АВ (или L) длины l. Рассмотрим непрерывную функцию f(x; у), определенную в точках дуги АВ. Разобьем кривую АВ точками 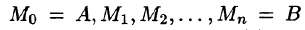
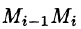
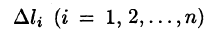
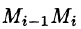
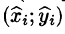
Ее называют интегральной суммой для функции f(x;y) по кривой АВ.
Пусть 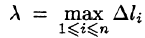
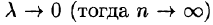
Таким образом, по определению,
Условие существования криволинейного интеграла I рода (существования предела интегральной суммы (55.1) при 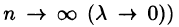
Теорема 55.1. Если функция f(х; у) непрерывна в каждой точке гладкой кривой (в каждой точке 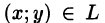
Аналогичным образом вводится понятие криволинейного интеграла от функции f(х; у; z) по пространственной кривой L.
Приведем основные свойства криволинейного интеграла по длине дуги (I рода).
если путь интегрирования L разбит на части 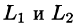
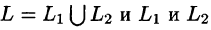
5. Если для точек кривой L выполнено неравенство
6. 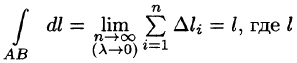
7. Если функция f(x; у) непрерывна на кривой АВ, то на этой кривой найдется точка 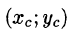
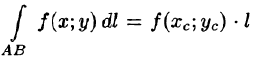
Вычисление криволинейного интеграла I рода
Вычисление криволинейного интеграла I рода может быть сведено к вычислению определенного интеграла. Приведем без доказательства правила вычисления криволинейного интеграла I рода в случаях, если кривая L задана параметрическим, полярным и явным образом.
Параметрическое представление кривой интегрирования
Если кривая АВ задана параметрическими уравнениями х = x(t), у = y(t), 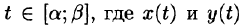
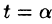
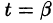
Аналогичная формула имеет место для криволинейного интеграла от функции f(x;y;z) по пространственной кривой АВ, задаваемой уравнениями
Явное представление кривой интегрирования
Если кривая АВ задана уравнением 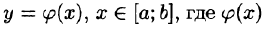
Подынтегральное выражение в правой части формулы (55.5) получается заменой в левой части 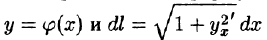
Пример 55.1. Вычислить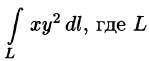
Решение: Уравнение прямой OA есть 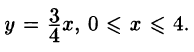
Полярное представление кривой интегрирования
Если плоская кривая L задана уравнением 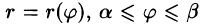
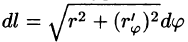
Подчеркнем, что нижний предел определенного интеграла в формулах (55.3)-(55.6) должен быть меньше верхнего.
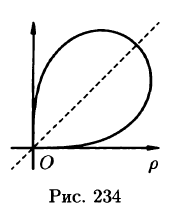
Пример 55.2. Вычислить 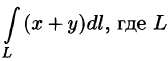
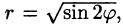
Решение: Кривая интегрирования изображена на рисунке 234. Воспользуемся формулой (55.6).
Так как
то, заметив, что 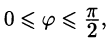
Некоторые приложения криволинейного интеграла I рода
Криволинейный интеграл I рода имеет разнообразные приложения в математике и механике.
Длина кривой
Длина I кривой АВ плоской или пространственной линии вычисляется по формуле
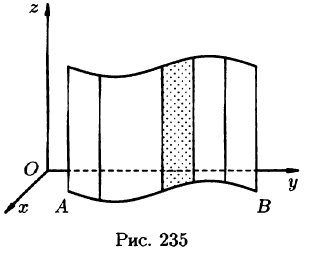
Плоиодь цилиндрической поверхности
Если направляющей цилиндрической поверхности служит кривая АВ, лежащая в плоскости Оху, а образующая параллельна оси Oz (см. рис. 235), то площадь поверхности, задаваемой функцией z = f(x; у), находится по формуле
Масса кривой
Масса материальной кривой АВ (провод, цепь, трос,…) определяется формулой 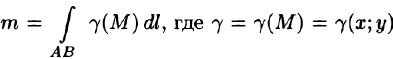
Разобьем кривую АВ на п элементарных дуг 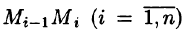
Пусть
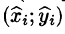
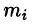
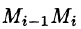
Суммируя, находим приближенное значение массы m:
За массу кривой АВ примем предел суммы (55.7) при условии, что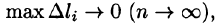
или, согласно формуле (55.2),
(Заметим, что предел существует, если кривая АВ гладкая, а плотность задана непрерывной в каждой точке АВ функцией.)
Статические моменты, центр тяжести
Статические моменты относительно осей Ох и Оу и координаты центра тяжести материальной кривой АВ определяются по формулам
Моменты инерции
Для материальной кривой АВ моменты 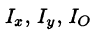
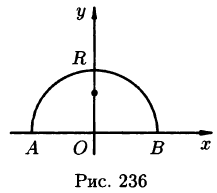
Пример 55.3. Найти центр тяжести полуокружности 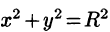
Решение: Из соображений симметрии ясно, что центр тяжести находится на оси Оу (см. рис. 236). Поэтому 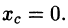
Знаменатель дроби — длина полуокружности. Поэтому
Для вычисления числителя воспользуемся параметрическими уравнениями окружности 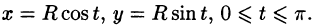
Следовательно,
Криволинейный интеграл второго рода
Решение задачи о вычислении работы переменной силы при перемещении материальной точки вдоль некоторой кривой (и других) приводит к понятию криволинейного интеграла II рода.
Криволинейный интеграл II рода определяется почти так же, как и интеграл I рода
Пусть в плоскости Оху задана непрерывная кривая АВ (или L) и функция Р(х;у), определенная в каждой точке кривой. Разобьем кривую АВ точками 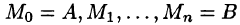
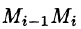
На каждой «элементарной дуге» 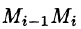
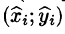
где 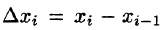
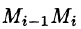
Сумму (56.1) называют интегральной суммой для функции Р(х;у) по переменной х. Таких сумм можно составить бесчисленное множество. (Отличие сумм (55.1) и (56.1) очевидно.)
Если при 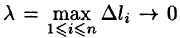
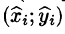
Итак,
Аналогично вводится криволинейный интеграл от функции Q(x;y) по координате у:
где 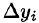
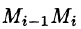
Криволинейный интеграл II рода общего вида
определяется равенством
Криволинейный интеграл
по пространственной кривой L определяется аналогично.
Теорема 56.1. Если кривая АВ гладкая, а функции Р(х; у) и Q(x; y) непрерывные на кривой АВ, то криволинейный интеграл II рода существует.
Отметим лишь некоторые свойства криволинейного интеграла II рода.
1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т. е.
(проекция дуги 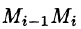
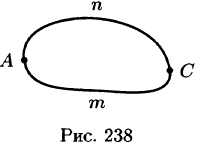
2.Если кривая АВ точкой С разбита на две части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям, т. е.
3.Если кривая АВ лежит в плоскости, перпендикулярной оси Ох, то
аналогично для кривой, лежащей в плоскости, перпендикулярной оси Оу :
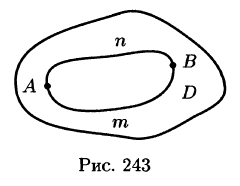
4.Криволинейный интеграл по замкнутой кривой (обозначается 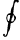
Действительно,
(см. рис. 238). С другой стороны,
Таким образом,
Вычисление криволинейного интеграла II рода
Вычисление криволинейного интеграла II рода, как и I рода, может быть сведено к вычислению определенного интеграла.
Параметрическое представление кривой интегрирования
Пусть кривая АВ задана параметрическими уравнениями х = x(t) и у = y (t), где функции x(t) и y(t) непрерывны вместе со своими производными x'(t) и y'(t) на отрезке 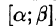
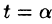
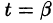
Преобразуем интегральную сумму к переменной t. Так как
то по формуле Лагранжа (см. (25.2)) имеем:
Выберем точку 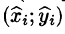
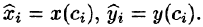
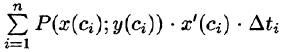
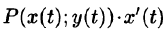
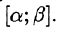
Аналогично получаем:
Складывая почленно полученные равенства (56.2) и (56.3), получаем:
Явное представление кривой интегрирования
Если кривая АВ задана уравнением 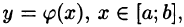
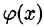
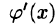
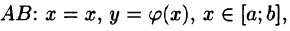
В частности,
Если АВ — гладкая пространственная кривая, которая описывается непрерывными на отрезке 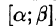
вычисляется по формуле
Замечание. Криволинейные интегралы I и II рода связаны соотношением
— углы, образованные касательной к кривой АВ в точке М(х, у) с осями Ох и Оу соответственно.
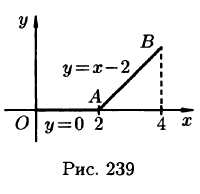
Пример 56.1. Вычислить
— ломаная ОАВ, где O(0; 0), A(2;0), В(4; 2).
Решение: Так как L = ОАВ = OA + АВ (см. рис. 239), то
Уравнение отрезка OA есть у = 0, 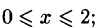
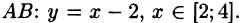
Согласно формуле (56.5), имеем:
Пример 56.2. Вычислить
— отрезок прямой в пространстве от точки А(1;0;2) до точки В(3;1;4).
Решение: Составим уравнение прямой, проходящей через точки А и В: 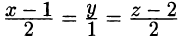
Формула Остроградского-Грина
Связь между двойным интегралом по области D и криволинейным интегралом по границе L этой области устанавливает формула Остроградского-Грина, которая широко применяется в математическом анализе.
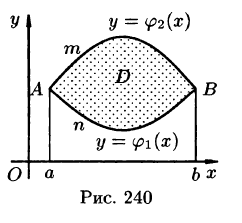
Пусть на плоскости Оху задана область D, ограниченная кривой, пересекающейся с прямыми, параллельными координатным осям не более чем в двух точках, т. е. область D — правильная.
Теорема 56.2. Если функции Р(х; у) и Q(x;y) непрерывны вместе со своими частными производными 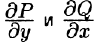
где L — гранив области D и интегрирование вдоль кривой L производится в положительном направлении (при движении вдоль кривой, область D остается слева).
Формула (56.8) называется формулой Остроградского-Грина.
Пусть 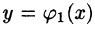
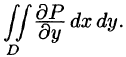
Или, согласно формуле (56.6),
Аналогично доказывается, что
Если из равенства (56.10) вычесть равенство (56.9), то получим формулу (56.8).
Замечание. Формула (56.8) справедлива и для произвольной области, которую можно разбить на конечное число правильных областей.
Пример 56.3. С помощью формулы Остроградского-Грина вылить
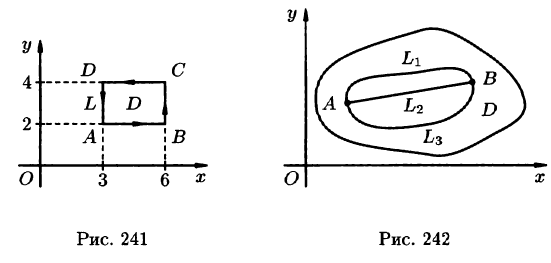
где L — контур прямоугольника с вершинами А(3;2), B(6; 2), С(6;4), D( 3;4).
Решение: На рисунке 241 изображен контур интегрирования. Поскольку
по формуле (56.8) имеем:
Условия независимости криволинейного интеграла II рода от пути интегрирования
Пусть 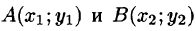
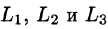
имеет, вообще говоря, свое значение.
Если же его значения по всевозможным кривым АВ одинаковы, то говорят, что интеграл I не зависит от вида пути интегрирования. В этом случае для интеграла I достаточно отметить лишь его начальную точку 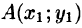
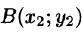
Записывают:
Каковы же условия, при которых криволинейный интеграл II рода не зависел от вида пути интегрирования?
Теорема 56.3. Для того чтобы криволинейный интеграл
не зависел от пути интегрирования в односвязной области D, в которой функции 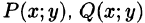
Докажем достаточность условия (56.12). Рассмотрим произвольный замкнутый контур 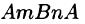
Учитывая свойства криволинейного интеграла, имеем:
т. e.
Полученное равенство означает, что криволинейный интеграл не зависит от пути интегрирования.
В ходе доказательства теоремы получено, что если выполняется условие 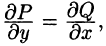
Верно и обратное утверждение.
Следствие 56.1. Если выполнено условие (56.12), то подынтегральное выражение 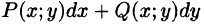
Тогда (см. (56.11)):
т. e.
Формула (56.14) называется обобщенной формулой Ньютона-Лейбница для криволинейного интеграла от полного дифференциала.
Следствие 56.2. Если подынтегральное выражение Pdx + Qdy есть полный дифференциал и путь интегрирования L замкнутый, то
Замечания.
- Чтобы не спутать переменную интегрирования х с верхним пределом х, переменную интегрирования обозначают другой буквой (например,
и т.д.).
- Функцию U = U(x; у), удовлетворяющую условию (56.12), можно найти, используя формулу
В качестве начальной точки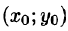
3. Аналогичные результаты справедливы для криволинейного интеграла
по пространственной кривой. Условие (56.12), равенство (56.13), формулы (56.14) и (56.15) имеют соответственно вид:
(см. пример 73.1).
Пример 56.4. Найти
Решение: Здесь 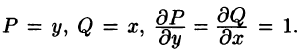
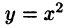
Пример 56.5. Убедиться, что выражение 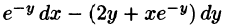
Решение: Для того чтобы указанное выражение являлось полным дифференциалом, необходимо выполнение условий (56.12):
— условия выполнены, следовательно,
А так как полный дифференциал имеет вид
(см. п. 44.3), то верны соотношения
Интегрируем по х первое из уравнений, считая у постоянным, при этом вместо постоянной интегрирования следует поставить 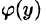
Подставляя полученное выражение во второе из уравнений (56.16), найдем 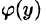
Таким образом,
Отметим, что функцию U проще найти, используя формулу (56.15):
Некоторые приложения криволинейного интеграла II рода
Площадь плоской фигуры
Площадь S плоской фигуры, расположенной в плоскости Оху и ограниченной замкнутой линией L, можно найти по формуле
при этом кривая L обходится против часовой стрелки.
Действительно, положив в формуле Остроградского-Грина (56.8) Р(х; у) = 0, Q(x; у) = х, получим:
или
Аналогично, полагая P = -у, Q = 0, найдем еще одну формулу для вычисления площади фигуры с помощью криволинейного интеграла:
Сложив почленно равенства (56.18) и (56.19) и разделив на два, получим:
Формула (56.17) используется чаще, чем формулы (56.18) и (56.19).
Работа переменной силы
Переменная сила 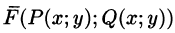
Разобьем кривую АВ точками 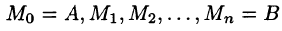
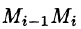
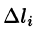
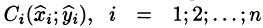
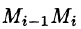
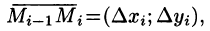
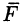
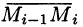
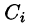
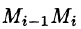
Тогда скалярное произведение 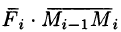
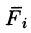
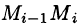
Приближенное значение работы А силы 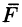
За точное значение работы А примем предел полученной суммы при
Замечание. В случае пространственной кривой АВ имеем:
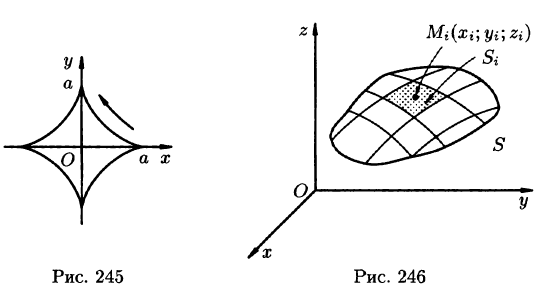
Пример 56.6. Найти площадь фигуры, ограниченной астроидой
Решение: При обхождении астроиды в положительном направлении параметр t изменяется от 0 до 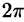
Пример 56.7. Найти работу силы 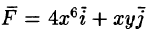
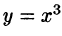
Решение: По формуле (56.20) находим:
Криволинейный интеграл
Пусть функция 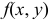
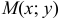
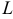
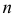
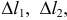
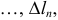
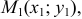
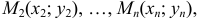
то она называется интегральной суммой функции 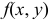
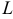
Криволинейным интегралом первого рода 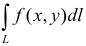
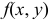
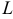
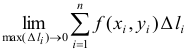
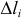
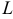
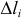
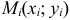
В прямоугольных координатах элемент дуги 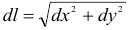
Если кривая 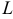
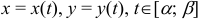
Если кривая 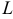
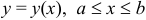
Если кривая 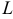
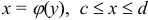
Физический смысл криволинейного интеграла первого рода. Масса 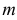
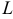
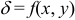
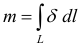
Свойства криволинейного интеграла первого рода
- При изменении направления интегрирования криволинейный интеграл первого рода не изменяет своего знака, т. е.
, где
— кривая
, пробегаемая в заданном направлении,
— кривая
, пробегаемая в противоположном направлении.
- Если кривая
с помощью некоторой точки разбита на части:
, то
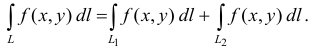
Криволинейным интегралом второго рода от пары функций 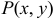
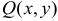
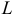
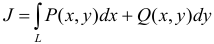
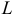
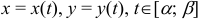
Если кривая 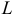
Свойства криволинейного интеграла второго рода
- При изменении направления интегрирования криволинейный интеграл второго рода изменяет свой знак, т. е.
.
- Если кривая
с помощью некоторой точки разбита на части:
, то
.
Циркуляцией называется криволинейный интеграл по замкнутой плоской линии 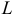
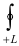
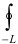
Обычно криволинейный интеграл 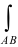
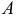
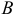
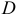
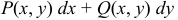
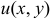
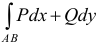
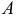
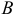
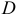
Выражение 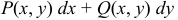
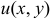
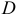
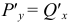
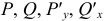
Полный дифференциал некоторой функции 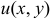
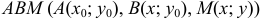
Полный дифференциал некоторой функции 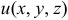
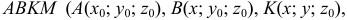
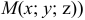
С помощью криволинейных интегралов вычисляются следующие величины:
1) Длина дуги 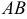
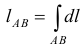
2) Площадь фигуры, расположенной в плоскости 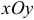
3) Масса 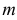
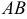
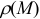
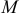
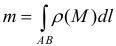
4) Координаты центра тяжести 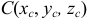
5) Работа 
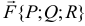
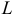
Формула Грина 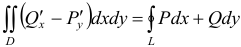
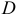
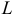
Пример №1
Вычислить криволинейный интеграл, сделать чертеж:
а) 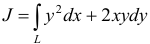
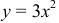
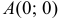
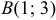
б) 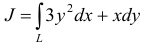
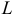
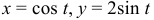
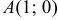
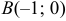
Решение:
а) Преобразуем криволинейный интеграл в определенный интеграл с переменной 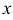
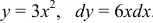
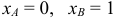
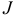
Ответ: 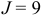
б) Найдем значение параметра 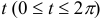
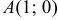
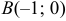
Преобразуем криволинейный интеграл в определенный с переменной 
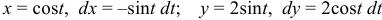
Ответ: 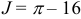
Пример №2
Проверить, является ли заданное выражение полным дифференциалом некоторой функции 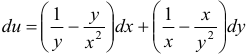
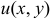
Решение:
Обозначим коэффициенты при дифференциалах 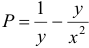
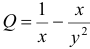
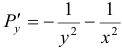
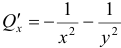
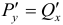
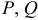
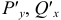
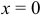
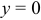
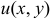
Найдем эту функцию:
где
Область определения функции 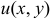
Ответ: 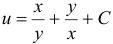
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Аналогично проектируя дугу AkAk–1 на ось Oy, получаем интеграл ∫ f (x; y)dy по координате y.
AB
Если на кривой определены две функции Р(x; y) и Q(x; y), тогда полный криволинейный интеграл 2-го рода записывается следующим образом:
∫ P (x; y)dx +Q(x; y)dy.
AB
Для случая пространственной кривой L формула криволинейного интеграла 2-го рода выглядит следующим образом:
∫ P (x; y;z)dx +Q(x; y;z)dy +R(x; y;z)dz.
AB
Криволинейные интегралы 2-го рода обладают свойствами линейности и аддитивности, однако теорема об оценке модуля интеграла и среднего значения неверны.
Вычисление криволинейного интеграла 2-го рода
Вычисление криволинейного интеграла 2-го рода производится с помощью опреденного интеграла.
Если кривая L задана параметрическими уравнениями x = φ(t) и y = ψ(t), где α ≤ t ≤ β, а функции φ(t) и ψ(t) имеют непрерывные производные. Пусть вдоль кривой L заданы кусочно-непрерывные функции Р(x; y) и Q(x; y). Тогда дифференциалы текущих координат x и y имеют вид: dx = φ'(t)dt, dy = ψ'(t)dt, а криволинейный интеграл выражается обыкновенным определенным интегралом по следующей формуле:
β
∫P (x; y)dx +Q(x; y)dy = ∫(P (ϕ(t );ψ(t ))ϕ'(t ) +Q(ϕ(t );ψ(t ))ψ'(t ))dt.
Lα
Если кривая L имеет явное задание y = y(x), где a ≤ x ≤ b, тогда криволинейный интеграл 2-го рода вычисляется по следующей формуле:
b
∫P (x; y)dx +Q(x; y)dy = ∫(P (x; y(x)) +Q(x; y(x))y ‘x ))dx.
Если кривая L имеет явное задание x = x(y), где c ≤ y ≤ d, тогда криволинейный интеграл 2-го рода вычисляется по следующей формуле:
31
d
∫P (x; y)dx +Q(x; y)dy = ∫(P (x( y); y)x ‘y +Q(x( y); y))dy.
Для случая пространственной кривой L, заданной уравнениями: x = φ(t), y = ψ(t), z = χ(t), где α ≤ t ≤ β, на которой определены три ку- сочно-непрерывные функции:
∫P (x; y;z)dx +Q(x; y;z)dy + R(x; y;z)dz =
L
β
= ∫α (P (ϕ(t );ψ(t );χ(t ))ϕ'(t ) +Q(ϕ(t );ψ(t );χ(t ))ψ'(t ) +R(ϕ(t );ψ(t );χ(t ))χ'(t ))dt.
Связь между криволинейными интегралами 1-го и 2-го рода
∫ Pdx +Qdy = ∫ (P cos α+Q cosβ)dl,
AB AB
где α, β – углы, образованные касательной к кривой L с осями координат.
В случае пространственного задания кривой L:
∫ Pdx +Qdy +Rdz = ∫ (P cos α+Q cosβ+R cos γ)dl.
AB AB
Формула Остроградского-Грина
Пусть функции Р(x; y) и Q(x; y) и их частные производные ∂P
∂Q ∂y
и ∂x непрерывны в простой области G. Тогда справедливо равенство
|
v∫ Pdx +Qdy = ∫∫( |
∂Q |
− |
∂P )dxdy, |
|
|
L |
G |
∂x |
∂y |
где криволинейный интеграл берется по границе L области G в положительном направлении.
Эта формула называется формулой Остроградского-Грина, она связывает криволинейный интеграл по границе с двойным интегралом
по самой области. Знак v∫ – означает интегрирование по замкнуто-
L
му контуру, в данном случае по границе области.
Обыкновенный (прямолинейный) определенный интеграл является частным случаем криволинейного интеграла, у которого линией интегрирования служит прямолинейный отрезок оси координат.
32
Обычно криволинейный интеграл зависит от линии интегрирования. Но если в некоторой односвязной области D выражение P(x; y)dx + Q(x; y)dy является полным дифференциалом, то криволинейный интеграл ∫ P (x; y)dx +Q(x; y)dy не зависит от ли-
AB
нии интегрирования, соединяющей точки А и В, а взятый по любой замкнутой линии, пролегающей в области D, равен нулю.
Вычисление криволинейного интеграла от полного дифференциала производится по следующей формуле:
∫ Pdx +Qdy = F (xB ; yB ) −F (xA ; yA ) .
AB
Примеры
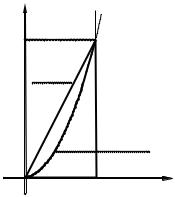
1. Найти значение криволинейного интеграла 2-го рода ∫ydx − xdy вдоль указанных путей интегрирования: L
а) L – прямая между точками O(0; 0), A(1; 2);
б) L – парабола y = kx2 между точками O(0; 0), A(1; 2);
в) L – ломаная ОВА, где O(0; 0), A(1; 2) B(1; 0).
Решение (а). С учетом координат точек, запишем уравнение прямой ОА: y = 2x, где 0 ≤ x ≤ 1 (рис. 18), найдем dy = 2dx. Подставим
винтеграл и получим
∫ydx − xdy = ∫1 (2xdx − x2dx )= 0.
Решение (б). Так как парабола проходит через точку A(1; 2), то k = 2. Найдем dy = 4xdx.
Подставим в интеграл и получим
|
∫ydx − xdy = ∫2 |
(2x2dx − x4xdx) = − |
2 |
. |
|
L |
0 |
3 |
|
Решение: (в). По свойству аддитивности криволинейного интеграла для участков ОВ и ВА (рис. 18) имеем:
∫ydx − xdy = ∫ ydx − xdy + ∫ ydx − xdy.
Найдем уравнения линии для участка ОВ: y = 0, 0 ≤ x ≤ 1 , dy = 0; для участка ВА: x =1, 0 ≤ y ≤ 2, dx = 0.
33
y
2 
y =2x
Рис. 18
Тогда интеграл будет равен
∫ ydx − xdy = ∫(0 − x 0)dx +∫( y 0 −1)dy = −2.
Задания для самостоятельной работы
1. Вычислить интеграл ∫ (4x + y)dx +(x +4 y)dy , где кривая АВ за-
AB
дана уравнением: y = x 4. Координаты точек A(1; 1), B(–1; 1). (Ответ: (–2).)
2. Вычислить криволинейный интеграл v∫ 2xdx −(x +2y)dy , где L –
L
контур периметра треугольника с вершинами А(–1; 0), В(0; 2), С(2; 0), пробегаемый по ходу часовой стрелки. (Ответ: 3.)
3. Даны точки О(0; 0; 0), А(3;–6;0), В(–2; 4; 5). Вычислить криволинейный интеграл 2-го рода ∫xy2dx + yz2dy − zx2dz :
|
L |
|
|
а) по прямолинейному отрезку ОВ |
(Ответ: 91.); |
б) по дуге АВ окружности, заданной уравнениями x 2 + y 2 +z 2 =45, 2x + y = 0 (при решении перейти к параметрическому виду уравнений,
|
полагая x = t). |
−271 |
1 |
||||
|
(Ответ: |
.) |
|||||
|
4 |
||||||
|
34 |

2.3.Физические и геометрические приложения криволинейных интегралов
Пусть L – материальная плоская кривая с линейной плотностью γ(x; y).
Тогда справедливы следующие формулы: Масса кривой: m = ∫γ(x; y)dl.
L
Статические моменты кривой относительно осей Ox и Oy:
Mx = ∫yγ(x; y)dl и My = ∫xγ(x; y)dl .
L L
Координаты центра тяжести пространственной дуги АВ :
|
x0 = |
∫ xρdl |
, y = |
∫ yρdl |
, z = |
∫ zρdl |
. |
|
AB |
AB |
AB |
||||
|
m |
0 |
m |
0 |
m |
||
Момент инерции кривой относительно начала координат:
I0 = ∫(x2 + y2 )γ(x; y)dl.
L
Моменты инерции кривой относительно осей Ox и Oy:
I x = ∫y2 γ(x; y)dl и I y = ∫x2 γ(x; y)dl .
L L
G G G
Работа переменной силы F (x; y) = P (x; y)i +Q(x; y) j при перемещении материальной точки единичной массы из точки А в точку В вдоль кривой АВ вычисляется по формуле:
A = ∫ P (x; y)dx +Q(x; y)dy.
AB
Вычисление площади S плоской фигуры, ограниченной замкнутой кривой L:
S= 1 v∫ xdy − ydx. 2 L
Примеры
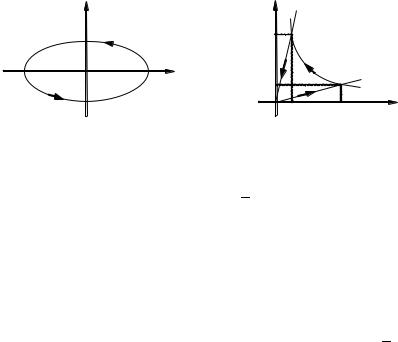
1. Найти площадь фигуры, ограниченной эллипсом x = a cos t, y = b sin t (рис. 19, а).
35
|
a |
y |
б |
y |
||||
|
b |
4 |
В |
|||||
|
–a |
0 |
a x |
1 |
А |
|||
|
– b |
0 |
1 |
4 |
x |
Рис. 19
Решение. Используем формулу S = 1 v∫ xdy − ydx. Преобразуем
2 L
криволинейный интеграл в обыкновенный с переменной t, для этого найдем дифференциалы dx = –a sin tdt, dy = b cos tdt. Тогда
|
1 |
1 |
2 π |
2 π |
||
|
S = |
v∫ xdy − ydx = |
∫ ab cos2 tdt +ab sin2 tdt = |
ab |
∫ dt = πab. |
|
|
2 |
2 |
2 |
|||
|
L |
0 |
0 |
2. Найти площадь фигуры, ограниченной линиями y = 4x, y = 1 x ,
4
xy = 4 (рис. 19, б).
Решение. Решая совместно уравнения линий, найдем точки их пересечения A(4; 1), B(1; 4). Граница искомой площади состоит из двух прямых линий и одной гиперболы (рис. 19, б). Тогда искомая площадь равна
|
S = |
1 |
∫ xdy − ydx + |
1 |
∫ xdy − ydx + |
1 |
∫ xdy − ydx = |
|||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||||
|
OA |
AB |
BO |
|||||||||||||||||||||||||
|
1 |
4 |
1 |
x |
1 |
1 |
4 |
1 |
0 |
|||||||||||||||||||
|
= |
∫ x |
− |
dx + |
∫ |
x − |
− x dx |
+ |
∫(x 4 −4x )dx = |
|||||||||||||||||||
|
2 |
4 |
2 |
x |
2 |
2 |
||||||||||||||||||||||
|
0 |
4 |
4 |
1 |
||||||||||||||||||||||||
|
1 |
4 |
1 |
dx |
0 |
x |
2 |
4 |
1 |
0 |
||||||||||||||||||
|
= |
∫ xdx −4∫ |
+2∫ xdx = |
−4 ln x |
+ x 2 |
= 4 ln 4. |
||||||||||||||||||||||
|
8 |
x |
||||||||||||||||||||||||||
|
0 |
4 |
1 |
16 |
0 |
4 |
1 |
|||||||||||||||||||||
3.Найти массу дуги АВ кривой y = lnx, где A(1; 0) и B(3; ln3), если
вкаждой ее точке линейная плотность пропорциональна квадрату абсциссы точки.
36

Решение. Используем формулу m = ∫ γ(x; y)dl . Преобразуем дан-
AB
ный криволинейный интеграл в обыкновенный с переменной x. Най-
|
дем производную y ′= |
1 |
, тогда dl = |
1 +( y‘)2 dx = |
1 + |
1 |
dx , γ = kx 2. |
|||||||||||||
|
x |
|||||||||||||||||||
|
Получаем |
x2 |
||||||||||||||||||
|
3 |
2 x2 |
+1 |
k |
3 |
2 |
1 |
2 |
k |
|||||||||||
|
m = ∫ |
γdl = k∫x |
∫(x |
|||||||||||||||||
|
dx = |
+1)2 d(x |
+1) |
= |
(10 10 |
−2 2). |
||||||||||||||
|
x |
2 |
2 |
3 |
||||||||||||||||
|
AB |
1 |
1 |
|||||||||||||||||
4. Найти массу отрезка прямой АВ: A(1; 4; 3), B(1; 0; 6), если в каждой ее точке линейная плотность равна γ = x 2 + y 2.
Решение. Составим каноническое уравнение прямой, проходя-
|
x −1 |
y −4 |
z −3 |
|||||||||||||||
|
щей через точки А и В: |
= |
= |
. Перейдем к параметри- |
||||||||||||||
|
1 −1 |
0 −4 |
6 −3 |
|||||||||||||||
|
ческому виду прямой: |
|||||||||||||||||
|
x −1 |
y −4 |
z −3 |
x =1, |
||||||||||||||
|
= |
= |
=t |
→ y = −4t +4 , |
||||||||||||||
|
0 |
−4 |
−3 |
|||||||||||||||
|
z =3t +3 . |
|||||||||||||||||
|
Найдем интервал изменения параметра t |
|||||||||||||||||
|
y = 4 t1 = 0 , |
|||||||||||||||||
|
y = 0 t2 =1. |
|||||||||||||||||
|
Элемент дуги dl = |
(xt′)2 +( yt′)2 +(zt′)2 dt = 12 +(−4)2 +32 dt =5dt . |
||||||||||||||||
|
Тогда масса отрезка |
|||||||||||||||||
|
1 |
1 |
95 |
|||||||||||||||
|
m = ∫ γdl =5∫(x 2 + y 2 ) dt =5∫(12 +(−4t +4)2 ) dt = |
. |
||||||||||||||||
|
3 |
|||||||||||||||||
|
L |
0 |
0 |
|||||||||||||||
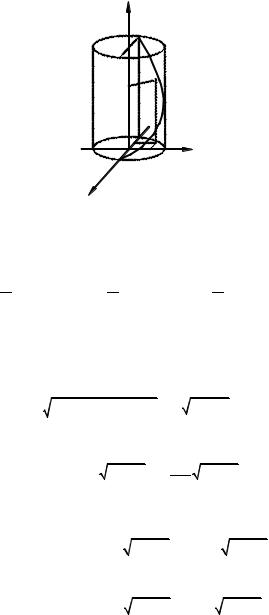
5.Найти координаты центра тяжести дуги АВ винтовой линии x = a cos t, y = a sin t , z = bt, если в каждой ее точке линейная плотность
равна аппликате этой точки, а параметр изменяется от tA = 0 до tB = π (рис. 20).
37
|
z |
||||||||||||
|
bπ |
||||||||||||
|
С● |
||||||||||||
|
–а |
0 |
а |
y |
|||||||||
|
а |
||||||||||||
|
x |
||||||||||||
|
Рис. 20 |
||||||||||||
|
Решение. Используем формулы |
||||||||||||
|
x = |
1 |
∫ |
xγdl, |
y = |
1 |
yγdl, |
z = |
1 |
zγdl. |
|||
|
c |
m |
c |
m ∫ |
c |
m ∫ |
|||||||
|
AB |
AB |
AB |
||||||||||
|
Найдем производные |
||||||||||||
|
x‘ = –asint, y‘ = acost, z‘ = b. |
||||||||||||
|
Тогда элемент дуги |
||||||||||||
|
dl = (x ′)2 +( y ′)2 +(z ′)2 dt = a2 +b2 dt |
||||||||||||
|
t |
t |
t |
||||||||||
|
так как плотность γ = bt, то масса дуги |
||||||||||||
|
m = ∫ γdl = ∫π bt a2 +b2 dt = bπ2 |
a2 +b2 . |
|||||||||||
|
AB |
0 |
2 |
||||||||||
|
Статические моменты равны |
||||||||||||
|
Syz |
= ∫ xγdl = ∫π acost bt |
a2 +b2 dt = −2ab |
a2 +b2 , |
|||||||||
|
AB |
0 |
|||||||||||
|
Sxz |
= ∫ yγdl = ∫π asint bt |
a2 +b2 dt = abπ |
a2 +b2 , |
|||||||||
|
AB |
0 |
|||||||||||
|
38 |

|
π |
b |
2 |
π |
3 |
|||||||||||||
|
S xy = ∫ z γdl = ∫bt bt a2 +b2 dt = |
a2 +b2 . |
||||||||||||||||
|
3 |
|||||||||||||||||
|
AB |
0 |
||||||||||||||||
|
Следовательно: x |
= |
Syz |
= − |
4a |
, |
y = |
Sxz |
= |
2a |
, z = |
Sxy |
= |
2bπ |
. |
|||
|
m |
π2 |
m |
π |
m |
3 |
||||||||||||
|
c |
c |
c |
6. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ, если А(хА; уА; zA) и B(хB; уB; zB).
Решение. Выберем прямоугольную систему координат так,GчтобыG направление оси Oz совпало с направлением силы тяжести F = mg (рис. 21). Тогда проекции этой силы на оси координат будут следующие: Fx = 0, Fy = 0, Fz = mg.
х
m
F =mg
В
zВ
z
Рис. 21
Работа переменной силы при перемещении точки по пространственной кривой вычисляется по следующей формуле:
A = ∫ P (x, y,z)dx +Q(x, y,z)dy +R(x, y,z)dz,
AB
где P, Q, R – проекции силы на оси координат Ох, Оу, Oz соответственно.
Получаем
zB
A = ∫ P (x, y,z)dx +Q(x, y,z)dy +R(x, y,z)dz =mg ∫ dz =mg(zB −zA ).
39

Задания для самостоятельной работы
1. Найти площадь, ограниченную астроидой x = acos3t, y = asin3t
(Ответ: 3πa2 ).
8
2. Найти площадь, ограниченную лемнискатой Бернулли (x 2 + y 2)2 = = 2a2(x2 – y2). (При расчете положить y = xtgt).
(Ответ: 2a 2).
3. В каждой точке плоскости наGматериальную точку действует сила, имеющая постоянную величину F и направление положительной оси Ох. Найти работу, совершаемую этой силой при движении точки поGдуге окружности x2 + y2 = R2, лежащей в первом четверти. (Ответ: FR ).
40
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Solving integrals/
xdy
Limits of integration:
from
to
The graph:
from
to
Enter:
{ piecewise-defined function here
The solution
You have entered
[src]
1 / | | x*1 dy | / 0
$$intlimits_{0}^{1} x 1, dy$$
Simplify
Detail solution
-
The integral of a constant is the constant times the variable of integration:
-
Add the constant of integration:
The answer is:
The answer (Indefinite)
[src]
/ | | x*1 dy = C + x*y | /
$$x,y$$
Simplify
The graph
Plot the graph f(x)
The answer
[src]
x
$$x$$
=
=
x
$$x$$
Simplify
The graph
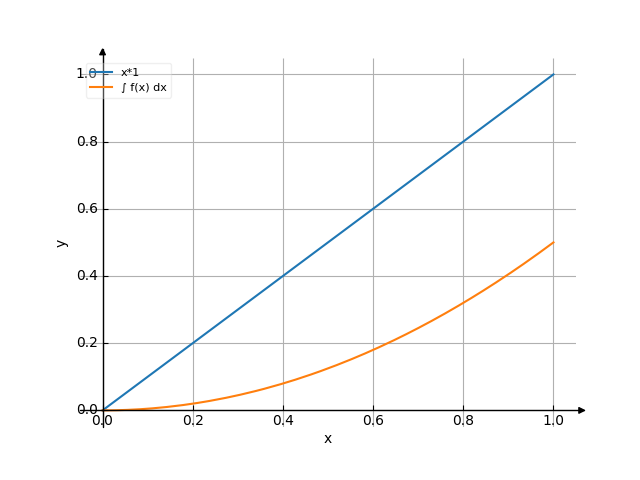
Use the examples entering the upper and lower limits of integration.
$begingroup$
I know this is a very simple question but why is this wrong?$$int(xdy+ydx)=int xdy+int ydx=xint dy+yint dx=2xy$$
I saw a similar question on Stack Exchange, but it was too complicated for me to understand. I am in 11th Grade and I have just done basic differentiation and integration for physics. Any help would be appreciated!
J.G.
114k7 gold badges74 silver badges135 bronze badges
asked Jul 7, 2020 at 6:02
$endgroup$
8
$begingroup$
Since $x,,y$ are in general not independent, you can’t treat $x$ as a constant as in $int xdy=xint dy$. Your original problem would make this clearer if you wrote $x(y)dy+y(x)dx$. In fact,$$int(xdy+ydx)=int d(xy)=xy+C.$$
answered Jul 7, 2020 at 6:05
J.G.J.G.
114k7 gold badges74 silver badges135 bronze badges
$endgroup$
3
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.

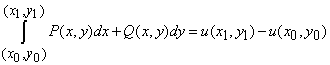
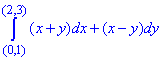
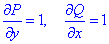
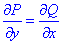
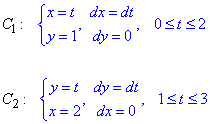
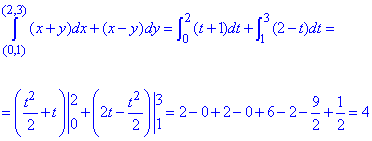
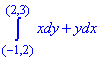
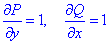
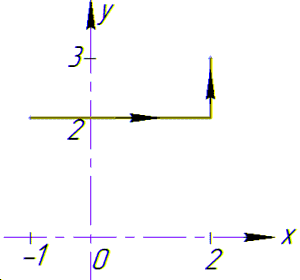
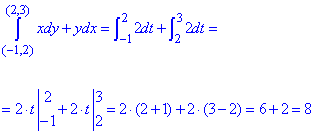
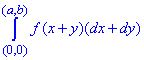
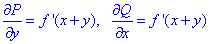
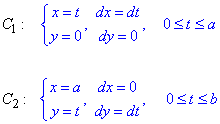
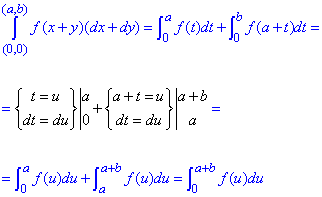
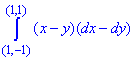
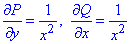
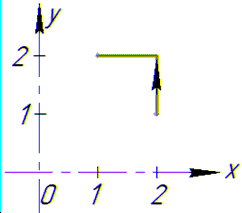
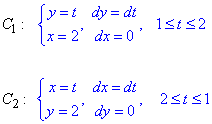
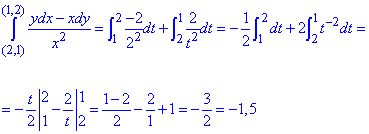
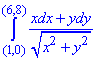
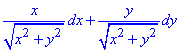
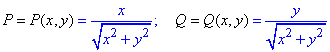
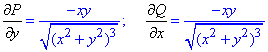
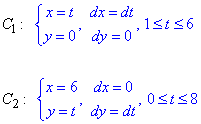
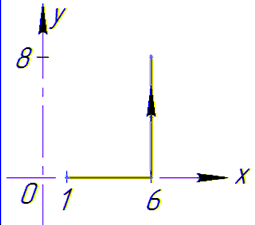
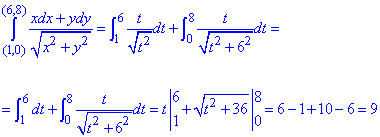


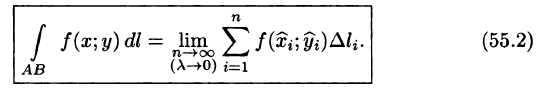
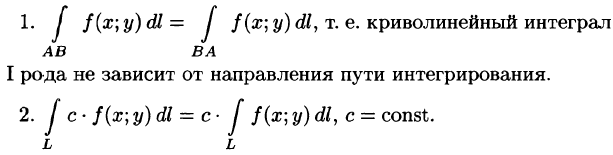
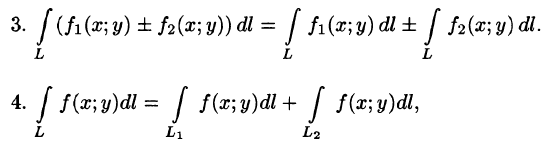
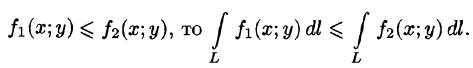
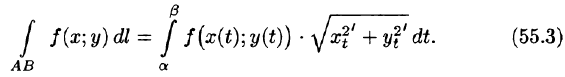
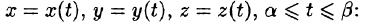
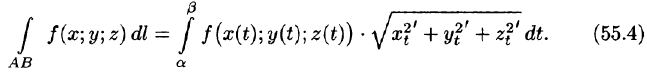
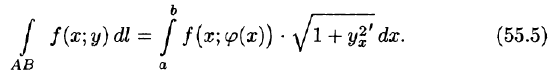
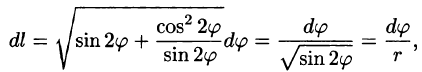
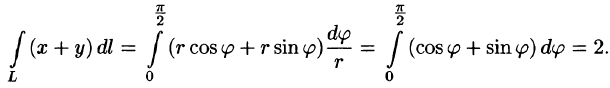
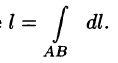
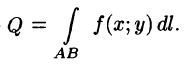
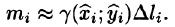
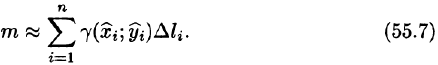
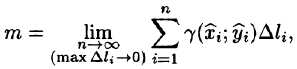
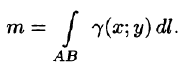
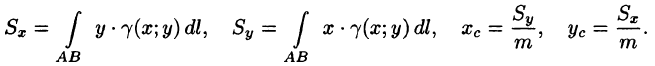
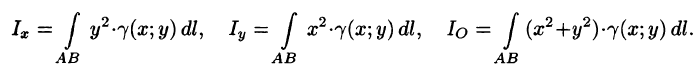
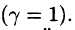
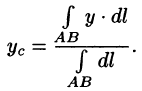
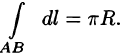
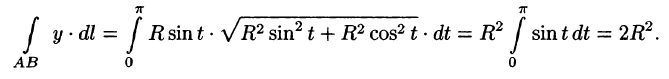
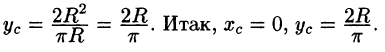
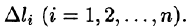
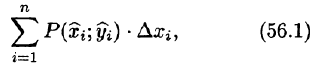
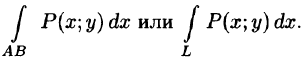
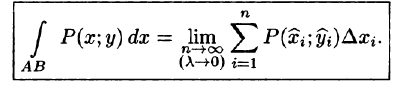
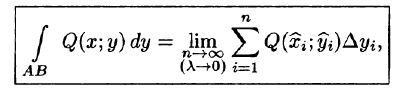
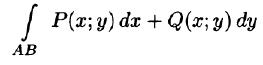
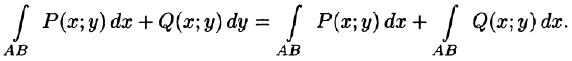
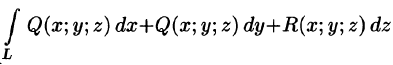
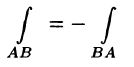
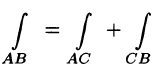
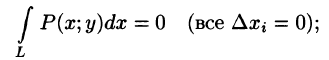
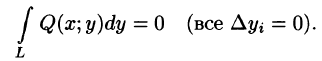
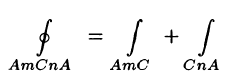
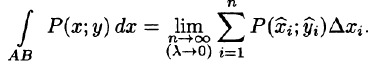
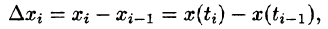
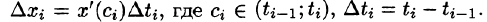
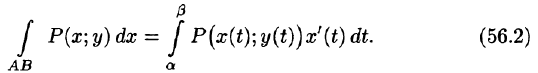
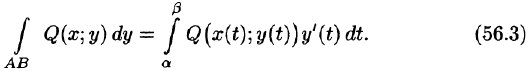
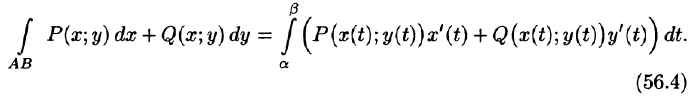
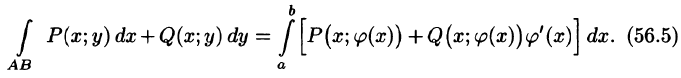
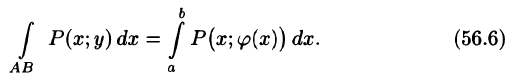
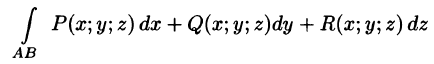
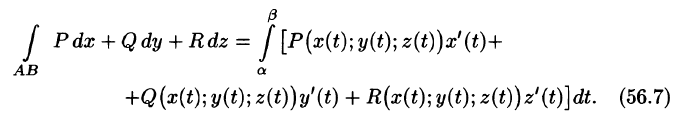
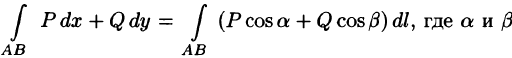
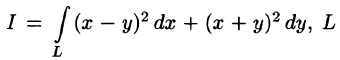
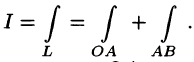
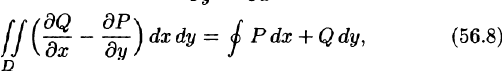
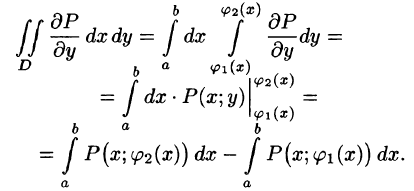
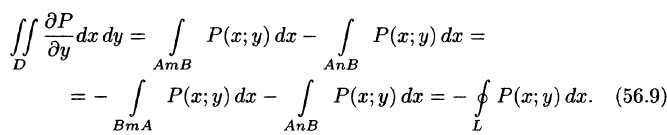
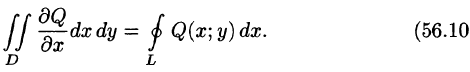
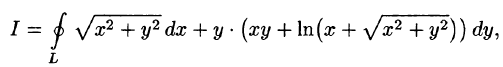
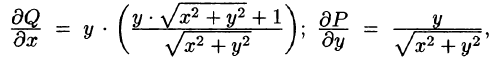
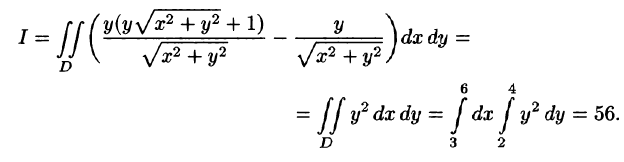
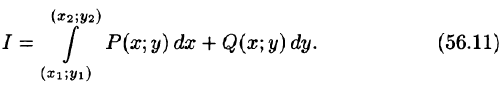
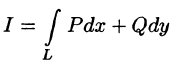

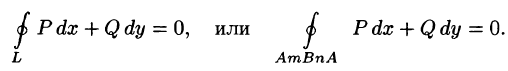
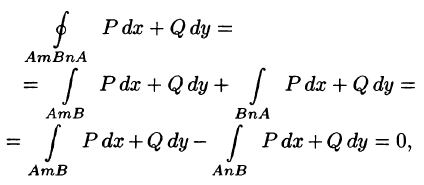
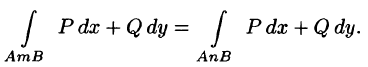
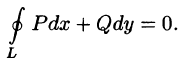
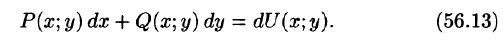
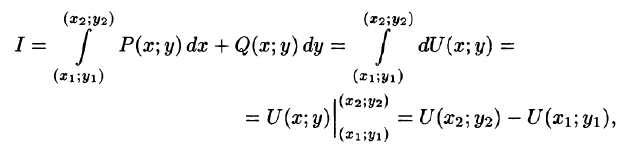
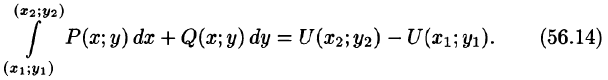
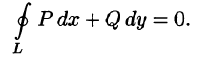
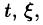 и т.д.).
и т.д.).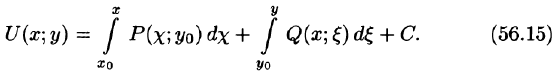

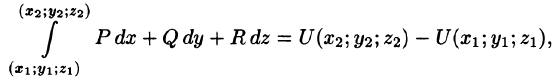
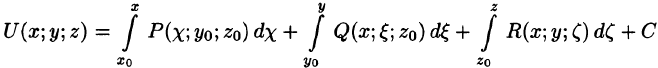
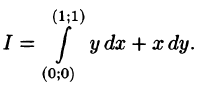
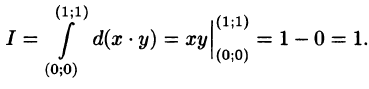
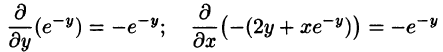
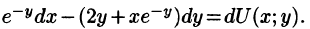
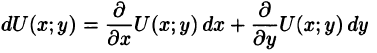
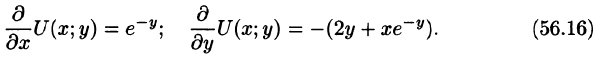
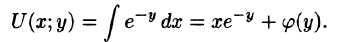
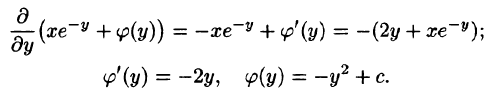
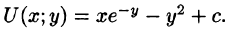
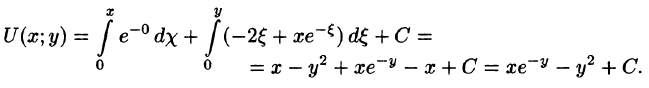
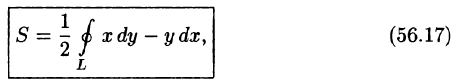
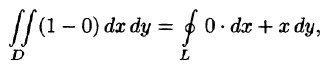


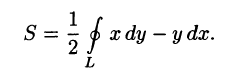
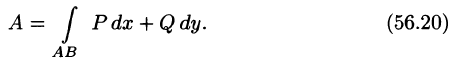
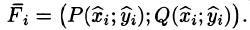
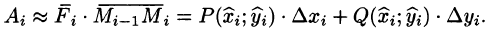
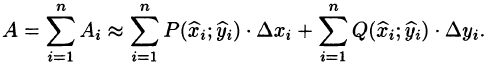
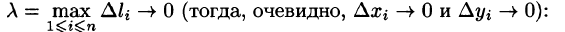
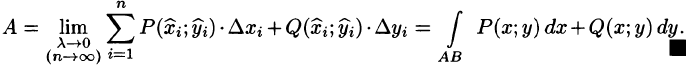
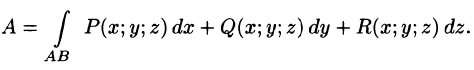
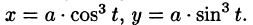
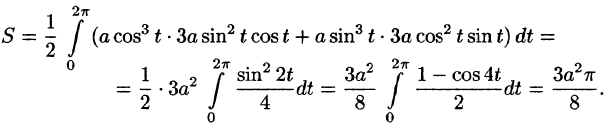
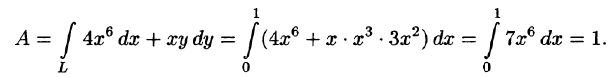
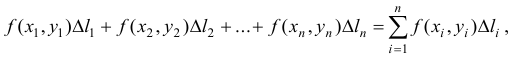
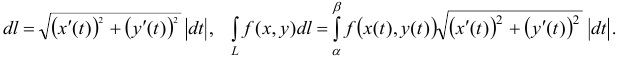
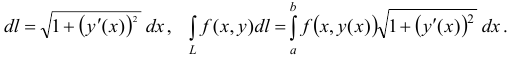
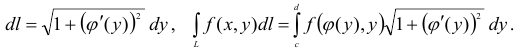
 , где
, где  — кривая
— кривая 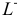 — кривая
— кривая 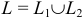 , то
, то 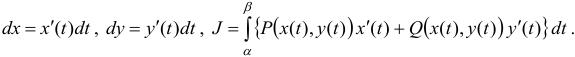
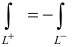 .
.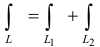 .
.