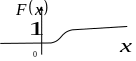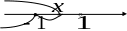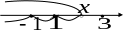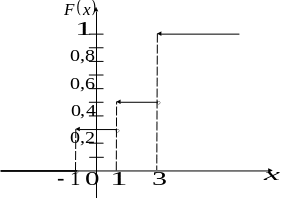Как найти интегральную функцию распределения случайной величины - Исправление недочетов и поиск решений вместе с Examum.ru

Функция распределения случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Пусть

– действительное число. Вероятность события,
состоящего в том, что

примет значение, меньшее

, то есть вероятность
события

обозначим через

. Разумеется, если

изменяется, то, вообще говоря, изменяется и

, то есть

– функция от

Функцией распределения называют функцию

, определяющую вероятность
того, что случайная величина

в результате испытания примет значение,
меньшее

, то есть:

Геометрически
это равенство можно истолковать так:

есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки

Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».

Функцию
распределения дискретной случайной величины

можно представить следующим соотношением:

Это
соотношение можно переписать в развернутом виде:

Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции

равна 1.

Свойства функции распределения

Свойство 1.

Значения
функции распределения принадлежат отрезку

Свойство 2.

– неубывающая функция, то есть:

,
если

Свойство 3.

Если возможные значения случайной величины
принадлежат интервалу

,
то:

при

;

при

Свойство 4.

Справедливо равенство:

Свойство 5.

Вероятность того, что непрерывная случайная
величина

примет одно определенное значение, равна нулю.

Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.

Заметим, что было бы неправильным думать, что
равенство нулю вероятности

означает, что событие

невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным

Свойство 6.

Если возможные значения непрерывной случайной величины
расположены на всей оси

,
то справедливы следующие предельные соотношения:

Свойство 7.

Функция распределения непрерывная слева, то есть:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Математическое ожидание
Дисперсия и среднее квадратическое отклонение

Примеры решения задач

Пример 1

Дан ряд
распределения случайной величины

	1	2	6	8
	0,2	0,3	0,1	0,4

Найти и изобразить ее функцию распределения.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Будем задавать различные значения

и находить для них

1. Если

,
то, очевидно,

в том числе и при

2. Пусть

(например

)

Очевидно, что и

3. Пусть

(например

);

Очевидно, что и

4. Пусть

Очевидно, что и

5. Пусть

Итак:

График функции распределения

Пример 2

Случайная
величина

задана функцией распределения:

Найти
вероятность того, что в результате испытания

примет значение:

а) меньше
0,2;

б) меньше
трех;

в) не
меньше трех;

г) не
меньше пяти.

Решение

а) Так
как при

функция

, то

то есть
при

б)

в)
События

противоположны, поэтому

Отсюда:

г) сумма
вероятностей противоположных событий равна единице, поэтому

Отсюда, в
силу того что при

функция

, получим:

Пример 3

Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики функций f(x) и F(x);

4)
вычислить математическое ожидание и дисперсию X;

5)
определить вероятность того, что X примет значение из
интервала (a,b).

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем отметить,
что:

Остается
найти выражение для

, когда х принадлежит интервалу

Получаем:

3) Построим графики функций:

График плотности распределения

График функции распределения

4) Вычислим
математическое ожидание:

В нашем случае:

Вычислим дисперсию:

Искомая дисперсия:

5) Вероятность того, что

примет значение из интервала

Задачи контрольных и самостоятельных работ

Задача 1

Закон
распределения случайной величины X задан таблицей.

Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.

F(1)=

M[X]=

D[X]=

Задача 2

Случайная
величины X задана функцией распределения

Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)

Задача 3

Дискретная
случайная величина X задана рядом распределения. Найти:

1)
функцию распределения F(x) и ее график;

2)
математическое ожидание M(X);

3)
дисперсию D(X).

	-5	5	25	45	65
	0.2	0.15	0.3	0.25	0.1

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

В задаче
дискретная случайная величина задана рядом распределения.

Найти

; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)

Задача 5

В задаче
непрерывная случайная величина X задана функцией
распределения F(x).

Найти a; f(x); M(X); D(X); P(X<0.2)

Начертить
графики функций f(x);F(x).

Задача 6

Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна

(

). Найти вероятность безотказной
работы устройства за время x больше либо равно T.

Задача 7

Функция
распределения непрерывной случайной величины задана выражением:

Найдите:

1)
параметр a;

2)
плотность вероятностей;

4) P(0<x<1)

Постройте
графики интегральной и дифференциальной функции распределения.

Задача 8

Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).

Задача 9

Дана
функция распределения F(х) случайной величины Х.

Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).

Задача 10

НСВ X имеет
плотность вероятности (закон Коши)

Найти:

а)
постоянную C=const;

б)
функцию распределения F(x);

в)
вероятность попадания в интервал -1<x<1

г)
построить графики f(x), F(x).

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Аналитически закон
распределения случайной величины можно
задать с помощью ее функции распределения.
Отметим, что с помощью функции распределения
или интегральной функции распределения
можно задать как дискретную, так и
непрерывную случайную величину.

Определение.
Функцией распределения
или интегральной
функцией
распределения
вероятностей
называется вероятность того, что
случайная величина

примет значение меньшее, чем произвольное
действительное число

,
т.е.

Свойства интегральной функции распределения

Свойство
1.
Областью определения функции

является все множество действительных
чисел

Доказательство.
Свойство
следует из определения интегральной
функции распределения.

Свойство
2.
Областью
изменения функции

является промежуток от нуля до единицы

Доказательство.
Так как по определению интегральная
функция – это вероятность события

,
то по свойствам вероятности

Свойство
3.
Предел
интегральной функции при

равен 1, а при

равен 0

Доказательство.
Из определения интегральной функции
распределения следует, что равенство

равносильно

.
Поэтому

Так
как событие

,
состоит в том, что случайная величина

в результате исхода испытания примет
какое-то действительное число, является
событием достоверным.

Найдем

Так
как

– это символ, меньше которого не может
быть никакое действительное число, то
событие

,
состоящее в том, что случайная величина
примет в результате исхода испытаний
значение меньшее

,
является событием невозможным.

Свойство
4.
Интегральная
функция распределения является
неубывающей функцией.

Доказательство.
Выберем два
действительных произвольных числа

так, чтобы

.

Тогда
событие

можно представить в виде суммы двух
несовместимых событий

Применив теорему
сложения для несовместных событий,
находим

или с учетом
определения интегральной функции
распределения имеем

. (1)

Так
как

,
то из равенства (1) получаем равенство

Таким
образом, доказано, что для любых значений

для которых выполняется неравенство

,
выполняется неравенство

следовательно,
функция

неубывающая на всей числовой прямой.

Свойство
5. Вероятность
того, что случайная величина примет
значение из промежутка

определяется по формуле

, (2)

т.е.
вероятность того, что случайная величина
примет значение из промежутка

,
равна приращению интегральной функции
распределения на этом промежутке.

Доказательство.
Формула (2) следует из формулы (1).

Прежде,
чем сформулировать остальные свойства
интегральной функции распределения,
уточним определение случайной величины.

Определение.
Случайная
величина
называется непрерывной,
если ее интегральная функция распределения
непрерывно дифференцируема.

Рассмотрим
теперь свойства интегральной функции
распределения, которые справедливы
лишь для непрерывных случайных величин.

Свойство
6. Если
случайная величина

непрерывна, то вероятность того, что
она примет любое отдельное возможное
значение

равна нулю

Доказательство.
По свойству 5 вероятность того, что
случайная величина

принимает значение из некоторого
промежутка

,
определяется по формуле

(3)

В
равенстве (3) перейдем к пределу при

,
получим

(4)

Так
как при

,
с одной стороны, получаем

, (4)

а,
с другой стороны, из непрерывности
случайной величины

следует непрерывность интегральной
функции распределения

,
а поэтому бесконечно малому приращению
аргумента

соответствует бесконечно малое приращение
функции

(6)

Подставляя найденные
значения пределов (5) и (6) в равенство
(4), получаем

Свойство
7. Если
случайная величина

непрерывна, то имеют место равенства

Доказательство.
Докажем,
например, первое равенство

Так
как событие

можно представить в виде суммы двух
несовместимых событий

то, применив теорему
сложения для двух несовместных событий,
находим

Остальные
равенства доказываются аналогично.

Р
ассмотрим
графики интегральной функции распределения.

а)
Если значения непрерывной случайной
величины заполняют бесконечный
промежуток

,
то ее график имеет вид изображенный
на рисунке 1.

б)
Если все значения непрерывной случайной
величины лежат на промежутке

,
то

при

,
т.к. значения случайной величины,
меньшее

невозможны,

при

,
т.к. событие

при

.
Следовательно, график интегральной
функции в этом случае имеет вид,
изображенный на рисунке 2.

в) График
интегральной функции распределения
для дискретной случайной величины,
заданной таблицей вида

			…
			…

имеет
ступенчатый вид. В точках возможных
значений

интегральная функция распределения
терпит разрыв первого рода, причем в
каждой из этих точек она непрерывна
слева и имеет разрыв справа. Величина
скачка равна вероятности соответствующего
значения случайной величины.

Пример
1.
Дискретная случайная величина

задана таблицей

	-1	1	3
	0,3	3	0,5

Найти интегральную
функцию распределения вероятностей и
построить ее график.

Решение.
Отметим
на числовой прямой возможность значения
случайной величины .

При построении
интегральной функции распределения
рассмотрим случаи:

	, в этом случае , т.к. на интервале не содержится возможных значений ;
	2) , в этом случае
	3) , в этом случае .
	4) , в этом случае .

Таким образом,
интегральную функцию распределения
можно записать в виде

П
остроим
график функции

График
функции имеет ступенчатый вид. В точках
возможных значений

функция имеет разрывы первого рода,
причем в каждой из этих точек функция
непрерывна слева и имеет разрыв справа.
Величина скачка в каждой точке разрыва
равна вероятности соответствующего
значения случайной величины.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Формулы онлайн: Случайные величины

В данном разделе вы найдете формулы по теории вероятностей в онлайн-варианте (в формате для скачивания — см. на странице Таблицы и формулы по теории вероятностей).

Каталог формул по теории вероятности онлайн

Случайные величины. Способы задания

Спасибо за ваши закладки и рекомендации

Ряд распределения дискретной случайной величины

Табличный вид:

$$
begin{array}{|c|c|}
hline
X_i & x_1 & x_2 & dots & x_n \
hline
p_i & p_1 & p_2 & dots & p_n \
hline
end{array}
$$

Сумма вероятностей всегда равна 1 (условие нормировки):

$$sum_{i=1}^{n} p_i=1$$

Примеры решенных задач с табличным законом распределения ДСВ

Функция распределения (интегральная функция распределения)

Функция распределения случайной величины $X$ определяется по формуле $F(x)=P(Xlt x)$. Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения $f(x)$, то функция распределения выражается как интеграл от плотности:

$$
F(x)=int_{-infty}^x f(t), dt.
$$

Плотность распределения (дифференциальная функция распределения)

Плотность распределения случайной величины $X$ определяется по формуле $f(x)=F'(x)$. Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки (площадь под кривой вероятности равна 1):

$$
int_{-infty}^{+infty} f(x), dx=1.
$$

Примеры решенных задач о НСВ

Вероятность попадания случайной величины в заданный интервал

Может быть вычислена двумя способами:

1) через функцию распределения

$$P(alpha lt X lt beta) = F(beta)-F(alpha).$$

2) через плотность распределения

$$P(alpha lt X lt beta) = int_{alpha}^{beta} f(x), dx.$$

Случайные величины. Числовые характеристики

Математическое ожидание случайной величины

1) Для дискретной случайной величины $X$, заданной рядом распределения:

$$M(X) = sum_{i=1}^{n} x_i cdot p_i.$$

2) Для непрерывной случайной величины $X$, заданной плотностью распределения:

$$M(X)=int_{-infty}^{+infty} f(x)cdot x, dx.$$

Статья и калькулятор о математическом ожидании

Выполним теорию вероятностей на отлично

Дисперсия случайной величины

По определению дисперсия – это второй центральный момент:

$$ D(X) =Mleft[ left(X-M(X)right)^2 right] =M(X^2)-left(M(X)right)^2.$$

1) Для дискретной случайной величины $X$:

$$ D(X)= sum_{i=1}^{n} x_i^2 cdot p_i — left(M(X)right)^2.$$

2) Для непрерывной случайной величины $X$:

$$M(X)=int_{-infty}^{+infty} f(x)cdot x^2, dx — left(M(X)right)^2.$$

Статья и калькулятор о дисперсии

Среднее квадратическое отклонение случайной величины

$$sigma (X) = sqrt{D(X)}.$$

Статья и калькулятор о СКО

Коэффициент вариации случайной величины

$$V(X) = frac{sigma(X)}{M(X)}.$$

Начальный момент r–го порядка случайной величины

определяется по формуле:

$$nu_r = M(X^r)$$

В частности, первый начальный момент – это математическое ожидание: $nu_1=M(X^1)=M(X).$

Центральный момент r – го порядка случайной величины

определяется по формуле:

$$mu_r = Mleft[ left(X-M(X)right)^r right]$$

В частности, второй центральный момент – это дисперсия:

$$mu_2 = Mleft[ left(X-M(X)right)^2 right] = D(X).$$

Асимметрия

$$
A_s = frac{mu_3}{sigma^3}.
$$

Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого (правая часть кривой более пологая), и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.

Эксцесс

$$
E = frac{mu_4}{sigma^4}-3.
$$

Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.

Спасибо за ваши закладки и рекомендации

Решенные задачи по теории вероятностей

Нужна готовая задача по терверу? Найдите на сайте-решебнике:

Подробно решим теорию вероятностей. Закажите сейчас!

Полезные ссылки

Онлайн калькуляторы
Формулы комбинаторики

Статьи по теории вероятностей
Более 200 готовых примеров

Источник

Интегральная функция распределения случайной величины и её свойства. Функция распределения дискретной случайно величины

Задание случайной величины её законом распределения не обладает общностью, так как его нельзя использовать, например, для непрерывных случайных величин. Кроме того, даже для дискретных случайных величин закон распределения не удовлетворяет практическим требованиям. Например, с точки зрения практики событие, состоящие в том, что некоторый прибор проработает, например, 1000 часов, не представляет интереса. Более важным является событие Х < 1000 или событие Х > 1000. Такое событие имеет вероятность, отличную от нуля, и при изменении Х вероятность события будет изменяться.

Следовательно, вероятность является функцией от х, которая и принимается в качестве интегральной функции распределения и которая является универсальной, пригодной для описания как непрерывных, так и дискретных случайных величин.

Определение 4. Интегральной функцией распределения вероятностей случайной величины Х называется функция F(х), соответствующая вероятности того, что в результате опыта случайная величина Х примет значение меньшее х – некоторого значения случайной величины.

Таким образом, по определению

F(x) = Р(X < х), т.е. (3.1)

На числовой оси Ох случайная величина х сщдержится в интервале (– ∞, х) (рисунок 3.4):

Рис. 3.4

Пример 9. Пусть для случайной величины X задан ряд распределения:

Х	х =1	х = 2	х = 3	х = 4	х = 5	х = 6
P	p= 0,4	p= 0,24	p=0,19	P=0,1	p=0,04	p= 0,03

Записать интегральную функцию распределения и построить ее график.

Решение. F(x) = P(X < x) = 0, х ≤ х=1; F (x) = P(X < x) = P(X = x)= = p = 0,4; 1 < х ≤ 2; F₂ (x) = P(X < x) = P (X = x) + P (X = x) = 0,4 + 0,24 = = 0,64; 2 < х ≤ 3.

Событие Х < х может быть осуществлено, когда Х принимает значения х₁ с вероятностью p= 0,4 или значение х с вероятностью p. В силу несовместности этих событии получается, что Р(Х < х) = p + p. Далее имеем

F(x) = P(X < x) = Р(X = x) + P(X = x) + P(X = x) = 0,4 + 0,24 + 0,19 = 0,83, 3< х ≤4;

F(x) = P(X < x) = 0,4 + 0,24+0,19 + 0,1 = 0,93, х< х ≤ х, 4 < х ≤ 5;

F(x) = P(X < x) = 0,4+0,24+0,19+0,1+0,04 = 0,97, х< х ≤ х, 5 < х ≤ 6;

F(x) = P(X>x) = 0,4 + 0,24 + 0,19 + 0,1 + 0,04 + 0,03 = 1, х > 6.

Рис. 3.5

Таким образом, функция F(х) здесь составная (ступенчатая) и она претерпевает разрыв 1-го рода в точках х_kи скачки этой функций равны p_k = = Р(Х = х_k) (k = 1, 2, 3, 4, 5, 6) (рисунок 3.5). Заметим, что функция распределе-ния для непрерывной случайной величины имеет форму плавной кривой (рисунок 3.6).

Источник