Как найти интенсивность естественного света

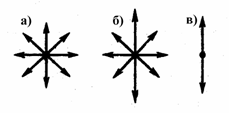
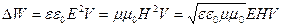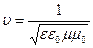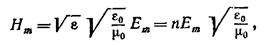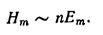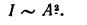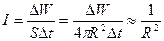Естественный
свет — оптическое излучение с быстро и
беспорядочно изменяющимися направлениями
напряжённости эл.-магн. поля, причём все
направления колебаний, перпендикулярные
к световым лучам, равновероятны.

Поляризованный
– свет, в котором направления колебаний
светового вектора упорядочены каким-либо
образом.

Частично-поляризованный
свет – если в результате каких-либо
внешних воздействий появляется
преимущественное направление колебаний
вектора Е.

Плоскополяризованный
– если колебания вектора Е происходят
только в одной плоскости.

Интенсивность
света после поляризатора определяется
законом Малюса. I=I₀*cos²α

I₀-интенсивность
до поляризатора; I
– интенсивность после поляризатора; α
– угол между вектором Е и плоскостью
поляризации.

Пусть
на 2 поляризатора падает естественный
свет.

I₁=1/2*I_ест

I₂=1/2*I_ест*cos²α=I₁*cos²α

Степень
поляризации луча Δ=(Imax-Imin)/(Imax*Imin)

22. Поляризация света при отражении и преломлении. Закон Брюстера.

Поляризованный
свет можно получить, используя отражение
или преломление света от диэлектрических
изотропных сред. Если угол падения света
на границу раздела двух диэлектриков
отличен от нуля, отраженный и преломленный
лучи оказываются частично поляризованными.
Степень поляризации того и другого луча
зависит от угла падения луча. У каждой
пары прозрачных сред существует такой
угол падения, при котором отраженный
свет становится полностью
плоскополяризованным, а преломленный
луч остается частично поляризованным,
но степень его поляризации при этом
угле максимальна. Этот угол называется
углом Бpюстеpа. Угол Брюстера определяется
из условия: tgφ_Бр=n₂₁=n₂/n₁

23. Естественный и поляризованный свет. Вращение плоскости поляризации.

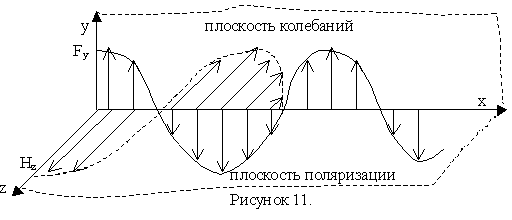
Плоскость,
в которой совершает колебания вектор
Е, называется плоскостью колебаний, а
вектор Н – плоскостью поляризации.

Если
колебания вектора Е упорядочены
каким-либо образом, свет называется
поляризованным. Если в одной плоскости
– плоско-поляризованным.

Если
колебания Е в одной плоскости преобладают
над другими – свет частично поляризованный.

В
естественном свете вектор Е не испытывает
асимметрии относительно направления
распространения луча.

Плоско
поляризованный свет получают с помощью
приборов – поляризаторов.

Интенсивность
света поле поляризаторов определяют
по закону Малюса: I=I_oCOS²α
, где I_o
– интенсивность
до поляризатора, I
– после, α – угол между Е и плоскостью
поляризации.

Степенью
поляризации луча называется величина,
равная: Δ=(I_max-I_min)/(I_max+I_min)

Для
естественного света Δ=0, для плоско
поляризованного Δ=1, для частично
поляризованного 0<Δ<1.

Плоско
поляризованный свет получается при
отражении от границы раздела двух сред,
если угол падения равен углу Брюстера:
tgα_бр=n₂₁=n₂/n₁

При
прохождении света через оптически
активное вещество вектор Е поворачивается.
Данное явление называется вращением
плоскости поляризации.

Угол
поворота плоскости поляризации для
кристаллов и чистых жидкостей: ϕ=αd;
для растворов: ϕ=[α]cd
, где d — расстояние, пройденное светом
в оптически активном веществе, a ([a]) —
так называемое удельное вращение,
численно равное углу поворота плоскости
поляризации света слоем оптически
активного вещества единичной толщины
(единичной концентрации — для растворов),
С — массовая концентрация оптически
активного вещества в растворе, кг/м3.
Удельное вращение зависит от природы
вещества, температуры и длины волны
света в вакууме.

Явление
вращения плоскости поляризации можно
объяснить с помощью двух предположений
Френеля:

1. Любая
   плоско поляризованная волна может быть
   представлена как 2 волны, поляризованные
   по кругу с правым и левым вращением

2. Скорости
   вращения в оптически активном веществе
   разные.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  12.04.2015451.58 Кб100VS.doc

• #
• #
• #
• #
• #
• #

Задача №5.147. Задачник 
Трофимова, Павлова.

Поляризованным называется
свет, в котором  направления колебаний скветового вектора  упорядочены каким-то
образом.

Интенсивность – это
среднее значение модуля потока энергии.

Анализатор – это устройсво
для определения характера и степени поляризации интересующего нас света, можно
использовать поляризатор.

Поляризатор – это
устройство для получения поляризованного света из естественного.

Плоскость поляризации, плоскость
колебаний – это плоскость, в которой колеблется световой вектор E в плоскополяризованной волне.

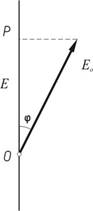
Закон Малюса – при падении
на поляризатор линейно-поляризованного света, вектор E_o которого составляет угол φ с
плоскостью пропускания P. Поляризатор пропускает
только ту состовляющую вектора E_o, которая параллельна плоскости прорускания Р,
т.е. φ. Интенсивность пропорциональна квадрату
модуля светового вектора, поэтому интенсивность прошедшего света φ.

Решение:

Интенсивность после прохождения
поляризатора для естественного света определяется по формуле

(1).

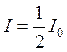
По  закону Малюса интенсивность
после поляризатора определяется как φ для естественного
света значение φ равновероятно. Следовательно доля света, прошедшего
поляризатор будет равна среднему значению φ = ½.

Так как поляризатор ортражает и
поглащает η света, т. е. интенсивность падающего света уменьшается на 2 η,
получим

 (2)

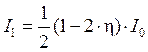
По закону Малюса при падении на
поляризатор поляризованного света интенсивность после поляризации равна

 (3)

В качстве анализатора используем
поляризатор повернутый на угол α. Для анализатора  (4) подставив сюда выражение для I₁ получим

 (5)

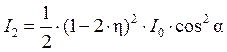
Отсюда выразим

 (6)

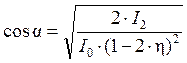
из условия  (7)

 (8)

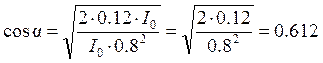
 (9)

Ответ:

Интенсивность света амплитуда светового вектора

§1 Естественный и поляризованный свет

Испускание кванта света происходит в результате перехода электрона из возбужденного состояния в основное. Электромагнитная волна, испускаемая в результате этого перехода, является поперечной, то есть вектора и взаимно перпендикулярны и перпендикулярны направлению распространения. Колебания вектора происходят в одной плоскости. Свет, в котором вектор колеблется только в одном направлении, называется плоско поляризованным светом (или электромагнитной волной). Поляризованным называется свет, в котором направления колебания вектора упорядочены каким-либо образом.

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают световые волна независимо друг от друга, поэтому световая волна, излучаемая телом в целом, харак­теризуется всевозможными равновероятными колебаниями светового вектора . Свет со всевозможными равновероятными ориентациями вектора называется естественным. Свет, в котором имеется преимущественное направление колебаний вектора и незначительная амплитуда колебаний вектора в других направлениях, называется частично поляризованным. В плоско поляризованном свете плоскость, в которой колеблется вектор , называется плоскостью поляризации, плоскость, в которой колеблется вектор , называется плоскостью колебаний.

Вектор называют световым вектором потому, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества.

Различает также эллиптически поляризованный свет: при распростра­нении электрически поляризованного света вектор описывает эллипс, и циркулярно поляризованный свет (частный случай эллиптически поляризованного света) — вектор описывает окружность (сравните со сложением взаимно перпендикулярных колебаний: возможны: прямая линия, эллипс и окружность).

Степенью поляризации называется величина

где I_max и I_min – максимальная и минимальная компоненты интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора (то есть Е_х и Е_у – составляющие). Для плоско поляризованного света Е_у = Е, Е_х = 0, следовательно, Р = 1. Для естественного света Е_у = Е_х = Е и Р = 0. Для частично поляризованного света Е_у = Е, Е_х = (0. 1)Еу, следовательно, 0

Если вектор в эллиптически поляризованном свете вращается при распространении света по часовой стрелке, то поляризация называется правой, против — левой. В эллиптически поляризованном свете колебания полностью упорядочены. К эллиптически поляризованному свету понятие степени поляризации не применимо, так что Р=1 всегда.

§2 Анализ поляризованного света при отражении и преломлении.

Закон Брюстера. Закон Малюса

Наиболее просто поляризационный свет можно получить из естественного света при отражении световой волны от границы раздела двух диэлектриков.

Если естественный свет падает на границу раздела двух диэлек­триков (например, воздух-стекло), то часть его отражается, а часть преломляется и распространяется во второй среде.

При угле падения, равном углу Брюстера і_Бр: 1. отраженный от границы раздела двух диэлектриков луч будет полностью поляризован в плоскости, перпендикулярной плоскости падения; 2. степень поляризации преломленного луча достигает максимального значения меньшего единицы; 3. преломленный луч будет поляризован частично в плоскости падения; 4. угол между отраженным и преломленным лучами будет равен 90°; 4. тангенс угла Брюстера равен относительному показателю преломления

n ₁₂ — показатель преломления второй среды относительно первой. Угол падения (отражения) — угол между падающим (отраженным) лучом и нормалью к поверхности. Плоскость падения — плоскость, проходящая через падающий луч и нормаль к поверхности.

Степень поляризации преломленного света может быть значительно повышена многократным преломлением при условии падения света на границу раздела под углом Брюстера. Если для стекла ( n = 1,53) степень поляризации преломленного луча составляет ≈15 %, то после преломления на 8-10 наложенных друг на друга стеклянных пластинках, вышедший свет будет практически полностью поляризован — стопа Столетова.

Поляризованный свет можно получить из естественного с помощью поляризаторов — анизотропных кристаллов, пропускающих свет только в одном направлении (исландский шпат, кварц, турмалин).

Поляризатор, анализирующий в какой плоскости поляризован свет, называется анализатором.

Если на анализатор падает плоско поляризованный свет амплитудой Е₀ и интенсивности I ₀ ( ), плоскость поляризации которого составляет угол φ с плоскостью анализатора, то падающее электромагнитное колебание можно разложить на два колебания; с амплитудами и , параллельное и перпендикулярное плоскости анализатора.

Сквозь анализатор пройдет составляющая параллельная плоскости анализатора, то есть составляющая , а перпендикулярная составлявшая будет задержана анализатором. Тогда интенсивность прошедшего через анализатор света будет равна ( ):

— закон Малюса

Закон Малюса : Интенсивность света, прошедшего через поляризатор, прямо пропорциональна произведению интенсивности падающего плоско поляризованного света I ₀ и квадрату косинуса угла между плоскостью падающего света и плоскостью поляризатора.

Если на поляризатор падает естественный свет, то интенсивность вышедшего из поляризатора света I ₀ равна половине I _ест , и тогда из анализатора выйдет

§ 3 Двойное лучепреломление

Все кристаллы, кроме кристаллов кубической система — изотропных кристаллов, являются анизотропными, то есть свойства кристаллов зависят от направления. Явление двойного лучепреломления впервые было обнаружено Барталином в 1667 г. на кристалле исландского шпата (разновидность СаСО₃). Явление двойного лучепреломления заклю­чается в следующем: луч света, падающий на анизотропный кристалл, разделяется в нем на два луча: обыкновенный и необыкновенный, распространяющиеся с разными скоростями в различных направлениях.

Анизотропные кристаллы подразделяются на одноосные и двуосные.

У одноосных кристаллов имеются одно направление, называемое оптической осью, при распространении вдоль которого не происходит разделения на обыкновенный и необыкновенный лучи. Любая прямая параллельная направлению оптической оси будет также являться оптической осью. Любая плоскость, проходящая через оптическую ось и падающий луч, называется главным сечением или главной плоскостью кристаллам.

Отличия между обыкновенными и необыкновенными лучами:

1. обыкновенный луч подчиняется законам преломления необыкновенный — нет;
2. обыкновенный луч поляризован перпендикулярно главной плоскости, плоскость поляризации необыкновенного луча перпендикулярна плоскости поляризованного обыкновенного луча;
3. кроме оптической оси обыкновенные и необыкновенные лучи распространяются в разных направлениях. Показатель преломления n₀ обыкновенного луча постоянен во всех направлениях, следовательно, фазовая скорость обыкновенного луча постоянна во всех направлениях. Показатель преломления n_е необыкновенного луча ( U_ф.е. ) зависит от направления.

Различие скоростей U _о и U _е для всех направлений, кроме направ­ления оптической оси, обуславливает явление двойного лучепреломления в одноосных кристаллах. У двуосных кристаллов имеется два направления, вдоль которых не происходит двойного лучепреломления.

Понятие обыкновенного и необыкновенного лучей имеет место пока эти лучи распространяются в кристалле, при выходе из кристалла эти понятия теряют смысл, то есть лучи отличаются только плоскостями поляризаций.

Природа двулучепреломления связана с тем, что обыкновенные и необыкновенные лучи имеют разные скорости, а так как , то для обыкновенного и необыкновенного лучей будут разные показатели преломления n ₀ и n _е , а так как то можно сказать, что перво­причиной двойного лучепреломления является анизотропия диэлектрич­еской проницаемости кристалла. Кристаллы, у которых V _е V ₀ ( n _е > n ₀ ) называются положительными, а у которых V _е > V ₀ ( n _е n ₀ )называются отрицательными.

Интенсивность света, связь интенсивности света с амплитудой светового вектора.

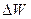
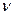
Интенсивностью света называют электромагнитную энергию , проходящую в единицу времени через единицу площади поверхности, перпендикулярной направлению распространения света. Частоты видимых световых волн лежат в пределах

= (,39 4-0,75)-10 15 Гц.

Ни глаз, ни какой-либо иной приемник световой энергии не может уследить за столь частыми изменениями потока энергии, вследствие чего они регистрируют усредненный по времени поток. Поэтому правильнее определить интенсивность как модуль среднего по времени значения плотности потока энергии, переносимой световой волной. Плотность потока электромагнитной энергии определяется выражением

(4.4)

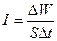
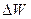
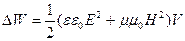
Поскольку световая волна- это электромагнитная волна, то складывается из энергии магнитного и электрического полей

(4.5)

где V- объем, занимаемый волновым полем.

Из уравнений Максвелла следует, что векторы напряженности электрического и магнитного полей в электромагнитной волне связаны соотношением

(4.6)

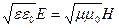
Поэтому выражение (4.5) можно записать следующим образом

Из уравнений Максвелла скорость распространения электромагнитных волн

Выделим некоторый объем волнового поля в форме параллелепипеда (рис.4.5)

Рис.4.5

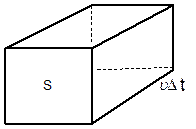
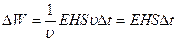
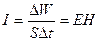
Тогда , по определению интенсивности

, используя выражение (4,6) и полагая, что в прозрачной среде m=1 получим

где n— показатель преломления среды, в которой распространяется волна. Таким образом, напряженность магнитного поля Н пропорционально напряженности электрического поля Е и n:

Тогда интенсивность волны будет определяться выражением

(4.7)

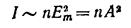
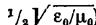
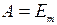
(коэффициент пропорциональности равен )- Следовательно, интенсивность света пропорциональна показателю преломления среды и квадрату амплитуды вектора напряженности электрического поля световой волны. Заметим, что при рассмотрении распространения света в однородной среде можно считать, что интенсивность пропорциональна квадрату амплитуды вектора напряженности электрического поля ( ) световой волны:

Однако в случае прохождения света через границу раздела сред выражение для интенсивности, не учитывающее множитель n, приводит к не сохранению светового потока.

Рассмотрим сферическую световую волну. Площадь сферического фронта волны 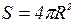, где R- радиус фронта волны. Согласно уравнению (4,4) находим интенсивность

Эти выражения показывают, что амплитуда сферической волны уменьшается пропорционально расстоянию от источника световых волн. Если R достаточно велико, т.е. источник находится очень далеко от области наблюдения, то фронт волны представляется частью сферической поверхности очень большого радиуса. Ее можно считать плоскостью. Волна, фронт волны которой представляется плоскостью, называется плоской, так как энергия волны во всех плоскостях, представляющих фронты волны в различные моменты времени остается постоянной, то амплитуда у такой волны постоянна.

.Понятие интерференции, наложение гармонических волн, условия когерентности.

Свет является электромагнитной волной. Сложение волн, распространяющихся в среде, определяется сложением соответствующих колебаний. Рассмотрим наиболее простой случай сложения электромагнитных волн (колебаний):

1) частоты их одинаковы,

2) направления электрических векторов совпадают.

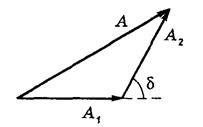
В этом случае для каждой точки среды, в которой происходит сложение волн, амплитуда результирующей волны для напряженности электрического поля определяется векторной диаграммой (рис.4.6)

Из диаграммы следует, что результирующая амплитуда определится следующим образом:

(4.8)

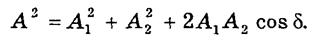
где d— разность фаз слагаемых волн (колебаний).

Результат сложения волн зависит от особенностей источников света и может быть различен.

Дата добавления: 2017-10-04 ; просмотров: 24979 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Интенсивность и световой вектор

Интенсивность света, связь интенсивности света с амплитудой светового вектора.

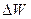
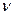
Интенсивностью света называют электромагнитную энергию , проходящую в единицу времени через единицу площади поверхности, перпендикулярной направлению распространения света. Частоты видимых световых волн лежат в пределах

= (,39 4-0,75)-10 15 Гц.

Ни глаз, ни какой-либо иной приемник световой энергии не может уследить за столь частыми изменениями потока энергии, вследствие чего они регистрируют усредненный по времени поток. Поэтому правильнее определить интенсивность как модуль среднего по времени значения плотности потока энергии, переносимой световой волной. Плотность потока электромагнитной энергии определяется выражением

(4.4)

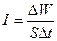
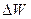
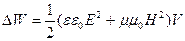
Поскольку световая волна- это электромагнитная волна, то складывается из энергии магнитного и электрического полей

(4.5)

где V- объем, занимаемый волновым полем.

Из уравнений Максвелла следует, что векторы напряженности электрического и магнитного полей в электромагнитной волне связаны соотношением

(4.6)

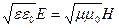
Поэтому выражение (4.5) можно записать следующим образом

Из уравнений Максвелла скорость распространения электромагнитных волн

Выделим некоторый объем волнового поля в форме параллелепипеда (рис.4.5)

Рис.4.5

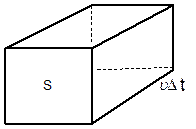
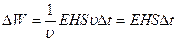
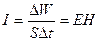
Тогда , по определению интенсивности

, используя выражение (4,6) и полагая, что в прозрачной среде m=1 получим

где n— показатель преломления среды, в которой распространяется волна. Таким образом, напряженность магнитного поля Н пропорционально напряженности электрического поля Е и n:

Тогда интенсивность волны будет определяться выражением

(4.7)

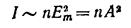
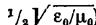
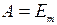
(коэффициент пропорциональности равен )- Следовательно, интенсивность света пропорциональна показателю преломления среды и квадрату амплитуды вектора напряженности электрического поля световой волны. Заметим, что при рассмотрении распространения света в однородной среде можно считать, что интенсивность пропорциональна квадрату амплитуды вектора напряженности электрического поля ( ) световой волны:

Однако в случае прохождения света через границу раздела сред выражение для интенсивности, не учитывающее множитель n, приводит к не сохранению светового потока.

Рассмотрим сферическую световую волну. Площадь сферического фронта волны 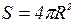, где R- радиус фронта волны. Согласно уравнению (4,4) находим интенсивность

Эти выражения показывают, что амплитуда сферической волны уменьшается пропорционально расстоянию от источника световых волн. Если R достаточно велико, т.е. источник находится очень далеко от области наблюдения, то фронт волны представляется частью сферической поверхности очень большого радиуса. Ее можно считать плоскостью. Волна, фронт волны которой представляется плоскостью, называется плоской, так как энергия волны во всех плоскостях, представляющих фронты волны в различные моменты времени остается постоянной, то амплитуда у такой волны постоянна.

.Понятие интерференции, наложение гармонических волн, условия когерентности.

Свет является электромагнитной волной. Сложение волн, распространяющихся в среде, определяется сложением соответствующих колебаний. Рассмотрим наиболее простой случай сложения электромагнитных волн (колебаний):

1) частоты их одинаковы,

2) направления электрических векторов совпадают.

В этом случае для каждой точки среды, в которой происходит сложение волн, амплитуда результирующей волны для напряженности электрического поля определяется векторной диаграммой (рис.4.6)

Из диаграммы следует, что результирующая амплитуда определится следующим образом:

(4.8)

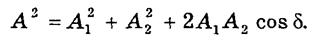
где d— разность фаз слагаемых волн (колебаний).

Результат сложения волн зависит от особенностей источников света и может быть различен.

Дата добавления: 2017-10-04 ; просмотров: 24919 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Интенсивность и давление света

Интенсивность света I в выбранной точке – это модуль средней по времени величины плотности потока энергии, которую световая волна переносит.

Определение плотности потока электромагнитной энергии возможно при помощи вектора Умова-Пойнтинга P → . Отсюда следует, что математический вид определения интенсивности света записывается в виде формулы:

I = » open=» P → = » open=» E → × H → .

По выражению усреднение проводится за период времени t , причем больший по сравнению с периодом колебания волны T t ≫ T . Интенсивность света записывается как:

I t = 1 T ∫ t t + T P → ( t ) d t .

В системе С И единицей измерения является В т м 2 .

Модули амплитуд ( E m и H m ) векторов напряженностей электрического E → и магнитного H → полей в электромагнитной волн записываются в виде отношения:

Имеем, что μ ≈ 1 . Необходимо выразить амплитуду H m :

где n = ε μ = ε при μ ≈ 1 является показателем преломления вещества, в котором распространяется свет.

Модуль среднего значения вектора Умова-Пойнтинга пропорционален произведению амплитуд E m · H m .

Интенсивность света не может быть измерена в связи с тем, что поле изменяется с высокой частотой ν = 10 15 Г ц , соответственно период колебаний составляет T = 10 — 15 с , а приемники колебаний обладают временем инерции существенно больше, чем 10 — 15 c .

Отсюда следует, что среднее значение интенсивности можно регистрировать. Также возможно измерение средней интенсивности, но не фазы поля.

Давление света

По закону сохранения при поглощении и отражении света телом ему сообщается импульс, равняющийся разности импульсов пучка света до и после этих процессов. Отсюда следует, что на тело действует сила, свет производит соответствующее давление на тело. Еще Кеплер выдвинул свое предположение о существовании давления света, которое было принято при рассмотрении отклонений хвостов комет от Солнца.

Последователи волновой теории отрицали давление света, отсутствие доказательств опытами о существовании светового давления служило аргументом против корпускулярной. То есть существование светового давления считалось следствием электромагнитной теории.

Если световая волна падает перпендикулярно плоскости поверхности тела и полностью поглощает свет, то определение давления p производится по формуле.

Где G считается плотностью импульса световой волны, P – модулем вектора Умова-Пойнтинга, с – скоростью света в вакууме.

Если происходит полное отражение света при помощи поверхности тела, то импульс, который при помощи него передается, имеет значение в 2 раза больше, также как и значение давления.

При падении световой волны на поверхность под углом относительно нормали, производя расчеты давления, применяют только перпендикулярную составляющую плотности потока энергии. Если имеются обычные условия, то давление крайне малое, то есть в 10 10 раз меньше атмосферного.

П.Н. Лебедев в 1899 году смог измерить световое давление. Для этого он применил крутильные весы, находящиеся в вакууме. Позже его опыты определения существования давления света подтвердили электромагнитную теорию света Максвелла.

Давление электромагнитных волн считается результатом воздействия электрического поля волны частицы вещества, которые обладают электрическим зарядом, движутся упорядоченно, на них действуют силы Лоренца.

Примеры

Определить давление, оказываемое плоской световой волной, падающей перпендикулярно относительно поверхности тела и поглощаемой телом. Значение амплитуды напряженности электрического поля равняется 2 В м .

Будем использовать формулу:

p = » open=» P c ( 1 . 1 ) .

Где » open=» P принимается за среднее значение модуля вектора Умова-Пойнтинга, c = 3 · 10 8 м с – за скорость света в вакууме.

Для нахождения среднего значения модуля вектора Умова-Пойнтинга необходимо использовать:

» open=» P = » open=» E · H ( 1 . 2 ) .

В условии имеем плоскую волну, тогда уравнение ее колебаний зафиксируем как:

E = E m cos ω t — k x , H = H m cos ω t — k x ( 1 . 3 ) .

Для нахождения значения амплитуды напряжения магнитного поля следует применить:

ε ε 0 E m = μ μ 0 H m ( 1 . 4 ) .

Когда для вакуума ε = 1 , μ = 1 , можно выразить из ( 1 . 4 ) H m . Получим:

H m = ε 0 μ 0 E m ( 1 . 5 ) ,

где μ 0 = 4 π · 10 — 7 Г н м , ε 0 = 1 4 π · 9 · 10 9 Ф м . Это говорит о том, что средним значением модуля вектора Умова-Пойнтинга будет:

» open=» P = » open=» E m cos ω t — k x · ε 0 μ 0 E m cos ω t — k x = ε 0 μ 0 E m 2 » open=» cos ω t — k x = = 1 2 ε 0 μ 0 E m 2 ( 1 . 6 ) .

Далее производим подстановку правой части выражения ( 1 . 6 ) в ( 1 . 1 ) вместо » open=» P , тогда искомое давление света:

p = 1 2 ε 0 μ 0 E m 2 c .

Заменим числовые значения и получим:

p = 1 2 · 3 · 10 8 1 4 π · 10 — 7 · 4 π · 9 · 10 9 · 4 = 4 120 π · 6 · 10 8 = 1 , 77 · 10 11 ( П а )

Ответ: 17 , 7 п П а .

Определить интенсивность I плоской световой волны, распространяющейся вдоль О х . Значение напряженности электрического поля волны равняется E m В м .

Из определения выявим интенсивность световой волны:

I = » open=» P ( 2 . 1 ) .

Запись модуля вектора Умова-Пойтинга для плоской световой волны обозначится как:

P = E H = E m H m cos 2 ω t — k x ( 2 . 2 ) .

Среднее значение » open=» P :

» open=» P = 1 2 E m H m 2 . 3 , так как » open=» cos 2 ω t — k x = 1 2 .

Сравнивая с примером 1 , можно произвести выражение амплитуды напряженности магнитного поля:

ε ε 0 E m = μ μ 0 H m → H m = ε ε 0 μ μ 0 E m ( 2 . 4 ) .

Из ( 2 . 1 ) , ( 2 . 3 ) , ( 2 . 4 ) получим:

Интенсивность и давление света

Вы будете перенаправлены на Автор24

Интенсивность света

Интенсивностью света ($I$) в избранной точке называют модуль средней по времени величины плотности потока энергии, которую световая волна переносит. В свою очередь плотность потока электромагнитной энергии определяют с помощью вектора Умова — Пойнтинга ($overrightarrow

$). Значит, в математическом виде определение интенсивности света можно записать как:

rightrangle right|=left|leftlangle overrightarrow times overrightarrow rightrangle right|left(1right),]

где усреднение производят за время ($t$) много большее, чем период ($T$) колебаний волны: ($tgg T$). Определение интенсивности света можно записать в виде:

Единицами измерения интенсивности света в $СИ$, обычно служат $frac .$

Модули амплитуд ($E_m и H_m$) векторов напряжённостей электрического ($overrightarrow $) и магнитного ($overrightarrow $) полей в электромагнитной волне связаны соотношением:

где считаем, что $mu approx 1.$ Выразим из (3) амплитуду $H_m$, получим:

где $n=sqrt =sqrt $ при $mu approx 1$- показатель преломления вещества, в котором распространяется свет. Из выражения (4) следует, что:

Модуль среднего значения вектора Умова — Пойнтинга пропорционален произведению амплитуд $E_m cdot H_m$, значит можно записать, что интенсивность света:

Интенсивность света не может быть измеряна в связи с тем, что поле изменяется с высокой частотой ($nu = ^ Гц$), соответственно период колебаний составляет $T= ^ с$, тогда как приемники колебаний имеют время инерции существенно больше, чем $ ^ с$. Следовательно, регистрировать мы можем среднее значение интенсивности. Кроме того, можно измерять среднюю интенсивность, но не фазу поля.

Готовые работы на аналогичную тему

Давление света

В соответствии с законом сохранения в случае, когда тело поглощает или отражает свет, ему сообщается импульс, который равен разности импульсов пучка света до и после поглощения или отражения. Значит, на тело действует сила, свет производит на тело соответствующее давление. Предположение о существовании давления света была выдвинута Кеплером, который рассматривал отклонение хвостов комет от Солнца.

Сторонниками волновой теории давление света отрицалось, отсутствие эмпирических доказательств существования светового давления считалось аргументом против корпускулярной теории света. Существование светового давления является следствием электромагнитной теории.

При перпендикулярном падении световой волны на плоскую поверхность тела, и полном поглощении света, его давление ($p$) определяют как:

где $G$ — плотность импульса световой волны, $P$ — модуль вектора Умова — Пойнтинга (надо отметить, что на практике часто используют его среднее значение), $c$ — скорость света в вакууме.

В случае полного отражения света поверхностью тела импульс, передаваемый светом в два раза больше, соответственно больше во столько же давление.

Если энергия световой волны поглощается телом частично, при этом плотность потока поглощаемой энергии ($P_

при этом плотность потока отражаемой энергии ($P_ $) выразим как:

Принимая во внимание выражения (8) и (9) давление определим:

Если световая волна падает на поверхность тела под углом к нормали, то при расчете давления используют только перпендикулярную составляющую плотности потока энергии. Давление света при обычных условиях кране мало, примерно в $ ^ $меньше атмосферного.

Первым световое давление измерил П.Н. Лебедев в 1899 г. Он использовал для этого крутильные весы, которые находились в вакууме. Значение опытов Лебедева в том, что существование давления света подтверждало электромагнитную теорию света Максвелла.

Итак, давление электромагнитных волн — результат того, что при воздействии электрического поля волны частицы вещества, обладающие электрическим зарядом, упорядочено движутся, на них действуют силы Лоренца.

Задание: Каким будет давление, которое оказывает плоская световая волна, которая падает перпендикулярно на поверхность тела и полностью телом поглощается? Амплитуда напряженности электрического поля при этом равна $2frac $.

Решение:

За основу решения задачи примем выражение:

где $leftlangle Prightrangle $ — среднее значение модуля вектора Умова — Пойнтинга, $c=3cdot ^8frac $ — скорость света в вакууме.

При этом среднее значение модуля вектора Умова — Пойнтинга найдем как:

[leftlangle Prightrangle =leftlangle Ecdot Hrightrangle left(1.2right).]

Так как по условию задачи мы имеем плоскую волну, то уравнение колебаний ее составляющих запишем как:

Для того чтобы найти значение амплитуды напряжения магнитного поля воспользуемся соотношением:

Используем то, что для вакуума $varepsilon $=1, $mu =1$, выразим из (1.4) $H_m$, имеем:

где $mu_0=4pi cdot ^ frac , varepsilon_0=frac ^9>frac $. В таком случае среднее значение модуля вектора Умова — Пойнтинга равно:

Подставим правую часть выражения (1.6) в формулу (1.1) вместо величины $leftlangle Prightrangle $, получим искомое давление света:

Ответ: $p=17,7пПа.$

Задание: Какой будет интенсивность ($I$), плоской световой волны, которая распространяется вдоль $оси X$? Амплитуда напряженности электрического поля волны при этом равна $E_m(frac )$.

Решение:

По определению интенсивность световой волны можно найти как:

[I=leftlangle Prightrangle left(2.1right).]

Для плоской световой волны модуль вектора Умова — Пойнтинга запишем как (см. Пример 1):

Тогда среднее значение $leftlangle Prightrangle $ можно выразить как:

[leftlangle Prightrangle =frac E_mH_mleft(2.3right),]

так как $leftlangle c ^2left(omega t-kxright)rightrangle =frac .$

При этом так же, как в примере 1, выразим амплитуду напряженности магнитного поля:

Используя выражения (2.1), (2.3) и (2.4), запишем:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 02 2022

Естественный
и поляризованный свет

Согласно
электромагнитной теории световые волны поперечны. В единственной
электромагнитной волне световой вектор  колеблется только в одной
плоскости. Значит, световая волна, по своей природе, поляризована. Однако же
свет, испускаемый большинством источников света, например, раскаленными
тавердыми телами,  не проявляет какой-либо поляризации. Почему? Потому, что
естественный свет никогда не состоит из единственной волны. Световая волна
состоит из множества цугов волн, испускаемых отдельными атомами совершенно
случайно, и плоскости колебаний каждого цуга ориентирована совершенно случайно.
В пучке естественного света колебания различных направлений представлены с
равной вероятностью (рис.28).

Рис.
28

Свет,
в котором направления колебаний каким-либо образом упорядочены, называется
поляризованным. Если колебания светового вектора происходят только в одной
плоскости, то такой свет называется плоско- либо линейно-поляризованным.
Плоскость, в которой происходят колебания светового вектора  называется
плоскостью колебаний. Эту же плоскость называют плоскостью поляризации.   

Для
получения плоско-поляризованного света пользуются устройствами, называемыми
поляризаторами. Поляризаторы свободно пропускают колебания в плоскости, которую
называют плоскостью поляризатора. Колебание амплитуды А, происходящее в плоскости, образующей
угол φ
с плоскостью поляризатора можно разложить на два колебания с амплитудами  и  (рис.29).

                                                 

                                                        Рис.
29

Первое
колебание пройдет через поляризатор, второе будет задержано. Интенсивность
прошедшей волны равна .
Интенсивность падающего на поляризатор света равна . Поэтому это
выражение примет вид:

.                                           
(26)

Это соотношение
называется законом Малюса.

Чтобы
узнать, данный пучок света поляризован или нет, пользуются поляризатором: если
при вращении поляризатора интенсивность проходящего пучка света остается
неизменной, изменяется только ориентация плоскости поляризации прошедшего
света, значит, падающий на поляризатор свет был не поляризован, если его
интенсивность изменяется от максимального до нуля, значит, свет, падающий на
поляризатор, плоско-поляризован. Поляризатор, используемый для такой цели,
называется анализатором. 

В
естественном свете все значения угла φ равновероятны,
поэтому доля интенсивности света, прошедшего через поляризатор равна среднему
значению ,
т.е. ½. Если естественный свет с интенсивностью  последовательно
проходит через поляризатор и анализатор, интенсивность света прошедшего через
анализатор, будет равна

.

Здесь φ
– угол между плоскостями анализатора и поляризатора.  Максимальная
интенсивность света, прошедшего через анализатор, равна.

                Свет, в котором
колебания светового вектора в одном направлении преобладают над колебаниями в
другом направлении, называется частично поляризованным. Такой свет может быть
рассмотрен как смесь естественного и плоско-поляризованного света. При
пропускании такого света через поляризатор его интенсивность света изменяется в
пределах  от максимал-ного  до
минимального.
Степень поляризации определяется как

.

         Если в
пространстве накладываются друг на друга две когерентные световые волны с
постоянной во времени разностью фаз, плоскости колебаний которых взаимно
перпендикулярны

то образуется результирующая волна,
световой вектор которого описывает эллипс и такой свет называется эллиптически
поляризованным. При разности фаз, равной π/2, и равенстве
амплитуд складываемых волн, получается свет поляризованный по кругу.
Эллиптически поляризованный свет получается при отражении от поверхности
металла.

Поляризация
света при отражении и преломлении

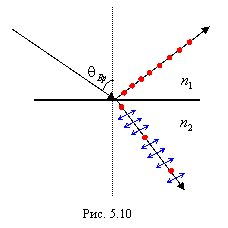
         Если угол
падения света на границу раздела двух диэлектриков оличен от нуля, то
отраженный и  преломленный лучи оказываются частично поляризованными. В
отраженном луче преобладают колебания, перпендикулярные к плоскости падения, в
преломленном – колебания в плоскости падения (рис.30). При угле падения,
удовлетворяющем условию

,                                    
                 (27)

     
Рис.30

(где — показатель
преломления второй среды относительно первой) отраженный свет полностью плоско
поляризован (рис.31).

Рис.31

Степень
поляризации преломленного света при этом достигает максимального значения,
однако он остается частично поляризованным. Формула (27) носит название закона
Брюстера и угол  носит название угла Брюстера.
При выполнении условия Брюстера преломленный луч
оказывается перпендикулярным к отраженному лучу. Физическая
суть поляризации при отражении от диэлектрика заключается в возбуждении
вынужденных колебаний электронов в атомах диэлектрика под воздействием падающей
световой волны и излучающих вторичные волны. Выделим один и электронов и разложим
его колебание на два колебания, одно из которых совершается в плоскости падения
(на рис. 32 сплошная линия), другое перпендикулярно плоскости падения
пунктирная линия.

Рис.32

 Каждому из
колебаний соответствует плоско-поляризованная световая волна. Колеблющийся
заряд в большей степени излучает в направлениях, перпендикулярных к направлению
колебаний, а в направлении колебаний не излучает. Сплошные и пунктирные
лепестки изображают диаграммы направленности излучений соответствующих
колебаний. Видно, что в направлении отраженного луча интенсивность излучения
колебаний, происходящих перпендикулярно к плоскости падения, максимальна и
достигает наибольшего значения при отражении под углом Брюстера. В падающем
естественном свете интенсивность колебаний в различных направлениях одинакова. 
Энергия этих колебаний распределяется между отраженным и преломленным лучами.
Если в отраженном луче преобладают колебания одного направления, то в силу
сохранения энергии, в преломленном луче более интенсивными должны быть колебания
другого направления. Отсюда следует, что преломленный свет поляризован
частично.

         Степень
поляризации преломленного луча можно увеличивать путем много кратного отражения
и преломления. На рис. 33 изображена стопа Столетова, состоящая из ряда параллельных
пластинок, ориентированных под углом Брюстера к падающему лучу.

Рис.33

На каждой границе
частично отражаются лучи, поляризованные только в плоскости падения, и в
результате многократных преломлений выходящий из стопы луч практически
оказывается полностью плоско- поляризованным в плоскости падения. 

Поляризация
света при  двойном лучепреломлении

         При
прохождении естественного света через некоторые кристаллы, падающий луч,
разделяется на два плоско-поляризованных луча. Отсюда и возник термин двойное
лучепреломление. Это явление впервые описал Эразм Бартоломинус (1669) (1625-1698).
Он наблюдал это явление на кристалле исландского шпата.

         Двойное
лучепреломление объясняется анизотропией показателя преломления кристалла. Если
кристалл анизотропен, то его диэлектрическая проницаемость по разным
направлениям, например, по осям х
и y
могут быть различными, различными будут и показатели преломления и
для
лучей, поляризованных вдоль координатных осей  с электрическими векторами Е_х  и Е_у. Если в вакууме оба луча
распространялись совместно, то попадая в кристалл, они преломятся под разными
углами и пространственно разойдутся. Оба луча будут распространяться с разной
скоростью и,
соответственно, пройдут различные оптические пути.

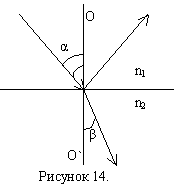
         При
двойном лучепреломлении один из лучей удовлетворяет обычному закону преломления
и лежит в одной плоскости с падающим лучом и нормалью. Этот луч называется
обыкновенным и обозначается буквой о.
Другой луч, называемый необыкновенным и обозначаемый буквой е, не подчиняется закону преломления
света: отношение не
остается постоянным при изменении угла падения и не лежит в одной плоскости с
падающим лучом и нормалью (рис.34а) Если на пластинку падает естественный свет
по нормали к поверхности (рис.34б ), то он расщепится на два луча.

Рис.34

Обыкновенный луч
пройдет через кристалл, не преломляясь, т.е. не изменяя своего направления.
Необыкновенный луч внутри кристалла отклонится и по выходе идет параллельно
обыкновенному лучу. При вращении пластинки вокруг обыкновенного луча
обыкновенный луч останется на месте, необыкновенный вращается вокруг него,
описывая внутри кристалла конус, вне кристалла – цилиндр.

         Явление
двойного лучепреломления наблюдается у всех прозрачных кристаллов, за
исключением кристаллов кубической системы. В так называемых одноосных
кристаллах имеется одно направление в кристалле, в котором не происходит
двойного лучепреломления. Это направление называется оптической осью кристалла.
Кристалл исландского шпата является одноосным кристаллом. В двуосных кристаллах
имеются две оптические оси (например, слюда, гипс). В одноосных кристаллах один
из лучей обыкновенный, другой необыкновенный. В двуосных кристаллах оба луча
являются необыкновенными.

         Любая
плоскость, проходящая через оптическую ось, называется главным сечением
кристалла. Обычно пользуются главным сечением проходящим через падающий луч.
Опыт показывает, что обыкновенный и необыкновенный лучи полностью поляризованы
во взаимно перпендикулярных плоскостях: плоскость колебаний обыкновенного луча
всегда перпендикулярна к главному сечению кристалла, поэтому его показатель
преломления не меняется при падении естественного света на кристалл под любым
углом. В необыкновенном луче колебания совершаются в плоскости главного
сечения, ориентация которой зависит от направления падающей световой волны: показатель
преломления необыкновенного луча изменяется в зависимости от угла падения.  По
выходе из кристалла лучи отличаются только направлением колебаний светового
вектора.

Чтобы
двоякопреломляющий кристалл использовать для получения поляризованного света,
один из лучей следует удалить. В некоторых кристаллах обыкновенный и
необыкновенный лучи поглощаются в разной степени. Это явление называется
оптическим дихроизмом. В кристалле турмалина дихроизм настолько высок, что
необыкновенный луч практически полностью поглощается на пути 1 мм. Естественный
луч выходит из пластинки такого кристалла полностью плоско-поляризованным в
одной плоскости. Такая пластинка будет поляризатором. Большое распространение
как поляризатор находит поляроид – целлулоидная пленка, в которую введено
большое количество одинаково ориентированных кристалликов сульфата иодистого
хинина (герапатита), в которых один из лучей поглощается на пути около 0,1 мм.

В
оптических приборах широкое применение получил поляризатор, называемый призмой
Николя (или просто николем). Она представляет собой призму из монокристалла
исландского шпата, разрезанную по диагонали и склеенную канадским бальзамом
(добывается из смолы канадской пихты). Показатель преломления канадского
бальзама  лежит между показателями
преломления обыкновенного  и  необыкновенного  лучей. Угол
падения подбирается таким, что обыкновенный луч на слое бальзама испытывает
полное внутреннее отражение, а необыкновенный свободно проходит через этот слой
и выходит из призмы (рис.35).

Рис.35

3.1. Поляризованный и естественный свет

3.2. Закон Малюса

3.3. Поляризация при отражении от диэлектриков. Закон Брюстера

3.4. Двойное лучепреломления

3.5. Искусственная оптическая анизотропия

3.6. Вращение плоскости поляризации

3.1. Поляризованный и естественный свет

Из теории Максвелла следует, что свет является поперечной электромагнитной волной. Вектор напряжённости электрического поля (электрический или световой вектор) и вектор напряжённости магнитного поля (магнитный вектор) в световой волне колеблется в направлении перпендикулярном скорости распространения волны.

Линейно поляризованной волной называется волна, вектор которой не изменяют направление колебаний в пространстве.

Уравнение плоской монохроматической линейно-поляризованной волны, распространяющейся в направлении оси ОХ:

,

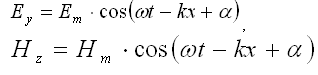
где ω – циклическая частота, — волновое число, υ – скорость распространения волны.

В каждой точке электромагнитного поля электрический вектор совершает гармонические колебания в плоскости XOY, которая называется плоскостью колебания.

Магнитный вектор колеблется в плоскости XOZ – в плоскости поляризации.

Световая волна со всевозможными одинаково вероятными направлениями колебаний электрического и магнитного векторов называется естественным светом.

В естественном свете плоскости поляризации меняют ориентацию в пространстве с течением времени.

Естественный свет можно представить в виде суперпозиции двух волн, которые поляризованы во взаимно-перпендикулярных плоскостях. Запишем уравнение естественного света только для электрического вектора волны:

;

,

где E_y, E_z – проекции электрического вектора на оси координат, α – сдвиг по фазе между колебаниями по Y и Z. Для естественного света E_oy=E_oz.

Частично поляризованным называется свет, если в нём есть преимущественное направление колебаний вектора

(E_oy>>E_oz) или (E_oz>>E_oy).

Частично поляризованный свет можно рассматривать как смесь одновременно распространяющихся в одном и том же направлении естественного и линейно поляризованного.

Поляризацией света называется выделение линейно поляризованного света естественного или частично поляризованного. Для этой цели используются специальные устройства, называемые поляризаторами.

Для определения характера и степени поляризации используют устройства, называемые анализаторами.

Поляризатор можно использовать в качестве анализатора.

Анализатор или поляризатор условно изображают в виде решётки, “прутья” которой параллельны направлению колебаний вектора в проходящем сквозь неё свете.

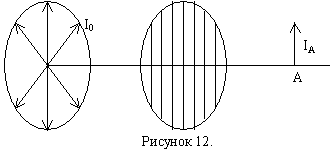
Если на такую решётку-анализатор падает естественный свет, то интенсивность проходящей волны не изменяется при вращении анализатора вокруг направления падающего луча вследствие того, что в естественном свете ни одно из направлений плоскости поляризации (плоскости колебаний) не является преобладающим.

,

где I₀ – интенсивность падающего естественного света,

k – коэффициент прозрачности анализатора,

I_А – интенсивность проходящего света.

На выходе из анализатора-поляризатора имеем линейно поляризованную волну.

Если падающий свет частично поляризован, то I_A при вращении анализатора изменяется в зависимости от ориентации его главной плоскости (т.е. направления прутьев) по отношению к преимущественному направлению колебаний вектора в падающем свете.

3.2. Закон Малюса

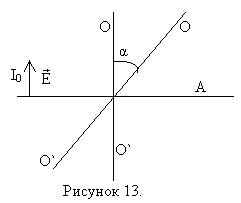
Пусть на анализатор падает линейно поляризованный свет интенсивностью I0. Оптическая ось анализатора О-О` (направление прутьев).

Определим интенсивность прошедшей волны в точке А, если анализатор повернуть на угол α вокруг направления распространения луча. Через анализатор пройдёт электрический вектор, величина . Т.к. интенсивность пропорциональна квадрату амплитуды, то — это и есть закон Малюса.

3.3. Поляризация при отражении от диэлектриков. Закон Брюстера

Направим на границу раздела двух диэлектриков (воздух, стекло) тонкий луч естественного света.

Часть световой волны отражается, а часть преломляется, распространяясь во второй среде. На рисунке: φ – угол падения луча, β – угол преломления, n₂ – показатель преломления стекла, n₁ — показатель преломления воздуха, n₁=1.

Если на пути отражённого и преломлённого луча поставить анализатор, то можно исследовать поляризацию при отражении и преломлении.

Оказалось, что в общем случае отражённый и преломлённый лучи поляризованы частично. При некотором строго определённом для данной пары сред (диэлектриков) значение угла падения отражённый свет оказывается линейно поляризованным. Угол падения в этом случае называется углом Брюстера (φ_Б) или углом полной поляризации и определяется законом Брюстера:

,

где n₂₁ – относительный показатель преломления среды.

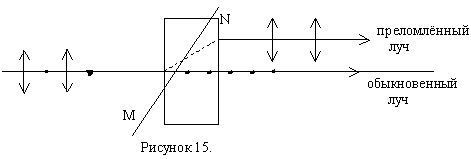
3.4. Двойное лучепреломление

В оптически анизотронных кристаллах наблюдается явление двойного лучепреломления, которое состоит в том, что луч света падающий на поверхность кристалла, раздваивается на два преломлённых луча.

MN – оптическая ось кристалла.

Оптическая ось кристалла – направление в оптически анизотронном кристалле, вдоль которого свет распространяется, не испытывая двойного лучепреломления. Главной плоскостью или главным сечением одностороннего кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось.

В одноосном кристалле один из преломлённых лучей подчиняется обычным законом преломления света. Этот луч лежит в плоскости падения. Волну, распространяющуюся вдоль направления этого луча, называют обыкновенной волной и обозначают буквой О. Показатель преломления для этой волны n₀.

Вдоль второго луча распространяется необыкновенная волна. Показатель преломления луча для неё n_е. угол преломления для необыкновенного луча зависит от того, как ориентирована поверхность пластинки по отношению к оптической оси кристалла MN. Угол преломления равен нулю в двух случаях:

а) если поверхность пластинки перпендикулярна к оптической оси (свет распространяется вдоль оптической оси, не испытывая двойного лучепреломления).

б) если поверхность пластинки параллельна оптической оси (свет распространяется в пластинке перпендикулярно оптической оси).

Двойное лучепреломление можно объяснить тем, что падающая на оптически анизотронный кристалл световая волна возбуждает две волны, распространяющиеся в кристалле эти по разным направлениям. В однослойном кристалле эти волны называются обыкновенными и необыкновенными волнами. Обыкновенные и необыкновенные волны линейно поляризованы во взаимно-перпендикулярных плоскостях.

В обыкновенной волне вектор направлен перпендикулярно к главной плоскости кристалла. Электрический вектор необыкновенной волны лежит в главной плоскости кристалла. Направления векторов в обыкновенных и необыкновенных волнах условно показаны на рисунке точками на обыкновенном луче и поперечными чёрточками на необыкновенном. Предполагается, что оба луча и пересекающая их оптическая ось MN кристалла лежат в плоскости рисунка.

3.5. Искусственная оптическая анизотропия

1. Оптически изотропное прозрачное вещество становится анизотропным, если его подвергнуть механической деформации. Это явление называется фотоупругостью, при одностороннем растяжении или сжатии изотропного тела вдоль оси OX оно приобретёт оптические свойства одноосного кристалла, оптическая ось которого параллельна ОХ . Разность показателей преломления обыкновенного (n_o) и необыкновенного (n_е) лучей в направлении перпендикулярном оси ОХ, пропорциональна нормальному напряжению .

n₀-n_е=к

где к- коэффициент пропорциональности, зависящий от свойств вещества.

2. Эффектом Керра называется возникновение оптической неоднородности у прозрачного изотропного диэлектрика, если его поместить во внешнее электрическое поле.

Под действием поля диэлектрик поляризуется и приобретает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором напряженности внешнего поля.

Разность показателей преломления поляризованного диэлектрика для необыкновенного и обыкновенного лучей монохроматического света, распространяющегося перпендикулярно направлению вектора Е, удовлетворяет закону Керра.

n_е-n₀=B_в

где -длина волны в вакууме, В_в-постоянная Керра.

3. Эффектом Коттона-Мутона называется возникновение оптической анизотропии у некоторых изотропных вещество при помещении их в сильное внешнее магнитное поле.

В однородном магнитном поле вещество преображает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором напряженности внешнего поля.

Разность показателей преломления вещества для необыкновенного и обыкновенного лучей монохроматического света при его распространении в направлении перпендикулярном вектору , пропорциональна .

с- постоянная Коттона — Мутона, -длина волны в вакууме.

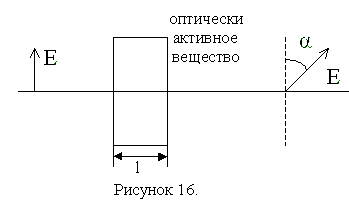
3.6. Вращение плоскости поляризации

При прохождении линейно поляризованного света через некоторые вещества, называемые оптически активными, плоскость поляризации света поворачивается вокруг направления распространения луча.

Оптически активны некоторые кристалла (кварц, киноварь и др.) чистые жидкости и растворы (скипидар, раствор сахара в воде и др.)

В оптически активных кристаллах и чистых жидкостях угол поворота плоскости поляризации пропорционален толщине слоя вещества, через который проходит свет:

Коэффициент пропорциональности называется удельным вращением, или постоянной вращения.

Угол поворота плоскости поляризации при прохождении света пути в оптически активном растворе равен

С — объемно-массовая концентрация оптически активного вещества в растворе, D- плотность раствора, к=С/D- долевая концентрация по массе, — удельная вращения, зависит от природы оптически активного вещества.

Оптически неактивная среда под действием внешнего магнитного поля приобретает способность вращать плоскость поляризации света, распространяющегося вдоль направления поля.

Это явление называется эффектом Фарадея, или магнитным вращением плоскости поляризации.

где — угол поворота плоскости поляризации,

-напряженность магнитного поля,

— длина пути световой волны,

V — постоянная Верде.