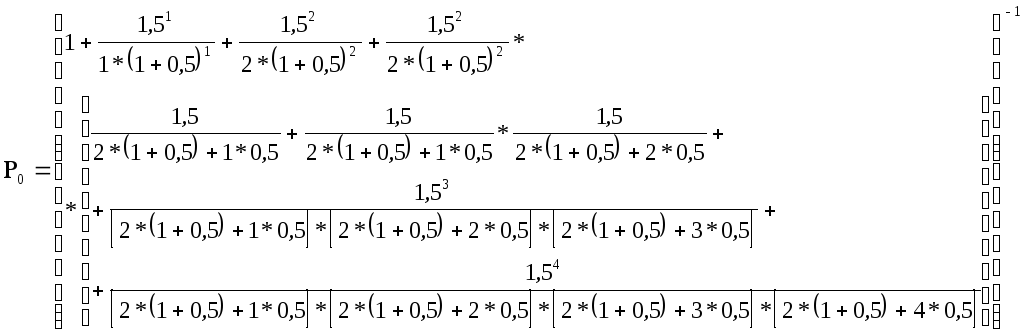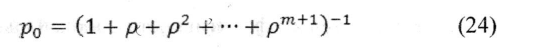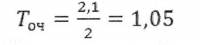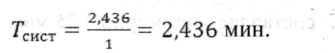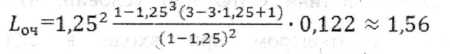Как найти интенсивность потока обслуживания - Исправление недочетов и поиск решений вместе с Examum.ru

Примеры задач для многоканальных СМО

Перейти к онлайн решению своей задачи

Многоканальная СМО с отказами в обслуживании

Пример. АТС имеет k линий связи. Поток вызовов — простейший с интенсивностью λ в минуту. Среднее время переговоров составляет t минут. Время переговоров имеет показательное распределение. Найти: а) вероятность того, что все линии связи заняты; б) относительную и абсолютную пропускные способности АТС; в) среднее число занятых линий связи. Определить оптимальное число линий связи, достаточное для того, чтобы вероятность отказа не превышала α.

k = 5; λ = 0.6; t = 3.5, α = 0.04.

Решение. Исчисляем показатели обслуживания многоканальной СМО:

Интенсивность потока обслуживания:

μ = 1/3.5 = 0.29

1. Интенсивность нагрузки.

ρ = λ • t_обс = 0.6 • 3.5 = 2.1

Интенсивность нагрузки ρ=2.1 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.

3. Вероятность, что канал свободен (доля времени простоя каналов).

Следовательно, 13% в течение часа канал будет не занят, время простоя равно t_пр = 7.5 мин.

Вероятность того, что обслуживанием:

занят 1 канал:

p₁ = ρ¹/1! p₀ = 2.1¹/1! • 0.13 = 0.26

заняты 2 канала:

p₂ = ρ²/2! p₀ = 2.1²/2! • 0.13 = 0.28

заняты 3 канала:

p₃ = ρ³/3! p₀ = 2.1³/3! • 0.13 = 0.19

заняты 4 канала:

p₄ = ρ⁴/4! p₀ = 2.1⁴/4! • 0.13 = 0.1

заняты 5 канала:

p₅ = ρ⁵/5! p₀ = 2.1⁵/5! • 0.13 = 0.0425 (вероятность того, что все линии связи заняты)

4. Доля заявок, получивших отказ.

Значит, 4% из числа поступивших заявок не принимаются к обслуживанию.

5. Вероятность обслуживания поступающих заявок.

В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому:

p_отк + p_обс = 1

Относительная пропускная способность: Q = p_обс.

p_обс = 1 — p_отк = 1 — 0.0425 = 0.96

Следовательно, 96% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.

6. Среднее число занятых линий связи

n_з = ρ • p_обс = 2.1 • 0.96 = 2.01 линии.

Среднее число простаивающих каналов.

n_пр = n — n_з = 5 — 2.01 = 3 канала.

7. Коэффициент занятости каналов обслуживанием.

K₃ = n₃/n = 2.01/5 = 0.4

Следовательно, система на 40% занята обслуживанием.

8. Абсолютная пропускная способность.

A = p_обс • λ = 0.96 • 0.6 = 0.57 заявок/мин.

9. Среднее время простоя СМО.

t_пр = p_отк • t_обс = 0.0425 • 3.5 = 0.15 мин.

12. Среднее число обслуживаемых заявок.

L_обс = ρ • Q = 2.1 • 0.96 = 2.01 ед.

Для определения оптимального число линий связи, достаточное для того, чтобы вероятность отказа не превышала 0.04, воспользуемся формулой:

Для наших данных:

где

Подбирая количество линий связей, находим, что при k=6, p_отк = 0.0147 < 0.04, p₀ = 0.12

Скачать решение

1. Коммерческая фирма занимается посреднической деятельностью по продаже автомобилей и осуществляет часть переговоров по 3 телефонным линиям. В среднем поступает 75 звонков в час. Среднее время предварительных переговоров справочного характера составляет 2 мин.

Рекомендации к решению задачи: здесь n = 3; λ = 75 ед. в час.; t = 2 мин. или μ = 30 ед. в час.

2. Пункт по ремонту квартир работает в режиме отказа и состоит из двух бригад. Интенсивность потока заявок λ, производительность пункта μ. Определить вероятность того, что оба каналы свободны, один канал занят, оба канала заняты, вероятность отказа, относительную и абсолютную пропускные способности, средне число занятых бригад.

Рекомендации к решению задачи: здесь n = 2; λ = 1.5 ед. в час.; μ = 1.8 ед. в час.

3. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр.
Среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок 0,25 (1/ч). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.

Рекомендации к решению задачи: здесь n = 3; λ = 0.25 ед. в час.; t_обс = 3 час.

Многоканальная СМО с ограниченной длиной очереди

1. Построить две модели многоканальной системы массового обслуживания – с бесконечной и ограниченной очередью. Вычислить Р₀ – вероятность простаивания всех каналов обслуживания, n_w – среднее число клиентов, ожидающих обслуживания, t_w – среднее время ожидания обслуживания, W – вероятность обязательного пребывания в очереди.

2. В мини-маркет поступает поток покупателей с интенсивностью 6 покупателей в 1 мин., которых обслуживают три контролера-кассира с интенсивностью 2 покупателя в 1 мин. длина очереди ограничена 5 покупателями.

Рекомендации к решению задачи: здесь n = 3; m = 5; λ = 6 ед. в мин.; μ = 2 ед. в мин.

3. На плодоовощную базу в среднем через 30 мин. прибывают автомашины с плодоовощной продукцией. Среднее время разгрузки одной машины составляют 1.5 ч. Разгрузку производят две бригады. На территории базы у дебаркадера могут находиться в очереди в ожидании разгрузки не более 4 автомашин.

Рекомендации к решению задачи: здесь n = 2; m = 4; λ = 2 ед. в час.; μ = 2/3 = 0.67 ед. в час.

4. На автомойку в среднем за час приезжают 9 автомобилей, но если в очереди уже находятся 4 автомобиля, вновь подъезжающие клиенты, как правило, не встают в очередь, а проезжают мимо. Среднее время мойки автомобиля составляет 20 мин., а мест для мойки всего два. Средняя стоимость мойки автомобиля составляет 70 руб. Определите среднюю величину потери выручки автомойки в течение дня.

Рекомендации к решению задачи: здесь n = 2; m = 4; λ = 9 ед. в час.; t_обс = 20 мин.

Величина потери выручки: S = t_{время работы мойки за день}λ•p_отк•70 руб. (ответ 5443.2 руб.)

5. Магазин получает овощи из теплиц. Автомобили с грузом прибывают с интенсивностью λ машин в день. Подсобные помещения позволяют обрабатывать и хранить товар, привезенный m автомобилями. В магазине работают n фасовщиков, каждый из которых в среднем может обрабатывать товар с одной машины в течении t_обсл. часов. Продолжительность рабочего дня при сменной работе составляет 12 часов. Определить емкость подсобных помещений при заданной вероятности Р* обсл. полной обработки товаров.

6. Имеется автозаправочная станция с 2-мя колонками. В очереди не может быть больше 3-х машин. Интенсивность и среднее время заправки равны 2.1 и 0.55. Найти вероятность простоя системы.

Решение:

Интенсивность потока обслуживания равна μ = 1/0.55 = 1.82. Отсюда, интенсивность нагрузки составит ρ = λ • t_обс = 2.1 • 0.55 = 1.16. Заметим, что интенсивность нагрузки ρ=1.16 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.

Поскольку 1.16<2, то процесс обслуживания будет стабилен.

Вероятность простоя системы выражается следующей формулой:

Следовательно, 28% в течение часа канал будет не занят, время простоя равно t_пр = 0.28*60 мин. = 16.9 мин.

Многоканальная СМО с неограниченной очередью

2. В расчетном узле магазина самообслуживания работают 3 кассы. интенсивность входного потока составляет 5 покупателей в минуту. интенсивность обслуживания каждого контролера-кассира составляет 2 покупателя минуту.

Рекомендации к решению задачи: здесь n = 3; λ = 5 ед. в мин.; μ = 2 ед. в мин.

В качестве количества заявок в очереди можно указать, например, m = 4. тогда будут рассчитаны соответствующие вероятность появления данных заявок.

3. В аудиторскую фирму поступает простейший поток заявок на обслуживание с интенсивностью λ = 1,5 заявки в день. Время обслуживания распределено по показательному закону и равно в среднем трем дням. Аудиторская фирма располагает пятью независимыми бухгалтерами, выполняющими аудиторские проверки (обслуживание заявок). Очередь заявок не ограничена. Дисциплина очереди не регламентирована. Определите вероятностные характеристики аудиторской фирмы как системы массового обслуживания, работающей в стационарном режиме.

Рекомендации к решению задачи: здесь n = 5; λ = 1.5 ед. в час.; t_обс = 3 ед. в час.

После решения необходимо заменить единицы измерения «час» на «дни».

4. В мастерской по ремонту холодильников работает n мастеров. В среднем в течение дня поступает в ремонт λ холодильников. Поток заявок пуассоновский. Время ремонта подчиняется экспоненциальному закону распределения вероятностей, в среднем в течение дня при семичасовом рабочем дне каждый из мастеров ремонтирует μ холодильников.

Требуется определить: 1) вероятность того, что все мастера свободны от ремонта холодильников, 2) вероятность того, что все мастера заняты ремонтом, 3) среднее время ремонта одного холодильника, 4) в среднем время ожидания начала ремонта для каждого холодильника, 5) среднюю длину очереди, которая определяет необходимое место для хранения холодильника, требующего ремонта, 6) среднее число мастеров, свободных от работы.

Источник

1.1.
Параметры
входящего потока заявок.

1.2.
Параметры структуры СМО:

число каналов
обслуживания — m;
число мест в
очереди — n;
средняя длительность
обслуживания заявки в канале —
;
интенсивность
потока обслуживания
.

2. Характеристики
СМО:

2.1.
Интенсивность выходного потока заявок
.

,
где

— интенсивность
потока обслуженных заявок;

— интенсивность
потока потерянных заявок;

(потери происходят
из-за ухода из СМО «нетерпеливых» заявок
и из-за отказов системы принять заявку
при заполненной очереди).

2.2.
Вероятность обслуживания.

,
где
— интенсивность входящего потока заявок.

2.3.
Вероятность потери заявок.

2.4.
Среднее время ожидания заявок в очереди
.

2.5.
Среднее время пребывания заявки в
системе (время реакции системы)
.

,
где
— среднее время обслуживания.

2.6.
Средняя длина очереди
.

2.7.
Среднее число занятых каналов обслуживания
.

2.8.
Среднее число заявок в системе.

Для СМО без
«выталкивания» заявок и ухода
«нетерпеливых» заявок справедливо
.
Критерий
эффективности СМО (Е) — некоторая функция
-показатель эффективности системы.

В общем виде
,
где— штраф за отказ системы принятьi-ю
заявку;

—
штраф за «выталкивание» i
— ой заявки;

— штраф за уход из
системы i
— ой заявки при превышении

допустимого
времени нахождения заявки в СМО;

M
— количество типов заявок.

Таким образом
критерий эффективности отражает потери
в СМО, вызванные отказами системы принять
заявку, уходом «нетерпеливых» заявок
и «выталкиванием» заявок, имеющих более
низкий приоритет, когда приходит заявка
с высшим приоритетом.

Пусть задано :

k
= 3;
= 6;= 15;= 9;= 0;

B
= 0,5; n
= 4; m
= 2;
= 0,1;= 25;

= 3;
= 2;= 10,

то есть имеется
двухпроцессорная система; число мест
в очереди — 4.

I Формулируем задачу в терминах смо:

Так как рассматриваемая
СМО — бесприоритетная, будем рассматривать
суммарный поток заявок с интенсивностью
с^-1.
Поток обслуживания
для одного канала имеет интенсивность
с^-1.
Находим приведенную
эффективность входного потока для
одного канала :
.
Находим интенсивность
потока уходов :
с^-1.
Находим приведенные
интенсивности потоков уходящих заявок
:

— уход из очереди;

— из каналов
обслуживания;

Рассматриваем возможные состояния системы :

z₀
— в системе нет заявок;
z₁
— в системе одна заявка, очередь
отсутствует;
z₂
— в системе 2 заявки, очередь отсутствует;
z₃
— 3 заявки : 2 заявки на обслуживании, 1 в
очереди;
z₄
— 4 заявки : 2 заявки на обслуживании, 2 в
очереди;
z₅
— 5 заявок : 3 заявки в очереди;
z₆
— 6 заявок : в очереди 4 заявки. Очередь
заполнена.

Вероятность
нахождения системы в i
— ом состоянии находим по формуле [2] :
;

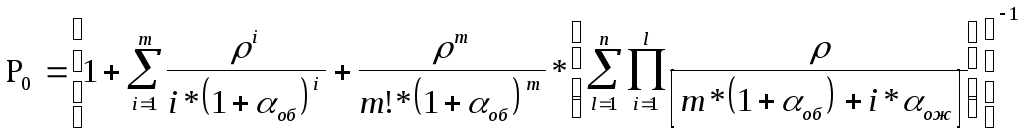
i=1,2,…,m;

l=1,2,…,n,
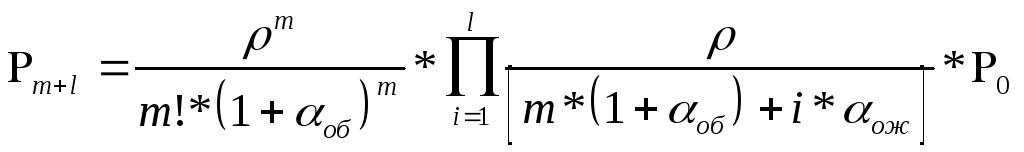
где l
— длина очереди.

Вероятность
состояния z₀
равна

Далее находим

P₀
= 0,3534 P₃
= 0,0757

P₁
= 0,3534 P₄
= 0,0284

P₂
= 0,1767 P₅
= 0,0095

P₆
= 0,0029.

(Для состояний z₀
— z₂
очередь отсутствует.)

Вычисляем характеристики смо :

Среднее число
занятых каналов

(в состоянии P₀
не занят ни один канал;

в состоянии P₁
занят 1 канал;

в состояниях P₂
— P₆
заняты 2 канала).

Средняя длина
очереди
.
Вероятность
отказов
.
Вероятность ухода
заявок из очереди
.
Вероятность ухода
заявки из системы во время обслуживания
.
Суммарная
вероятность ухода «нетерпеливых»
заявок
.
Вероятность потерь
заявок
.
Вероятность
обслуживания заявки
.

Соседние файлы в папке Обработка данных

Источник

Привет, мой друг, тебе интересно узнать все про расчет показателей эффективности одноканальной смо с ограниченной очередью, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
расчет показателей эффективности одноканальной смо с ограниченной очередью, одноканальная смо с ограниченной очередью , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.

Рассмотрим одноканальную систему массового обслуживания с ожиданием, в которую поступает
простейший поток заявок с интенсивностью X; интенсивность обслуживания и, (т.е. в среднем непрерывно
занятый канал будет выдавать 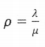обслуженных заявок в единицу (времени).
Длительность обслуживания — случайная величина, подчиненная показательному закону распределения.
Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди
уже стоят m-заявок, она покидает систему не обслуженной.

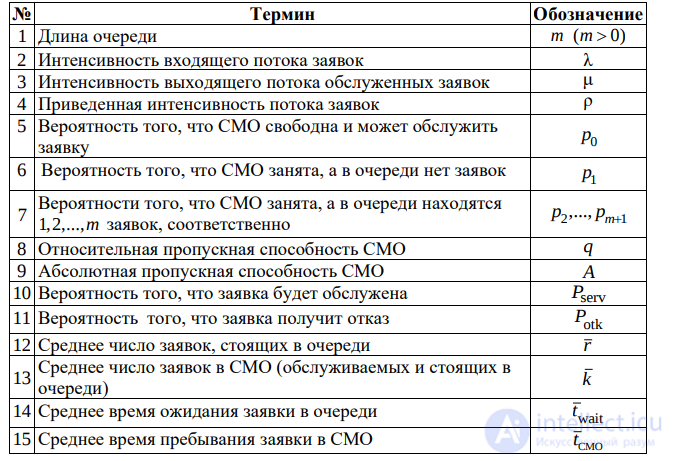
Список используемых терминов и обозначений

Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди уже стоят m-заявок, она покидает систему не обслуженной.
В качестве показателей эффективности одноканальной
СМО с ограниченной длиной очереди будем рассматривать:
А — абсолютную пропускную способность СМО;
Q — относительную пропускную способность;
Ротк — вероятность отказа;
Lсист — среднее число находящихся в системе заявок;
Теист_ среднее время пребывания заявки в системе;
Lоч — средняя длина очереди;
Точ — среднее время ожидания в очереди.

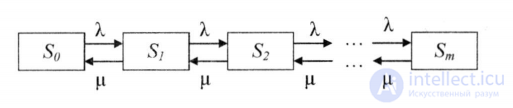
Размеченный граф состояний представлен на рисунке 9.

Рис. 9. Одноканальная СМ О с ограниченной длинной очереди

So — канал обслуживания свободен;
S1 — канал обслуживания занят, но очереди нет;
S2 — канал обслуживания занят, в очереди стоит 1 заявка;

***
Sm — канал обслуживания занят, в очереди все m заявок, любая следующая заявка получает отказ.
Вероятности состояний определяются уравнениями:

Отсюда получаем, что если р 1, то

Тогда остальные предельные вероятности находятся по формулам:

Постановка задачи
Параметры m , λ и μ известны.
Требуется найти

Формулы для расчетов
Приведенная интенсивность потока заявок вычисляется, как и в предыдущих параграфах, по формуле

Вероятности вычисляются по следующим формулам:

Поскольку заявка получает отказ, если СМО занята, а в очереди находятся m заявок, то

Далее получаем

Кроме того, справедливы формулы

Пример 10.
Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более пяти машин одновременно (m = 5) . Об этом говорит сайт https://intellect.icu . Если
в очереди уже находятся пять машины, очередная машина, прибывшая к станции, в очередь не становится. Поток
машин, прибывающих для заправки, имеет интенсивность λ = 2 (машина в минуту). Интенсивность потока
обслуживания составляет μ = 2.

Определите характеристики СМО и сделайте вывод об эффективности ее работы.

Решение.

Среднее число находящихся в системе заявок:

Среднее время пребывания машины в системе:

Средняя длина очереди:
Среднее время ожидания в очереди:

Каждому седьмому клиенту отказывают в обслуживании => эффективность СМО низкая.

Пример 11.
В небольшом магазине самообслуживания установлено, что поток покупателей является простейшим с интенсивностью λ = 1 покупатель в минуту. В этом магазине установлен один кассовый аппарат, позволяющий добиться такой производительности труда, при которой среднее время обслуживания одного клиента составляет примерно 1,25 мин. покупателя в минуту.

Определите характеристики СМО при условии, что очередь ограничена контролером при входе в зал самообслуживания: m = 3 покупателей.

Решение: Найдем интенсивность потока обслуживания:

Найдем приведенную интенсивность потока заявок:

Найдем предельные вероятности:

Вероятность отказа:

Относительная пропускная способность СМО:

Абсолютная пропускная способность СМО:

покупателей в мин.
Среднее число покупателей у кассы:

Среднее время пребывания покупателя у кассы:

Среднее число покупателей в очереди:

т.е. среднее число покупателей, ожидающих в очереди у кассы, равно 1,56.
Среднее время ожидания покупателя в очереди:

Вероятность простоя кассира мала, среднее время оживания покупателя не большое, вероятность отказа примерно 0,297. Таким образом, можно сказать, что система работает эффективно.

Задачи для самоконтроля

1. На автомойке один блок для обслуживания и есть место для очереди. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины — 10 минут. Найдите все средние характеристики СМО.

Ответ

2. Автосервис (пост диагностики) представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих обслуживания ограничено и равно 3. Если все стоянки заняты, то есть в очереди уже находятся три автомобиля, то очередной автомобиль, прибывший в автосервис на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по показательному закону Пуассона и имеет интенсивность 0,85 (автомобиля в час). Время диагностики распределено по показательному закону и в среднем равно 1,05 час. Определите вероятностные характеристики работы СМО и сделайте вывод об эффективности ее работы.

Ответ:

Как ты считаеешь, будет ли теория про расчет показателей эффективности одноканальной смо с ограниченной очередью улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое расчет показателей эффективности одноканальной смо с ограниченной очередью, одноканальная смо с ограниченной очередью
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория массового обслуживания

Источник