Как найти интервал длин волн

Решение.
Данный ион гелия считаем водородоподобным. Для водородоподобных ионов справедлива формула Бальмера для определения длины волны:

[ begin{align}
  & nu =ccdot Rcdot {{Z}^{2}}cdot (frac{1}{{{m}^{2}}}-frac{1}{{{n}^{2}}}), nu =frac{c}{lambda }, \
 & frac{1}{{{lambda }_{nm}}}=Rcdot {{Z}^{2}}cdot (frac{1}{{{m}^{2}}}-frac{1}{{{n}^{2}}}), {{lambda }_{nm}}=frac{1}{Rcdot {{Z}^{2}}cdot (frac{1}{{{m}^{2}}}-frac{1}{{{n}^{2}}})},{{lambda }_{max }}=frac{{{m}^{2}}cdot {{n}^{2}}}{Rcdot {{Z}^{2}}cdot ({{n}^{2}}-{{m}^{2}})} (1). \
 & frac{1}{{{lambda }_{min }}}=frac{Rcdot {{Z}^{2}}}{{{m}^{2}}}, n=infty . \
 & {{lambda }_{min }}=frac{{{m}^{2}}}{Rcdot {{Z}^{2}}} (2). \
end{align} ]

В серии Бальмера электрон переходит на второй энергетический уровень, m = 2.
Для определения максимальной длины волны n = 3, минимальной n = ∞.
с = 3∙10⁸ м/с, с – скорость света, R – постоянная Ридберга,
R = 1,097737∙10⁷ м^-1.
Z = 2, порядковый номер гелия.

[ begin{align}
  & {{lambda }_{max }}=frac{{{2}^{2}}cdot {{3}^{2}}}{1,097737cdot {{10}^{7}}cdot {{2}^{2}}cdot ({{3}^{2}}-{{2}^{2}})}=1,639cdot {{10}^{-7}}. \
 & {{lambda }_{min }}=frac{{{2}^{2}}}{1,097737cdot {{10}^{7}}cdot {{2}^{2}}}=0,91cdot {{10}^{-7}}. \
end{align} ]

Ответ: λ_mах = 1,639∙10^-7 м, λ_min = 0,91∙10^-7 м.

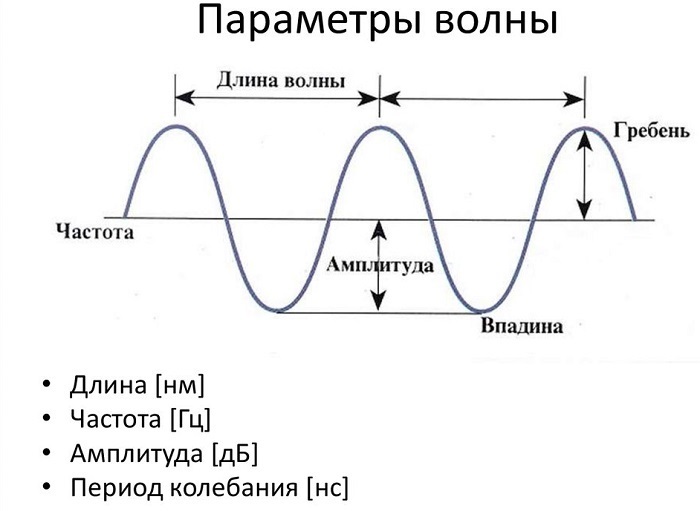
Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной. 

Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

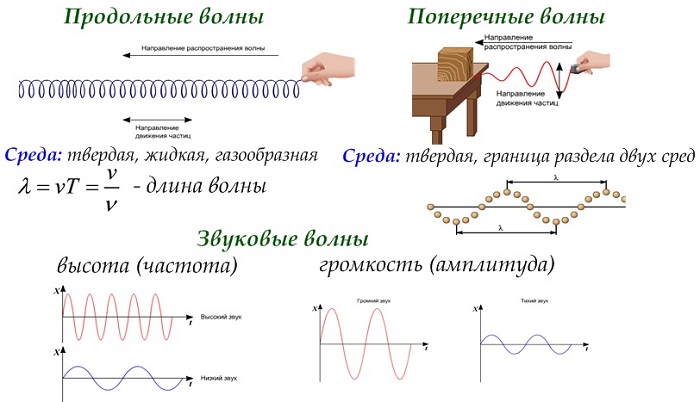
Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества. 

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

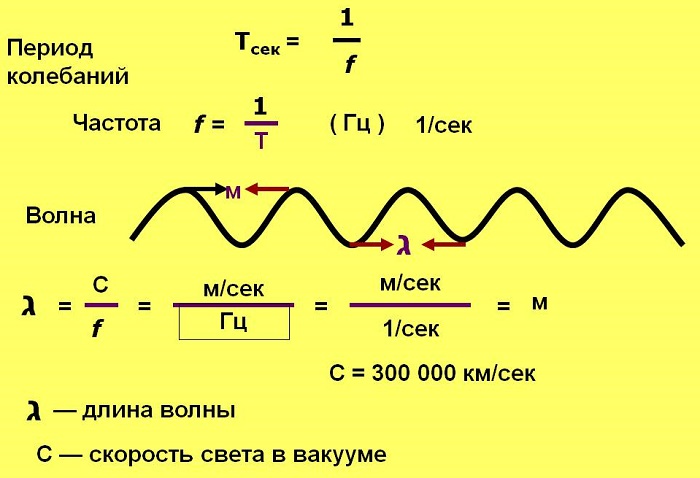
Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10⁸ м/с поделить на длину в метрах.

Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

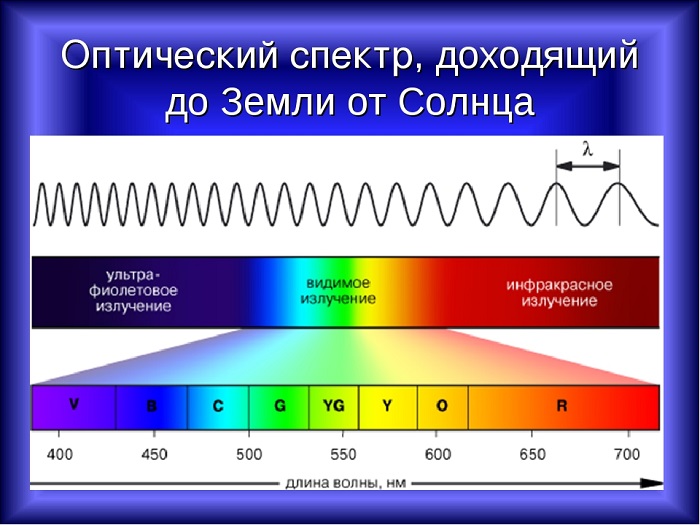
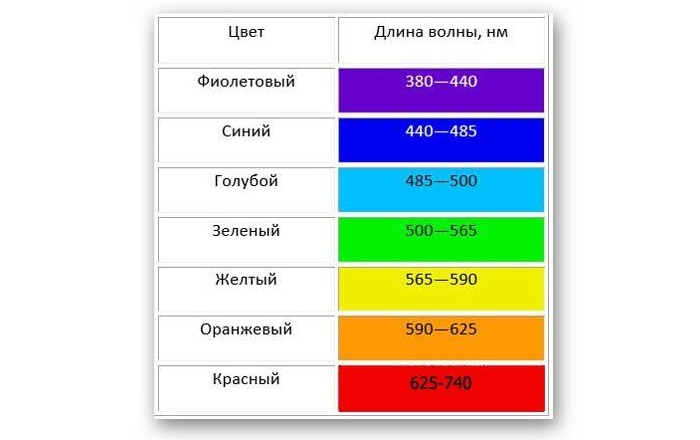
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

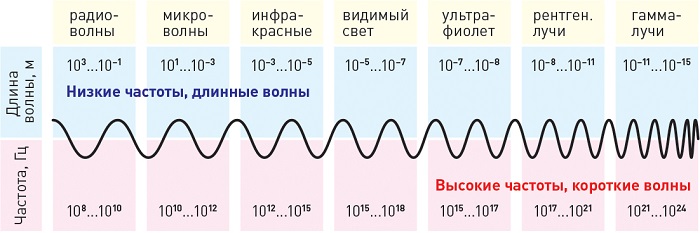
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания. 

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Найти интервал длин звуковых волн, воспринимаемых человеком, если диапазон их частот от 20 до 20000 Гц. Скорость звука в воздухе равна 340 м в сек

Длина волны равна расстоянию, которое проходит, распространяясь, волна за время, равное одному периоду.  Как и в случае механического движения пройденное расстояние выражается произведением скорости на время. 

Период колебаний есть величина, обратная частоте.        $T=frac{1}{f}$              (2) 

(2) подставим в (1)

Ответ: человек воспринимает звуковые волны длиной от 1,7 см до 17 м

2018-07-04   

Рассчитать и изобразить в шкале длин волн спектральные интервалы, в которых заключены серии Лаймана, Бальмера и Пашена для атомарного водорода. Выделить на этой шкале видимую область спектра.

Решение:

Из общей формулы для перехода $n_{2} rightarrow n_{1}$

$hbar omega = E_{H} left ( frac{1}{n_{1}^{2} } — frac{1}{n_{2}^{2} } right )$

где $E_{H} = 13,65 эВ$. Тогда

(1) Серия Лаймана, $n_{1} = 1, n_{2} = 2,3$. Таким образом

$hbar omega geq frac{3}{4} E_{H} = 10,238 эВ$

Это соответствует $lambda = frac{2 pi c hbar}{ hbar omega} = 0,121 мкм$

и линии Лаймана $lambda leq 0,121 мкм$, предел серии при $0,0909 мкм$

(2) Серия Бальмера: $n_{2} = 2, n_{3} = 3,4,$

$hbar omega geq E_{H} left ( frac{1}{4} — frac{1}{9} right ) = frac{5}{36} E_{H} = 1,876 эВ$

Это соответствует

$lambda = 0,65 мкм$

и серия Бальмера $lambda leq 0,65 мкм$, предел серии при $lambda = 0,363 мкм$.

(3) Серия Пашена: $n_{2} = 3, n_{1} = 4,5, cdots$

$h omega geq E_{H} left ( frac{1}{9} — frac{1}{16} right ) = frac{7}{144} E_{H} = 0,6635 эВ$

Это соответствует $lambda = 1,869 мкм$

предел серии при $lambda = 0,818 мкм$

 Готовое решение: Заказ №8389

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Физика

 Дата выполнения: 28.09.2020

 Цена: 227 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№1 3. Найти интервал длин волн, в котором заключена спектральная серия Бальмера ионов He+.

Решение.

Когда атом переходит из состояния с большей энергией En в состояние с меньшей энергией Ek, испускается фотон. Длина волны для водородоподобного иона определяется обобщённой формулой Бальмера: , где м – постоянная Ридберга; – зарядовое число ядра. Для серии Бальмера ( , ) имеем: . Выразим длину волны: ;