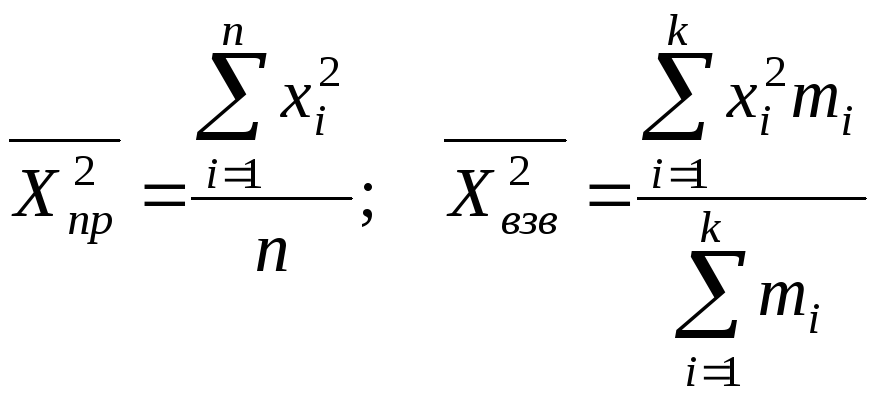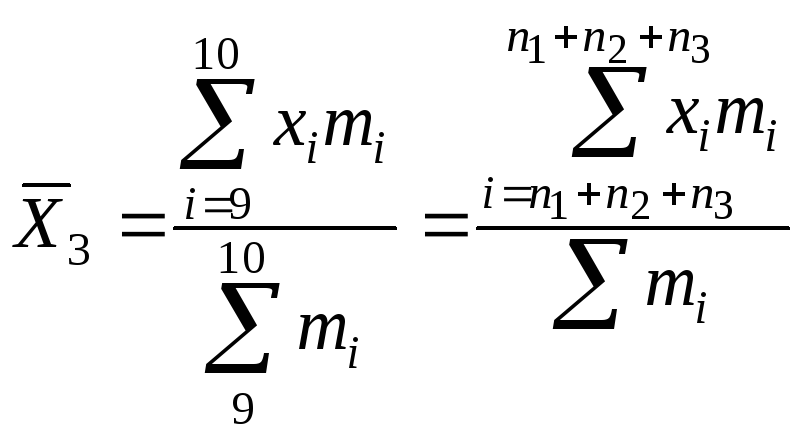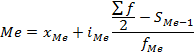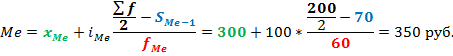,(20)
где
–
нижняя граница медианного интервала;
– величина медианного интервала;
–
накопленная частота (или частость)
интервала, предшествующего медианному;
–
половина суммы всех частот (или частостей);
– частота медианного интервала.
При
исчислении медианы интервального
вариационного ряда сначала находят
интервал, содержащий медиану. Для этого
используют накопленные частоты (или
частости). Медианному
интервалу соответствует первая из
накопленных частот (или частостей),
превышающая половину всего объёма
совокупности.
Пример:
процент выполнения норм выработки (х).
|
Интервалы |
xi |
mi |
Накопленные |
|
90–100 |
95 |
3 |
3 |
|
100–110 |
105 |
8 |
11 |
|
110–120 |
115 |
7 |
18 |
|
120–130 |
125 |
2 |
20 |
|
Σ |
– |
20 |
– |
Первая из накопленных
частот превышает 0,5·Σmi,
т.е. 10:
0,5·Σmi,
= 10.
Значит медианный
интервал (100–110):
=
100; 
= 3;
k
=
100 – 100 = 10; 
= 3;
11. Мода
В математической
статистике модой
называют вариант, наиболее
часто встречающийся в данном вариационном
ряду.
Для дискретного
ряда мода
определяется по наибольшей частоте и
соответствует
варианту с наибольшей частотой.
Мода для непрерывного
(интервального с равными интервалами)
ряда исчисляется по формуле:
,(21)
где
хМо(min) —
нижняя граница модального интервала;
mМо —
частота модального интервала;
mМо–1 —
частота интервала, предшествующего
модальному;
mМо+1
— частота интервала, последующего за
модальным;
ki
— величина модального интервала.
Может
быть: одна мода –
унимодальное распределение;
две моды –
бимодальное распределение;
три и более –
мультимодальное распределение.
Модальный интервал
определяется по набольшей частоте.
Пример:
|
Интервалы |
mi |
|
90–100 |
3 |
|
100–110 |
8 |
|
110–120 |
7 |
|
120–130 |
2 |
|
Σ |
20 |
Модальный интервал
(100–110), т.к. он имеет наибольшую частоту.
хМо(min)
= 100
k
=
10 mМо–1
= 3;
mМо
= 8; mМо+1
= 7;
Мо
≈108,3
Показатели колеблемости (вариации) признака
Такие признаки,
как заработная плата, профессия, число
членов семьи, возраст и т.д. — варьируют.
Для измерения
вариации признака математическая
статистика применяет ряд показателей.
12.
Вариационный размах (R),
или широта распределения
R
= xmax
– xmin
(22)
применялся в
формуле (8.6)
xmax
— наибольший вариант вариационного
ряда.
xmin
— наименьший вариант вариационного
ряда.
R
представляет
собой величину неустойчивую, зависящую
от случайных обстоятельств. Она
применяется в качестве приблизительной
оценки вариации.
Среднее
линейное отклонение
невзвешенное
взвешенное
(23)
13
Дисперсия (средний квадрат отклонения)
невзвешенная
взвешенная
(24)
У
прощённая
формула дисперсии
,
(25)
где
14.
Среднее квадратическое отклонение
(с.к.о.)
(26)
15.
Коэффициент вариации (υ)
(27)
Применяется
только для признака, принимающего только
положительные значения.
Если ν > 40%, то это
говорит о большой колеблемости признака
в изучаемой совокупности (например
большая колеблемость товарооборота в
регионе).
–коэффициент
осцилляции
–коэффициент
вариации по среднему линейному
отклонению.
16.
Свойства дисперсии
1. σ2(С)
= 0, где
С –
const.
2. Если все
значения вариантов признака Х уменьшить
на постоянную величину, то дисперсия
не изменится.
3. Если все
значения вариантов признака Х увеличить
в k
раз, то дисперсия увеличится в k2
раз.
4. Вычисление
дисперсии методом отсчёта от условного
нуля (методом моментов).
(28)
17.
Частные средние и частные дисперсии
Пусть вся совокупность
разбита на l
групп. Для каждой группы вариантов
вариационного ряда можно вычислить
средние, которые называются частными
средними
и дисперсии, которые называются частными
дисперсиями или внутригрупповыми
дисперсиями.
Пусть l
групп:
(29)
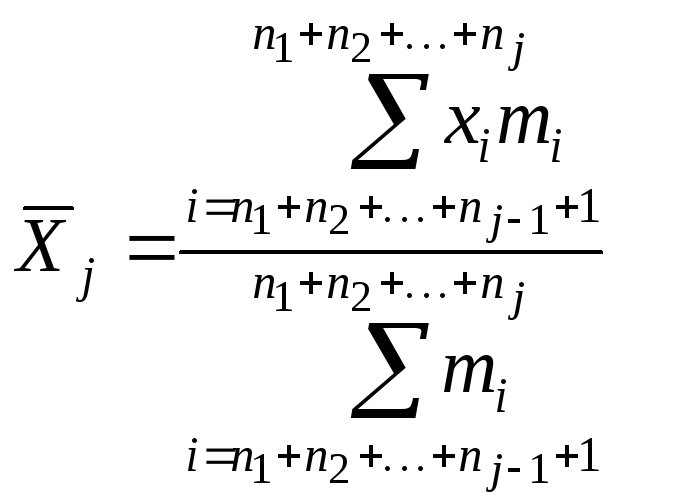
j=1,
2, …, l;
Σmi
= Nj
– объём j-ой
группы
–частная средняя
j-ой
группы
(30)
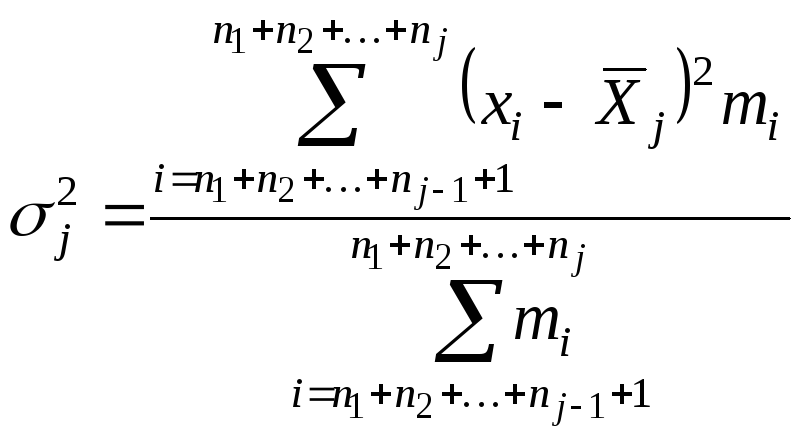
Частные средние
могут не совпадать с общей средней
.
Убедимся в этом:
|
n1 |
n2 |
n3 |
|
x1 |
x4 |
x9 |
|
m1 |
m4 |
m9 |
Разбили на три
группы. l=3.
Группы не пересекаются
n1
+ n2
+ … + nl
= k
|
n1, |
k |
|
3 |
m1
+ m2
+ m3
= N1
– объём 1ой
группы (сумма
частот в 1ой
группе)
m4
+ m5
+ … + m8
= N2
– объём 2ой
группы
m9
+ m10
= N3
– объём 3ей
группы
Nj
– объём jтой
группы
j
= 1, 2, … , l
или
i
= 3 + 5 + 1 = 8 + 1 = 9
Итак
,
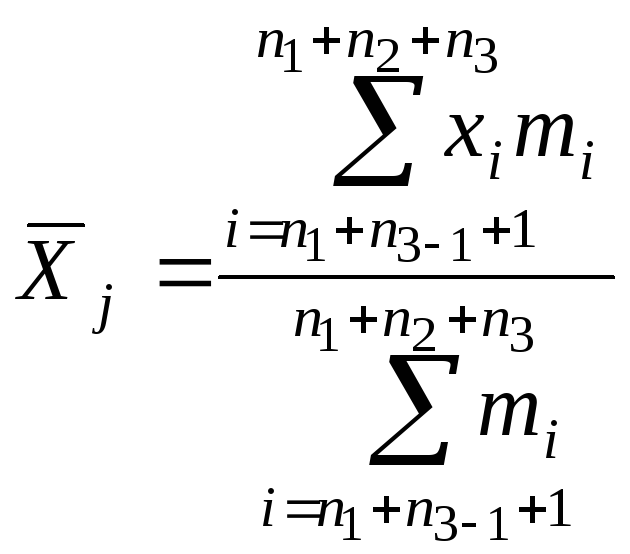
где j
= 1, 2, …, l
Отсюда видно, как
получается формула (29).
Соседние файлы в папке 11-03-2014_20-15-21
- #
- #
Как найти доверительный интервал для медианы (шаг за шагом)
17 авг. 2022 г.
читать 1 мин
Мы можем использовать следующую формулу для расчета верхней и нижней границ доверительного интервала для медианы генеральной совокупности:
j: nq – z√ nq(1-q)
k: nq + z√ nq(1-q)
куда:
- n: размер выборки
- q: квантиль интереса. В качестве медианы мы будем использовать q = 0,5.
- z: z-критическое значение
Округляем j и k до следующего целого числа. Результирующий доверительный интервал находится между j -м и k -м наблюдениями в данных упорядоченной выборки.
Обратите внимание, что z-значение, которое вы будете использовать, зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Источник: эта формула взята из «Практической непараметрической статистики», 3-е издание, автор У. Дж. Коновер .
В следующем пошаговом примере показано, как рассчитать доверительный интервал для медианы генеральной совокупности, используя следующие выборочные данные из 15 значений:
Примеры данных: 8, 11, 12, 13, 15, 17, 19, 20, 21, 21, 22, 23, 25, 26, 28
Шаг 1: Найдите медиану
Во-первых, нам нужно найти медиану выборочных данных. Это оказывается средним значением 20 :
8, 11, 12, 13, 15, 17, 19, 20 , 21, 21, 22, 23, 25, 26, 28
Шаг 2: Найдите j и k
Предположим, мы хотим найти 95% доверительный интервал для медианы генеральной совокупности. Для этого нам нужно сначала найти j и k :
- j: nq – z√ nq(1-q) = (15)(0,5) – 1,96√ (15)(0,5)(1-0,5) = 3,7
- k: nq + z√ nq(1-q) = (15)(0,5) + 1,96√ (15)(0,5)(1-0,5) = 11,3
Мы округлим j и k до ближайшего целого числа:
- Дж: 4
- к: 12
Шаг 3: Найдите доверительный интервал
95% доверительный интервал для медианы будет между j = 4 -м и k = 12 -м наблюдениями в наборе выборочных данных.
4 -е наблюдение равно 13, а 12 -е наблюдение равно 23:
8, 11, 12, 13 , 15, 17, 19, 20, 21, 21, 22, 23 , 25, 26, 28
Таким образом, 95% доверительный интервал для медианы оказывается равным [13, 23] .
Дополнительные ресурсы
Как найти доверительный интервал для пропорции
Как найти доверительный интервал для среднего
Как найти доверительный интервал для стандартного отклонения
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
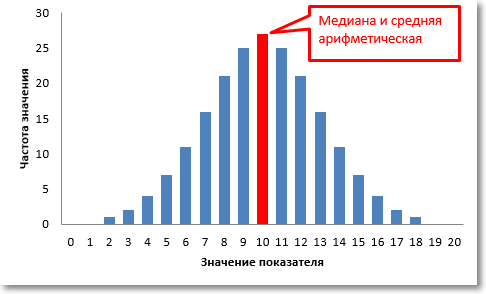
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
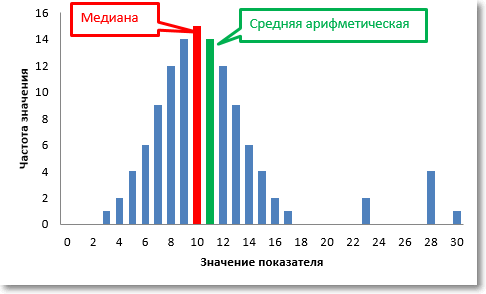
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
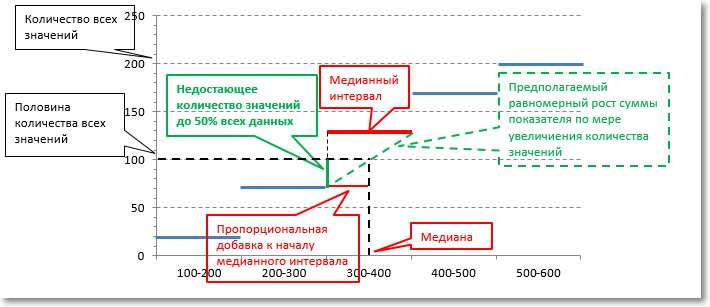
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
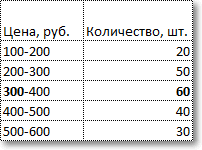
Для примера рассчитаем медиану по следующим данным.
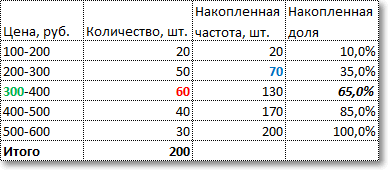
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:
(8.17 – формула Медианы)
где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:
Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
Загрузка…
В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.
Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.
Понятие медианы
Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.
То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.
Формула для расчета медианы
Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.
Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.
Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:
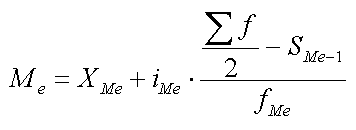
где: Me — медиана;
Xme — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);
ime — величина медианного интервала;
f — частота (сколько раз в ряду встречается то или иное значение);
Sme-1 — сумма частот интервалов предшествующих медианному интервалу;
fme — число значений в медианном интервале (его частота).
Пример вычисления медианы
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.
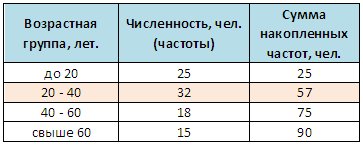
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).
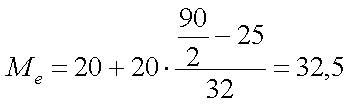
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.
Особенности медианы
- Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки;
- Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.
Источники
- Медиана // Википедия. URL: http://ru.wikipedia.org/wiki/Медиана_(статистика) (дата обращения: 23.10.2013)
- Минашкин В. Г. и др. Курс лекций по теории статистики. – М.: МЭСИ, 2001.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Медиана // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/mediana (дата обращения: 26.05.2023).