Как найти интервал наибольшего целого числа - Исправление недочетов и поиск решений вместе с Examum.ru

1 idea: well, I think you have to kinda sort the list anyway, but you can’t go with merge or quick sort. But if you have memory, you could use idea from counting sort for integers.

So you can create array of 0 and 1, from 0 to max int value, then fill it with ones if you have value and then find maximum continous array

2 idea: create dictionary of values, find min and max — all O(N) operations:

dict = {1: 1, 3: 3, 4: 4, 5: 5, 6: 6, 7: 7, 10: 10}
min = 1
max = 10

then, go like i in range(min, max) and and find longest continuous subset

>>> d = [1, 3, 5, 7, 4, 6, 10]
>>> s = set(d)
>>> mind = min(d)
>>> maxd = max(d)
>>> a, b, j = 0, 0, 0

>>> for i in range(mind, maxd):
        if i not in s:
            if (b - a) < (i - j - 1):
                a, b = j, i - 1
            j = i + 1

>>> a, b
(3, 7)

but this could be slow for sparse lists like [1, 9000, 100000]

EDIT: based on super great answer of Grigor Gevorgyan, here’s the code for O(N) dictionary solution in Python (I just love it’s simplicity!!!)

l = [1, 3, 5, 7, 4, 6, 10]
d = {x:None for x in l}
print d
for (k, v) in d.iteritems():
    if v is not None: continue
    a, b = d.get(k - 1), d.get(k + 1)
    if a is not None and b is not None: d[k], d[a], d[b] = k, b, a
    elif a is not None: d[a], d[k] = k, a
    elif b is not None: d[b], d[k] = k, b
    else: d[k] = k
    print d

m = max(d, key=lambda x: d[x] - x)
print m, d[m]

output:

{1: None, 3: None, 4: None, 5: None, 6: None, 7: None, 10: None}
{1: 1, 3: None, 4: None, 5: None, 6: None, 7: None, 10: None}
{1: 1, 3: 3, 4: None, 5: None, 6: None, 7: None, 10: None}
{1: 1, 3: 4, 4: 3, 5: None, 6: None, 7: None, 10: None}
{1: 1, 3: 5, 4: 3, 5: 3, 6: None, 7: None, 10: None}
{1: 1, 3: 6, 4: 3, 5: 3, 6: 3, 7: None, 10: None}
{1: 1, 3: 7, 4: 3, 5: 3, 6: 3, 7: 3, 10: None}
{1: 1, 3: 7, 4: 3, 5: 3, 6: 3, 7: 3, 10: 10}
3 7

Источник

Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.

Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.

Виды числовых промежутков

На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.

078e9

Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.

159

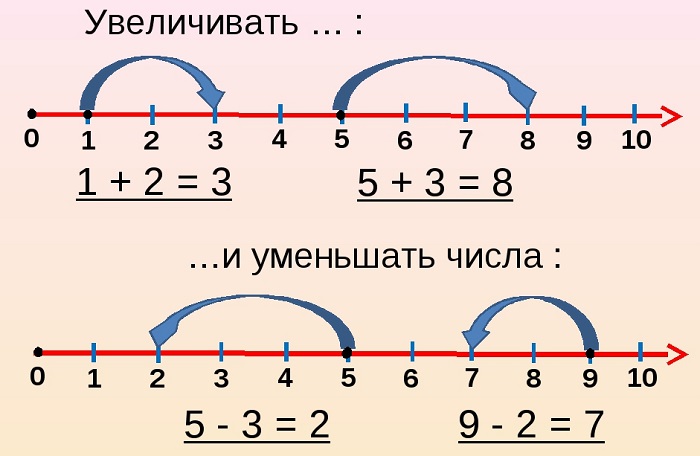
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.

На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.

Открытый числовой луч

Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.

Точки расположены по одну сторону от определенной переменной, признанной началом координат.

Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:

(-∞; А);
(А; +∞).

Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».

Также можно охарактеризовать неравенством:

х < А;
х > А.

Знак зависит от расположения луча относительно А.

Замкнутый числовой луч

Замкнутый луч отличается от открытого тем, что к множеству относится А.

Также ему соответствует условие:

х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
х ≥ А (значение больше или равно А) или [А; +∞).

При графическом изображении А в этом случае закрашивается, на рисунке она черная.

Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.

Числовой отрезок

Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.

При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.

Обозначается отрезок, например, -7 ≤ х ≤ 3. Запись читается следующим образом: «отрезок от минус семи до трех».

Интервал

Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.

Обозначается, например, 5 < х < 13. Читается запись как «интервал от пяти до тринадцати».

Полуинтервал

Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.

Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.

Обозначение может выглядеть, например, так -2 ≤ х < 9, «полуинтервал от минус двух до девяти».

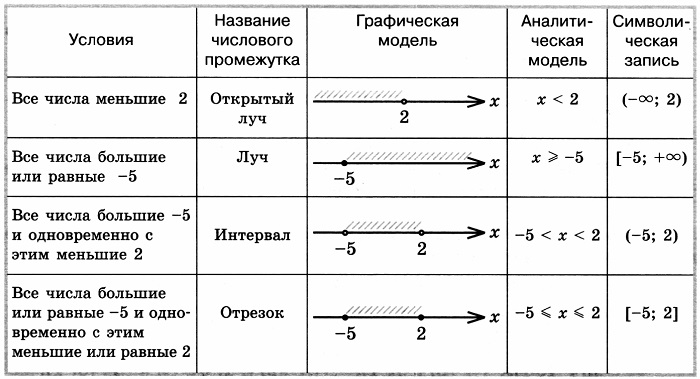
Таблица числовых промежутков

Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.

Наглядное изображение поможет восприятию и закреплению материала.

Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.

Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.

Источник

Числовые промежутки

Виды числовых промежутков
Открытый и замкнутый луч
Отрезок
Интервал и полуинтервал

Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.

Виды числовых промежутков

Название	Изображение	Неравенство	Обозначение
Открытый луч		x > a	(a; +∞)
	x < a	(-∞; a)
Замкнутый луч		x ⩾ a	[a; +∞)
	x ⩽ a	(-∞; a]
Отрезок		a ⩽ x ⩽ b	[a; b]
Интервал		a < x < b	(a; b)
Полуинтервал		a < x ⩽ b	(a; b]
	a ⩽ x < b	[a; b)

В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.

Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.

Открытый и замкнутый луч

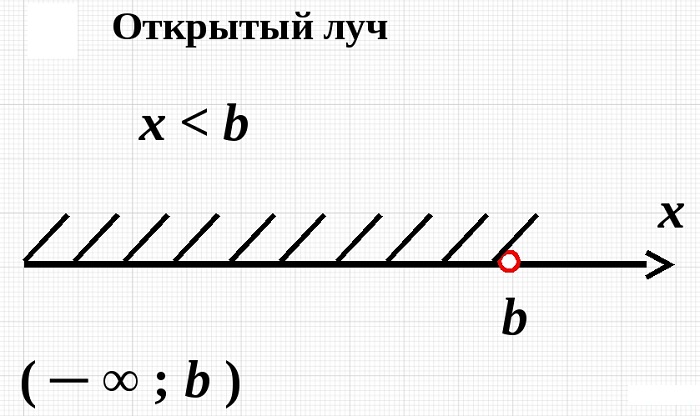
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.

Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:

Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности.

Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:

Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.

Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:

Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности и числовой луч от минус бесконечности до двух. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.

Отрезок

Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.

Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх.

Интервал и полуинтервал

Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.

Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх.

Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:

Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3, и полуинтервал от минус двух до трёх, включая минус два.

Источник

Интервалы между простыми чиcлами — это разности между двумя последовательными простыми числами. n-ый интервал, обозначаемый g_n~ , — это разность между n+1-м и n-ым простыми числами, то есть

$g_n = p_{n + 1} - p_n.~$

Мы имеем: . Последовательность g_n~ интервалов между простыми хорошо изучена. Иногда рассматривают функцию g(p_n)~ вместо g_n~

Первые 30 интервалов между простыми числами следующие:

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14 последовательность A001223 в OEIS.

Содержание

1 Простые замечания
2 Численные результаты
3 Дальнейшие результаты
- 3.1 Верхние оценки
- 3.2 Нижние оценки
4 Гипотезы о интервалах между простыми числами
5 Интервалы между простыми как арифметическая функция
6 См. также
7 Примечания
8 Ссылки

Простые замечания

Для любого простого числа P, символом P# мы будем обозначать праймориал P, то есть произведение всех простых чисел, не превосходящих P. Если Q — это простое число, следующее за P, то последовательность

является последовательностью из Q-2 последовательных составных чисел, поэтому существуют интервалы между простыми длины не меньше, чем Q-1 . Следовательно, существуют сколь угодно большие интервалы между простыми числами, и для любого простого P существует n такое, что (Очевидно, что для этого мы можем выбрать n таким, что p_n~ будет наибольшим простым числом, не превосходящим P#+2~ .). Другой способ увидеть, что существуют сколь угодно большие интервалы между простыми должны существовать использует тот факт, что множество простых чисел имеет нулевую плотность, согласно теореме о распределении простых чисел.

На самом деле, интервал между простыми величины P может встретиться между простыми, гораздо меньшими, чем P#. Например, самая первая последовательность из 71 последовательных составных чисел находится между 31398 и 31468, в то время как 71# является 27-значным числом.

Уже среднее значение интервалов между простыми растет как натуральный логарифм n.

С другой стороны, гипотеза о простых близнецах утверждает, что g_n=2~ для бесконечно многих n.

Интервалы между простыми могут быть оценены сверху и снизу с помощью функции Якобсталя последовательность A048670 в OEIS

Численные результаты

На 2009 г. наибольший известный интервал между числами, определенными как вероятно простые, имеет длину 2254930, с 86853-значными вероятно простыми был найден H. Rosenthal и J. K. Andersen.^[1] Наибольший известный интервал между простыми числами — это интервал длины 337446, с 7996-значными простыми найден T. Alm, J. K. Andersen и Francois Morain.^[2]

Будем говорить, что g_n~ является максимальным интервалом, если для всех k<n~ будет .

Первые 75 максимальных интервалов (n не приводится)

От 1 до 25

#	g_n	p_n
1	1	2
2	2	3
3	4	7
4	6	23
5	8	89
6	14	113
7	18	523
8	20	887
9	22	1129
10	34	1327
11	36	9551
12	44	15683
13	52	19609
14	72	31397
15	86	155921
16	96	360653
17	112	370261
18	114	492113
19	118	1349533
20	132	1357201
21	148	2010733
22	154	4652353
23	180	17051707
24	210	20831323
25	220	47326693

От 26 до 50

#	g_n	p_n
26	222	122164747
27	234	189695659
28	248	191912783
29	250	387096133
30	282	436273009
31	288	1294268491
32	292	1453168141
33	320	2300942549
34	336	3842610773
35	354	4302407359
36	382	10726904659
37	384	20678048297
38	394	22367084959
39	456	25056082087
40	464	42652618343
41	468	127976334671
42	474	182226896239
43	486	241160624143
44	490	297501075799
45	500	303371455241
46	514	304599508537
47	516	416608695821
48	532	461690510011
49	534	614487453523
50	540	738832927927

От 51 до 75

#	g_n	p_n
51	582	1346294310749
52	588	1408695493609
53	602	1968188556461
54	652	2614941710599
55	674	7177162611713
56	716	13829048559701
57	766	19581334192423
58	778	42842283925351
59	804	90874329411493
60	806	171231342420521
61	906	218209405436543
62	916	1189459969825483
63	924	1686994940955803
64	1132	1693182318746371
65	1184	43841547845541059
66	1198	55350776431903243
67	1220	80873624627234849
68	1224	203986478517455989
69	1248	218034721194214273
70	1272	305405826521087869
71	1328	352521223451364323
72	1356	401429925999153707
73	1370	418032645936712127
74	1442	804212830686677669
75	1476	1425172824437699411

Дальнейшие результаты

Верхние оценки

Постулат Бертрана утверждает, что для любого k всегда существует хотя бы одно простое число между k и 2k, поэтому, в частности, $p_{n+1}<2p_n~$ , откуда .

Теорема о распределении простых чисел говорит, что «средняя длина» интервалов между простым p и следующим простым числом имеет порядок ln p~ . Фактическая длина интервалов может быть больше или меньше этого значения. Однако, из теоремы о распределении простых чисел можно вывести, верхную оценку для длины интервалов простых чисел: для любого существует такое N, что для всех n>N~ будет .

Hoheisel первым показал^[3] что существует такое постоянное

$pi(x + x^theta) - pi(x) sim frac{x^theta}{ln x}$

при

отсюда следует, что

для достаточно большого n.

Отсюда следует, что интервалы между простыми становятся сколь угодно меньше по отношению к простым: частное $frac{g_n}{p_n}$ стремится к нулю при n стремящемся к бесконечности.

Hoheisel получил возможное значение 32999/33000 для theta . Эта оценка была улучшена до 249/250 by Хейлборном,^[4] и до $theta = frac{3}{4} + varepsilon$ для любого by Чудаковым.^[5]

Основное улучшение было получено Ингамом,^[6], который показал, что если

для некоторой константы c>0 , где O используется в смысле нотации O большое, то

$pi(x + x^theta) - pi(x) sim frac{x^theta}{ln x}$

для любого $theta > frac{1+4c}{2+4c}$ . Здесь, как обычно, zeta обозначает дзета функцию Римана, а pi (x) — функция числа простых чисел не превосходящих x. Известно, что допускается $c > frac{1}{6}$ , откуда в качестве theta можно взять любое число, большее $frac{5}{8}$ . Из результата Ингама сразу следует, что всегда существует простое число между числами n^3 и (n+1)^3 для достаточно больших n. Заметим, что ещё не доказана гипотеза Линделёфа, которая утверждает, что в качестве c может быть выбрано любое положительное число, но из неё следует, что всегда существует простое число между n^2 and (n+1)^2 для достаточно больших n (см. также Гипотеза Лежандра). Если эта гипотеза верна, то возможно, что необходима ещё более строгая гипотеза Крамера.

Хаксли показал, что можно выбрать $theta = frac{7}{12}$ .^[7]

Последний результат принадлежит Baker, Harman and Pintz, показавшим, что theta может быть взято равным 0,525.^[8]

В 2005, Daniel Goldston, Janos Pintz и Cem Y?ld?r?m доказали, что

$liminf_{nto+infty}frac{g_n}{ln p_n}=0$

и позже улучшили это^[9] до

$liminf_{nto+infty}frac{g_n}{sqrt{ln p_n}(ln ln p_n)^2}<infty$

Нижние оценки

Роберт Ранкин доказал, что существует константа c>0 такая, что неравенство

$g_n > frac{cln nlnln nlnlnlnln n}{(lnlnln n)^2}$

сохраняется для бесконечно многих значений n. Наилучшее известное значение для c на текущий момент — это $c=2e^{gamma}~$ , где gamma~ — постоянная Эйлера-Маскерони.^[10] Пауль Эрдёш предлагает приз в $5,000 за доказательство или опровержение того, что константа c в неравенстве выше может быть сколь угодно большой.^[11]

Гипотезы о интервалах между простыми числами

Primegap function

Здесь возможны ещё лучшие результаты, чем те, которые могут быть получены при предположении истинности гипотезы Римана. Harald Cramer доказал, что если гипотеза Римана верна, то интервалы g(p_n)~ удовлетворяют соотношению

$g(p_n) = O(sqrt{p_n} ln p_n),$

(здесь используется нотация O большое). Позже он предположил, что интервалы растут гораздо меньше. Грубо говоря, он предположил, что

В данный момент на это указывают численные расчеты. Для более детальной информации см. Гипотеза Крамера.

Гипотеза Андрики утверждает, что

$g(p_n) < 2sqrt{p_n} + 1.$

Это слабое усиление гипотезы Лежандра, которая утверждает, что между любой парой квадратов натуральных чисел существует хотя бы одно простое число.

Интервалы между простыми как арифметическая функция

Интервал g_n~ между n-ым и n+1 -ым простым числом является примером арифметической функции. В таком контексте обычно её обозначают d_n~ и называют разностью между простыми.^[11] Разность между простыми не является мультипликативной и не является аддитивной.

См. также

Гипотеза Римана
Гипотеза Крамера
Открытые проблемы в теории чисел

Примечания

↑ Largest known prime gap
↑ A proven prime gap of 337446
↑ Hoheisel, G. (1930). «Primzahlprobleme in der Analysis». Sitzunsberichte der Koniglich Preussischen Akademie der Wissenschaften zu Berlin 33: 3–11.
↑ Heilbronn, H. A. (1933). «Uber den Primzahlsatz von Herrn Hoheisel». Mathematische Zeitschrift 36 (1): 394–423. DOI:10.1007/BF01188631.
↑ Tchudakoff, N. G. (1936). «On the difference between two neighboring prime numbers». Math. Sb. 1: 799–814.
↑ Ingham, A. E. (1937). «On the difference between consecutive primes». Quarterly Journal of Mathematics 8 (1): 255–266. DOI:10.1093/qmath/os-8.1.255.
↑ Huxley, M. N. (1972). «On the Difference between Consecutive Primes». Inventiones Mathematicae 15 (2): 164–170. DOI:10.1007/BF01418933.
↑ Baker, R. C. (2001). «The difference between consecutive primes, II». Proceedings of the London Mathematical Society 83 (3): 532–562. DOI:10.1112/plms/83.3.532.
↑ arΧiv:0710.2728
↑ Pintz, J. (1997). «Very large gaps between consecutive primes». J. Number Theory 63 (2): 286–301. DOI:10.1006/jnth.1997.2081.
↑ ¹ ² Guy R. K. Unsolved problems in number theory. — Third. — New York: Springer, 2004. — P. 31. — ISBN 0387208607

Ссылки

Thomas R. Nicely, Some Results of Computational Research in Prime Numbers — Computational Number Theory. This reference web site includes a list of all first known occurrence prime gaps.
Weisstein, Eric W. Prime Difference Function (англ.) на сайте Wolfram MathWorld.
Шаблон:Planetmath reference
Chris Caldwell, Gaps Between Primes

Источник