Функциональные ряды Функциональный ряд и его область сходимости
Пусть u1(x),
u2(x),
… , un(x),
… – последовательность функций,
определенных на некотором множестве
X.
Ряд вида
,
(20)
членами которого
являются функции, называется функциональным.
Придавая в (20) x
различные числовые значения из множества
X,
будем получать различные числовые ряды.
В частности, при x=x0X
получим числовой ряд
.
Этот числовой ряд может быть сходящимся
или расходящимся. Если он сходится, то
x0
называется точкой
сходимости функционального ряда
(20) .
Множество всех
точек сходимости функционального ряда
называют его областью
сходимости
и обозначают ее через D.
Очевидно, Dx.
В частных случаях, множество D
может совпадать или не совпадать с
множеством X,
или же может быть и пустым множеством.
В последнем случае функциональный ряд
расходится в каждой точке множества X.
Вид области D
для произвольного функционального ряда
может быть различным: вся числовая ось,
интервал, объединение интервалов и
полуинтервалов и т.д. В простейших
случаях, при исследовании функциональных
рядов на сходимость, можно применить
рассмотренные выше признаки сходимости
числовых рядов, если под x
понимать фиксированное число.
Определения:
Сумма первых n
членов функционального ряда Sn(x)=u1(x)+
u2(x)+…+
un(x)
называется
n-ой
частичной суммой,
а функция ,
определенная в области D,–
суммой
функционального ряда.
Функция Rn(x)
= S(x)-Sn(x)
, определенная
в области D,
называется
остатком
ряда.
Функциональный
ряд называется абсолютно
сходящимся
на множестве DX,
если в каждой точке D
сходится ряд .
Степенные ряды
Частным случаем
функциональных рядов являются степенные
ряды.
Определение.
Степенным рядом
называется
функциональный ряд
(21)
члены которого
являются произведениями постоянных C0
,
C1
, … , Cn
,…
на степенные функции от разности x-x0
с целыми неотрицательными показателями
степеней, точка x0
называется
центром
степенного ряда.
Пример
27.
Ряд
– степенной ряд с центром в точке x0=0.
Ряд
– степенной ряд с центром в точке x0=-3.
Ряд
– функциональный ряд.
Исследование
степенного ряда на сходимость, а именно
нахождение области сходимости степенного
ряда, является одним из главных вопросов.
Ответ на этот вопрос можно получить ,
используя теорему Абеля.
ТЕОРЕМА 10.
(Теорема
Абеля)
-
Если степенной
ряд сходится при x=x1
(x1x0),
то он сходится, и притом абсолютно, для
всех x,
удовлетворяющих неравенству
|x—x0
|<|x1-x0|.
-
Если степенной
ряд расходится при x=x2
, то он расходится для всех x,
удовлетворяющих неравенству
|x—x0
|>|x2—x0|.
Опираясь на теорему
Абеля можно доказать, что существует
такое положительное число R,
что для всех x,
удовлетворяющих неравенству |x—x0|<R,
ряд сходится абсолютно и расходится
при всех x,
для которых |x—x0|>R.
Число R
называется радиусом
сходимости
ряда ,
а интервал (x0—R,
x0—R)
– интервалом
сходимости.
В частном случае
интервал сходимости степенного ряда
может совпадать со всей числовой осью
(в этом случае R=)
или может превращаться в точку (в этом
случае R=0).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
Пример 28.
Найти интервал сходимости степенного
ряда
.
Решение. Первый
способ.
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда :
.
Применим признак Даламбера:
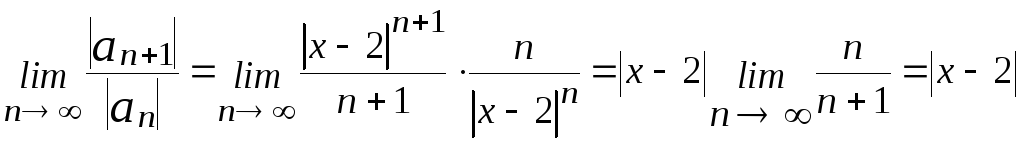
Если |x-2|<1,
то ряд сходится. Итак, -1<x-2<1,
1<x<3
– интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках x=1
и x=3,
исследуется отдельно.
При x=1
из данного ряда получаем ряд
,
который условно сходится.
При x=3
получаем гармонический ряд
, который расходится.
Итак, данный ряд
сходится абсолютно при 1<x<3
и условно при .x=1.
Второй способ
решения.
Если для степенного ряда (2) существует

то радиус сходимости степенного ряда
можно вычислить по формуле

(22)
или 
В нашем случае
и ,
поэтому 
Так как x0=2
– центр степенного ряда, то (x0—R,
x0+R)=(1;3)
– интервал сходимости данного ряда.
Сходимость ряда
на концах интервала сходимости исследована
выше.
Итак, данный ряд
сходится абсолютно при 1<x<3
и условно при х=1.
Соседние файлы в папке Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функциональные и степенные ряды
Возьмем последовательность натуральных чисел n{n} и поставим каждому n{n} в соответствие функцию fn(x)f_n (x). Если функции fn(x)f_n (x) определены на некотором множестве x∈Ex in E, E⊂RE subset R, то на множестве EE определено выражение:
f1(x)+f2(x)+f3(x)+…+fn(x)+…,f_1 (x)+f_2 (x)+f_3 (x)+ ldots +f_n (x)+ ldots,
состоящее из функций fn(x)f_n (x), которое называется функциональным рядом.
В общем виде функциональный ряд записывается как:
∑n=1∞fn(x)sumlimits_{n=1}^{infty} f_n(x)
Примеры функциональных рядов
1+cosx2!+cos2×3!+cos3×4!+…+cosnx(n+1)!+…=∑n=1∞cosnx(n+1)!1+frac{cos x}{2!}+frac{cos 2x}{3!}+frac{cos 3x} {4!} +ldots +frac{cos nx}{(n+1)!}+ldots=sumlimits_{n=1}^{infty}frac{cos nx} {(n+1)!}
ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}
Степенные ряды являются одним из видов функциональных рядов и в общем виде записываются как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости степенного ряда.
Примеры степенных рядов
12+2!(x−5)4+3!(x−5)28+…+(n+1)!(x−5)n2n+1+…=∑n=0∞(n+1)!(x−5)n2n+1frac{1}{2}+frac{2!(x-5)}{4}+frac{3!(x-5)^2}{8}+ldots +frac{(n+1)!(x-5)^n}{2^{n+1}}+ldots =sum limits_{n=0} ^{infty} frac{(n+1)!(x-5)^n}{2^{n+1}}
ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}
Сходимость степенных рядов
Сумму SnS_n первых nn членов степенного ряда называют nn–й частичной суммой:
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)nS_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n
Если при определенном значении x∈Ex in E существует конечный предел:
limn→∞Sn(x)=S(x)limlimits_{n to infty } S_n (x) = S (x)
то ряд называется сходящимся, а значение S(x)S(x) называют суммой ряда. Если сходится ряд, составленный из абсолютных величин его членов, то такой ряд называется абсолютно сходящимся.
Если степенной ряд сходится в точке x=x1x=x_1, то он сходится абсолютно и при:
∣x∣<∣x1∣|x|<|x_1 |
Если степенной ряд расходится в точке x=x2x=x_2, то он расходится и при:
∣x∣>∣x2∣|x|>|x_2 |
Интервалом сходимости степенного ряда является:
(x0−R,x0+R)(x_0-R,x_0+R)
Здесь RR – радиус сходимости степенного ряда. Степенной ряд расходится при:
∣x−x0∣>R|x-x_0 |>R
Для граничных точек интервала
∣x−x0∣>R|x-x_0 |>R
степенной ряд может, как сходится, так и расходится, для чего требуется дополнительное изучение.
Основные признаки сходимости
Приведем основные признаки, используемые для определения сходимости степенных рядов.
1-й признак сравнения
Пусть даны два ряда с положительными членами:
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
причем, un≤vnu_n le v_n для всех номеров, начиная с некоторого nn. Тогда:
-
Если ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n сходится, то сходится и ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n
-
Если ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n расходится, то расходится и ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
2-й признак сравнения
Пусть даны два ряда с положительными членами:
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
и существует конечный и отличный от нуля предел:
limn→∞unvn≠0limlimits_{n to infty } dfrac{ u_n }{ v_n }ne 0
Тогда ряды
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
сходятся или расходятся одновременно.
Признак Лейбница для знакочередующихся рядов
При исследовании степенных рядов на сходимость часто используется признак Лейбница для знакочередующихся рядов. Ряд, содержащий как положительные, так и отрицательные члены, называют знакопеременным.
Ряд вида:
b1−b2+b3−b4+…+(−1)n+1bn+1+…=∑k=1∞(−1)k+1bk+1b_1-b_2+b_3-b_4+ ldots +{(-1)}^{n+1}b_{n+1}+ldots=sumlimits_{k=1} ^ {infty}{(-1)}^{k+1}b_{k+1},
когда любые два соседних члена имеют противоположные знаки, называется знакочередующимся.
Очевидно, каждый знакочередующийся ряд является знакопеременным.
В случае, когда выполняется два условия:
b1>b2>b3>b4>…>bn>…b_1>b_2>b_3>b_4> ldots >b_{n}> ldots, т.е когда члены ряда по модулю монотонно убывают
и
limn→∞an=0limlimits_{n to infty }{a_n}=0, т.е. когда общий член ряда стремится к нулю при n→∞n to infty, ряд сходится. Если, помимо этого, сходится ряд
b1+b2+b3+b4+…+bn+1+…=∑k=1∞bk+1b_1+b_2+b_3+b_4+ ldots + b_{n+1}+ldots=sumlimits_{k=1} ^ {infty} b_{k+1}
составленный из модулей исходного ряда, то такой ряд называют абсолютно сходящимся. Если признак Лейбница выполняется, но, при этом, ряд из абсолютных значений не сходится, то такой ряд называют условно сходящимся.
Признак Даламбера
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
и существует конечный предел
limn→∞un+1un=1limlimits_{n to infty } dfrac{ u_{n+1} }{ u_n }=1
Тогда, если l<1l<1, то данный ряд сходится; если же l>1l>1, то – расходится. Если l=1l=1 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
Признак Коши
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
такой, что существует конечный предел
limn→∞unn=1limlimits_{n to infty } sqrt [n] { u_n }=1
Тогда, если l<1l<1, то ряд сходится. В случае, если l>1l>1, то ряд расходится. Если же l=1l=1, то вопрос о сходимости рядя требует дополнительного исследования.
Интегральный признак сходимости
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
для которого существует положительная, непрерывная и монотонно убывающая на промежутке [1,+∞)[1, +infty) функция f(x)f(x) такая, что f(n)=an,n=1,2,…f(n)=a_n, n=1,2, ldots
Тогда данный ряд и несобственный интеграл ∫0∞f(x)dxintlimits_0^infty f(x) dx сходятся или расходятся одновременно.
Примеры исследования степенных рядов
Пример 1
Найти область сходимости ряда
∑n=1∞(x−1)n+12n(n+1)sum limits_{n=1} ^{infty} dfrac{(x-1)^{n+1}}{2^n {(n+1)}}
Используем признак Даламбера. Учитывая, что
∣an+1an∣=∣(x−1)(n+1)+12n+1(n+1+1):(x−1)n+12n(n+1)∣=∣(x−1)n+2(x−1)n+1⋅2n2n+1⋅n+1n+2∣=∣x−1∣2⋅n+1n+2Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x-1)^{(n+1)+1}}{2^{n+1}(n+1+1)}: dfrac {(x-1)^{n+1}}{2^n(n+1)}Bigr|= Bigl| dfrac {(x-1)^{n+2}}{(x-1)^{n+1}}cdot dfrac {2^n}{2^{n+1}}cdot dfrac {n+1}{n+2}Bigr|=dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}
находим:
limn→∞∣an+1an∣=limn→∞(∣x−1∣2⋅n+1n+2)=∣x−1∣2⋅limn→∞1+1n1+2n=∣x−1∣2limlimits_{n to infty }Bigl| dfrac{a_{n+1}}{a_n} Bigr|= limlimits_{n to infty} left(dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}right)= dfrac {|x-1|}{2} cdot limlimits_{n to infty }dfrac{1+dfrac{1}{n}}{1+dfrac{2}{n}}=dfrac {|x-1|}{2}
Для определения требуемых значений xx решаем неравенство:
∣x−1∣2<1⇔−1<x−12<1⇔−2<x−1<2⇔−1<x<3dfrac{|x-1|}{2}<1 Leftrightarrow -1<dfrac{x-1}{2}<1 Leftrightarrow -2<x-1<2 Leftrightarrow -1<x<3
Таким образом, при x∈(−1,3)x in (-1,3) ряд сходится абсолютно, а при $ x notin (-1,3) $ ряд расходится. Это означает, что (−1,3)(-1,3) – интервал сходимости данного ряда.
Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−1x=-1 и x=3x=3.
При x=3x=3 получаем ряд
∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(3−1)n+12n(n+1)=∑n=1∞2n+12n(n+1)=∑n=1∞2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(3-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2}{n+1}
Применим 2-й признак сравнения и проведем сравнение этого ряда с гармоническим:
∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}
Получаем:
limn→∞(2n+1:1n)=limn→∞(2nn+1)=limn→∞(21+1n)=2≠0limlimits_{n to infty }left( dfrac{2}{n+1}:dfrac{1}{n}right)= limlimits_{n to infty }left( dfrac{2n}{n+1}right)=limlimits_{n to infty }left( dfrac{2}{1+dfrac{1}{n}}right)=2 ne 0
Как известно, гармонический ряд расходится. Так как полученный предел отличен от нуля, то ряды
∑n=1∞2n+1sum limits_{n=1} ^{infty} dfrac{2}{n+1} и ∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}
сходятся или расходятся одновременно. В данном случае, они расходятся, и, следовательно, исходный ряд при x=2x=2 расходится.
При x=−1x=-1 получаем ряд
∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(−1−1)n+12n(n+1)=∑n=1∞(−2)n+12n(n+1)=∑n=1∞(−1)n+1⋅(2)n+12n(n+1)=∑n=1∞(−1)n+1⋅2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(-1-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-1)^{n+1}cdot (2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{ (-1)^{n+1}cdot 2}{n+1}
Как было показано, этот ряд не является абсолютно сходящимся, так как ряд, составленный из абсолютных значений:
∑n=1∞∣(−1)n+1⋅2n+1∣=∑n=1∞2n+1sum limits_{n=1} ^{infty}Bigl| dfrac{ (-1)^{n+1}cdot 2}{n+1} Bigl|=sum limits_{n=1} ^{infty} dfrac {2}{n+1}
расходится.
Используя признак Лейбница, выясним сходимость данного знакочередующегося ряда. Очевидно, что неравенство:
bn>bn+1⇔2n+1>2(n+1)+1⇔2n+1>2n+2b_n>b_{n+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{(n+1)+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{n+2}
выполнено для всех n=1,2,3,…n=1,2,3, ldots
Выполняется и второе условие:
limn→∞an=limn→∞3n+2=0limlimits_{n to infty } a_n = limlimits_{n to infty } dfrac{3}{n+2}=0
Оба условия признака Лейбница выполнены. Это означает, что знакочередующийся ряд
∑n=1∞(−1)n+13n+2sum limits_{n=1} ^{infty} (-1)^{n+1} dfrac {3}{n+2}
сходится. Так как этот ряд не является абсолютно сходящимся, то знакочередующийся ряд сходится условно.
Таким образом, областью сходимости исходного ряда является промежуток:
x∈[−1,3)x in [-1,3)
Пример 2
Найти область сходимости ряда
∑n=2∞(x+3)nnln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}
Используем признак Даламбера. Учитывая, что
∣an+1an∣=∣(x+3)n+1(n+1)ln3(n+1):(x+3)nnln3n∣=∣(x+3)n+1(x+3)n⋅nn+1⋅ln3nln3(n+1)∣=∣x+3∣⋅nn+1⋅ln3nln3(n+1)Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(n+1)ln^3{(n+1)}}: dfrac {(x+3)^n}{nln^3{n}}Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(x+3)^n}cdot dfrac {n}{n+1}cdot dfrac {ln^3{n}}{ln^3{(n+1)}}Bigr|=|x+3| cdot dfrac{n}{n+1} cdot dfrac{ln^3{n}}{ln^3{(n+1)}}
находим c помощью правила Лопиталя:
limn→+∞∣an+1an∣=limn→+∞(∣x+3∣⋅nn+1⋅ln3nln3(n+1))=∣x+3∣⋅limn→∞11+1n⋅(limn→∞lnnln(n+1))3=∣x+3∣⋅limn→∞1n1n+1=∣x+3∣limlimits_{n to +infty } Bigl| dfrac {a_{n+1}}{a_n}Bigr| = limlimits_{n to +infty } left( |x+3| cdot dfrac {n}{n+1}cdot dfrac{ln^3{n}}{ln^3{(n+1)}} right)=|x+3| cdot limlimits_{n to infty } dfrac {1}{1+dfrac{1}{n}} cdot {left(limlimits_{n to infty } dfrac {ln{n}}{ln{(n+1)}}right)}^3= |x+3| cdot limlimits_{n to infty } dfrac{dfrac{1}{n}}{dfrac{1}{n+1}}=|x+3|
Для определения требуемых значений x решаем неравенство:
∣x+3∣<1⇔−1<x+3<1⇔−4<x<−2|x+3|<1 Leftrightarrow -1<x+3<1 Leftrightarrow -4<x<-2
Таким образом, при x∈(−4,−2)x in (-4,-2) ряд сходится абсолютно, а при x∉(−4,−2)x notin (-4,-2) ряд расходится. Это означает, что (−4,−2)(-4,-2) – интервал сходимости данного ряда.
Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−4x=-4 и x=−2x=-2.
При x=−4x=-4 получаем ряд
∑n=2∞(x+3)nnln3n=∑n=2∞(−4+3)nnln3n=∑n=2∞(−1)nnln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-4+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}
Воспользуемся интегральным признаком. Возьмем функцию:
f(x)=1xln3xf(x)=dfrac{1}{x ln^3{x}}
Очевидно, что для любых x1>x2>2x_1>x_2>2:
1x2ln3×2>1x1ln3×1⇒f(x2)>f(x1)dfrac{1}{x_2 ln^3{x_2}}>dfrac{1}{x_1 ln^3{x_1}} quad Rightarrow quad f(x_2 )>f(x_1 )
Найдем неопределенный интеграл
∫dxxln3x=∫d(lnx)xln3x=(−12)(lnx)−2+C=−12ln2x+Cint dfrac {dx}{x ln^3 {x}}=int dfrac {d(ln{x})}{x ln^3 {x}}=left( -dfrac{1}{2}right)(ln{x})^{-2}+C= -dfrac{1}{2 ln^2{x}}+C
Далее:
∫2∞f(x)dx=∫2∞dxxln3x=limd→+∞∫2ddxxln3x=limd→+∞(−12ln2x∣2d)=limd→+∞(−12ln2d+12ln22)=12ln22intlimits_2^infty f(x) dx=intlimits_2^infty dfrac {dx}{x ln^3 {x}}=limlimits_{d to +infty }intlimits_2^d dfrac{dx}{xln^3 {x}}=limlimits_{d to +infty }left( -dfrac{1}{2 ln^2{x}}Bigr|_2^d right) = limlimits_{d to +infty } left(-dfrac{1}{2 ln^2{d}}+dfrac{1}{2 ln^2{2}} right) = dfrac{1}{2 ln^2{2}}
Таким образом, несобственный интеграл сходится. Это значит, что ряд
∑n=2∞1nln3nsum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}
также сходится, а ряд
∑n=2∞(−1)nnln3nsum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}
сходится абсолютно.
При x=−2x=-2 получим ряд
∑n=2∞(x+3)nnln3n=∑n=2∞(−2+3)nnln3n=∑n=2∞1nln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-2+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}
Как было показано, этот ряд сходится абсолютно. Следовательно, область сходимости исходного ряда – промежуток [−4,−2][-4, -2].
Тест по теме “Степенные ряды”
Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).
Например, исходный ряд 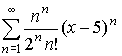
Правила ввода функций:
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, (x-4)n, записываем как(x-4)^n. - Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)
Пример. 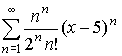
Решение.
Общий вид степенного ряда 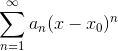
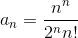
Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:
|x-x0|<R или x0-R<x<x0+R
Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.
Найдем радиус сходимости ряда, используя формулу Даламбера:
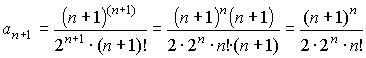
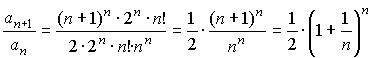
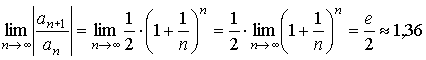
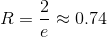
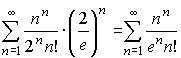
Для исследования сходимости этого ряда используем формулу Стирлинга 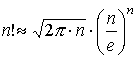
Получим ряд сравнения. Этот ряд расходится.
Проверим сходимость ряда при 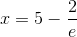
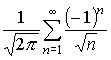
Этот ряд сходится (по признаку Лейбница).
Итак, мы получили область сходимости исходного ряда:
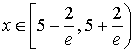
Пример 1:
Найти область сходимости ряда:
Решение от преподавателя:
Пример 2:
Найти область сходимости ряда:
Решение от преподавателя:
Пример 3:
Найти область сходимости ряда:
Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где:
R — радиус сходимости. Вычислим его:
x1 = 2 — 1 = 1
x2 = 2 + 1 = 3
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (1;3)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = 1
Получаем ряд:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
б) По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется.
Ряд сходится, значит, x = 1 — точка сходимости.
При x = 3
получаем ряд:
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 3 — точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x [1;3)
Пример 4:
Исследовать область сходимости функционального ряда:
Решение от преподавателя:
Пример 5:
Найти область сходимости степенного ряда:
Решение от преподавателя:
Пример 6:
Найти область сходимости ряда:
Решение от преподавателя:


при любом х – ряд расходится всюду.
Пример 7:
Найти область сходимости ряда:
Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где:
R — радиус сходимости. Вычислим его:
x1 = -1 — 2 = -3
x2 = -1 + 2 = 1
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-3;1)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = -3
Получаем ряд:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется
1<2<3
б) По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница не выполняется.
Ряд расходится, значит, x = -3 — точка расходимости.
При x = 1
получаем ряд:
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 1 — точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x (-3;1)
Пример 8:
Найти область сходимости ряда:
Решение от преподавателя:


Следовательно, ряд сходится, если
и расходится, если
Если x=4/9, то ряд принимает вид 
Если x=2/3, то ряд принимает вид 


Окончательно получаем область сходимости исходного ряда: [4/9;2/3).
Пример 9:
Найдите множество абсолютной (условной) сходимости ряда:
Решение от преподавателя:
Пример 10:
Найти область сходимости ряда:
Решение от преподавателя:


Следовательно, ряд сходится, если
и расходится, если
Если x=-3/7, то ряд принимает вид 
Если x=-1/7, то ряд принимает вид 
Окончательно получаем область сходимости исходного ряда: [-3/7;-1/7].
Пример 11:
Найдите множества абсолютной (условной) сходимости ряда
Решение от преподавателя:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
Проверяем выполнение признака Лейбница:
Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю, то ряд сходится.
Ряд знакочередующийся. Составим ряд из абсолютных величин членов данного ряда
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
Второе условие Лейбница выполняется.
Данный ряд сходится, так как удовлетворяет условиям признака Лейбница для знакочередующихся рядов.
Следовательно, ряд условно сходящийся.
Следовательно, сходится условно и исходный ряд.
Область сходимости ряда:(-∞; +∞)
Пример 12:
Найти область сходимости ряда:
Решение от преподавателя:



Такой ряд сходится, если
Однако 

Пример 13:
Найти область сходимости ряда:
Решение от преподавателя:
По признаку Лейбница ряд расходится
Т. о., область сходимости имеет вид (-1; 1)
Пример 14:
Найти область сходимости ряда:
Решение от преподавателя:


Следовательно, ряд сходится, если
и расходится, если
Если x=1/6, то ряд принимает вид 
Если x=3/2, то ряд принимает вид 
Окончательно получаем область сходимости исходного ряда: 
Пример 15:
Найти область сходимости ряда:











































