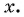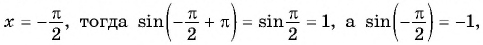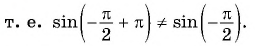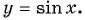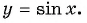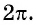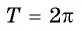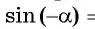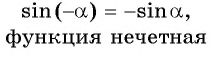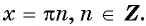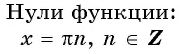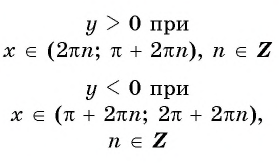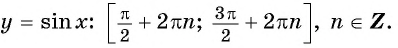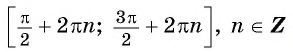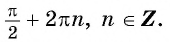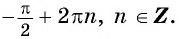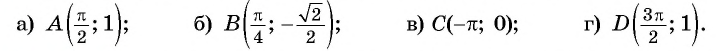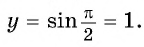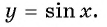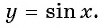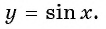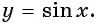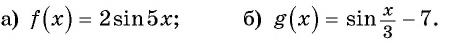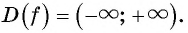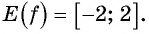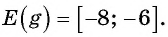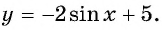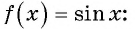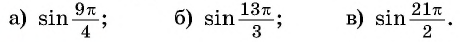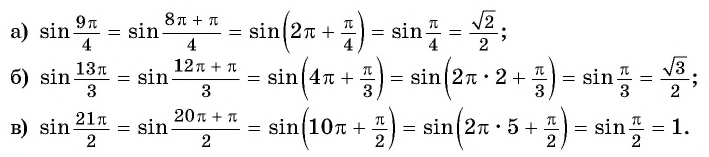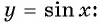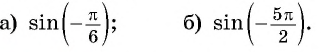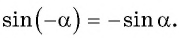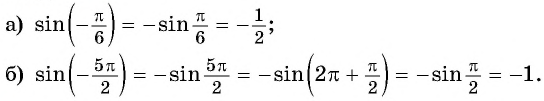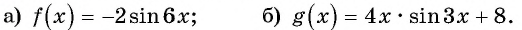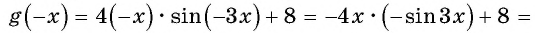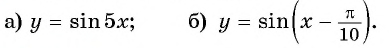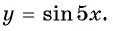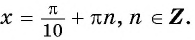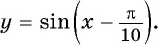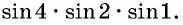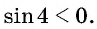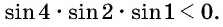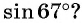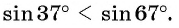Таблицы DPVA.ru — Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru: 
|
|||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 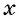
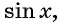
Рассмотрим свойства функции 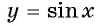
Область определения функции y=sin x
Областью определения функции 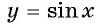
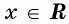
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 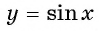
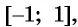
Графически это означает, что график функции 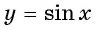
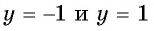
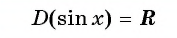
Периодичность функции y=sin x
Периодичность функции 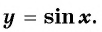
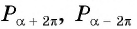
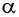
Говорят, что число 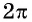
Определение:
Функция 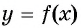
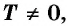
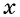
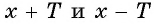
Чтобы определить, является ли функция периодической с периодом 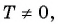
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 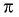
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 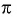
Периодом функции 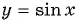
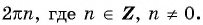
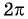
Функция 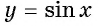
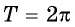
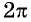
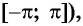
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 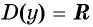
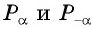
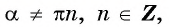
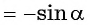
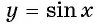
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
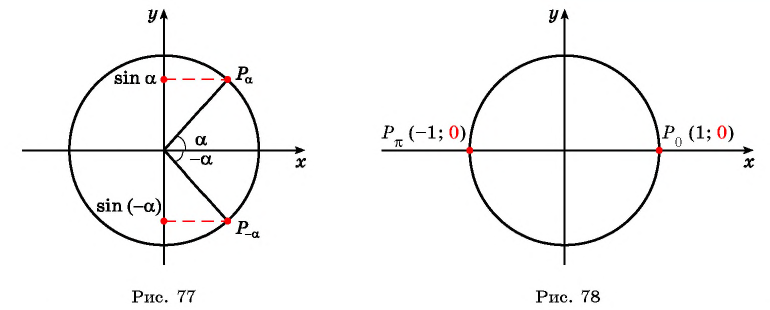
Нули функции y=sin x
Нули функции. Ординаты точек 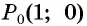
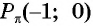
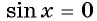
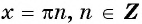
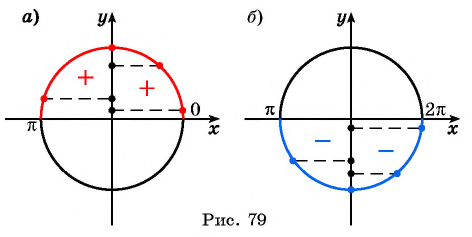
Промежутки знакопостоянства функции y=sin x
На промежутках 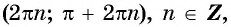
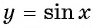
На промежутках 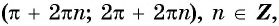
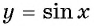
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 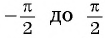
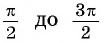
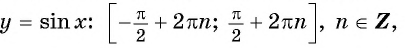
Функции 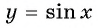
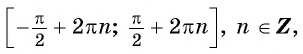
Наибольшее значение функции 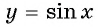
Наименьшее значение функции 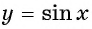
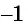
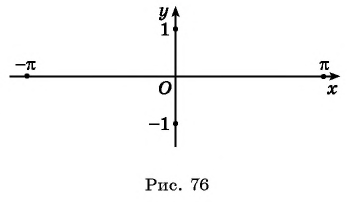
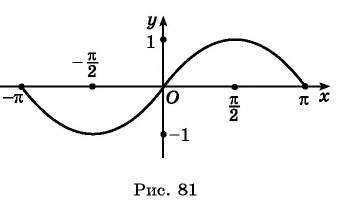
На основании проведенного исследования построим график функции 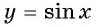
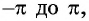
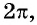
На этом периоде функция
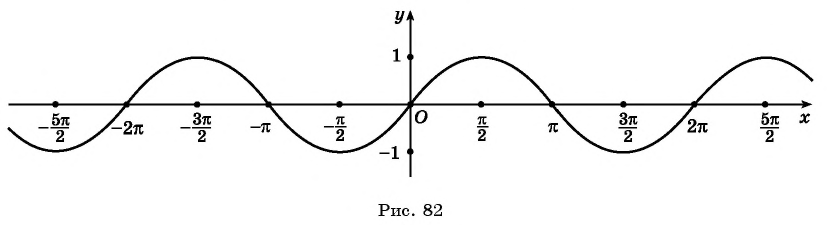
На рисунке 81 изображена часть графика функции 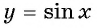
Перенесем эту часть на другие периоды и получим график функции 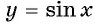
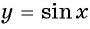
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 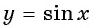
Решение:
а) Подставим в формулу 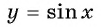
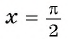
Полученное значение функции равно ординате точки 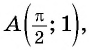
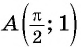
б) При 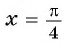
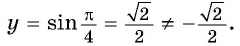
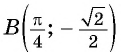
в) При 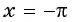
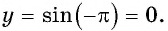
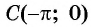
г) При 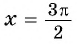
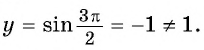
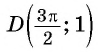
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 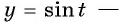
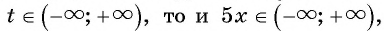
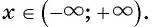
Множеством значений функции 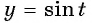
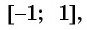
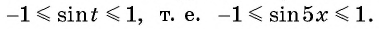
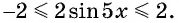
б) 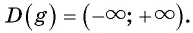
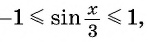
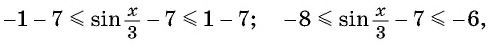
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 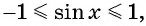
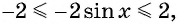
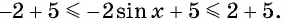
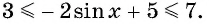
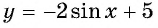
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 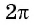
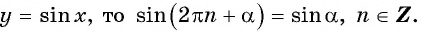
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 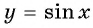
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
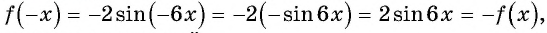
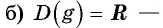
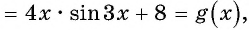
Пример №7
Найдите нули функции:
Решение:
а) Пусть 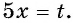
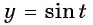
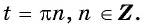
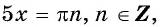
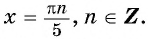
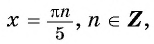
б) Пусть 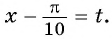
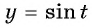
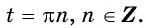
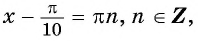
Таким образом, числа 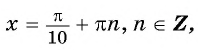
Пример №8
Определите знак произведения
Решение:
Так как 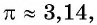
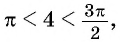
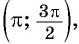
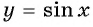
Углы 2 радиана и 1 радиан принадлежат промежутку 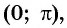
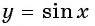
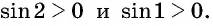
Пример №9
Что больше: 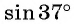
Решение. Так как функция 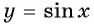
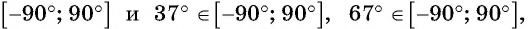
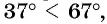
Пример №10
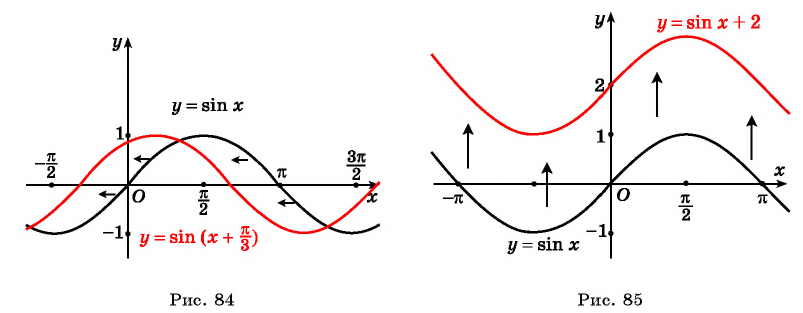
Постройте график функции:
Решение:
а) График функции 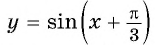
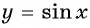
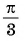
б) График функции 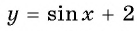
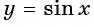
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
Область определения: (D(x)=R).
(y(-x)=-y(x)) — нечётная.
Построение графика этой функции происходит таким же способом, как и графика функции
y=cosx
, начиная с построения, например, на отрезке
0;π
.
Но можно упростить, применив формулу
sinx=cosx−π2
, которая показывает, что график функции
y=sinx
можно получить путём сдвига графика функции
y=cosx
вдоль оси абсцисс вправо на
π2
.
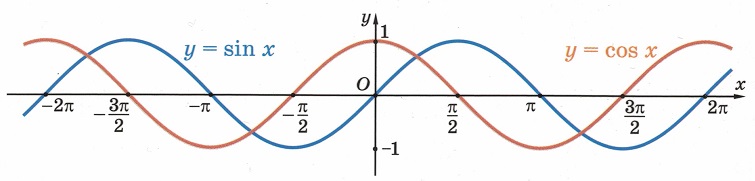
Кривая, являющаяся графиком функции
y=sinx
, называется синусоидой.
1. Область определения — множество
ℝ
всех действительных чисел.
2. Множество значений — отрезок
−1;1
.
3. Функция
y=sinx
имеет период (T =)
2π
.
4. Функция
y=sinx
является нечётной.
5. Нули функции:
x=πn,n∈ℤ
;
наибольшее значение равно (1) при
x=π2+2πn,n∈ℤ
;
наименьшее значение равно (-1) при
x=−π2+2πn,n∈ℤ
;
значения функции положительны на интервале
0;π
, с учётом периодичности функции на интервалах
2πn;π+2πn,n∈ℤ
;
значения функции отрицательны на интервале
π;2π
, с учётом периодичности функции на интервалах
π+2πn;2π+2πn,n∈ℤ
.
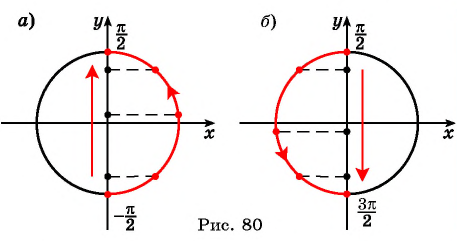
— возрастает на отрезках
−π2;π2
, с учётом периодичности функции на отрезках
−π2+2πn;π2+2πn,n∈ℤ
;
— убывает на отрезке
π2;3π2
, с учётом периодичности функции на отрезках
π2+2πn;3π2+2πn,n∈ℤ
.
ВИДЕО УРОК
Периодические функции.
Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:
f(х + Т) = f(х) = f(х – Т).
Число Т называют периодом функции у = f(х).
Из этого
определения сразу следует, что если Т –
период функции
у = f(х), то
2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т
– также периоды
функций. Значит у периодической функции бесконечно много периодов.
Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.
Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.
График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.
График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)
Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на
± Т, ±
2Т, ± 3Т, …
Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках
(–Т/2; 0) и (Т/2; 0) или
(0; 0) и (Т; 0).
ПРИМЕР:
Рассмотрим функцию
у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:
f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).
Следовательно, при любом
значении х
f(x + 1) = f(x).
А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.
График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.
Периодичность тригонометрических функций.
Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.
Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.
Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то
sin (α + 2π) = sin α или
sin (α + 360°) = sin α
и
cos (α + 2π)
= cos α или
cos (α + 360°) = cos α.
Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.
Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:
sin (α + 2kπ) = sin α или
sin (α + 360°k) = sin α
и
cos (α + 2kπ) = cos α или
cos (α + 360°k) = cos α,
где k – любое целое
число.
Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.
Периодом функции sin α и cos α
является 2π или 360°.
Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.
Построим точку М‘,
симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.
Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому
sin α = у, cos α = х,
sin (α + π) = –у,
cos (α + π) = –х.
Отсюда
и, следовательно,
tg (α + π) = tg α,
сtg (α + π)
= сtg α.
отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:
tg (α + kπ) = tg α,
сtg (α + kπ) = сtg α.
где k – любое целое
число.
Периоды функций
y = A sin (ωx + φ) и
y = A cos (ωx + φ)
вычисляются по формуле
T = 2π/ω,
а период функции
y = A tg (ωx + φ)
по формуле
T = π/ω.
Если период функции y = f(x) равен T1, а период функции y = g(x) равен T2, то период функций
y = f(x) + g(x) и
y = f(x) – g(x)
равен наименьшему числу, при делении которого
на T1 и T2 получаются целые числа.
ПРИМЕР:
Найти
период функции
y = 3 sin (x – 2) + 7 соs πx.
РЕШЕНИЕ:
Период
функции
y = 3 sin (x – 2)
равен
T1 = 2π/1 = 2π.
Период
функции
y = 7 соs πx
равен
T2 = 2π/π = 2.
Периода
у функции
y = 3 sin (x – 2) + 7 соs πx
не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.
ОТВЕТ:
Периода
не существует.
ПРИМЕР:
Доказать
следующее утверждение:
tg
3850° = tg 250°.
РЕШЕНИЕ:
Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:
tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.
ПРИМЕР:
Доказать
следующее утверждение:
сos (–13π) = –1.
РЕШЕНИЕ:
Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
ПРИМЕР:
Доказать
следующее утверждение:
sin (–7210°) = – sin 10°.
РЕШЕНИЕ:
Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:
sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.
ПРИМЕР:
Найти основной период функции
sin 7х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
sin 7х = sin 7(х + t) = sin (7х + 7t)
так как 2πk период синуса, то получим:
sin (7х + 7t) = sin (7х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти основной период функции
соs 0,3х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)
так как 2πk период косинуса, то получим:
соs (0,3х + 0,3t) = соs (0,3х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти период функции:
y = 5sin 2x + 2ctg 3х.
РЕШЕНИЕ:
Период функции
y = 5sin 2x
равен Т1 = 2𝜋/2 = π,
а период функции
y = 2ctg 3х
равен Т2 = 𝜋/3.
Наименьшее число, при делении которого на
Т1 = π и Т2 = 𝜋/3
– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.
ПРИМЕР:
Найти период функции:
y = 9sin (5x + π/3) – 4cоs (7х + 2).
РЕШЕНИЕ:
Находим периоды слагаемых. Период функции
y = 9sin (5x + π/3)
равен Т1 = 2𝜋/5,
а период функции
y = 4cоs (7х + 2)
равен Т2 = 2𝜋/7.
Очевидно, что период заданной функции равен
Т = 2π.
ПРИМЕР:
Найти период функции:
y = 3sin πx + 8tg (х + 5).
РЕШЕНИЕ:
Период функции
y = 3sin πx
равен Т1 = 2π/π = 2,
а период функции
y = 8tg (х + 5)
равен Т2 = 𝜋/1 = π.
Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
ПРИМЕР:
Найти период функции:
y = sin 3x + соs 5х.
РЕШЕНИЕ:
Период функции
y = sin 3x
равен Т1 = 2π/3,
а период функции
y = соs 5х
равен Т2 = 2π/5.
Приведём к общему знаменателю периоды:
Т1 = 10π/15, Т2 = 6π/15.
Тогда наименьшее общее кратное (НОК) будет:
НОК (10π; 6π)
= 30π.
Теперь найдём период заданной функции:
Т = 30π/15 = 2π.
Задания к уроку 5
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
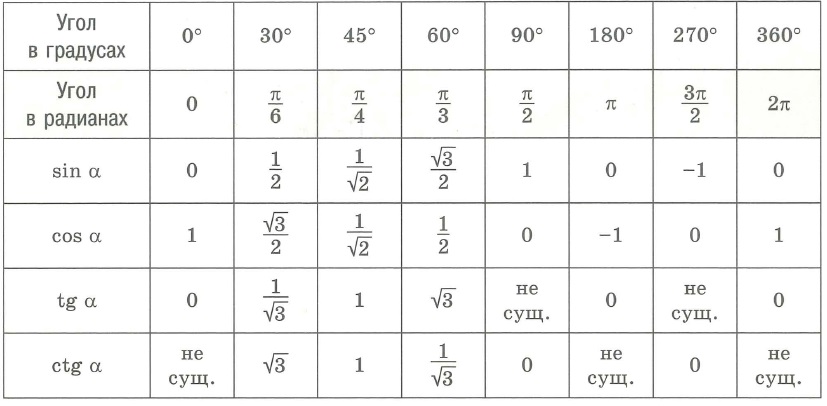
- Урок 4. Натуральные тригонометрические таблицы
- Урок 6. Область определения и область значения тригонометрических функций
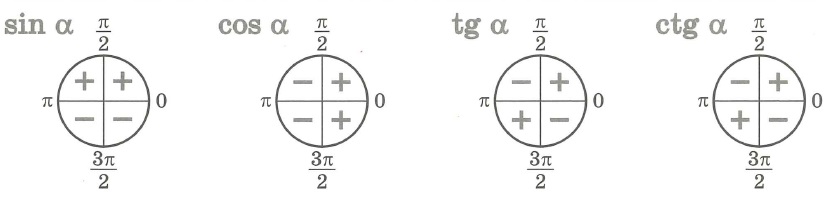
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
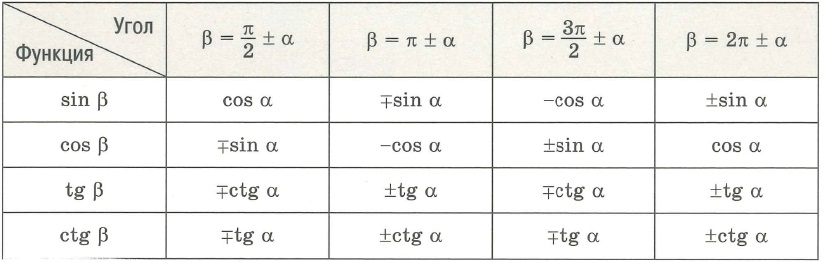
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
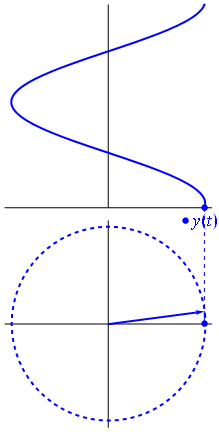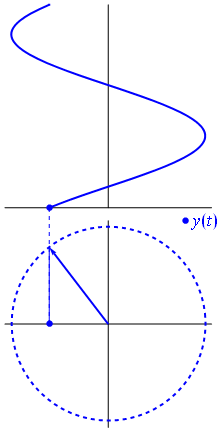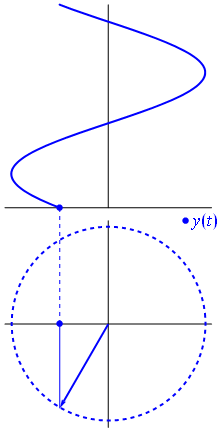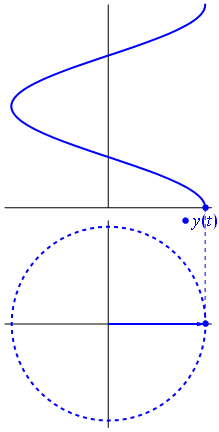
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Как определить промежутки по окружности
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Способы отбора корней в тригонометрических уравнениях
Класс: 10
Автор проекта:
Шелкова Полина,
Класс: 10
Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]
sinx−(cos 2 x−sin 2 x)=0;
sinx−(1−sin 2 x−sin 2 x)=0;
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
Вернемся к замене:
б) Рассмотрим три способа отбора корней, попадающих в отрезок 
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни:
3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
http://b4.cooksy.ru/articles/kak-opredelit-promezhutki-po-okruzhnosti
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/










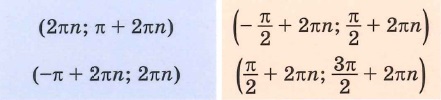
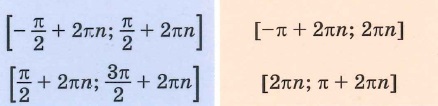




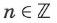

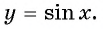
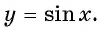
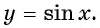
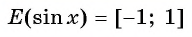
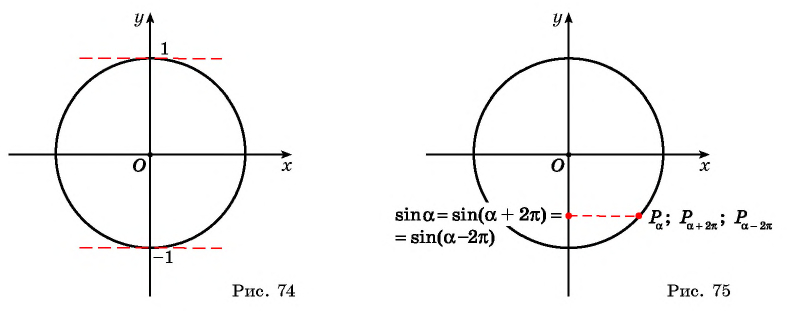
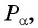
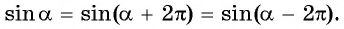
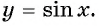
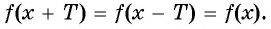
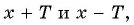 если
если 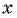 принадлежит области определения функции;
принадлежит области определения функции;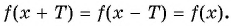
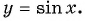
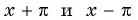 принадлежат области определения функции, так как
принадлежат области определения функции, так как 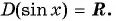
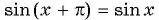 для всех
для всех