Как найти интервал убывания параболы

В предложенном Вами примере необходимо найти промежутки убывания и возрастания квадратичной функции, поэтому для начала Вам требуется найти абсциссу вершины параболы, являющейся графиком этой самой квадратичной функции. Формула для ее нахождения выглядит так:

Подставляя значения из нашего примера, получим х0=10. Поскольку коэффициент а в нашем случае положителен (он равен 1/4), то заданная функция убывает на промежутке (–∞, 10) и возрастает на промежутке (10, +∞).

Можно использовать и другой метод. Находим производную заданной функции:

f'(x)=x/2-5

и определяем ее нули:

х1=10.

Функция будет убывающей в интервале, в котором производная меньше нуля, и возрастает в интервале, в котором производная больше. В нашем случае получаем все тот же ответ: она убывает на промежутке (–∞, 10) и возрастает на промежутке (10, +∞).

Содержание

• — Как определять возрастание и убывание функции?
• — Как определить возрастает или убывает функция парабола?
• — Как доказать что функция является убывающей?
• — Что такое промежутки монотонности?
• — Как найти область монотонности функции?
• — Как определить монотонная функция?
• — Как понять где возрастает парабола?
• — Как определить промежутки Знакопостоянства квадратичной функции?
• — Что такое гипербола и парабола?
• — Как понять что функция возрастает?
• — Как понять возрастает или убывает функция 7 класс?
• — Что такое убывающая функция?
• — Что такое промежутки монотонности функции?
• — Что такое промежутки монотонности квадратичной функции?
• — Как определить на каком промежутке функция возрастает?

Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x) . Если на промежутке f′(x)<0 , то на этом промежутке функция убывает; если на промежутке f′(x)>0 , то на этом промежутке функция возрастает.

Как определять возрастание и убывание функции?

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

1. найти область определения функции;
2. найти производную функции;
3. решить неравенства и на области определения;
4. к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Как определить возрастает или убывает функция парабола?

Графиком любой квадратичной функции является парабола. Ветви ее направлены либо вверх, либо вниз, в зависимости от знака коэффициента а. Если ветви направлены вверх, то квадратичная функция сначала убывает от –∞ до самой вершины параболы, а затем начинает возрастать от вершины до +∞.

Как доказать что функция является убывающей?

Функция является убывающей, если для большего значения аргумента соответствует меньшее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции убывают, то заданная функция убывает.

Что такое промежутки монотонности?

Промежутки монотонности функции y = f (x) — это такие интервалы значений аргумента х, при которых функция y = f (x) возрастает либо убывает. …

Как найти область монотонности функции?

Для исследования функции на монотонность необходимо:

1. найти её производную ;
2. найти критические точки функции как решения уравнения ;
3. определить знак производной на каждом из промежутков, на которые критические точки разбивают область определения функции;

Как определить монотонная функция?

Монотонная функция — это функция, которая всё время либо возрастает, либо убывает. Функция y=f(x) называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.

Как понять где возрастает парабола?

Теория: Графиком квадратичной функции y = a x 2 ( a ≠ 0 ) является парабола, вершина которой находится в начале координат. … Если при возрастании значений аргумента (x) возрастают также значения функции (y), то функция является возрастающей.

Как определить промежутки Знакопостоянства квадратичной функции?

Алгоритм нахождения промежутков знакопостоянства квадратичной функции y = ax2 + bx + c:

1. найти корни уравнения ax2 + bx + c = 0, нанести их на числовую прямую;
2. если корни есть, то они разобьют числовую прямую на несколько промежутков – это и будут промежутки знакопостоянства.

Что такое гипербола и парабола?

Ключевое отличие: Парабола — это коническое сечение, которое создается, когда плоскость разрезает коническую поверхность параллельно стороне конуса. Гипербола создается, когда плоскость разрезает коническую поверхность, параллельную оси.

Как понять что функция возрастает?

Функция является возрастающей, если для большего значения аргумента соответствует большее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции тоже возрастают, то заданная функция возрастает.

Как понять возрастает или убывает функция 7 класс?

линейная функция или возрастает, или убывает. Если k>0, то линейная функция y = kx + m возрастает; если k<0, то линейная функция y = kx + m убывает.

Что такое убывающая функция?

Функция называется убыва́ющей, если большему значению аргумента соответствует не большее (по другой терминологии — меньшее) значение функции.

Что такое промежутки монотонности функции?

Определение 2: Промежутки области определения, на которых функция возрастает или убывает, называются промежутками монотонности функции.

Что такое промежутки монотонности квадратичной функции?

Монотонность, промежутки знакопостоянства квадратичной функции … Функция убывает на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. Промежутки убывания и возрастания функции называются промежутками монотонности функции.

Как определить на каком промежутке функция возрастает?

Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x) . Если на промежутке f′(x)<0 , то на этом промежутке функция убывает; если на промежутке f′(x)>0 , то на этом промежутке функция возрастает.

Интересные материалы:

Что произошло со Швабриным в конце произведения?
Что произошло в 1984 Apple?
Что произошло в ссср в 1977?
Что проходят на астрономии?
Что проводят сосуды?
Что раньше использовалось в баскетболе вместо колец?
Что раньше носили вместо трусов?
Что расширяется при нагревании тела?
Что рассказал смотритель рассказчику о Дуне?
Что разделяет Северную и Евразию?

	(a > 0) (коэффициент (a) положительный)	(a < 0) (коэффициент (a) отрицательный)
	Ветви параболы направлены вверх	Ветви параболы направлены вниз
	Функция убывает, если x∈(−∞;0 , возрастает, если x∈0;+∞	Функция возрастает, если x∈(−∞;0 , убывает, если x∈0;+∞
	Наибольшее значение функции: нет	Наибольшее значение функции: (y = 0)
	Наименьшее значение функции: (y = 0)	Наименьшее значение функции: нет
	Функция положительная ((y > 0)), если x∈(−∞;0)∪(0;+∞) (график находится выше оси (Ox))	Интервалы, в которых значение функции положительное:  нет
	Интервалы, в которых значение функции отрицательное: нет	Функция отрицательная ((y < 0)), если x∈(−∞;0)∪(0;+∞) (график находится ниже оси (Ox))

Что такое возрастание функции

В начале прочитаем определение возрастания функции.

Определение сложно понять без наглядного примера.
Поэтому сразу перейдём к разбору задачи на возрастание функции.

По-другому можно сказать, что, если каждому бóльшему значению « x »
соответствует бóльшее значение « y », значит,
функция « y(x) » возрастает.

x2 > x1 y( x2 ) > y( x1 )

Обязательное условие возрастания функции

Давайте разберем определение возрастания функции на конкретном примере.

Разбор примера

Возрастающей или убывающей является функция « y = 9x − 4 » ?

Для начала определим
область определения функции
« y = 9x − 4 ».

y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.

Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.

Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.

Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».

x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4

Для второй точки возьмем « x = 1 ».

x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5

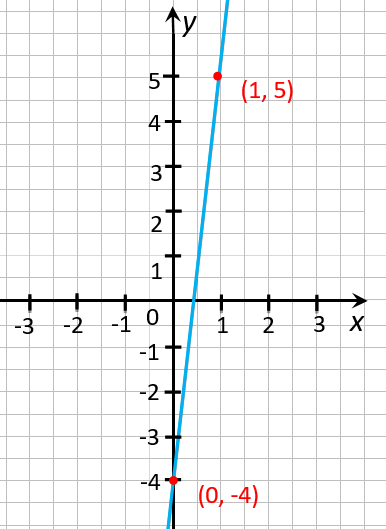
Отметим две полученные
точки «(0; −4)» и «(1; 5)» на

координатной плоскости
и проведем через них прямую.

Докажем, что функция
« y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и
аналитически
(по ее формуле).

Как определить по графику, что функция возрастает

По определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.

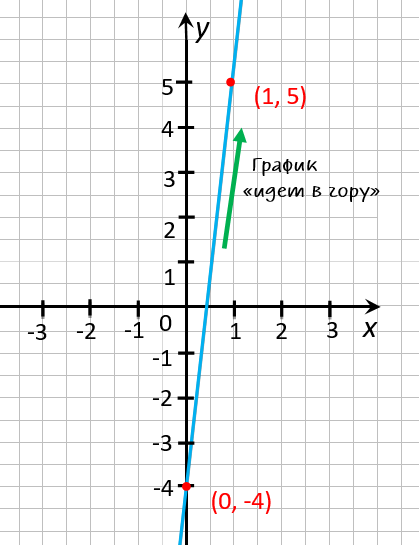
На рисунке ниже видно, что график функции « y = 9x − 4 »
«идет в гору». Другими словами, при увеличении « x »
↑ растет
значение « y » ↑.

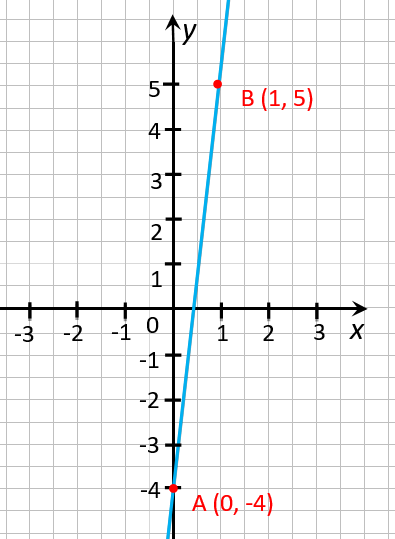
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».

У первой точки « (·)A »
координаты:
x₁ = 0 ;   y₁ = − 4

У второй точки « (·)B » координаты:
x₂ = 1 ;   y₂ = 5

На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x₂ > x₁ )»
растет
« y ↑ ( y₂ > y₁ ) ».
Поэтому график зрительно «идет в гору».

Как по формуле доказать, что функция возрастает

Вернёмся к нашей функции
« y = 9x − 4 ».

По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?

Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.

По определению возрастания функции нам нужно доказать, что при
« x₂ > x₁ » увеличивается значение функции
« y( x₂ ) > y( x₁ ) ».

Но как нам найти значения функции
« y( x₁ )» и
«y( x₂ ) »?

Для нахождения « y( x₁ )» и
«y( x₂ ) »

достаточно подставить « x₁ » и
« x₂ » в исходную формулу « y = 9x − 4 ».

y( x₁ ) = 9x₁ − 4
y( x₂ ) = 9x₂ − 4

Теперь запишем обязательное условие возрастания функции.

x2 > x1 y( x2 ) > y( x1 )

Обязательное условие возрастания функции

Подставим в неравенство
« y( x₂ ) >
y( x₁ ) » полученные формулы

« y( x₁ ) = 9x₁ − 4» и
« y( x₂ ) = 9x₂ − 4 » .

y( x₂ ) > y( x₁ )
9x₂ − 4 > 9x₁ − 4

Упростим полученное
неравенство.

9x₂ − 9x₁ > − 4 + 4
9x₂ − 9x₁ > 0

Вынесем общий множитель
в левой части неравенства.

9(x₂ − x₁) > 0

Разделим левую и правую часть на «9».

При делении нуля на любое число получается ноль.

x₂ − x₁ > 0
x₂ > x₁

Мы доказали, что выполняется исходное условие возрастания функции «x₂ > x₁».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.

В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».

---

Посмотрим другой пример, где требуется доказать, что функция возрастает.

Разбор примера

Доказать, что функция возрастает на всей области определения: y = 13x − 1

По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.

x2 > x1 y( x2 ) > y( x1 )

Обязательное условие возрастания функции

Вместо « y( x₁ )» и
«y( x₂ ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.

Что и требовалось доказать.

Что такое убывание функции

Как по графику понять, что функция убывает

Разбор примера

Доказать, что функция убывает на всей области определения: y = 1 − 3x

По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.

Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.

Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».

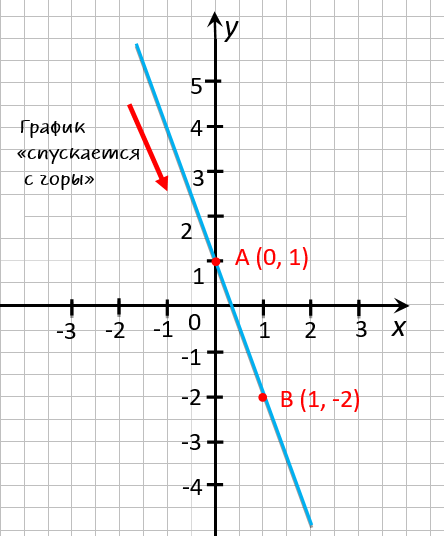
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».

На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.

Как по формуле доказать, что функция убывает

Вернёмся к нашей функции
« y = 1 − 3x ».

По ее графику мы поняли, что функция убывает, так как график «спускается с горы». Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?

Давайте разберем на примере функции
« y = 1 − 3x ». Докажем, что она убывает
на всей своей области определения.

x2 > x1 y( x2 ) < y( x1 )

Обязательное условие убывания функции

Подставим « y( x₁ )» и
«y( x₂ ) » в
формулу функции « y = 1 − 3x » и упростим полученное неравенство.

Умножим на « −1 » левую и правую часть неравенства. При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.

−x₂ < −x₁ | · (−1)

x₂ > x₁

Что и требовалось доказать.

Как по графику функции определить
возрастание и убывание

Потренируемся только по графику функции определять промежутки возрастания и убывания функции.

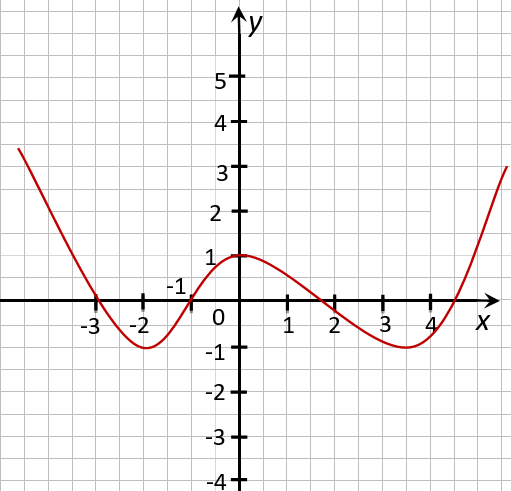
Разбор примера

На рисунке ниже изображён график функции, определенной на множестве действительных чисел.
Используя график, найдите промежутки возрастания и промежутки убывания функции.

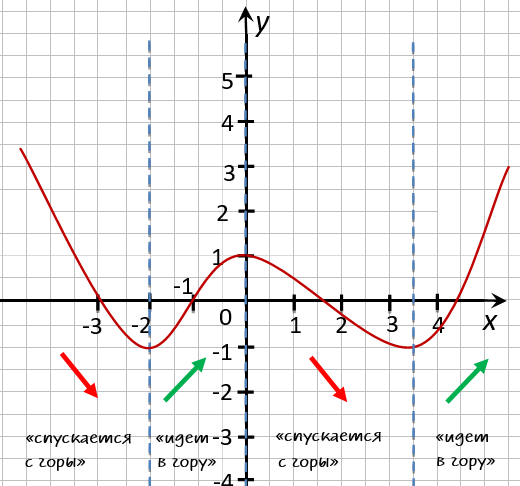
Отметим с помощью штриховых линий промежутки, где график функции убывает
(«спускается с горы») и где он возрастает («идет в гору»).

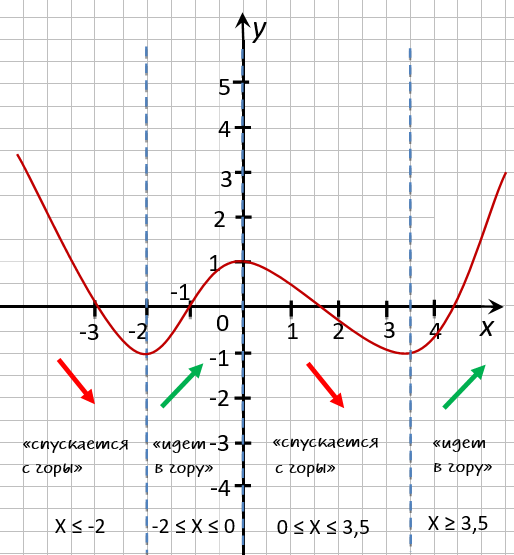
Запишем через знаки неравенств,
какие значения принимает « x » на полученных промежутках.
Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их
концы входят в промежуток, то есть используем знаки нестрогого неравенства.

Остаётся записать полученные промежутки возрастания и убывания функции в ответ.

Ответ:

• функция убывает при
     x ≤ −2;     0 ≤ x ≤ 3,5
• функция возрастает при
      −2 ≤ x ≤ 0 ;     x ≥ 3,5

Более грамотно будет записать ответ с помощью специальных
математических символов.

Ответ:

• функция убывает на промежутках    
  x ∈ (−∞ ; −2] ∪ [0; 3,5]
• функция возрастает на промежутках     x ∈ [−2 ; 0] ∪ [3,5 ; +∞]

При каких значениях
« m »
функция является убывающей или возрастающей

Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.

Разбор примера

При каких значениях « m » функция

« y = mx − m − 3 + 2x » является убывающей?

Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.

x2 > x1 y( x2 ) < y( x1 )

Обязательное условие убывания функции

Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче. Вместо
« x »
подставим « x₁ » и « x₂ ».

Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.

mx₂ − m − 3 + 2x₂ − mx₁
+ m
+ 3
− 2x₁
< 0

Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.

mx₂ − mx₁
− m + m − 3 + 3 + 2x₂ − 2x₁

< 0

mx₂ − mx₁ + 2x₂ − 2x₁

< 0

Вынесем общие множители за скобки.

m( x₂ − x₁) + 2(x₂ − x₁)

< 0

Теперь
вынесем общий множитель

« ( x₂ − x₁ ) ».

( x₂ − x₁) (m + 2)

< 0

Вспомним обязательное условие убывания функции.

x2 > x1 y( x2 ) < y( x1 )

Обязательное условие убывания функции

Преобразуем исходное условие убывания функции « x₂ > x₁ ».
Перенесем все в левую часть.

x₂ > x₁

x₂ − x₁ > 0

По условию убывания функции
« x₂ − x₁ > 0 »,
значит, чтобы
произведение
«( x₂ − x₁) (m + 2)

» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.

+	·	−	< 0
(x2 − x1)	·	(m + 2)	< 0

Решим полученное неравенство.

m + 2 < 0
m < −2

Ответ: при «m < −2» функция
« y = mx − m − 3 + 2x »
является убывающей.

---

Ваши комментарии

Оставить комментарий:

---