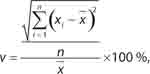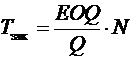Как найти интервал времени между заказами

Расчет
интервала времени между заказами можно
производить следующим образом:

I
= N:S/ОРЗ

N —
количество рабочих дней в году, дни;

S —
потребность в заказываемом продукте,
шт.;

ОРЗ —
оптимальный размер заказа, шт.

Полученный
с помощью формулы интервал времени
между заказами не может рассматриваться,
как обязательный к применению. Он может
быть скорректирован на основе экспертных
оценок. Например, при полученном расчетном
результате (4 дня), возможно, использовать
интервал в 5 дней, чтобы производить
заказы один раз в неделю.

Исходные
данные для расчета параметров системы
следующие:

• потребность
  в заказываемом продукте, шт.;

• интервал
  времени между заказами, дни;

• время
  поставки, дни;

• возможная
  задержка поставки, дни.

Гарантийный
(страховой) запас, позволяет обеспечивать
потребность на время предполагаемой
задержки поставки (под возможной
задержкой поставки также подразумевается
максимально возможная задержка).
Восполнение гарантийного запаса
производится входе последующих поставок
через пересчет размера заказа таким
образом, чтобы его поставка увеличила
запас до желательного максимального
уровня.

Так
как в рассматриваемой системе момент
заказа, заранее определен и не меняется
ни при каких обстоятельствах, постоянно
пересчитываемым параметром является
именно размер заказа. Его вычисление
основывается на прогнозируемом уровне
потребления до момента поступления
заказа на склад организации. Расчет
размера заказа в системе с фиксированным
интервалом времени между заказами
производится по формуле:

РЗ
= МЖЗ – ТЗ +ОП

РЗ —
размер заказа, шт.;

МЖЗ —
желательный максимальный запас, шт.;

ТЗ —
текущий запас, шт.;

ОП —
ожидаемое потребление за время поставки,
шт.

Как
видно из формулы, размер заказа
рассчитывается таким образом, что при
условии точного соответствия фактического
потребления за время поставки ожидаемому
поставка пополняет запас на складе до
желательного максимального уровня.
Разница между желательным максимальным
и текущим запасом определяет величину
заказа, необходимую для восполнения
запаса до желательного максимального
уровня на момент расчета, а ожидаемое
потреблениеза время поставки обеспечивает
это восполнение в момент осуществления
поставки.

Список использованной литературы

1. Сергеев
   В.И., Сергеев И.В. Логистические системы
   мониторинга цепей поставок: Учеб.пособие.
   — М.: ИНФРА-М, 2003, 172с.

2. Логистика:
   Учебник. / Под ред. Б.А. Аникина. — 3-е изд.,
   перераб. и допол. — М.: ИНФРА-М, 2005, 368с.

3. Основы
   логистики: Учебник для вузов/Под ред.
   В.В.Щербакова. –СПб.: Питер, 2009.

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Одним из ключевых элементов оптимизации цепей поставок является процесс управления запасами в рамках всей цепи поставок. Создание интегрированной системы управления запасами позволит минимизировать общие активы цепи, связанные с запасами.

Высокие уровни запасов на протяжении всей цепи поставок являются симптомом низких показателей функционирования системы. Как правило, большие объемы запасов продукции объясняются опасением возникновения дефицита, что может привести к сбоям в работе цепи поставок, а для производственных предприятий — к полной остановке производства, а это влечет за собой серьезные убытки. Чтобы избежать подобной ситуации и обеспечить высокие уровни обслуживания при низких уровнях запасов, необходимо устранить источники нестабильности и неопределенности в цепи поставок.

Классическая модель управления запасами является детерминированной моделью и предназначена для оптимизации размера текущей части запаса. В торговых организациях при управлении товарными запасами речь идет об оптимизации размера заказа (партии закупки или поставки), а в управлении товарными (сбытовыми) запасами готовой продукции предприятий-производителей — об оптимизации партий отгрузки товара.

Обратите внимание. Оптимизация размера заказа (партии поставки) означает, что необходимо найти такое его количественное значение, которое потребует минимальных затрат на формирование и содержание текущего запаса при заданных условиях.

Методика решения данной задачи базируется на том, что различные составляющие затрат изменяются разнонаправлено при изменении размера партии поставки. Следовательно, существует такой размер партии закупки, который обеспечивает минимум общих (суммарных) затрат, связанных с формированием и содержанием запаса. Наименьшие затраты будут определять оптимальную стратегию закупки материального ресурса в заданных условиях, то есть минимум удельных затрат является критерием оптимальности выбора размера заказа (объема партии поставки) и максимального уровня текущего запаса.

Классическая экономико-математическая модель запасов имеет следующий вид:

h / Q = 2 × k × b,

где h — стоимость содержания единицы запасов в единицу времени;

Q — оптимальный размер партии поставки;

k — условно-постоянные затраты, связанные с закупкой и поставкой одной партии;

b — среднесуточный расход (продажа) материального ресурса.

Эту модель теории управления запасами называют формулой Уилсона (Вилсона) по имени ее автора (R. H. Wilson).

Проведем разделение товаров на группы с применением АВС-классификации (по доле среднегодового запаса позиции в общем объеме товарных запасов), а также XYZ-классификацию, учитывающую неравномерность спроса на различные товарные позиции. Построим совмещенную матрицу АBC-XYZ. Ассортимент товаров, среднегодовые запасы, среднеквартальные объемы продаж по каждой товарной позиции представлены в табл. 1.

Таблица 1. Ассортимент товаров, среднегодовые запасы и среднеквартальные объемы продаж
№ позиции	Среднегодовой запас по позиции, тыс. руб.	Реализация, тыс. руб.
I кв.	II кв.	III кв.	IV кв.
1	30	60	250	60	40
2	450	650	140	20	420
3	500	200	1280	270	330
4	3460	1460	80	50	1770
5	230	50	10	30	130
6	430	730	60	25	700
7	30	60	900	10	30
8	1240	3200	70	1350	2850
9	1400	40	35	30	0
10	50	370	130	40	540
11	210	410	450	370	490
12	30	30	80	50	30
13	1400	40	30	35	0
14	50	370	150	130	540
15	210	410	430	450	490
16	30	50	40	30	30
17	3300	2300	2700	1900	2800
18	1350	470	220	310	290
19	150	50	80	150	60
20	110	60	30	130	50
21	790	20	25	700	25
22	10	1400	10	30	30
23	25	490	30	25	30
24	130	30	70	130	25
25	10	10	30	450	10

Выполним АВС-классификацию с использованием табл. 2. При разбиении на группы используем следующие границы интервалов групп:

• группа А ≤ 80 %;
• 80 % < группа В ≤ 90 %;
• 90 % < группа С ≤ 100 %.

Таблица 2. Расчеты и результат АВС-классификации
Исходные данные	Упорядоченный список	Группа
№ позиции	Средний запас по позиции, %	Доля запаса по позиции в общем объеме запаса*, %	№ позиции	Средний запас по позиции, %	Доля запаса по позиции в общем объеме запаса, %	Доля нарастающим итогом**, %
1	30	0,192	4	3460	22,144	22,144	А
2	450	2,88	17	3300	21,12	43,264	А
3	500	3,2	9	1400	8,96	52,224	А
4	3460	22,144	13	1400	8,96	61,184	А
5	230	1,472	18	1350	8,64	69,824	А
6	430	2,752	8	1240	7,936	77,76	А
7	30	0,192	21	790	5,056	82,816	В
8	1240	7,936	3	500	3,2	86,016	В
9	1400	8,96	2	450	2,88	88,896	В
10	50	0,32	6	430	2,752	91,648	С
11	210	1,344	5	230	1,472	93,12	С
12	30	0,192	11	210	1,344	94,464	С
13	1400	8,96	15	210	1,344	95,808	С
14	50	0,32	19	150	0,96	96,768	С
15	210	1,344	24	130	0,832	97,6	С
16	30	0,192	20	110	0,704	98,304	С
17	3300	21,12	10	50	0,32	98,624	С
18	1350	8,64	14	50	0,32	98,944	С
19	150	0,96	1	30	0,192	99,136	С
20	110	0,704	7	30	0,192	99,328	С
21	790	5,056	12	30	0,192	99,52	С
22	10	0,064	16	30	0,192	99,712	С
23	25	0,16	23	25	0,16	99,872	С
24	130	0,832	22	10	0,064	99,936	С
25	10	0,064	25	10	0,064	100	С
Итого	15 625	100	—	15 625	100	—	—

*Доля запаса по позиции в общем объеме запаса рассчитывается как средний запас по позиции × 100 / 15 625.

**Доля нарастающим итогом рассчитывается как сумма доли нарастающим итогом предыдущей позиции с долей запаса по позиции в общем объеме запаса.

Проведение XYZ-анализа выполняется с использованием табл. 3. При разбиении на группы используется классический вариант:

• группа Х < 10 %;
• 10 % ≤ группа Y < 25 %;
• группа Z ≥ 25 %.

Таблица 3. XYZ-анализ
№ позиции	Упорядоченный список
Реализация, тыс. руб.	Коэффициент вариации, %	№ позиции	Группа
I кв.	II кв.	III кв.	IV кв.
1	60	250	60	40	83,46	6,65	15	X
2	650	140	20	420	90,63	10,4	11	Y
3	200	1280	270	330	84,85	14,69	17	Y
4	1460	80	50	1770	93,19	22,11	16	Y
5	50	10	30	130	82,82	28,37	18	Z
6	730	60	25	700	88,85	43,08	12	Z
7	60	900	10	30	150,28	45,94	19	Z
8	3200	70	1350	2850	66,88	55,8	20	Z
9	40	35	30	0	59,29	56,71	14	Z
10	370	130	40	540	73	59,29	9	Z
11	410	450	370	490	10,4	59,29	13	Z
12	30	80	50	30	43,08	65,94	24	Z
13	40	30	35	0	59,29	66,88	8	Z
14	370	150	130	540	56,71	73	10	Z
15	410	430	450	490	6,65	82,82	5	Z
16	50	40	30	30	22,11	83,46	1	Z
17	2300	2700	1900	2800	14,69	84,85	3	Z
18	470	220	310	290	28,37	88,85	6	Z
19	50	80	150	60	45,94	90,63	2	Z
20	60	30	130	50	55,8	93,19	4	Z
21	20	25	700	25	152,21	139,07	23	Z
22	1400	10	30	30	162,22	150,25	25	Z
23	490	30	25	30	139,07	150,28	7	Z
24	30	70	130	25	65,94	152,21	21	Z
25	10	30	450	10	150,25	162,22	22	Z

где xi — значение спроса в i-м периоде;

— среднее арифметическое (среднемесячное, среднеквартальное, среднегодовое) значение спроса по оцениваемому периоду;

n — количество периодов (месяцев, кварталов, лет), за которые проведена оценка.

Построение матрицы ABC-XYZ проводится по результатам выполненных ранее АВС- и XYZ-классификаций (табл. 4).

Таблица 4. Матрица ABC-XYZ
Показатель	X	Y	Z
A	—	17	4, 9, 13, 18, 8
B	—	—	21, 3, 2
C	15	11, 16	6, 5, 19, 24, 20, 10, 14, 1, 7, 12, 23, 22, 25

Пример 1

Рассмотрим построение модели с фиксированным размером заказа. Выполним расчеты параметров модели и представим в табл. 5 движение запаса при отсутствии задержек в поставках на 30 дней.

Исходные данные:

• расчетный период — 30 дн.;
• объем потребности — 300 ед.;
• оптимальных размер заказа — 60 ед.;
• время выполнения заказа — 3 дн.;
• время задержки поставки — 1 день;
• остаток запаса на 1-е число — 50 ед.

Таблица 5. Движение запаса при отсутствии задержек в поставках на 30 дней
Показатель	Значение
Объем потребности, ед.	300
Оптимальный размер заказа, ед.	60
Время выполнения заказа, дн.	3
Время задержки поставки, дн.	1
Ожидаемое дневное потребление, ед./день	300 / 30 = 10
Срок расходования заказа, дн.	60 / 10 = 6
Ожидаемое потребление за время выполнения заказа, ед.	10 × 3 = 30
Максимальное потребление за время выполнения заказа, ед.	(3 + 1) × 10 = 40
Страховой (гарантийный) запас, ед.	10 × 1 = 10
Пороговый уровень запаса, ед.	30 + 10 = 40
Максимальный желательный запас, ед.	60 + 10 = 70

Страховой запас (Zs) рассчитывается по следующей формуле:

Zs = Sд × tзп,

где Sд — ожидаемое дневное потребление запаса, ед.;

tзп — время задержки поставки, дн.

Ожидаемое дневное потребление запаса (Sд) рассчитывается исходя из ожидаемой потребности в запасе за весь период:

Sд = S / N,

где S — объем потребности в запасе;

N — количество рабочих дней в плановом периоде.

Пороговый уровень запаса (ПУ):

ПУ = ОП + Zs,

ОП = Sд × tвз,

где ОП — ожидаемое потребление за время выполнения заказа, ед.;

tвз — время выполнения заказа, дн.

Максимальный желательный запас (МЖЗ):

МЖЗ = Zs + Q`,

где Q` — оптимальный размер заказа, ед.

Движение запаса приводится в табл. 6.

Таблица 6. Движение запаса
Дни	Запас	Расход	Приход
1	50	10
2	40	10	Заказ
3	30	10
4	20	10
5	10	10
6	60	10	60
7	50	10
8	40	10	Заказ
9	30	10
10	20	10
11	10	10
12	60	10	60
13	50	10
14	40	10	Заказ
15	30	10
16	20	10
17	10	10
18	60	10	60
19	50	10
20	40	10	Заказ
21	30	10
22	20	10
23	10	10
24	60	10	60
25	50	10
26	40	10	Заказ
27	30	10
28	20	10
29	10	10
30	60	10	60

Пример 2

Построим модель с фиксированным интервалом времени между заказами. Для этого выполним расчеты параметров модели и представим движение запаса при отсутствии задержек в поставках.

Исходные данные:

• расчетный период — 360 дн.;
• объем потребности — 1520 ед.;
• оптимальных размер заказа — 40 ед.;
• время выполнения заказа — 3 дн.;
• время задержки поставки — 1 день;
• остаток запаса на 1-е число — 50 ед.

Первый заказ делается в первый день.

Выполним расчеты параметров модели и представим движение запаса при отсутствии задержек в поставках на 45 дней.

Расчеты параметров модели выполнены в табл. 7.

Таблица 7. Расчет параметров
Показатель	Значение
Объем потребности, ед.	1520
Интервал времени между заказами, дн.	360 × 40 / 1520 = 9,3
Время выполнения заказа, дн.	3
Время задержки поставки, дн.	1
Ожидаемое дневное потребление, ед./день	1520 / 360 = 4,2
Ожидаемое потребление за время выполнения заказа, ед.	4 × 3 = 12
Максимальное потребление за время выполнения заказа, ед.	(4 + 1) × 3 = 15
Страховой (гарантийный) запас, ед.	4 × 1 = 4
Максимальный желательный запас, ед.	40 + 4 = 44

Фиксированный интервал времени между заказами (tмз, дн.) определяется на основе предварительно рассчитанного оптимального размера заказа по формуле:

tмз = N × Q` / S,

где N — количество рабочих дней в плановом периоде;

Q` — оптимальный размер заказа;

S — объем потребности в запасе.

Исходные данные для расчета параметров модели:

• объем потребности в запасе;
• интервал времени между заказами;
• время выполнения заказа;
• время задержки поставки.

Расчетные параметры:

• страховой запас;
• максимальный желательный запас.

Через фиксированные интервалы времени требуется пополнение запаса до максимально желательного уровня (МЖЗ). Размер очередного заказа рассчитывается по формуле:

Q = МЖЗ – ZТ + ОП – Zt,

где ZT — уровень текущего запаса при выдаче заказа;

Zt — объем запаса в пути, не полученного к моменту выдачи заказа.

Движение запаса и расчет размера заказа приводится в табл. 8.

Таблица 8. Движение запаса и расчет размера заказа
Дни	Запас	Расход	Приход
1	50	4	Заказ 1 (44 – 50 + 12 = 6)
2	46	4	—
3	42	4	—
4	38 + 6 = 44	4	6
5	40	4	—
6	36	4	—
7	32	4	—
8	28	4	—
9	24	4	—
10	20	4	Заказ 2 (44 – 20 + 12 = 36)
11	16	4	—
12	12	4	—
13	12 + 34 = 46	4	34
14	42	4	—
15	38	4	—
16	34	4	—
17	30	4	—
18	26	4	—
19	22	4	Заказ 3 (44 – 22 + 12 = 34)
20	18	4	—
21	14	4	—
22	14 + 34 = 48	4	34
23	44	4	—
24	40	4	—
25	36	4	—
26	32	4	—
27	28	4	—
28	24	4	Заказ 4 (44 – 24 + 12 = 32)
29	20	4	—
30	16	4	—
31	12 + 32 = 44	4	32
32	40	4	—
33	36	4	—
34	32	4	—
35	28	4	—
36	24	4	—
37	22	4	Заказ 5 (44 – 22 + 12 = 34)
38	18	4	—
39	14	4	—
40	10 + 34 = 44	4	34
41	40	4	—
42	36	4	—
43	32	4	—
44	28	4	—
45	24	4	—

Сущность СУЗ с фиксированным интервалом времени между заказами

Определить величину интервала времени между заказами можно на основе расчетного оптимального размера заказа (EOQ), а также исходя из графика работы предприятия, сроков выполнения заказов, транспортных издержек и др.

При известном оптимальном размере заказа (EOQ) и плановой потребности в продукции (Q) за период N интервал времени между заказами определяют по формуле:

Преимущество данной СУЗ – относительная простота управления, так как тщательный ежедневный контроль состояния запаса не требуется, заказы и поставки осуществляются в строго определенные моменты времени, поэтому их проще планировать. В связи с этим, данную модель рекомендуют использовать для управления широкой номенклатурой запасов невысокого приоритета (т.е. группа «С» согласно АВС-классификации). Данная система нормально работает в условиях стабильного спроса или при небольших колебаниях величины отгрузки и потому подходит для категории запасов «Х» по XYZ-классификации.

Параметры СУЗ с фиксированным интервалом времени между заказами

Исходные данные для расчета параметров обозначенной СУЗ следующие:

«Модель системы управления запасами с фиксированным интервалом времени между заказами» 👇

• плановая потребность в товарах на определенный период времени, нат. ед.;
• интервал времени между заказами, дни.
• время осуществления поставки, дни;
• максимально возможная отсрочка поставки, дни.

Основными расчетными параметрами СУЗ являются:

• гарантийный запас −это уровень запаса, который создается с целью обеспечения бесперебойной работы предприятия в случае сбоев в поставках;
• максимально желательный запас −это уровень запаса, который определяет максимально целесообразную загрузку площадей с точки зрения минимизации совокупных затрат;
• размер заказа – определяется каждый раз в день осуществления заказа, заказа таким образом, чтобы очередная поставка пополнила запас до максимально желательного уровня по формуле:

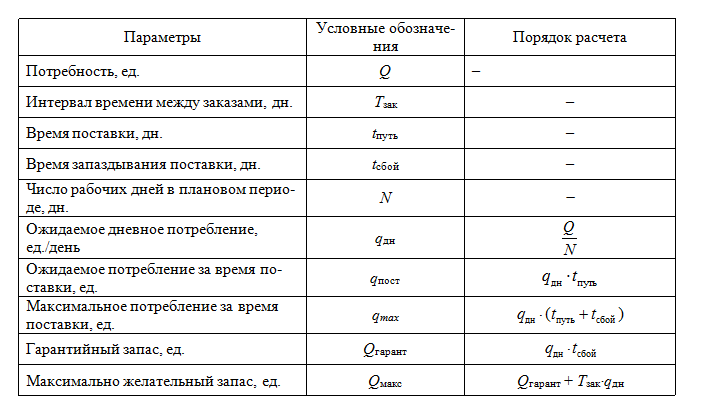
Формулы для расчета параметров обозначенной СУЗ приведены в таблице ниже.

Графическое моделирования работы СУЗ с фиксированным интервалом времени между заказами

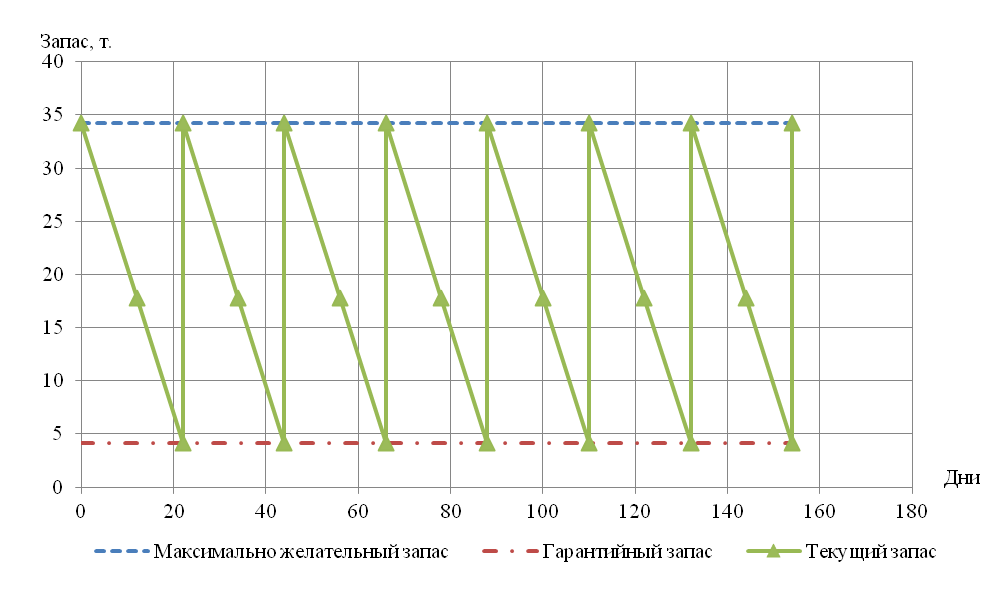
График работы СУЗ строят в декартовой системе координат, где по оси абсцисс обозначаю время, а по оси ординат – уровень запаса в каждый момент времени. В первую очередь на график СУЗ с фиксированным интервалом времени между заказами наносят рассчитанные даты заказов, максимально желательный запас и гарантийный запас. Если иное не оговорено условиями задачи, дата первого заказа определяется как разница между интервалом времени между заказами и временем поставки.

Далее строят линию текущего запаса в каждый момент времени по следующему алгоритму:

1. построение графика начинают с 0 отметки на шкале времени, предполагая, что уровень запаса в данной точке равен максимально желательному;
2. находят и отмечают на графике объем текущего запаса на складе на момент осуществления заказа;
3. находят и отмечают на графике дату поставки и объем заказа на складе на момент поставки;
4. определяют размер заказа;
5. находят и отмечают на графике дату поставки и объем запаса на складе на момент поставки;
6. производят пополнение запаса на размер заказываемой партии;
7. этапы алгоритма повторяют необходимое число раз для охвата горизонта планирования.

Пример графика СУЗ с фиксированным интервалом времени между заказами представлен на рисунке.
Графики систем управления запасами подобного рода называют «пилообразная диаграмма».

Система управления запасами. Фиксированный интервал времени

Журнал: ФармОбоз.

В предыдущей статье была подробно описана системы управления запасами с фиксированным размером заказа. Сегодня мы изучим систему с фиксированным интервалом времени. После этого этапа изучения данной тематики появляется возможность приступить к разработке собственных систем управления запасами.

Итак, система управления запасами с фиксированным интервалом времен. Отличительной особенностью данной системы является стандартный расчетный промежуток времени, через который производится заказ поставщику на закупку. При этом постоянно пересматривается размер партии.

После всплеска или спада продаж, а также в после задержки поставки система восстанавливается достаточно быстро благодаря стабильному интервалу времени и возможности изменения объема заказываемой партии.

Графически система управления запасами с фиксированным интервалом времени представлена на рисунке 1. Здесь, как и в системе с фиксированным размером запаса обязательно присутствуют расчетные величины:

• Страховой запас, который предназначен для обеспечения спроса на случай различных критических ситуаций.
• Максимальный товарный запас. Он является ориентиром для расчета нормируемого коэффициента оборачиваемости. Также служит показателем нормальности работы системы. Определяется следующим образом — интервал времени между поставками умножается на ожидаемое потребление за время поставки, а затем добавляется объем страхового запаса.

Кроме этих расчетных величин также присутствует расчет интервала между поставками: сначала определяется количество поставок (общая годовая потребность в товаре относится к оптимальному размеру партии), затем число рабочих дней в году делим на количество поставок.

Рисунок 1 – Система управления запасами с фиксированным интервалом времени

Общий расчет параметров системы представлен в таблице 1.

 Таблица 1 – Расчет параметров системы управления запасами с фиксированным интервалом времени между заказами

При работе системы управления запасами с фиксированным интервалом времени действуют все те же тонкости и нюансы, как и в системе управления запасами, описанной в предыдущей публикации. Речь идет об отношении к дефициту, возможности автоматизации процессов по управлению запасами, периодичность пересмотра систем управления запасами, точность прогнозирования и анализ ассортимента, а также возможности влияния закупщиком на срок поставки и сок реакции.

Теперь стоит перейти к изучению того, каким образом данная система функционирует, как восстанавливается после проявления различных внезапных факторов (скачки или спады спроса, недопоставки, сдвиг сроков поставки, и т.д.). За основу возьмем все тот же пример с лекарственным препаратом «Кетанов», к которому мы обращаемся на всем протяжении цикла публикаций по тематике «Управление запасами».

Итак, исходные данные:

1. годовой спрос равен  9238 единицы.
2. оптимальный размер заказа – 125 единиц.
3. время поставки – 2 дня.
4. возможная задержка поставки – 1,5 дня.
5. страховой запас – 90 единиц.
6. вероятность поддержания запаса – 95%.
7. 360 рабочих дней в году.

 Ниже (Таблица 2) приведен расчет параметров системы.

Таблица 2 – Расчет параметров системы управления запасами с фиксированным интервалом времени.

Предлагаю на данных учета препарата «Кетанов» рассмотреть, каким образом будет работать система управления запасами с фиксированным интервалом времени. В таблице 3 можно увидеть, в какие моменты происходит расчет размера партии, и то каким образом это происходит.

Таблица 3 – Карточка учета лекарственного препарата «Кетанов» с указанием момента и объема заказа.

Графически движение товара «Кетанов» представлено на рисунке 3.

Вернемся на время к таблице 3 и вспомним еще раз, каким образом определяется объем заказываемой партии. Логика при определении размера заказ следующая:

• При достижении контрольной даты (в нашем случае на третий день после получения предыдущего заказа, или иначе заказ оформляем через каждые пять дней) необходимо определить тот объем, которого не хватает до достижения «Максимально Желательного Уровня Запаса» (МЖЗ). То есть Максимально Желательный Запас – Текущий запас.

 Напомню, Текущий запас – это объем остатка на складе на момент контроля.

•  Далее необходимо прогнозное значение спроса на время поставки. То есть определяется тот объем препарата, который будет реализован во время поставки этой партии. В нашем примере за прогнозное значение ежедневного спроса был принят средний объем продаж. На практике чаще всего применяют такой же подход из-за простоты, хотя он не всегда корректен. Он обеспечивает достаточно точные данные, если товар стабилен в спросе. Наш препарат «Кетанов» как раз весьма популярен и стабилен. Для товаров с более непредсказуемым спросом точнее было бы применять технологии прогнозирования. Особенно это важно при более длительных сроках поставки.
• Затем суммируются эти две части (Рисунок 2).

 Рисунок 2 – Схема расчета объема заказываемой партии

Рисунок 3 – Движение лекарственного препарата «Кетанов» за май и июнь

Как видно на рисунке 3, система в принципе ведет себя вполне устойчиво. Только в начале цикла уровень запаса был близок к нулю, но это связано исключительно с условиями нашего примера. Мы в исходных данных имели входящий остаток, равный 10 единицам препарата «Кетанов».

А в общем ситуация в данном примере следующая:

1. За пределы рекомендуемого максимального уровня запаса система вышла 6 раз, но несильно превышая допустимый уровень МЖЗ.
2. И пять дней остаток был ниже уровня страхового запаса. Близкий к нулю всего один раз в начале мая.

 А общие результаты по эффективности данной системы управления запасами для нашего примера приведены в таблице 4.

 Таблица 4 – Анализ эффективности системы управления запасами

Но принимать решение на этом этапе о целесообразности применения этой системы для лекарственного средства «Кетанов» пока рано. Мы пока рассмотрели случай стабильных поставок. В нашем примере ни разу не было сбоя в поставках, что на практике практически невозможно. Поэтому для наглядности мы проведем тот же эксперимент, который проводили в предыдущей публикации (смотреть статью «Система управления запасами. Фиксированный размер заказа»). Немного сместим сроки поставок. Примем задержку в поставках одиннадцатого мая на четыре дня (поставка будет пятнадцатого числа). И двадцатого июня на три дня (поставка – двадцать третьего июня). 

Движение товара при условии нестабильности поставок представлено в таблице 5.

 Таблица 5 – Движение препарата «Кетанов» при условии нестабильности срока поставок

Здесь стоит отметить, каким образом определяется размер партии, если в аптеку не поступила ранее заказанная партия. В таком случае технология следующая (в таблице 5 смотри дату 14 мая):
Q_z = МЖЗ – ТЗ + Qт ожид – ТП,
Где:

МЖЗ – максимально желательный уровень запаса, ед.

ТЗ – текущий запас, ед.

 Qт ожид – ожидаемое потребление за время поставки, ед.

ТП – товары в пути, то есть партия ранее заказанная, но пока не поставленная поставщиком, ед.

 А вот изменение в сроках поставки от 23 июня (таблица 5) приходится на дату следующего заказа. Таким образом, если заказ оформляется до оприходования задержанной партии, то эта партия также будет товаром в пути. Если после того, как она поставлена на приход, то процедура определения объема потребной партии происходит по стандартной методике.

И еще один момент. При задержках поставки не смещается подача следующих заказов поставщику. Это происходит потому, что в системе стабилен интервал времени между заказами (в нашем примере это 5 дней).

Теперь посмотрим, насколько эффективна в данном случае оказалась система. Выдержала она испытания или нет. На рисунке 4 представлена графическая интерпретация поведения препарата «Кетанов». Здесь наглядно видно, что ситуацию от дефицита спасает два раза страховой запас.  Именно для этого он и предназначен. При этом стоит отметить, что сама система довольно быстро восстанавливается. Но, если бы такие сбои в поставках были бы гораздо чаще, то такой уровень страхового запаса не спас от возникновения неудовлетворенного спроса. Товар «Кетанов» был бы постоянно в дефиците. И проблема не в системе управления запасами, а в неточных расчетах страхового запаса. Напомню, что в алгоритме расчета уровня страхового запаса участвуют данные о стабильности поставок. Если данные, принимаемые в расчетах неточные, то страховой запас оказывается ниже, чем этого требует ситуация.

 Рисунок 4 — Движение лекарственного препарата «Кетанов» за май и июнь с учетом задержек в поставках

И, наконец, благодаря таблице 6 можно ознакомиться с эффективностью системы управления запасами с учетом задержек в поставках.

Таблица 6 — Эффективность системы управления запасами с фиксированным интервалом времени с учетом задержек в поставках для препарата «Кетанов»

На взгляд автора, система выдержала испытание. А Вы как считаете?

            Еще несколько слов о данной системе. Она, как правило, применяется для товаров стабильных. Возвращаясь к XYZ – анализу, для товаров группы X. Это связано с тем, что при работе с этой группой товаров нет необходимости постоянно контролировать уровень запаса. В нашем примере мы это делаем раз в пять дней. Другой вариант применения системы управления запасами с фиксированным интервалом времени проявляется. Когда наш поставщик диктует нам сроки заказов и поставок.

Например, поставщик определяет для нашей аптеки день, когда будет осуществляться поставка — среда. При условии работы поставщика без выходных. Такая ситуация уже не совпадает с нашими расчетами. Что же делать в таком случае? Придется отклонить возможность использования оптимального размера партии (хотя для ориентира определять его все равно стоит). Нужно будет при расчетах системы учитывать прогнозное значение ежедневного спроса и период между поставками. В таком случае уровень максимально желательного запаса повысится, а коэффициент оборачиваемости упадет. То есть денежные средства будут использоваться менее эффективно. Но при этом уровень сервиса для наших клиентов будет поддерживаться на весьма высоком уровне (в нашем случае 95%).