Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | — | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f»(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x — 3.
Решение: Находим производную: f′(x) = 2x — 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
Е
сли
для всех точек отрезка
при
выполняется равенство
,
то функция
называется возрастающей
на
.
При
выполнении условий
,
функция
называется убывающей
на
.
Интервалы,
в которых функция
только
возрастает или только убывает, называются
интервалами
монотонности
функции.
П
ризнак
возрастания.
Дифференцируемая функция
возрастает на отрезке
тогда и только тогда, когда её производная
.
П
ризнак
убывания.
Дифференцируемая функция
убывает на отрезке
тогда и только тогда, когда её производная
.
В
точках, отделяющих интервалы монотонности
функции, производная функции обращается
в нуль или не существует. Эти точки
называются критическими.
Для
нахождения интервалов монотонности
функции
необходимо
найти все её критические точки и
установить знак производной в каждом
из интервалов, на которые критические
точки разбивают область существования
функции.
Пример
7.13.
Найдите интервалы монотонности функции
.
Ф
ункция
определена на всей числовой оси. Найдём
её производную.
.
Найдём
критические точки, приравняв производную
к нулю.
— критические.
Результаты исследования занесём в
таблицу:
|
|
|
|
|
|
|
|
|
+ |
|
+ |
||
|
|
|
|
|
|
Т
аким
образом, функция
возрастает а интервалах
и
,
а убывает на интервале
.
§ 6. Экстремум функции. Необходимый признак.
Т
очка
называется точкой
максимума
(maximum)
функции
,
если значение функции в этой точке
больше её значений во всех точках
некоторого интервала, содержащего точку
,
т.е.
для любого
(
—
мало
по величине).
Т
очка
называется точкой
минимума
(minimum)
функции
,
если значение функции в этой точке
меньше её значений во всех точках
некоторого интервала, содержащего точку
,
т.е.
.
Точки,
в которых функция достигает максимума
или минимума, называются точками
экстремума
функции, а значения функции в этих точках
называют экстремальными.
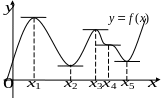
Ф
ункция,
заданная кривой на рисунке выше, в точках
и
достигает максимума, в точках
и
—
минимума, в точке
—
экстремума нет. Очевидно, что функция
имеет производную, равную нулю в
критических точках. Касательная к кривой
в этих точках параллельна оси
.
Необходимый
признак экстремума.
Если дифференцируемая функция достигает
в некоторой точке экстремума, то её
производная в этой точке равна нулю или
не существует.
§ 7. Достаточные признаки экстремума функции.
П
ервый
достаточный признак.
Пусть функция
непрерывна в некотором интервале,
содержащем критическую точку
и дифференцируема во всех точках этого
интервала (кроме, быть может самой точки
).
Тогда, если:
а)
при
,
при
,
то в точке
функция
достигает максимума;
б)
при
,
при
,
то в точке
функция
достигает
минимума.
В
торой
достаточный признак экстремума.
Пусть функция
имеет
в точке
производную
и
непрерывную вторую производную
.
Тогда, если
в точке
будет максимум, а если
в точке
будет минимум.
Пример
7.14. В
примере 7.13 точки
являются точками экстремума. В точке
функция достигает максимума, в точке
функция достигает минимума.
Пример
7.15.
Издержки предприятия выражаются формулой
,
где
—
объём производства. При каком объёме
производства средние издержки будут
минимальными?
С
редние
издержки выражаются формулой
.
Найдем минимум этой функции.
.
.
Найдем
вторую производную функции.
,
значит, по второму достаточному признаку
экстремума при
средние издержки достигают минимума.
Соседние файлы в предмете Высшая математика
- #
- #
Исследование функций должно начинаться с установления области определения и интервалов монотонности. Для этого студент должен обладать хорошими знаниями поведения элементарных функций и последующим теоретическим материалом.
Функция 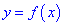
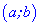
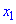
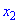
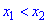
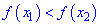
Для того чтобы функция 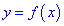
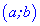
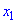
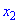
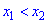
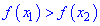
Как возрастающие, так и убывающие функции называются монотонными, а интервалы в которых
функция возрастает или убывает – интервалами монотонности.
Область возрастания и убывания функции 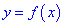
некотором интервале производная больше нуля 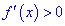
если же наоборот 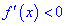
Интервалы монотонности могут прилегать друг к другу или точками, где производная равна нулю
или точками, где производная не существует. Эти точки называются критическими точками.
Для того, чтобы найти интервалы монотонности функции 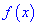
1) найти область определения функции 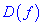
2) вычислить производную данной функции;
3) найти критические точки из условия равенства нулю производной 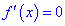
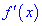
4) разделить критическими точками область определения на интервалы, в каждом из которых определить знак производной.
На интервалах где производная положительная функция возрастает, а где отрицательная — убывает.
————————————
Примеры.
Рассмотрим задачу из сборника В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах» на нахождение интервалов монотонности функции.
1. (3.36.10)
Функция существует во всех точках где определен логарифм и он не обращается в нуль, а также где функция под корнем принимает неотрицательные значения. На основе этого находим
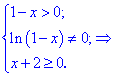
Итак, областью определения будут два интервала
2. (3.36.11)
С подкоренной функцией ведем себя как и в предыдущем примере, а функция 
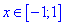
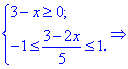
Единственным промежутком, который удовлетворяет эти условия являются следующий
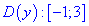
3. (3.36.13)
Область определения функции находим из двух условий
Первое условие дает две точки
в которых функция не существует.
С второго условия получим
Исследуем поведение функции в интервалах монотонности на которые разбивают заданные точки. Для этого
выбираем произвольные точки 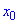
Функция 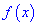
Вместе с первым условием получим следующую область определения
——————————
Рассмотрим примеры исследования монотонности функции из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика» .
І. (5.705) Показать, что функция 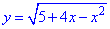
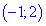
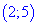
1) Областью определения функции будет множество значений для которых подкоренная функция принимает неотрицательные значения.
Решим квадратное уравнение
Определим знак функции на всем интервале
Таким образом получим следующую область определения
2) Найдем производную
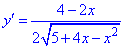
3) Приравняем ее к нулю и найдем критические точки:
Не стоит забывать и о точках, в которых производная не существует. Это корни уравнения в
знаменателе. Итак производная существует на интервале 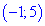
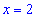
4) Знаки производной: подставляем 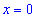
Так что на интервале 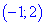
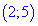
ІІ. (5.715) Найти интервалы монотонности функции
1. Областью определения будет множество точек 
основе этого получим
Итак
2) Найдем производную функции
3) Находим критические точки
Другая точка, где производная не существует это 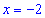
Таким образом получили два интервала монотонности 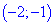
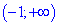
4) Выясним где функция возрастает, а где убывает. Подставим точки 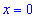
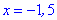
производной
Исследуемая функция на интервале 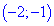
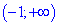
При исследовании функций на монотонность определите все критические точки в которых производная равна нулю или не существует. Также не забывайте при этом учитывать область определения функции. Остальное зависит от Ваших знаний свойств элементарных функции, поскольку именно на их основе построены все задачи, которые Вам задают преподаватели.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Наибольшее и наименьшее значение функции на отрезке
- Локальный экстремум функции. Примеры
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
Содержание:
- Монотонность функции, основные понятия и определения
- Связь монотонности функции с ее производной
Монотонность функции, основные понятия и определения
Определение
Функция $y=f(x)$ называется строго возрастающей на
промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.
$f(x) uparrow : x_{1} lt x_{2} Rightarrow fleft(x_{1}right) lt fleft(x_{2}right)$
Пример
Функция $y=x^{2}$ является возрастающей на промежутке
$[0 ; 1]$, так как:
для $0 lt 1 : f(0)=0^{2}=0 lt f(1)=1^{2}=1$
Определение
Функция $f(x)$ называется строго убывающей на
промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.
$f(x) downarrow : x_{1} lt x_{2} Rightarrow fleft(x_{1}right)>fleft(x_{2}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Функция $y=x^{2}$ является строго убывающей на
промежутке $[-1 ; 0]$, так как:
для $-1 lt 0 : f(-1)=(-1)^{2}=1>f(0)=0^{2}=0$
Функция $y=f(x)$ строго возрастающая или строго убывающая
на промежутке называется монотонной на этом промежутке.
Определение
Функция $y=f(x)$ называется неубывающей на промежутке,
если из неравенства $x_{1} lt x_{2}$ следует неравенство
$fleft(x_{1}right) leq fleft(x_{2}right)$.
Функция $y=f(x)$ называется невозрастающей на
промежутке, если из неравенства $x_{1} lt x_{2}$ следует
неравенство $fleft(x_{1}right) geq fleft(x_{2}right)$.
Связь монотонности функции с ее производной
Теорема
(Об условии возрастания/убывания монотонной функции)
Если производная функции $f^{prime}(x)>0$ на некотором
промежутке $X$, то функция
$y=f(x)$ возрастает на этом промежутке; если же
$f^{prime}(x) lt 0$ на промежутке
$X$, то функция
$y=f(x)$ убывает на этом промежутке.
Замечание
Обратное утверждение формулируется несколько иначе. Если функция возрастает на промежутке, то
$f^{prime}left(x_{0}right) geq 0$ или не существует.
Пример
Задание. Исследовать функцию $y=x^{3}$ на монотонность на всей числовой прямой.
Решение. Найдем производную заданной функции:
$y^{prime}=left(x^{3}right)^{prime}=3 x^{2}$
Для любого действительного $x$:
$y^{prime}(x)=3 x^{2} geq 0$, а поэтому делаем вывод, что заданная функция
возрастает на всей действительной оси.
Ответ. Функция $y=x^{3}$ возрастает на всей действительной оси.
Читать дальше: понятие экстремума функции.
Алгебра и начала математического анализа, 11 класс
Урок №15. Возрастание и убывание функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение промежутков монотонности функции,
2) Определение алгоритма нахождения промежутков возрастания и убывания функции,
3) Решение задачи на нахождения промежутков возрастания и убывания функции
Глоссарий по теме
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
- Найти D(f)
- Найти f‘(x).
- Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) <f(x2)
2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) >f(x2)
Теоремы
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1.Найдем область определения функции.
D(y) =
2.Найдем производную функции.
y’ = (x – 1)(-9x – 1)
3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так как на интервале 
Так как на интервале 
Так как на интервале 
Так как в точках 
Следовательно, функция возрастает на 


Ответ: Функция возрастает на
Функция убывает на 

№2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
y‘ =
- Функция возрастает на
; функция убывает на
.
Ответ: Функция возрастает на 
функция убывает на 

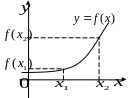
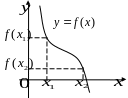
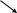



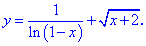
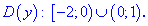
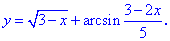
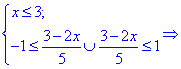
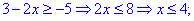
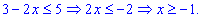
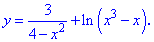
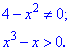
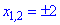
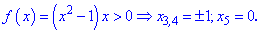
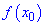
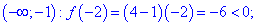
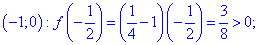
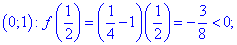
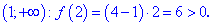
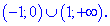
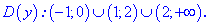
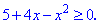
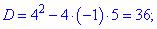
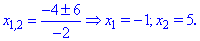
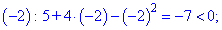
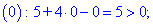
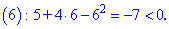
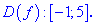
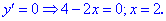
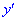
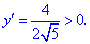
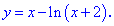
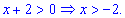
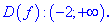
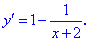
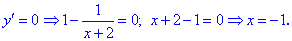
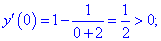
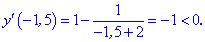







 ; функция убывает на
; функция убывает на  .
.